Unit 8 : Matrices and determinants of order 2
8.0 Introductory activity
A pharmacist buys two types of drugs in boxes A and B. On the first day
he bought 5 boxes of drug A and 4 boxes of drug B and he paid 35,000Frw.
On the second day, the pharmacist bought 3 boxes of drug A and 6 boxes
of drug B and paid 30,000Frw.
a) Arrange what the pharmacist bought according to their types in asimple table as follows:
b) Discuss and explain in your own words how you can determine the
cost for the box of drug A and the cost for drug B.
objectives
After completing this unit, I will be able to:
» Define matrices.
» Perform operations on matrices of order 2.
» Determine determinant of matrix.» Determine the inverse of a matrix of order 2.
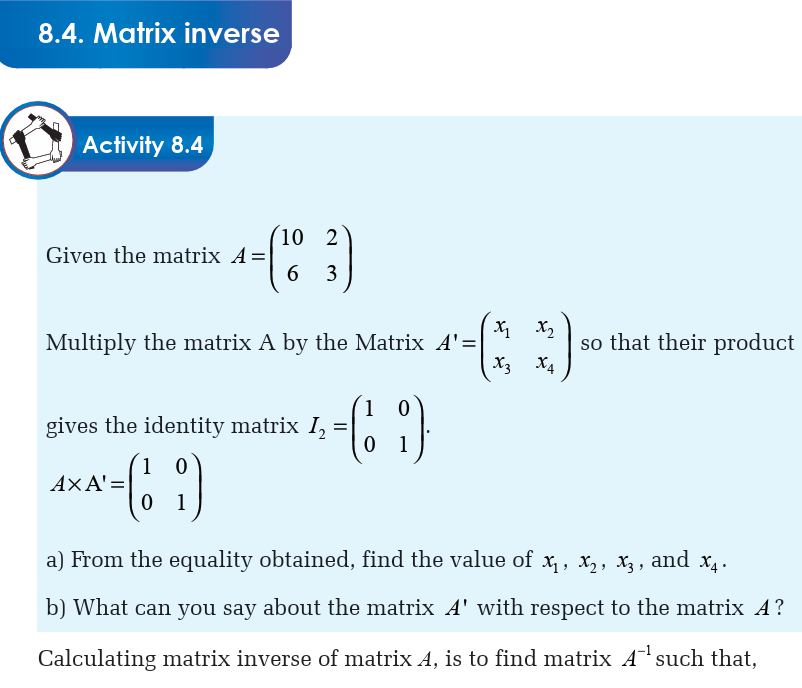
8.1. Square Matrices of order two
Activity 8.1
A shop sold 20 cell phones and 31 computers in a particular month.
Another shop sold 45 cell phones and 23 computers in the same
month. Present this information as an array of rows and columns.
A matrix is every set of numbers or terms arranged in a rectangular shape,
forming rows and columns. In square matrix of order two, the number of
rows is equal to the number of columns equal to 2 and it has the followingform;
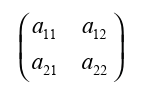
If we compare these data and the boxes of drugs bought by the pharmacist,
we find the following:
the elements 1 and 4 are on the first row, they look like the quantity of
drug of type A (1) and the quantity of drug of type B (4) bought by thepharmacist on the first day.
The element 3 and 11 are on the second row. They look like the quantity
of drug of type A (3) and the quantity of drug of type B (11) bought by thepharmacist on the second day.

Application activity 8.1
Give five examples of matrices of order two.
8.2. Operations on matrices
Example 8.3
There are two pharmacists Gerard and Jane who bought boxes of drugs in
two different days.
On the first Day, Gerard bought 13 boxes of nystatin and 4 boxes of
Amoxicillin. On the second day, he bought 6 boxes of nystatin and 10
boxes of Amoxicillin.
For Jane, she bought 7 boxes of nystatin and 10 boxes of Amoxicillin on the
first day. On the second day she bought 3 boxes of nystatin and 4 boxes of
Amoxicillin.
a) Organise in the matrix A the number of drugs bought by Gerard in the
two days, and the matrix B of drugs bought by Jane.
b) Write the matrix showing the total number of drugs bought by the two
pharmacists Gerard and Jane.c) Interpret the matrix obtained in b).
c) On the first day, Gerard and Jane bought20 boxes of nystatin and 14
boxes of Amoxycillin. On the second day, they bought 9 boxes of nystatinand 14 boxes of Amoxycillin.
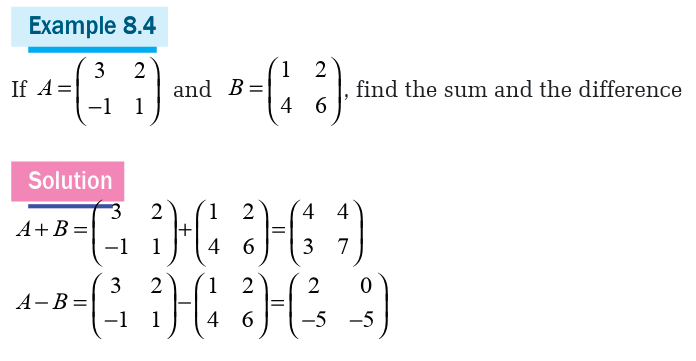


Example 8.6
According to information from the American Red Cross, the distributionof blood types in the United States is as shown in the accompanying table.
(a) Write a 2x2 matrix depicting the distribution of blood types A and O by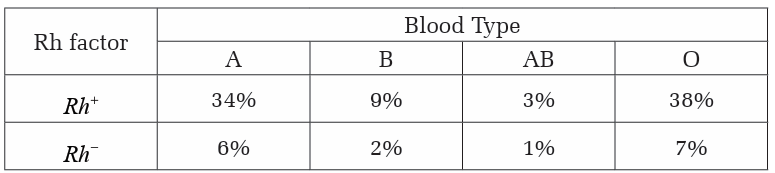
Rh factor, using decimals as entries.
(b) On any given day in the United States, 38,000 units of blood are needed.
Use scalar multiplication to determine the number of units needed
each day in the United States by blood type A and O, assuming daily
distributions match the percentages above.(c) State in words what this means about the number of units of O+


Multiplying matrices
Two matrices A and B of order two can be multiplied together.
The element of the product matrix is obtained by multiplying every
element in row i of matrix A by each element of column j of matrix B andthen adding them together.

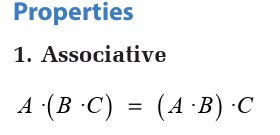

Commuting matrices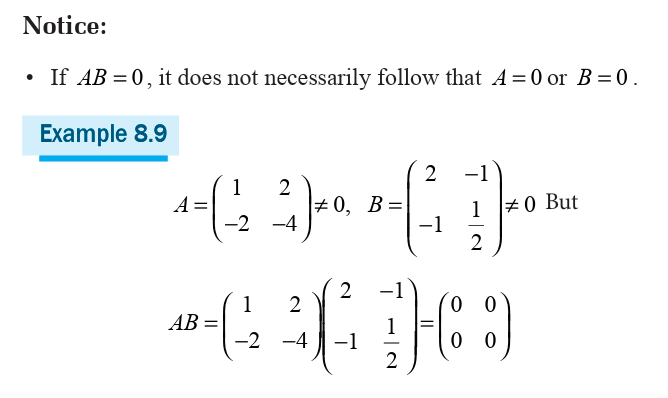
In general the multiplication of matrices is not commutative, i.E, AB≠ BA
, but we can have the case where two matrices A and B satisfy AB= BA. Inthis case A and B are said to be commuting.




Example 8.12

3. If a determinant switches two parallel rows or columns, its determinant
changes sign.


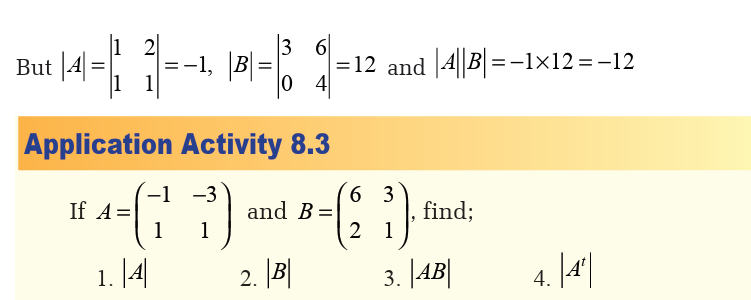




Example 8.23
A pharmacist buys different boxes for Cefalexin and Cloxacillin. On the
first day he bought 5 boxes of Cefalexin and 4 boxes of Cloxacillin and he
paid 35,000Frw.
On the second day, the pharmacist bought 3 boxes of Cefalexin and 6 boxes
of Cloxacillin and paid 30,000Frw.
a) Let x be the cost of one box of Cefalexin and y the cost of one box
of Cloxacillin. Write the product of matrices that model this situation:
matrix with the numbers of boxes bought by the column matrix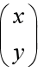
unknowns.
b) From, the obtained matrix, write the two equations obtained after
multiplication.
c) Solve the equation to deduce the value x and y.d) After solving this problem, try to explain the role of matrices in medicine.

Thus, the cost of one box of Cefalexin is 5,000Frw and the cost of one
box of Cloxacillin is 2,500Frw.
d) After solving this problem, we see that matrices can be used to solve
problem related to the calculation of the number of drugs or otherproducts used in medicine.
Example 8.24
A movie theater sells tickets for $8 each. When there are special clients,
she allows them a discount of $2.
One evening the theater sold 525 tickets and took in $3580 in revenue.How many of each type of ticket were sold?


Unit summary
1. A matrix is every set of numbers or terms arranged in a rectangular
shape, forming rows and columns.
2. Two matrices are equal if the elements of the two matrices that occupythe same position are equal.


End unit assesment


