Topic outline
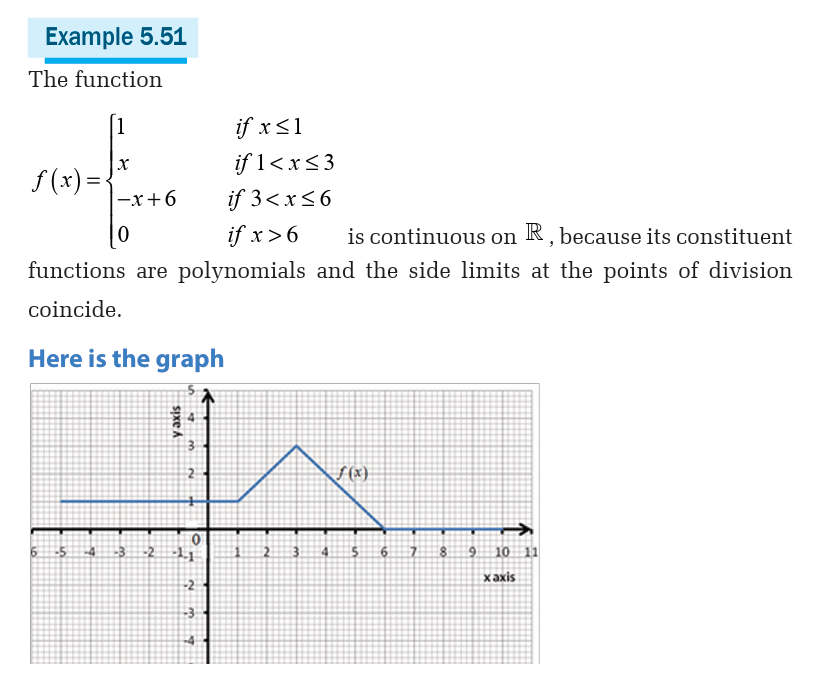
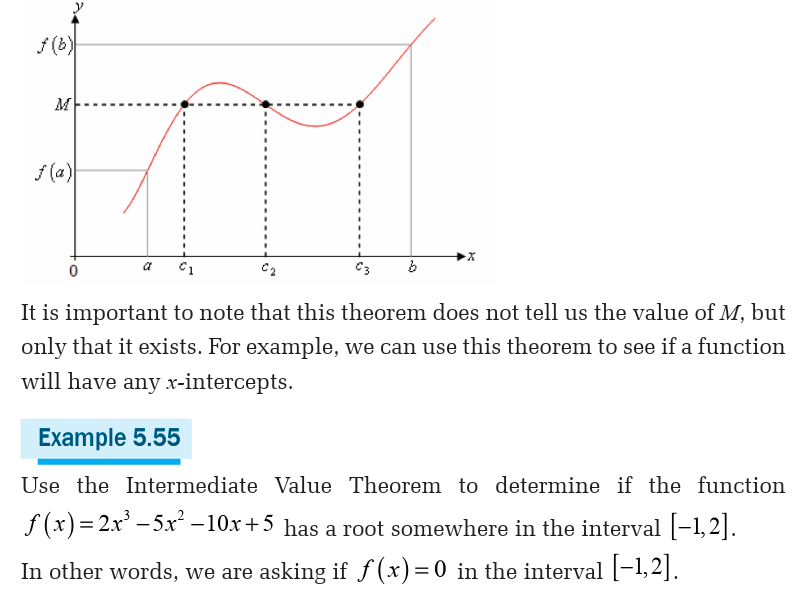
Unit 1 :Set IR of real numbers
1.0 Introductory activityFrom the following diagram, discuss and work out the given tasks:
1. How many sets of numbers do you know? List them down and give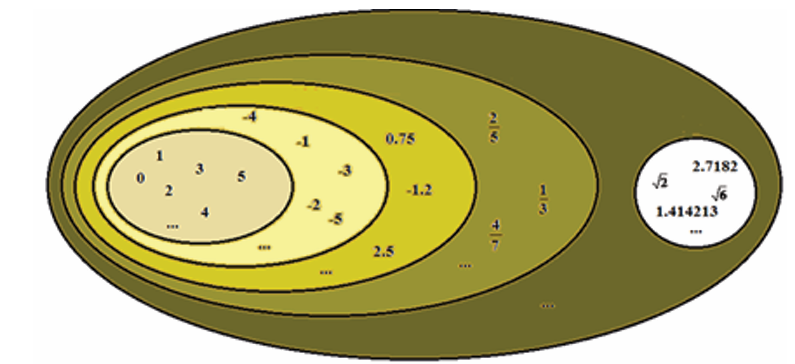
reasons for your answer.
2. Using a mathematical dictionary or the internet, define the sets of
numbers you listed in (1).
3. Give an example of element for each set of numbers you listed.4. Establish the relationship between the set of numbers that you listed.
Objectives
After completing this unit, I will be able to:
» Define absolute value of a real number and solve
simple equations involving absolute value.
» Define powers and their properties.
» Define radicals and their properties.
» Define decimal logarithms of a real numbers andsolve simple logarithmic equations.
1.1. Subsets and properties of operations in the set real numbers
Activity 1.1
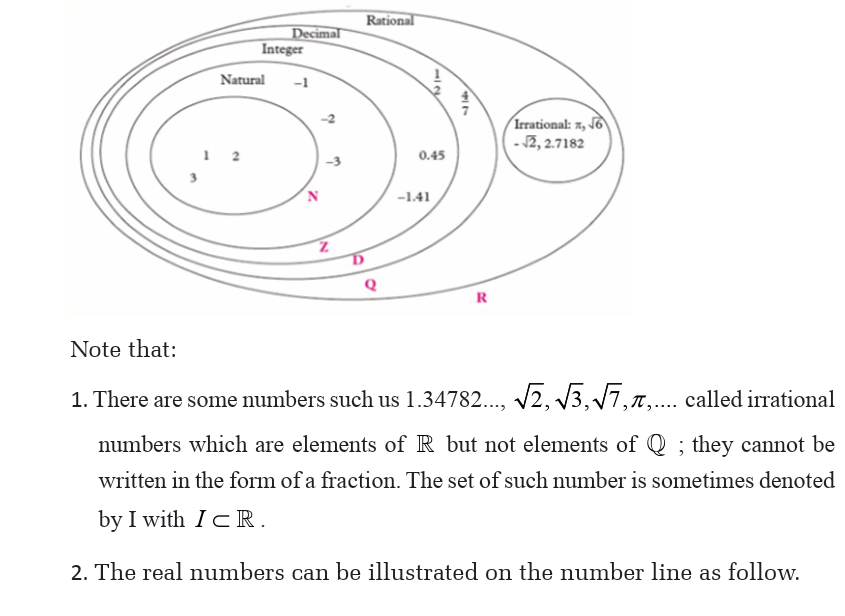
a. Carry out a research on sets of numbers to determine the meaning of
natural numbers, integers, rational numbers and irrational numbers.
Use knowledge from your findings to classify numbers in the givenlist into natural numbers, integers, rational numbers and irrational



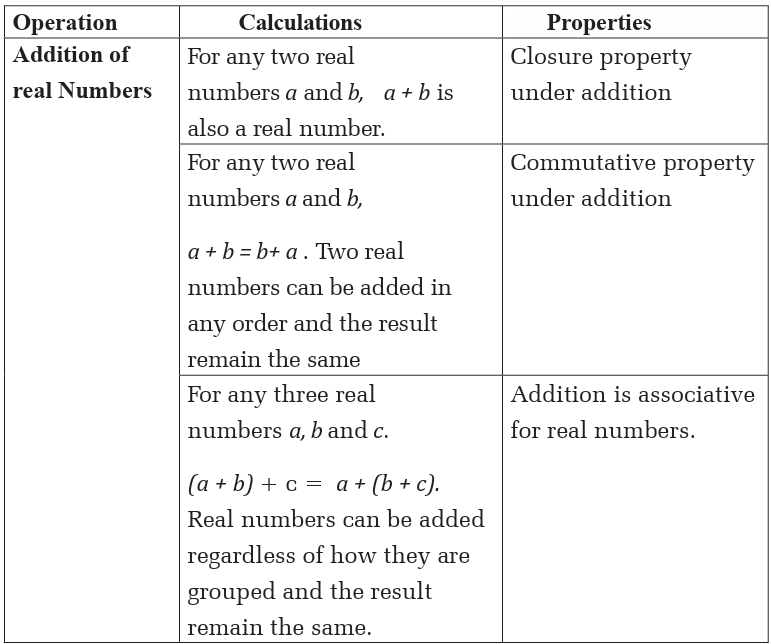
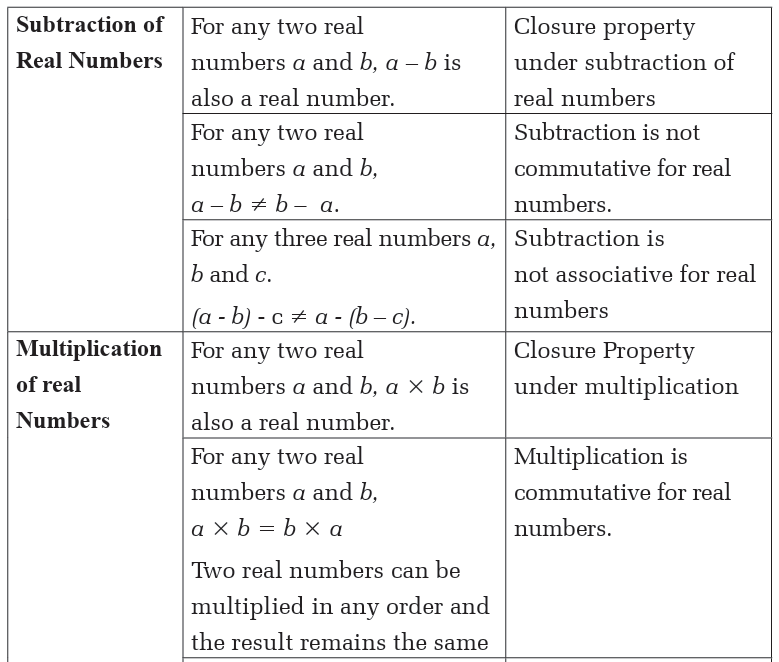
The following table shows the addition, subtraction, multiplication anddivision of real numbers and the related properties.

Application Activity 1.1
1. Plot a number line and locate elements of the following subsets ofreal numbers.

1.2. Positive and negative numbers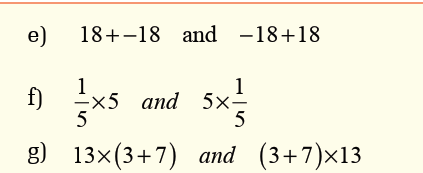
Activity 1.2
1. By means of thermometer, a Doctor recorded the temperature of a patientat different times of the same day.

a) When the lowest temperature of a patient was recorded?
b) What was the difference in temperature between 6:00 and 21:00?
c) What was the difference in temperature between 9:00 and 12:00?
d) At midnight the temperature was 0.25 degrees above 21:00. What was
the temperature at midnight?
Extreme high and low temperatures contribute directly to deaths from
cardiovascular and respiratory disease, particularly among elderly
people. In Quebec, Canada, it was observed that on July 6th 1921 the
highest temperature recorded in Ville-Marie was 40 oC and on February
5th 1923 the lowest temperature recorded in Doucet was -54.4 oC. Do you
think this records can happen or was happened in Africa? Consult the
link (https://en.wikipedia.org/wiki/List_of_countries_and_territories_
by_extreme_temperatures) and find out the lowest temperature(oC)
recorded on January 28th 2005 in Mecheria , Algeria and the lowesttemperature(oC) recorded on February 11th 1935 in Ifrane, Morocco.
The most commonly used numbers in arithmetic are integers, which are
positive and negative whole numbers including zero. Positive integers
are 1, 2, 3, 4, 5 and so on. The negative integers are -1, -2, -3, -4, -5 and
so on.
Integers (positive and negative numbers) can be represented on a
number line and the number line can be used to perform addition and
subtraction.
Example 1.1:
1) Use a number line, locate -2 and -5. Then perform the following
operation using a number line: (-2)+(-5)=
Solution
“negative 2 minus negative 5” meaning that (-2) + 5 (adding theopposite).
Integers (positive and negative numbers) have the real-life applications
and situations where one can find the use of plus and minus-valuedintegers.
• When scientists measure the temperature of the water and some
chemical compound, then the mixture is said to be cold, if the
thermometer (or any other measuring device) gives a negative
value.
• −67.8 °C (−90.0 °F) is the record temperature of Verkhoyansk and
Oymyako of the country Russia. Here, even countries and many
cities of the world are represented using negative numbers for
freezing climates and positive numbers for hot summer weather.
• During banking or when involved in any other financial procedures,
minus sign denotes debit value and the positive sign represents a
credit value. So, if the balance check sheet for your debit card
states – 14 500, then you have a loan amount of 14 500 Frw to be
debated in the bank.
Application Activity 1.2
1. Water freezes at 0oC. Is the temperature in a freezer,
a) Equal to 0oC?
b) Lower than 0oC?
c) Greater than 0oC?
2. Here are six temperatures, in Celsius degrees.
6 -10 5 -4 0 2
Write them in order, starting with the lowest.
3. Here are the midday temperatures, in degrees Celsius, of five citieson the same day.
a) Which city was the warmest?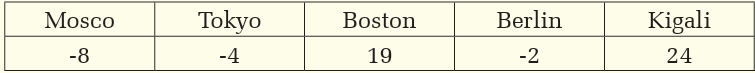
b) Which city was the coldest?
c) What is the difference between the temperatures of Berlin and
Boston?
4. Some frozen food is stored at -8oC. During a power cut the
temperature increases by 1oC every minute. Copy and completethis table to show the temperature of the food.
5. In a certain city, the temperature was -7 oC in the morning and
dropped by 10oC in the afternoon. What is the new temperature?1.3. Rounding and estimating decimal numbers.
Activity 1.3
As a pharmacy technician, you will encounter decimals nearly every
day. Medications are frequently prescribed in decimals, and you will
find that many dosage calculations will be worked out using thedecimal format.
1. Use calculator to work out
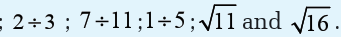
What do you notice?
2. How can you write the answer for instance when dividing 22 by 7,
calculating square root of 3 ? Explain?
The word “Decimal” means “based on 10” and comes from the Latin
word: decima which means «a tenth part”. Decimal numbers are used
in situations which call for more precision than whole numbers provide.
As with whole numbers, a digit in a decimal number has a value which
depends on the place of the digit. The places to the left of the decimal
point are ones, tens, hundreds, and so on, just as with whole numbers.
The following illustration shows the decimal place value for variouspositions:
Each digit in a number has a ‘place value’ (related to one). The value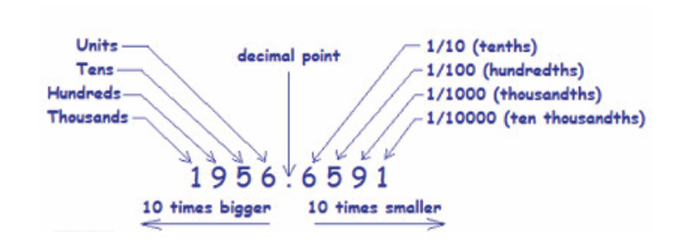
depends on the position of the digit in that number. Each position can
be thought of as columns. Each column is a power of ten.For example, let’s look at 56.39
A recurring decimal is a decimal fraction where a digit repeats itself
indefinitely.
Rounding numbers is a method of summarizing a number to make
calculations easier to solve. Rounding decreases the accuracy of a
number. Rounding to a specified integer or decimal is important whenanswers need to be given to a particular degree of accuracy.
The Rules for Rounding:
1. Choose the last digit to keep.
2. If the digit to the right of the chosen digit is 5 or greater, increase the
chosen digit by 1.
3. If the digit to the right of the chosen digit is less than 5, the chosen
digit stays the same.
4. All digits to the right are now removed.
Example 1.3
What is 7 divided by 9 rounded to 3 decimal places?
Solution
7÷ 9 =0.7777777...
So, by respecting rule 2, then 7÷ 9 = 0.778
Estimating decimal numbers.
Estimating is a very important skill in solving Mathematics problems. It helps
to be able to estimate the answer to check if your calculations are correct.
Some simple methods of estimation:
• Rounding
Example 1: 273.34+ 314.37=?
If we round to the tens We get 270 +310 which is much easier and
quicker. We know that 273.34 +314.37 should equal approximately 580.
• Compatible Numbers
Example 2: 527× 12 ?
1.4. Fractions and equivalent fractions
Activity 1.4Refer to the figures and answer the related questions
a) What fraction of the large square is black?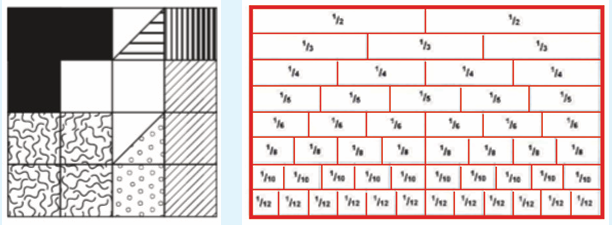
b) What fraction of the large square has vertical lines?
c) What fraction of the large square has diagonal lines?
d) What fraction of the large square has wavy lines?
e) What fraction of the large square has dots?
f) What fraction of the large square is unshaded?
g) What fraction of the large square has the horizontal line?h) What is the relationship between
• Fractions are representations of “parts of a whole”. A fraction is a part of a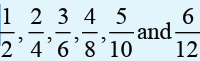
whole: the denominator (bottom number) represents how many equal parts
the whole is split into; the numerator (top number) represents the amount of
those parts
• Equivalent fractions are two or more fractions that are all equal.
The second figure in activity above shows that each row has been
split into different fractions: top row into 2 halves, bottom row 12twelfths. An equivalent fraction splits the row at the same place.
therefore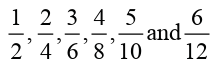 are all equal and equivalent fractions.
are all equal and equivalent fractions.
Doctors often use fractions to figure out what the right dose is. There
is a medicine that can treat patients who are having a stroke (a blood
clot that stops blood flow going to part of the brain). The dose of
the medication is (9/10) times the body weight in kilograms. So if
a patient weighs 70 kg, doctors have to multiply 99/100x (70) = 63
mg of medication. Then (1/10) of that is given right away (6.3 mg),
followed by the rest (63-6.3=56.7 mg) over an hour. The nurses
who give the medication have to do more to figure out how much
medication has to be given every minute on a pump. If there is a
math mistake, then the patient might get too little medication-then
it probably won’t work. If they get too much medication, they might
have bleeding in the brain. So doctors have to be sure they do it right.
Calculators and several people do the math to make sure everyoneagrees
Application Activity 1.4
1. Given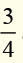 . Find the equivalent fraction by multiplying 4.
. Find the equivalent fraction by multiplying 4.
2. The order reads 1/400 gr. The vial is labelled 1/300g =20 drops.How many drops are to be given?
1.5. Ratios, proportions and rates.
Activity 1.5
1. you survey your friends about their favourite course in associate
nursing program and you find that 8 out of 12 prefer Maternal and
Child health.
a) Write in simplest form the fraction that represents those who do
not prefer Maternal and Child health.
b) Which fraction best communicates the survey results?
c) Express to percentage, the fraction of those who prefer Maternaland Child health.
2. At a certain clinic, an hospitalized person had to pay 17,500FRW for
consultation, 45,000FRW for medicine, and 30,000FRW for room in3days. If the patient was insured by RSSB who pay 85% of the cost,
a. How much money did the RSSB pay for the patient?
b. How much money did the patient pay on his/her own?
3. Consider the table below which shows the relationship betweenthe ages (in year) and quantity of medicine (in ml) to be take.
a. Draw the graph of the number of medicine (in ml) against ages
(in year)
b. Describe the graph you have drawn in (a) above.
4. Consider the relationship between the speed and time taken by acar to cover a fixed distance of 320 km.
Take 20 km/h to be the original speed.
(i) What do you notice when the speed is doubled?
(ii) Plot the graph of speed against time.(iii) Describe the graph you drew to your classmates.
5. A pulse is measured as 17 beats over 15 seconds. What is the heart
rate per minute?
1. A ratio is a comparison of two quantities. The ratio of a to b can also
be expressed as a:b or a/b. This relation gives us how many times one
quantity is equal to the other quantity. In simple words, the ratio is
the number which can be used to express one quantity as a fraction
of the other ones.
Ratio Formula:
Assume that, we have two quantities (or two numbers) and we have to
find the ratio of these two, then the formula for ratio is defined as; a:
b ⇒ a/b, where a and b could be any two quantities.
Example 1.5The ratio of 2 to 4 is represented as 2:4 = 1:2.
Example 1.6
Consider a class that has 20 male students and 80 female students. We
can think about this in several ways. We could express this simply as the
ratio of men to women and write the relationship as 20:80 or 20/80. We can
also simplify this by dividing both the numerator and the denominator by a
number that divides evenly into both
the numerator and the denominator.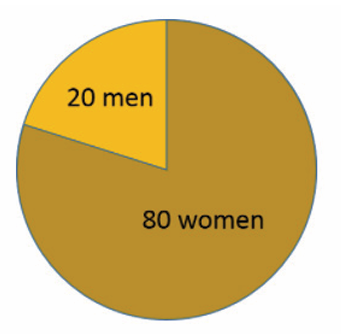
In this case, we could divide both by 20 to simplify this to a 1:4 ratio
(or 1/4 ratio). This indicates that for every man, there are four women.
We could also consider this from the inverse perspective, i.e., the
number of women relative to the number of men; in this case the ratio
of women to men is 80/20 which is equivalent to 4 to 1, i.e., there are
four women for every man.
Note that Equivalent ratios are ratios that have the same value. Given a
ratio, we can generate equivalent ratios by multiplying both parts of the
ratio by the same value.
2. Proportion is an equation which defines that the two given ratios are
equivalent to each other. A proportion is a type of ratio that relates a part to a
whole.
Proportion Formula:
Assume that, in proportion, the two ratios are a:b and c:d. The
two terms ‘b’ and ‘c’ are called ‘means or mean term,’ whereas the
Example 1.7
The time taken by train to cover 100km per hour is equal to the time
taken by it to cover the distance of 500km for 5 hours. Such as 100km/
hr = 500km/5hrs.
Example 1.8
In the class with 20 men and 80 women, the total class size is 100, and
the proportion of men is 20/100 or 20%. The proportion of women is
80/100 or 80%. In both of these proportions the size of part of the class
is being related to the size of the entire class.
Difference Between Ratio and Proportion
To understand the concept of ratio and proportion, go through thedifference between ratio and proportion given here.
Example 1.9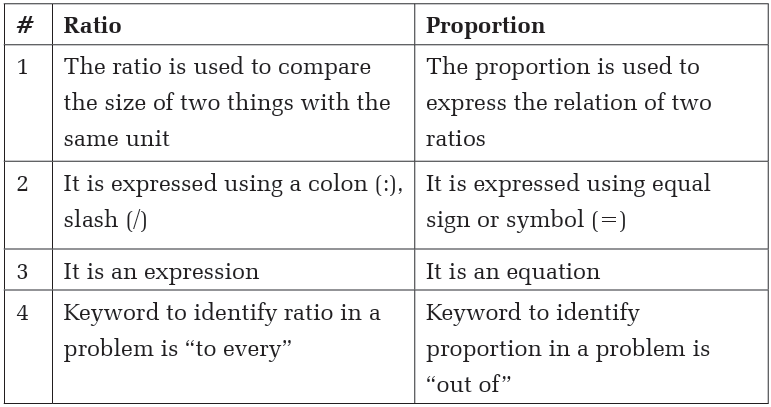
The information on mortality from bird flu shows that 44 died and the other
79 lived could be expressed as a simple ratio, which compares the number who
died to the number who survived. 44/79 or 44:79 would be two ways of expressing
this simple ratio. The ratio of those who died relative to those who lived was 44
to 79.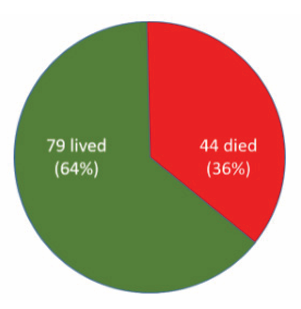
Alternatively, we might want to focus on the proportion who lived. In
total, 123 people were infected, and 44 of these died. Therefore, the
proportion who died was 44/123, which could be expressed as a
decimal fraction (0.36) or as a percentage (36%). This proportion is
referred to as the “case-fatality” rate, although strictly speaking, it is a
proportion and not a rate.
3. Rate: Rates are a special type of ratio that incorporate the dimension of
time into the denominator. Familiar examples include measurements
of speed (kilometers per hour.
Example 1.10
If a car travels 24 kilometres in 2 hours, its average speed is a rate of 24
kilometres / 2 hours = 12 kilometres/hr.
Note that some commonly used measurements of health outcomes are
referred to as “rates” even though they are actually proportions.
For example:
• A mortality rate is the proportion of deaths occurring over a span of
time in a population.
• An attack rate is the proportion of people developing an infectious
disease after exposure to a pathogen.
• A case-fatality rate is the proportion of individuals who die after
developing a disease.
Application of ratios, proportions and rates in nursing
Nurses use ratios, proportions and rates when administering medication.
1. Nurses need to be able to understand the doctor’s orders.
Example 1.11
A doctor’s order may be given as: 25 mcg/kg/min. If the patient
weighs 52kg, how many milligrams should the patient receive in one
hour? In order to do this, nurses must convert micrograms (mcg) to
milligrams (mg). If 1mcg = 0.001mg, we can find the amount (in mg)
of 25mcg by setting up a proportion.
2. Nurses use proportions to Calculate Intravenous Infusion rates and drops per
minute (dpm), by considering the following:
• The total volume to be given, which is often written on the
prescription in mLs.• The time over which the volume is to be given, often in minutes
Example 1.12
If 1500mLs of 0.9% sodium chloride fluid is to be given over 10 hours,
what is the infusion rate for delivery? If the IV administration set has a
drop factor of 20, what will you set the drop rate at?
Solution :There are 2 parts to this question1) calculating the infusion rate (mL/hr)
If the drug is in solution (e.g. oral, IV, IM, SC) the correct dose to be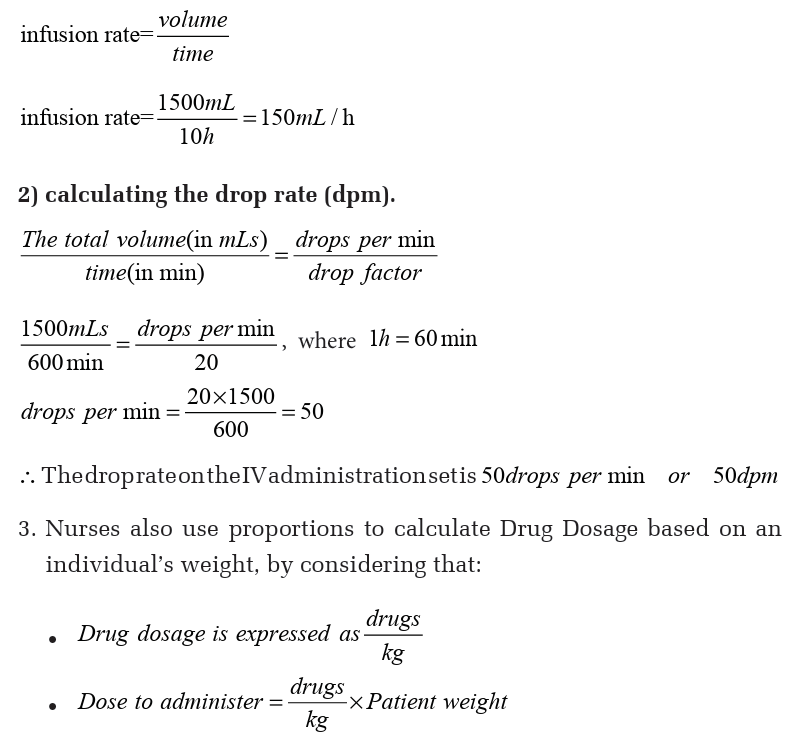
administered, may need to be drawn from a stock solution. This is a
medication solution that contains a ratio of drug (either as solute or
solid) in a diluent (refresh these concepts in section 10 Dilutions usingthe expression solute in diluent).

Example 1.13
Mr. Small weights 60kg. He has been ordered a drug with a dosage of
10 mg per kg. How much drug should be administered? If the drug
is available in a stock solution of 250mg/5mL, what volume of drug
solution should be administered?
Solution: There are two parts to this question1) The dose of drug to give (in mg);
Application Activity 1.5
1. A first year, physiology subject has 36 males and 48 females, whereas
the clinical practice subject has 64 males and 80 females. You are
asked to work out which cohort has the largest male to female ratio.
2. Yasmin is checking the IV fluid infusion on Mrs Cannon at the start
of the shift. She sees from the fluid balance sheet that Mrs Cannon
has received 320 mL over the past 4 hours. Mrs Cannon is to receive
the full litre bag. How many hours would you expect it to take to
infuse the full litre?
3. Apply your understanding of proportional thinking to solve the
following:
a) A patient is prescribed 150mg of soluble aspirin. We only have
300mg tablets on hand. How many tablets should be given?
b) A solution contains fluoxetine 20mg/5mL. How many milligrams
of fluoxetine are in 40mL of solution?
c) A stock has the strength of 5000units per mL. What volume
must be drawn up into an injection to give 6500units?
d) An intravenous line has been inserted in a patient. The total
volume to be given is 1200mL over 5hours at a drop factor of
15drops/mL. How many drops per minute will the patient
receive?
e) Penicillin syrup contains 200mg of penicillin in 5mL of water.
If a patient requires 300mg of penicillin how much water will be
required to make the syrup?
4. What fraction of H2 O2is hydrogen? Calculate it’s percentage.
1.6. Absolute value and its properties
Activity 1.6.1
Draw a number line and state the number of units that are between;
Absolute value of a number is the distance of that number from the
original (zero point) on a number line. The symbol is used to denote
is used to denotethe absolute value.

Example 1.15
Find x in the following
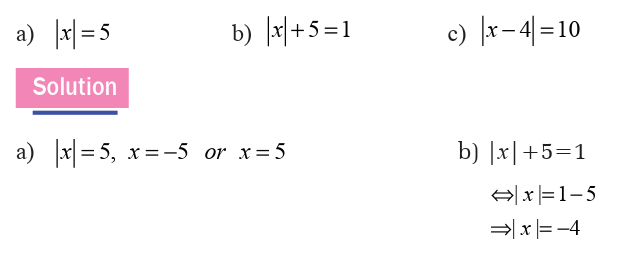
There is no value of x since the absolute value of x must be a positive real number.

Properties of the Absolute Value
Opposite numbers have equal absolute value.

1.7. Powers and radicals
Powers in IR
Activity 1.7.1
Peter suggested that his allowance be changed. He wanted $2
the first week, with his allowance to be doubled each week. Hisparent investigated the suggestion using this table
1. Complete the table to find how many dollars Peter would be paid each
of the first five weeks.
2. How much would Peter be paid the seventh week? The tenth week?3. Do you think his parent will agree with his suggestion? Explain.


These properties help us to simplify some powers.
There is no general way to simplify the sum of powers, even when the
powers have the same base. For instance,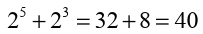 and 40 is
and 40 is
not an integer power of 2. But some products or ratios of powers can besimplified using repeated multiplication model of an

1.A hummingbird has a mass of about 10-2 kg . Show that this mass is 0.01
Radicals in real numbers
Activity 1.7.2Evaluate the following powers


Example 1.23


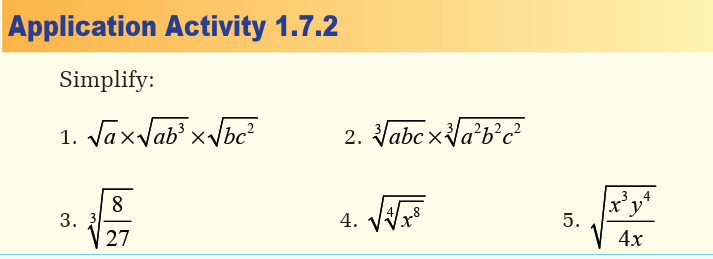
Operations on radicals
When adding or subtracting the radicals, we may need to simplify if we
have similar radicals. Similar radicals are the radicals with the sameindices and same bases.
Addition and subtraction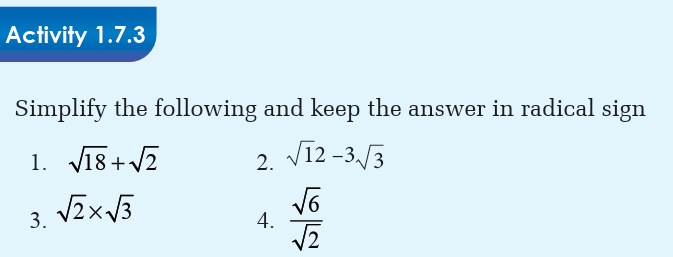
When adding or subtracting the radicals we may need to simplify if we
have similar radicals. Similar radicals are the radicals with the sameindices and same bases.


Rationalizing the denominator
Activity 1.7.4Make the denominator of each of the following rational;
Rationalizing is to convert a fraction with an irrational denominator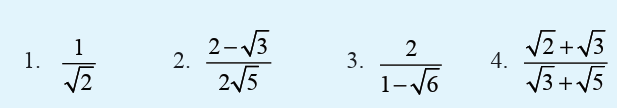
to a fraction with rational denominator. To do this, if the denominator
involves radicals, we multiply the numerator and denominator by theconjugate of the denominator.



Example 1.27
log (100) = ?We are required to find the power to which 10 must be raised to obtain 100



Co-logarithm
Co-logarithm, sometimes shortened to colog, of a number is the
logarithm of the reciprocal of that number, equal to the negative of thelogarithm of the number itself,

4. Rationalizing is to convert a fraction with an irrational denominator
to a fraction with rational denominator. To do this, if the denominator
involves radicals we multiply the numerator and denominator bythe conjugate of the denominator.
5. The decimal logarithm of a positive real number x is defined to bea real number y for which 10 must be raised to obtain x. We write

5. Contractors are tilling the bathroom floor in new house. The floor
measures 288 cm by 192 cm. They are using square tiles with sides
measuring 24 cm. How many tiles will they need?
6. Esther’s little brother is playing with a set of collared blocks. Each
block has edges measuring 4 cm. What is the volume of one of the
blocks?
7. Humans breathe about 15 breaths in a minute. The average breath at
rest contains 0.76 liter of air. About how many liters of air will you
breathe while at rest for 25 minutes?
8. Density is the ratio of a substance’s mass to its volume. A volume of
20 cubic centimeters of gold has a mass of 386 grams. Express the
density of gold as a unit rate.
9. A lion’s heart beats 12 times in 16seconds. How many times does alion’s heart beat in 60seconds?.
a)How many people were tested negative?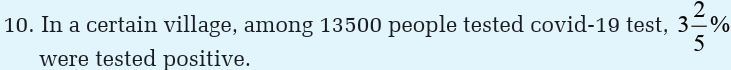
b)How many people were tested positive?
11. Ingabire, Mugenzi and Gahima have jointly invested in buying and
selling of shares in the Rwanda stock exchange market. In one sale
as they invested different amount of money, they realised a gain of
1 080 000 Frw and intend to uniquely share it in the ratio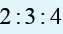
respectively. How much did Mugenzi get?

Unit 2: Fundamentals of Trigonometry
2.0 Introductory activity
The angle of elevation of the top of the Cathedral from a point 280
m away from the base of its steeple on level ground is 600. By usingtrigonometric concepts, find the height of the cathedral.
Objectives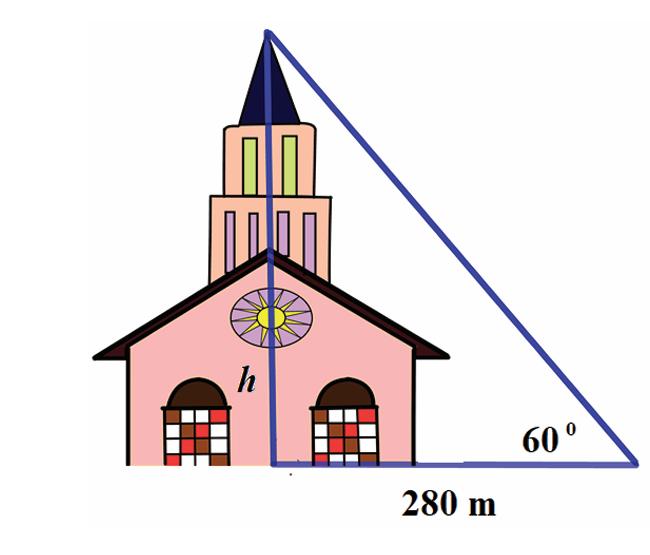
After completing this unit, I will be able to:
» Define sine, cosine, and tangent (cosecant, secant and
cotangent) of any angle – know special values.
» Convert radians to degree and vice versa.
» Use trigonometric identities.» Apply trigonometric formulae in real world problems.
2.1. Trigonometric concepts
Activity 2.1Consider the following diagram
Trigonometry is the study of how the sides and angles of a triangle are
related to each other. A rotation angle is formed by rotating an initial
side through an angle, about a fixed point called vertex, to terminal
position called terminal side.
Trigonometric concepts contribute to various medical testing and
interpretation of those test results. Some of the uses are,
1.Electrocardiography: The measurement of electrical activities in the
heart. Through this process, it is possible to determine how long the
electrical wave takes to travel from one part of the heart to the next
by showing if the electrical activity is normal or slow, fast or irregular.
2.Pulmonary function testing: a spirometer is used to measure the
volume of air inhaled and exhaled while breathing by recording
the changing volume over time. The output of a spirogram can be
quantified using trigonometric equations and generally, it is possible
to describe any repeating rhythms of lung capacity.
A rational angle is drawn in what is called standard position if the initialside is on the positive x-axis and the vertex of the angle is at the origin.
Angles in standard position that have a common terminal side are called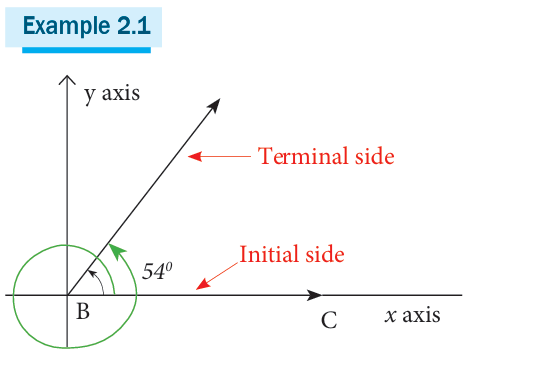
co-terminal angles; the measure of smallest positive rotation angle is
called principal angle. Angle is positive if rotated in a counterclockwise
direction and negative when rotated clockwise.
Angles are named according to where their terminal sides lie. For
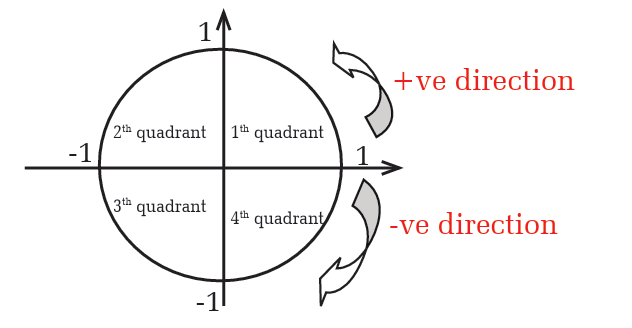
instance, the x-axis and y-axis divide a plane into four quadrants asfollow.
Example 2.2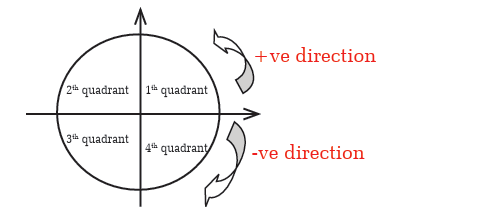
Draw each of the following angles in standard position and show thereangles which are co-terminal to 300 ?
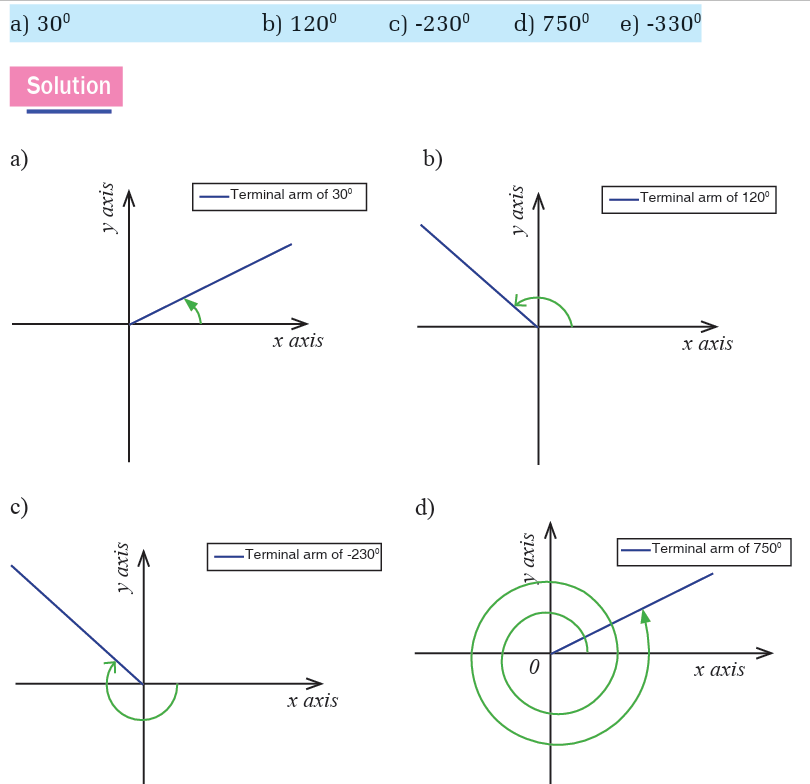
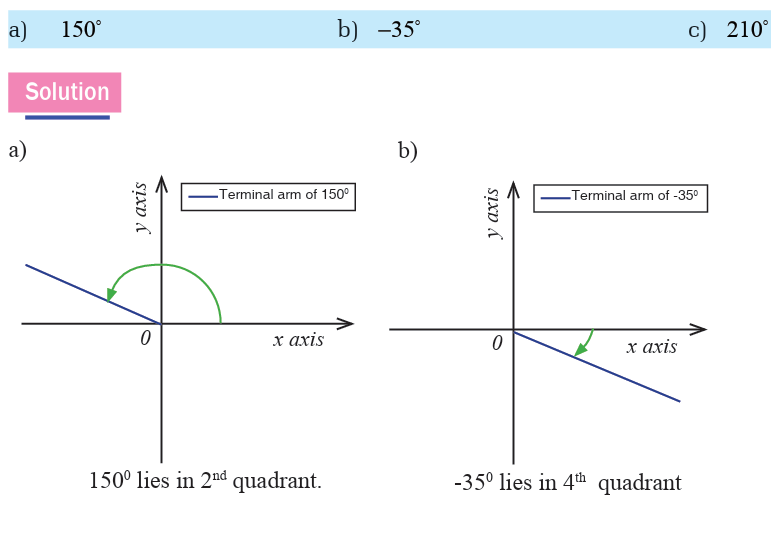
Example 2.3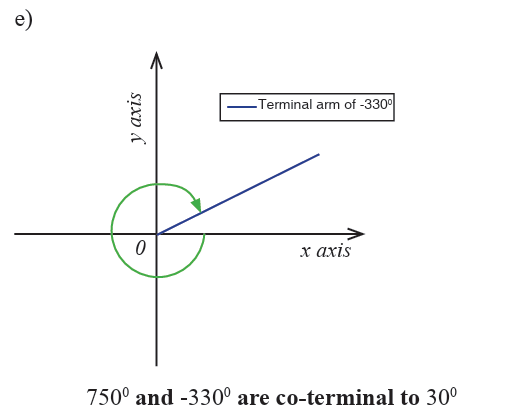
Draw each of the following angles in standard position and indicate inwhich quadrant the terminal side is.
Application Activity 1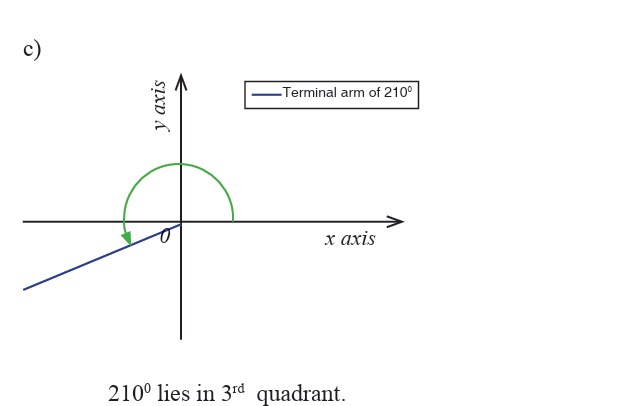
1. Draw each of the following angles in standard position and show
the angles which are co-terminal to 200?
a) 200 b) -2000 c) 7400 d) -3400
2. Draw each of the following angles in standard position and
indicate in which quadrant the terminal side is.
a) 400 b) -2350 c) 2800
2.1.1. Measure of an angle
Activity 2.2
The amount we rotate the angle is called the measure of the angle andis measured in following units:



Example 2.7
An angle which measures 82 grades, 7 decigrades, 2 centigrades and 5
milligrades will be denoted by
82G ,725
c) Radian
A central angle of a circle is an angle with a vertex at the centre of a
circle. An intercepted arc is the portion of the circle with endpoints on
the sides of the central angle and remaining points within the interior
of the angle.
When a central angle intercepts an arc that has the same length as aradius of the circle, the measure of the angle is defined to be one radian.
Like degrees, radian measures the amount of the rotation from the initial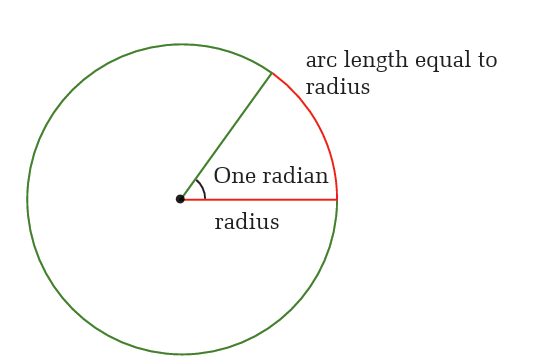
side to the terminal side of an angle.


Application Activity 2
1. Convert 220 grades to radians and degrees.2. Convert 1240 degrees to radians and grades.
Activity 2.3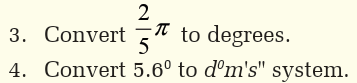
Construct two right angled triangles, one of which is an
enlargement of the other.
How is the side opposite to the right angle (or the longest side) called?
For both triangles, consider an angle and compute the following ratios.
• Opposite side to the considered angle and hypotenuse.
• Adjacent side and hypotenuse.
• Opposite side to the considered angle and adjacent side.
How can you conclude?Consider the following circle with radius r.
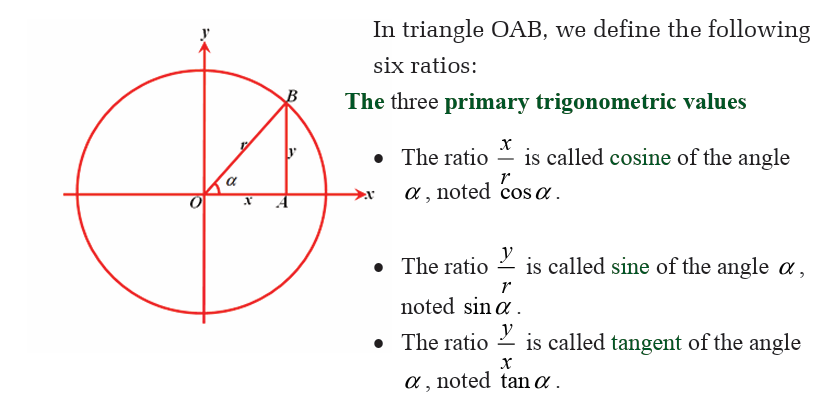

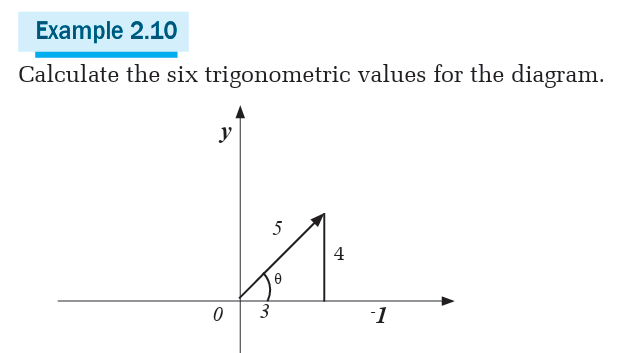




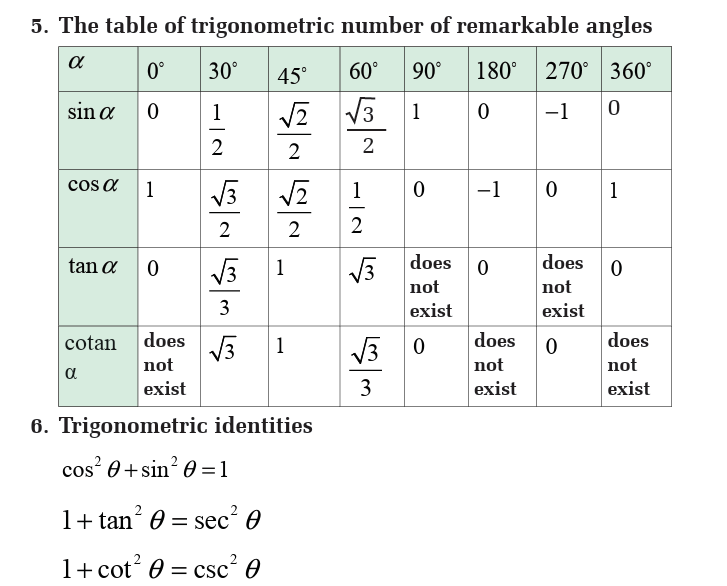
Trigonometric Number of special Angles 300, 450, 600
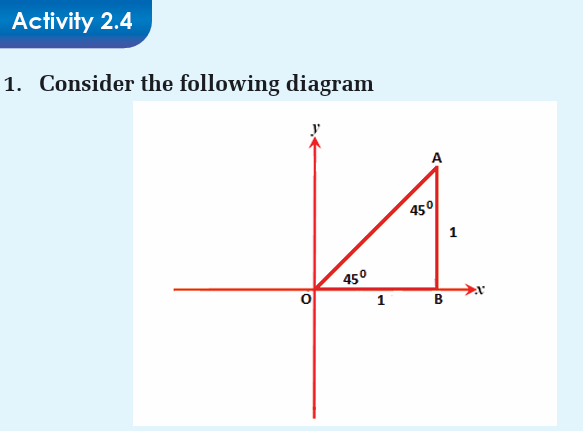
From pythagoras theorem, definition of trigonometric ratios and
given diagrams, find sin 450, cos 450 and tan 4502. Consider the following diagram
As these angles are often used, it is better to keep in your mind their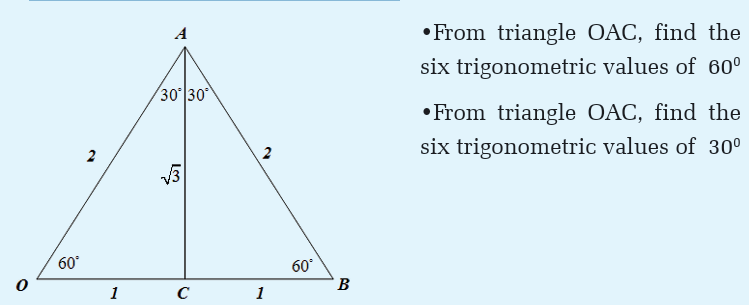
trigonometric ratios in fraction form.

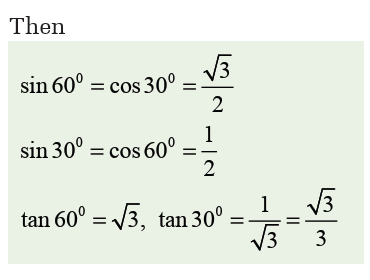
Application Activity 2.4
The following diagram shows which primary trigonometric values are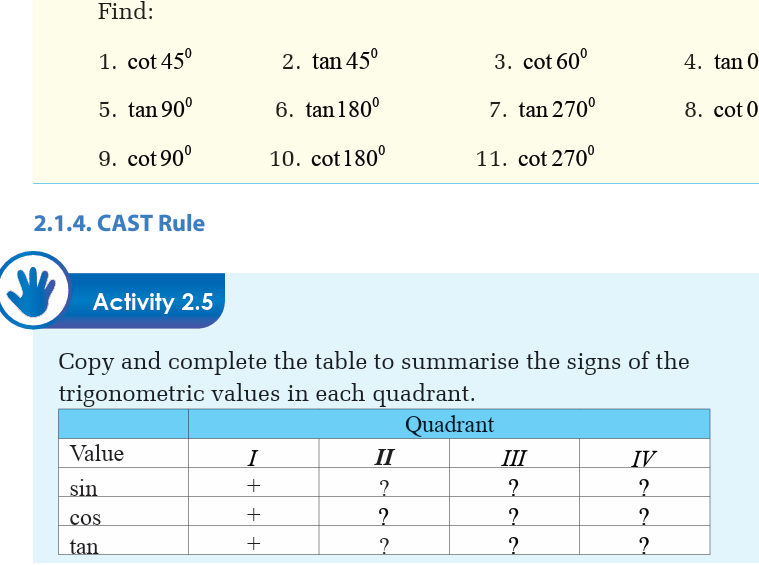
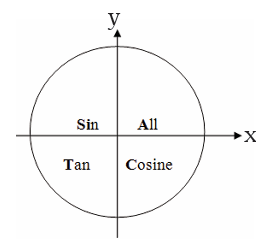
positive in each quadrant. This is called the CAST rule.
Sine is positive in first and second quadrant but negative in third and fourth quadrant.
Cosine is positive in the first and fourth quadrant but negative in second and third
quadrant.
Tangent is positive in in the first and third quadrants but negative in second and fourthquadrant.
Application Activity 2.5



Application Activity 6
2. Triangle and applications
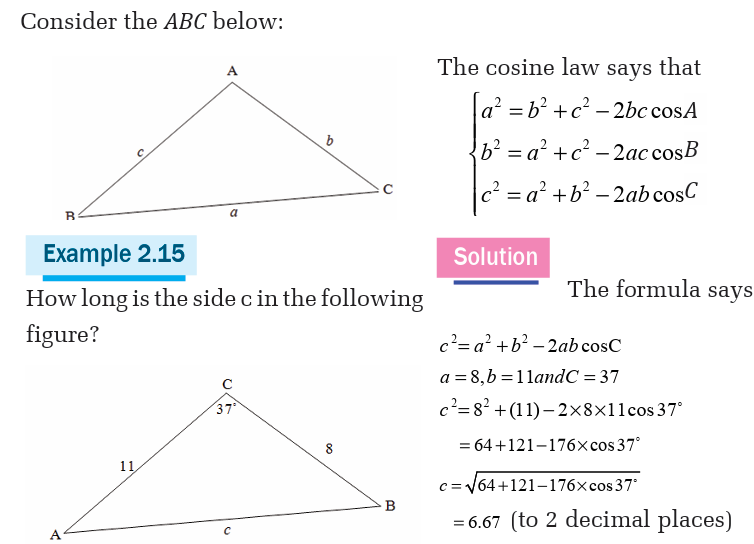
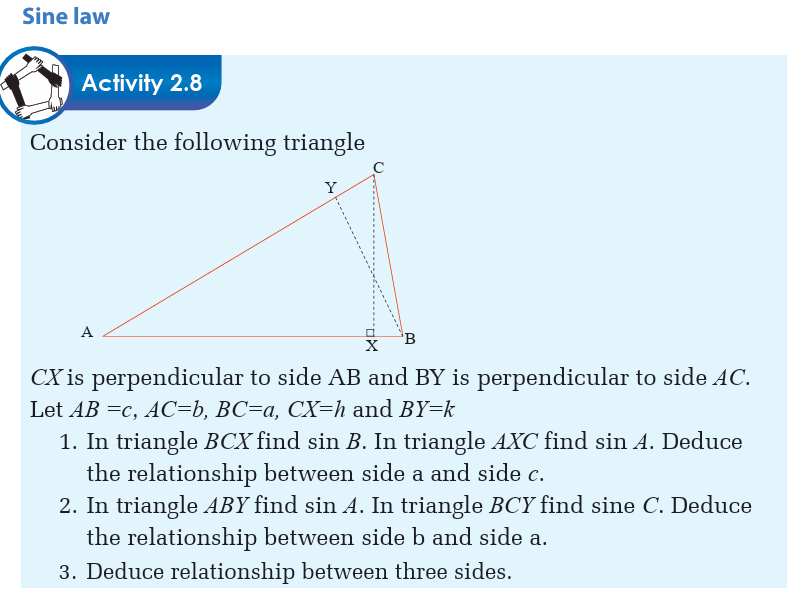
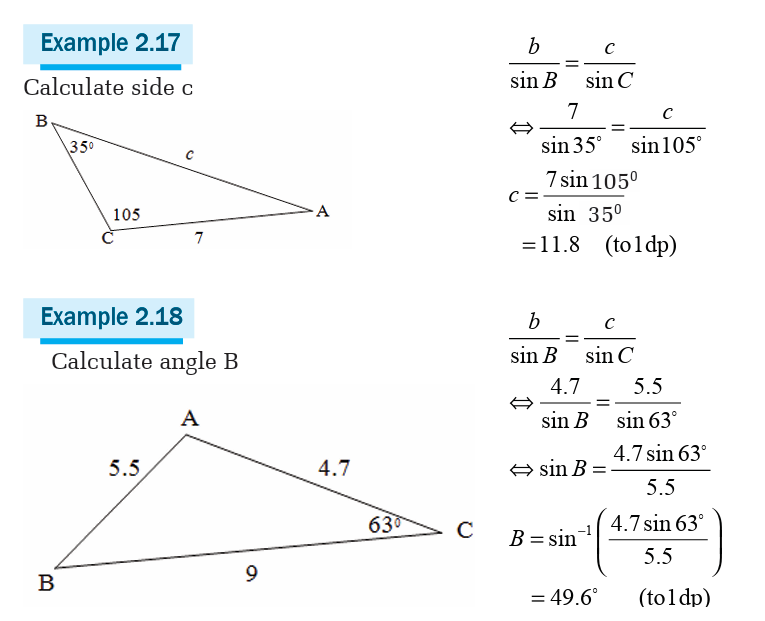
Solving triangle
Solving a triangle is to find the length of its sides and measures of its
angles. There are two methods for solving a triangle: cosine law andsine law.
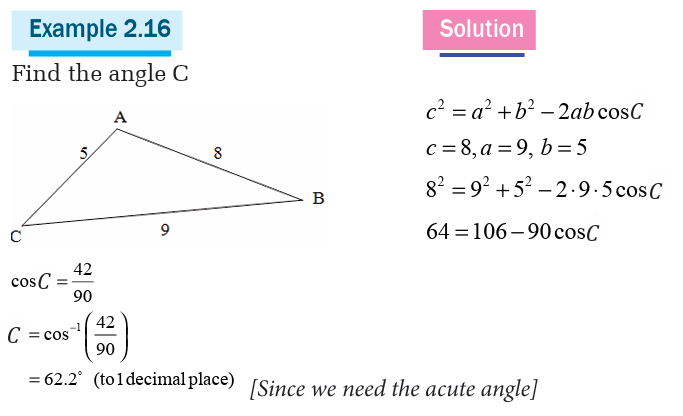
Cosine law
Activity 7
Cosine law (also known as cosine formula or cosine rule) relates the
lengths of sides to the cosine of one of the angles as follow.
Application Activity 2.7

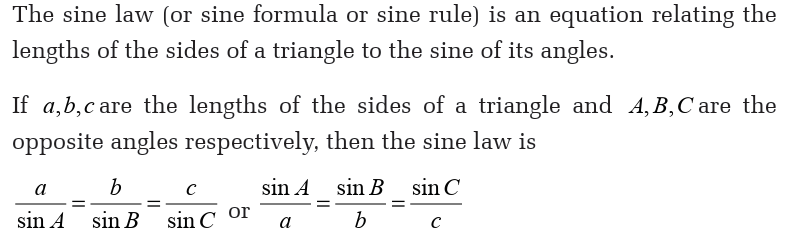

Applications
Many real situations involve right triangles. Using angles and
trigonometric functions, we can solve problems involving right triangle.We have already seen how to solve a triangle.
1. Bearings and air navigation
Similarly, if B is south of A then the bearing of A from B is 180o, and if B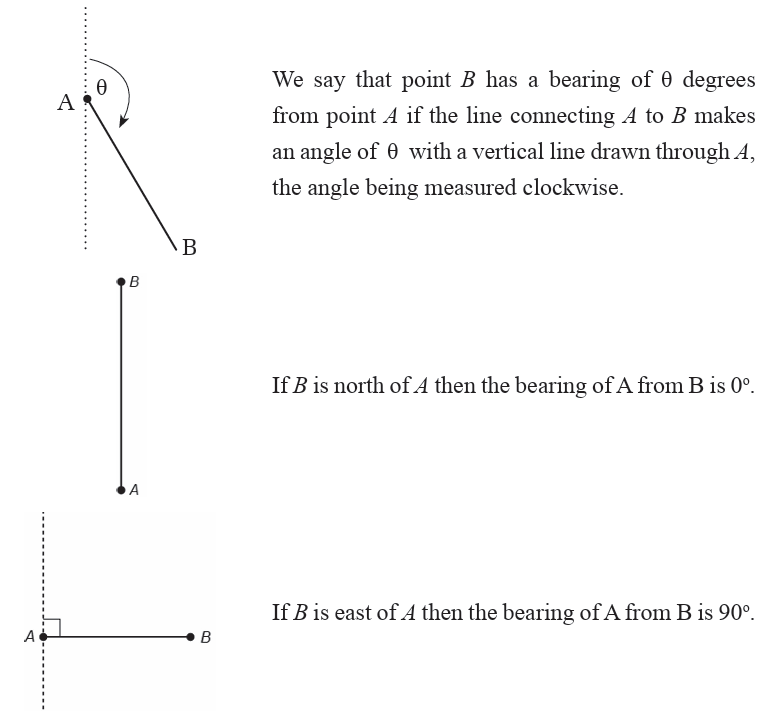
is west of A then the bearing of A from B is 270o. The bearing can be any
number between 0 and 360, because there are 360 degrees in a circle.
We can also use right triangles to find distances using angles given as
bearings.
In navigation, a bearing is the direction from one object to another.
Further, angles in navigation and surveying may also be given in terms
of north, east, south, and west. For example, N 700E refers to an angle
from the north, towards the east, while N700 W refers to an angle from
the north, towards the west.
Example 2.19
A ship travels on a N500 E course. The ship travels until it is due north
of a port which is 10 kilometers due east of the port from which the shiporiginated. How far did the ship travel?

Example 2.20
An airplane flies on a course of S 300E , for 150 km. How far south is theplane from where it originated?
2. Angle of elevation and angle of depression
You can use right triangles to find distances, if you know an angle of
elevation or an angle of depression. The figure below shows each of
these kinds of angles.
Suppose that an observer is standing at the top of a building and looking
straight ahead at the birds (horizontal line). The observer must lower
his/her eyes to see the car parked (slanting line). The angle formedbetween the two lines is called the angle of depression.
Suppose that an observer is standing at the top of a building and looking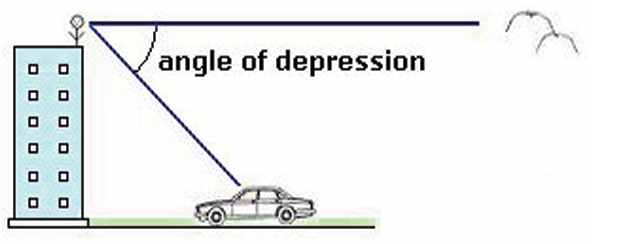
straight ahead at the birds (horizontal line). The observer must raise his/
her eyes to see the airplane (slanting line). The angle formed betweenthe two lines is called the angle of elevation.
The angle of elevation of the top of a pole measures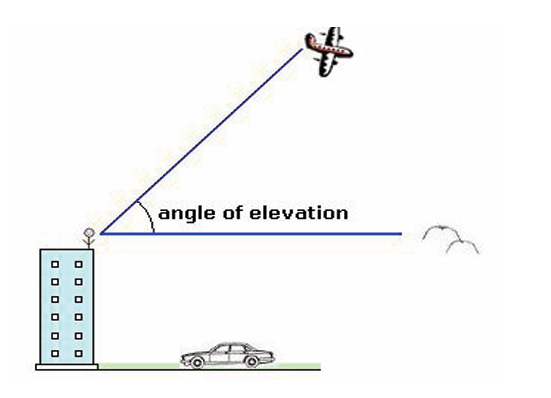
480 from a point on the ground 18 metres away from its base.
Find the height of the flagpole.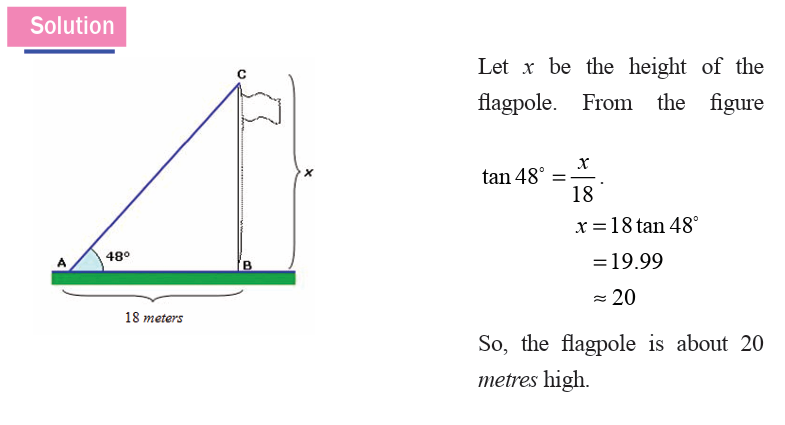
Example 2.22
An airplane is flying at a height of 2 kilometres above the level ground.
The angle of depression from the plane to the foot of a tree is 15o. Findthe distance that the air plane must fly to be directly above the tree.
Let x be the distance the airplane must fly to be directly above the tree.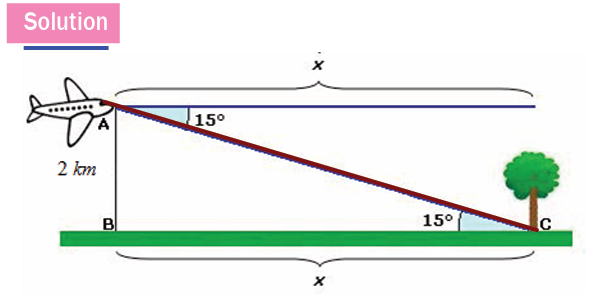
The level ground and the horizontal are parallel, so the alternate interiorangles are equal in measure.
So, the airplane must fly about 7.46 kilometres to be directly above the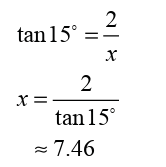
tree.
3. Inclined plane
An inclined plane, also known as a ramp, is a flat supporting surface
tilted at an angle, with one end higher than the other, used as an aid
for raising or lowering a load. On the inclined plane the weight of
the object causes the object to push into and, the object slides, to rub
against the surface of the incline. Also the weight causes the object tobe pulled down the slant of the incline. The component that pushes the

the same as the angle of the incline, as shown below

Unit summary
1. Trigonometry is the study of how the sides and angles of a triangle
are related to each other. A rotation angle is formed by rotating an
initial side through an angle, about a fixed point called vertex, to
terminal position called terminal side. Angle is positive if rotated in a
counterclockwise direction and negative when rotated clockwise.2. The amount we rotate the angle is called the measure of the angle and
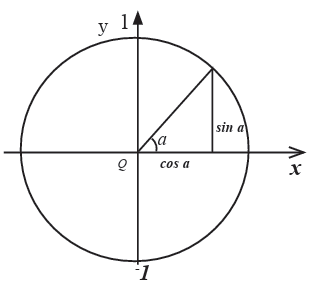
4. The unit circle is a circle of radius one centered at the origin (0,0) in
the Cartesian coordinate system in the Euclidian plane. In the unit
circle, the coordinate axes delimit four quadrants that are numbered in
an anticlockwise direction. Each quadrant measures 90 degrees, meansthat the entire circle measures 360 degrees or radians.

End Unit assesment

9. A point P is 90 m away from a vertical flagpole, which is 11 m high. What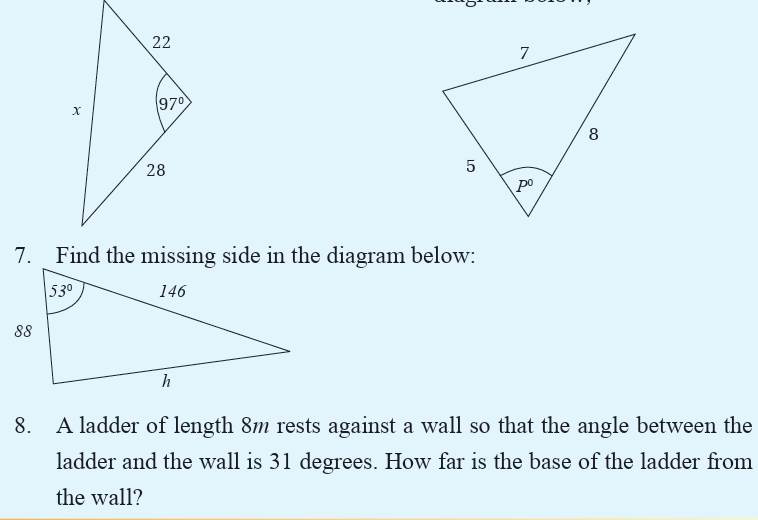
is the angle of elevation to the top of the flagpole from P?
10. A ship sails 200 km on a bearing of 243.7 degrees
a) How far south has it travelled?
b) How far west has it travelled?
11. An aircraft flies 500 km on a bearing of 100 degrees and then 600 km on
a bearing of 160 degrees. Find the distance and bearing of the finishing
point from the starting point.
12. A plane is flying at a constant height of 8000 m. It flies vertically above
me and 30 seconds later the angle of elevation is 74 degrees. Find the
speed of the plane in metres/second.
13. Convert 81013'08'' to decimal degree.
14. Convert 117.65720 to d0 m' s" system.
15. Convert 2.9370 to d0 m' s" system.16. Convert 75019'35'' to the nearest tenth degree.
Unit 3: Linear, quadratic equations and inequalities
3.0 Introductory activity
1. By the use of library and computer lab, do the research and explain
the linear equation.
2. If x is the number of pens for a learner, the teacher decides to give
him/her two more pens. What is the number of pens will he/she have?3. Complete the following table called table of value to indicate the
4. Find out an example of problem from the real life situation that can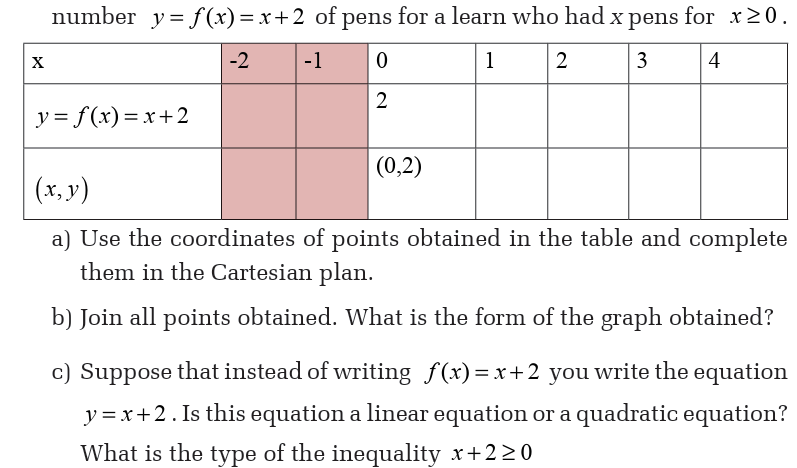
be solved by the use of linear equation in one unknown
5. Smoke jumpers are fire fighters who parachute into areas near forest
fires. Jumpers are in free fall from the time they jump from a plane
until they open their parachutes. The function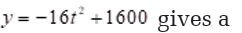
jumper’s height in metre after seconds for a jump from.
a) How long is free fall if the parachute opens at 1000 m?
b) Complete a table of values for t = 0, 1, 2, 3, 4, 5 and 6.
objectives
After completing this unit, I will be able to:
» Solve equation of the first degree and second degree.
» Solve inequality of the first degree and second degree.
» Solve a system of linear equations.
» Use equations and inequalities to solve word
problems.» Apply equations and inequalities in real life problems.
3.1. Equations and inequalities in one unknown
EquationsActivity 3.1.1


Example 3.2
Mugisha’s target heart rate is 130 beats/min. This is 58beats/min morethan his resting heart rate. Find his resting heart rate.
II. Uwamahoro measures her heart rate at 123 beats per minute. This
is 55beats per minute more than her resting heart rate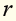 . Write and
. Write and
solve an equation to find Uwamahoro’s resting heart rate.
Venus’s average distance from the Sun is 108million km. this distance
is 42million km less than the average distance from the Sun to Earth.
Write and solve an equation to find Earth’s average distance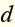 from the Sun.
from the Sun.
Equations products / quotients
Activity 3.1.2State the method you can use to solve the following equations.
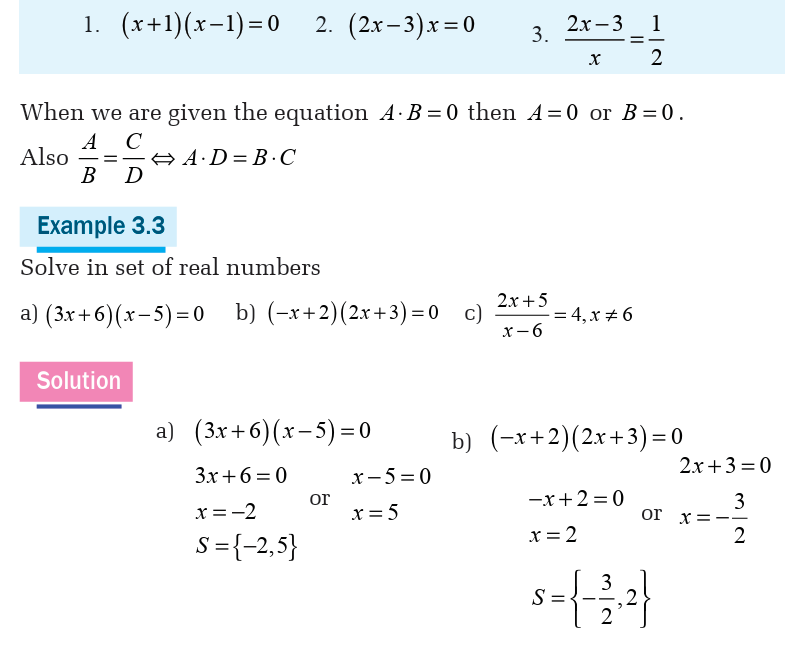

Inequalities
Activity 3.1.3
Find the value(s) of x such that the following statements are true
Suppose that we have the inequality x+3<10 In this case, we have
an inequality with one unknown. Here, the real value of x satisfies that
this inequality is not unique. For example, 1 is a solution but 3 is also
a solution. In general, all real numbers less than 7 are solutions. In thiscase, we will have many solutions combined in an interval.
Now, the solution set of x+3 <10 is an open interval containing allreal numbers less than 7 whereby 7 is excluded. How?
We solve this inequality as follows;
Recall that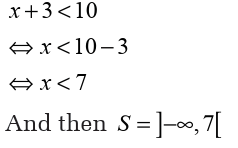
• When the same real number is added or subtracted from each side
of the inequality, the direction of the inequality is not changed.
• The direction of the inequality is not changed if both sides are
multiplied or divided by the same positive real number and
is reversed if both sides are multiplied or divided by the samenegative real number.
Since any real number times zero is zero and zero is greater than -18,
then the solution set is the set of real numbers.

Solution
A serving of low sodium food has at most 140mg per serving.
Let s be the number of milligrams of sodium in a serving of low sodiumfood.
II) Use the table in example 4. A certain food is labelled sodium free.
Write an inequality for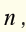 the number of milligrams of sodium in
a serving of
the number of milligrams of sodium in
a serving of this sodium-free food.
III) High-fiber foods have at least 5g of fiber per serving. Write an inequality to
represent this situation. Let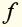 be the number of grams of fiber per serving
be the number of grams of fiber per serving of high -fiber food.
Inequalities products / quotients
Activity 3.1.4State the method you can use to solve the following inequalities
Suppose that we need to solve the inequality of the form
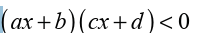
. For this inequality, we need the set of all real numbers that make the
left hand side to be negative. Suppose also that we need to solve the
inequality of the form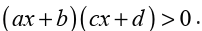
. For this inequality, we need the set of all real numbers that make the left hand side to
be positive. We follow the following steps:
a) First we solve for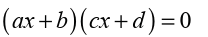
b) We construct the table called sign table, find the sign of each
factor and then the sign of the product or quotient if we are given
a quotient.
For the quotient, the value that makes the denominator to be zero is
always excluded in the solution. For that value, we use the symbol ||
in the row of quotient sign.c) Write the interval considering the given inequality sign.

Application Activity 3.1.4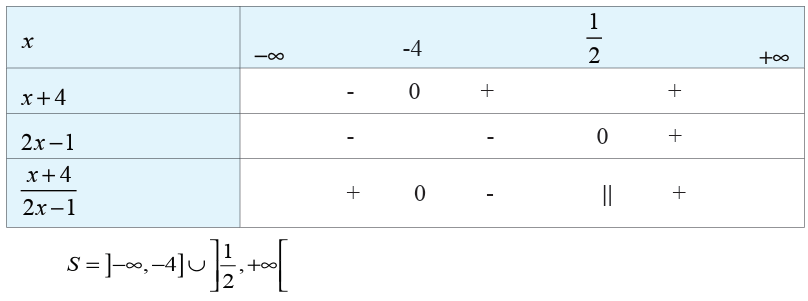
Solve the following inequalities:
Inequalities involving absolute value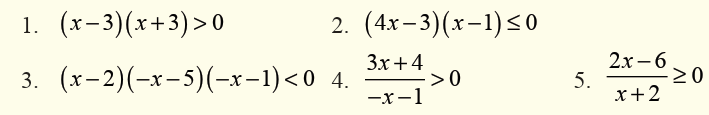
Activity 3.1.5
State the set of all real numbers whose number of units from zero,
on number line, are
1. greater than 4
2. less than 6Hint Draw a number line




Equations and inequalities in real life problems
Activity 3.1.6
How can you do the following?
1. A father is 30 years older than his son. 5 years ago he was four times
as old as his son. What is the son’s age?
2. Betty spent one fifth of her money on food. Then she spent half of
what was left for a haircut. She bought a present for 7,000 francs.
When she got home, she had 13,000 francs left. How much did
Betty have originally?
Equations can be used to solve real life problems.
To solve real life problems, follow the following steps:
a) Identify the variable and assign symbol to it.
b) Write down the equation.
c) Solve the equation.
d) Interpret the result. There may be some restrictions on the variable.
Example 3.11
Kalisa is four times as old as his son, and his daughter is 5 years younger
than his brother. If their combined ages amount to 73 years, find the ageof each person.
110 kg of cement are required.
440 kg of sand are required.
660 kg of aggregate are required.
Example 3.13
John has 1,260,000 Francs in an account with his bank. If he deposits
30,000 Francs each week into the account, how many weeks will he
need to have more than 1,820,000 Francs on his account?
Solution
Let x be the number of weeks
We have;
total amount of deposits to be made + the current balance > total
amount wanted.
That is;
30,000x + 1,260,000 > 1,820,00030,000x > 1,820,000 _ 1,260,000
Application Activity 3.1.6
1. The sum of two numbers is 25. One of the numbers exceeds the
other by 9. Find the numbers.
2. The difference between the two numbers is 48. The ratio of the
two numbers is 7:3. What are the two numbers?
3. The length of a rectangle is twice its breadth. If the perimeter is
72 metre, find the length and breadth of the rectangle.
4. Aaron is 5 years younger than Ron. Four years later, Ron will be
twice as old as Aaron. Find their present ages.
5. Sam and Alex play in the same soccer team. Last Saturday Alex
scored 3 more goals than Sam, but together they scored less than
9 goals. What are the possible number of goals Alex scored?
6. Joe enters a race where he has to cycle and run. He cycles a
distance of 25 km, and then runs for 20 km. His average running
speed is half of his average cycling speed. Joe completes the racein less than 2½ hours, what can we say about his average speeds?
3.2. Simultaneous equations in two unknowns
Combination (or addition or elimination) method
Activity 3.2.1
For each of the following, find two numbers to be multiplied tothe equations such that one variable will be eliminated;
We try to combine the two equations such that we will remain with one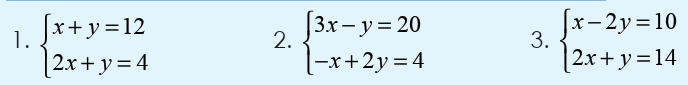
equation with one unknown. We find two numbers to be multiplied oneach equation and then add up such that one unknown is cancelled.


We find the value of one unknown in one equation and put it in another
equation to find the value of the remaining unknown.



In order to use Cramer’s rule, x’s must be in the same position and y’s in the same position.
Consider the following system:

solution
First rearrange the system such that x’s will be in the same position andy’s will be in the same position.
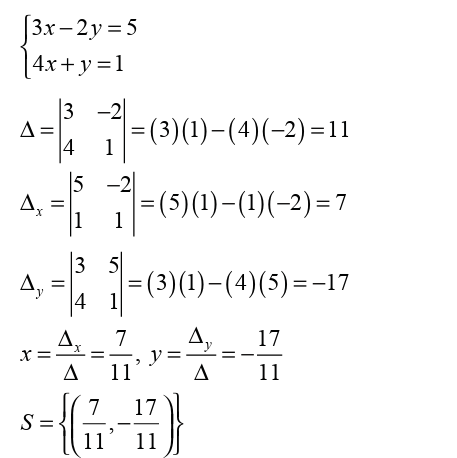
Example 3.25


2. Plot the obtained points in xy plane and join these points to obtain
the lines. Two points for each equation give one line.
3. What is the point of intersection for two lines?
Some systems of linear equations can be solved graphically. To do this,
follow the following steps:
1. Find at least two points for each equation.
2. Plot the obtained points in xy plane and join these points
to obtain the lines. Two points for each equation give
one line.
3. The point of intersection for two lines is the solution forthe given system

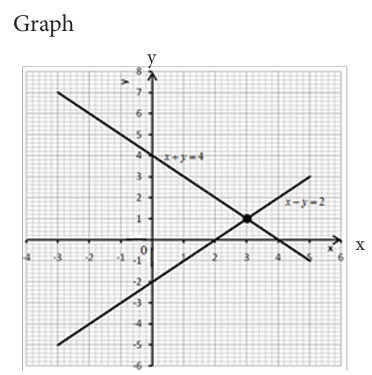
The two lines intersect at point (3,1). Therefore the solution is S={(3,1)}.

We see that the two lines are parallel and do not intersect. Therefore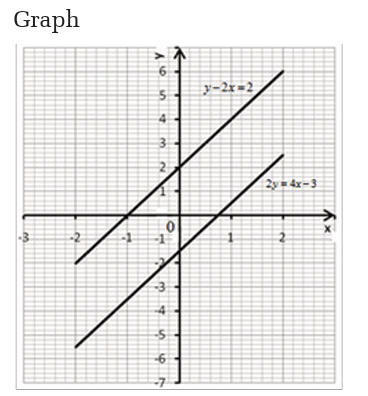
there is no solution. Note that the gradients of the two lines are thesame.
We see that the two lines coincide as a single line. In such case there is
an infinite number of solutions.
Solving word problems using simultaneous equations
Activity 3.2.5
How can you do the following question?
Margie is responsible for buying a week’s supply of food and
medication for the dogs and cats at a local shelter. The food and
medication for each dog costs twice as much as those supplies
for a cat. She needs to feed 164 cats and 24 dogs. Her budget is
$4240. How much can Margie spend on each dog for food and
medication?
To solve word problems, follow the following steps:
a) Identify the variables and assign symbol to them.
b) Express all the relationships, among the variables using equations.
c) Solve the simultaneous equations
d) Interpret the result. There may be some restrictions on the
variables.
Example 3.30
Peter has 23 coins in his pocket. Some of them are 5 Frw coins and
the rest are 10 Frw coins. The total value of coins is 205 Frw . Find the
number of 10 Frw coins and the number of 5 Frw coins.
Solution
Let x be the number of 10 Frw coins and y be the number of 5 Frw coins.Then,
Example 3.31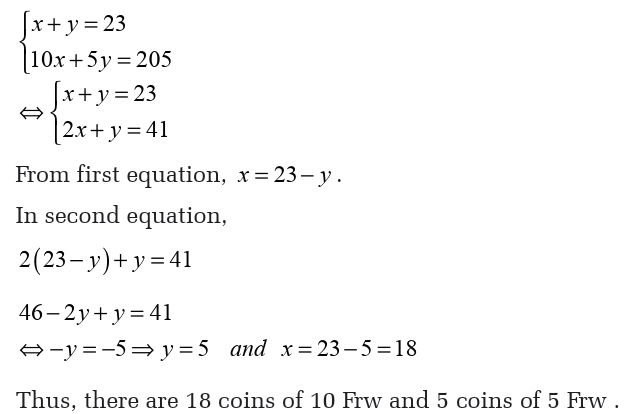
Cinema tickets for 2 adults and 3 children cost 1,200 Frw . The cost for
3 adults and 5 children is 1,900 Frw. Find the cost of an adult ticket and
the cost of a child ticket.
Solution
Let x be the cost of an adult ticket and y be the cost of a child ticket,then
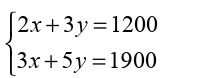
Application Activity 3.2.5
1. A test has twenty questions worth 100 points. The test consists of True/
False questions worth 3 points each and multiple choice questions
worth 11 points each. How many multiple choice questions are on
the test?
2. Two small pitchers and one large pitcher can hold 8 cups of water.
One large pitcher minus one small pitcher constitutes 2 cups of water.
How many cups of water can each pitcher hold?
3. The state fair is a popular field trip destination. This year, the senior
class at High School A and the senior class at High School B both
planned trips there. The senior class at High School A rented and
filled 8 vans and 8 buses with 240 students. High School B rented
and filled 4 vans and 1 bus with 54 students. Every van had the same
number of students in it as did the buses. Find the number of students
in each van and in each bus.
4. The sum of the digits of a certain two-digit number is 7. Reversing its
digits increases the number by 9. What is the number?
5. A boat traveled 210 miles downstream and back. The trip downstream
took 10 hours. The trip back took 70 hours. What is the speed of theboat in still water? What is the speed of the current?
3.3 Quadratic equations and inequalities
Quadratic equations by factorizing or finding square roots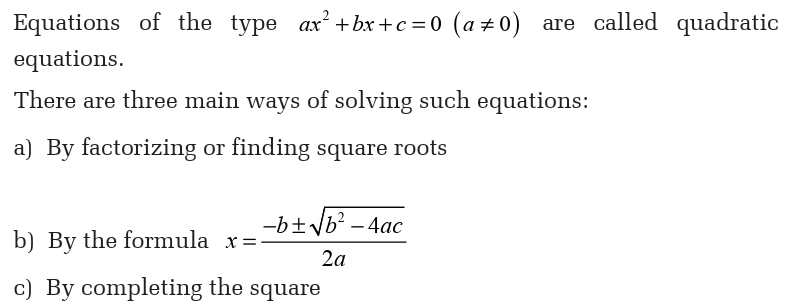
Activity 3.3.1
Smoke jumpers are firefighters who parachute into areas near forest
fires. Jumpers are in free fall from the time they jump from a plane
until they open their parachutes.The function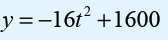
gives a jumper’s height y gives a jumper’s height t seconds for a jump from
1600m.How long is free fall if the parachute opens at 1000m?
The method of solving quadratic equations by factorization should only
be used if is readily factorized by inspection.
The method of solving quadratic equations by factorization should onlybe used if is readily factorized by inspection.
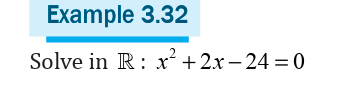

Before solving quadratic equations by completing the square, let’s look
at some examples of expanding a binomial by squaring it.
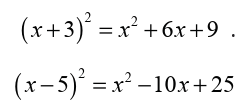


Application Activity 3.3.2
Solve in set of real numbers the following equations by completingthe square


In fact,

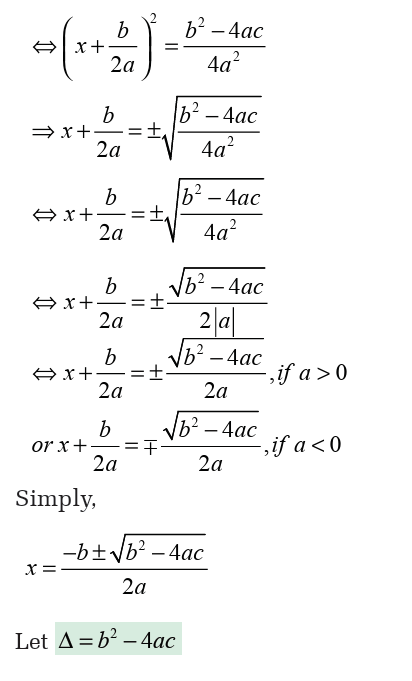

As we saw it, in this equation the sum of two roots is 7 and the product
is 10. To find those roots we can think about two numbers such thattheir sum is 7 and their product is 10. Those numbers are 2 and 5. Thus
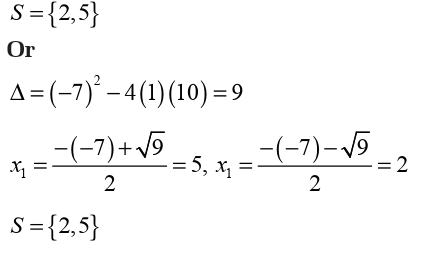

Factor form of a quadratic expression
Activity 3.3.4
In each of the following, remove brackets and discuss about theresult and original form.




So, the basic process is to check that the equation is reducible to a
quadratic form, then make a quick substitution to turn it into a
quadratic equation. In most cases, to make the check that it’s reducible
to quadratic form, all we really need to do is to check that one of theexponents is twice the other.
b) Nested radicals
Activity 3.3.6


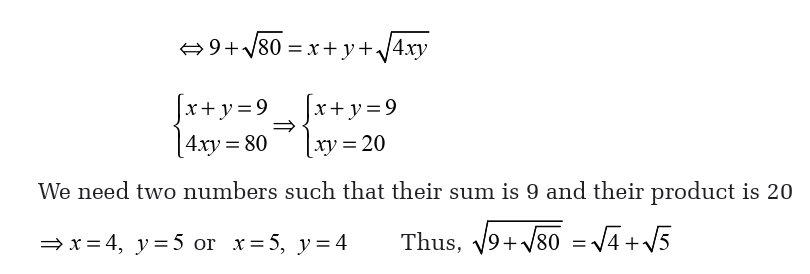

c) Irrational equations
Activity 3.3.7Consider the following equation
1. Square both sides of the equation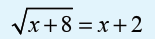
2. Solve the obtained equation
3. Verify that the obtained solutions are solution of the original
equation and then give the solution set of the original equation
(given equation)
Irrational equation is the equation involving radical sign. We will see
the case the radical sign is a square root.
To solve an irrational equation, follow these steps:
a) Isolate a radical in one of the two members and pass it to another
member of the other terms which are also radical.
b) Square both members.
c) Solve the equation obtained.
d) Check if the solutions obtained verify the initial equation.
e) If the equation has several radicals, repeat the first two steps of theprocess to remove all of them.

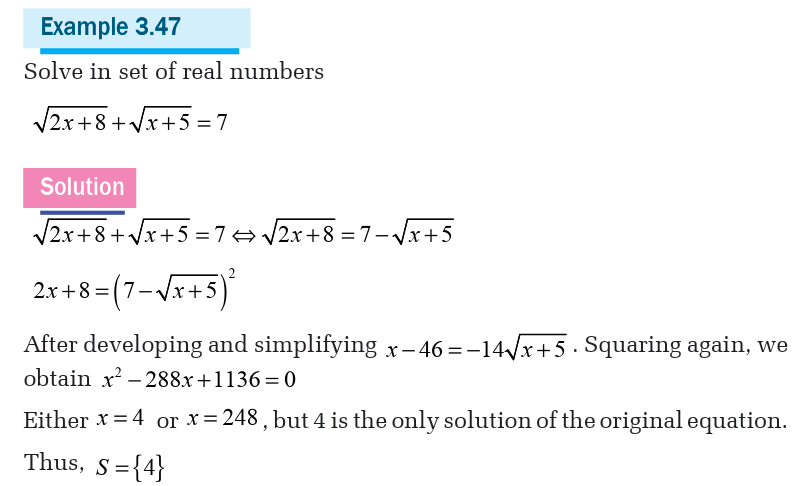
We saw how to solve the inequality product like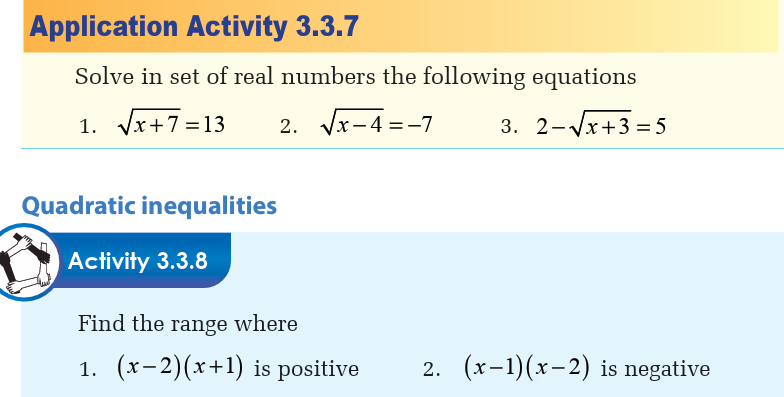
(ax+b)(cx+d)>0. If we find the product of the left hand side, the result
will be a quadratic expression of the form (ax2+bx+c).
Then to solve the inequality of the second degree like ax2+bx+c>0 we
need to put the expression ax2+bx+c in factor form and use the method
to solve inequality product.
If the expression to be transformed in factor form has no factor form,we find its sign by replacing the unknown by any chosen real number.
We may find that the expression is always positive or always negative.
If the expression to be transformed in factor form has a repeated root,
it is zero at that root and positive or negative elsewhere depending oncoefficient of x2.


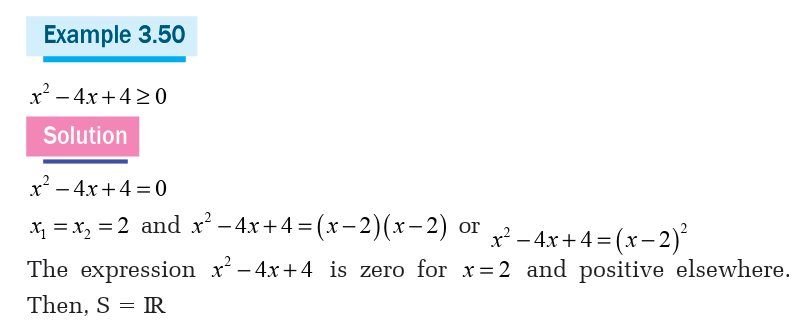


3.4. Applications
Activity 3.4.1
1. Explain how linear equations can be used in daily life1.
2. Give three examples of where you think quadratic equations are
useful in daily life
a) Supply and demand analysis
Market equilibrium is when the amount of product produced is equal
to the amount of quantity demanded. We can see equilibrium on a
graph when the supply function and the demand function intersect,
like shown on the graph below. Max can then figure out how to pricehis new lemonade products based on market equilibrium.
Example 3.53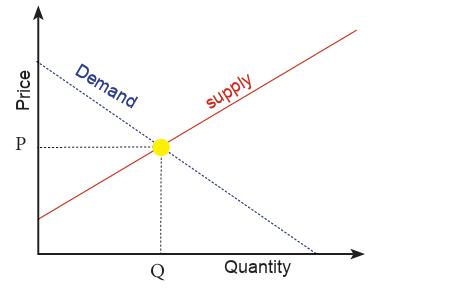
Assume that in a competitive market the demand schedule is and the
supply schedule is p=60+0.4q (p=price, q=quantity). If the market is
in equilibrium then the equilibrium price and quantity will be where
the demand and supply schedules intersect. As this will correspond to
a point which is on both the demand schedule and the supply schedule
the equilibrium values of p and q will be such that both equations hold.To find the equilibrium quantity set 420- 0.2q = 60 + 0.4q
b) Linear motion
Linear motion is a motion along a straight line, and can therefore be
described mathematically using only one spatial dimension. The linear
motion can be of two types: uniform linear motion with constant
velocity or zero acceleration; non uniform linear motion with variablevelocity or non-zero acceleration.
Example 3.54
Some examples of linear motion are given below:
1. An athlete running 100m along a straight track
2. Parade of the soldiers
3. Car moving at constant speed
4. A bullet targeted from the pistol
5. A man swimming in the straight lane
6. Train moving in a straight track
7. Object dropped from a certain height
8. Balancing equation
c) Balancing equation
In chemistry, to balance the chemical equation we set the reactants andproducts equal to each other.
d)Health care
In medicine, equations are used for modelling medication situations
and solve related problems.
Example 3.56
NSHUTI works as a nurse. According to her daily schedule, she has
to give Medication dosage to 60 patients’ daily. One day she took 1
longer than the expected, and therefore she gave Medication dosage to
3patients less per hour than anticipated.How long did she expected to give Medication dosage to 60 patients?

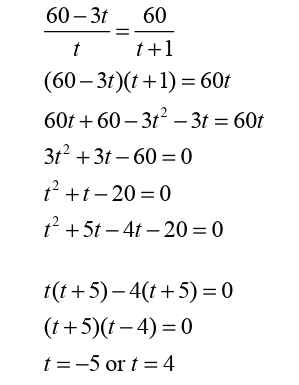
• Ignore the negative value as it is not valid.
• Therefore, she expected to give Medication dosage to 60 patients
in 4 hours.
e) Figuring out a profit
Sometimes calculating a business’ profit requires using a quadratic
function. If you want to sell something (even something as simple as
lemonade) you need to decide how many things to produce so thatyou’ll make a profit.
Example 3.57
Let us say that you’re selling glasses of lemonade, and you want to make
12 glasses. You know, however, that you’ll sell a different number of
glasses depending on how you set your price. At 100 francs per glass,
you are not likely to sell any, but at 10 francs per glass, you will probably
sell 12 glasses in less than a minute. So, to decide where to set your
price, use P as a variable. Let’s say you estimate the demand for glasses
of lemonade to be at 12 - P. Your revenue, therefore, will be the price
times the number of glasses sold: P(12 - P), or 12P–P2. Using however
much your lemonade costs to produce, you can set this equation equal
to that amount and choose a price from there.
f) Quadratics in Athletics
In athletic events that involve throwing things, quadratic equations are
highly useful.
Example 3.58
Say, for example, you want to throw a ball into the air and have your
friend catch it, but you want to give her the precise time it will take the
ball to arrive.
To do this, you would use the velocity equation, which calculates the
height of the ball based on a parabolic (quadratic) equation. So, say
you begin by throwing the ball at 3 meters, where your hands are. Also
assume that you can throw the ball upward at 14 meters per second, and
that the earth’s gravity is reducing the ball’s speed at a rate of 5 meters
per second squared. This means that we can calculate the height, using
the variable t for time, in the form of h=3+14t –5t2 . If your friend’s
hands are also at 3 metres in height, how many seconds will it take the
ball to reach her? To answer this, set the equation equal to 3 = h, and
solve for t. The answer is approximately 2.8 seconds.
g) Finding a Speed
Quadratic equations are also useful in calculating speeds. Avid kayakers,
for example, use quadratic equations to estimate their speed when goingup and down a river.
Example 3.59
Assume a kayaker is going up a river, and the river moves at 2 km/hr.
Say he goes upstream -- against the current -- at 15 km, and the trip takes
him 3 hours to go there and return. Remember that time = distance /
speed. Let v = the kayak’s speed relative to land, and let x = the kayak’s
speed in the water. So, we know that, while traveling upstream, the
kayak’s speed is v = x - 2 (subtract 2 for the resistance from the river
current), and while going downstream, the kayak’s speed is v = x + 2.
The total time is equal to 3 hours, which is equal to the time goingupstream plus the time going downstream, and both distances are 15km.
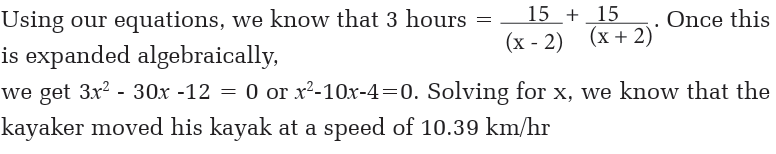
Application Activity 3.4.1
1) A pot of water has a temperature of 250c How many degrees should youraise the temperature to boil the water at 1000c

he high and low production levels during the month.
Unit summary
1. An equation is statement that the values of two mathematical
expressions are equal while an inequality is a statement that thevalues of two mathematical that are not equal.
3. To solve real life problems, follow the following steps: • Identify the variable and assign symbol to it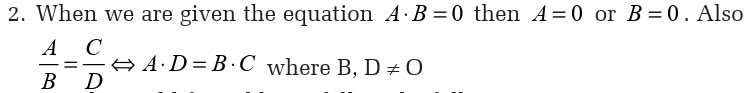
• Write down the equation
• Solve the equation
• Interpret the result. There may be some restrictions on thevariable.
Algebraically, there are three methods for solving this system: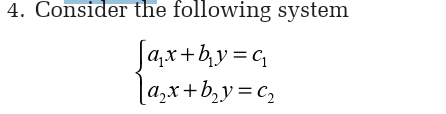
combination method, substitution method and Cramer’s rule. Some
systems of linear equations can be solved graphically. To do this,
follow the following steps:
• Find at least two points for each equation.
• Plot the obtained points in xy plane and join these points to
obtain the lines. Two points for each equation give one line.
• The point of intersection for two lines is the solution for thegiven system

9. Irrational equation is the equation involving radical sign. We solve
irrational equations by squaring both sides. By substituting all
obtained solutions in the given equation, those which dont satisfy
the given equation are rejected.
10. Application
Supply and demand analysis
Market equilibrium is when the amount of product produced is equal
to the amount of quantity demanded. Max can then figure out how to
price his new lemonade products based on market equilibrium.
Linear motion
Linear motion is a motion along a straight line, and can therefore be
described mathematically using only one spatial dimension.
Balancing equation
In chemistry, to balance the chemical equation we set the reactants
and products equal to each other.
Calculating Areas
People frequently need to calculate the area of things like rooms,
boxes or plots of land.
Figuring Out a Profit
Sometimes calculating a business’ profit requires using a quadratic
function. If you want to sell something (even something as simple as
lemonade) you need to decide how many things to produce so that
you’ll make a profit.
Quadratics in Athletics
In athletic events that involve throwing things, quadratic equations
are highly useful.
Finding a Speed
Quadratic equations are also useful in calculating speeds. Avid
kayakers, for example, use quadratic equations to estimate theirspeed when going up and down a river.

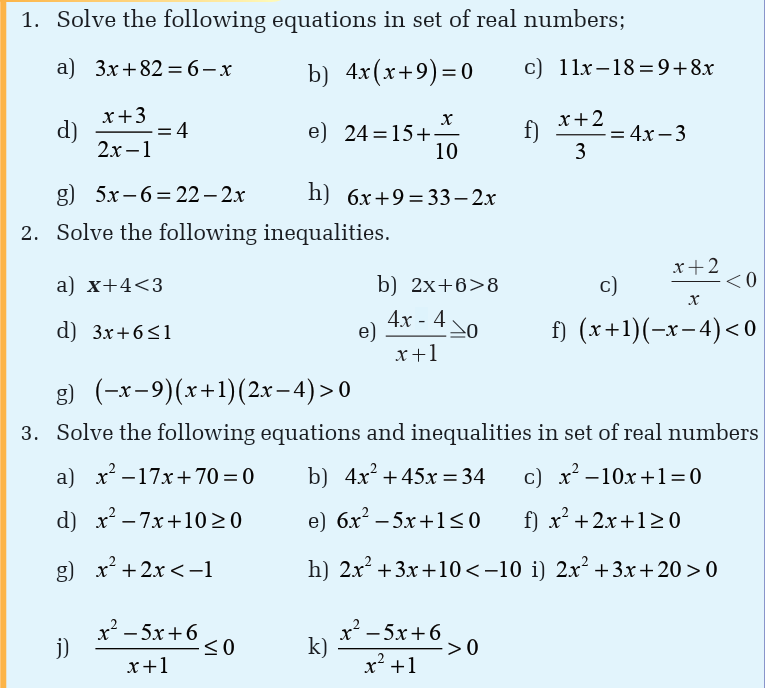
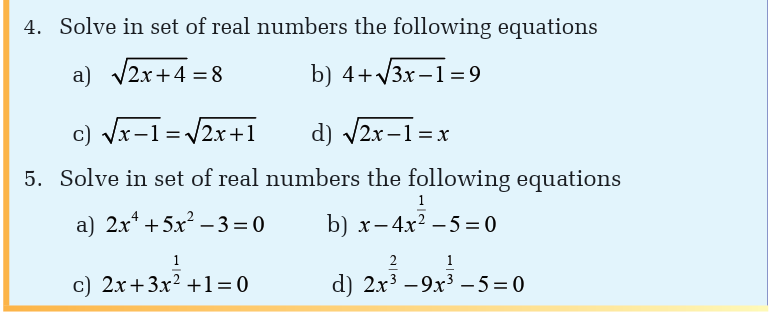
7. The senior classes at High School A and High School B planned separate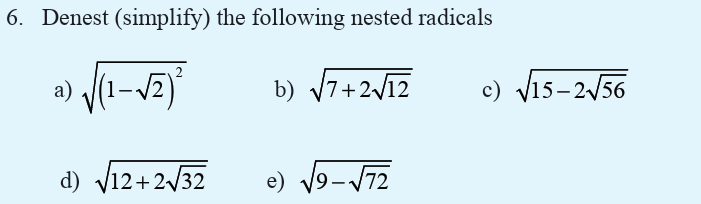
trips to Akagera National Park. The senior class at High School A rented
and filled 1 van and 6 buses with 372 students. High School B rented
and filled 4 vans and 12 buses with 780 students. Each van and each bus
carried the same number of students. How many students can a van carry?
How many students can a bus carry?
8. Brenda’s school is selling tickets to a spring musical. On the first day of
ticket sales the school sold 3 senior citizen tickets and 9 child tickets for a
total of $75. The school took in $67 on the second day by selling 8 senior
citizen tickets and 5 child tickets. What is the price each of one senior
citizen ticket and one child ticket?
9. A number is divided into two parts, such that one part is 10 more than the
other. If the two parts are in the ratio 5 : 3, find the number and the two
parts.
10. Robert’s father is 4 times as old as Robert. After 5 years, father will be
three times as old as Robert. Find their present ages.
11. The sum of two consecutive multiples of 5 is 55. Find these multiples.
12. The difference in the measures of two complementary angles is 12°. Find
the measure of the angles.
13. The cost of two tables and three chairs is $705. If the table costs $40 more
than the chair, find the cost of the table and the chair.
14. The velocity v m/s of a ball thrown directly up in the air is given by v =
20 – 5t, where t is the time in seconds. At what times will the velocity be
between 5 m/s and 15 m/s?
15. A rectangular room fits at least 7 tables that each have 1 square meter of
surface area. The perimeter of the room is 16 m. What could the width and
length of the room be?
16. A picture has a height that is 4/3 of its width. It is to be enlarged to have an
area of 192 square metres. What will be the dimensions of the enlargement?
17. The product of two consecutive negative integers is 1122. What are
the numbers?
18. A garden measuring 12 meters by 16 meters is to have a pedestrian pathway
installed all around it, increasing the total area to 285 square meters. What
will be the width of the pathway?
19. You have to make a square-bottomed, unlidded box with a height of three
metres and a volume of approximately 42 cubic metres. You will be taking
a piece of cardboard, cutting three- metres squares from each corner,
scoring between the corners, and folding up the edges. What should be thedimensions of the cardboard, to the nearest quarter metres?
Unit 4 :Polynomial, Rational and irrational functions
4.0 Introductory activity
1. Consider the following sentences:
i. The function of the heart is to pump blood
ii. Last Saturday, my sister got married; the arrangement of chairs in the
main hall was in function of the number of guests.
iii. The area of a square is function of the length of its side.
Explain what is meant by the word “Function” in each of the three sentences
above.
2. Any function involves at least two variables. Identify the “independentvariable” and the “dependent variable” in the following functions:
4. If we agree that the set of all possible values, the independent variable
can assume is called the “ Domain” of the function and the set of all
possible values, the dependent value can assume is called the “Range”
of the function, determine the range and the domain of each of the
functions in part (2) above.
Objectives
After completing this unit, I will be able to:
» Demonstrate an understanding of operations on
polynomials, rational and irrational functions, and
find the composite of two functions.
» Identify a function as a rule and recognize rules that
are not functions.
» Determine the domain and range of a function
» Find whether a function is even , odd , or neither
» Construct composition of functions.
4.1. Generalities on numerical functions
Activity 4.1
In the following arrow diagram, for each of the elements of set A,state which element of B is mapped to it.
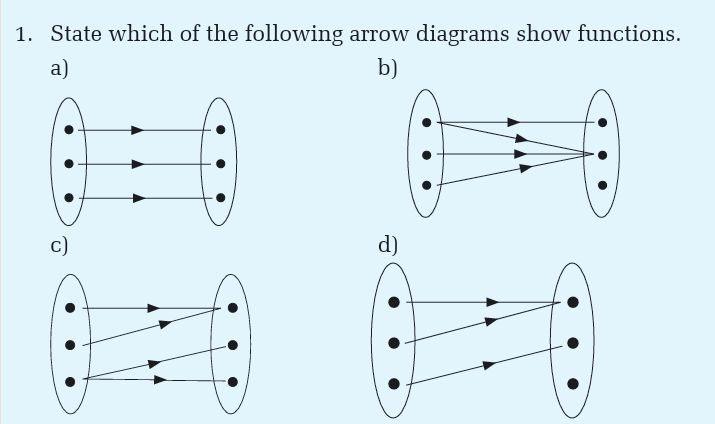
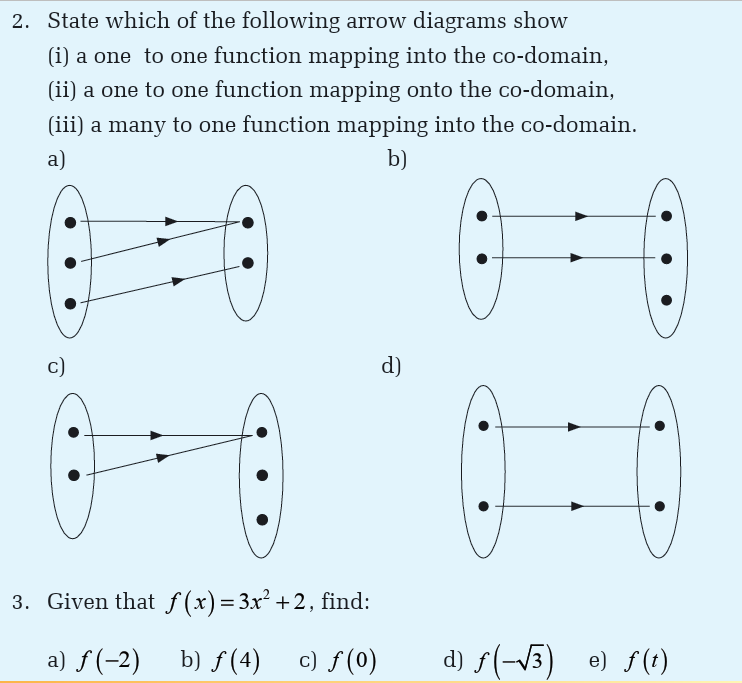
A function is a rule that assigns to each element in a set A one and only one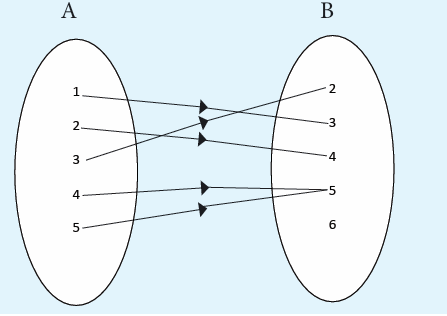
element in set B. We can even define a function as any relationship which
takes one element of one set and assigns to it one and only one element of
second set. The second set is called a co-domain. The set A is called thedomain, denoted by Domf.
Example 4.1
Four children, Ann, Bob, Card and David, are given a spelling test whichis market out of 5; their marks for the test are shown in the arrow diagram:
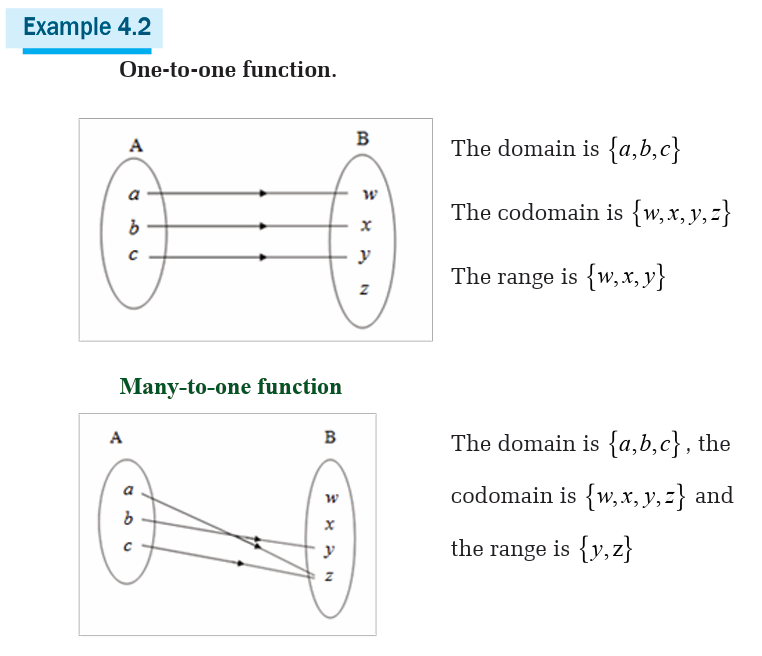
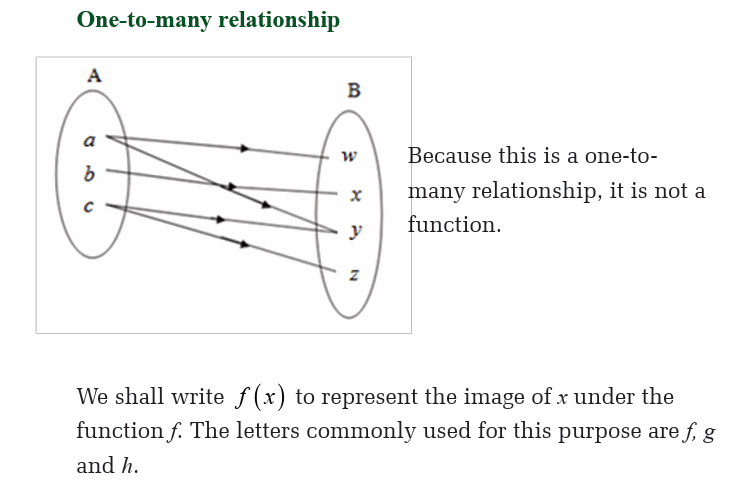
Functions for which each element of the domain is associated onto a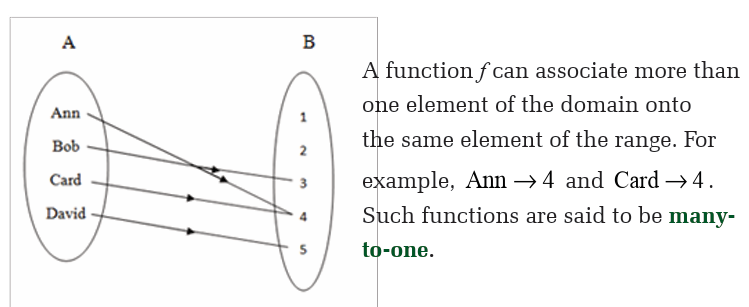
different element of the range are said to be one-to-one. Relationships
which are one-to-many can occur, but from our preceding definition, theyare not functions.


4. You have ever followed a speech talking about NDI
UMUNYARWANDA . You have been said that Rwandans have
been divided and now they want to be unified. From the types of
relationship (in Mathematics), complete this sentence: We have
been made……to……by colonialists, NDI UMUNYARWANDA ismaking us……to……
4.2. Classification of functions
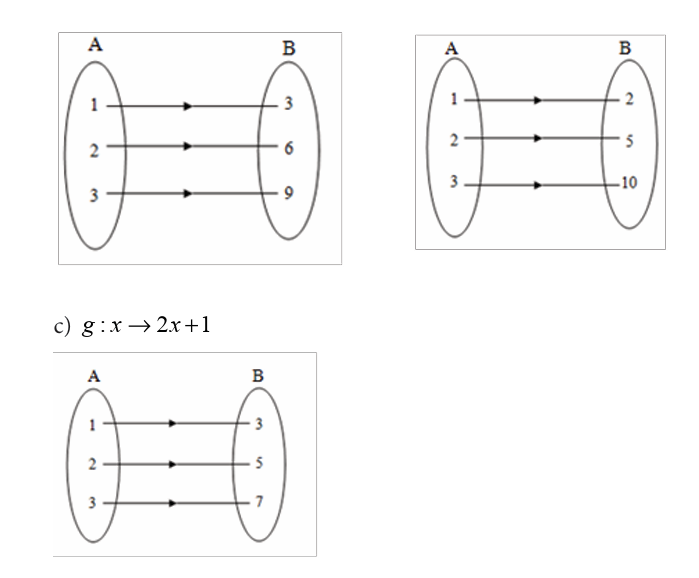
Activity 4.2
State which of the following functions is a polynomial, rationalor irrational function
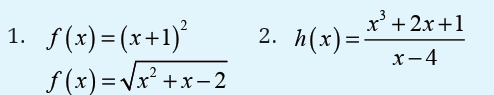
a) Constant function
A function that assigns the same value to every member of its domain iscalled a constant function C.


Application Activity 4.2
Observe the given functions and categorize them into polynomial,rational or irrational functions.
4.3. Finding domain of definition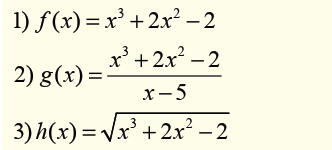
Activity 4.3.1
Case 3: The given function is an irrational function
Activity 4.3.2
For each of the following functions, give a range of values of thevariable x for which the function is not defined.




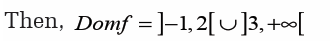
Example 4.18
The following functions map an element x of the domain onto its image y.
For each of the three functions below, state
(i) the domain for which the function is defined,
(ii) the corresponding range of the function,(iii) whether the function is one-to-one or many-to-one.
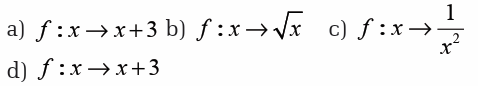


4.4. Operations on functions
Activity 4.4
Just as numbers can be added, subtracted, multiplied and divided to produce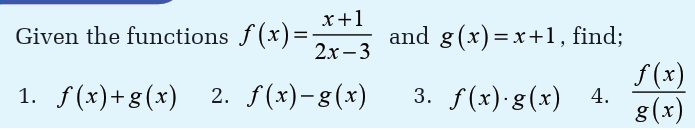
other numbers, there is a useful way of adding, subtracting, multiplying
and dividing functions to produce other functions. These operations aredefined as follows:
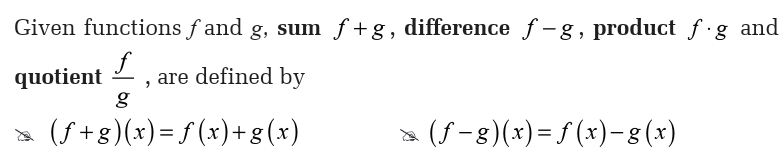






4.5 Parity of function
Odd and even functions
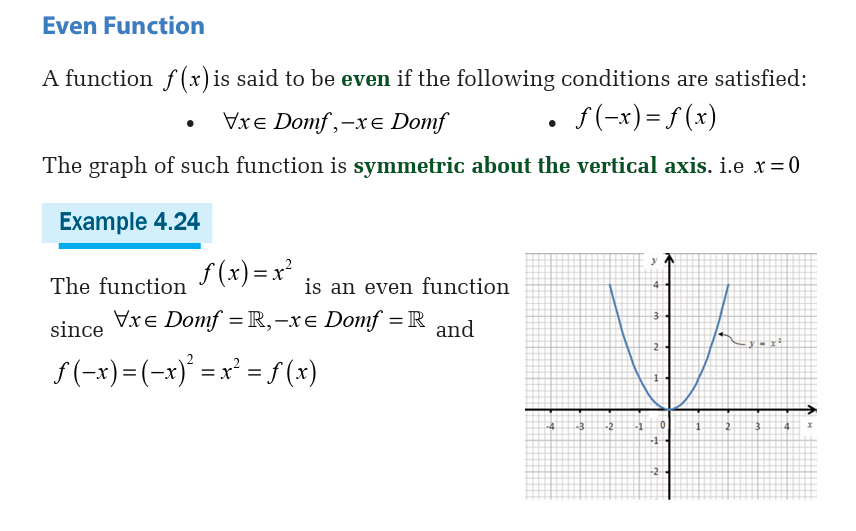
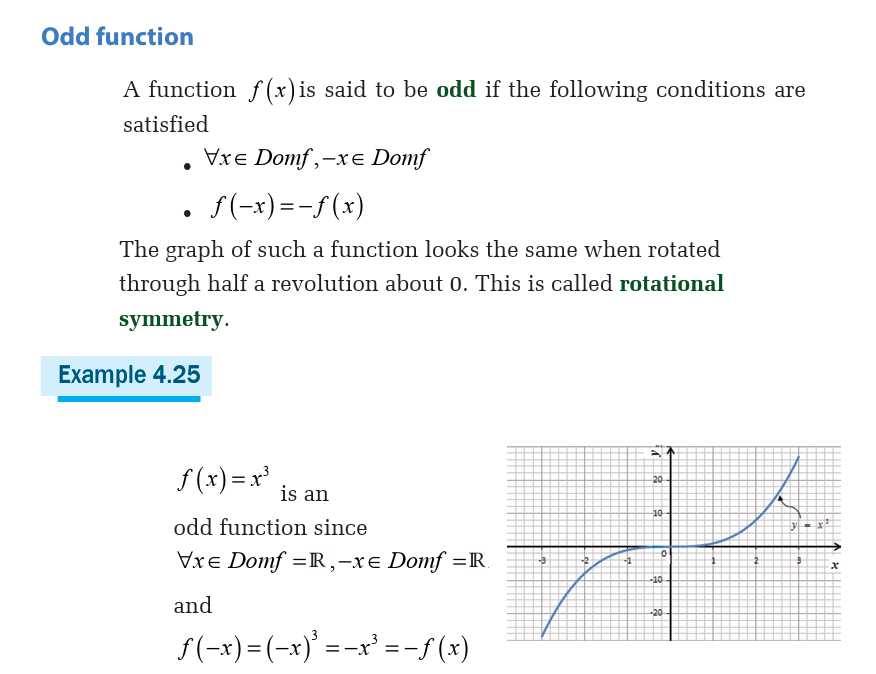
Activity 4.5

4.6. Factorization of polynomials
Activity 4.6
For each expression above, identify the common factors for both terms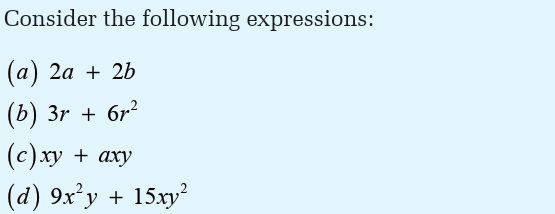
and rewrite the expression in factor form. Compare your results with
those of other classmates.
In arithmetic, you are familiar with factorization of integers into primefactors.

a) How many terms does each result have?
b) Find out the common characteristics for the all above expressions.What is the highest and lowest exponent for the variable
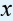 in all expressions?
in all expressions?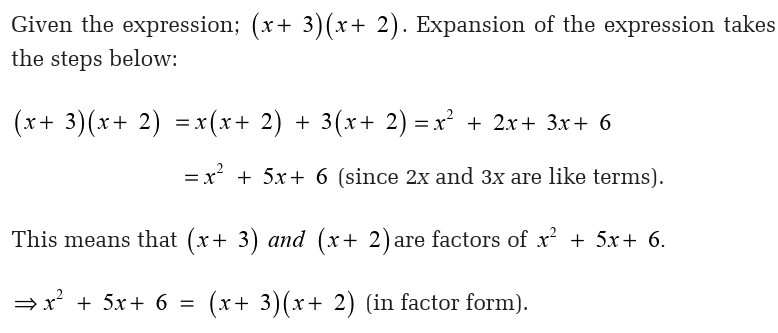
a) The coefficient of the highest degree of this trinomial is 1,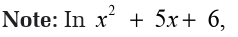
b) The coefficient of the linear term is 5, the sum of the constant terms
in the binomial factors, and
c) The constant term is 6, the product of the constant terms in the
binomial factors.Generally,
1. List all the possible pairs of integers whose product equals the
constant term.
2. Identify the only pair whose sum equals the coefficient of the linear
term.
3. Rewrite the given expression with the linear term split as per the
factors in 2 above.
4. Factorise your new expression by grouping, i.e. taking two terms at a
time.5. Check that the factors are correct by expanding and simplifying.
Example 4.27
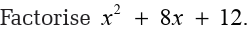

Note: Since all the terms in the example are positive, the negative pairs of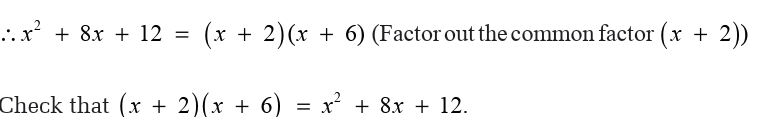
factors of 12 could have been omitted altogether.
Note that:
• If the third term in the split form of the expression is negative, wefactor out the negative common factor.
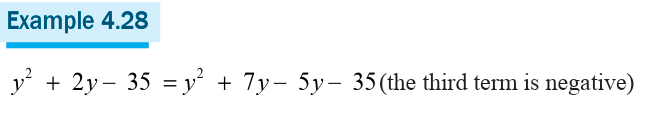
Each binomial expansion has three terms
The first term is the square of the first term of the binomial
The third term is the square of the second term of the given binomialThe middle term is twice the product of the two terms of the binomial
Remarks
If a trinomial is a perfect square,
1. The first term must be a perfect square.
2. The last term must be a perfect square.
3. The middle term must be twice the product of numbers that weresquared to give the first and last terms.


4.8. Graphs of linear and quadratic functions
Activity 4.8 1.Copy and complete the tables below.
2. Use the coordinates from each table to plot the graphs on separate
Cartesian planes.3. What is your conclusion about the shapes of the graphs?
4.8.1 Linear functions
Definition of linear function

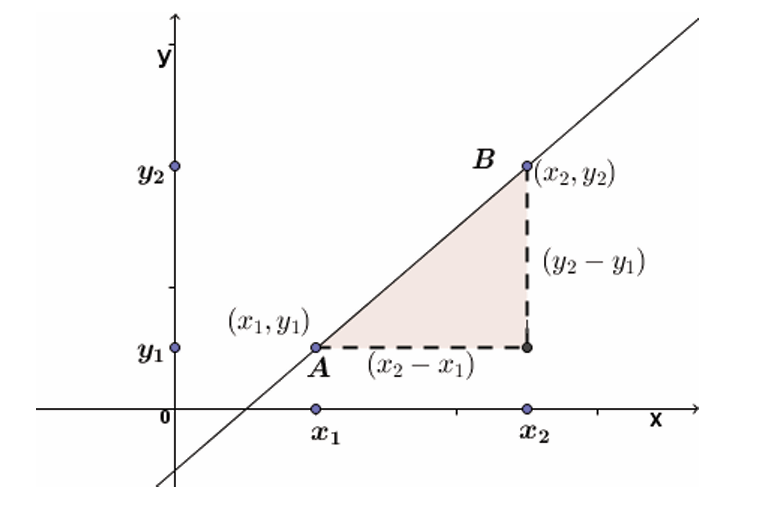
In the Cartesian plane, the gradient of a line is the measure of its slope
or inclination to the x-axis. It is defined as the ratio of the change in
y-coordinate (vertical) to the change in the x-coordinate (horizontal).
When drawing a graph of a linear function, it is sufficient to plot only
two points and these points may be chosen as the x and y intercepts of
the graph. In practice, however, it is wise to plot three points. If the three
points lie on the same line, the working is probably correct, if not you havea chance to check whether there could be an error in your calculation.
From the table the coordinates (x, y) are
When drawing the graph, the dependent variable is marked on the vertical axis
generally known as the y – axis. The independent variable is marked on the
horizontal axis also known as the OX --axis
4.8.2 Quadratic function
Definition of quadratic functionA polynomial equation in which the highest power of the variable is 2 is
Table of values are used to determine the coordinates that are used to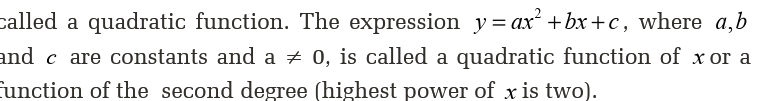
draw the graph of a quadratic function. To get the table of values, we
need to have the domain (values of an independent variable) and then
the domain is replaced in a given quadratic function to find range (values
of dependent variables). The values obtained are useful for plotting the
graph of a quadratic function. All quadratic function graphs are parabolicin nature

Graph of quadratic function
The graph of a quadratic function can be sketched without table of values
as long as the following are known.
• The vertex
• The x-intercepts• The y-intercept

4.9. Applications
Activity 4.9
Give three examples of where you think functions can be used in
daily life.
Polynomials are used to describe curves of various types; people use them
in the real world to graph curves. For example, roller coaster designers may
use polynomials to describe the curves in their rides. Polynomials can be
used to figure how much of a garden’s surface area can be covered with
a certain amount of soil. The same method applies to many flat-surface
projects, including driveway, sidewalk and patio construction.
Functions are important in medicine, building structures (houses,
businesses,…), vehicle design, designing games, to build computers
(formulas that are used to plug to computer programs), knowing how much
change you should receive when making a purchase, driving (amount of
gas needed for travel).
In the health field, polynomials are used for example to predict how
patients will metabolise medication over time. When painkillers move
through the bloodstream, enzymes start to break them down. Over time,the body moves more and more of the drug from the blood..



Unit summary
1. A function f is a rule that assigns to each element in a set A one and
only one element in set B. The second set is called a co-domain. The
set A is called the domain, denoted by Domf. The set of all possible
values of f(x) as x varies over the domain is called the range2. A function that is expressible as ratio of two polynomials is called



12. Polynomials are used to describe curves of various types; people
use them in the real world to graph curves. Functions are important
in calculating medicine, building structures (houses, businesses,…),
vehicle design, designing games, to build computers (formulas that
are used to plug to computer programs), knowing how much change
you should receive when making a purchase, driving (amount of gasneeded for travel).
End Unit Assesment
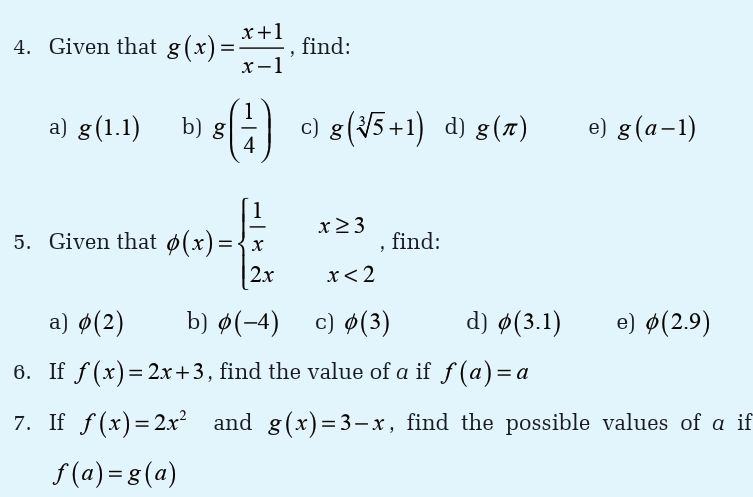

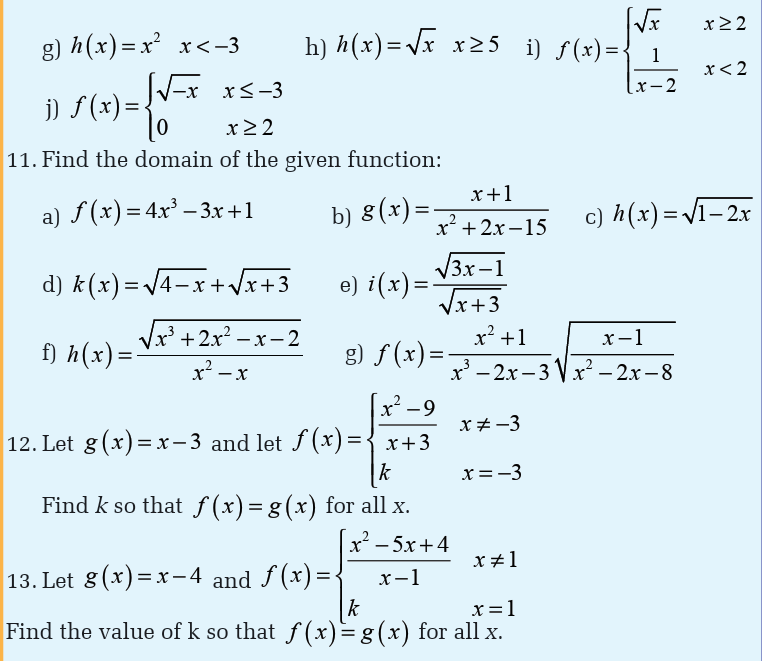

Unit 5 :Limits of polynomial, rational and irrational functions
5.0 Introductory activity
To find the value of a function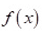 when x approaches 2, a student used
when x approaches 2, a student used a calculator and dressed a table as follows:
objectives
After completing this unit, I will be able to:
» Calculate limits of certain elementary functions.
» Apply informal methods to explore the concept of a limit
including one sided limits.
» Solve problems involving continuity.
» Use the concepts of limits to determine the asymptotes
to the rational and polynomial functions.» Develop calculus reasoning.
5.1. Concepts of limits
Neighbourhood of a real number
Activity 5.1.1
Study the following political map of Lesotho, Swaziland and
South Africa. What can you say about the boundaries of Lesotho
and Swaziland?What is the actual name of Swaziland?
A set N is called a neighbourhood of point p if there exists an open interval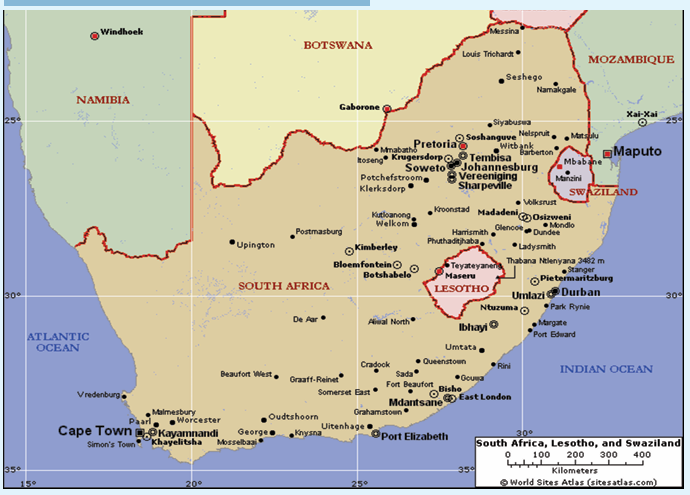
I such that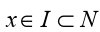 . The collection of all neighbourhoods of a point is
. The collection of all neighbourhoods of a point is
called the neighbourhood system at the point.
A deleted neighbourhood of a point p (sometimes called a puncturedneighbourhood) is a neighbourhood of p without p itself
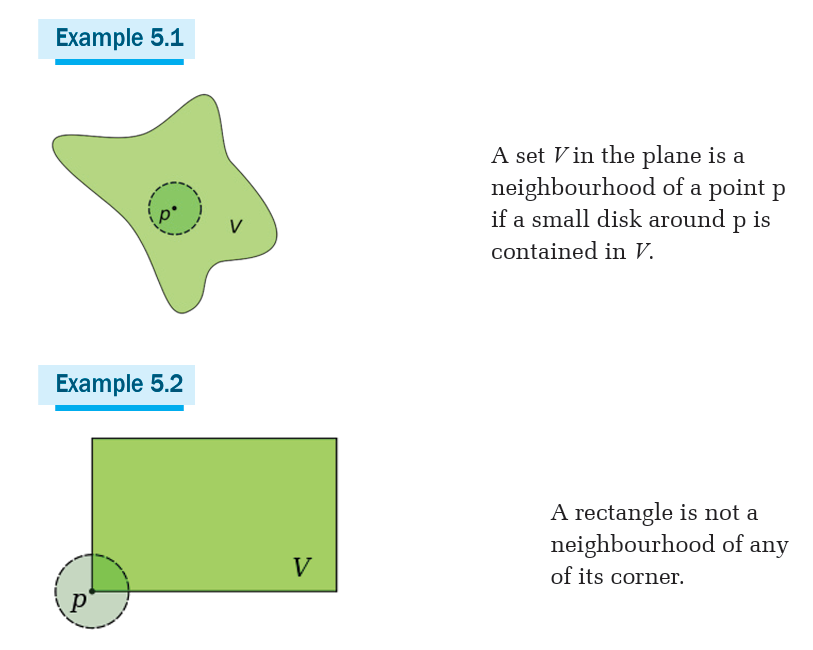
Application Activity 5.1.1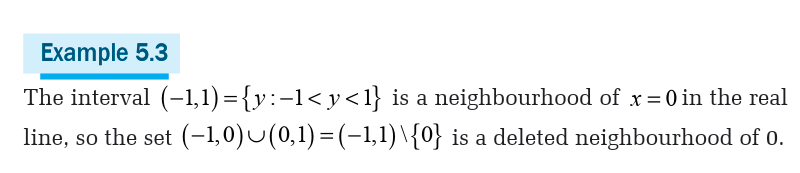
1. Apart from The Kingdom of Lesotho, give two examples of
countries or Cities in the world that are surrounded by a single
country or city.
2. Give three examples of intervals that are neighbourhoods of -5?
3. Is a circle a neighborhood of each of its points? Why?
4. Draw any plane and show three points on that plane for which
the plane is their neighborhood.
Note:
A deleted neighbourhood of a given point is not in fact a neighbourhood
of the point. The concept of deleted neighbourhood occurs in thedefinition of the limit of a function.
Limit of a functionActivity 5.1.2

To find limit of a function
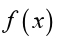 as x approaches a, first we need to
as x approaches a, first we need to
substitute that value a in the function and see what happens. The limitcan exist or not.



5.2. One sided limits
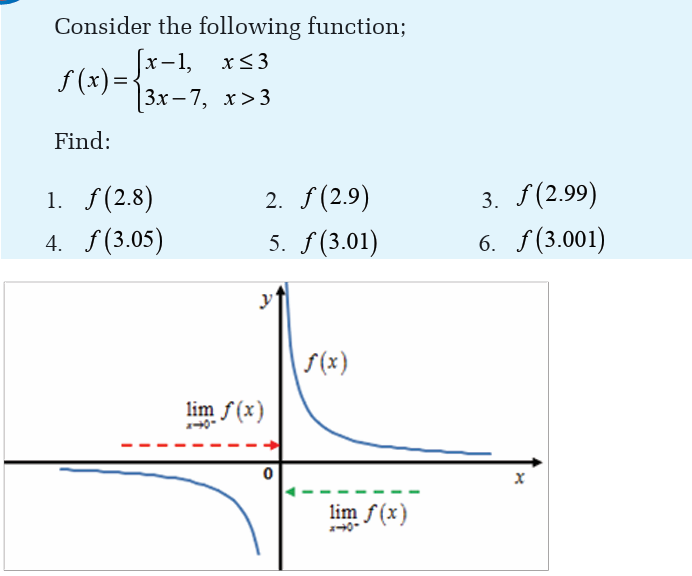
Activity 5.2




Infinite limits
A function whose values grow arbitrarily large can sometimes be said to
have an infinite limit. Since infinity is not a number, infinite limits arenot really limits at all but they provide a way of describing the behavior of



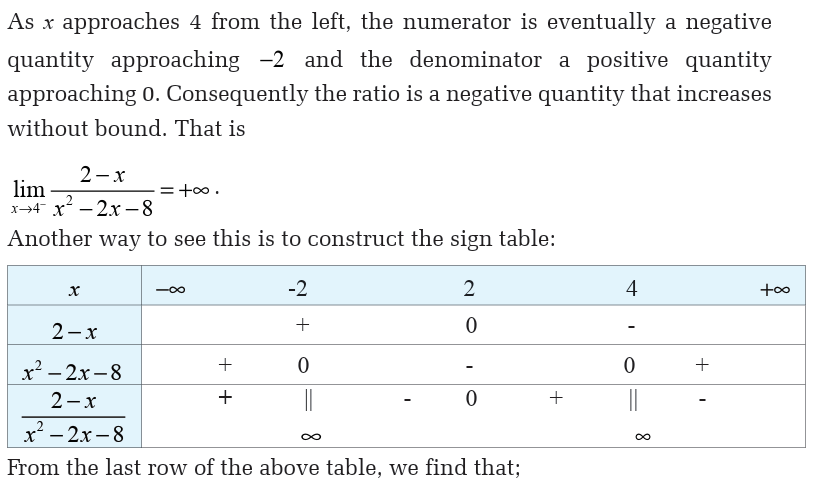


Beware!
So, we have dealt with almost every basic algebraic operation involvinginfinity. There are three cases that we have not dealt with yet. These are




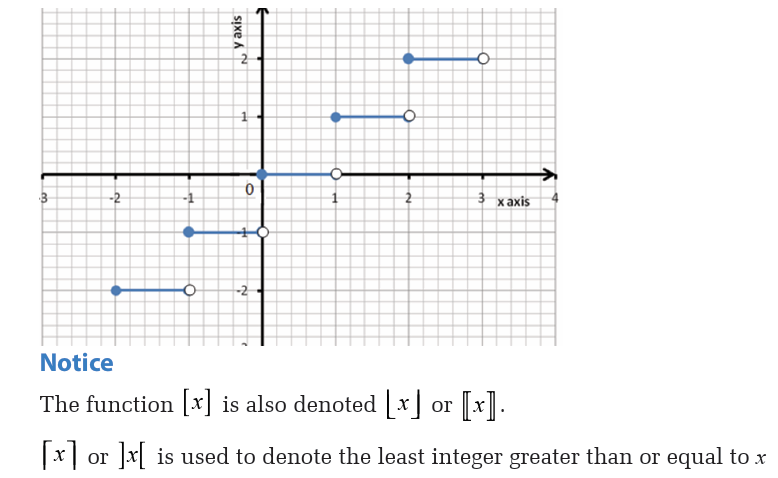
To find a limit graphically, we must understand each component of the
limit to ensure the graph is used properly to evaluate the limit.
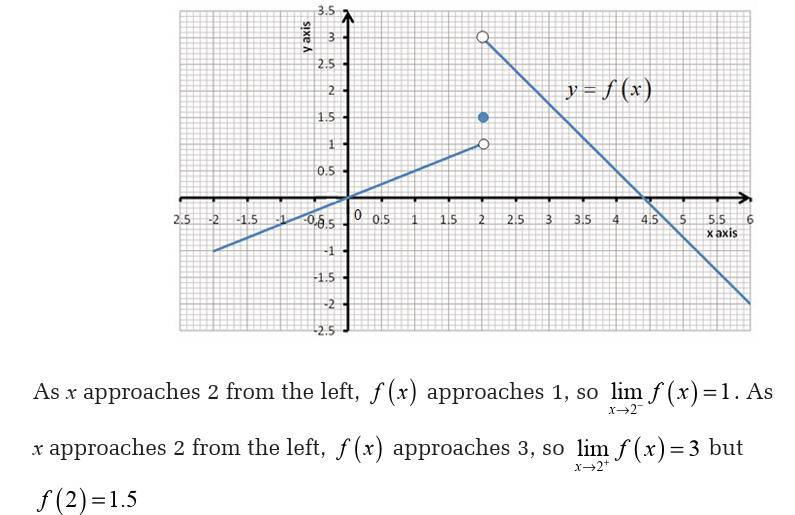
Example 23Let f be the function whose graph is shown below,
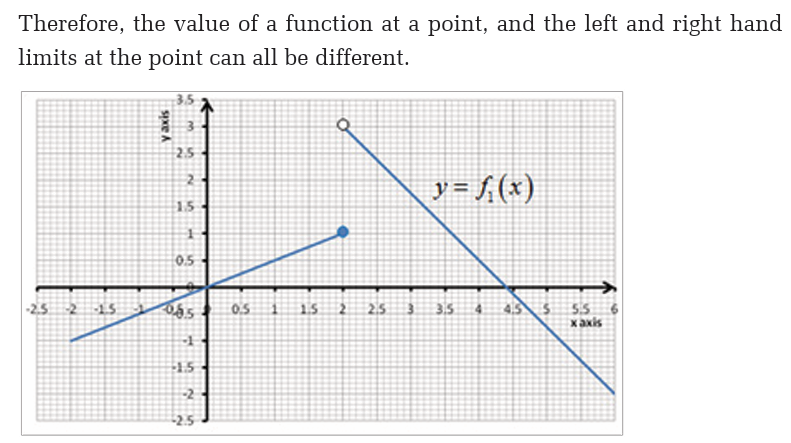
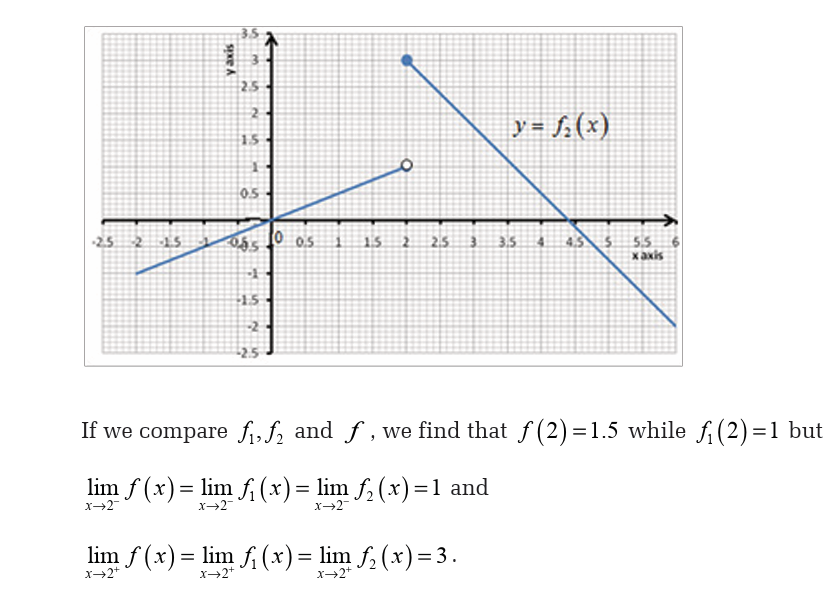
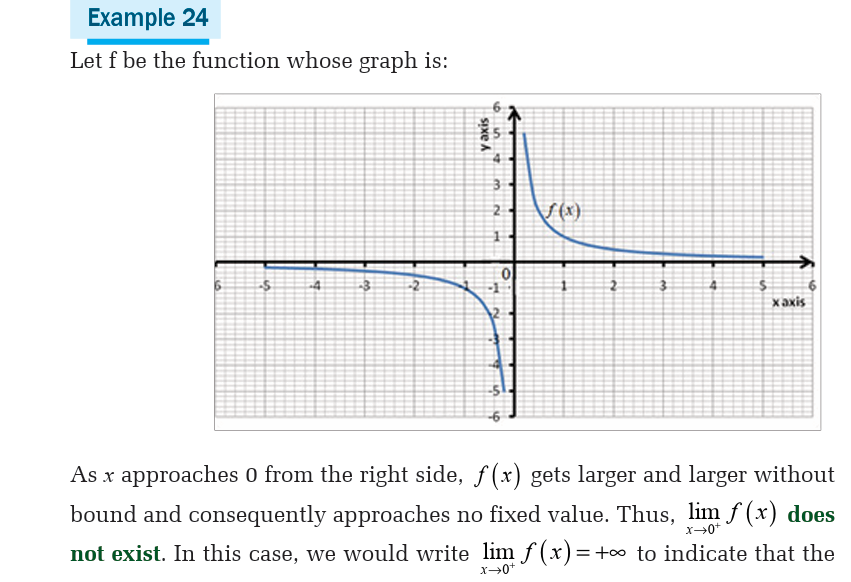

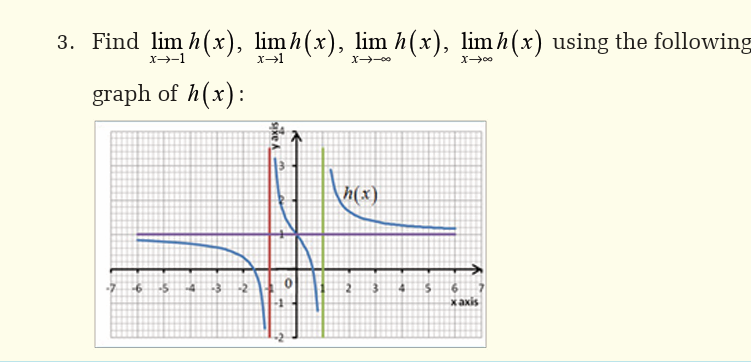
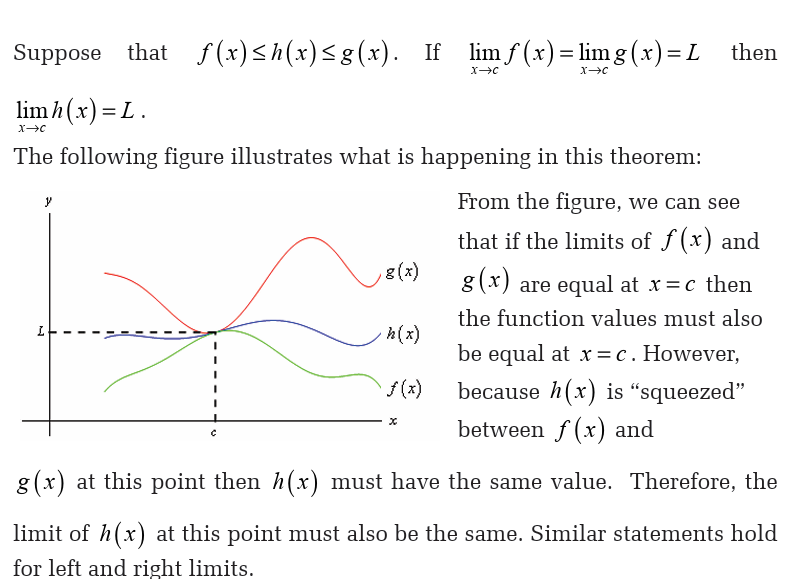
5.4. The squeeze theorem and operations on limits






5.5. Indeterminate cases



Or Since we have a rational function and degree of numerator is equal
to the degree of denominator, to find the limit as x tends to infinity, we
need to divide the coefficients of the highest degree for numerator anddenominator. That is the limit is given by
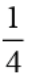
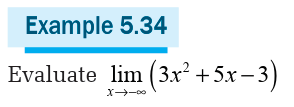








Note that the limits involving indeterminate form
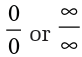
can be evaluated by successive derivatives of numerator and denominator.
This method is called L’Hôpital rule.We will see this in application of derivatives.




















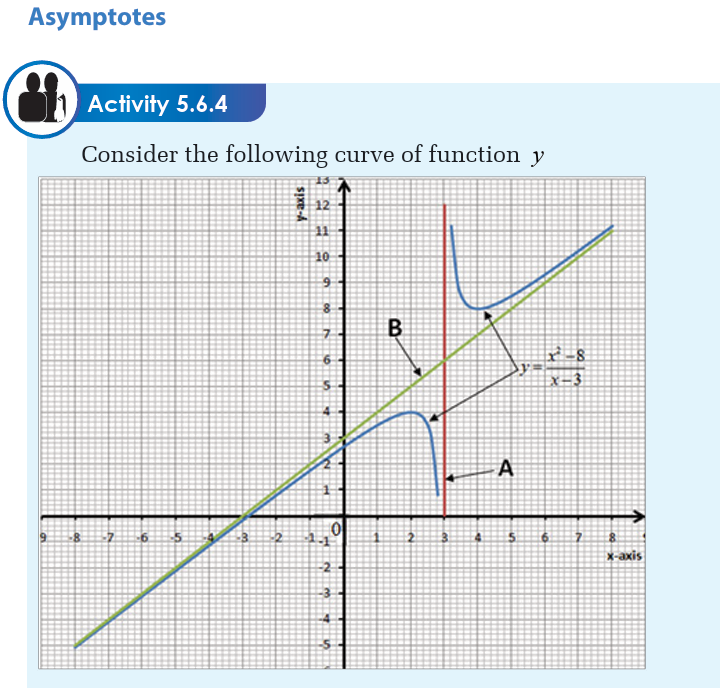
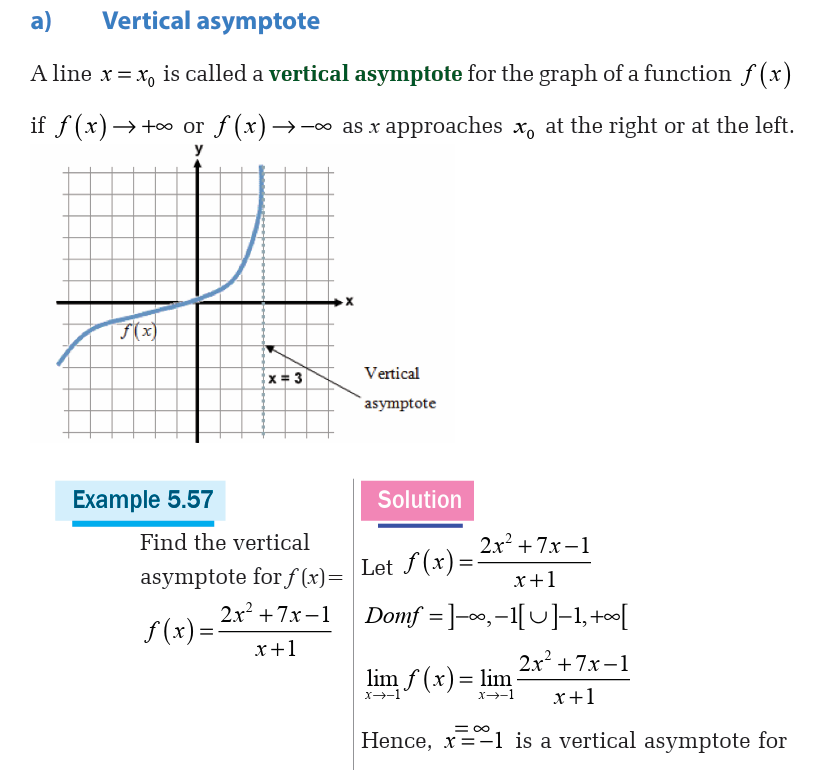
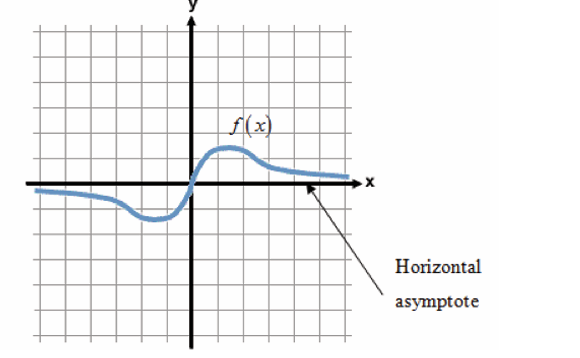
Types of asymptotes
There are three types of asymptotes:
• Vertical asymptote,
• Horizontal asymptote and• Oblique asymptote.
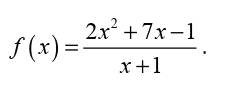







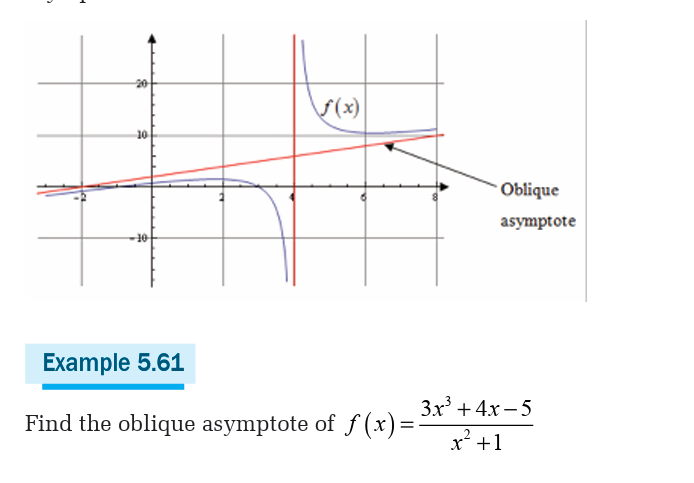









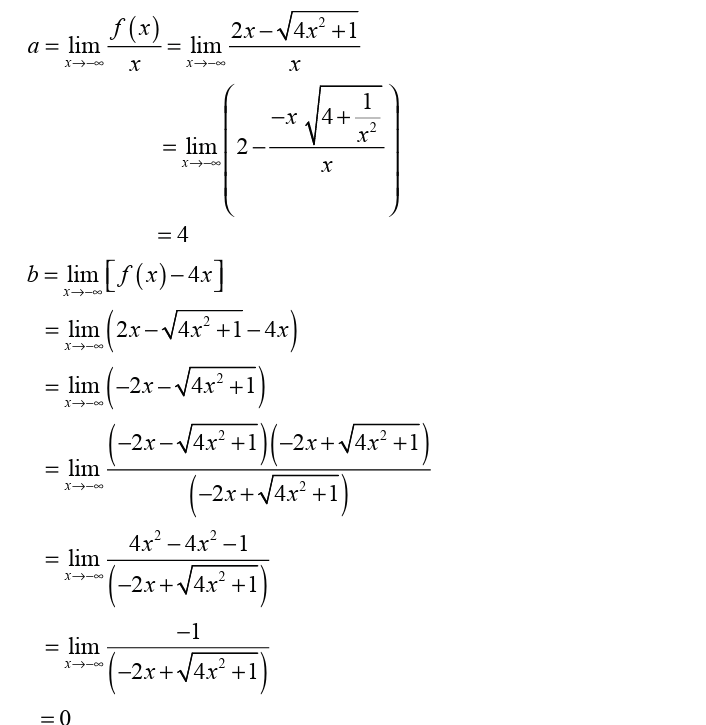



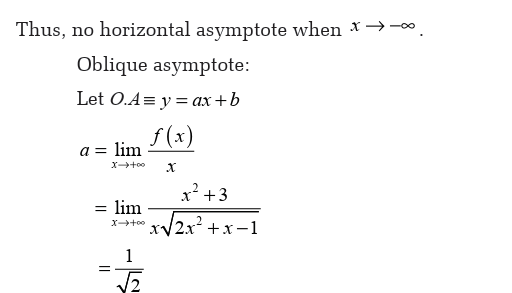
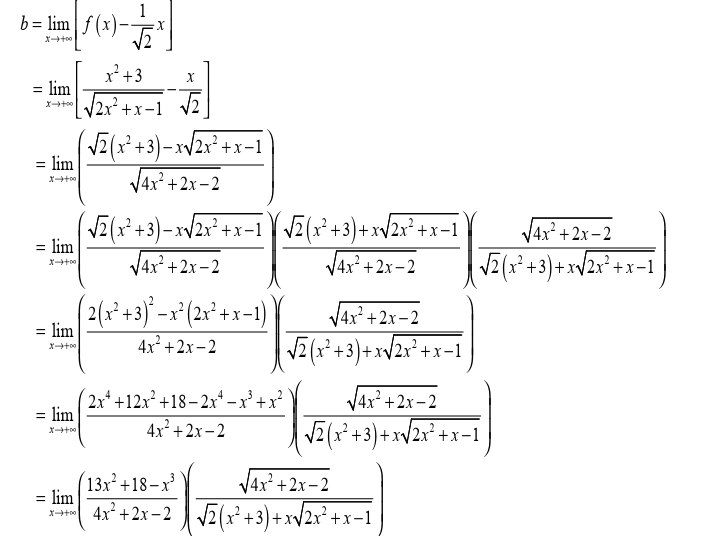
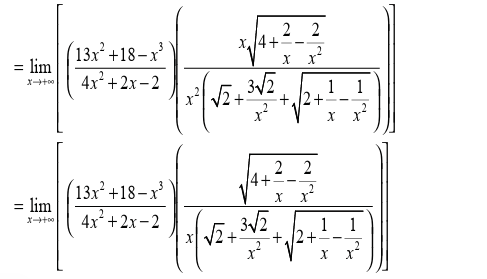
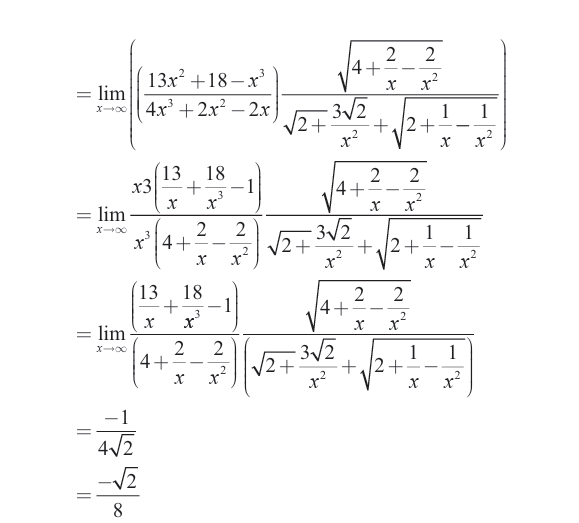



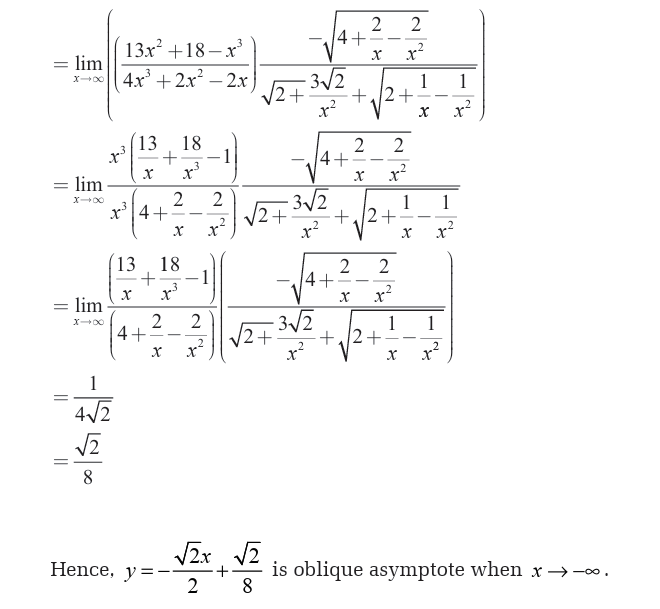


Limits can be applied in different fields in real life. In economics the
average cost per unit sold is calculated using limits.In physics, the velocity and acceleration are calculated using limits,etc.
1. Instantaneous rate of change of a function
The instantaneous rate of change of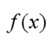 of at a, also called the rate of change of
of at a, also called the rate of change of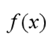 at a, is defined to be the limit of the average rate of change
at a, is defined to be the limit of the average rate of change
of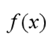 over shorter and shorter intervals around a.
over shorter and shorter intervals around a.
Since the average rate of change is a difference quotient of the form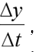
, the instantaneous rate of change is a limit of difference quotient. In practice,we often approximate a rate of change by one of these difference quotients.
2. Instantaneous velocity
Instantaneous velocity of a moving body is the limit of average velocityover an infinitesimal interval of time.
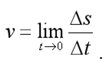

Unit summary








Unit 6 : Differentiation of polynomial, rational and irrational functions
6.0 Introductory activity
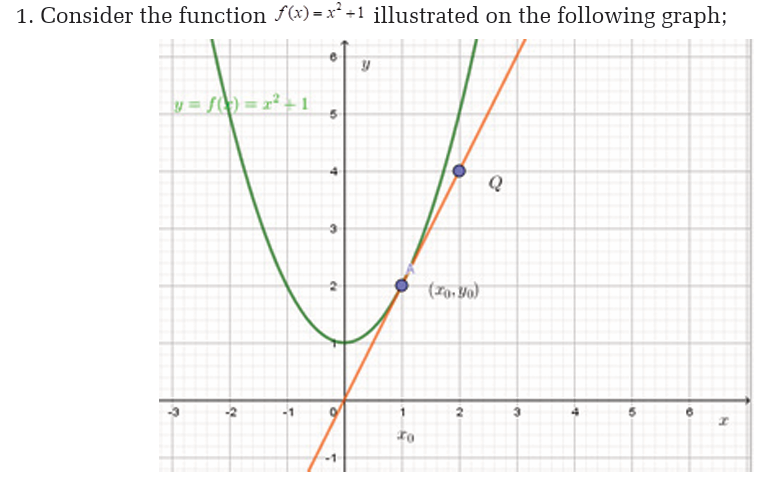
2) Go in library or computer lab, do research and make a short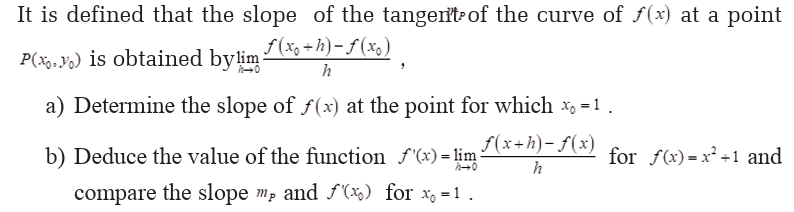
presentation on the following:
a. Derivative of a functionb. Find 2 examples of applications of derivatives.
objectives
After completing this unit, I will be able to:
» Use properties of derivatives to differentiate
polynomial, rational ad irrational functions
» Use first principles to determine the gradient of the
tangent line to a curve at a point.
» Apply the concepts of and techniques of
differentiation to model, analyze and solve rates or
optimization problems in different situations.
» Use the derivative to find the equation of a linetangent or normal to a curve at a given point.
6.1. Concepts of derivative of a function
Definition
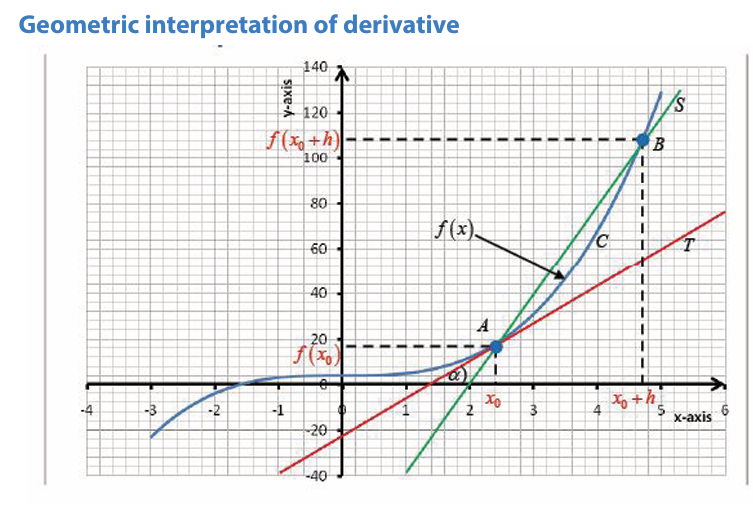
Activity 6.1.1Consider the following figure


provided that the limit exists.


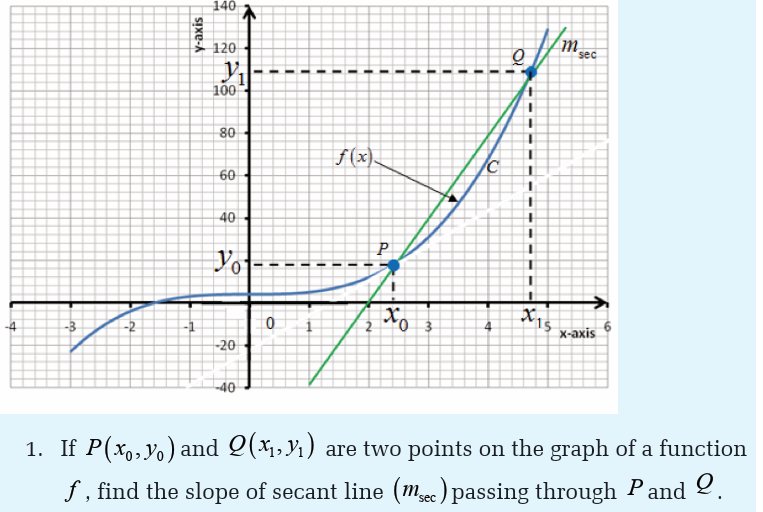
Right-hand and left-hand derivatives
Activity 6.1.2



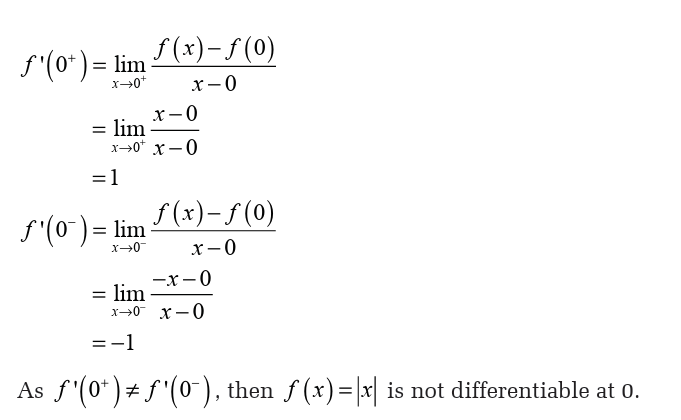














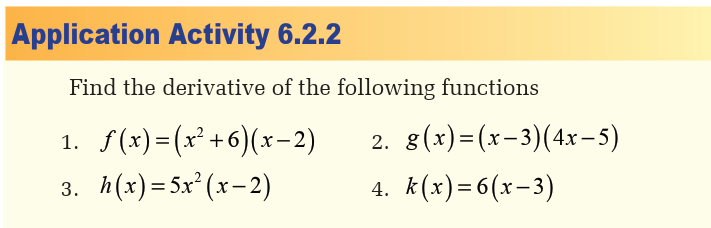





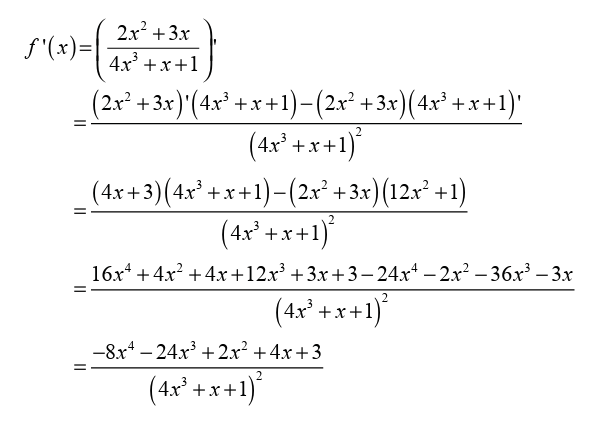




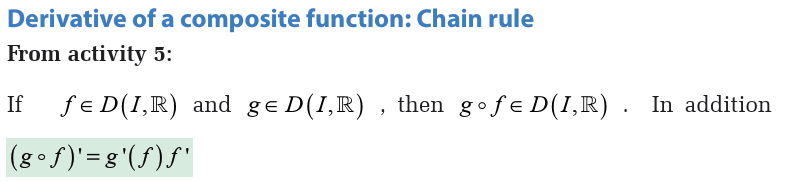








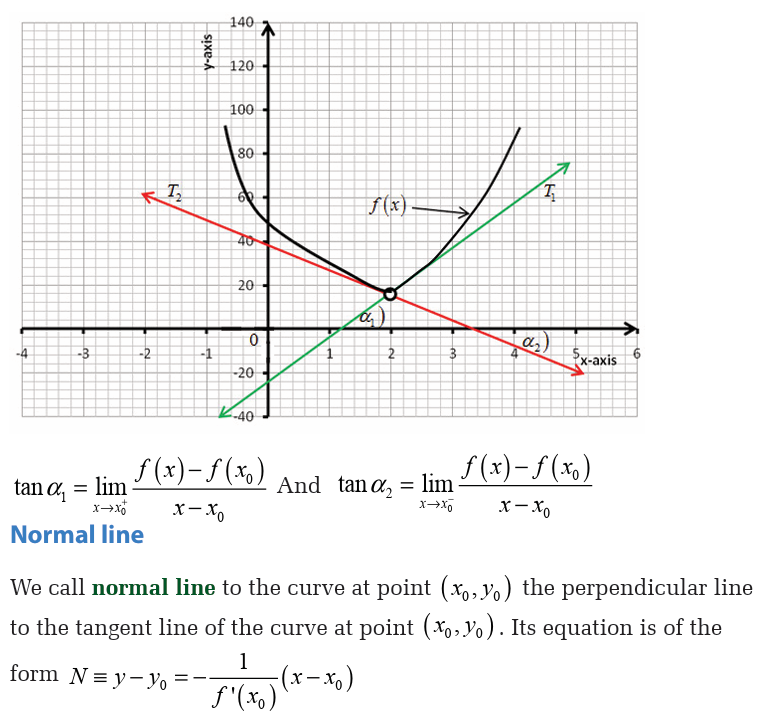
a) Find the point where the tangent line is parallel to the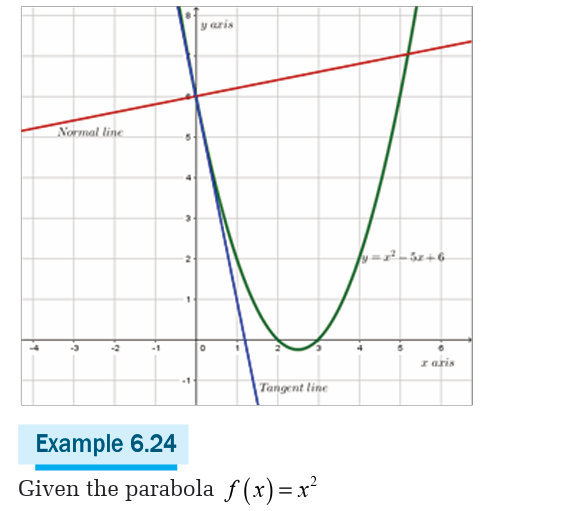
bisector of the first quadrant.
b) Find the tangent line to the curve of this function at point(2,4 )

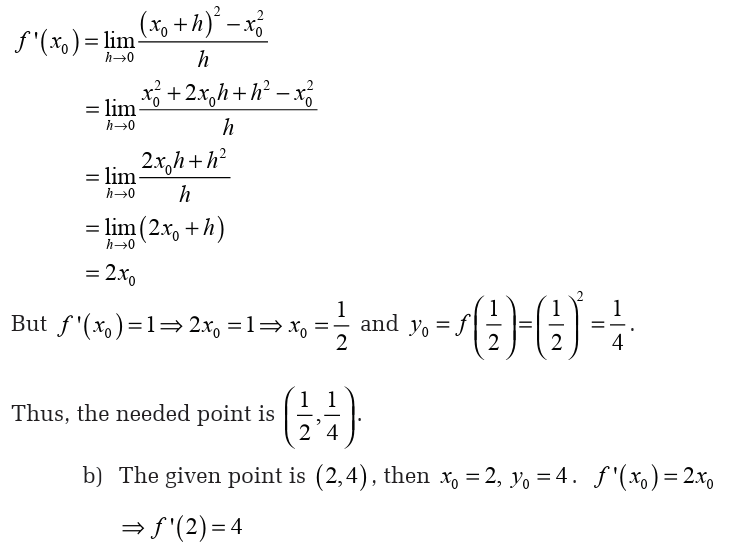

Rates of change
The purpose here is to remind ourselves one of the more important
applications of derivatives. That is the fact that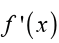 represents the rate
represents the rate
of change of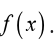



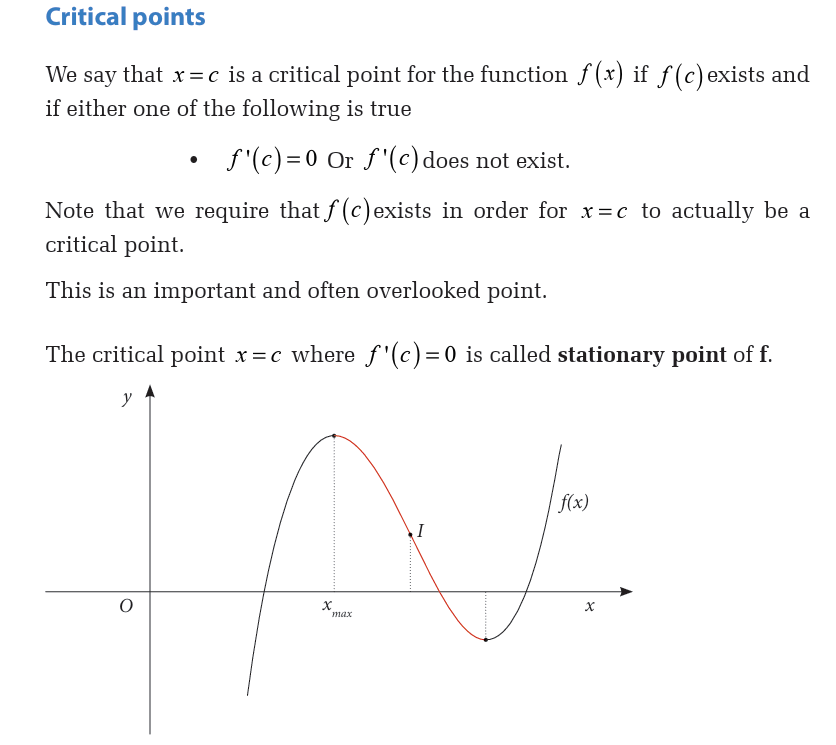

Now, our derivative is a polynomial and so will exist everywhere.
Therefore the only critical points will be those values of x which make thederivative zero. So, we must solve
Because this is the factored form of the derivative, it’s pretty easy to identify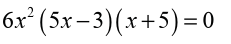
the three critical points. They are,
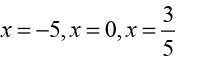
Example 6.29
Let us determine all the critical points for the function
To find the derivative, it’s probably easiest to do a little simplification before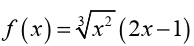
we actually differentiate. Let’s multiply the root through the parenthesis
and simplify as much as possible.
This will allow us to avoid using the product rule when taking thederivative.
We will need to be careful with this problem. When faced with a negative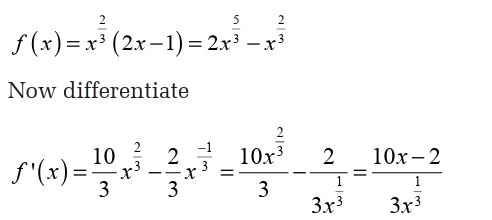
exponent it is often best to eliminate the minus sign in the exponent as
we did above. This is not really required but it can make our life easier onoccasion if we do that.

Now, we have two issues to deal with. First the derivative will not exist
if there is division by zero in the denominator. So we need to solve,
So, we can see from this that the derivative will not exist at
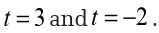
However, these are not critical points since the function will also not exist
at these points. Recall that in order for a point to be a critical point the
function must actually exist at that point.
At this point, we have to be careful. The numerator does not factor, but that
does not mean that there are not any critical points where the derivative is
zero. We can use the quadratic formula on the numerator to determine ifthe fraction as a whole is ever zero.
a) Verify that the function is continuous on the interval
b) Find all critical points of that are in the interval
that are in the interval 
This makes sense if you think about it.
Since we are only interested in what the function is doing in this
interval, we do not care about critical points that fall outside the
interval.
c) Evaluate the function at the critical points found in a) above and
the end points.d) Identify the absolute extrema.
It looks like we will have two critical points,
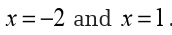 Note that we
Note that we
actually want something more than just the critical points. We only want
the critical points of the function that lie in the interval in question. Both
of these do fall in the interval as so we will use both of them.
Now we evaluate the function at the critical points and the end points ofthe interval.




guaranteed to have both an absolute maximum and an absolute minimum
for the function somewhere in the interval. The theorem doesn’t tell us
where they will occur or if they will occur more than once, but at least it
tells us that they do exist somewhere. Sometimes, all that we need to know
is that they do exist. This theorem doesn’t say anything about absolute
extrema if we aren’t working on an interval.
The requirement that a function be continuous is also required in order forus to use the theorem.
This function is not continuous at x = 0 as we move in towards zero the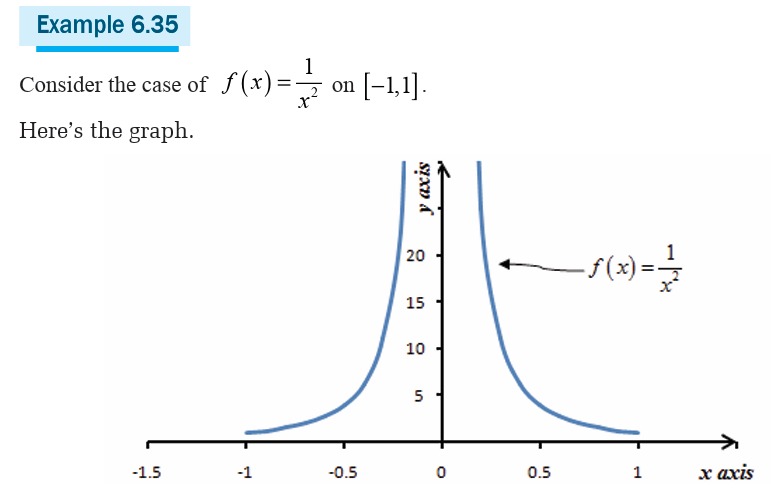
function is approaching infinity. So, the function does not have an absolute
maximum. Note that it has an absolute minimum however. In fact theabsolute minimum occurs twice at both
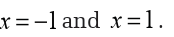
If we changed the interval a little to say,
the function would now have both absolute extrema. We may only run into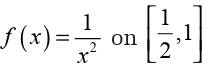
problems if the interval contains the point of discontinuity. If it doesn’t,
then the theorem will hold.
We should also point out that just because a function is not continuous at
a point, that doesn’t mean that it won’t have both absolute extrema in aninterval that contains that point.
This graph is not continuous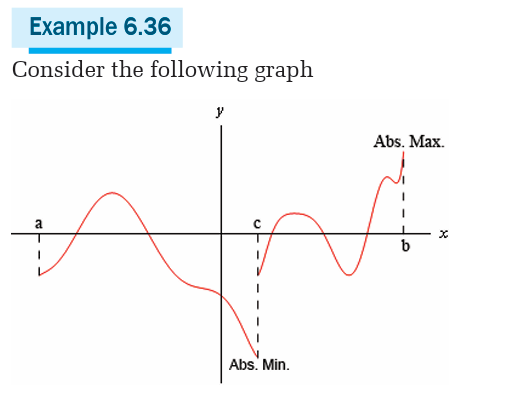
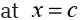 yet it does have both an absolute
yet it does have both an absolutemaximum
Also note that, in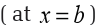 and an absolute minimum
and an absolute minimum 
this case one of the absolute extrema occurred at the point of discontinuity,
but it doesn’t need to. The absolute minimum could just have easily been
at the other end point or at some other point interior to the region. The
point here is that this graph is not continuous and yet does have both
absolute extrema
The point of all this is that we need to be careful to only use the extreme
value theorem when the conditions of the theorem are met and not
misinterpret the results if the conditions are not met.
Note
In order to use the extreme value theorem, we must have an interval and the
function must be continuous on that interval. If we don’t have an interval
and/or the function isn’t continuous on the interval, then the function mayor may not have absolute extrema.
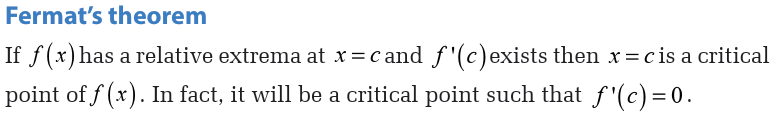

Example 6.38
Clearly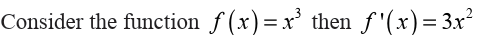
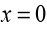 is a critical point.
is a critical point.
However this function has no relative
extrema of any kind. So, critical points do not have to be relative extrema.
Also note that this theorem says nothing about absolute extrema. An
absolute extrema may or may not be a critical point.
Increasing and decreasing of a function
In the previous lines we saw how to use the derivative to determine the
absolute minimum and maximum values of a function. However, there is
a lot more information about a graph that can be determined from the first
derivative of a function.The main idea we will be looking at here, we will
be identifying all the relative extrema of a function.
We know from our work in previous lines that the first derivative,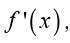
is the rate of change of the function. We used this idea to identify where afunction was increasing, decreasing or not changing. Let us see definitions:
Now, recall that earlier we constantly used the idea that if the derivative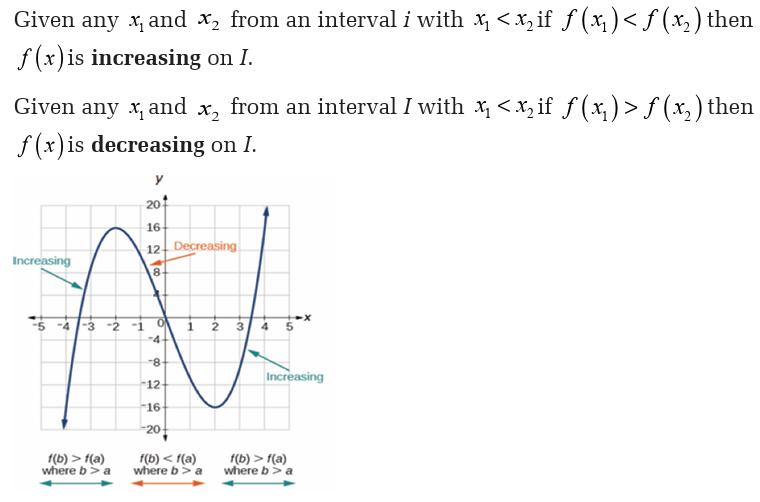
of a function was positive at a point then the function was increasing at
that point and if the derivative was negative at a point then the function
was decreasing at that point. We also used the fact that if the derivative of
a function was zero at a point then the function was not changing at that
point. We used these ideas to identify the intervals in which a function isincreasing and decreasing. This can be summarised in the following fact.

From the factored form of the derivative, we see that we have three critical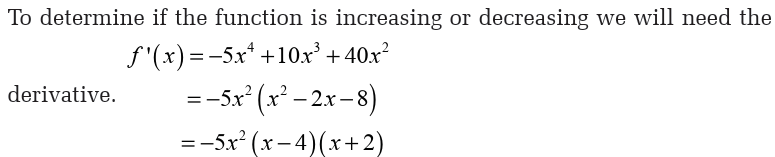
points: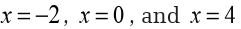 We will need these in a bit.
We will need these in a bit.
We now need to determine where the derivative is positive and where it’s
negative. Since the derivative is a polynomial, it is continuous and so we
know that the only way for it to change signs is to first go through zero.
In other words, the only place that the derivative may change signs is at
the critical points of the function. We have now got another use for critical
points. So, we will build sign table of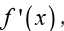 graph the critical points
graph the critical points
and pick test points from each region to see if the derivative is positive ornegative in each region.

Concavity of a function
In the lines, we saw how we could use the first derivative of a function to
get some information about the graph of a function. In following lines, we
are going to look at the information that the second derivative of a functioncan give us about the graph of a function.
So a function is concave up if it “opens” up and the function is concave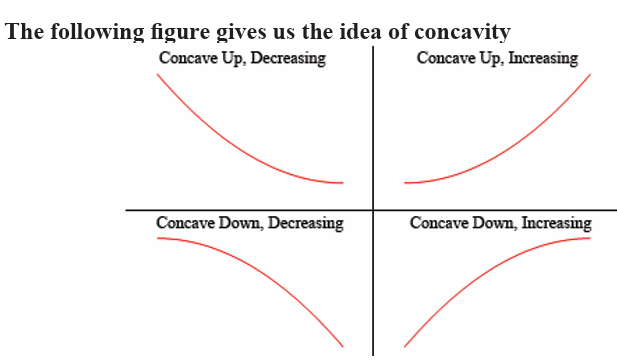
down if it “opens” down. Notice as well that concavity has nothing to do
with increasing or decreasing. A function can be concave up and either
increasing or decreasing. Similarly, a function can be concave down andeither increasing or decreasing.
So, as you can see, in the two upper graphs all of the tangent lines sketched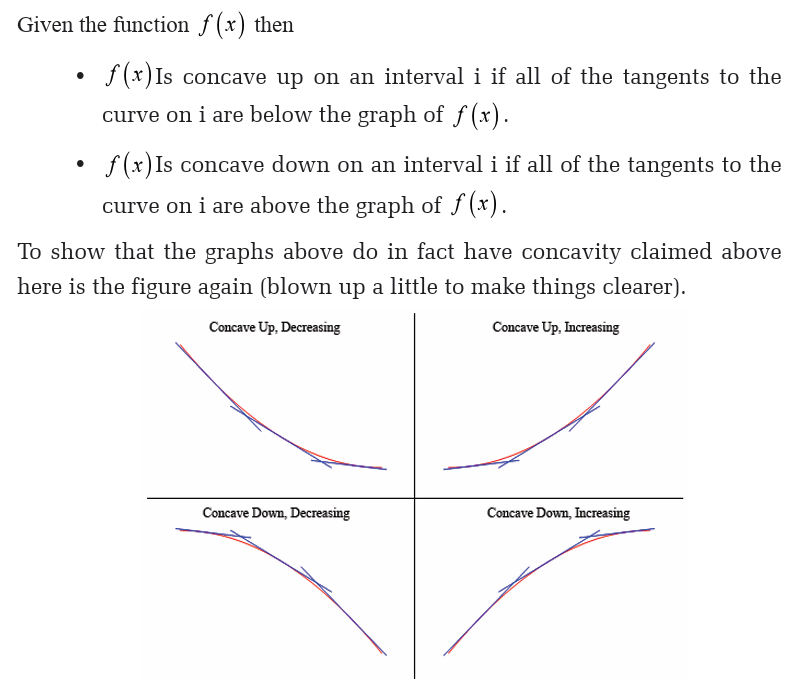
in are all below the graph of the function and these are concave up. In the
lower two graphs all the tangent lines are above the graph of the functionand these are concave down.
There’s one more definition that we need to get out of the way.
A point is called an inflection point if the function is continuous at
is called an inflection point if the function is continuous at
the point and the concavity of the graph changes at that point.
Now that we have all the concavity definitions out of the way, we need
to bring the second derivative into the mix. The following fact relates thesecond derivative of a function to its concavity.
Notice that this fact tells us that a list of possible inflection points will
be those points where the second derivative is zero or doesn’t exist. Be
careful, however, to not make the assumption that just because the second
derivative is zero or doesn’t exist that the point will be an inflection point.
We will only know that it is an inflection point once we determine the
concavity on both sides of it. It will only be an inflection point if theconcavity is different on both sides of the point.
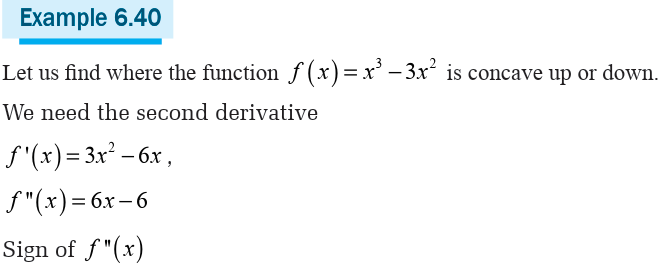



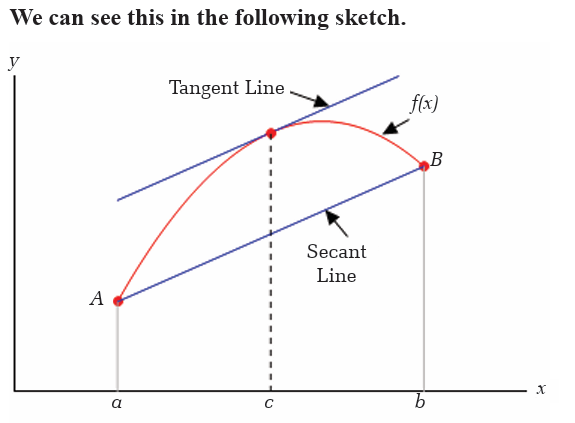
Example 6.42
Let us determine all the numbers c which satisfy the conclusions of the mean value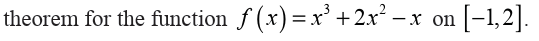
There isn’t really a whole lot to this problem other than to notice that since is a polynomial, it is both continuous and differentiable (i.E, the
is a polynomial, it is both continuous and differentiable (i.E, the derivative exists) on the interval given.
Now, to find the numbers that satisfy the conclusions of the mean value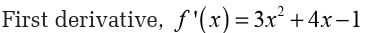
theorem all we need to do is plug this into the formula given by the meanvalue theorem.
Note that in both of these facts we are assuming the functions are continuous
and differentiable on the interval [ a,b] ,
L’hôpital’s rule
Back on the section of limits, we saw methods for dealing with the followinglimits:


Applications of differentiation in medicine
Application of differentiation to find the Concentration of drugs.
Example 6.45
The concentration C (in milligrams per milliliter) of a drug in a patient’s
blood-stream is monitored over 10minute intervals for 2 hours, where t
is measured in minutes, as shown in the table. Find the average rate ofchange over each interval.
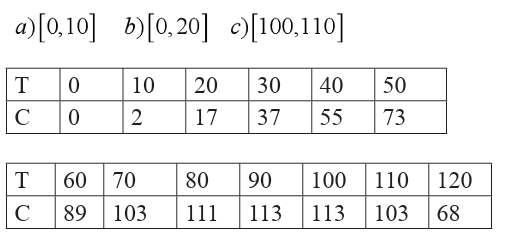

Example 6.46
As blood moves from the heart through the major arteries out to the
capillaries and back through the veins, the systolic blood pressure
continuously drops. Consider a person whose systolic blood pressure P(in millimeters of mercury) is given by


Application of differentiation to find effectiveness E of a pain
killing drug t hours after entering the bloodstream
Example 6.48
The effectiveness E (on a scale from 0 to 1) of a pain-killing drug t hoursafter entering the bloodstream is given by.

Solution

Unit summary





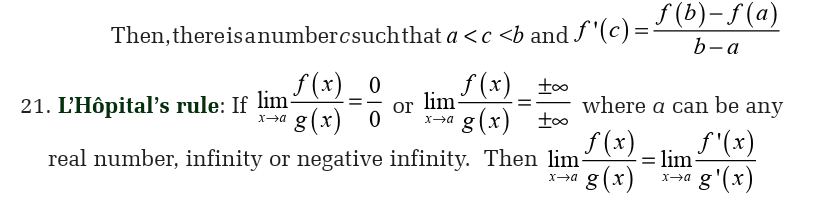
End Unit Assesment



Unit 7 :Vector space of real numbers
7.0 Introductory activity

objectives
After completing this unit, I will be able to:
» Find the norm of a vector.
» Calculate the scalar product of two vectors.
» Calculate the angle between two vectors.
» Apply and transfer the skills of vectors to other area ofknowledge.


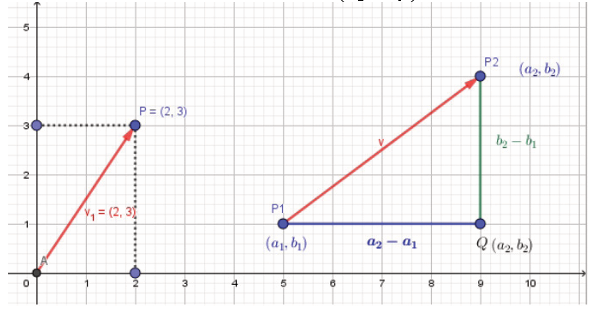
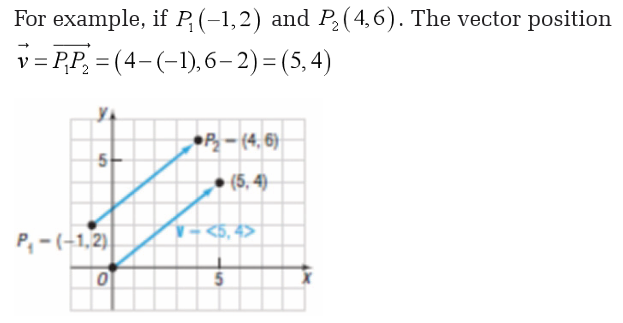

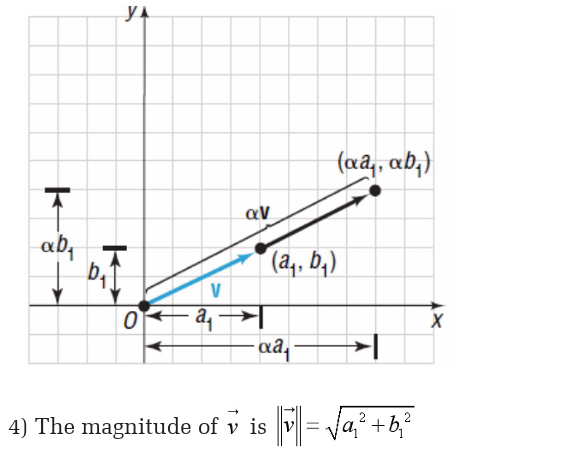


Scalar product and properties
The scalar product or dot product (or sometimes inner product) is an
algebraic operation that takes two coordinate vectors and returns a single
number.
Algebraically, it is the sum of the products of the corresponding coordinatesof the two vectors. That is, the scalar product of vectors
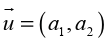 and
and
We can illustrate this scalar product in terms of work done by a force on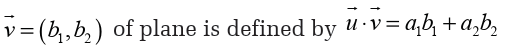
the body:
Suppose that a person is holding a heavy weight at rest. This person may
say and feel he is doing hard work but in fact none is being done on the
weight in the scientific sense. Work is done when a force moves its point
of application along the direction of its line of action.
If the constant force F and the displacement S are in the same direction
and we define the work W done by the force on the body by W= F .S

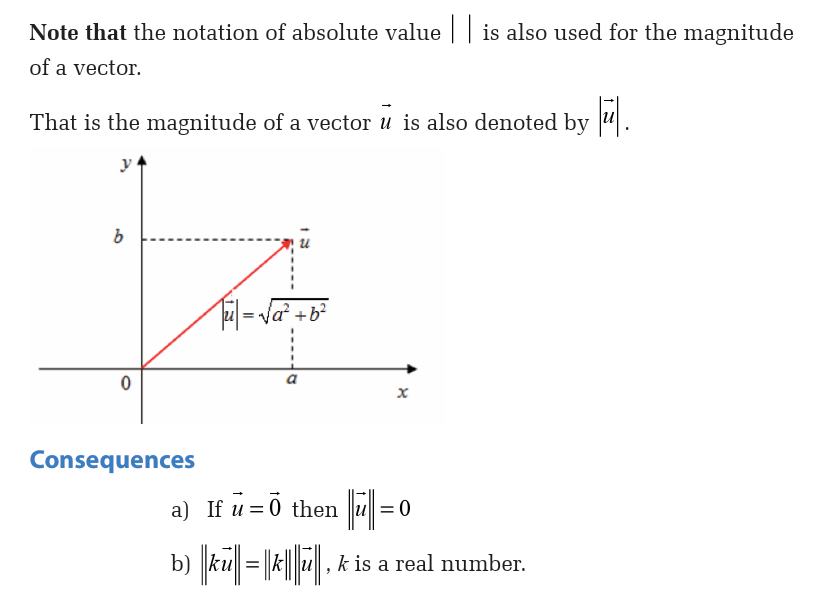

Example 7.5
The figure below shows a girl pulling a wagon with a force of 50Newtons.
How much work is done in moving the wagon 100 meters if the handlemakes an angle of 30 degrees with the ground?
Solution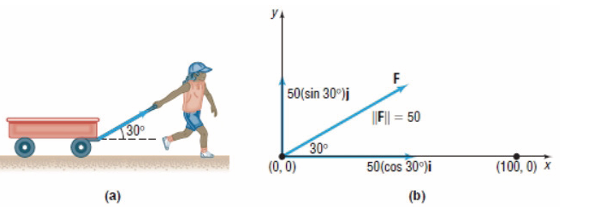
Let us position the vector in the cartesian plane in such a way the wagon
moved from the origin O(0,0) to the point P(100,0). The motion is from Oto P.

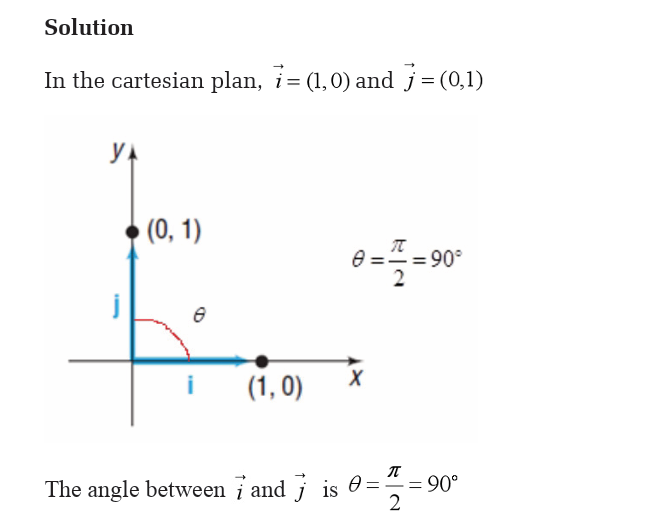

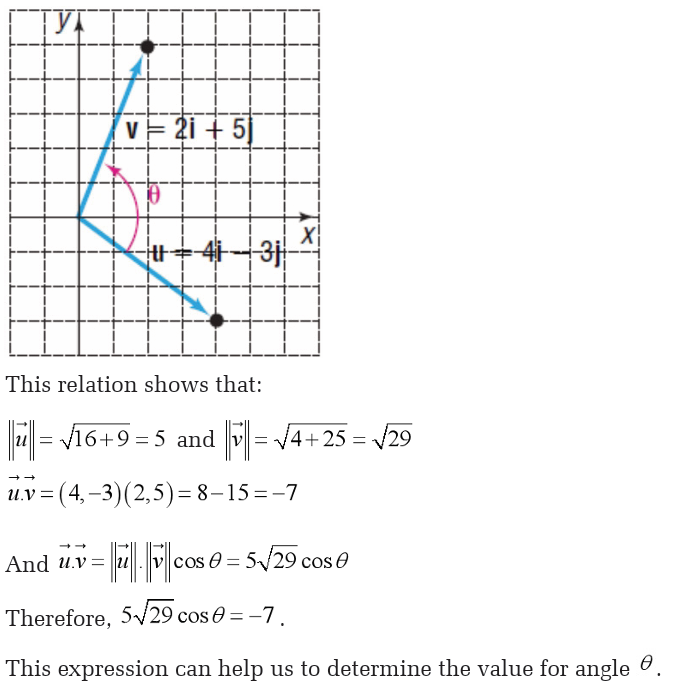

We can illustrate the scalar product in terms of work done by the force on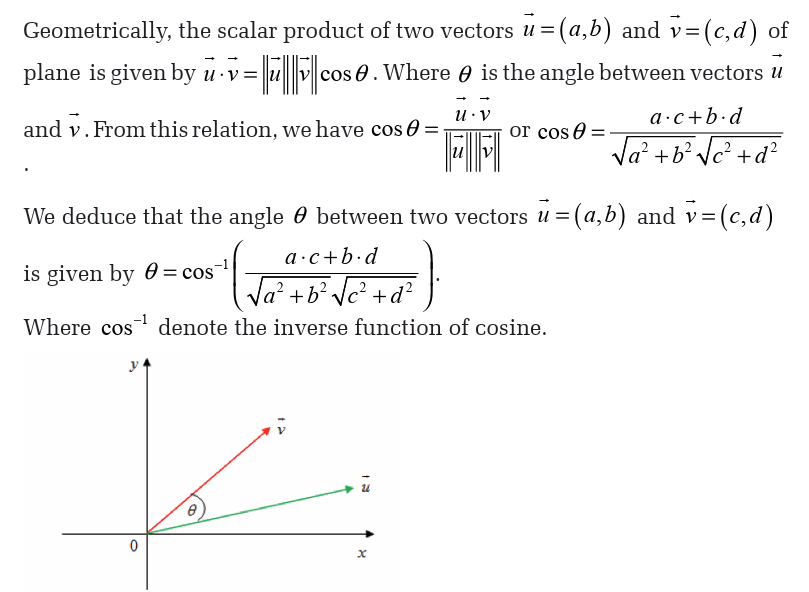
the body:
If the constant force F and the displacement S are in the same direction,
the work W done by the force on the body is W= F .S
If the force does not act in the direction in which motion occurs but an angle
to it , then the work done is defined as the product of the component ofthe force in the direction of motion and the displacement in that direction.
Notice
• Two vectors are perpendicular if the angle between them is a multiple
of a right angle.
• Two vectors are parallel and with the same direction if the angle
between them is a multiple of a zero angle.
• Two vectors are parallel and with the opposite direction if the anglebetween them is a multiple of a straight angle.



Application
In physics,
, calculate the value of k
Vectors are fundamental in the physical sciences. They can be used to
represent any quantity that has magnitude, has direction, and which adheres
to the rules of vector addition. An example is velocity, the magnitude of
which is speed. For example, the velocity 7 meters per second upward
could be represented by the vector (0,7). Another quantity represented by a
vector is force, since it has a magnitude and direction and follows the rules
of vector addition. Vectors also describe many other physical quantities,
such as linear displacement, displacement, linear acceleration, angular
acceleration, linear momentum, and angular momentum. Other physical
vectors, such as the electric and magnetic field, are represented as a systemof vectors at each point of a physical space; that is, a vector field.
In geography,Vectors can be used in air plane navigation
Use of vectors in real life
Vectors are used whenever some quantity has a size and a direction.
The most important vectors in basic physics are probably position and
momentum. These are used to calculate an object’s motion. Some other
useful vectors in physics are velocity which tells you how fast an object’s
moving and current density which tells you how the total current is
distributed around the conductor.
In chemistry, vectors are used to consider bond polarity; there are chemical
bonds where one side is slightly negatively charged, and the other is
slightly positively charged. This creates an electric field pointing from the
positive to the negative end, which needs to be considered in chemistry
calculations.
Vectors can also be used with other shapes to produce vector graphics.
These are images which are produced using a set of instructions. When
you save the image, the instructions are stored in the computer memory as
another type of image.
In many fields, vectors are useful for solving systems which are represented
by many simultaneous equations. You arrange the system as the product
of a matrix (taken as a vector of vectors) multiplied by a vector, which givesa vector output.
In medicine, the mathematics definition implies that vectors are used to
calculate speed of blood flow to and from the heart or air through the
lungs.
On the other hand, the medical field takes vectors as animals, insects
or means (wind, water, etc) that carry germs, viruses, bacteria, or fungal
spores within or outside their bodies from one location to another where itdoes or does not result in disease.
Unit summary



Unit 8 : Matrices and determinants of order 2
8.0 Introductory activity
A pharmacist buys two types of drugs in boxes A and B. On the first day
he bought 5 boxes of drug A and 4 boxes of drug B and he paid 35,000Frw.
On the second day, the pharmacist bought 3 boxes of drug A and 6 boxes
of drug B and paid 30,000Frw.
a) Arrange what the pharmacist bought according to their types in asimple table as follows:
b) Discuss and explain in your own words how you can determine the
cost for the box of drug A and the cost for drug B.
objectives
After completing this unit, I will be able to:
» Define matrices.
» Perform operations on matrices of order 2.
» Determine determinant of matrix.» Determine the inverse of a matrix of order 2.
8.1. Square Matrices of order two
Activity 8.1
A shop sold 20 cell phones and 31 computers in a particular month.
Another shop sold 45 cell phones and 23 computers in the same
month. Present this information as an array of rows and columns.
A matrix is every set of numbers or terms arranged in a rectangular shape,
forming rows and columns. In square matrix of order two, the number of
rows is equal to the number of columns equal to 2 and it has the followingform;
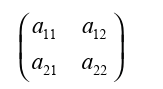
If we compare these data and the boxes of drugs bought by the pharmacist,
we find the following:
the elements 1 and 4 are on the first row, they look like the quantity of
drug of type A (1) and the quantity of drug of type B (4) bought by thepharmacist on the first day.
The element 3 and 11 are on the second row. They look like the quantity
of drug of type A (3) and the quantity of drug of type B (11) bought by thepharmacist on the second day.

Application activity 8.1
Give five examples of matrices of order two.
8.2. Operations on matrices
Example 8.3
There are two pharmacists Gerard and Jane who bought boxes of drugs in
two different days.
On the first Day, Gerard bought 13 boxes of nystatin and 4 boxes of
Amoxicillin. On the second day, he bought 6 boxes of nystatin and 10
boxes of Amoxicillin.
For Jane, she bought 7 boxes of nystatin and 10 boxes of Amoxicillin on the
first day. On the second day she bought 3 boxes of nystatin and 4 boxes of
Amoxicillin.
a) Organise in the matrix A the number of drugs bought by Gerard in the
two days, and the matrix B of drugs bought by Jane.
b) Write the matrix showing the total number of drugs bought by the two
pharmacists Gerard and Jane.c) Interpret the matrix obtained in b).
c) On the first day, Gerard and Jane bought20 boxes of nystatin and 14
boxes of Amoxycillin. On the second day, they bought 9 boxes of nystatinand 14 boxes of Amoxycillin.
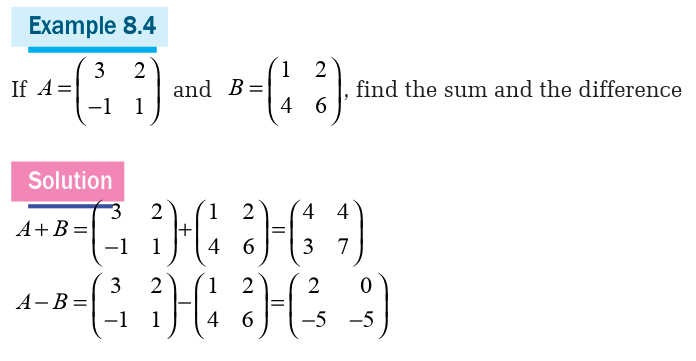


Example 8.6
According to information from the American Red Cross, the distributionof blood types in the United States is as shown in the accompanying table.
(a) Write a 2x2 matrix depicting the distribution of blood types A and O by
Rh factor, using decimals as entries.
(b) On any given day in the United States, 38,000 units of blood are needed.
Use scalar multiplication to determine the number of units needed
each day in the United States by blood type A and O, assuming daily
distributions match the percentages above.(c) State in words what this means about the number of units of O+

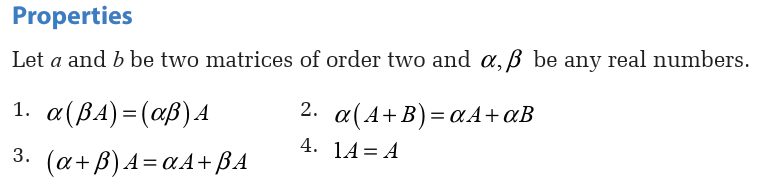
Multiplying matrices
Two matrices A and B of order two can be multiplied together.
The element of the product matrix is obtained by multiplying every
element in row i of matrix A by each element of column j of matrix B andthen adding them together.

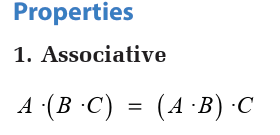

Commuting matrices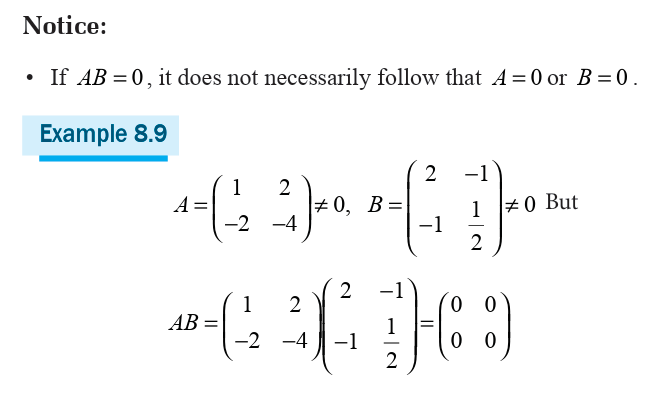
In general the multiplication of matrices is not commutative, i.E, AB≠ BA
, but we can have the case where two matrices A and B satisfy AB= BA. Inthis case A and B are said to be commuting.




Example 8.12

3. If a determinant switches two parallel rows or columns, its determinant
changes sign.


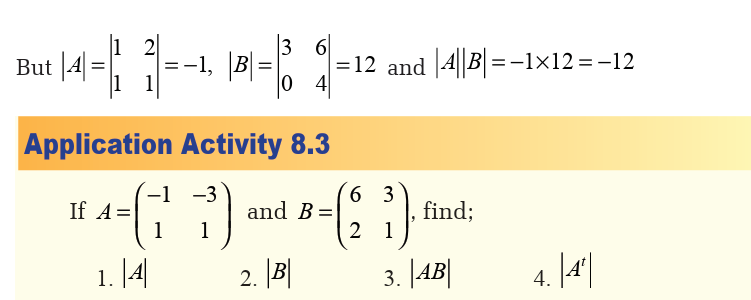
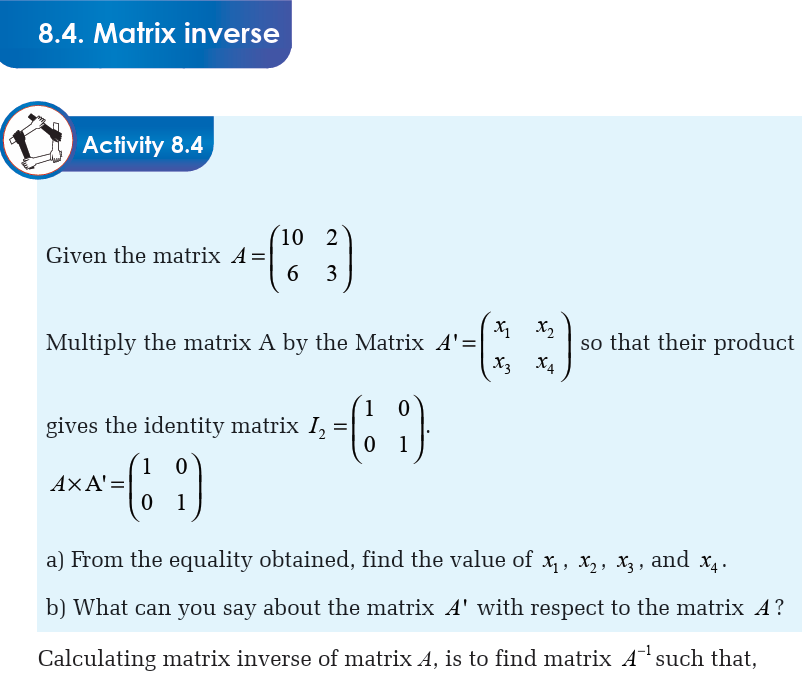




Example 8.23
A pharmacist buys different boxes for Cefalexin and Cloxacillin. On the
first day he bought 5 boxes of Cefalexin and 4 boxes of Cloxacillin and he
paid 35,000Frw.
On the second day, the pharmacist bought 3 boxes of Cefalexin and 6 boxes
of Cloxacillin and paid 30,000Frw.
a) Let x be the cost of one box of Cefalexin and y the cost of one box
of Cloxacillin. Write the product of matrices that model this situation:
matrix with the numbers of boxes bought by the column matrix
unknowns.
b) From, the obtained matrix, write the two equations obtained after
multiplication.
c) Solve the equation to deduce the value x and y.d) After solving this problem, try to explain the role of matrices in medicine.

Thus, the cost of one box of Cefalexin is 5,000Frw and the cost of one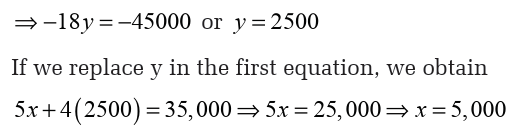
box of Cloxacillin is 2,500Frw.
d) After solving this problem, we see that matrices can be used to solve
problem related to the calculation of the number of drugs or otherproducts used in medicine.
Example 8.24
A movie theater sells tickets for $8 each. When there are special clients,
she allows them a discount of $2.
One evening the theater sold 525 tickets and took in $3580 in revenue.How many of each type of ticket were sold?


Unit summary
1. A matrix is every set of numbers or terms arranged in a rectangular
shape, forming rows and columns.
2. Two matrices are equal if the elements of the two matrices that occupythe same position are equal.


End unit assesment


Unit 9 : Measures of dispersion
9.0 Introductory activity
1. During 6 consecutive days, a fruit-seller has recorded the number offruits sold per type.
a) Which type of fruits had the highest number of fruits sold?
b) Which type of fruits had the least number of fruits sold?
c) What was the total number of fruits sold that week?
d) Find out the average number of fruits sold per day.
2. During the welcome test of Mathematics out of 10 , 10 student-teachers
of year one of Nursing scored the following marks: 3, 5,6,3,8,7,8,4,8 and 6.
a) Determine the mean mark of the class.
b) What is the mark that was obtained by many students?
c) Compare and discuss the difference between the mean mark of the
class and the mark for every student-teacher. What advice could you
give to the Mathematics teacher?
Objectives
After completing this unit, I will be able to:
» Determine the measures of dispersion of a given
statistical series.
» Apply and explain the standard deviation as the
more convenient measure of the variability in the
interpretation of data.
» Express the coefficient of variation as a measure of the
spread of a set of data as a proportion of its mean.
Statistics data show that even though you can observe equal means for
two different series, the spread, or variation from the mean, can be quite
different. If this variation is small, the data are more consistently spread
vis Avis the mean.
For the spread or variability of a data set observed in medicine, three
measures are commonly used: range, variance, and standard deviation.
In the ordinary level we have already defined the range R as the difference
between the largest value and the smallest value.
R = highest value - lowest value.The two last measures are going to be discussed in this unit.
distance each value is from the mean. A variance of zero indicates that
all the values are identical. Variance is always non-negative: a small
variance indicates that the data points tend to be very close to the mean
and hence to each other, while a high variance indicates that the data
points are very spread out around the mean and from each other.The variance is denoted and defined by:
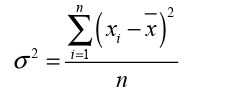


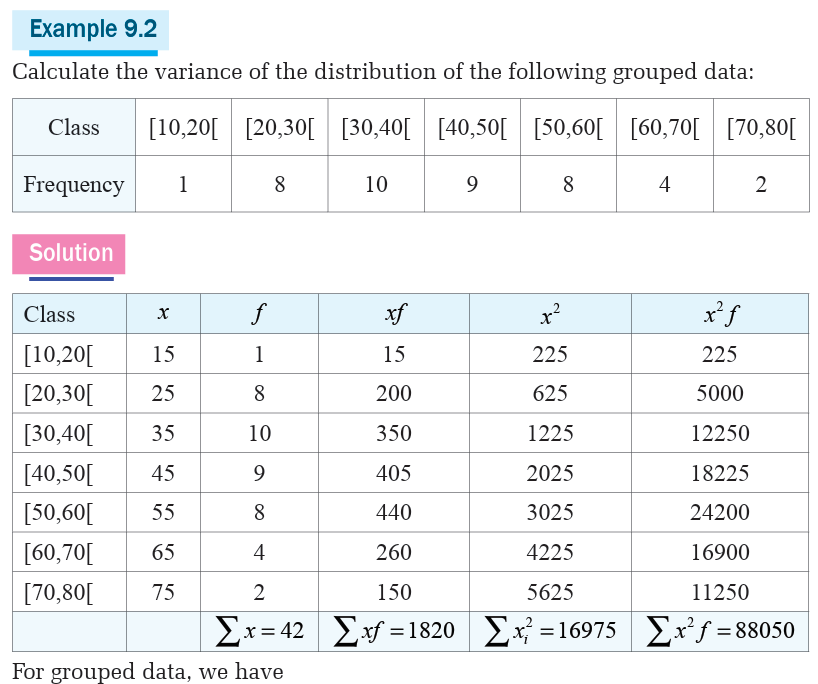
Sample Variance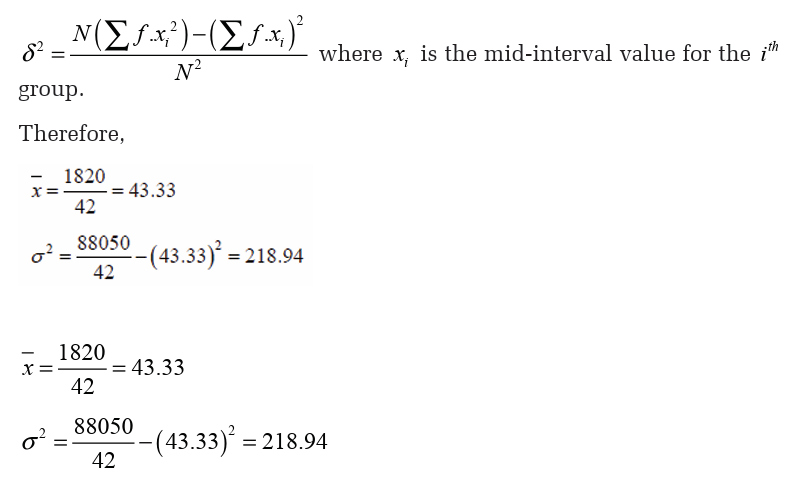
If the data used are a sample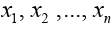 of the population, the sample
of the population, the sample
variance is defined as: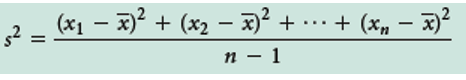
where n is the number of items in the sample and x the sample mean.
If the standard deviation of the set A is less than the standard deviation of
the set B, it indicates that the data of the set A are more clustered around
the mean than those of the set B.
Application Activity 9.1
Find the variance of the following set of data:
1. 1,3,2,1,2,5,4,0,2,6 2. 3,2,1,5,4,6,0,4,7,8
3. 1,5,6,7,6,4,2,6,3 4. 5,4,5,5,4,5,4,4,5,35. 8,7,6,8,6,5,6,4,1
The standard deviation has the same dimension as the data, and hence is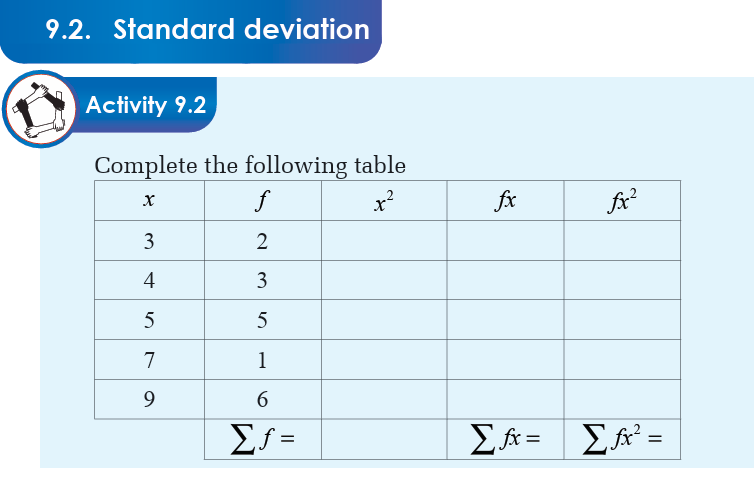
comparable to deviations from the mean. We define the standard deviation
to be the square root of the variance.Thus, the standard deviation is denoted and defined by;
The following results follow directly from the definitions of mean and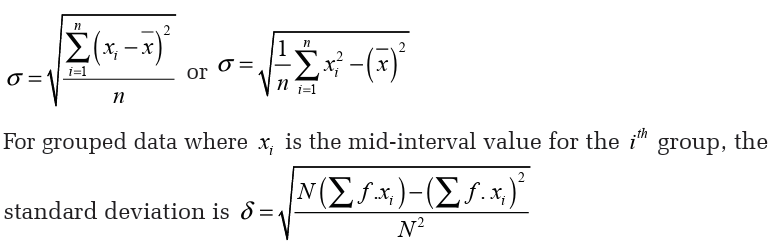
standard deviation:
• When all the data values are multiplied by a constant a, the newmean and new standard deviation are equal to a times the original

Example 9.3
The six runners in a 200 meter race clocked times (in seconds) of 24.2,
23.7, 25.0, 23.7, 24.0, 24.6
a) Find the mean and standard deviation of these times.
b) These readings were found to be 10% too low due to faultytimekeeping. Write down the new mean and standard deviation.
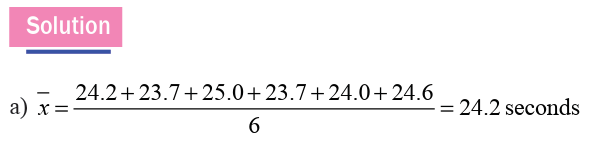
The method which uses the formula for the standard deviation is not
necessarily the most efficient. Consider the following:
Example 9.4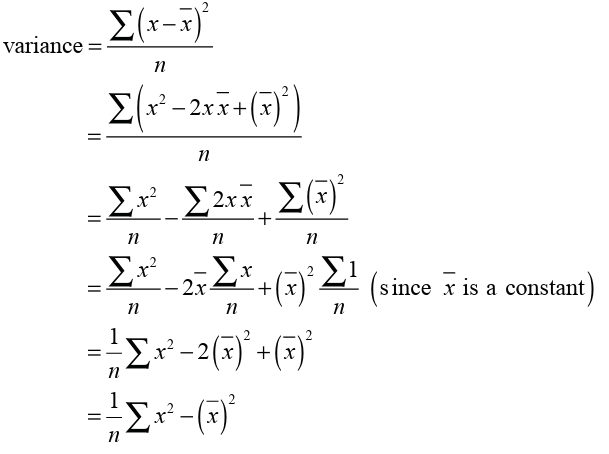
The heights (in meters) of six children are 1.42, 1.35, 1.37, 1.50, 1.38 and1.30. Calculate the mean height and the standard deviation of the heights.
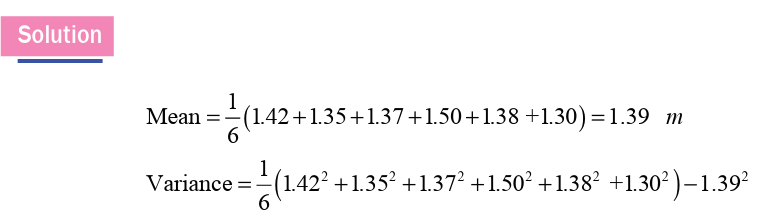
Example 9.5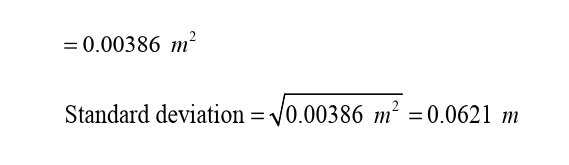
The number of customers served lunch in a restaurant over a period of 60days is as follows:
Find the mean and standard deviation of the number of customers served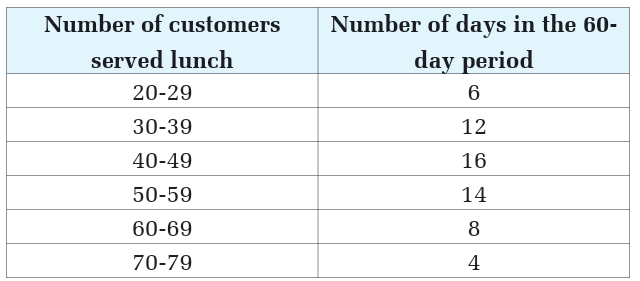
lunch using this grouped data.
Application Activity 9.3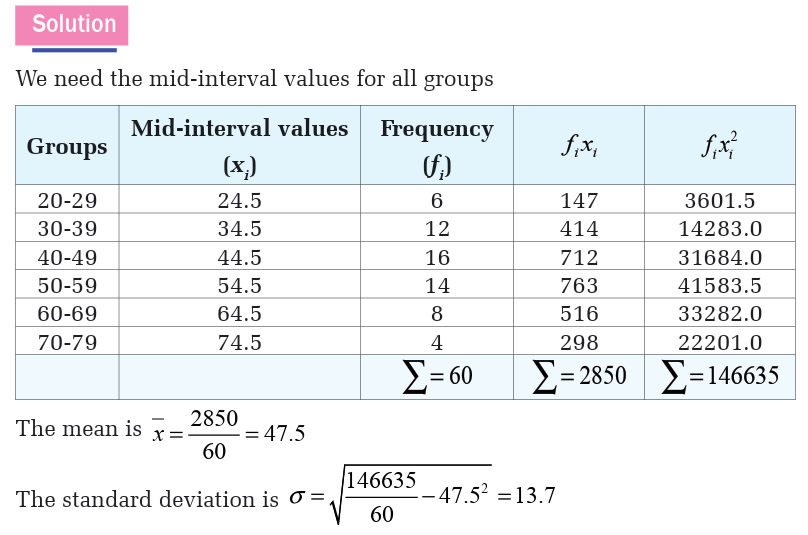
Find the standard deviation of the following set of data
1. 202,205,207,203,205,206,207,209
2. 1009,1011,1008,1007,1012,1010,106
3. 154,158,157,156,155,154,159
4. 7804,7806,7805,7807,78085. 56,54,55,59,58,57,55
The coefficient of variation measures variability in relation to the mean (or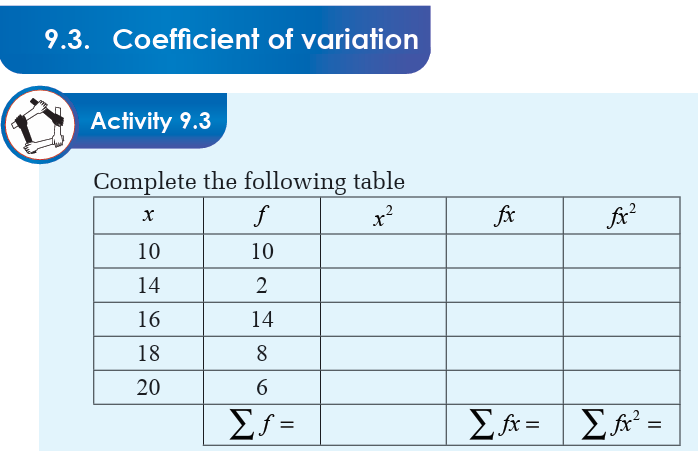
average) and is used to compare the relative dispersion in one type of data
with the relative dispersion in another type of data. It allows us to compare
the dispersions of two different distributions if their means are positive.
The greater dispersion corresponds to the value of the coefficient of greater
variation.
The coefficient of variation is a calculation built on other calculations: thestandard deviation and the mean as follows:
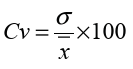

9.4. Applications
A large standard deviation indicates that the data points can spread far
from the mean and a small standard deviation indicates that they are
clustered closely around the mean.
Standard deviation is often used to compare real-world data against amodel to test the model.
Example 9.7
In industrial applications, the weight of products coming off a production
line may need to legally be some value. By weighing some fraction of the
products an average weight can be found, which will always be slightly
different from the long term average. By using standard deviations, a
minimum and maximum value can be calculated that the averaged weight
will be within some very high percentage of the time (99.9% or more).
If it falls outside the range then the production process may need to becorrected.
Example 9.8
Consider the average daily maximum temperatures for two cities, one
inland and one on the coast. It is helpful to understand that the range of
daily maximum temperatures for cities near the coast is smaller than for
cities inland. Thus, while these two cities may each have the same average
maximum temperature, the standard deviation of the daily maximum
temperature for the coastal city will be less than that of the inland city as
on any particular day, the actual maximum temperature is more likely to
be farther from the average maximum temperature for the inland city than
for the coastal one.
In finance, standard deviation is often used as a measure of the risk
associated with price-fluctuations of a given asset (stocks, bonds, property,
etc.), or the risk of a portfolio of assets, Standard deviation provides aquantified estimate of the uncertainty of future returns.
Unit summary
1. Variance measures how far a set of numbers is spread out. The varianceis denoted and defined by
2. The standard deviation has the same dimension as the data, and hence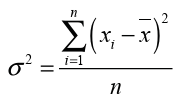
is comparable to deviations from the mean. We define the standard
deviation to be the square root of the variance. Thus, the standarddeviation is denoted and defined by
3. The coefficient of variation measures variability in relation to the mean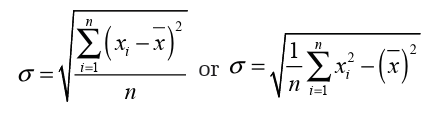
(or average) and is used to compare the relative dispersion in one type of
data with the relative dispersion in another type of data. The coefficientof variation is
4. Application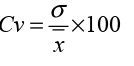
A large standard deviation indicates that the data points can spread far
from the mean and a small standard deviation indicates that they are
clustered closely around the mean. Standard deviation is often used to
compare real-world data against a model to test the model. Standard
deviation is often used as a measure of the risk associated with price
fluctuations of a given asset (stocks, bonds, property, etc.), or the risk of
a portfolio of assets. Standard deviation provides a quantified estimateof the uncertainty of future returns.
End Unit Assesment
1. The mean of 200 items was 50. Later on it was discovered that two
items were misread as 92 and 8 instead of 192 and 88. Find the
correct mean.2. Calculate the mean and standard deviation of the following series:

3. Find the mean of:
a) 6, 10, 4, 13, 11, 9, 1, 6, 12 b) 193, 195, 202, 190, 189, 195
4. Find the mean and standard deviation of 25.2, 22.8, 22.1, 25.3, 24.6,25.0, 24.3 and 22.7.



Unit 10 : Elementary probability
10.0 Introductory activity
1. Use the library or the internet to search on counting techniques used todetermine outcomes for different random experiments.
2. There are 2 roads joining A and B and 3 roads joining B and C. Writedown different roads from A to C via B. How many are they?
3. When a card is selected from an ordinary deck of 52 cards, one assumes
that the deck has been shuffled, and each card has the same chance of
being selected. Let A be the event of selecting a black card,
a) If n is the number of black cards in the pack, what is the value of n?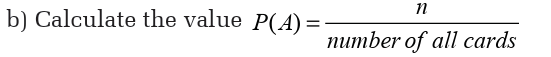
c) If P(A )is the probability of electing a black card, deduce thedefinition of probability for any event E.
objectives
After completing this unit, I will be able to:
» solve problems involving factorial notation,
» determine the number of permutations of n different
objects taken r at a time,
» determine the number of permutations of n different
objects,
» determine the number of permutations of n different
objects taken r at a time for a given condition,
» determine the number of combinations of r objects
chosen from n different objects,
» determine the number of combinations of r objects
chosen from n different objects for a given condition,
» use properties of combinations for finding coefficients
in Pascal’s triangle,
» solve problems involving permutations and
combinations,
» find probability of events,» determine probability of an equiprobable sample space
10.1. Permutations and arrangements
Activity 10.1
1. There are 4 roads joining A and B and 3 roads joining B and C.Write down different roads from A to C via B. How many are they?
c) Toss simultaneously a coin with two sides H and T and a
die with six sides 1 through 6, write down different possibleoutcomes that can appear. How many are they?
It is often necessary to count the ways in which a certain task can be
performed. In some cases, the total number of possible ways is very large,
and becomes impractical to write down all possible choices.
To solve such problems related to counting, we refer to the theory called
“Combinatorial analysis or combinatorics”.
In this theory, there are three basic counting principles that will help us to
count in a more systematic way: The first is the multiplication principle;
the other two, which follow from it, are rules concerning permutations and
combinations.
Principle of counting
Some terms:
Experiment: any human activity, like tossing a die.
Trial: small experiment contained in a large experiment. For example,
tossing simultaneously a coin and a die may be regarded as an experiment
consisting of two smaller experiments, tossing a coin (experiment 1)
followed by tossing a die (experiment 2). Here experiment 1 and experiment2 are called trials.
The set S of all possible outcomes of a given experiment is called the sample
space. A particular outcome, i.e., an element in S, is called a sample point.
An event A is a set of outcomes or, in other words, a subset of the samplespace S.

A probability experiment is a chance process that leads to well-defined
results called outcomes.An outcome is the result of a single trial of a probability experiment.
Example 10.1
For example, tossing simultaneously a coin and a die may be regarded
as an experiment consisting of two smaller experiments, tossing a coin
(experiment 1) followed by tossing a die (experiment 2). Here experiment1 and experiment 2 are trials. Point on a side of a die is an outcome.
Notice:
Die (plural dice): small cube of plastic, ivory, bone, or wood, marked oneach side with one to six sports, usually used in pairs in games of chance.
Successive experiments
Basic product principle of counting
“If experiment 1 has m possible outcomes and if for each outcome of
experiment 1, experiment 2 has n possible outcomes, then an experiment
of performing experiment 1 and experiment 2 simultaneously, called
experiment 1 and 2, has m× n possible outcomes.”
Example 10.2
In tossing simultaneously a coin with two sides a and b and a die with six
sides 1 through 6, how many possible outcomes will appear?
Solution
The tossing may be regarded as an experiment (experiment 1 & 2) consisting
of two smaller experiments, tossing a coin (experiment 1) followed by
tossing a die (experiment 2).
Experiment 1 has 2 outcomes.
Experiment 2 has 6 outcomes.
So experiment 1 & 2 has 2 ×6 = 12 outcomes.
Example 10.3
There are 5 roads joining A and B and 3 roads joining B and C how many
different roads from A to C via B?
Solution
Here;
From A to B we have 5 roads.
From B to C we have 3 roads.
Thus, the number of roads from A to C via B is 3 ×5 = 15
Note that this multiplication rule only applies when the experiments are
independent, i.E, the choice made for one experiment does not affect the
choice made for any of other experiments.
Example 10.4
A man has three choices of the way in which he travels to work; he can
walk, go by car or go by train. How many different ways can he arrange histravel for the five working days in a week?
Solution
This man has 3 choices on Monday: walk, car or train
3 Choices on Tuesday: walk, car or train
Similarly on Wednesday, Thursday and Friday he has 3 choices.
Then there are 5 successive operations, each of which can be performed
in 3 ways. Thus, the total number of choices he has is 3 ×3× 3 ×3× 3= 243
choices.
Example 10.5
A car license plate is to contain three letters of the alphabet, the first of
which must be r, s, t or u, followed by three decimal digits. How manydifferent license plates are possible?
Solution
The first letter can be chosen in 4 different ways, the second and third
letters in 26 different ways each, and each of the three digits can be chosen
in ten ways.
Hence there are 4 ×26× 26 ×10 ×10× 10 = 2,704,000 . possible plates
Example 10.6:
Imagine that we wish to experimentally manipulate growth conditions
for plants. We want to grow plants in pots in a green-house at two
different levels of fertilizer (low and high) and four different temperatures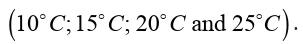
If we want three replicates of each possible combination of fertilizer and
temperature treatment, how many pots will we need?
Solution
From the principle, we see that we will need:2 · 4 · 3 = 24 pots for our experiment.
Application 10.1
1. There are 4 roads joining A and B and 5 roads joining B and C. How
many different roads from A to C via B?
2. A car license plate is to contain two letters of the alphabet, the first
of which must be A or B, followed by 6 decimal digits. How many
different license plates are possible?
Permutations
Activity 10.2
Consider three letters A, B and C written in a row, one after
another.
• Form all possible different words from three letters A, B and C
(not necessarily sensible).
In fact, each arrangement is a possible permutation of the letters A, B
and C; for example ABC, ACB,…
• How many arrangements are they possible for three letters A, B and C?
How to calculate the number of permutations without having to
list them all
From different arrangement of three letters a, b and c, the first letter to
be written down can be chosen in 3 ways. The second letter can then
be chosen in 2 ways because there are 2 remaining letters to be written
down and the third letter can be chosen in 1 way because it is only one
letter remaining to be written down. Thus, the three operations can be
performed in
3× 2× 1 =6 ways.
This suggests the following fact:
Fact: Permutations of n objects
The number of different permutations of n different objects (unlike objects)in a row is
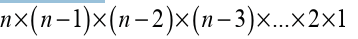
Example 10.8
Five children are to be seated on a bench. In how many ways can they be
seated? How many arrangements are they, if the youngest child has to sitat the left end of the bench?
Solution
Since there are five children, the first child can be chosen in 5 ways, the
next child in 4 ways, the next in 3 ways, the next in 2 ways and the last in1 way. Then, the number of ways is
Now, if the youngest child has to sit at the left end of the bench, this place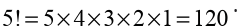
can be filled in only 1 way. The next child can then be chosen in 4 ways,the next in 3 ways and so on. Thus, the number of total arrangement is
Example 10.9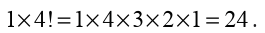
Three different mathematics books and five other books are to be arranged
on a bookshelf. Find:
a) the number of possible arrangements of the books.
b) the number of possible arrangements if the three mathematics
books must be kept together.
Solution
We have 8 books altogether.
a) since we have 8 books altogether, the first book can be chosen in 8
ways, the next in 7 ways, the next in 6 ways and so on. Thus, the total
arrangement is 8! = 40,320
b) since the 3 mathematics books have to be together, consider these bound
together as one book. There are now 6 books to be arranged and these
can be performed in 6! = 720.
Note that we have taken the three mathematics books as one book; these
three books can be arranged in 3! = 6 ways.
Thus, the total number of arrangements is 720× 6 =4,320.
Application activity 10.2
1. Four different English books, five different Biology books and ten
other books are to be arranged on a bookshelf. Find
a) the number of possible arrangements of the books.
b) the number of possible arrangements if the three Biologybooks must be kept together?
Permutations of indistinguishable objects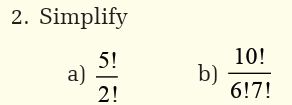
Activity 10.3
Consider the arrangements of four letters in the word “BOOM”.
• Write down all possible different arrangements.
• How many arrangements are they possible of four letters in the
word “BOOM”?
In the same way,
• Write down all possible different arrangements of five letters in
the word “CLASS”.
• How many arrangements are they possible of five letters in the
word “CLASS”?
Consider the arrangements of six letters in the word “avatar” (a title usedfor the movie).


Application activity 10.3
1. How many arrangements can be made from the letters of the word
ENGLISH?
2. How many arrangements can be made from the letters of English
alphabet?
3. In how many ways can 4 red, 3 yellow and 2 green discs be arrangedin a row, if discs of the same color are indistinguishable?
Circular arrangements
Activity 10.4
Take 5 different note books
• Put them on a circular table
• Fix one note book
• Try to interchange other 4 note books as possible
• How many different way obtained?Remember that there is one note book will not change it place.

Example 10.13
Four men Peter, Rogers, Smith and Thomas are to be seated at a circular table. Inhow many ways can this be done?
Solution
Suppose peter is seated at some particular place. The seats on his left can
be filled in 3 ways, the next seat can then be filled in 2 ways and theremaining seat in 1 way.

Example 10.14
Nine beads, all of different colors are to be arranged on a circular wire. Two
arrangements are not considered to be different if they appear the same
when the ring is turned over. How many different possible arrangementsare there?
When viewed from one side, these arrangements are only different in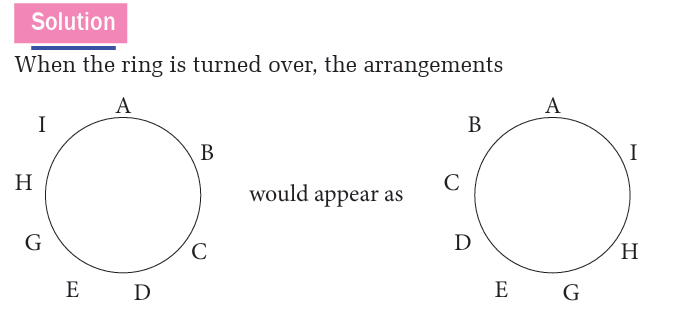
that one is a clockwise arrangement and the other is anticlockwise. If one
bead is fixed, there are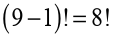 ways of arranging the remaining beads
ways of arranging the remaining beads
relative to the fixed one.
But, half of these arrangements will appear the same as the other half when
the ring is turned over, because for every clockwise arrangement there is
a similar anticlockwise arrangement. Hence, number of arrangements is
Application Activity 10.4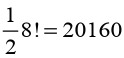
1. Five men Eric, Peter, John, Smith and Thomas are to be seated at a
circular table. In how many ways can this be done?
2. Eleven different books are placed on a circular table. In how manyways can this be done?
Mutually exclusive situation
Activity 10.5
When you go to a restaurant you will be asked if you wish to have a
soup or juice. Will you pick one, the other or both?
Two experiments 1 and 2 are mutually exclusive, if when experiment
1 occurs, experiment 2 cannot occur. Likewise, if experiment 2 occurs,experiment 1 cannot occur.
Basic sum principle of counting
In such cases, the number of permutations of either experiment 1
or experiment 2 occuring can be obtained by adding the number of
permutations of experiment 1 to the number of permutations of experiment 2.
This suggests the following result:
“If experiment 1 has m possible outcomes and if experiment 2 has n possible
outcomes, then an experiment which might be experiment 1 or experiment
2, called experiment 1 or 2, has m +n possible outcomes.”
Example 10.15
In tossing an object which might be a coin (with two sides h and t) or a die
(with six sides 1 through 6), how many possible outcomes will appear?
Solution
• The experiment may be t
• Tossing a coin (experiment 1) or tossing a die (experiment 2), or just
experiment 1 or 2.
• So the number of outcomes is 2+ 6 = 8 according to the above basic
sum principle of counting.
Example 10.16
How many different four digit numbers, end in a 3 or a 4, can be formed
from the figures 3,4,5,6 if each figure is used only once in each number.
Solution
We need the numbers that end in 3: the last digit can be chosen in one way,
as it must be a 3, the first digit can then be chosen in 3 ways, the second in
2 ways and the third in 1 way. Thus, there are 1 ×3× 2× 1= 6 numbers that
end in a 3.
Similarly, there are 1× 3× 2× 1= 6 numbers that end in a 4.
The number that ends in a 3 cannot also end in a 4, so these are mutually
exclusive situations.
Thus, there are 6+6 =12 numbers ending either in a 3 or in a 4.
Alternatively, this can be solved as follows:
The last digit can be chosen in 2 ways (3 or 4); the first digit can be chosen
in 3 ways, the second in 2 ways and the third in 1 way, i.e, 2 ×3 × 2 ×1= 12
numbers end either in a 3 or in a 4.
The number of permutations in which a certain experiment 1 occurs
will clearly be mutually exclusive with those permutations in which thatexperiment does not occur. Thus,
Example 10.17
In how many ways can five people Smith, James, Clark, Brown and John,
be arranged around a circular table in each of following cases:
a) Smith must sit next to Brown.b) Smith must not sit next to Brown.
Solution
There are five people.
a) Since Smith and Brown must sit next to each other, consider these
two bound together as one person. There are now, 4 people to seat.
Fix one of these, and then the remaining 3 people can be seated in 3 ×2× 1= 6
ways relative to the one who was fixed.
In each of these arrangements, smith and brown are seated together in
a particular way. Smith and Brown could now change the seats giving
another 6 ways of arranging the five people. Total number of arrangements
is 6×2 =12.
b) If Smith must not sit next to Brown, then this situation is
a mutually exclusive with the situation in a).
Total number of arrangements of 5 people at a circular table is
Thus, if Smith must not sit next to Brown, the number of arrangements is
24 -12 = 12 .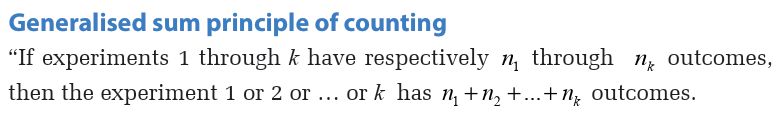
Example 10.18
How many even numbers containing one or more digits can be formed
from the digits 2, 3, 4, 5, 6 if no digit may be repeated?
Solution
Since the required numbers are even, last digit must 2 or 4 or 6. Note that
there are 5 digits.
So we can form one digit, two digits, three digits, four digits or five digits
as follows:
One digit: 2 or 4 or 6. That is 3 numbers.
Two digits: 3 ways to choose the last and 4 ways to choose the first. Thatis 3× 4 = 12 numbers.
Three digits: 3 ways to choose the last, 4 ways to choose the first and 3
ways to choose the second. That is 3× 4 ×3= 36
Four digits: 3 ways to choose the last, 4 ways to choose the first, 3 ways to
choose the second and 2 ways to choose the fourth. That is 3 × 4 ×3 ×2= 72
Five digits: 3 ways to choose the last, 4 ways to choose the first, 3 ways to
choose the second, 2 ways to choose the fourth and 1 way to choose the
fifth. That is 3 × 4 × 3 × 2 ×1= 72
Adding, we have 3 +12+ 36+ 72+ 72 = 195 even numbers in total.
Application activity 10.5
1. How many odd numbers containing one or more digits can be
formed from the digits 2, 3, 4, 5, 6, 7 if no digit may be repeated?
2. How many even numbers containing 2 digits can be formed from
the digits 2, 3, 4 if no digit may be repeated?
3. How many numbers containing three digits can be formed from thedigits 1, 2, 3, 4, 5, 6, 7, 8 if no digit may be repeated?
Distinguishable permutations
Activity 10.6
Make a selection of any three letters from the word “KNOW” and fillthem in 3 empty spaces.
Write down all different possible permutations of 3 letters selected
from the letters of the word “KNOW”.
How many are they?
Consider the number of ways of placing 3 of the letters a, b, c, d, e, f, g in3 empty spaces.

Example 10.21
How many different arrangements are there of 3 letters chosen from theword COMBINATION?
Solution
There are 11 letters including two O’s, two I’s and two N’s. to find the total
number of different arrangements we consider the possible arrangementsas four mutually exclusive situations.

Application activity 10.6
1. How many permutations are there of 4 letters chosen from letters
of the word ENGLISH?
2. How many permutations are there of 2 letters chosen from letters
of the word PACIFIC?
3. How many permutations are there of 5 letters chosen from letters
A, B, C, D, E, F, and G.
4. How many permutations are there of 10 letters chosen from Englishalphabet.
10.2. Combinations
Activity 10.7
Take 3 different mathematics books and 4 unlike English books so
that you will have 7 books altogether. Form different groups each
containing 2 mathematics books and 2 English books. How manygroups obtained?
From permutation of r unlike objects selected from n different objects, we
have seen that the order in which those objects are placed is important. Butwhen considering the number of combinations of r unlike objects selected

Example 10.22
From a group of 5 men and 7 women, how many different committees
consisting of 2 men and 3 women can be formed?
Solution
• Experiment 1: select 2 men from 5.
• Experiment 2: select 3 women from 7.
• Experiment of forming a committee: experiment 1 & 2.• Number of possible outcomes of experiment 1 is
• That is, the desired number of possible outcomes of the experiment
of forming a committee is 350.
Example 10.23
A committee of three men and one woman is obtained from five men andthree women. In how many ways can the members be chosen?
Example 10. 24
Suppose that you wish to plant 5 grass species in a plot. You can chooseamong 12 different species. How many choices do you have?

Example 10.25
In a sample of 50 people, 21 had type O blood, 22 had type A blood, 5 had
type B blood, and 2 had type AB blood. Set up a table of those numbers andfind the probability that a person has type O blood.


Application activity 10.7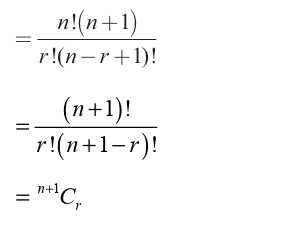
1. A committee of four men and two women is obtained from 10 men
and 12 women. In how many ways can the members be chosen?
2. A group containing 4 Mathematics books and 5 Physics books is
formed from 9 Mathematics books and 10 Physics books. Howmany groups can be formed?



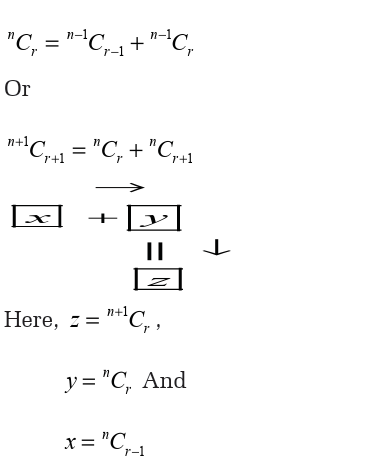
A simple construction of this triangle proceeds in the following manner: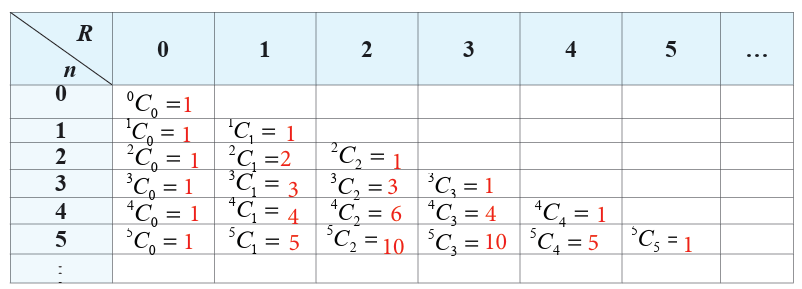
• On row 0, write only the number 1.
• Then, to construct the elements of following rows, add the number
above and to the left with the number above to the right to find the
new value.
• If either the number to the right or left is not present, substitute a
zero in its place. For example, the first number in the first row is 0 +1= 1
, whereas the numbers 1 and 3 in the third row are added toproduce the number 4 in the fourth row.
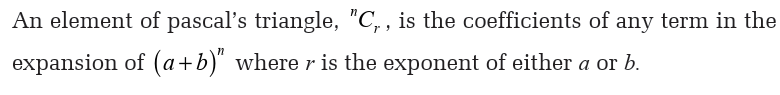



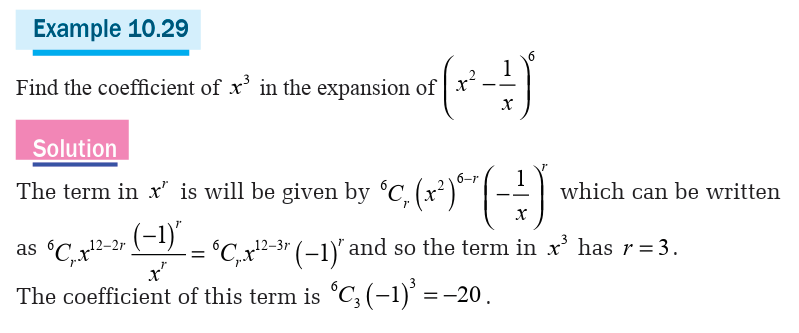
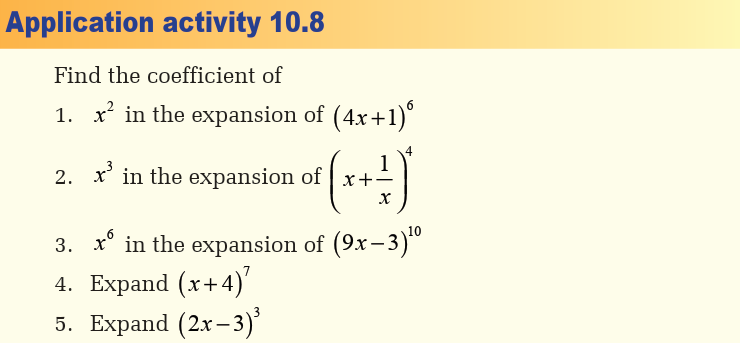
1. Suppose that you are choosing one card;
(i) How many cards can be chosen?
(ii) How many kings can be chosen?
(iii) How many aces of hearts can be chosen?
2. If a spade card has been declared to be a trump card. How many
trumps of Jack can be chosen?
Probability is the chance that something will happen.
The concept of probability can be illustrated in the context of game of
52 playing cards. In a park of deck of 52 playing cards, cards are divided
into four suits of 13 cards each. If a player selects a card at random (by
simple random sampling), then each card has the same probability of
being selected.
In most sampling situations we are generally not concerned with
sampling a specific individual but instead we concern ourselves with
the probability of sampling certain types of individuals. For example, for
our case of a deck of 52 playing cards, what is the probability of selecting
a queen? Selecting a queen is the event and selecting any card from 52
cards is an experiment.
Random experiments and events
A random experiment is an experiment that, atleast theoretically, may be
repeated as often as we want and whose outcome cannot be predicted, the
roll of a die. Each time experiment is repeated, an elementary outcome is
obtained. The set of all elementary outcomes of a random experiment is
called the sample space, which is denoted by
discrete or continuous.
Discrete sample space:
. Sample space may be
• Firstly, the number of possible outcomes is finite.
• Secondly, if the number of possible outcomes is countably infinite,
which means that there is an infinite number of possible outcomes,
Then the outcomes can be put in a one-to-one correspondence withthe positive integers.
Example 1.30
If a die is rolled and the number that shows up is noted, then
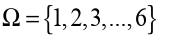
Example 1.31
If a die is rolled until a “6” is obtained, and the number of rolls made before getting
first “6” is counted, then we have that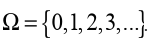
Continuous sample space:
If the sample space contains one or more intervals, the sample space is
then uncountable infinite.
Example 1.32A die is rolled until a “6” is obtained and the time needed to get this first “6” is
An event is a set of elementary outcomes. That is, it is a subset of the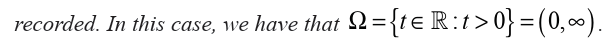
sample space.
In particular, every elementary outcome is an event, and so is the sample
space itself.
Remarks:
• An elementary outcome is sometimes called a simple event, whereas
a compound event is made up of at least two elementary outcomes.• To be precise, we should distinguish between the elementary outcome
Example 1.33
Consider the experiment that consists in rolling a die and recording the
number that shows up. Let A be the event “the even number is shown” and
B be the event “the odd number less than 5 is shown”. Define the events A
and B.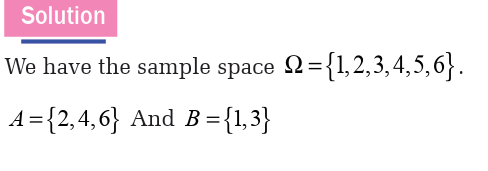
Definitions
• Two or more events which have an equal probability of occurrence are
said to be equally likely, i.e. If on taking into account all the conditions,
there should be no reason to accept any one of the events in preference
over the others. Equally, likely events may be simple or compound events.
• Two events, A and B are said to be incompatible (or mutually exclusive)
if their intersection is empty. We then write that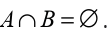
• Two events, A and B are said to be exhaustive if they satisfy the condition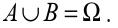
• An event which is sure to occur at every performance of an experiment
is called a certain event connected with the experiment. For example,
“Head or Tail’ is a certain event connected with tossing a coin. Face-1 or
face-2, face-3, ……, face-6 is a certain event connected with throwing a die.
• An event which cannot occur at any performance of the experiment is
called an impossible event. Following are such examples
i. ‘Seven’ in case of throwing a die.
ii. ‘Sum=13’ in case of throwing a pair of dice.
• Two events are said to be equivalent or identical if one of them implies
and implied by other. That is, the occurrence of one event implies the
occurrence of the other and vice versa. For example, “even face” and
“face-2” or “face-4” or “face-6” are two identical events.
• The outcomes which make necessary the happening of an event in a
trial are called favourable events. For example; if two dice are thrown,
the number of favourable events of getting a sum 5 is four, i.e., (1, 4), (2,
3), (3, 2) and (4, 1).
Example 10.32
Consider the experiment that consists in rolling a die and recording the
number that shows up.
Therefore, A and C are incompatible events.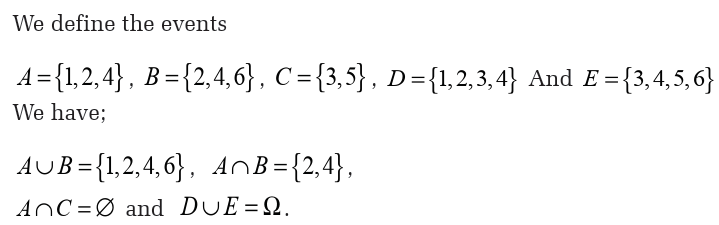
D and E are exhaustive events.

Example 1.35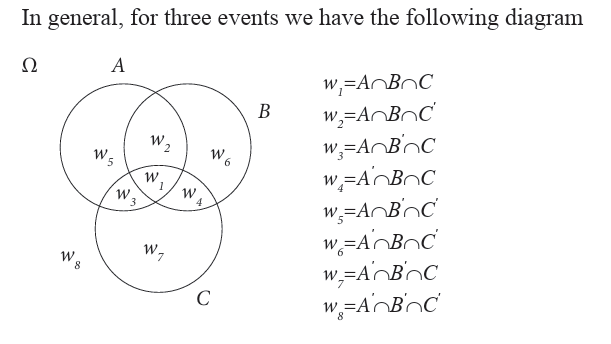
In the experiment of tossing a coin:
Where;
(i) A : the event of getting a “head” and
(ii) B : the event of getting a “tail”
Events “A” and “B” are said to be equally likely events. Both the events have
the same chance of occurrence.
Example 1.36
Consider the experiment that consists in choosing at random from the list
2, 3, 5, 7, 11, 13, 17, 19. The event that the chosen number is not prime
number is impossible events since all numbers are prime numbers.
Example 1.37
Consider the experiment that consists in rolling a die. The event of rolling
a number that is not 8 is a certain event.
Application activity 10.9
1. A box contains 5 red, 3 blue and 2 green pens. If a pen is chosen
at random from the box, then which of the following is an
impossible event?
a) Choosing a red pen.
b) Choosing a blue pen.
c) Choosing a yellow pen.
d) None of the above.
2. A spinner has 9 equal sectors numbered 1 to 9. If you spin the
spinner, then which of the following is a certain event?
a) Landing on a number less than 9.
b) Landing on a number less than 12.
c) Landing on a number greater than 1.
d) None of the above.
3. Which of the following are mutually exclusive events when a day of the
week is chosen at random?
a) Choosing a Monday or choosing a Wednesday.
b) Choosing a Saturday or choosing a Sunday.
c) Choosing a weekday or choosing a weekend day.
d) All of the above.
4. A die is tossed, tell whether the following events are exhaustive or not.
a) X = Get prime number ; Y = Get multiple of 2 ; Z = Get 1.
b) X = Get prime numbers; Y = Get composite numbers; Z = Get 1.c) X = an odd number; Y = an even number.
10.4. Properties and formulas
Activity 10.4
Consider the letters of the word “PROBABILITY”.
a) How many letters are in this word
b) How many vowels are in this word? What is the ratio of numbers
of vowels to the total number of letters?
c) How many consonants are in this word? what is the ratio of the
numbers of consonants to total number of lettersd) Let A be the set of all vowels and B the set of all consonants. Find


Example 10.38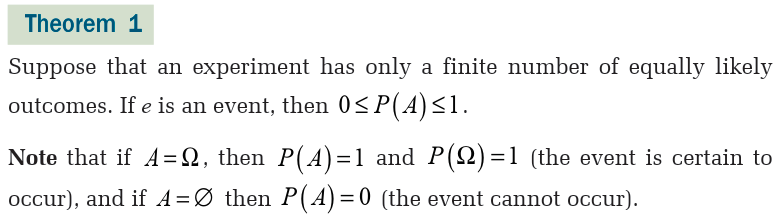
A letter is chosen from the letters of the word “MATHEMATICS”. What is
the probability that the letter chosen is an “A”?
Solution
Since two of the eleven letters are a’s, we have two favorable outcomes.
There are eleven letters, so we have 11 possible outcomes.Thus, the probability of choosing a letter a is
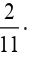
Example 10.39
A medical study tests a new medicine on 3500 people. It is effective for
3,010 people. Find the experimental probability that the medicine is
effective. Then, predict the number of people in a group of 6,000 for whomthe medicine will be effective.
Solution
From the definition, the probability of an event is the quotient of the
number of times that event occurs by the number of times experiment isdone.


Application activity 10.4
1. A letter is chosen from the letters of the word “MATHEMATICS”.
What is the probability that the letter chosen is
a) M? b) T?
2. An integer is chosen at random from the set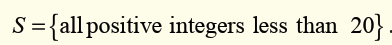
Let A be the event of
choosing a multiple of 3 and let B be the event of choosing an oddnumber. Find;



Example 10.42
In a group of 20 adults, 4 out of the 7 women and 2 out of the 13 men wear
glasses. What is the probability that a person chosen at random from the
group is a woman or someone who wears glasses?
Solution
Let A be the event: “the person chosen is a woman”.B be the event: “the person chosen wears glasses”.
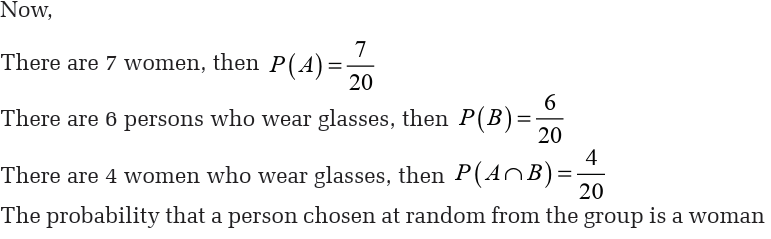
Application activity 10.11
1. A fair die is rolled, what is the probability of getting a even number
or prime number?
2. Two fair dice are rolled, what is the probability of getting a sum thatis divisible by 2 or 4?
Mutually exclusive events
Activity 10.12
A book is drawn from a bookshelf containing 15 books of which
5 are Mathematics books and 10 are English books. If A is the
event: “a book is a Mathematics book” and B is the event: “abook is an English book”, find:
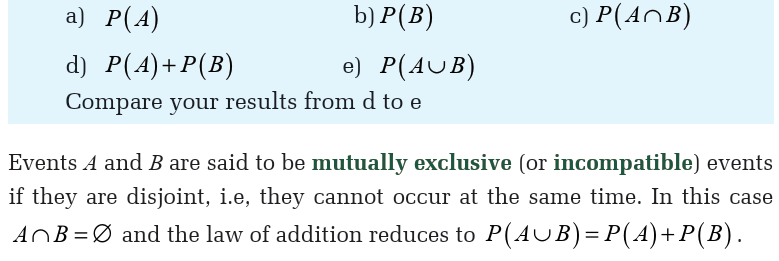
Example 10.44
A card is drawn at random from an ordinary pack of 52 playing cards. Findthe probability that the card drawn is a club or a diamond.

Application Activity 10.12
1. If A and B are mutually exclusive events, given the probability of A
Exhaustive events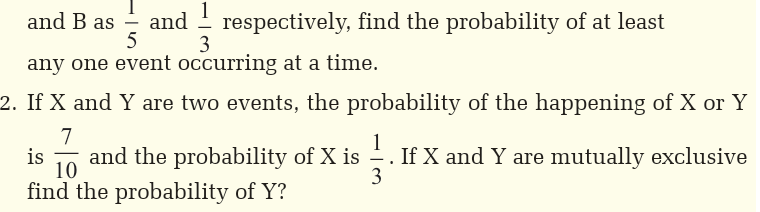
Activity 10.13An integer is chosen at random from the set
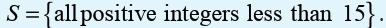 Let A be the event of choosing an
Let A be the event of choosing an odd number and let B be the event of choosing an even number. Find:

What can you say about result in a. and result in b.?


Example 10.43
Events A and B are such that they are both mutually exclusive andexhaustive. Find the relation between these two events.
Thus, if events A and B are such that they are both mutually exclusive and
exhaustive, then they are complementary.
Application activity 10.13
In a class of a certain school, there are 12 girls and 20 boys. If a
teacher wants to choose one learner to answer the asked question
a) What is the probability that the chosen learner is a girl?
b) What is the probability that the chosen learner is a boy?
c) If teacher doesn’t care on the gender, what is the probabilityof choosing any learners?
Unit summary
1. Combinatorial analysis is a mathematical theory of counting.
2. Experiment: any human activity.
Trial: small experiment contained in a large experiment.Outcome called event: a result of an experiment.


11. Probability is the chance that something will happen-how likely it is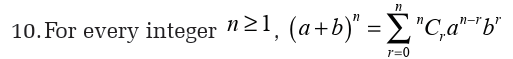
that some event will happen.
12. A random experiment is an experiment that, at least theoretically,
may be repeated as often as we want and whose outcome cannot be
predicted, the roll of a die.
13. Each time experiment is repeated, an elementary outcome is obtained.
14. The set of all elementary outcomes of a random experiment is called
the sample space, which is denoted by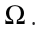
15. Discrete sample space: Firstly is the number of possible outcomes is
finite.
16. Continuous sample space: If the sample space contains one or more
intervals, the sample space is then uncountable infinite.
17. An event is a set of elementary outcomes. That is, it is a subset of the
sample space.
18. Two or more events which have an equal probability of occurrence
are said to be equally likely, i.e. if on taking into account all the
conditions, there should be no reason to except any one of the events
in preference over the others. Equally likely events may be simple or
compound events.
19. Two events, A and B are said to be incompatible (or mutually exclusive)
if their intersection is empty. We then write that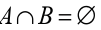
20. Two events, A and B are said to be exhaustive if they satisfy the condition
21. An event which is sure to occur at every performance of an experiment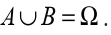
is called a certain event connected with the experiment.
22. An event which cannot occur at any performance of the experiment
is called an impossible event.
23. Two events are said to be equivalent or identical if one of them
implies and implied by other. That is, the occurrence of one event
implies the occurrence of the other and vice versa.
24. The outcomes which make necessary the happening of an event in
a trial are called favourable events.
25. If E is an event, then ' E is the event which occurs when E does notoccur. Events E and ' E are said to be complementary events.
End unit assessment
1. If there are three different roads joining town A to town B and four
different roads joining town B to town C, in how many different ways
can I travel from A to C via B and return if:
a) there are no restrictions,
b) I am not able to return on any road I used on the outwards
journey?
2. How many 3-digits numbers can be formed using only the digits 1,
2, 3, 5, 7 and 8? How many of these numbers are even? How many
are less than 500?
3. There are three roads joining town X to town Y; three more roads join
Y to z and two roads join Z to A. How many different routes are there
from X to A passing through Y and Z?
4. In how many ways can a group of ten children be arranged in a line?
5. In how many ways can eight different books be arranged on a
bookshelf?
6. The letters a, b, c and d are to be arranged in a row with each letterbeing used once and once only. In how many ways can this be done?
9. There are ten teams in the local football competition. In how many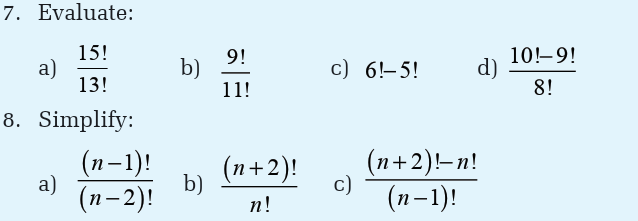
ways can the first four places in the premiership table be filled?
10. In how many different ways can five identical blue balls, two
identical red balls and a yellow ball be arranged in a row?
11. Find the number of arrangements of four different letters chosen
from the word PROBLEM which:
a) begin with a vowel.
b) end with a consonant.
12. With his breakfast, a man sometimes has tea, sometimes coffee and
sometimes fruit juice, but never more than one of these on any one
day. Find the number of possible arrangements he can have in a
period of 4 days if:
a) he always has a drink of some sort,
b) he may choose not to have a drink on certain days.
13. How many numbers greater than 300 can be formed from the figures
4, 3, 2 and 1 if each figure can be used not more than once in each
number and all the figures need not be used each time?
14. A box contains 14 colored discs which are identical except for their
color. There are 5 red discs, 4 green discs, 4 blue discs and 2 yellow.
In how many ways can the 14 discs be arranged in a row?
15. Find the number of different three-letter arrangements that can be
made from the letters of the word ISOSCELES.
How many of these arrangements will contain:
a) no E’s at all,
b) at least one E,
c) no vowels at all,
d) at least one vowel
16. A basketball team of 6 is to be chosen from 11 available players. In
how many ways can this be done if:
a) there no restrictions,
b) 3 of the players are automatically selected,
c) 3 of the players are automatic in selections and 2 other players
are injured and cannot play?
17. In how many ways can 9 people be placed in cars which can
take 2, 3 and 4 passengers respectively, assuming that the seating
arrangements inside the cars are not important?
18. A group consists of 5 boys and 8 girls. In how many ways can a team
of four be chosen, if the team contains:
a) no girl.
b) not more than one girl.
c) atleast two boys?
19. Find the number of ways that 9 children can be divided into:
a) a group of 5 and a group of 4 children,
b) three groups of 3 children.
20. a) A small holiday hotel advertises for a manager and 7 other
members of staff. There are 4 applicants for the position of
manager and 10 other people apply for the other jobs at the hotel.
Find the number of different ways of selecting a group of people
for the 8 jobs.
b) The hotel has 4 single rooms, 6 double rooms and 5 family rooms.
For a particular week, 4 individuals book single rooms, 3 couples
book double rooms and 3 families book family rooms. Given that
all the rooms are available for that week, find the number of
different possible arrangements of booking amongst the rooms.
c) One afternoon, 12 guests organize a game requiring 2 teams of 6.
Find the number of different ways of selecting the teams.
d) Given that the 12 guests consist of 6 adults and 6 children and
that each team must contain atleast 2 adults, find the number ofdifferent ways of selecting the teams.





41. Which of the following is an experiment?
a) Tossing a coin, b) Rolling a single die,c) Choosing a marble from a jar, d) All of the above.
42. Which of the following is an outcome?
a) Rolling a pair of dice, b) Landing on red,
c) Choosing 2 marbles from a jar, d) None of the above.
43. Which of the following experiments does not have equally likely
outcomes?
a) Choose a number at random between 1 and 7, b) Toss a coin,
c) Choose a letter at random from the word SCHOOL, d) None of the above.
44. A glass jar contains 5 red, 3 blue and 2 green jelly beans. If a jelly
bean is chosen at random from the jar, then which of the following
is an impossible event?
a) Choosing a red jelly bean, b) Choosing a blue jelly bean,
c) Choosing a yellow jelly bean, d) None of the above.
45. A spinner has 7 equal sectors numbered 1 to 7. If you spin the
spinner, then which of the following is a certain event?
a) Landing on a number less than 7,
b) Landing on a number less than 8,
c) Landing on a number greater than 1,
d) None of the above.
46. Tickets numbered 1 to 20 are mixed up and then a ticket is drawn at
random. What is the probability that the ticket drawn has a number
which is a multiple of 3 or 5?
47. A bag contains 2 red, 3 green and 2 blue balls. Two balls are drawn at
random. What is the probability that none of the balls drawn is blue?
48. In a box, there are 8 red, 7 blue and 6 green balls. One ball is picked
up randomly. What is the probability that it is neither red nor green?
49. In a class, there are 15 boys and 10 girls. Three students are selected
at random. What is the probability that 1 girl and 2 boys are selected?
50. From a pack of 52 cards, two cards are drawn together at random.
What is the probability of both the cards being kings?
51. One card is drawn at random from a pack of 52 cards. What is the
probability that the card drawn is a face card (Jack, Queen and King
only)?
52. An integer is chosen at random from the first 200 positive integers.
Find the probability that the number is:
a) divisible by 2
b) divisible by 7
c) divisible by 2 and 7
d) divisible by neither 2 nor 7
53. The letters of the word FACETIOUS are arranged in a row. Find the
probability that:
a) the first 2 letters are consonants,
b) all the vowels are together.
