Unit 7 :Vector space of real numbers
7.0 Introductory activity

objectives
After completing this unit, I will be able to:
» Find the norm of a vector.
» Calculate the scalar product of two vectors.
» Calculate the angle between two vectors.
» Apply and transfer the skills of vectors to other area ofknowledge.






Scalar product and properties
The scalar product or dot product (or sometimes inner product) is an
algebraic operation that takes two coordinate vectors and returns a single
number.
Algebraically, it is the sum of the products of the corresponding coordinatesof the two vectors. That is, the scalar product of vectors
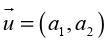 and
and
We can illustrate this scalar product in terms of work done by a force on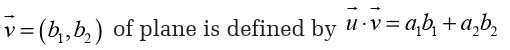
the body:
Suppose that a person is holding a heavy weight at rest. This person may
say and feel he is doing hard work but in fact none is being done on the
weight in the scientific sense. Work is done when a force moves its point
of application along the direction of its line of action.
If the constant force F and the displacement S are in the same direction
and we define the work W done by the force on the body by W= F .S


Example 7.5
The figure below shows a girl pulling a wagon with a force of 50Newtons.
How much work is done in moving the wagon 100 meters if the handlemakes an angle of 30 degrees with the ground?
Solution
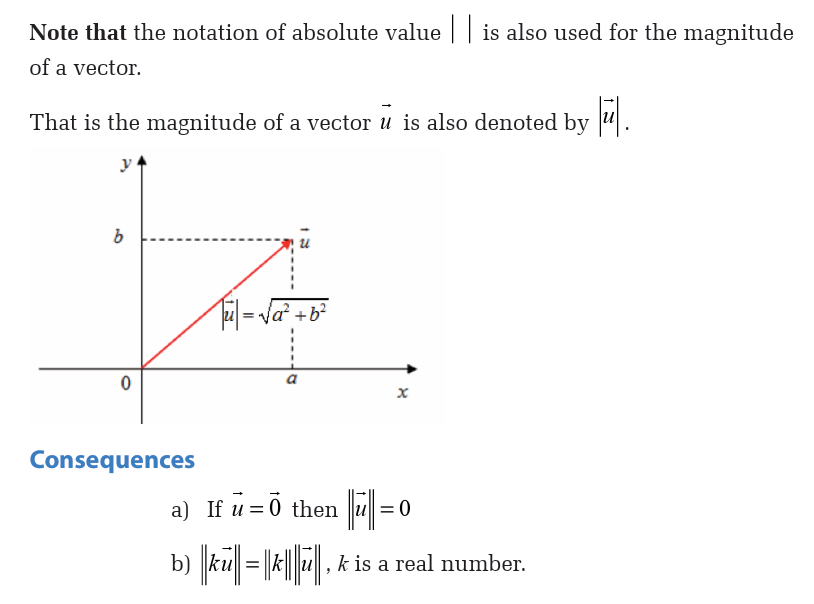
Let us position the vector in the cartesian plane in such a way the wagon
moved from the origin O(0,0) to the point P(100,0). The motion is from Oto P.



We can illustrate the scalar product in terms of work done by the force on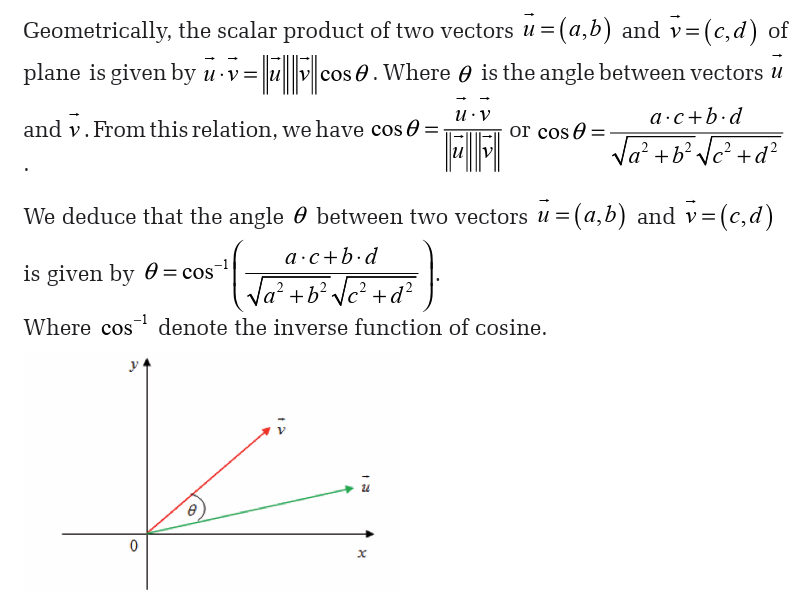
the body:
If the constant force F and the displacement S are in the same direction,
the work W done by the force on the body is W= F .S
If the force does not act in the direction in which motion occurs but an angle
to it , then the work done is defined as the product of the component ofthe force in the direction of motion and the displacement in that direction.
Notice
• Two vectors are perpendicular if the angle between them is a multiple
of a right angle.
• Two vectors are parallel and with the same direction if the angle
between them is a multiple of a zero angle.
• Two vectors are parallel and with the opposite direction if the anglebetween them is a multiple of a straight angle.



Application
In physics,
, calculate the value of k
Vectors are fundamental in the physical sciences. They can be used to
represent any quantity that has magnitude, has direction, and which adheres
to the rules of vector addition. An example is velocity, the magnitude of
which is speed. For example, the velocity 7 meters per second upward
could be represented by the vector (0,7). Another quantity represented by a
vector is force, since it has a magnitude and direction and follows the rules
of vector addition. Vectors also describe many other physical quantities,
such as linear displacement, displacement, linear acceleration, angular
acceleration, linear momentum, and angular momentum. Other physical
vectors, such as the electric and magnetic field, are represented as a systemof vectors at each point of a physical space; that is, a vector field.
In geography,Vectors can be used in air plane navigation
Use of vectors in real life
Vectors are used whenever some quantity has a size and a direction.
The most important vectors in basic physics are probably position and
momentum. These are used to calculate an object’s motion. Some other
useful vectors in physics are velocity which tells you how fast an object’s
moving and current density which tells you how the total current is
distributed around the conductor.
In chemistry, vectors are used to consider bond polarity; there are chemical
bonds where one side is slightly negatively charged, and the other is
slightly positively charged. This creates an electric field pointing from the
positive to the negative end, which needs to be considered in chemistry
calculations.
Vectors can also be used with other shapes to produce vector graphics.
These are images which are produced using a set of instructions. When
you save the image, the instructions are stored in the computer memory as
another type of image.
In many fields, vectors are useful for solving systems which are represented
by many simultaneous equations. You arrange the system as the product
of a matrix (taken as a vector of vectors) multiplied by a vector, which givesa vector output.
In medicine, the mathematics definition implies that vectors are used to
calculate speed of blood flow to and from the heart or air through the
lungs.
On the other hand, the medical field takes vectors as animals, insects
or means (wind, water, etc) that carry germs, viruses, bacteria, or fungal
spores within or outside their bodies from one location to another where itdoes or does not result in disease.
Unit summary



