Unit 5 :Limits of polynomial, rational and irrational functions
5.0 Introductory activity
To find the value of a function
when x approaches 2, a student used a calculator and dressed a table as follows:
objectives
After completing this unit, I will be able to:
» Calculate limits of certain elementary functions.
» Apply informal methods to explore the concept of a limit
including one sided limits.
» Solve problems involving continuity.
» Use the concepts of limits to determine the asymptotes
to the rational and polynomial functions.» Develop calculus reasoning.
5.1. Concepts of limits
Neighbourhood of a real number
Activity 5.1.1
Study the following political map of Lesotho, Swaziland and
South Africa. What can you say about the boundaries of Lesotho
and Swaziland?What is the actual name of Swaziland?
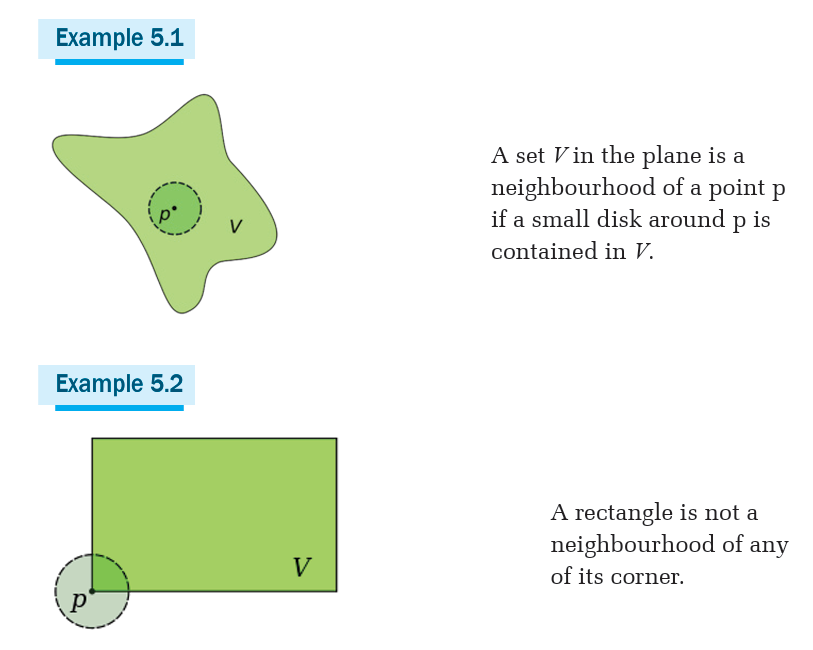
A set N is called a neighbourhood of point p if there exists an open interval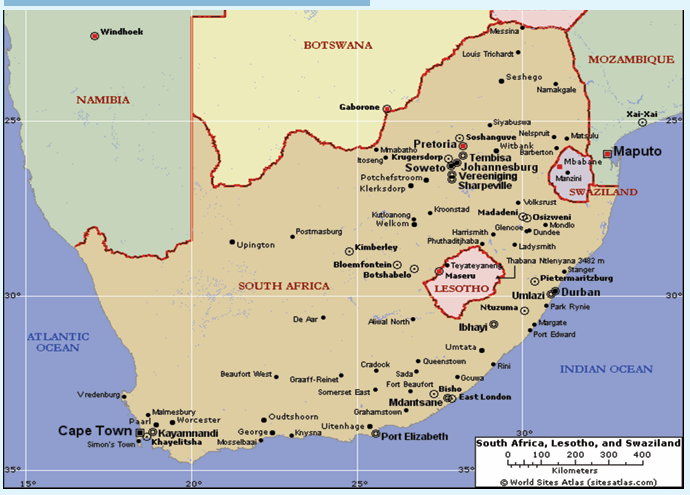
I such that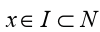
. The collection of all neighbourhoods of a point is
called the neighbourhood system at the point.
A deleted neighbourhood of a point p (sometimes called a puncturedneighbourhood) is a neighbourhood of p without p itself
Application Activity 5.1.1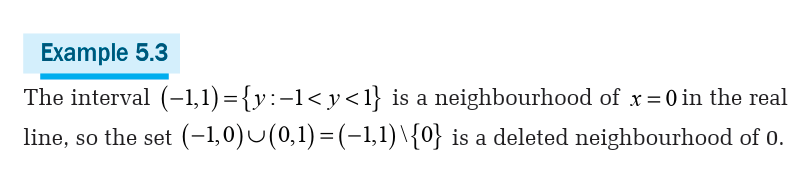
1. Apart from The Kingdom of Lesotho, give two examples of
countries or Cities in the world that are surrounded by a single
country or city.
2. Give three examples of intervals that are neighbourhoods of -5?
3. Is a circle a neighborhood of each of its points? Why?
4. Draw any plane and show three points on that plane for which
the plane is their neighborhood.
Note:
A deleted neighbourhood of a given point is not in fact a neighbourhood
of the point. The concept of deleted neighbourhood occurs in thedefinition of the limit of a function.
Limit of a functionActivity 5.1.2
To find limit of a function
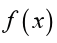as x approaches a, first we need to
substitute that value a in the function and see what happens. The limitcan exist or not.
5.2. One sided limits
Activity 5.2
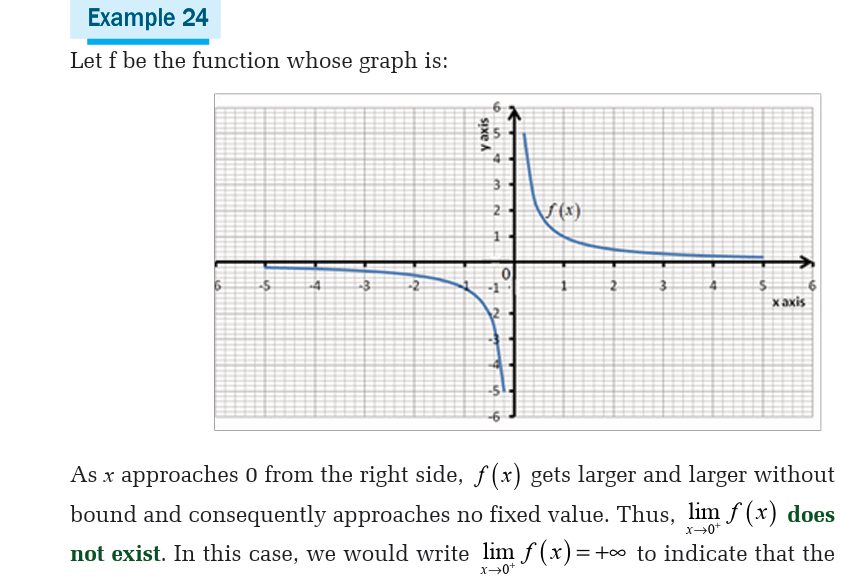
Infinite limits
A function whose values grow arbitrarily large can sometimes be said to
have an infinite limit. Since infinity is not a number, infinite limits arenot really limits at all but they provide a way of describing the behavior of
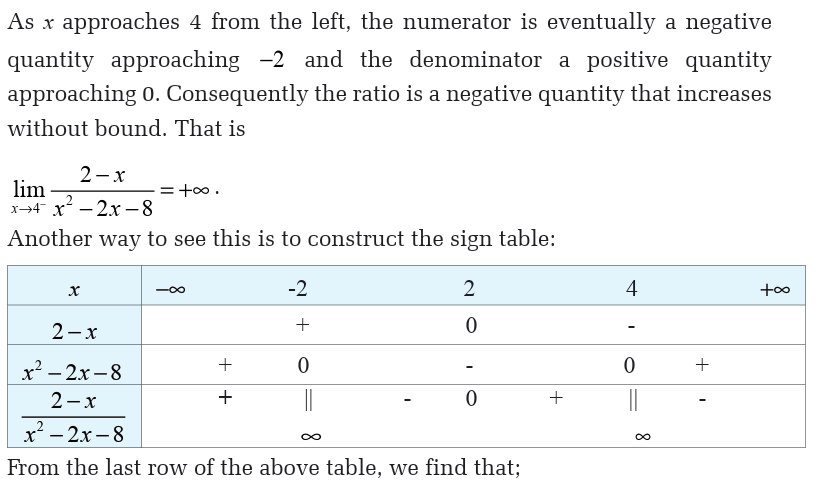
Beware!
So, we have dealt with almost every basic algebraic operation involvinginfinity. There are three cases that we have not dealt with yet. These are
To find a limit graphically, we must understand each component of the
limit to ensure the graph is used properly to evaluate the limit.
Example 23Let f be the function whose graph is shown below,
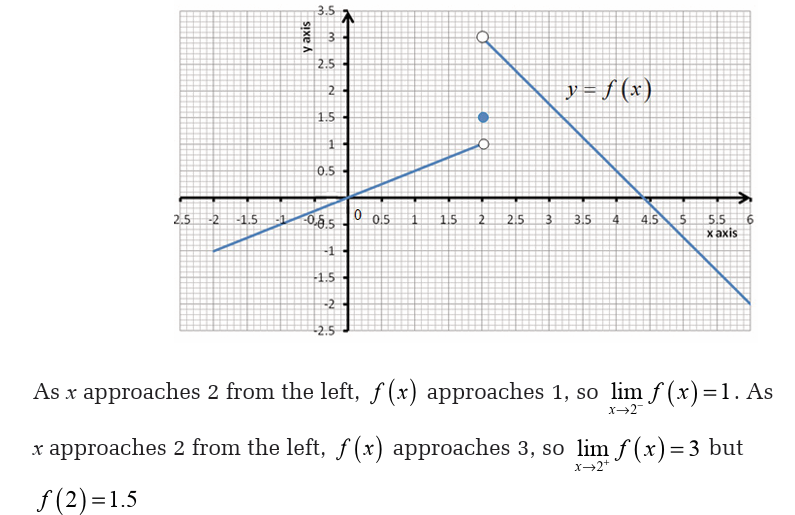
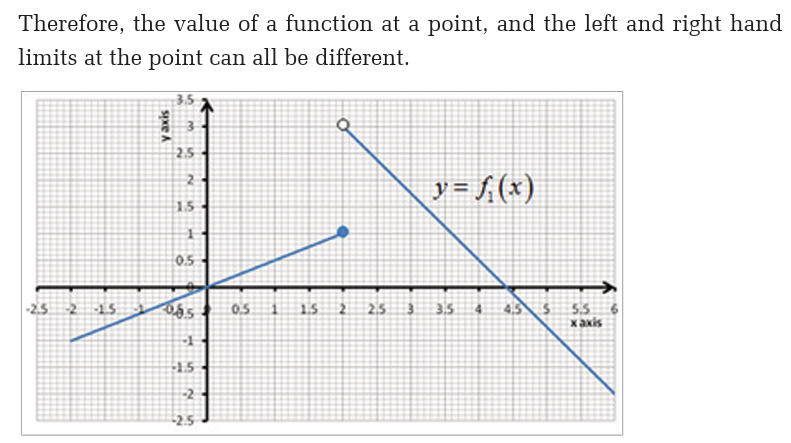
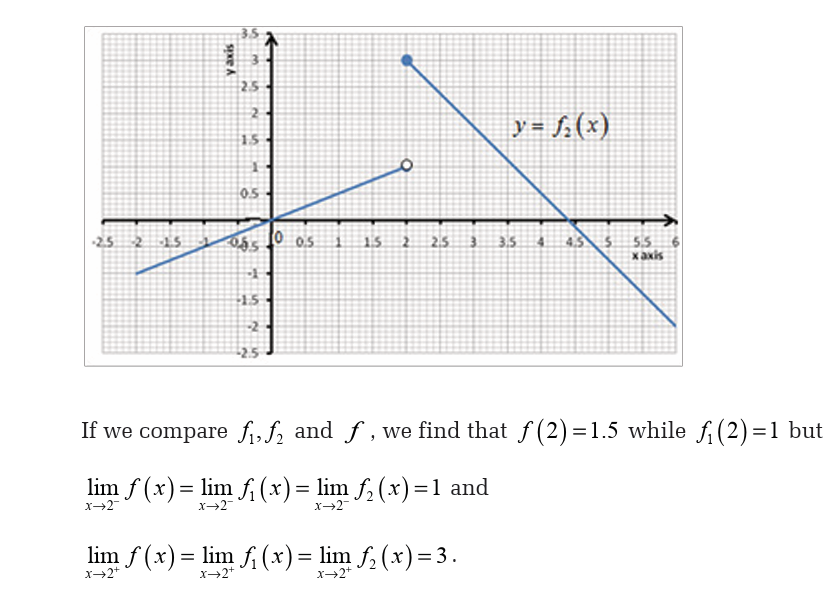
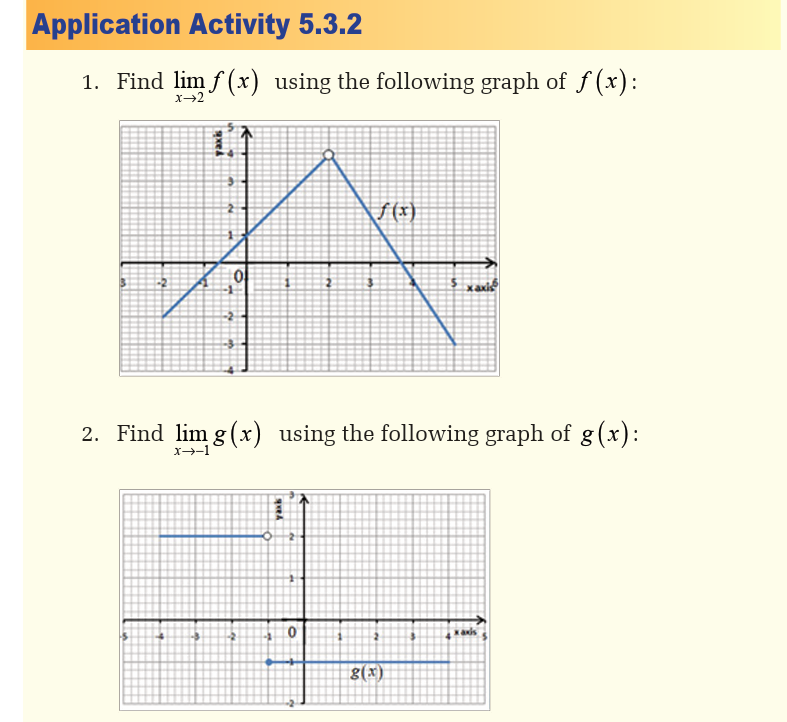
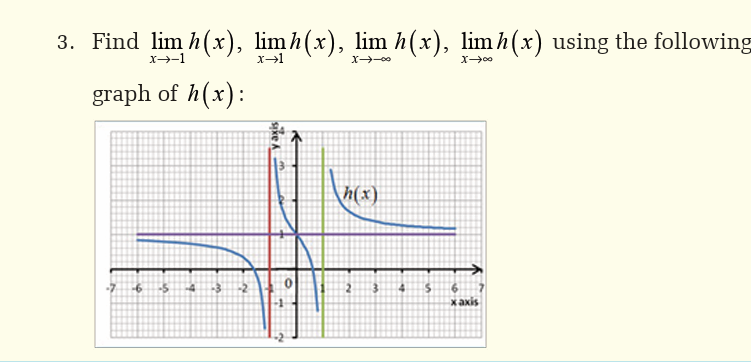
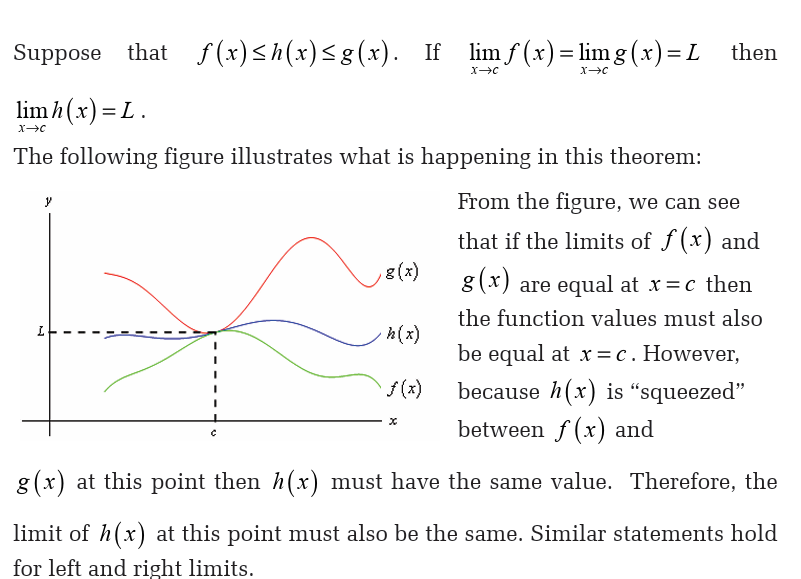
5.4. The squeeze theorem and operations on limits
5.5. Indeterminate cases
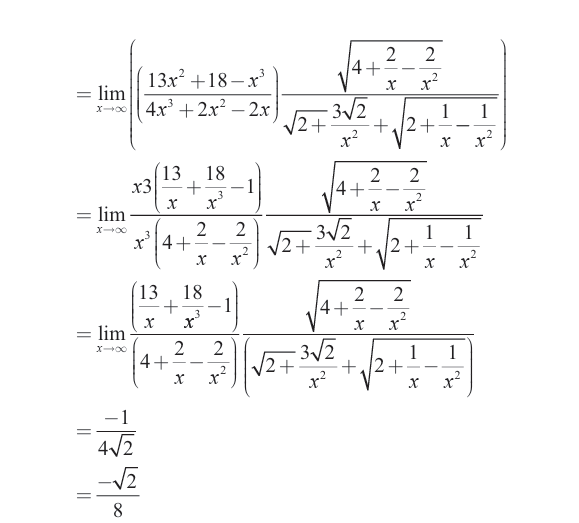
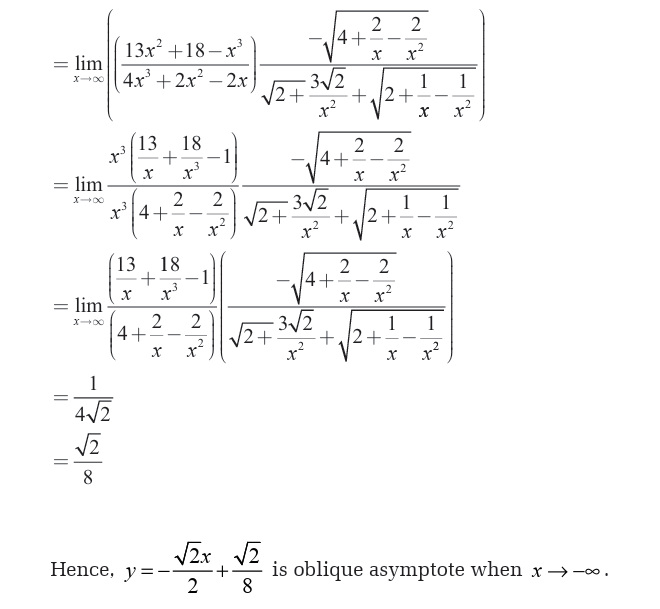
Or Since we have a rational function and degree of numerator is equal
to the degree of denominator, to find the limit as x tends to infinity, we
need to divide the coefficients of the highest degree for numerator anddenominator. That is the limit is given by
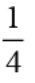
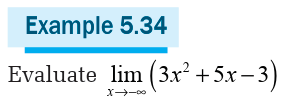
Note that the limits involving indeterminate form
can be evaluated by successive derivatives of numerator and denominator.
This method is called L’Hôpital rule.We will see this in application of derivatives.
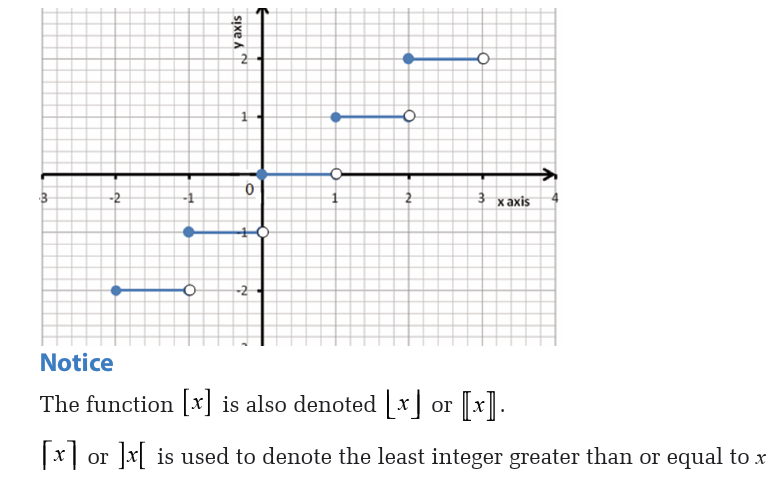
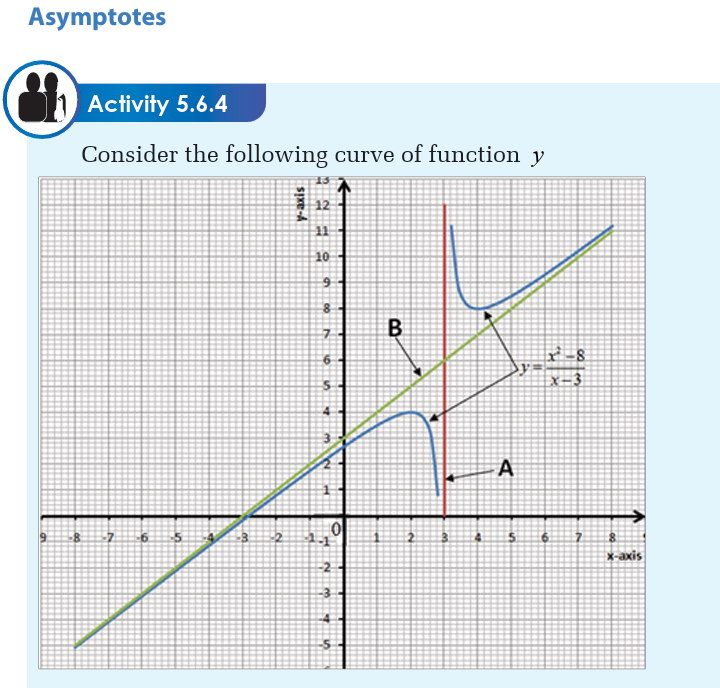
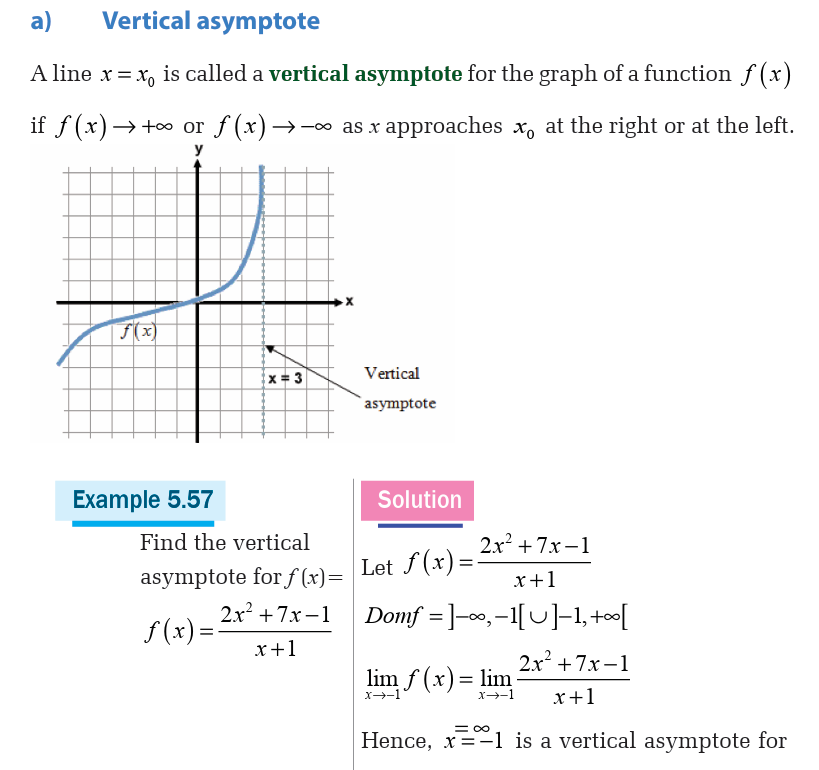
Types of asymptotes
There are three types of asymptotes:
• Vertical asymptote,
• Horizontal asymptote and• Oblique asymptote.
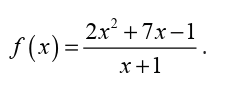
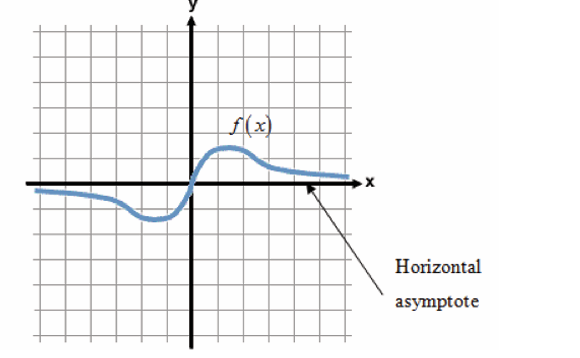
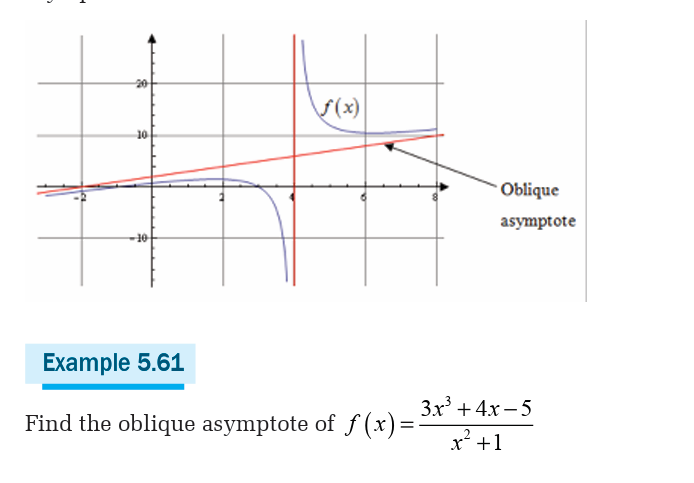
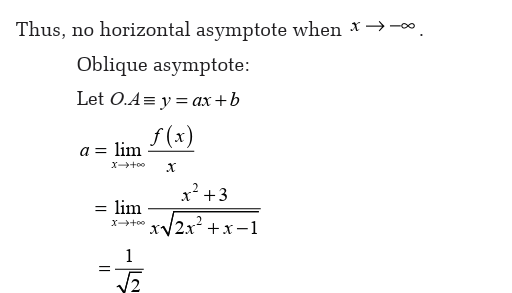
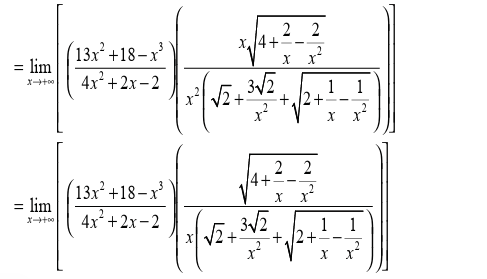
Limits can be applied in different fields in real life. In economics the
average cost per unit sold is calculated using limits.In physics, the velocity and acceleration are calculated using limits,etc.
1. Instantaneous rate of change of a function
The instantaneous rate of change of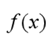
of at a, also called the rate of change of
at a, is defined to be the limit of the average rate of change
of over shorter and shorter intervals around a.
Since the average rate of change is a difference quotient of the form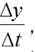
, the instantaneous rate of change is a limit of difference quotient. In practice,we often approximate a rate of change by one of these difference quotients.
2. Instantaneous velocity
Instantaneous velocity of a moving body is the limit of average velocityover an infinitesimal interval of time.
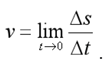
Unit summary
