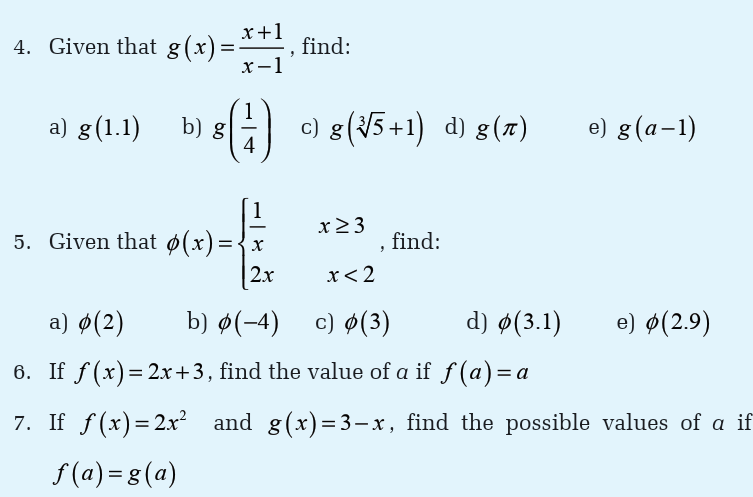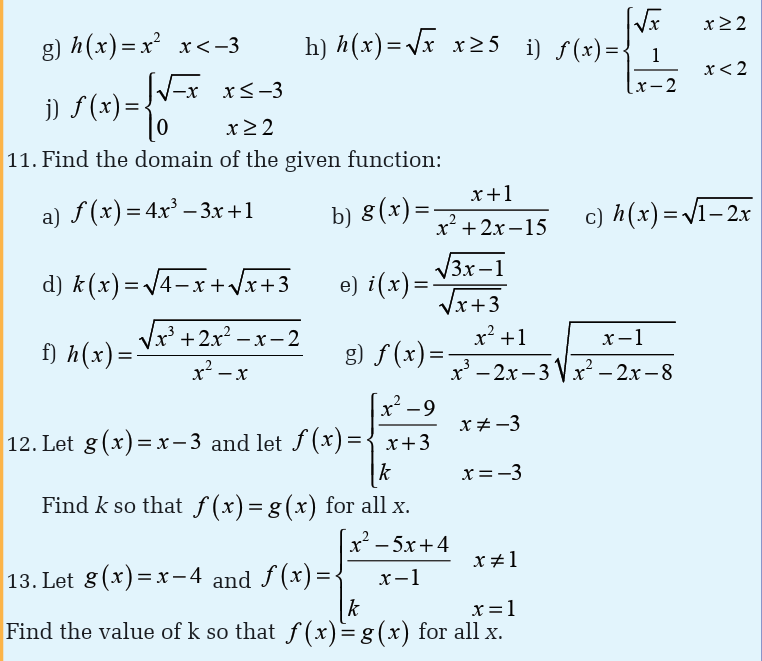Unit 4 :Polynomial, Rational and irrational functions
4.0 Introductory activity
1. Consider the following sentences:
i. The function of the heart is to pump blood
ii. Last Saturday, my sister got married; the arrangement of chairs in the
main hall was in function of the number of guests.
iii. The area of a square is function of the length of its side.
Explain what is meant by the word “Function” in each of the three sentences
above.
2. Any function involves at least two variables. Identify the “independentvariable” and the “dependent variable” in the following functions:
4. If we agree that the set of all possible values, the independent variable
can assume is called the “ Domain” of the function and the set of all
possible values, the dependent value can assume is called the “Range”
of the function, determine the range and the domain of each of the
functions in part (2) above.
Objectives
After completing this unit, I will be able to:
» Demonstrate an understanding of operations on
polynomials, rational and irrational functions, and
find the composite of two functions.
» Identify a function as a rule and recognize rules that
are not functions.
» Determine the domain and range of a function
» Find whether a function is even , odd , or neither
» Construct composition of functions.
4.1. Generalities on numerical functions
Activity 4.1
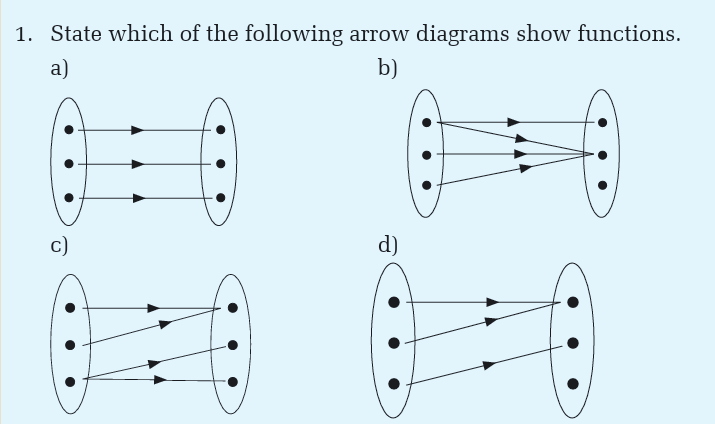
In the following arrow diagram, for each of the elements of set A,state which element of B is mapped to it.
A function is a rule that assigns to each element in a set A one and only one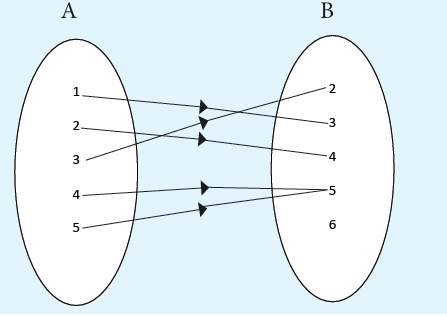
element in set B. We can even define a function as any relationship which
takes one element of one set and assigns to it one and only one element of
second set. The second set is called a co-domain. The set A is called thedomain, denoted by Domf.
Example 4.1
Four children, Ann, Bob, Card and David, are given a spelling test whichis market out of 5; their marks for the test are shown in the arrow diagram:
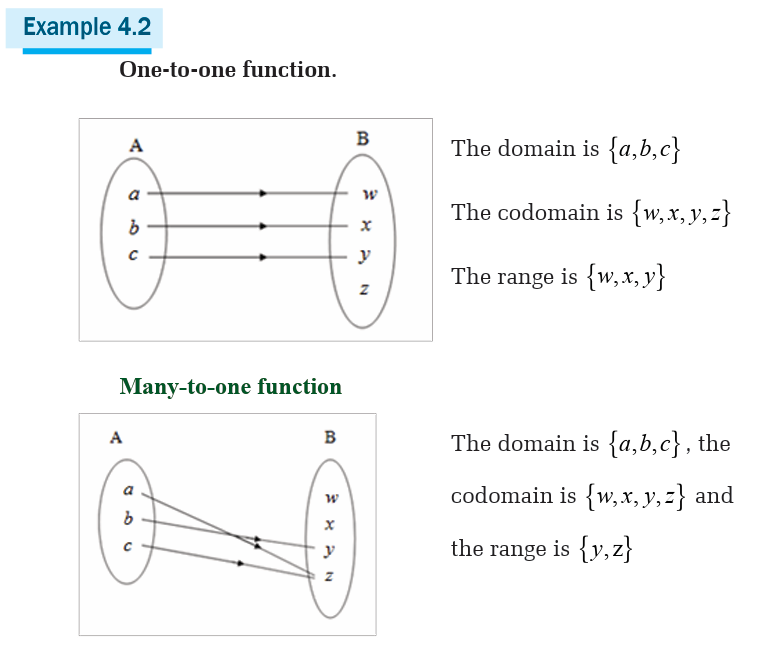
Functions for which each element of the domain is associated onto a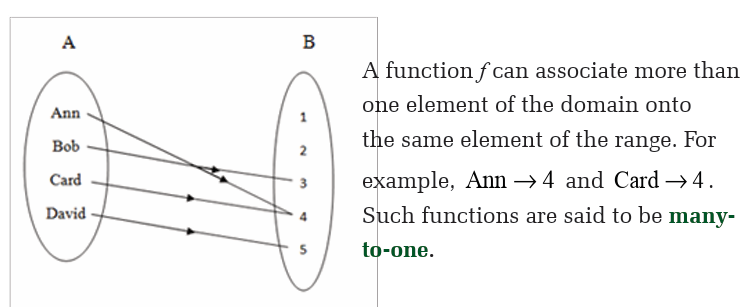
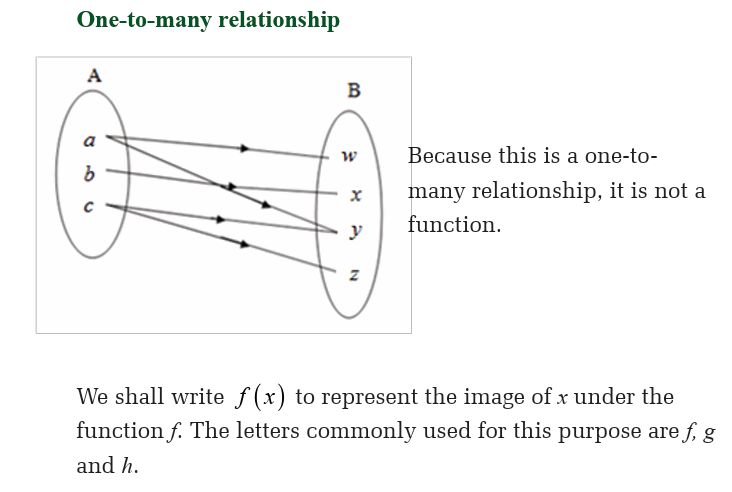
different element of the range are said to be one-to-one. Relationships
which are one-to-many can occur, but from our preceding definition, theyare not functions.



4. You have ever followed a speech talking about NDI
UMUNYARWANDA . You have been said that Rwandans have
been divided and now they want to be unified. From the types of
relationship (in Mathematics), complete this sentence: We have
been made……to……by colonialists, NDI UMUNYARWANDA ismaking us……to……
4.2. Classification of functions
Activity 4.2
State which of the following functions is a polynomial, rationalor irrational function
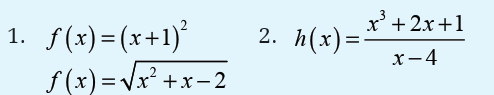
a) Constant function
A function that assigns the same value to every member of its domain iscalled a constant function C.


Application Activity 4.2
Observe the given functions and categorize them into polynomial,rational or irrational functions.
4.3. Finding domain of definition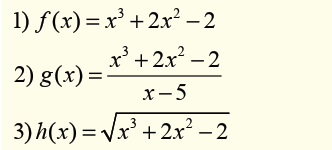
Activity 4.3.1
Case 3: The given function is an irrational function
Activity 4.3.2
For each of the following functions, give a range of values of thevariable x for which the function is not defined.




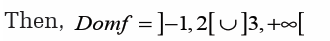
Example 4.18
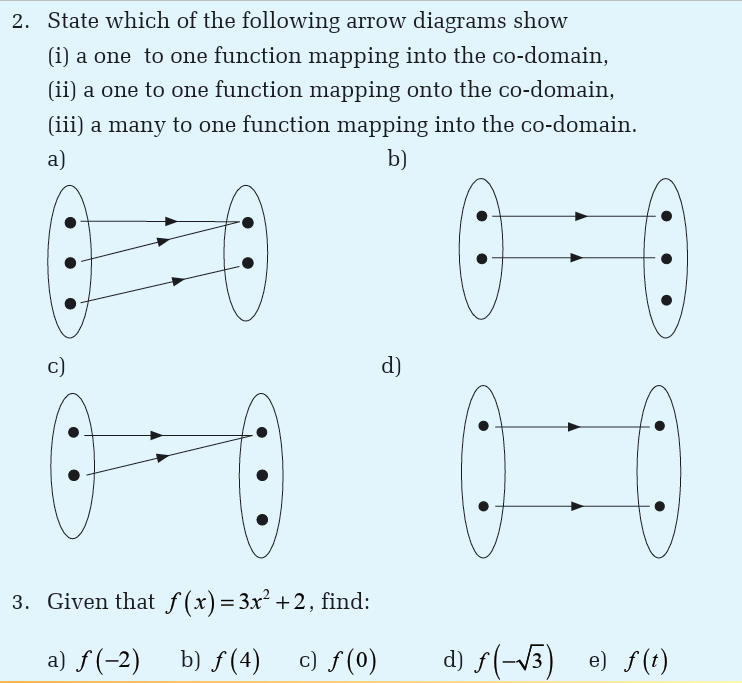
The following functions map an element x of the domain onto its image y.
For each of the three functions below, state
(i) the domain for which the function is defined,
(ii) the corresponding range of the function,(iii) whether the function is one-to-one or many-to-one.
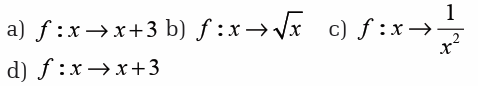


4.4. Operations on functions
Activity 4.4
Just as numbers can be added, subtracted, multiplied and divided to produce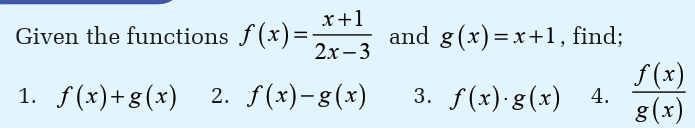
other numbers, there is a useful way of adding, subtracting, multiplying
and dividing functions to produce other functions. These operations aredefined as follows:
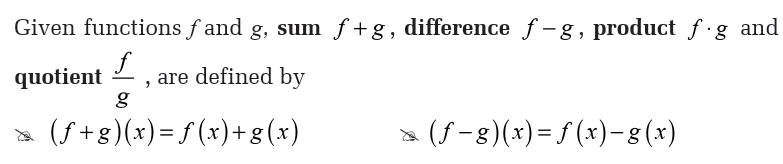






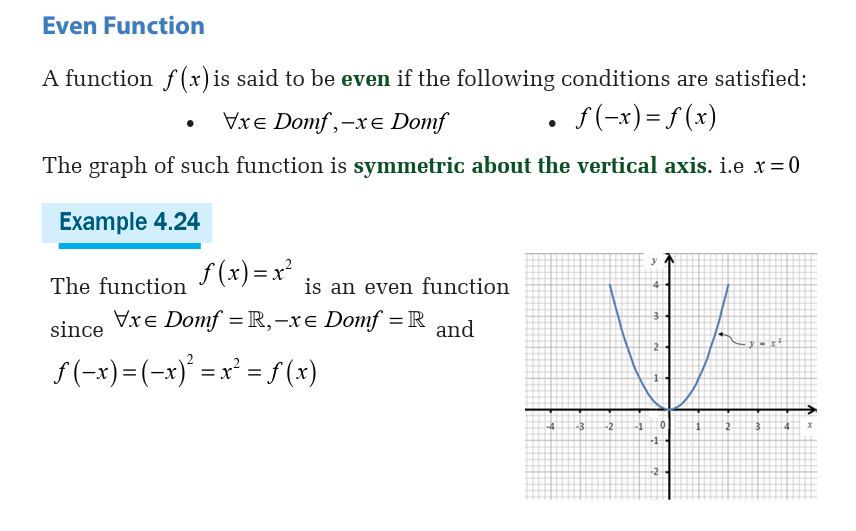
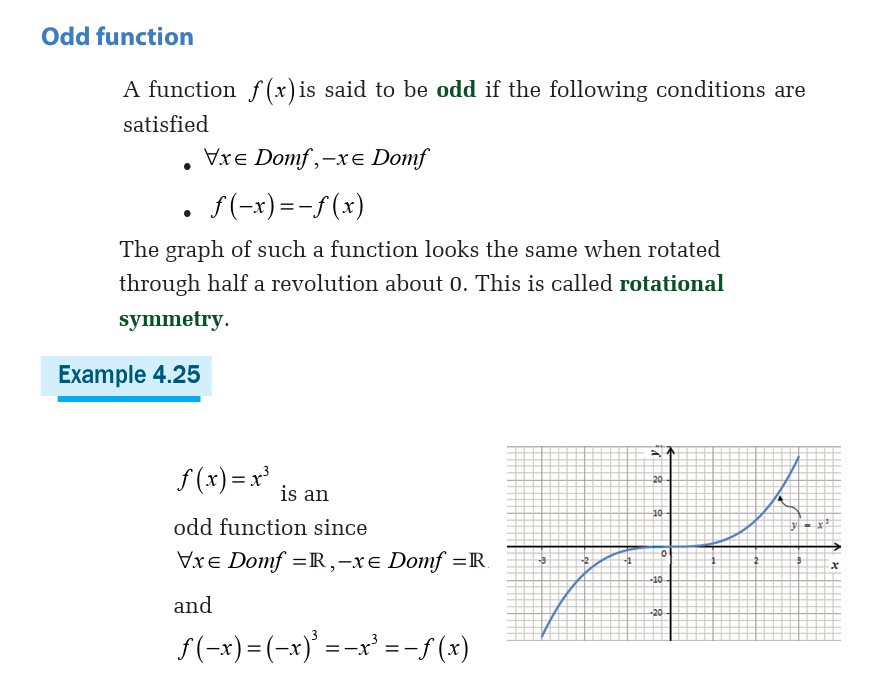
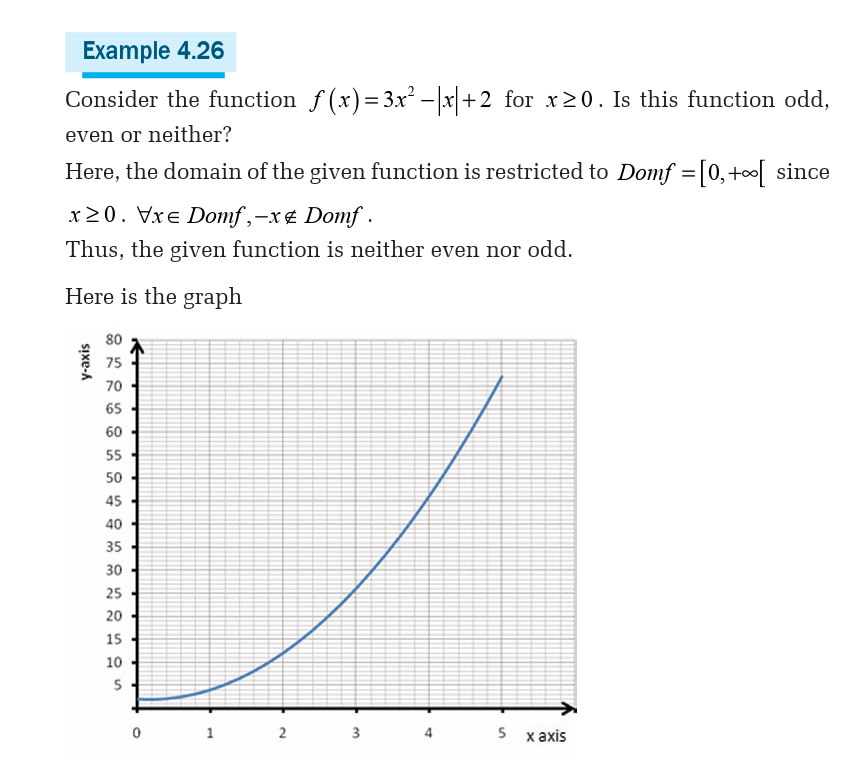
4.5 Parity of function
Odd and even functions
Activity 4.5
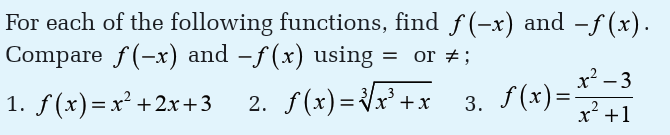

4.6. Factorization of polynomials
Activity 4.6
For each expression above, identify the common factors for both terms
and rewrite the expression in factor form. Compare your results with
those of other classmates.
In arithmetic, you are familiar with factorization of integers into primefactors.

a) How many terms does each result have?
b) Find out the common characteristics for the all above expressions.What is the highest and lowest exponent for the variable
 in all expressions?
in all expressions?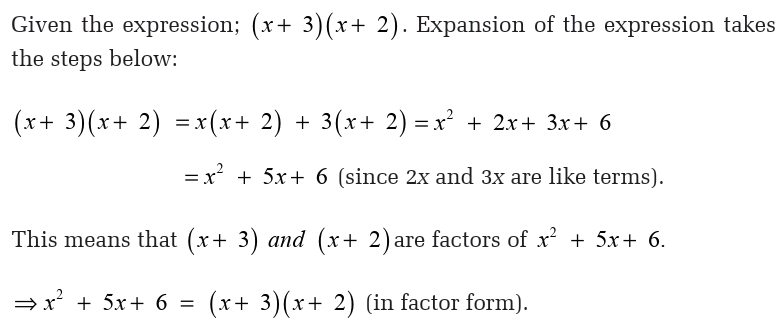
a) The coefficient of the highest degree of this trinomial is 1,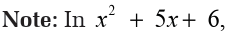
b) The coefficient of the linear term is 5, the sum of the constant terms
in the binomial factors, and
c) The constant term is 6, the product of the constant terms in the
binomial factors.Generally,
1. List all the possible pairs of integers whose product equals the
constant term.
2. Identify the only pair whose sum equals the coefficient of the linear
term.
3. Rewrite the given expression with the linear term split as per the
factors in 2 above.
4. Factorise your new expression by grouping, i.e. taking two terms at a
time.5. Check that the factors are correct by expanding and simplifying.
Example 4.27
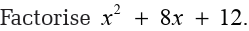

Note: Since all the terms in the example are positive, the negative pairs of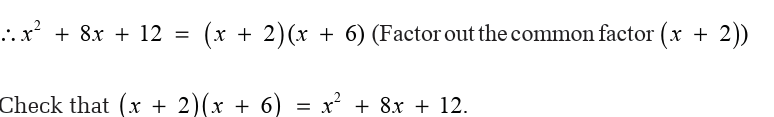
factors of 12 could have been omitted altogether.
Note that:
• If the third term in the split form of the expression is negative, wefactor out the negative common factor.
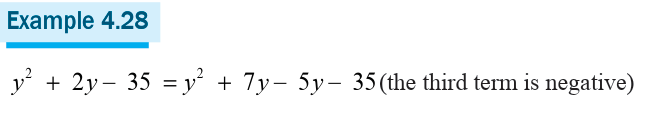
Each binomial expansion has three terms
The first term is the square of the first term of the binomial
The third term is the square of the second term of the given binomialThe middle term is twice the product of the two terms of the binomial
Remarks
If a trinomial is a perfect square,
1. The first term must be a perfect square.
2. The last term must be a perfect square.
3. The middle term must be twice the product of numbers that weresquared to give the first and last terms.


4.8. Graphs of linear and quadratic functions
Activity 4.8 1.Copy and complete the tables below.
2. Use the coordinates from each table to plot the graphs on separate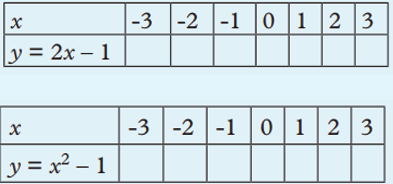
Cartesian planes.3. What is your conclusion about the shapes of the graphs?
4.8.1 Linear functions
Definition of linear function

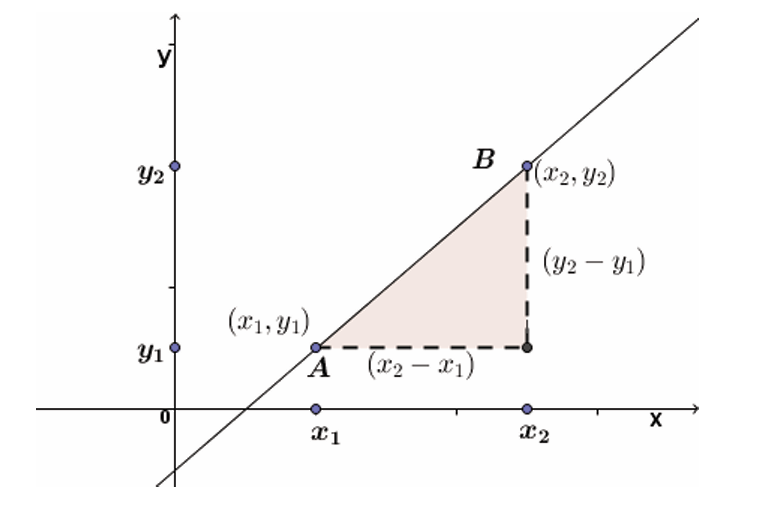
In the Cartesian plane, the gradient of a line is the measure of its slope
or inclination to the x-axis. It is defined as the ratio of the change in
y-coordinate (vertical) to the change in the x-coordinate (horizontal).
When drawing a graph of a linear function, it is sufficient to plot only
two points and these points may be chosen as the x and y intercepts of
the graph. In practice, however, it is wise to plot three points. If the three
points lie on the same line, the working is probably correct, if not you havea chance to check whether there could be an error in your calculation.
From the table the coordinates (x, y) are
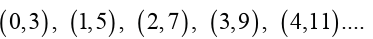
When drawing the graph, the dependent variable is marked on the vertical axis
generally known as the y – axis. The independent variable is marked on the
horizontal axis also known as the OX --axis
4.8.2 Quadratic function
Definition of quadratic functionA polynomial equation in which the highest power of the variable is 2 is
Table of values are used to determine the coordinates that are used to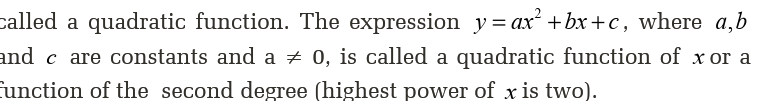
draw the graph of a quadratic function. To get the table of values, we
need to have the domain (values of an independent variable) and then
the domain is replaced in a given quadratic function to find range (values
of dependent variables). The values obtained are useful for plotting the
graph of a quadratic function. All quadratic function graphs are parabolicin nature

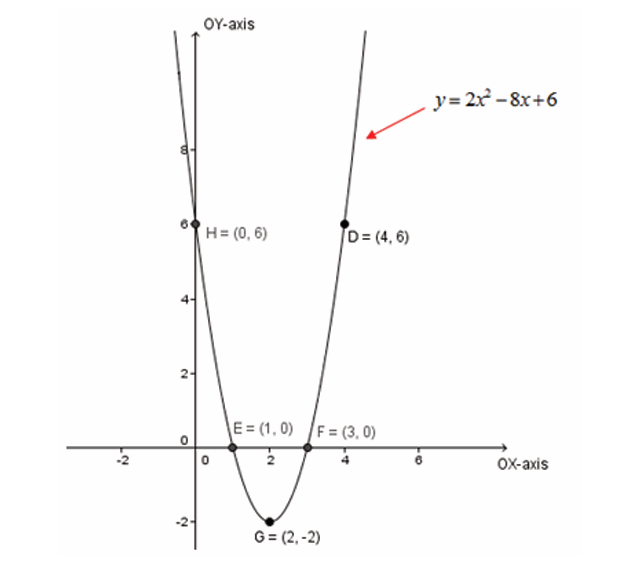
Graph of quadratic function
The graph of a quadratic function can be sketched without table of values
as long as the following are known.
• The vertex
• The x-intercepts• The y-intercept

4.9. Applications
Activity 4.9
Give three examples of where you think functions can be used in
daily life.
Polynomials are used to describe curves of various types; people use them
in the real world to graph curves. For example, roller coaster designers may
use polynomials to describe the curves in their rides. Polynomials can be
used to figure how much of a garden’s surface area can be covered with
a certain amount of soil. The same method applies to many flat-surface
projects, including driveway, sidewalk and patio construction.
Functions are important in medicine, building structures (houses,
businesses,…), vehicle design, designing games, to build computers
(formulas that are used to plug to computer programs), knowing how much
change you should receive when making a purchase, driving (amount of
gas needed for travel).
In the health field, polynomials are used for example to predict how
patients will metabolise medication over time. When painkillers move
through the bloodstream, enzymes start to break them down. Over time,the body moves more and more of the drug from the blood..



Unit summary
1. A function f is a rule that assigns to each element in a set A one and
only one element in set B. The second set is called a co-domain. The
set A is called the domain, denoted by Domf. The set of all possible
values of f(x) as x varies over the domain is called the range2. A function that is expressible as ratio of two polynomials is called



12. Polynomials are used to describe curves of various types; people
use them in the real world to graph curves. Functions are important
in calculating medicine, building structures (houses, businesses,…),
vehicle design, designing games, to build computers (formulas that
are used to plug to computer programs), knowing how much change
you should receive when making a purchase, driving (amount of gasneeded for travel).
End Unit Assesment