S4 : Mathematics

 3.0 Introductory activity
 1. By the use of library and computer lab, do the research and explain 
the linear equation. 
2. If x is the number of pens for a learner, the teacher decides to give 
him/her two more pens. What is the number of pens will he/she have? 

3. Complete the following table called table of value to indicate the

4. Find out an example of problem from the real life situation that can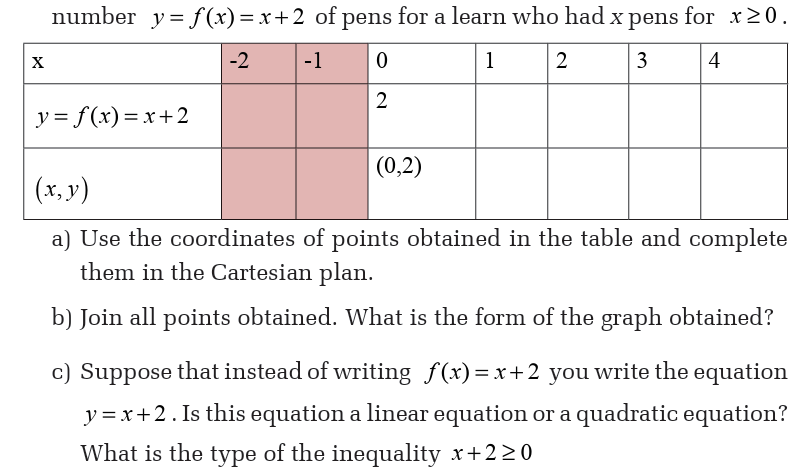 
be solved by the use of  linear equation in one unknown
 5. Smoke jumpers are fire fighters who parachute into areas near forest 
fires. Jumpers are in free fall from the time they jump from a plane 
until they open their parachutes. The function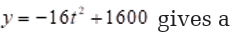 

jumper’s height in metre after seconds for a jump from. 

a) How long is free fall if the parachute opens at 1000 m?
 b) Complete a table of values for t = 0, 1, 2, 3, 4, 5 and 6.
 
objectives
 After completing this unit, I will be able to:
 » Solve equation of the first degree and second degree.
 » Solve inequality of the first degree and second degree.
 » Solve a system of linear equations.
 » Use equations and inequalities to solve word 
problems.

 » Apply equations and inequalities in real life problems.

 3.1. Equations and inequalities in one unknown 
Equations

Activity 3.1.1

Example 3.2

Mugisha’s target heart rate is 130 beats/min. This is 58beats/min more 

than his resting heart rate. Find his resting heart rate.

II. Uwamahoro measures her heart rate at 123 beats per minute. This 
is 55beats per minute more than her resting heart rate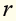 . Write and 
solve an equation to find Uwamahoro’s resting heart rate.
 Venus’s average distance from the Sun is 108million km. this distance 
is 42million km less than the average distance from the Sun to Earth. 
Write and solve an equation to find Earth’s average distance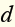  from the Sun.

Equations products / quotients
 Activity 3.1.2

 State the method you can use to solve the following equations.

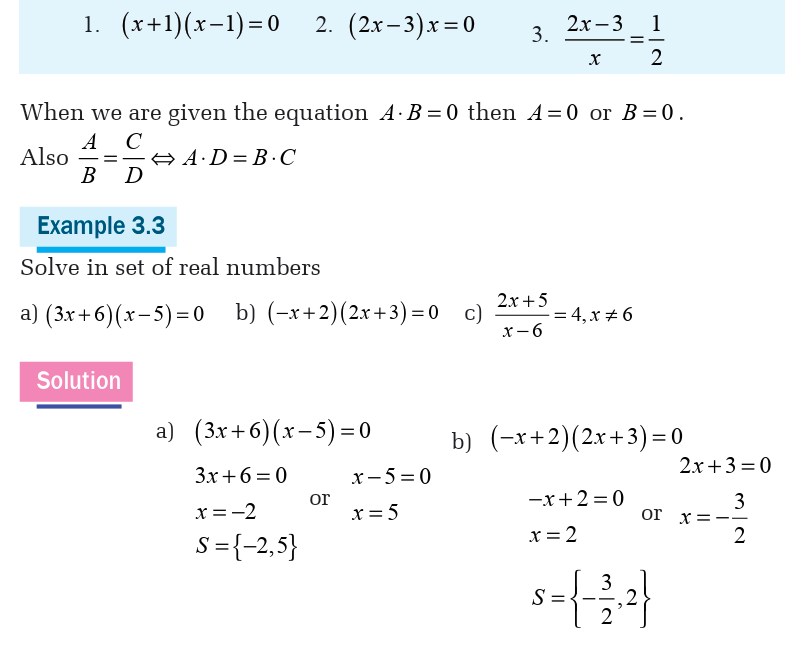
Inequalities

Activity 3.1.3

Find the value(s) of x such that the following statements are true

Suppose that we have the inequality x+3<10 In this case, we have
an inequality with one unknown. Here, the real value of x satisfies that 
this inequality is not unique. For example, 1 is a solution but 3 is also 
a solution. In general, all real numbers less than 7 are solutions. In this 

case, we will have many solutions combined in an interval. 

Now, the solution set of x+3 <10  is an open interval containing all 

real numbers less than 7 whereby 7 is excluded. How?

We solve this inequality as follows;

 Recall that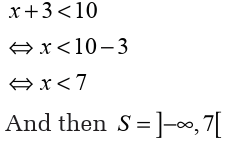
• When the same real number is added or subtracted from each side 
of the inequality, the direction of the inequality is not changed.
 
• The direction of the inequality is not changed if both sides are 
multiplied or divided by the same positive real number and 
is reversed if both sides are multiplied or divided by the same 

negative real number.

 Since any real number times zero is zero and zero is greater than -18, 

then the solution set is the set of real numbers. 

Solution

 A serving of low sodium food has at most 140mg per serving.
 Let s be the number of milligrams of sodium in a serving of low sodium 

food.

II) Use the table in example 4. A certain food is labelled sodium free.
Write an inequality for the number of milligrams of sodium in a serving of 

this sodium-free food.

 III) High-fiber foods have at least 5g of fiber per serving. Write an inequality to 
represent this situation. Let be the number of grams of fiber per serving 

of high -fiber food.

Inequalities products / quotients
Activity 3.1.4

State the method you can use to solve the following inequalities

 Suppose that we need to solve the inequality of the form 
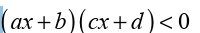
. For this inequality, we need the set of all real numbers that make the 
left hand side to be negative. Suppose also that we need to solve the 
inequality of the form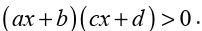 
 . For this inequality, we need the set of all real numbers that make the left hand side to
be positive. We follow the following steps:
 a) First we solve for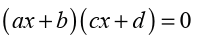 
b) We construct the table called sign table, find the sign of each 
factor and then the sign of the product or quotient if we are given 
a quotient. 
For the quotient, the value that makes the denominator to be zero is 
always excluded in the solution. For that value, we use the symbol || 
in the row of quotient sign.

c) Write the interval considering the given inequality sign.

Application Activity 3.1.4 

 Solve the following inequalities:

Inequalities involving absolute value
Activity 3.1.5
State the set of all real numbers whose number of units from zero, 
on number line, are
 1. greater than 4
 2. less than 6

 Hint Draw a number line

Equations and inequalities in real life problems

 Activity 3.1.6
How can you do the following?
 1. A father is 30 years older than his son. 5 years ago he was four times 
as old as his son. What is the son’s age?
 2. Betty spent one fifth of her money on food. Then she spent half of 
what was left for a haircut. She bought a present for 7,000 francs. 
When she got home, she had 13,000 francs left. How much did 
Betty have originally?
Equations can be used to solve real life problems. 
To solve real life problems, follow the following steps:
 a) Identify the variable and assign symbol to it.
 b) Write down the equation.
 c) Solve the equation.
 d) Interpret the result. There may be some restrictions on the variable.
 
Example 3.11
 Kalisa is four times as old as his son, and his daughter is 5 years younger 
than his brother. If their combined ages amount to 73 years, find the age 

of each person.

 110 kg of cement are required.
 440 kg of sand are required.
 660 kg of aggregate are required.
 
Example 3.13
John has 1,260,000 Francs in an account with his bank. If he deposits 
30,000 Francs each week into the account, how many weeks will he 
need to have more than 1,820,000 Francs on his account?

Solution
 Let x be the number of weeks
 We have;
 total amount of deposits to be made + the current balance > total 
amount wanted.
 That is;
 30,000x + 1,260,000 > 1,820,000

 30,000x > 1,820,000 _ 1,260,000

Application Activity 3.1.6
 1. The sum of two numbers is 25. One of the numbers exceeds the 
other by 9. Find the numbers. 
2. The difference between the two numbers is 48. The ratio of the 
two numbers is 7:3. What are the two numbers?
 3. The length of a rectangle is twice its breadth. If the perimeter is 
72 metre, find the length and breadth of the rectangle.
 4. Aaron is 5 years younger than Ron. Four years later, Ron will be 
twice as old as Aaron. Find their present ages. 
5. Sam and Alex play in the same soccer team. Last Saturday Alex 
scored 3 more goals than Sam, but together they scored less than 
9 goals. What are the possible number of goals Alex scored?
 6. Joe enters a race where he has to cycle and run. He cycles a 
distance of 25 km, and then runs for 20 km. His average running 
speed is half of his average cycling speed. Joe completes the race 

in less than 2½ hours, what can we say about his average speeds?

3.2. Simultaneous equations in two unknowns

Combination (or addition or elimination) method
Activity 3.2.1
 For each of the following, find two numbers to be multiplied to 

the equations such that one variable will be eliminated;

We try to combine the two equations such that we will remain with one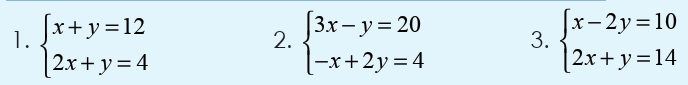 
equation with one unknown. We find two numbers to be multiplied on 

each equation and then add up such that one unknown is cancelled.

We find the value of one unknown in one equation and put it in another 

 equation to find the value of the remaining unknown.

In order to use Cramer’s rule, x’s must be in the same position and y’s in the same position. 

 Consider the following system:

solution
 First rearrange the system such that x’s will be in the same position and 

y’s will be in the same position.

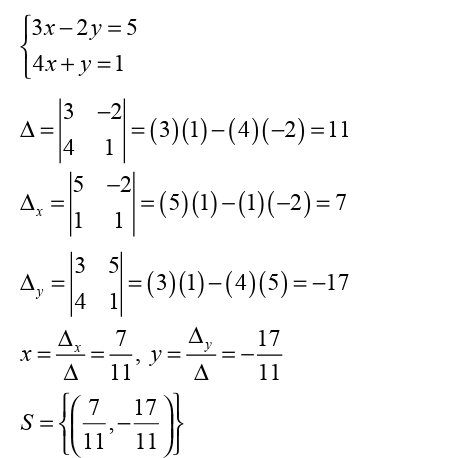
Example 3.25

2. Plot the obtained points in xy plane and join these points to obtain 
the lines. Two points for each equation give one line.
 3. What is the point of intersection for two lines?
 Some systems of linear equations can be solved graphically. To do this, 
follow the following steps:
 1. Find at least two points for each equation.
 2. Plot the obtained points in xy plane and join these points 
to obtain the lines. Two points for each equation give 
one line.
 3. The point of intersection for two lines is the solution for 

the given system

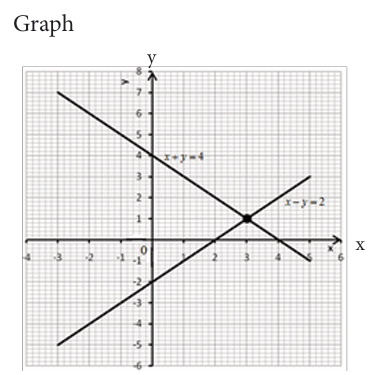
The two lines intersect at point (3,1). Therefore the solution is S={(3,1)}.

We see that the two lines are parallel and do not intersect. Therefore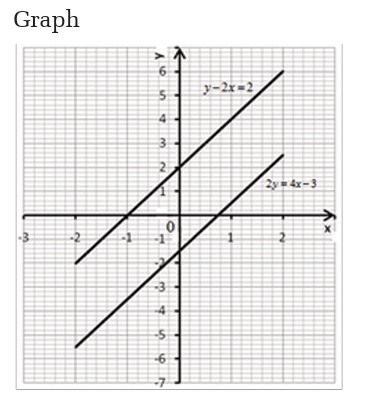 
there is no solution. Note that the gradients of the two lines are the 

same.

We see that the two lines coincide as a single line. In such case there is 

an infinite number of solutions.

Solving word problems using simultaneous equations
 Activity 3.2.5
 How can you do the following question?
 Margie is responsible for buying a week’s supply of food and 
medication for the dogs and cats at a local shelter.  The food and 
medication for each dog costs twice as much as those supplies 
for a cat.  She needs to feed 164 cats and 24 dogs.  Her budget is 
$4240.  How much can Margie spend on each dog for food and 
medication?

To solve word problems, follow the following steps:
 a) Identify the variables and assign symbol to them.
 b) Express all the relationships, among the variables using equations.
 c) Solve the simultaneous equations
d) Interpret the result. There may be some restrictions on the 
variables.
 
Example 3.30
 Peter has 23 coins in his pocket. Some of them are 5 Frw coins and 
the rest are 10 Frw coins. The total value of coins is 205 Frw . Find the 
number of 10 Frw coins and the number of 5 Frw coins.
 Solution
 Let x be the number of 10 Frw coins and y be the number of 5 Frw  coins. 

Then,

 Example 3.31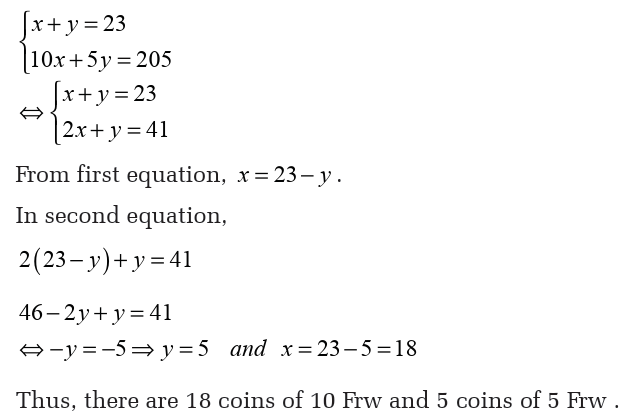
 Cinema tickets for 2 adults and 3 children cost 1,200 Frw . The cost for 
3 adults and 5 children is 1,900 Frw. Find the cost of an adult ticket and 
the cost of a child ticket.
 
Solution
 Let x  be the cost of an adult ticket and y be the cost of a child ticket, 

then

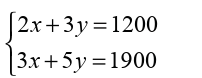
Application Activity 3.2.5
 1. A test has twenty questions worth 100 points.  The test consists of True/
 False questions worth 3 points each and multiple choice questions 
worth 11 points each.  How many multiple choice questions are on 
the test?
 2. Two small pitchers and one large pitcher can hold 8 cups of water.  
One large pitcher minus one small pitcher constitutes 2 cups of water.  
How many cups of water can each pitcher hold?
 3. The state fair is a popular field trip destination. This year, the senior 
class at High School A and the senior class at High School B both 
planned trips there. The senior class at High School A rented and 
filled 8 vans and 8 buses with 240 students. High School B rented 
and filled 4 vans and 1 bus with 54 students. Every van had the same 
number of students in it as did the buses. Find the number of students 
in each van and in each bus.
 4. The sum of the digits of a certain two-digit number is 7. Reversing its 
digits increases the number by 9. What is the number?
5.  A boat traveled 210 miles downstream and back. The trip downstream 
took 10 hours. The trip back took 70 hours. What is the speed of the 

boat in still water? What is the speed of the current?

3.3 Quadratic equations and inequalities

Quadratic equations by factorizing or finding square roots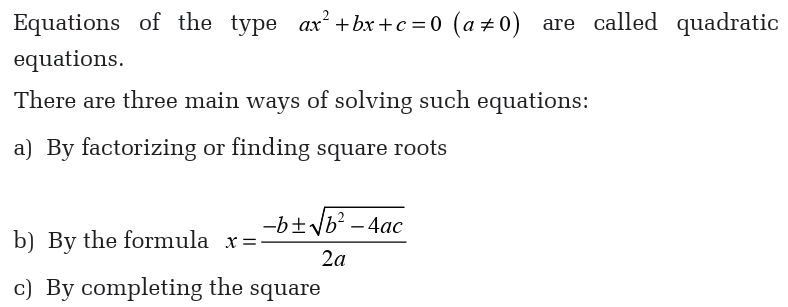
Activity 3.3.1
Smoke jumpers are firefighters who parachute into areas near forest
fires. Jumpers are in free fall from the time they jump from a plane
until they open their parachutes.The function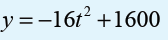 
gives a jumper’s height y gives a jumper’s height t seconds for a jump from
1600m.How long is free fall if the parachute opens at 1000m?
The method of solving quadratic equations by factorization should only 
be used if is readily factorized by inspection.
 The method of solving quadratic equations by factorization should only 

be used if is readily factorized by inspection. 

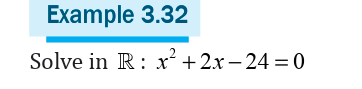
Before solving quadratic equations by completing the square, let’s look 

at some examples of expanding a binomial by squaring it.

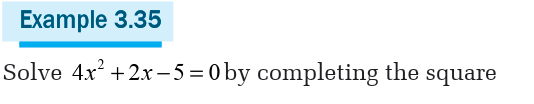
Application Activity 3.3.2
 Solve in set of real numbers the following equations by completing 

the square

In fact,

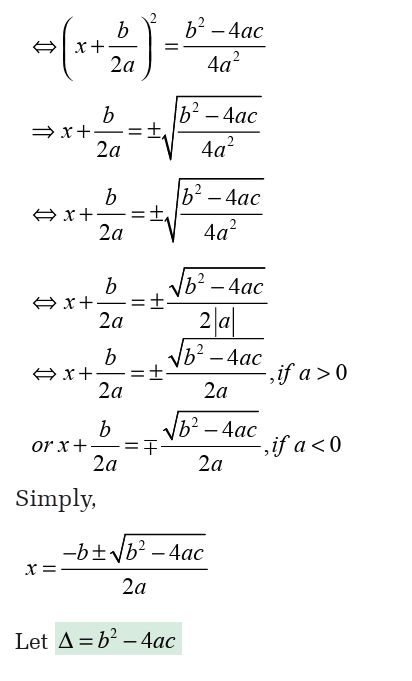
As we saw it, in this equation the sum of two roots is 7 and the product 
is 10. To find those roots we can think about two numbers such that 

their sum is 7 and their product is 10. Those numbers are 2 and 5. Thus 

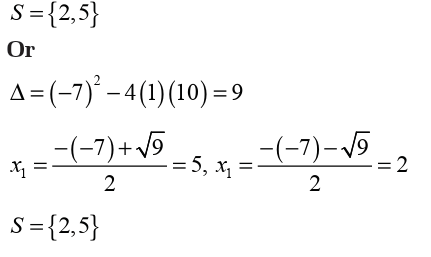
Factor form of a quadratic expression
Activity 3.3.4
 In each of the following, remove brackets and discuss about the 

result and original form.

 So, the basic process is to check that the equation is reducible to a 
quadratic form, then make a quick substitution to turn it into a 
quadratic equation.  In most cases, to make the check that it’s reducible 
to quadratic form, all we really need to do is to check that one of the 

exponents is twice the other. 

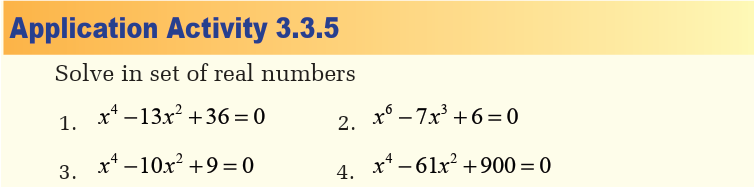
b) Nested radicals

Activity 3.3.6

c) Irrational equations
Activity 3.3.7

Consider the following equation

 1. Square both sides of the equation
 2. Solve the obtained equation
 3. Verify that the obtained solutions are solution of the original 
equation and then  give the solution set of the original equation 
(given equation)
 Irrational equation is the equation involving radical sign. We will see 
the case the radical sign is a square root.
 To solve an irrational equation, follow these steps:
 a) Isolate a radical in one of the two members and pass it to another 
member of the other terms which are also radical.
 b) Square both members.
 c) Solve the equation obtained. 
d) Check if the solutions obtained verify the initial equation.
 e) If the equation has several radicals, repeat the first two steps of the 

process to remove all of them.

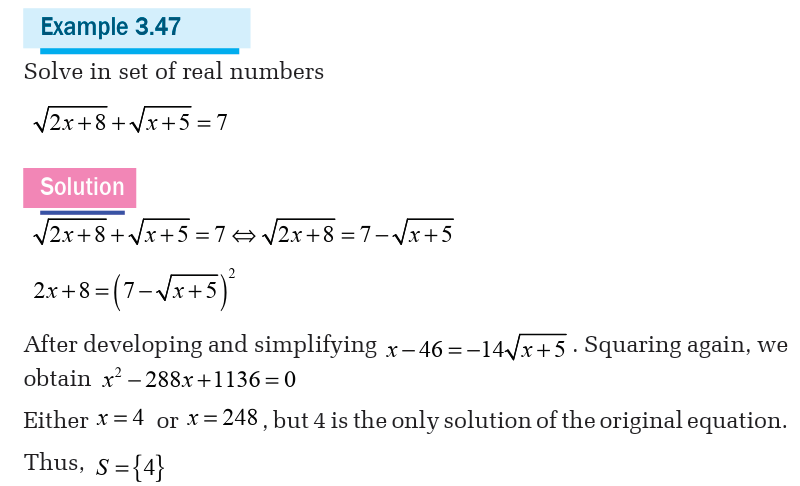
We saw how to solve the inequality product like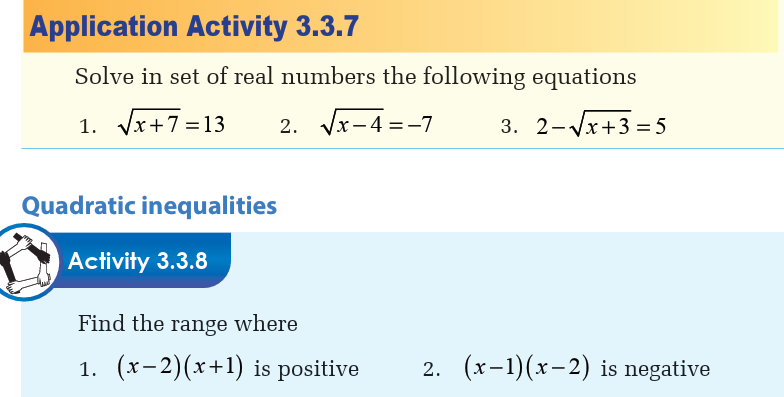
 (ax+b)(cx+d)>0. If we find the product of the left hand side, the result 
will be a quadratic expression of the form (ax²+bx+c). 
Then to solve the inequality of the second degree like ax²+bx+c>0 we 
need to put the expression ax²+bx+c in factor form and use the method 
to solve inequality product.
 If the expression to be transformed in factor form has no factor form, 

we find its sign by replacing the unknown by any chosen real number. 

We may find that the expression is always positive or always negative. 
If the expression to be transformed in factor form has a repeated root, 
it is zero at that root and positive or negative elsewhere depending on 

coefficient of x².

3.4. Applications
 Activity 3.4.1
 1. Explain how linear equations can be used in daily life1.
 2. Give three examples of where you think quadratic equations are 
useful in daily life
 
a)   Supply and demand analysis
 Market equilibrium is when the amount of product produced is equal 
to the amount of quantity demanded. We can see equilibrium on a 
graph when the supply function and the demand function intersect, 
like shown on the graph below. Max can then figure out how to price 

his new lemonade products based on market equilibrium. 

 Example 3.53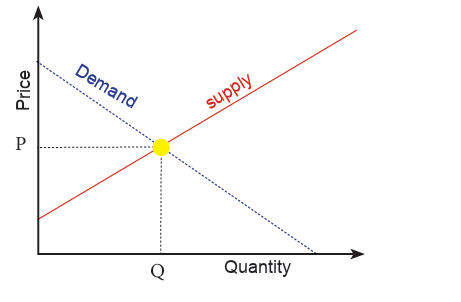 
Assume that in a competitive market the demand schedule is   and the 
supply schedule is  p=60+0.4q (p=price, q=quantity). If the market is 
in equilibrium then the equilibrium price and quantity will be where 
the demand and supply schedules intersect. As this will correspond to 
a point which is on both the demand schedule and the supply schedule 
the equilibrium values of  p and q will be such that both equations hold. 

To find the equilibrium quantity set 420- 0.2q = 60 + 0.4q

b)    Linear motion
 Linear motion is a motion along a straight line, and can therefore be 
described mathematically using only one spatial dimension. The linear 
motion can be of two types: uniform linear motion with constant 
velocity or zero acceleration; non uniform linear motion with variable 

velocity or non-zero acceleration. 

Example 3.54 
Some examples of linear motion are given below:
 1. An athlete running 100m along a straight track
 2. Parade of the soldiers
3. Car moving at constant speed
4. A bullet targeted from the pistol 
5. A man swimming in the straight lane
6.  Train moving in a straight track
7. Object dropped from a certain height
8. Balancing equation

c)   Balancing equation
 In chemistry, to balance the chemical equation we set the reactants and 

products equal to each other. 

 d)Health care
 In medicine, equations are used for modelling medication situations 
and solve related problems.

Example 3.56 
NSHUTI works as a nurse. According to her daily schedule, she has 
to give Medication dosage to 60 patients’ daily. One day she took 1 
longer than the expected, and therefore she gave Medication dosage to 
3patients less per hour than anticipated.

 How long did she expected to give Medication dosage to 60 patients? 

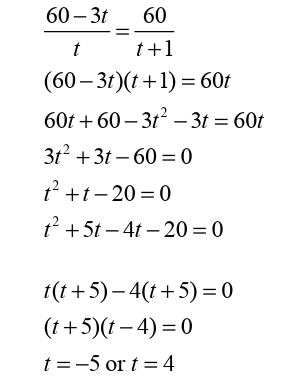
 • Ignore the negative value as it is not valid.
 • Therefore, she expected to give Medication dosage to 60 patients 
in 4 hours.
 e)   Figuring out a profit
 Sometimes calculating a business’ profit requires using a quadratic 
function. If you want to sell something (even something as simple as 
lemonade) you need to decide how many things to produce so that 

you’ll make a profit. 

Example 3.57 
Let us say that you’re selling glasses of lemonade, and you want to make 
12 glasses. You know, however, that you’ll sell a different number of 
glasses depending on how you set your price. At 100 francs per glass, 
you are not likely to sell any, but at 10 francs per glass, you will probably 
sell 12 glasses in less than a minute. So, to decide where to set your 
price, use P as a variable. Let’s say you estimate the demand for glasses 
of lemonade to be at 12 - P. Your revenue, therefore, will be the price 
times the number of glasses sold: P(12 - P), or 12P–P2. Using however 
much your lemonade costs to produce, you can set this equation equal 
to that amount and choose a price from there.

f) Quadratics in Athletics
 In athletic events that involve throwing things, quadratic equations are 
highly useful. 

Example 3.58 
Say, for example, you want to throw a ball into the air and have your 
friend catch it, but you want to give her the precise time it will take the 
ball to arrive. 
To do this, you would use the velocity equation, which calculates the 
height of the ball based on a parabolic (quadratic) equation. So, say 
you begin by throwing the ball at 3 meters, where your hands are. Also 
assume that you can throw the ball upward at 14 meters per second, and 
that the earth’s gravity is reducing the ball’s speed at a rate of 5 meters 
per second squared. This means that we can calculate the height, using 
the variable t for time, in the form of h=3+14t –5t2 . If your friend’s 
hands are also at 3 metres in height, how many seconds will it take the 
ball to reach her? To answer this, set the equation equal to 3 = h, and 
solve for t. The answer is approximately 2.8 seconds.

g) Finding a Speed
 Quadratic equations are also useful in calculating speeds. Avid kayakers, 
for example, use quadratic equations to estimate their speed when going 

up and down a river. 

 Example 3.59
 Assume a kayaker is going up a river, and the river moves at 2 km/hr. 
Say he goes upstream -- against the current -- at 15 km, and the trip takes 
him 3 hours to go there and return. Remember that time = distance / 
speed. Let v = the kayak’s speed relative to land, and let x = the kayak’s 
speed in the water. So, we know that, while traveling upstream, the 
kayak’s speed is v = x - 2 (subtract 2 for the resistance from the river 
current), and while going downstream, the kayak’s speed is v = x + 2. 
The total time is equal to 3 hours, which is equal to the time going 

upstream plus the time going downstream, and both distances are 15km. 

Application Activity 3.4.1

1) A pot of water has a temperature of 25⁰c How many degrees should you

raise the temperature to boil the water at 100⁰c

he high and low production levels during the month.

Unit summary
 1. An equation is statement that the values of two mathematical 
expressions are equal while an inequality is a statement that the 

values of two mathematical that are not equal. 

  3. To solve real life problems, follow the following steps: • Identify the variable and assign symbol to it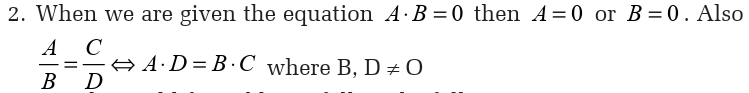
• Write down the equation
 • Solve the equation
 • Interpret the result. There may be some restrictions on the 

variable.

 Algebraically, there are three methods for solving this system: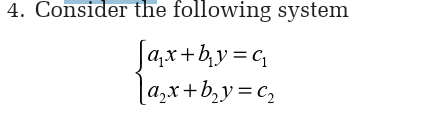 
combination method, substitution method and Cramer’s rule. Some 
systems of linear equations can be solved graphically. To do this, 
follow the following steps:
 • Find at least two points for each equation.
 • Plot the obtained points in xy plane and join these points to 
obtain the lines. Two points for each equation give one line.
 • The point of intersection for two lines is the solution for the 

given system

9. Irrational equation is the equation involving radical sign. We solve 
irrational equations by squaring both sides. By substituting all 
obtained solutions in the given equation, those which dont  satisfy 
the given equation are rejected. 
10. Application

 Supply and demand analysis
 Market equilibrium is when the amount of product produced is equal 
to the amount of quantity demanded. Max can then figure out how to 
price his new lemonade products based on market equilibrium. 

Linear motion
 Linear motion is a motion along a straight line, and can therefore be 
described mathematically using only one spatial dimension. 

Balancing equation
 In chemistry, to balance the chemical equation we set the reactants 
and products equal to each other. 

Calculating Areas 
People frequently need to calculate the area of things like rooms, 
boxes or plots of land. 

Figuring Out a Profit
 Sometimes calculating a business’ profit requires using a quadratic 
function. If you want to sell something (even something as simple as 
lemonade) you need to decide how many things to produce so that 
you’ll make a profit. 

Quadratics in Athletics
 In athletic events that involve throwing things, quadratic equations 
are highly useful. 

Finding a Speed
 Quadratic equations are also useful in calculating speeds. Avid 
kayakers, for example, use quadratic equations to estimate their 

speed when going up and down a river. 

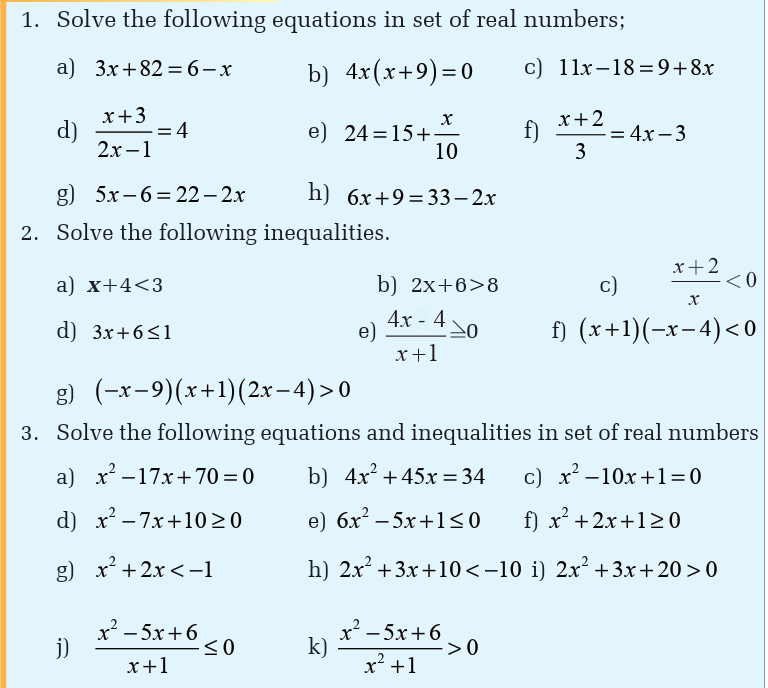
7. The senior classes at High School A and High School B planned separate 
trips to Akagera National Park. The senior class at High School A rented 
and filled 1 van and 6 buses with 372 students. High School B rented 
and filled 4 vans and 12 buses with 780 students. Each van and each bus 
carried the same number of students. How many students can a van carry? 
How many students can a bus carry?
 8. Brenda’s school is selling tickets to a spring musical. On the first day of 
ticket sales the school sold 3 senior citizen tickets and 9 child tickets for a 
total of $75. The school took in $67 on the second day by selling 8 senior 
citizen tickets and 5 child tickets. What is the price each of one senior 
citizen ticket and one child ticket?
 9. A number is divided into two parts, such that one part is 10 more than the 
other. If the two parts are in the ratio 5 : 3, find the number and the two 
parts.
 10. Robert’s father is 4 times as old as Robert. After 5 years, father will be 
three times as old as Robert. Find their present ages.
 11. The sum of two consecutive multiples of 5 is 55. Find these multiples.
 12. The difference in the measures of two complementary angles is 12°. Find 
the measure of the angles.
 13. The cost of two tables and three chairs is $705. If the table costs $40 more 
than the chair, find the cost of the table and the chair. 
14. The velocity v m/s of a ball thrown directly up in the air is given by v = 
20 – 5t, where t is the time in seconds. At what times will the velocity be 
between 5 m/s and 15 m/s?
 15. A rectangular room fits at least 7 tables that each have 1 square meter of 
surface area. The perimeter of the room is 16 m. What could the width and 
length of the room be?
16. A picture has a height that is 4/3 of its width. It is to be enlarged to have an 
area of 192 square metres. What will be the dimensions of the enlargement?
 17. The product of two consecutive negative integers is 1122. What are 
the numbers?
 18. A garden measuring 12 meters by 16 meters is to have a pedestrian pathway 
installed all around it, increasing the total area to 285 square meters. What 
will be the width of the pathway?
 19. You have to make a square-bottomed, unlidded box with a height of three 
metres and a volume of approximately 42 cubic metres. You will be taking 
a piece of cardboard, cutting three- metres squares from each corner, 
scoring between the corners, and folding up the edges. What should be the 

dimensions of the cardboard, to the nearest quarter metres?