Unit 2: Fundamentals of Trigonometry
2.0 Introductory activity
The angle of elevation of the top of the Cathedral from a point 280
m away from the base of its steeple on level ground is 600. By usingtrigonometric concepts, find the height of the cathedral.
Objectives
After completing this unit, I will be able to:
» Define sine, cosine, and tangent (cosecant, secant and
cotangent) of any angle – know special values.
» Convert radians to degree and vice versa.
» Use trigonometric identities.» Apply trigonometric formulae in real world problems.
2.1. Trigonometric concepts
Activity 2.1Consider the following diagram
Trigonometry is the study of how the sides and angles of a triangle are
related to each other. A rotation angle is formed by rotating an initial
side through an angle, about a fixed point called vertex, to terminal
position called terminal side.
Trigonometric concepts contribute to various medical testing and
interpretation of those test results. Some of the uses are,
1.Electrocardiography: The measurement of electrical activities in the
heart. Through this process, it is possible to determine how long the
electrical wave takes to travel from one part of the heart to the next
by showing if the electrical activity is normal or slow, fast or irregular.
2.Pulmonary function testing: a spirometer is used to measure the
volume of air inhaled and exhaled while breathing by recording
the changing volume over time. The output of a spirogram can be
quantified using trigonometric equations and generally, it is possible
to describe any repeating rhythms of lung capacity.
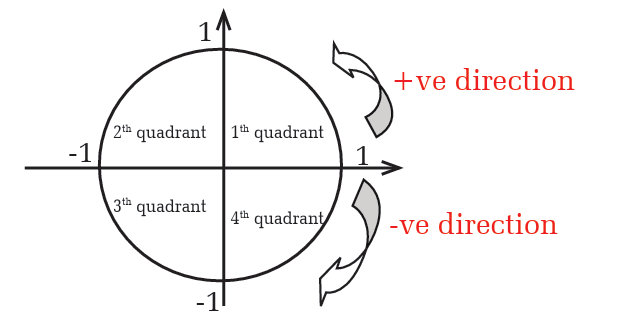
A rational angle is drawn in what is called standard position if the initialside is on the positive x-axis and the vertex of the angle is at the origin.
Angles in standard position that have a common terminal side are called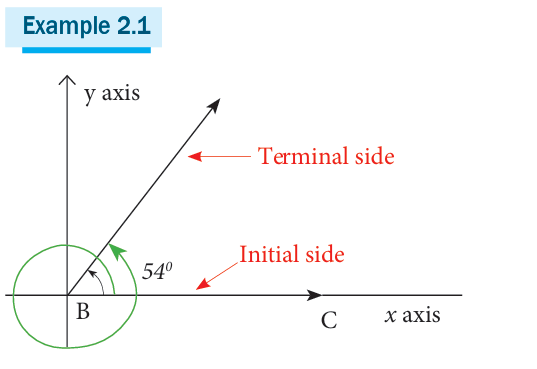
co-terminal angles; the measure of smallest positive rotation angle is
called principal angle. Angle is positive if rotated in a counterclockwise
direction and negative when rotated clockwise.
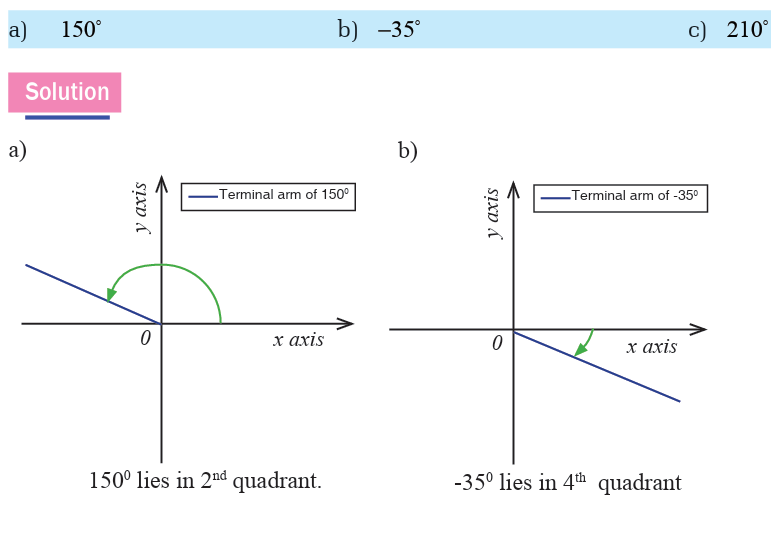
Angles are named according to where their terminal sides lie. For
instance, the x-axis and y-axis divide a plane into four quadrants asfollow.
Example 2.2
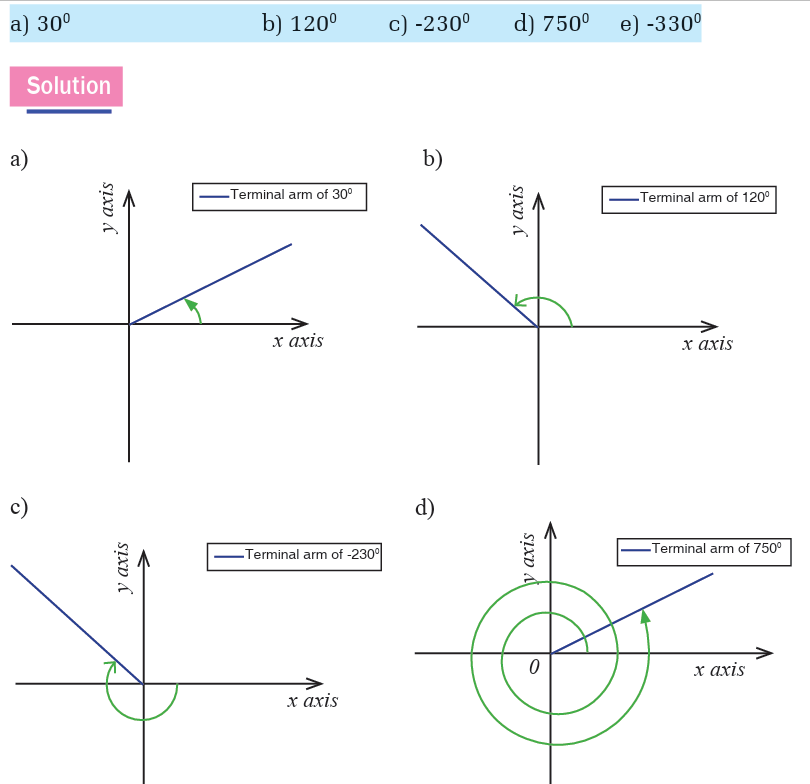
Draw each of the following angles in standard position and show thereangles which are co-terminal to 300 ?
Example 2.3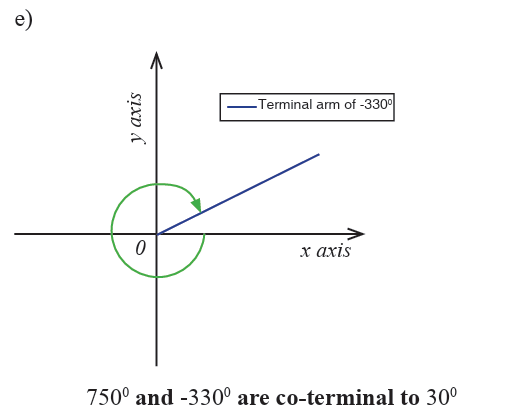
Draw each of the following angles in standard position and indicate inwhich quadrant the terminal side is.
Application Activity 1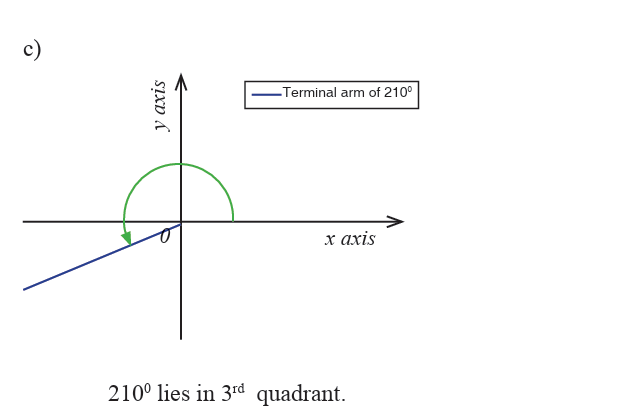
1. Draw each of the following angles in standard position and show
the angles which are co-terminal to 200?
a) 200 b) -2000 c) 7400 d) -3400
2. Draw each of the following angles in standard position and
indicate in which quadrant the terminal side is.
a) 400 b) -2350 c) 2800
2.1.1. Measure of an angle
Activity 2.2
The amount we rotate the angle is called the measure of the angle andis measured in following units:



Example 2.7
An angle which measures 82 grades, 7 decigrades, 2 centigrades and 5
milligrades will be denoted by
82G ,725
c) Radian
A central angle of a circle is an angle with a vertex at the centre of a
circle. An intercepted arc is the portion of the circle with endpoints on
the sides of the central angle and remaining points within the interior
of the angle.
When a central angle intercepts an arc that has the same length as aradius of the circle, the measure of the angle is defined to be one radian.
Like degrees, radian measures the amount of the rotation from the initial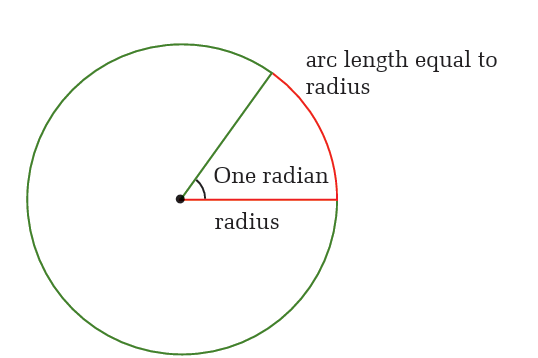
side to the terminal side of an angle.


Application Activity 2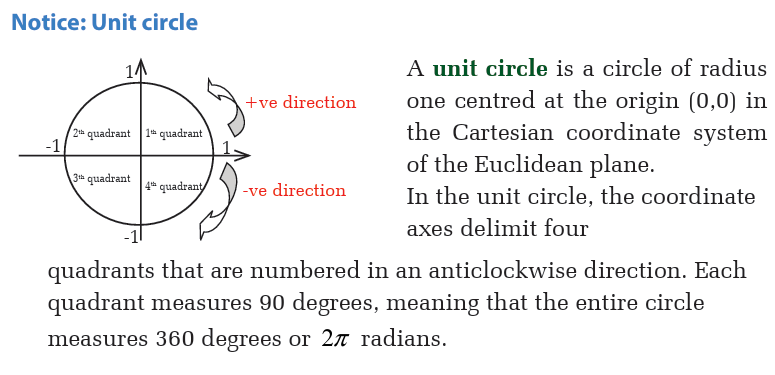
1. Convert 220 grades to radians and degrees.2. Convert 1240 degrees to radians and grades.
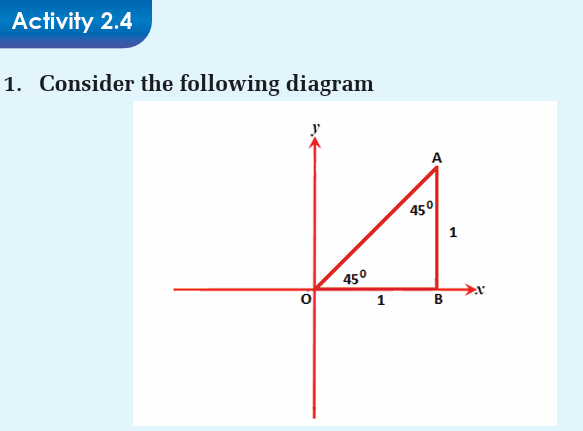
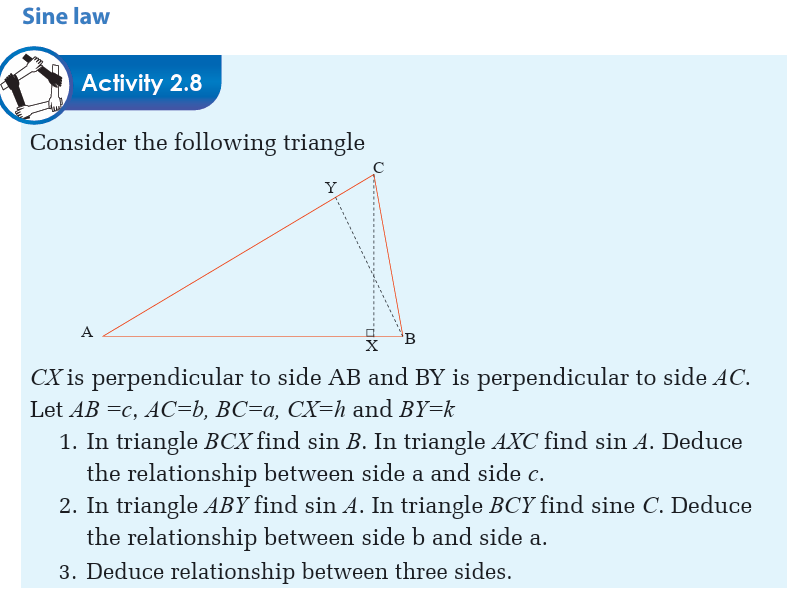
Activity 2.3
Construct two right angled triangles, one of which is an
enlargement of the other.
How is the side opposite to the right angle (or the longest side) called?
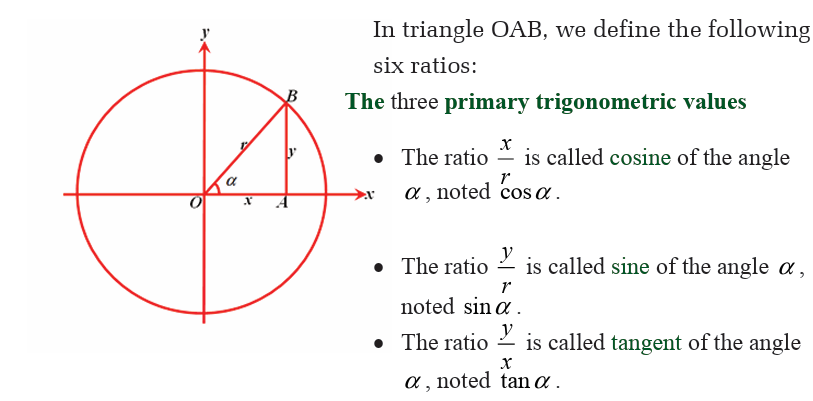
For both triangles, consider an angle and compute the following ratios.
• Opposite side to the considered angle and hypotenuse.
• Adjacent side and hypotenuse.
• Opposite side to the considered angle and adjacent side.
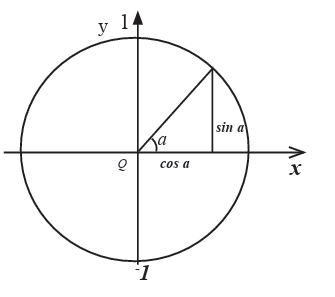
How can you conclude?Consider the following circle with radius r.





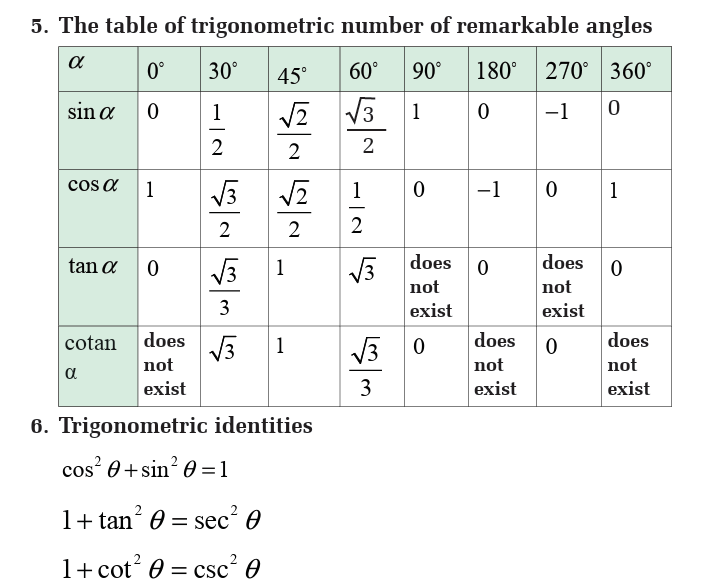
Trigonometric Number of special Angles 300, 450, 600
From pythagoras theorem, definition of trigonometric ratios and
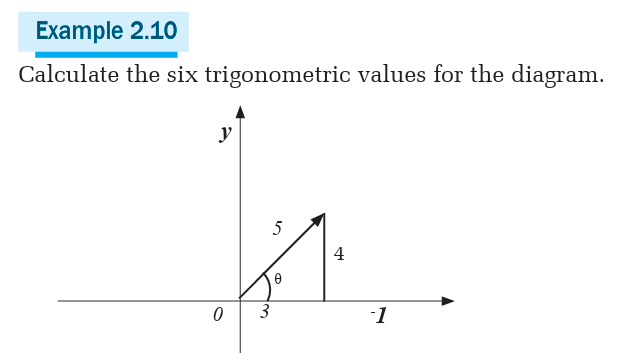
given diagrams, find sin 450, cos 450 and tan 4502. Consider the following diagram
As these angles are often used, it is better to keep in your mind their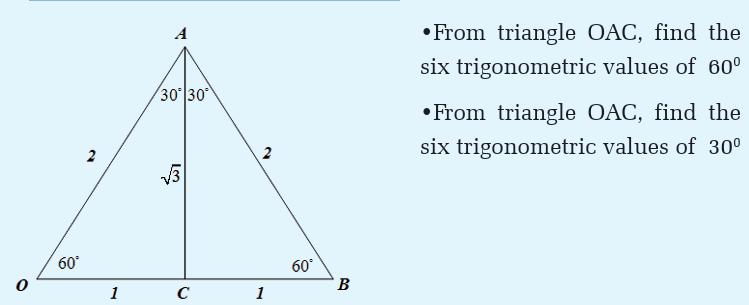
trigonometric ratios in fraction form.

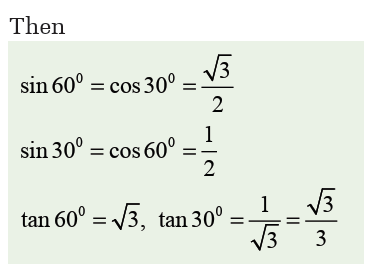

Application Activity 2.4
The following diagram shows which primary trigonometric values are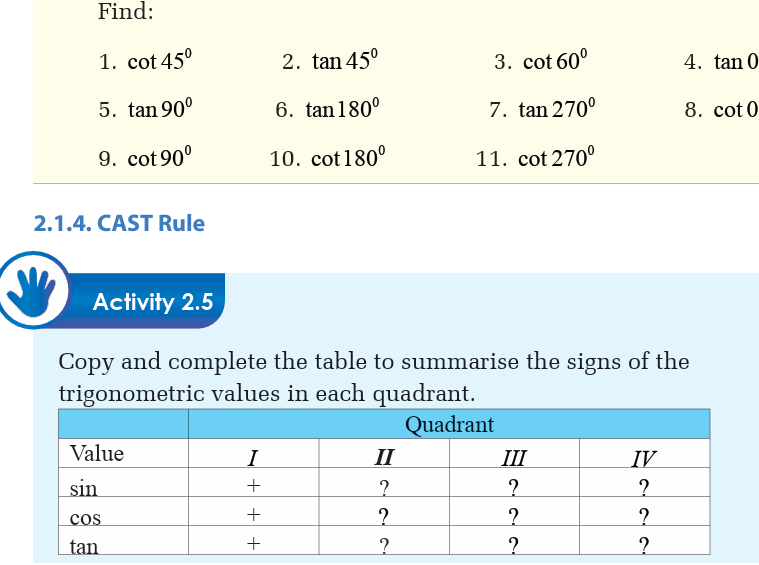
positive in each quadrant. This is called the CAST rule.
Sine is positive in first and second quadrant but negative in third and fourth quadrant.
Cosine is positive in the first and fourth quadrant but negative in second and third
quadrant.
Tangent is positive in in the first and third quadrants but negative in second and fourthquadrant.
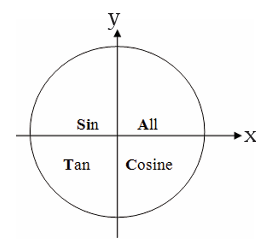
Application Activity 2.5



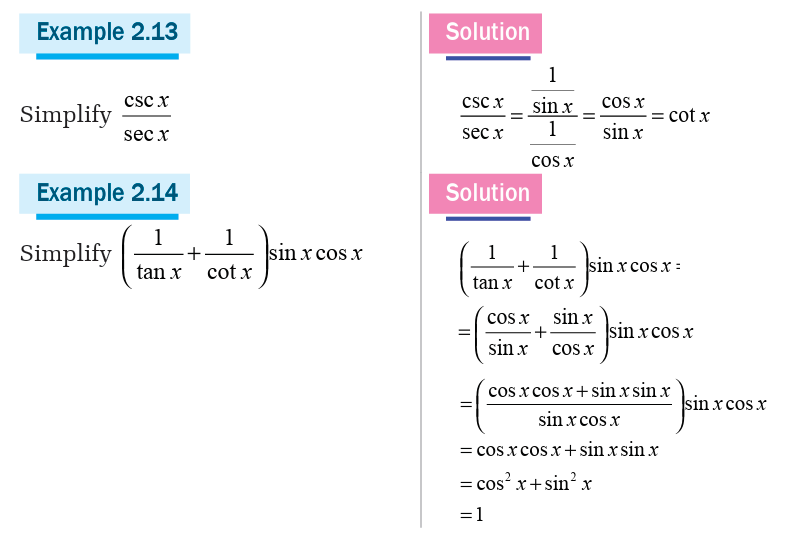
Application Activity 6
2. Triangle and applications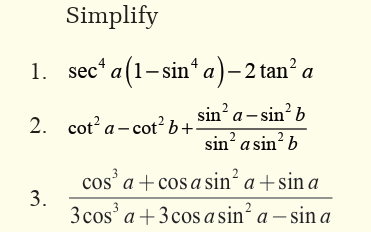
Solving triangle
Solving a triangle is to find the length of its sides and measures of its
angles. There are two methods for solving a triangle: cosine law andsine law.
Cosine law
Activity 7
Cosine law (also known as cosine formula or cosine rule) relates the
lengths of sides to the cosine of one of the angles as follow.
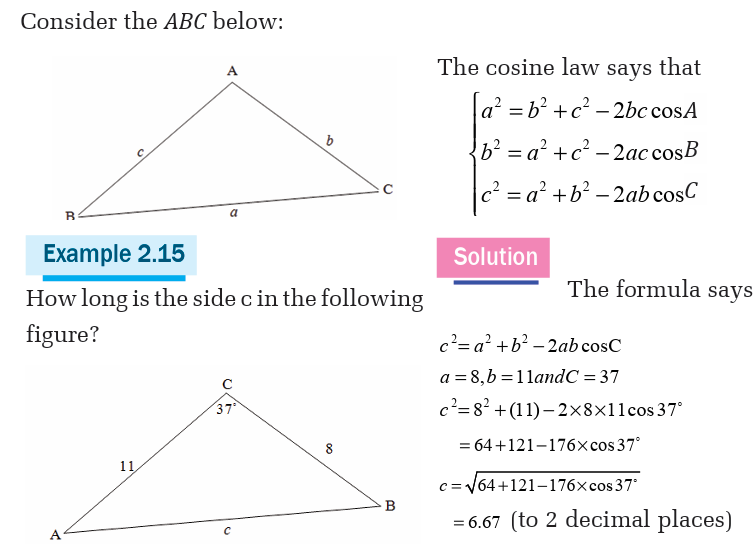
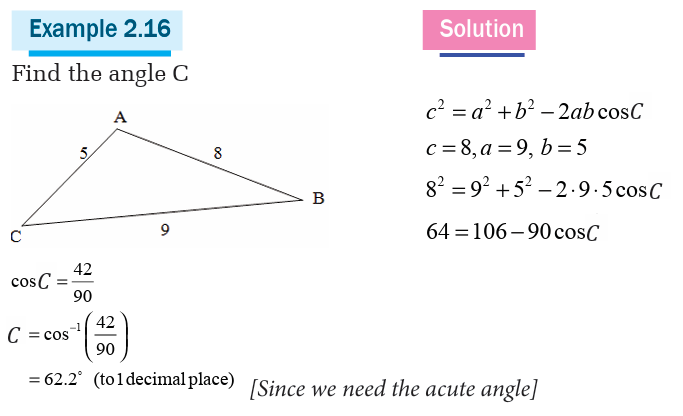
Application Activity 2.7

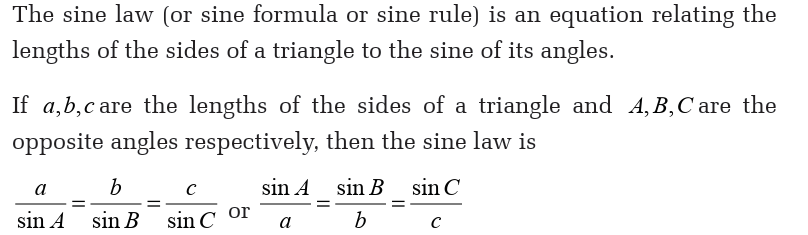

Applications
Many real situations involve right triangles. Using angles and
trigonometric functions, we can solve problems involving right triangle.We have already seen how to solve a triangle.
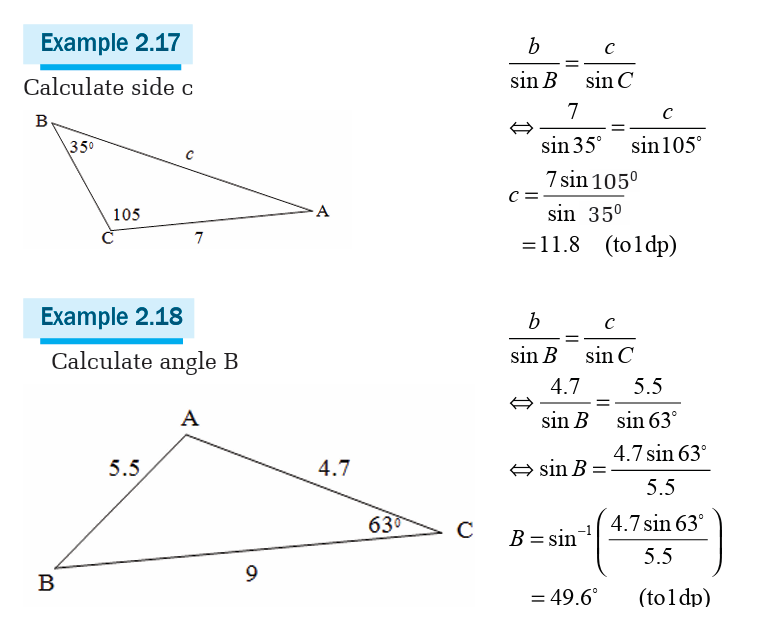
1. Bearings and air navigation
Similarly, if B is south of A then the bearing of A from B is 180o, and if B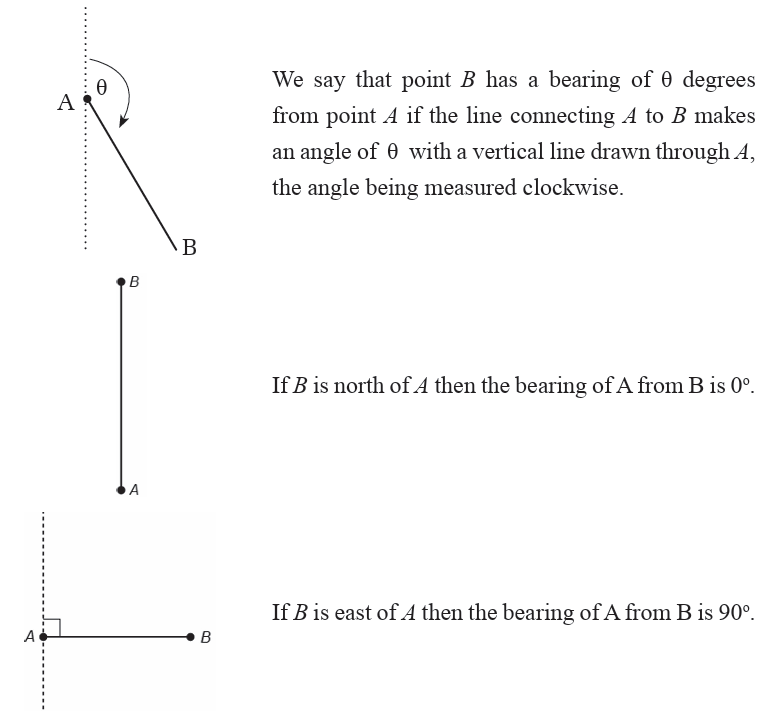
is west of A then the bearing of A from B is 270o. The bearing can be any
number between 0 and 360, because there are 360 degrees in a circle.
We can also use right triangles to find distances using angles given as
bearings.
In navigation, a bearing is the direction from one object to another.
Further, angles in navigation and surveying may also be given in terms
of north, east, south, and west. For example, N 700E refers to an angle
from the north, towards the east, while N700 W refers to an angle from
the north, towards the west.
Example 2.19
A ship travels on a N500 E course. The ship travels until it is due north
of a port which is 10 kilometers due east of the port from which the shiporiginated. How far did the ship travel?

Example 2.20
An airplane flies on a course of S 300E , for 150 km. How far south is theplane from where it originated?
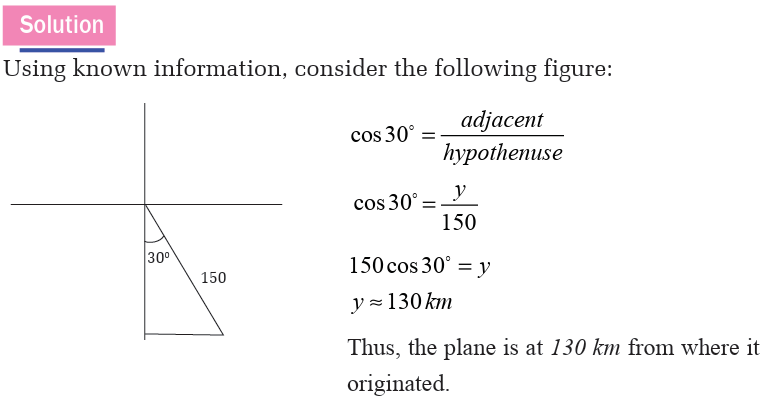
2. Angle of elevation and angle of depression
You can use right triangles to find distances, if you know an angle of
elevation or an angle of depression. The figure below shows each of
these kinds of angles.
Suppose that an observer is standing at the top of a building and looking
straight ahead at the birds (horizontal line). The observer must lower
his/her eyes to see the car parked (slanting line). The angle formedbetween the two lines is called the angle of depression.
Suppose that an observer is standing at the top of a building and looking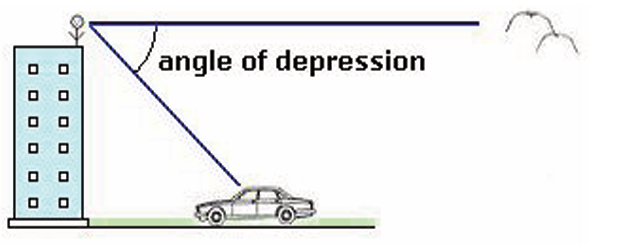
straight ahead at the birds (horizontal line). The observer must raise his/
her eyes to see the airplane (slanting line). The angle formed betweenthe two lines is called the angle of elevation.
The angle of elevation of the top of a pole measures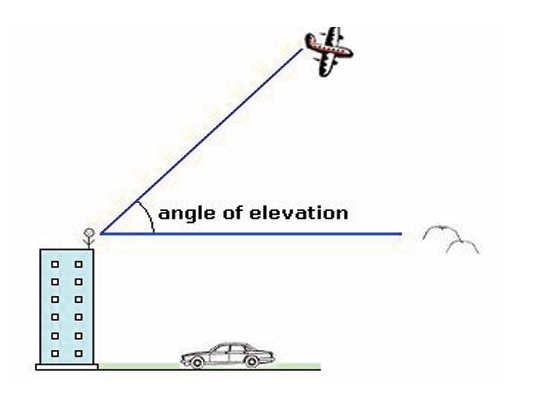
480 from a point on the ground 18 metres away from its base.
Find the height of the flagpole.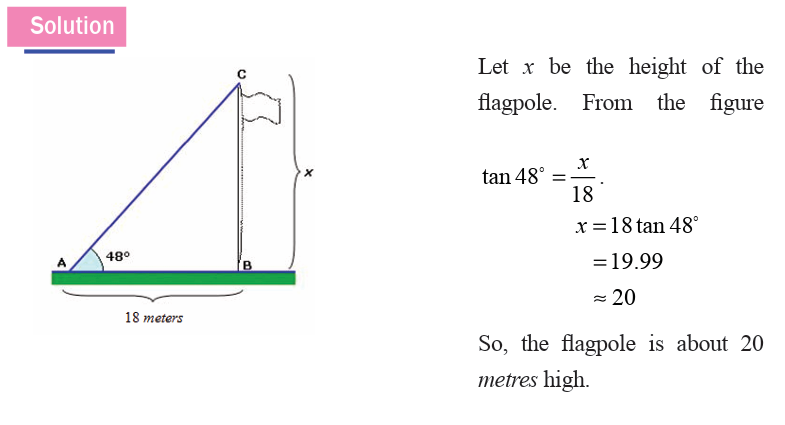
Example 2.22
An airplane is flying at a height of 2 kilometres above the level ground.
The angle of depression from the plane to the foot of a tree is 15o. Findthe distance that the air plane must fly to be directly above the tree.
Let x be the distance the airplane must fly to be directly above the tree.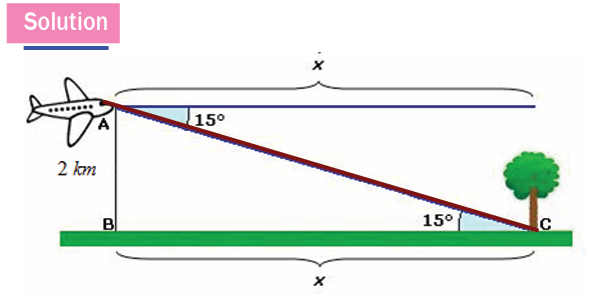
The level ground and the horizontal are parallel, so the alternate interiorangles are equal in measure.
So, the airplane must fly about 7.46 kilometres to be directly above the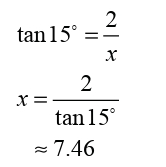
tree.
3. Inclined plane
An inclined plane, also known as a ramp, is a flat supporting surface
tilted at an angle, with one end higher than the other, used as an aid
for raising or lowering a load. On the inclined plane the weight of
the object causes the object to push into and, the object slides, to rub
against the surface of the incline. Also the weight causes the object tobe pulled down the slant of the incline. The component that pushes the

the same as the angle of the incline, as shown below

Unit summary
1. Trigonometry is the study of how the sides and angles of a triangle
are related to each other. A rotation angle is formed by rotating an
initial side through an angle, about a fixed point called vertex, to
terminal position called terminal side. Angle is positive if rotated in a
counterclockwise direction and negative when rotated clockwise.2. The amount we rotate the angle is called the measure of the angle and
4. The unit circle is a circle of radius one centered at the origin (0,0) in
the Cartesian coordinate system in the Euclidian plane. In the unit
circle, the coordinate axes delimit four quadrants that are numbered in
an anticlockwise direction. Each quadrant measures 90 degrees, meansthat the entire circle measures 360 degrees or radians.

End Unit assesment

9. A point P is 90 m away from a vertical flagpole, which is 11 m high. What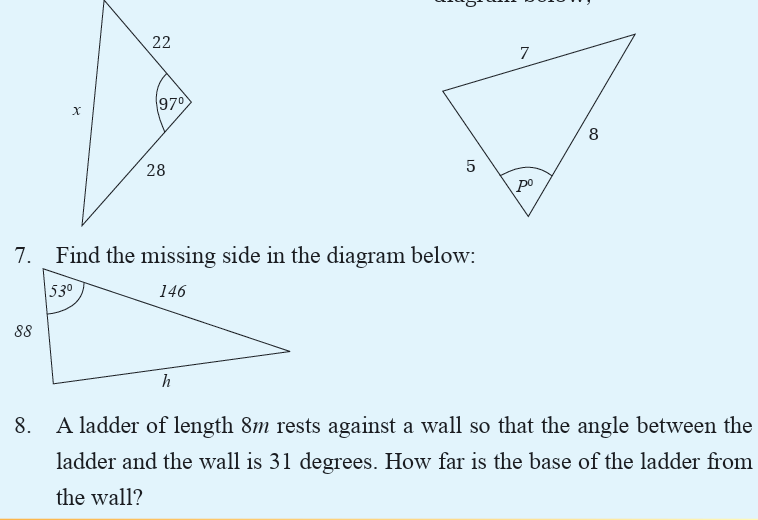
is the angle of elevation to the top of the flagpole from P?
10. A ship sails 200 km on a bearing of 243.7 degrees
a) How far south has it travelled?
b) How far west has it travelled?
11. An aircraft flies 500 km on a bearing of 100 degrees and then 600 km on
a bearing of 160 degrees. Find the distance and bearing of the finishing
point from the starting point.
12. A plane is flying at a constant height of 8000 m. It flies vertically above
me and 30 seconds later the angle of elevation is 74 degrees. Find the
speed of the plane in metres/second.
13. Convert 81013'08'' to decimal degree.
14. Convert 117.65720 to d0 m' s" system.
15. Convert 2.9370 to d0 m' s" system.16. Convert 75019'35'' to the nearest tenth degree.
