S4 : Mathematics

 10.0 Introductory activity
 1. Use the library or the internet to search on counting techniques used to 

determine outcomes for different random experiments.

2. There are 2 roads joining A and B and 3 roads joining B and C. Write 

down different roads from A to C via B.  How many are they?

 3. When a card is selected from an ordinary deck of 52 cards, one assumes 
that the deck has been shuffled, and each card has the same chance of 
being selected. Let A be the event of selecting a black card, 
a) If n is the number of black cards in the pack, what is the value of n?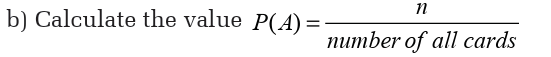

 c) If  P(A )is the probability of electing a black card, deduce the 

definition of  probability for any event E. 

 objectives
 After completing this unit, I will be able to:
 » solve problems involving factorial notation,
 » determine the number of permutations of n different 
objects taken r at a time,
 » determine the number of permutations of n different 
objects,
 » determine the number of permutations of n different 
objects taken r at a time for a given condition,
 » determine the number of combinations of r objects 
chosen from n different objects,
 » determine the number of combinations of r objects 
chosen from n different objects for a given condition,
 » use properties of combinations for finding coefficients 
in Pascal’s triangle,
 » solve problems involving permutations and 
combinations,
 » find probability of events,

 » determine probability of an equiprobable sample space

 10.1. Permutations and arrangements
 Activity 10.1
 1. There are 4 roads joining A and B and 3 roads joining B and C. 

Write down different roads from A to C via B.  How many are they?

 c) Toss simultaneously a coin with two sides H and T and a 
die with six sides 1 through 6, write down different possible 

outcomes that can appear. How many are they?

 It is often necessary to count the ways in which a certain task can be 
performed. In some cases, the total number of possible ways is very large, 
and becomes impractical to write down all possible choices. 
To solve such problems related to counting, we refer to the theory called 
“Combinatorial analysis or combinatorics”. 
In this theory, there are three basic counting principles that will help us to 
count in a more systematic way: The first is the multiplication principle; 
the other two, which follow from it, are rules concerning permutations and 
combinations. 

Principle of counting
 Some terms:
 Experiment: any human activity, like tossing a die.
 Trial: small experiment contained in a large experiment. For example, 
tossing simultaneously a coin and a die may be regarded as an experiment 
consisting of two smaller experiments, tossing a coin (experiment 1) 
followed by tossing a die (experiment 2). Here experiment 1 and experiment 

2 are called trials.

The set S of all possible outcomes of a given experiment is called the sample 
space. A particular outcome, i.e., an element in S, is called a sample point. 
An event A is a set of outcomes or, in other words, a subset of the sample 

space S.

 

A probability experiment is a chance process that leads to well-defined 
results called outcomes.

 An outcome is the result of a single trial of a probability experiment.

Example 10.1
 For example, tossing simultaneously a coin and a die may be regarded 
as an experiment consisting of two smaller experiments, tossing a coin 
(experiment 1) followed by tossing a die (experiment 2). Here experiment 

1 and experiment 2 are trials. Point on a side of a die is an outcome.

Notice:
 Die (plural dice): small cube of plastic, ivory, bone, or wood, marked on 

each side with one to six sports, usually used in pairs in games of chance.

Successive experiments
 Basic product principle of counting
 “If experiment 1 has m possible outcomes and if for each outcome of 
experiment 1, experiment 2 has n possible outcomes, then an experiment 
of performing experiment 1 and experiment 2 simultaneously, called 
experiment 1 and 2, has m× n  possible outcomes.”

Example 10.2
 In tossing simultaneously a coin with two sides a and b and a die with six 
sides 1 through 6, how many possible outcomes will appear?
 
Solution
 The tossing may be regarded as an experiment (experiment 1 & 2) consisting 
of two smaller experiments, tossing a coin (experiment 1) followed by 
tossing a die (experiment 2).
 Experiment 1 has 2 outcomes.
 Experiment 2 has 6 outcomes.
 So experiment 1 & 2 has 2 ×6 = 12 outcomes.
 
Example 10.3
There are 5 roads joining A and B and 3 roads joining B and C how many 
different roads from A to C via B?
 
Solution
 Here;
 From A to B we have 5 roads.
 From B to C we have 3 roads.
 Thus, the number of roads from A to C via B is 3 ×5 = 15

Note that this multiplication rule only applies when the experiments are 
independent, i.E, the choice made for one experiment does not affect the 
choice made for any of other experiments.  

Example 10.4
 A man has three choices of the way in which he travels to work; he can 
walk, go by car or go by train. How many different ways can he arrange his 

travel for the five working days in a week?

Solution

 This man has 3 choices on Monday: walk, car or train
                          3 Choices on Tuesday: walk, car or train
 Similarly on Wednesday, Thursday and Friday he has 3 choices. 
Then there are 5 successive operations, each of which can be performed 
in 3 ways. Thus, the total number of choices he has is 3 ×3× 3 ×3× 3= 243 
choices.
 
Example 10.5
 A car license plate is to contain three letters of the alphabet, the first of 
which must be r, s, t or u, followed by three decimal digits. How many 

different license plates are possible?

Solution
 The first letter can be chosen in 4 different ways, the second and third 
letters in 26 different ways each, and each of the three digits can be chosen 
in ten ways.
 Hence there are  4 ×26× 26 ×10 ×10× 10 = 2,704,000 . possible plates

 Example 10.6: 
 Imagine that we wish to experimentally manipulate growth conditions 
for plants. We want to grow plants in pots in a green-house at two 
different levels of fertilizer (low and high) and four different temperatures 

If we want three replicates of each possible combination of fertilizer and 
temperature treatment, how many pots will we need?
 
Solution
 From the principle, we see that we will need:

 2 · 4 · 3 = 24 pots for our experiment.

Application 10.1
 1. There are 4 roads joining A and B and 5 roads joining B and C. How 
many different roads from A to C via B?
 2. A car license plate is to contain two letters of the alphabet, the first 
of which must be A or B, followed by 6 decimal digits. How many 
different license plates are possible?
 Permutations
 
Activity 10.2
 Consider three letters A, B and C written in a row, one after 
another. 
• Form all  possible different words from three letters A, B and C 
(not necessarily sensible).
 In fact, each arrangement is a possible permutation of the letters A, B 
and C; for example ABC, ACB,…
 • How many arrangements are they possible for three letters A, B and C?
 
How to calculate the number of permutations without having to 
list them all
 From different arrangement of three letters a, b and c, the first letter to 
be written down can be chosen in 3 ways. The second letter can then 
be chosen in 2 ways because there are 2 remaining letters to be written 
down and the third letter can be chosen in 1 way because it is only one 
letter remaining to be written down. Thus, the three operations can be 
performed in 
3× 2× 1 =6 ways. 
This suggests the following fact:

Fact: Permutations of n objects 
The number of different permutations of n different objects (unlike objects) 

in a row is 

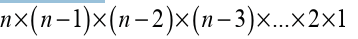
 Example 10.8
 Five children are to be seated on a bench. In how many ways can they be 
seated? How many arrangements are they, if the youngest child has to sit 

at the left end of the bench?

 Solution
 Since there are five children, the first child can be chosen in 5 ways, the 
next child in 4 ways, the next in 3 ways, the next in 2 ways and the last in 

1 way. Then, the number of ways is 

Now, if the youngest child has to sit at the left end of the bench, this place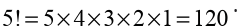 
can be filled in only 1 way. The next child can then be chosen in 4 ways, 

the next in 3 ways and so on. Thus, the number of total arrangement is 

 Example 10.9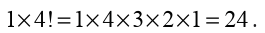
 Three different mathematics books and five other books are to be arranged 
on a bookshelf. Find:
 a) the number of possible arrangements of the books.
 b) the number of possible arrangements  if the three mathematics 
books must be kept together.
 
Solution
 We have 8 books altogether.
 a) since we have 8 books altogether, the first book can be chosen in 8 
ways, the next in 7 ways, the next in 6 ways and so on. Thus, the total 
arrangement is 8! = 40,320
b) since the 3 mathematics books have to be together, consider these bound 
together as one book. There are now 6 books to be arranged and these 
can be performed in 6! = 720.
Note that we have taken the three mathematics books as one book; these 
three books can be arranged in 3! = 6 ways.
 Thus, the total number of arrangements is  720× 6 =4,320.

Application activity 10.2
 1. Four different English books, five different Biology books and ten 
other books are to be arranged on a bookshelf. Find 
a) the number of possible arrangements of the books.
 b) the number of possible arrangements  if the three Biology 

books must be kept together?

Permutations of indistinguishable objects
 Activity 10.3
 Consider the arrangements of four letters in the word “BOOM”. 
• Write down all possible different arrangements. 
• How many arrangements are they possible of four letters in the 
word “BOOM”?
 In the same way, 
• Write down all possible different arrangements of five letters in 
the word “CLASS”. 
• How many arrangements are they possible of five letters in the 
word “CLASS”?
 Consider the arrangements of six letters in the word “avatar” (a title used 

for the movie).

Application activity 10.3
 1. How many arrangements can be made from the letters of the word 
ENGLISH?
 2. How many arrangements can be made from the letters of English 
alphabet?
 3. In how many ways can 4 red, 3 yellow and 2 green discs be arranged 

in a row, if discs of the same color are indistinguishable?

Circular arrangements
 Activity 10.4
 Take 5 different note books
 • Put them on a circular table
 • Fix one note book
 • Try to interchange other 4 note books as possible 
• How many different way obtained?

 Remember that there is one note book will not change it place.

Example 10.13

Four men Peter, Rogers, Smith and Thomas are to be seated at a circular table. In 

how many ways can this be done?

 Solution
 Suppose peter is seated at some particular place. The seats on his left can 
be filled in 3 ways, the next seat can then be filled in 2 ways and the 

remaining seat in 1 way.

Example 10.14

Nine beads, all of different colors are to be arranged on a circular wire. Two 
arrangements are not considered to be different if they appear the same 
when the ring is turned over. How many different possible arrangements 

are there?

 When viewed from one side, these arrangements are only different in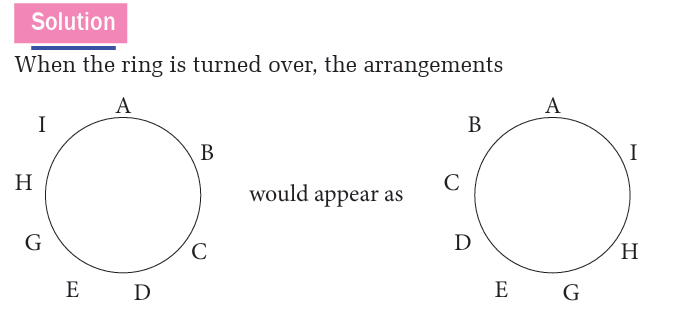 
that one is a clockwise arrangement and the other is anticlockwise. If one 
bead is fixed, there are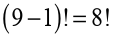 ways of arranging the remaining beads 
relative to the fixed one.
 But, half of these arrangements will appear the same as the other half when 
the ring is turned over, because for every clockwise arrangement there is 
a similar anticlockwise arrangement. Hence, number of arrangements is 

Application Activity 10.4
 1. Five men Eric, Peter, John, Smith and Thomas are to be seated at a 
circular table. In how many ways can this be done?
 2. Eleven different books are placed on a circular table. In how many 

ways can this be done?

Mutually exclusive situation
 Activity 10.5
 When you go to a restaurant you will be asked if you wish to have a 
soup or juice. Will you pick one, the other or both?
 Two experiments 1 and 2 are mutually exclusive, if when experiment 
1 occurs, experiment 2 cannot occur. Likewise, if experiment 2 occurs, 

experiment 1 cannot occur.

Basic sum principle of counting 
In such cases, the number of permutations of either experiment 1 
or experiment 2 occuring can be obtained by adding the number of 
permutations of experiment 1 to the number of permutations of experiment 2.
 This suggests the following result:  
“If experiment 1 has m possible outcomes and if experiment 2 has n possible 
outcomes, then an experiment which might be experiment 1 or experiment 
2, called experiment 1 or 2, has m +n  possible outcomes.”

 Example 10.15
 In tossing an object which might be a coin (with two sides h and t) or a die 
(with six sides 1 through 6), how many possible outcomes will appear?
 
Solution
 • The experiment may be t
 • Tossing a coin (experiment 1) or tossing a die (experiment 2), or just 
experiment 1 or 2.
 • So the number of outcomes is 2+ 6 = 8 according to the above basic 
sum principle of counting.
 Example 10.16
 How many different four digit numbers, end in a 3 or a 4, can be formed 
from the figures 3,4,5,6 if each figure is used only once in each number.
 
Solution
 We need the numbers that end in 3: the last digit can be chosen in one way, 
as it must be a 3, the first digit can then be chosen in 3 ways, the second in 
2 ways and the third in 1 way. Thus, there are 1 ×3× 2× 1= 6 numbers that 
end in a 3.
 
Similarly, there are 1× 3× 2× 1= 6 numbers that end in a 4.
 The number that ends in a 3 cannot also end in a 4, so these are mutually 
exclusive situations.
 Thus, there are 6+6 =12 numbers ending either in a 3 or in a 4.

Alternatively, this can be solved as follows:
The last digit can be chosen in 2 ways (3 or 4); the first digit can be chosen 
in 3 ways, the second in 2 ways and the third in 1 way, i.e, 2 ×3 × 2 ×1= 12
numbers end either in a 3 or in a 4.
 
 The number of permutations in which a certain experiment 1 occurs 
will clearly be mutually exclusive with those permutations in which that 

experiment does not occur. Thus,

 Example 10.17
 In how many ways can five people Smith, James, Clark, Brown and John, 
be arranged around a circular table in each of following cases:
 a) Smith must sit next to Brown.

 b) Smith must not sit next to Brown.

 Solution
 There are five people.
 a) Since Smith and Brown must sit next to each other, consider these 
two bound together as one person. There are now, 4 people to seat. 
Fix one of these, and then the remaining 3 people can be seated in 3 ×2× 1= 6
ways relative to the one who was fixed.
 In each of these arrangements, smith and brown are seated together in 
a particular way. Smith and Brown could now change the seats giving 
another 6 ways of arranging the five people. Total number of arrangements 
is 6×2 =12.

b) If Smith must not sit next to Brown, then this situation is 
a mutually exclusive with the situation in a). 
Total number of arrangements of 5 people at a circular table is 
Thus, if Smith must not sit next to Brown, the number of arrangements is 
24 -12 = 12 .


 Example 10.18
 How many even numbers containing one or more digits can be formed 
from the digits 2, 3, 4, 5, 6 if no digit may be repeated?
 
Solution
 Since the required numbers are even, last digit must 2 or 4 or 6. Note that 
there are 5 digits.
 So we can form one digit, two digits, three digits, four digits or five digits 
as follows:
 One digit:  2 or 4 or 6. That is 3 numbers.
 Two digits: 3 ways to choose the last and 4 ways to choose the first. That 

is 3× 4 = 12 numbers.

Three digits: 3 ways to choose the last, 4 ways to choose the first and 3 
ways to choose the second. That is 3× 4 ×3= 36
 Four digits: 3 ways to choose the last, 4 ways to choose the first, 3 ways to 
choose the second and 2 ways to choose the fourth. That is 3 × 4 ×3 ×2= 72
 Five digits: 3 ways to choose the last, 4 ways to choose the first, 3 ways to 
choose the second, 2 ways to choose the fourth and 1 way to choose the 
fifth. That is  3 × 4 × 3 × 2 ×1=  72
Adding, we have 3 +12+ 36+ 72+ 72 = 195 even numbers in total.

Application activity 10.5
1. How many odd numbers containing one or more digits can be 
formed from the digits 2, 3, 4, 5, 6, 7 if no digit may be repeated?
 2. How many even numbers containing 2 digits can be formed from 
the digits 2, 3, 4 if no digit may be repeated?
 3. How many numbers containing three digits can be formed from the 

digits 1, 2, 3, 4, 5, 6, 7, 8 if no digit may be repeated?

Distinguishable permutations

 Activity 10.6
 Make a selection of any three letters from the word “KNOW” and fill 

them in 3 empty spaces.

 Write down all different possible permutations of 3 letters selected 
from the letters of the word “KNOW”.
 How many are they? 
Consider the number of ways of placing 3 of the letters a, b, c, d, e, f, g in 

3 empty spaces.

 Example 10.21
 How many different arrangements are there of 3 letters chosen from the 

word COMBINATION?

Solution 
There are 11 letters including two O’s, two I’s and two N’s. to find the total 
number of different arrangements we consider the possible arrangements 

as four mutually exclusive situations.

Application activity 10.6
 1. How many permutations are there of 4 letters chosen from letters 
of the word ENGLISH?
 2. How many permutations are there of 2 letters chosen from letters 
of the word PACIFIC?
 3. How many permutations are there of 5 letters chosen from letters 
A, B, C, D, E, F, and G.
 4. How many permutations are there of 10 letters chosen from English 

alphabet.

10.2. Combinations

 Activity 10.7
 Take 3 different mathematics books and 4 unlike English books so 
that you will have 7 books altogether. Form different groups each 
containing 2 mathematics books and 2 English books. How many 

groups obtained?

 From permutation of r unlike objects selected from n different objects, we 
have seen that the order in which those objects are placed is important. But 

when considering the number of combinations of r unlike objects selected 

Example 10.22
 From a group of 5 men and 7 women, how many different committees 
consisting of 2 men and 3 women can be formed?
 
Solution
 • Experiment 1: select 2 men from 5.
 • Experiment 2: select 3 women from 7.
 • Experiment of forming a committee: experiment 1 & 2.

 • Number of possible outcomes of experiment 1 is 

• That is, the desired number of possible outcomes of the experiment 
of forming a committee is 350.

 Example 10.23
 A committee of three men and one woman is obtained from five men and 

three women. In how many ways can the members be chosen?

Example 10. 24
 Suppose that you wish to plant 5 grass species in a plot. You can choose 

among 12 different species. How many choices do you have?

Example 10.25

In a sample of 50 people, 21 had type O blood, 22 had type A blood, 5 had 
type B blood, and 2 had type AB blood. Set up a table of those numbers and 

find the probability that a person has type O blood.

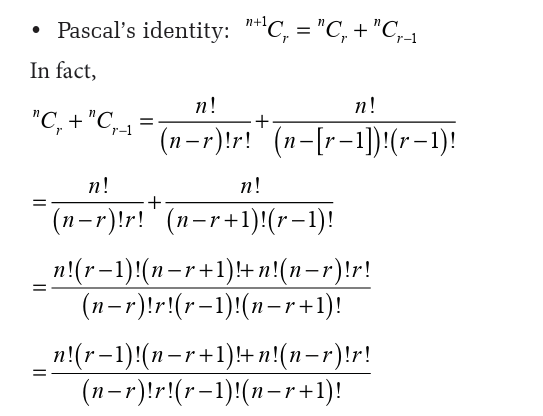
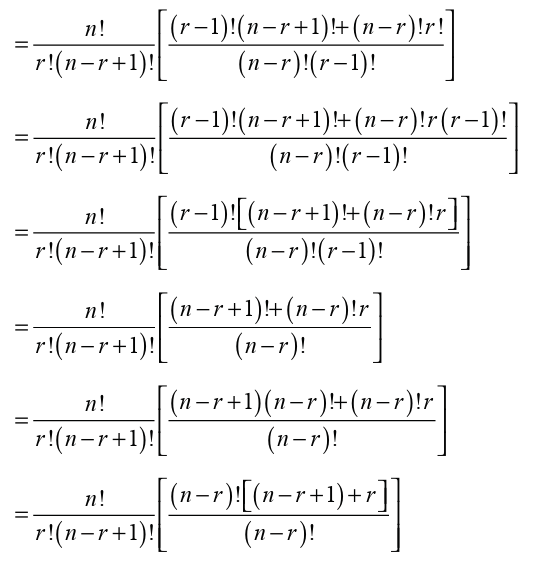
Application activity 10.7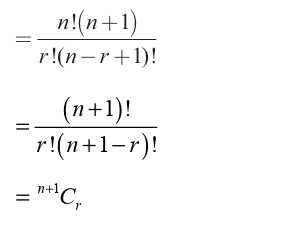
 1. A committee of four men and two women is obtained from 10 men 
and 12 women. In how many ways can the members be chosen?
 2. A group containing 4 Mathematics books and 5 Physics books is 
formed from 9 Mathematics books and 10 Physics books. How 

many groups can be formed?

 

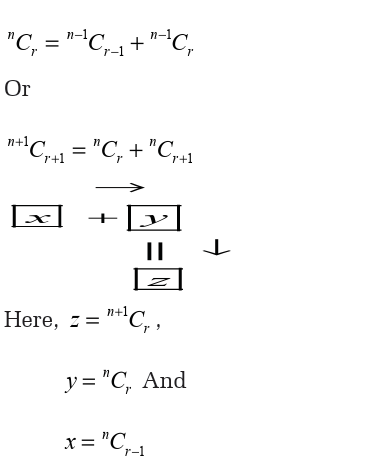
A simple construction of this triangle proceeds in the following manner: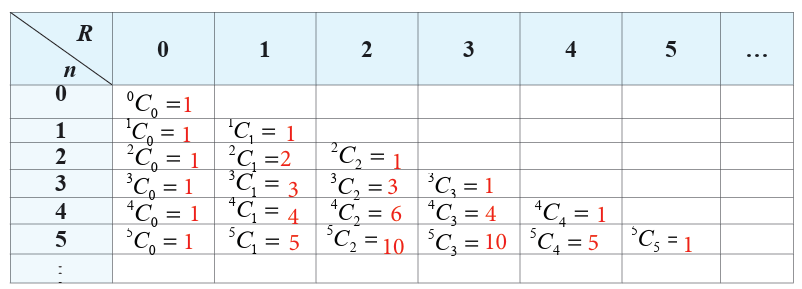 
• On row 0, write only the number 1. 
• Then, to construct the elements of following rows, add the number 
above and to the left with the number above to the right to find the 
new value. 
• If either the number to the right or left is not present, substitute a 
zero in its place. For example, the first number in the first row is 0 +1= 1
 , whereas the numbers 1 and 3 in the third row are added to 

produce the number 4 in the fourth row.

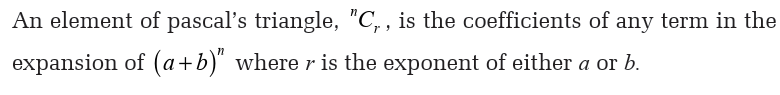
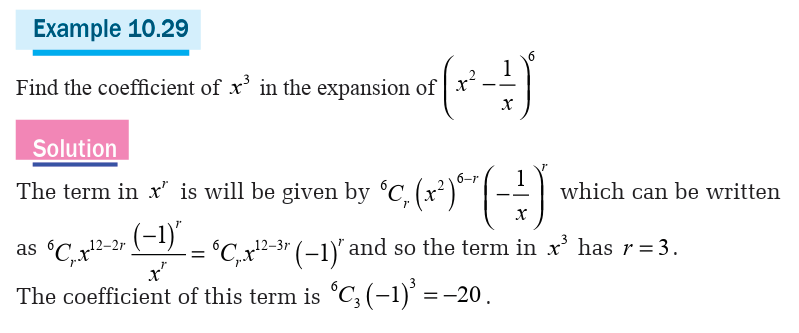
 1. Suppose that you are choosing one card;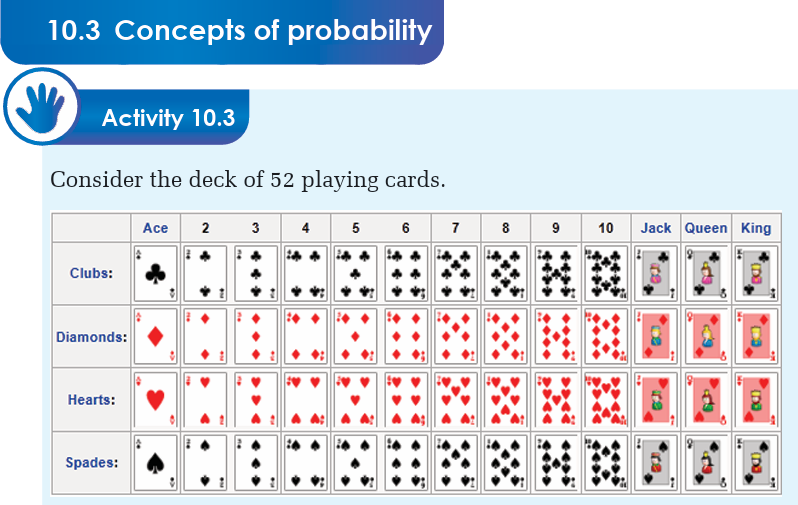
 (i) How many cards can be chosen?
 (ii) How many kings can be chosen?
 (iii) How many aces of hearts can be chosen?
 2. If a spade card has been declared to be a trump card. How many 
trumps of Jack can be chosen?

Probability is the chance that something will happen. 
The concept of probability can be illustrated in the context of game of 
52 playing cards. In a park of deck of 52 playing cards, cards are divided 
into four suits of 13 cards each. If a player selects a card at random (by 
simple random sampling), then each card has the same probability of 
being selected.

 In most sampling situations we are generally not concerned with 
sampling a specific individual but instead we concern ourselves with 
the probability of sampling certain types of individuals. For example, for 
our case of a deck of 52 playing cards, what is the probability of selecting 
a queen? Selecting a queen is the event and selecting any card from 52 
cards is an experiment.
 
Random experiments and events
 A random experiment is an experiment that, atleast theoretically, may be 
repeated as often as we want and whose outcome cannot be predicted, the 
roll of a die. Each time experiment is repeated, an elementary outcome is 
obtained. The set of all elementary outcomes of a random experiment is 
called the sample space, which is denoted by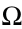 
discrete or continuous.
 
Discrete sample space: 
. Sample space may be 
• Firstly, the number of possible outcomes is finite. 
• Secondly, if the number of possible outcomes is countably infinite, 
which means that there is an infinite number of possible outcomes, 
Then the outcomes can be put in a one-to-one correspondence with 

the positive integers. 

Example 1.30

If a die is rolled and the number that shows up is noted, then 

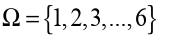
Example 1.31
 If a die is rolled until a “6” is obtained, and the number of rolls made before getting 
first “6” is counted, then we have that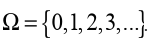 
Continuous sample space: 
If the sample space contains one or more intervals, the sample space is 
then uncountable infinite. 

Example 1.32

 A die is rolled until a “6” is obtained and the time needed to get this first “6” is 

 An event is a set of elementary outcomes. That is, it is a subset of the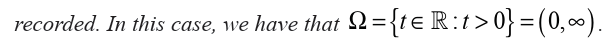 
sample space. 
In particular, every elementary outcome is an event, and so is the sample 
space itself.
 
Remarks:
 • An elementary outcome is sometimes called a simple event, whereas 
a compound event is made up of at least two elementary outcomes.

 • To be precise, we should distinguish between the elementary outcome 

Example 1.33

Consider the experiment that consists in rolling a die and recording the 
number that shows up. Let A be the event “the even number is shown” and 
B be the event “the odd number less than 5 is shown”. Define the events A 
and B.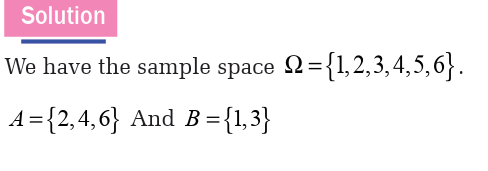

Definitions
 • Two or more events which have an equal probability of occurrence are 
said to be equally likely, i.e. If on taking into account all the conditions, 
there should be no reason to accept any one of the events in preference 
over the others. Equally, likely events may be simple or compound events.
• Two events, A and B are said to be incompatible (or mutually exclusive)
if their intersection is empty. We then write that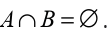 
• Two events, A and B are said to be exhaustive if they satisfy the condition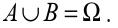

 • An event which is sure to occur at every performance of an experiment 
is called a certain event connected with the experiment. For example, 
“Head or Tail’ is a certain event connected with tossing a coin. Face-1 or 
face-2, face-3, ……, face-6 is a certain event connected with throwing a die.
 • An event which cannot occur at any performance of the experiment is 
called an impossible event. Following are such examples
 i. ‘Seven’ in case of throwing a die.
 ii.  ‘Sum=13’ in case of throwing a pair of dice.
 • Two events are said to be equivalent or identical if one of them implies 
and implied by other. That is, the occurrence of one event implies the 
occurrence of the other and vice versa. For example, “even face” and 
“face-2” or “face-4” or “face-6” are two identical events.
 • The outcomes which make necessary the happening of an event in a 
trial are called favourable events. For example; if two dice are thrown, 
the number of favourable events of getting a sum 5 is four, i.e., (1, 4), (2, 
3), (3, 2) and (4, 1).

 Example 10.32
 Consider the experiment that consists in rolling a die and recording the 
number that shows up.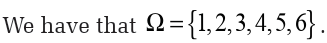

Therefore, A and C are incompatible events.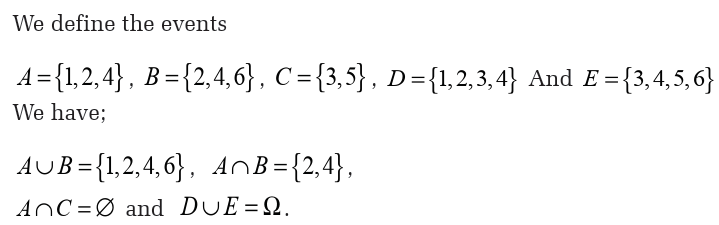 

D and E are exhaustive events.

Example 1.35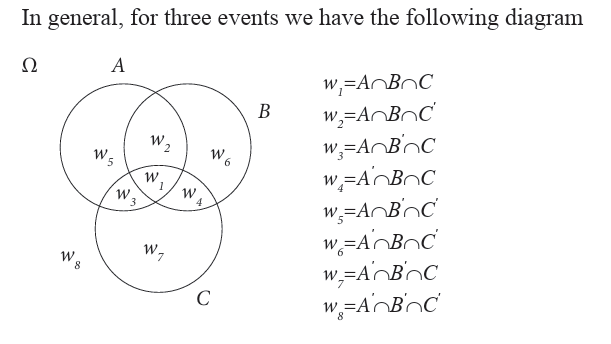
 In the experiment of tossing a coin: 
Where;
 (i) A : the event of getting a “head” and 
(ii) B : the event of getting a “tail”
 Events “A” and “B” are said to be equally likely events. Both the events have 
the same chance of occurrence. 

Example 1.36
 Consider the experiment that consists in choosing at random from the list 
2, 3, 5, 7, 11, 13, 17, 19. The event that the chosen number is not prime 
number is impossible events since all numbers are prime numbers.
 
Example 1.37
 Consider the experiment that consists in rolling a die. The event of rolling 
a number that is not 8 is a certain event. 

Application activity 10.9
 1. A box contains 5 red, 3 blue and 2 green pens. If a pen is chosen 
at random from the box, then which of the following is an 
impossible event? 
a) Choosing a red pen.
 b) Choosing a blue pen.
 c) Choosing a yellow pen.
 d) None of the above.
 2. A spinner has 9 equal sectors numbered 1 to 9. If you spin the 
spinner, then which of the following is a certain event? 
a) Landing on a number less than 9.
 b) Landing on a number less than 12.
 c) Landing on a number greater than 1.
 d) None of the above.
3. Which of the following are mutually exclusive events when a day of the 
week is chosen at random? 
a) Choosing a Monday or choosing a Wednesday.
 b) Choosing a Saturday or choosing a Sunday. 
c) Choosing a weekday or choosing a weekend day. 
d) All of the above. 
4. A die is tossed, tell whether the following events are exhaustive or not.
 a) X = Get prime number ; Y = Get multiple of 2 ; Z = Get 1.
 b) X = Get prime numbers; Y = Get composite numbers; Z = Get 1.

 c) X = an odd number; Y = an even number.

10.4. Properties and formulas 
Activity 10.4
 Consider the letters of the word “PROBABILITY”.
 a) How many letters are in this word  
b) How many vowels are in this word? What is the ratio of numbers 
of vowels to the total number of letters?
 c) How many consonants are in this word? what is the ratio of the 
numbers of consonants to total number of letters

 d) Let A be the set of all vowels and B the set of all consonants. Find

 Example 10.38
 A letter is chosen from the letters of the word “MATHEMATICS”. What is 
the probability that the letter chosen is an “A”?
 
Solution
 Since two of the eleven letters are a’s, we have two favorable outcomes. 
There are eleven letters, so we have 11 possible outcomes. 

Thus, the probability of choosing a letter a is 

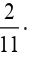
Example 10.39

A medical study tests a new medicine on 3500 people. It is effective for 
3,010 people. Find the experimental probability that the medicine is 
effective. Then, predict the number of people in a group of 6,000 for whom 

the medicine will be effective. 

Solution
 From the definition, the probability of an event is the quotient of the 
number of times that event occurs by the number of times experiment is 

done.

Application activity 10.4
 1. A letter is chosen from the letters of the word “MATHEMATICS”. 
What is the probability that the letter chosen is 
a) M?                  b)                          T?
 2. An integer is chosen at random from the set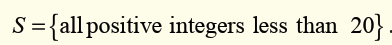 

Let A be the event of 
choosing a multiple of 3 and let B be the event of choosing an odd 

number. Find;

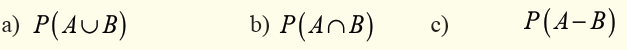
 Example 10.42
 In a group of 20 adults, 4 out of the 7 women and 2 out of the 13 men wear 
glasses. What is the probability that a person chosen at random from the 
group is a woman or someone who wears glasses?
 
Solution
 Let A be the event: “the person chosen is a woman”.

      B be the event: “the person chosen wears glasses”.

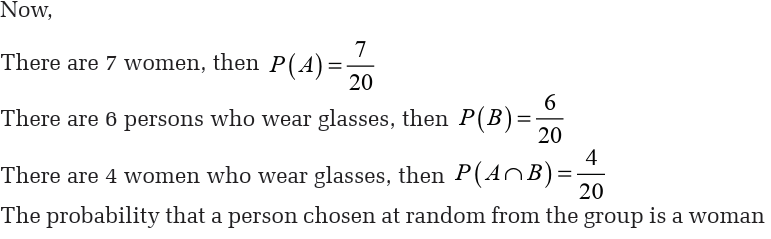
Application activity 10.11
 1. A fair die is rolled, what is the probability of getting a even number 
or prime number?
 2. Two fair dice are rolled, what is the probability of getting a sum that 

is divisible by 2 or 4?

Mutually exclusive events
Activity 10.12
 A book is drawn from a bookshelf containing 15 books of which 
5 are Mathematics books and 10 are English books. If A is the 
event: “a book is a Mathematics book” and B is the event: “a 

book is an English book”, find:

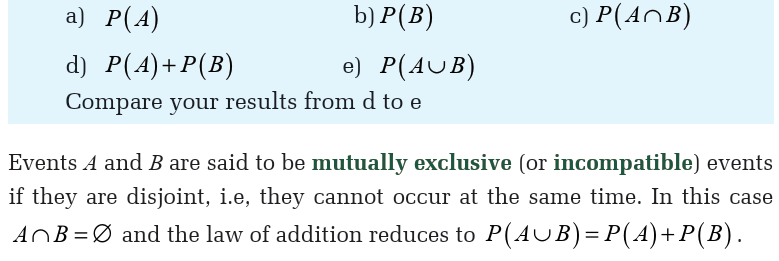
 Example 10.44
 A card is drawn at random from an ordinary pack of 52 playing cards. Find 

the probability that the card drawn is a club or a diamond.

Application Activity 10.12

1. If A and B are mutually exclusive events, given the probability of A

Exhaustive events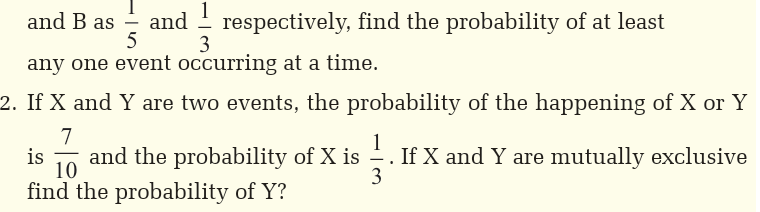
 Activity 10.13

 An integer is chosen at random from the set 

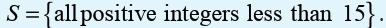  Let A be the event of choosing an 

odd number and let B be the event of choosing an even number. Find:

What can you say about result in a. and result in b.?

Example 10.43
 Events A and B are such that they are both mutually exclusive and 

exhaustive. Find the relation between these two events.

Thus, if events A and B are such that they are both mutually exclusive and 
exhaustive, then they are complementary.
 
Application activity 10.13
 In a class of a certain school, there are 12 girls and 20 boys. If a 
teacher wants to choose one learner to answer the asked question
 a) What is the probability that the chosen learner is a girl?
 b) What is the probability that the chosen learner is a boy?
 c) If teacher doesn’t care on the gender, what is the probability 

of choosing any learners?

Unit summary
 1. Combinatorial analysis is a mathematical theory of counting.
 2. Experiment: any human activity.
 Trial: small experiment contained in a large experiment. 

Outcome called event: a result of an experiment.

11. Probability is the chance that something will happen-how likely it is 
that some event will happen. 
12. A random experiment is an experiment that, at least theoretically, 
may be repeated as often as we want and whose outcome cannot be 
predicted, the roll of a die. 
13. Each time experiment is repeated, an elementary outcome is obtained. 
14. The set of all elementary outcomes of a random experiment is called 
the sample space, which is denoted by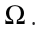 
15. Discrete sample space: Firstly is the number of possible outcomes is 
finite. 
16. Continuous sample space: If the sample space contains one or more 
intervals, the sample space is then uncountable infinite. 
17. An event is a set of elementary outcomes. That is, it is a subset of the 
sample space. 
18. Two or more events which have an equal probability of occurrence 
are said to be equally likely, i.e. if on taking into account all the 
conditions, there should be no reason to except any one of the events 
in preference over the others. Equally likely events may be simple or 
compound events. 
19. Two events, A and B are said to be incompatible (or mutually exclusive) 
if their intersection is empty. We then write that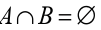 
20. Two events, A and B are said to be exhaustive if they satisfy the condition

21. An event which is sure to occur at every performance of an experiment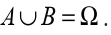 
is called a certain event connected with the experiment. 
22. An event which cannot occur at any performance of the experiment 
is called an impossible event. 
23. Two events are said to be equivalent or identical if one of them 
implies and implied by other. That is, the occurrence of one event 
 implies the occurrence of the other and vice versa. 
24. The outcomes which make necessary the happening of an event in 
a trial are called favourable events. 
25. If E is an event, then ' E is the event which occurs when E does not 

occur. Events E and ' E are said to be complementary events.

 End unit assessment
 1. If there are three different roads joining town A to town B and four 
different roads joining town B to town C, in how many different ways 
can I travel from A to C via B and return if:
 a) there are no restrictions,
 b) I am not able to return on any road I used on the outwards 
journey?
 2. How many 3-digits numbers can be formed using only the digits 1, 
2, 3, 5, 7 and 8? How many of these numbers are even? How many 
are less than 500?
 3. There are three roads joining town X to town Y; three more roads join 
Y to z and two roads join Z to A. How many different routes are there 
from X to A passing through Y and Z?
 4. In how many ways can a group of ten children be arranged in a line?
 5. In how many ways can eight different books be arranged on a 
bookshelf?
 6. The letters a, b, c and d are to be arranged in a row with each letter 

being used once and once only. In how many ways can this be done?

9. There are ten teams in the local football competition. In how many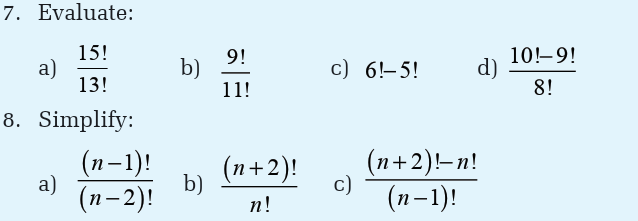 
ways can the first four places in the premiership table be filled?
 10. In how many different ways can five identical blue balls, two 
identical red balls and a yellow ball be arranged in a row?
 11. Find the number of arrangements of four different letters chosen 
from the word PROBLEM which:
 a) begin with a vowel.
 b) end with a consonant.
 12. With his breakfast, a man sometimes has tea, sometimes coffee and 
sometimes fruit juice, but never more than one of these on any one 
day. Find the number of possible arrangements he can have in a 
period of 4 days if:
 a) he always has a drink of some sort,
 b) he may choose not to have a drink on certain days.
 13. How many numbers greater than 300 can be formed from the figures 
4, 3, 2 and 1 if each figure can be used not more than once in each 
number and all the figures need not be used each time?
 14. A box contains 14 colored discs which are identical except for their 
color. There are 5 red discs, 4 green discs, 4 blue discs and 2 yellow. 
In how many ways can the 14 discs be arranged in a row?
 15. Find the number of different three-letter arrangements that can be 
made from the letters of the word ISOSCELES.
 How many of these arrangements will contain:
 a) no E’s at all,   
b)  at least one E,
c) no vowels at all,  
d)  at least one vowel
16. A basketball team of 6 is to be chosen from 11 available players. In 
how many ways can this be done if:
 a) there no restrictions,
 b) 3 of the players are automatically selected,
 c) 3 of the players are automatic in  selections and 2 other players 
are injured and cannot play? 
17. In how many ways can 9 people be placed in cars which can 
take 2, 3 and 4 passengers respectively, assuming that the seating 
arrangements inside the cars are not important?
 18. A group consists of 5 boys and 8 girls. In how many ways can a team 
of four be chosen, if the team contains:
 a) no girl.
 b) not more than one girl.
 c) atleast two boys?
 19. Find the number of ways that 9 children can be divided into:
 a) a group of 5 and a group of 4 children,
 b) three groups of 3 children. 
20. a) A small holiday hotel advertises for a manager and 7 other 
members of staff. There are 4 applicants for the position of 
manager and 10 other people apply for the other jobs at the hotel. 
Find the number of different ways of selecting a group of people 
for the 8 jobs.
 b) The hotel has 4 single rooms, 6 double rooms and 5 family rooms. 
For a particular week, 4 individuals book single rooms, 3 couples 
book double rooms and 3 families book family rooms. Given that 
all the rooms are available for that week, find the number of
 different possible arrangements of booking amongst the rooms.
 c) One afternoon, 12 guests organize a game requiring 2 teams of 6. 
Find the number of different ways of selecting the teams.
 d) Given that the 12 guests consist of 6 adults and 6 children and 
that each team must contain atleast 2 adults, find the number of 

different ways of selecting the teams.

41. Which of the following is an experiment?

a) Tossing a coin,                                     b) Rolling a single die,

c) Choosing a marble from a jar,       d) All of the above.

42. Which of the following is an outcome? 
a) Rolling a pair of dice,                         b)  Landing on red,
 c) Choosing 2 marbles from a jar,    d)  None of the above.

 43. Which of the following experiments does not have equally likely 
outcomes? 
a) Choose a number at random between 1 and 7,           b) Toss a coin,
c) Choose a letter at random from the word SCHOOL,   d) None of the above.
 
44. A glass jar contains 5 red, 3 blue and 2 green jelly beans. If a jelly 
bean is chosen at random from the jar, then which of the following 
is an impossible event?    
a) Choosing a red jelly bean,               b) Choosing a blue jelly bean,
c) Choosing a yellow jelly bean,        d) None of the above.
45. A spinner has 7 equal sectors numbered 1 to 7. If you spin the 
spinner, then which of the following is a certain event? 
a) Landing on a number less than 7,
 b) Landing on a number less than 8, 
c) Landing on a number greater than 1,
 d) None of the above.
 46. Tickets numbered 1 to 20 are mixed up and then a ticket is drawn at 
random. What is the probability that the ticket drawn has a number 
which is a multiple of 3 or 5? 
47. A bag contains 2 red, 3 green and 2 blue balls. Two balls are drawn at 
random. What is the probability that none of the balls drawn is blue? 
48. In a box, there are 8 red, 7 blue and 6 green balls. One ball is picked 
up randomly. What is the probability that it is neither red nor green? 
49. In a class, there are 15 boys and 10 girls. Three students are selected 
at random. What is the probability that 1 girl and 2 boys are selected?
 50. From a pack of 52 cards, two cards are drawn together at random. 
What is the probability of both the cards being kings?
 51. One card is drawn at random from a pack of 52 cards. What is the 
probability that the card drawn is a face card (Jack, Queen and King 
only)?
 52. An integer is chosen at random from the first 200 positive integers. 
Find the probability that the number is:
 a) divisible by 2
 b) divisible by 7
 c) divisible by 2 and 7
 d) divisible by neither 2 nor 7
 53. The letters of the word FACETIOUS are arranged in a row. Find the 
probability that:
 a) the first 2 letters are consonants,
 b) all the vowels are together.