Unit 2: Fundamentals of Trigonometry►

Unit 1 :Set IR of real numbers

  • Unit 1 :Set IR of real numbers

    1.0 Introductory activity

     From the following diagram, discuss and work out the given tasks: 

    r

    1. How many sets of numbers do you know? List them down    and give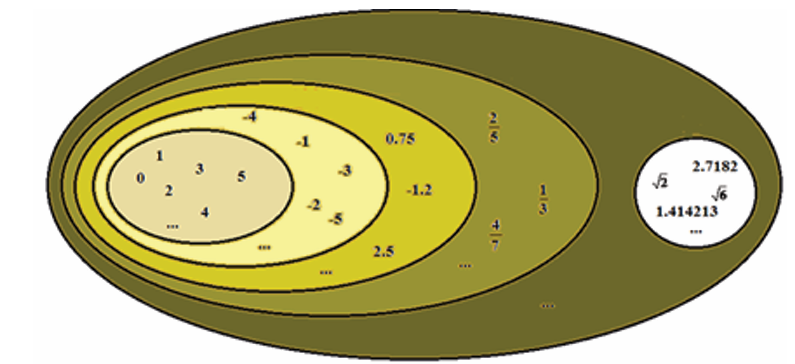 
    reasons for your answer. 
    2. Using a mathematical dictionary or the internet, define the sets of 
    numbers you listed in    (1). 
    3. Give an example of element for each set of numbers you listed.

    4. Establish the relationship between the set of numbers that you listed.

    Objectives
     After completing this unit, I will be able to:
     » Define absolute value of a real number and solve 
    simple equations involving absolute value.
     » Define powers and their properties.
     » Define radicals and their properties.
     » Define decimal logarithms of a real numbers and 

    solve simple logarithmic equations.

     1.1. Subsets and properties of operations in the set real numbers
    Activity 1.1
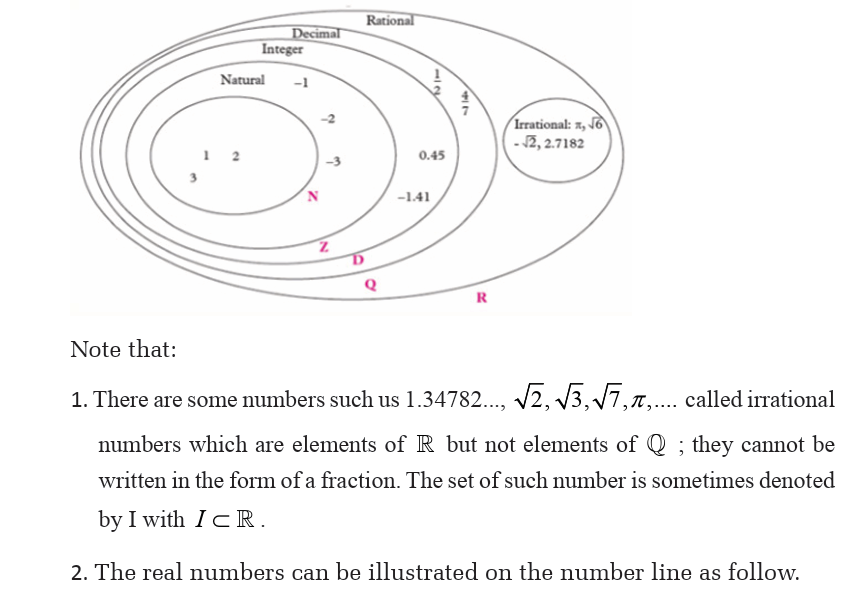
    a. Carry out a research on sets of numbers to determine the meaning of 
    natural numbers, integers, rational numbers and irrational numbers. 
    Use knowledge from your findings to classify numbers in the given 

    list into natural numbers, integers, rational numbers and irrational 





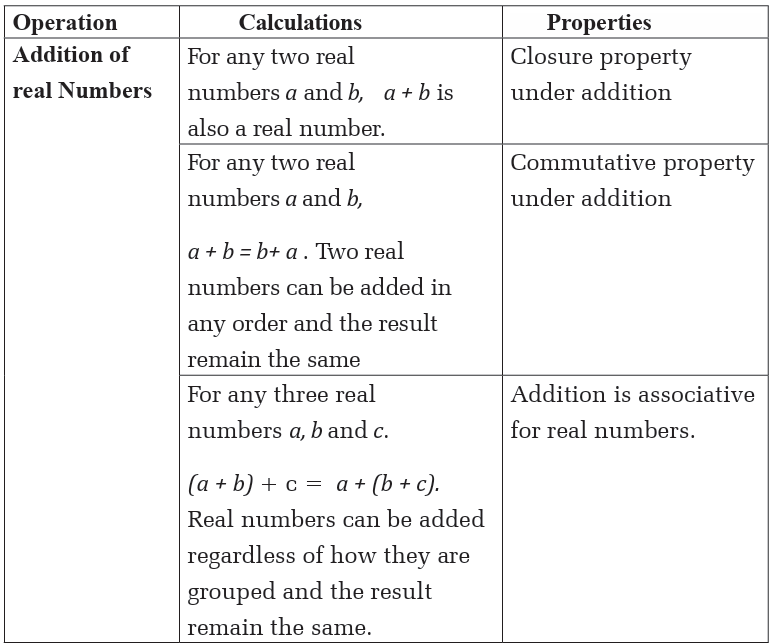
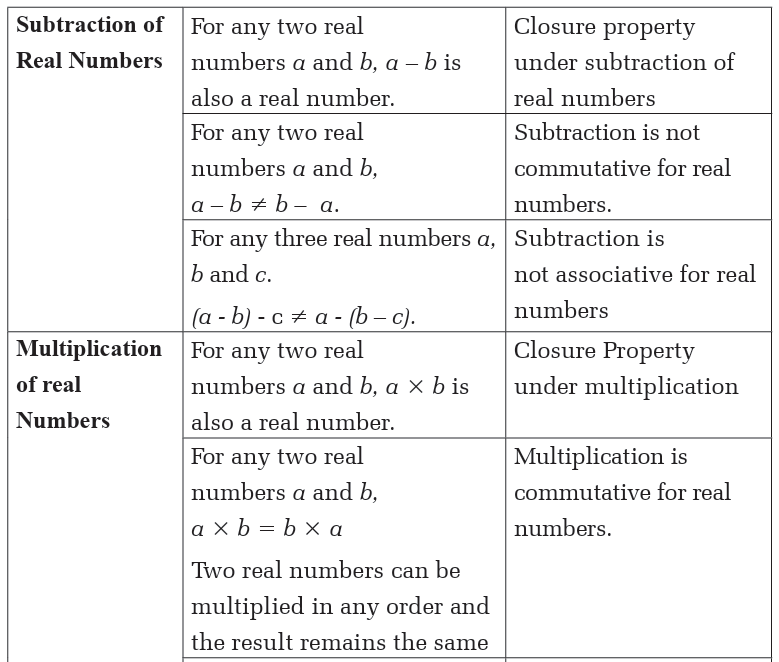
    The following table shows the addition, subtraction, multiplication and 

    division of real numbers and the related properties.

     Application Activity 1.1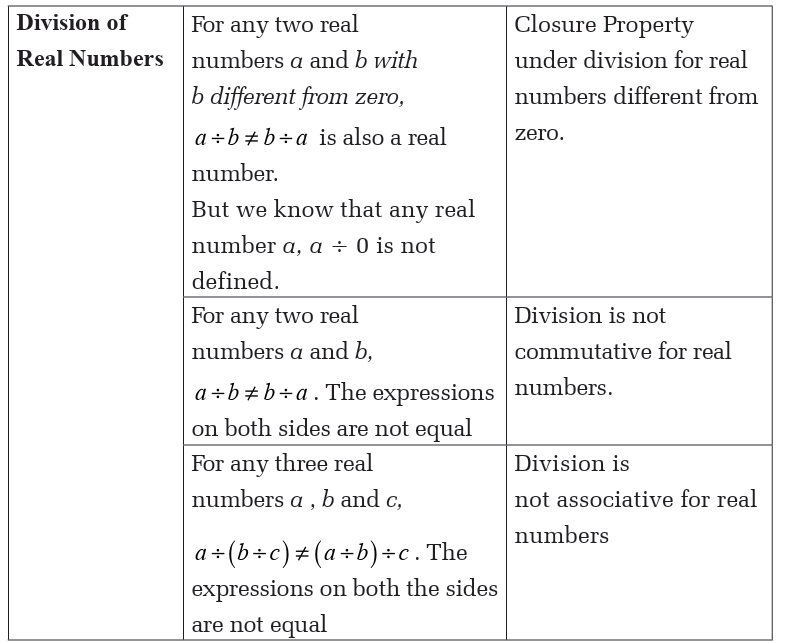
     1. Plot a number line and locate elements of the following subsets of 

    real numbers. 

     1.2. Positive and negative numbers
     Activity 1.2
     1. By means of thermometer, a Doctor recorded the temperature of a patient 

    at different times of the same day.



     a) When the lowest temperature of a patient  was recorded?
     b) What was the difference in temperature between 6:00 and 21:00?
     c) What was the difference in temperature between 9:00 and 12:00?
     d) At midnight the temperature was 0.25 degrees above 21:00. What was 
    the temperature at midnight?
     
    Extreme high and low temperatures contribute directly to deaths from 
    cardiovascular and respiratory disease, particularly among elderly 
    people. In Quebec, Canada, it was observed that on July 6th 1921 the 
    highest temperature recorded in Ville-Marie was 40 oC and on February 
    5th 1923 the lowest temperature recorded in Doucet  was -54.4 oC. Do you 
    think this records can happen or was happened in Africa?  Consult the 
    link (https://en.wikipedia.org/wiki/List_of_countries_and_territories_
     by_extreme_temperatures)  and find out the lowest temperature(oC) 
    recorded on January 28th 2005 in Mecheria , Algeria and the lowest 

    temperature(oC) recorded on February 11th 1935 in Ifrane, Morocco. 


    The most commonly used numbers in arithmetic are integers, which are 
    positive and negative whole numbers including zero. Positive integers 
    are 1, 2, 3, 4, 5 and so on. The negative integers are -1, -2, -3, -4, -5 and 
    so on.
     Integers (positive and negative numbers) can be represented on a 
    number line and the number line can be used to perform addition and 
    subtraction.
     
    Example 1.1: 
    1) Use a number line, locate -2 and -5. Then perform the following 
    operation using a number line:          (-2)+(-5)= 
    Solution
     “negative 2 minus negative 5” meaning that (-2) + 5 (adding the 

    opposite). 

     Integers (positive and negative numbers) have the real-life applications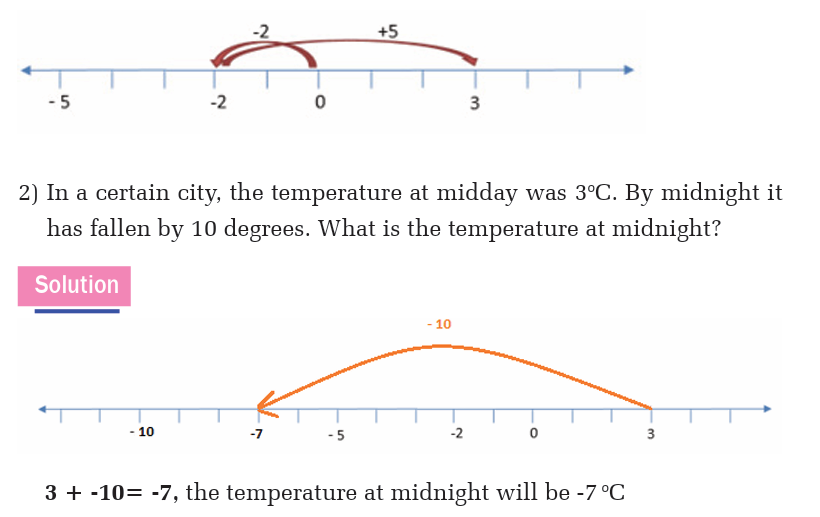 
    and situations where one can find the use of plus and minus-valued 

    integers.

    • When scientists measure the temperature of the water and some 
    chemical compound, then the mixture is said to be cold, if the 
    thermometer (or any other measuring device) gives a negative 
    value. 
    • −67.8 °C (−90.0 °F) is the record temperature of Verkhoyansk and 
    Oymyako of the country Russia. Here, even countries and many 
    cities of the world are represented using negative numbers for 
    freezing climates and positive numbers for hot summer weather.
     • During banking or when involved in any other financial procedures, 
    minus sign denotes debit value and the positive sign represents a 
    credit value. So, if the balance check sheet for your debit card 
    states – 14 500, then you have a loan amount of 14 500 Frw to be 
    debated in the bank. 

    Application Activity 1.2
     1. Water freezes at 0oC. Is the temperature in a freezer,  
    a) Equal to 0oC?
     b) Lower than 0oC?
     c) Greater than 0oC?
     2. Here are six temperatures, in Celsius degrees.
     6          -10            5        -4        0         2
     Write them in order, starting with the lowest.
     3. Here are the midday temperatures, in degrees Celsius, of five cities 

    on the same day.

     a) Which city was the warmest?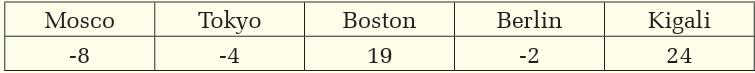
     b) Which city was the coldest?
     c) What is the difference between the temperatures of Berlin and 
    Boston?
    4. Some frozen food is stored at -8oC. During a power cut the 
    temperature increases by 1oC every minute.  Copy and complete 

    this table to show the temperature of the food.

     5. In a certain city, the temperature was -7 oC in the morning and 
    dropped by 10oC in the afternoon. What is the new temperature?

     1.3.  Rounding and estimating decimal numbers.  

    Activity 1.3
     As a pharmacy technician, you will encounter decimals nearly every 
    day. Medications are frequently prescribed in decimals, and you will 
    find that many dosage calculations will be worked out using the 

    decimal format.

    1. Use calculator to work out 

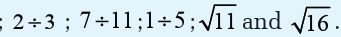
    What do you notice? 

    2. How can you write the answer for instance when dividing 22 by 7, 
    calculating square root of 3 ?  Explain? 
    The word “Decimal” means “based on 10” and comes from the Latin 
    word: decima which means «a tenth part”. Decimal numbers are used 
    in situations which call for more precision than whole numbers provide. 
    As with whole numbers, a digit in a decimal number has a value which 
    depends on the place of the digit. The places to the left of the decimal 
    point are ones, tens, hundreds, and so on, just as with whole numbers.
     The following illustration shows the decimal place value for various 

    positions:

    Each digit in a number has a ‘place value’ (related to one). The value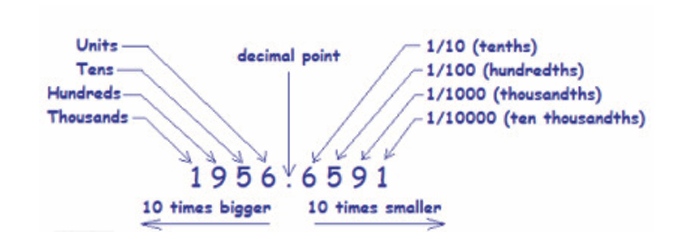 
    depends on the position of the digit in that number. Each position can 
    be thought of as columns. Each column is a power of ten. 

    For example, let’s look at 56.39 

    A recurring decimal is a decimal fraction where a digit repeats itself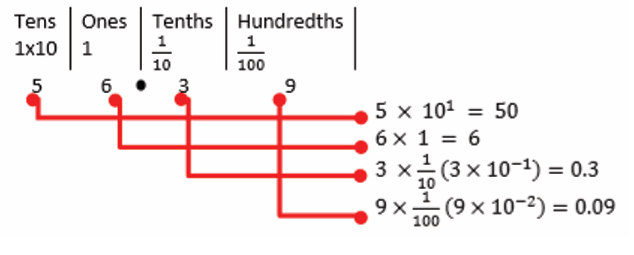 

    indefinitely. 

    Rounding numbers is a method of summarizing a number to make 
    calculations easier to solve. Rounding decreases the accuracy of a 
    number.  Rounding to a specified integer or decimal is important when 

    answers need to be given to a particular degree of accuracy.  

    The Rules for Rounding:
     1. Choose the last digit to keep.  
    2. If the digit to the right of the chosen digit is 5 or greater, increase the 
    chosen digit by 1.
     3. If the digit to the right of the chosen digit is less than 5, the chosen 
    digit stays the same. 
    4. All digits to the right are now removed.

     Example 1.3
     What is 7 divided by 9 rounded to 3 decimal places?
     Solution 
    7÷ 9 =0.7777777...
     
    So, by respecting rule 2, then      7÷ 9 = 0.778
     
    Estimating decimal numbers.
     Estimating is a very important skill in solving Mathematics problems.  It helps 
    to be able to estimate the answer to check if your calculations are correct. 
    Some simple methods of estimation:
     • Rounding
     Example 1:  273.34+ 314.37=?
    If we round to the tens  We get  270 +310 which is much easier and
     quicker. We know that 273.34 +314.37 should equal approximately 580.

         • Compatible Numbers
    Example 2: 527× 12 ?

     1.4.  Fractions and equivalent fractions  
    Activity 1.4

     Refer to the figures and answer the related questions  

    a) What fraction of the large square is black?
    b) What fraction of the large square has vertical lines?
    c) What fraction of the large square has diagonal lines?
    d) What fraction of the large square has wavy lines?
    e) What fraction of the large square has dots?
    f) What fraction of the large square is unshaded?
    g) What fraction of the large square has the horizontal line?

    h) What is the relationship between 

     • Fractions are representations of “parts of a whole”. A fraction is a part of a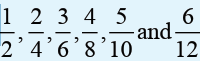 
    whole: the denominator (bottom number) represents how many equal parts 
    the whole is split into; the numerator (top number) represents the amount of 
    those parts 
    • Equivalent fractions are two or more fractions that are all equal. 
    The second figure in activity above shows that each row has been 
    split into different fractions: top row into 2 halves, bottom row 12 

    twelfths. An equivalent fraction splits the row at the same place. 

    therefore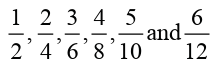  are all equal and equivalent fractions. 
    Doctors often use fractions to figure out what the right dose is. There 
    is a medicine that can treat patients who are having a stroke (a blood 
    clot that stops blood flow going to part of the brain). The dose of 
    the medication is (9/10) times the body weight in kilograms. So if 
    a patient weighs 70 kg, doctors have to multiply 99/100x (70) = 63 
    mg of medication. Then (1/10) of that is given right away (6.3 mg), 
    followed by the rest (63-6.3=56.7 mg) over an hour. The nurses 
    who give the medication have to do more to figure out how much 
    medication has to be given every minute on a pump. If there is a 
    math mistake, then the patient might get too little medication-then 
    it probably won’t work. If they get too much medication, they might 
    have bleeding in the brain. So doctors have to be sure they do it right. 
    Calculators and several people do the math to make sure everyone 

    agrees

    Application Activity 1.4
     1. Given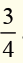 . Find the equivalent fraction by multiplying 4.
     2. The order reads 1/400 gr. The vial is labelled 1/300g =20 drops. 

    How many drops are to be given? 

    1.5. Ratios, proportions and rates. 
     Activity 1.5
    1. you survey your friends about their favourite course in associate 
    nursing program  and you find that 8 out of 12 prefer Maternal and 
    Child health. 
    a) Write in simplest form the fraction that represents those who do 
    not prefer Maternal and Child health.
     b) Which fraction best communicates the survey results?
     c) Express to percentage, the fraction of those who prefer Maternal 

    and Child health.

     2. At a certain clinic, an hospitalized person had to pay 17,500FRW for 
    consultation, 45,000FRW for medicine, and 30,000FRW for room in 

    3days. If the patient was insured by RSSB who pay 85% of the cost, 

    a. How much money did the RSSB pay for the patient?
     b. How much money did the patient pay on his/her own? 

    3. Consider the table below which shows the relationship between 

    the ages (in year) and quantity of medicine (in ml) to be take.

     a. Draw the graph of the number of medicine (in ml) against ages 
    (in year) 
    b. Describe the graph you have drawn in (a) above.
     4. Consider the relationship between the speed and time taken by a 

    car to cover a fixed distance of 320 km.

    Take 20 km/h to be the original speed.
     (i) What do you notice when the speed is doubled? 
    (ii) Plot the graph of speed against time. 

    (iii) Describe the graph you drew to your classmates.

     5. A pulse is measured as 17 beats over 15 seconds. What is the heart 
    rate per minute?
     1. A ratio is a comparison of two quantities. The ratio of a to b can also 
    be expressed as a:b or a/b. This relation gives us how many times one 
    quantity is equal to the other quantity. In simple words, the ratio is 
    the number which can be used to express one quantity as a fraction 
    of the other ones.
     Ratio Formula:
     Assume that, we have two quantities (or two numbers) and we have to 
    find the ratio of these two, then the formula for ratio is defined as; a: 
    b ⇒ a/b, where a and b could be any two quantities.
     
    Example 1.5

     The ratio of 2 to 4 is represented as 2:4 = 1:2.

    Example 1.6
     Consider a class that has 20 male students and 80 female students. We 
    can think about this in several ways. We could express this simply as the 
    ratio of men to women and write the relationship as 20:80 or 20/80. We can 
    also simplify this by dividing both the numerator and the denominator by a 
    number that divides evenly into both 
    the numerator and the denominator.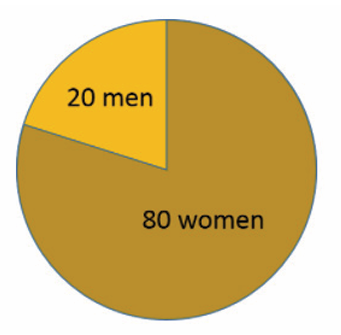

     In this case, we could divide both by 20 to simplify this to a 1:4 ratio 
    (or 1/4 ratio). This indicates that for every man, there are four women. 
    We could also consider this from the inverse perspective, i.e., the 
    number of women relative to the number of men; in this case the ratio 
    of women to men is 80/20 which is equivalent to 4 to 1, i.e., there are 
    four women for every man.

    Note that Equivalent ratios     are ratios that have the same value. Given a 
    ratio, we can generate equivalent ratios by multiplying both parts of the 
    ratio by the same value.
     2. Proportion is an equation which defines that the two given ratios are 
    equivalent to each other. A proportion is a type of ratio that relates a part to a 
    whole.
     Proportion Formula:
     Assume that, in proportion, the two ratios are a:b  and  c:d. The 
    two terms ‘b’ and ‘c’ are called ‘means or mean term,’ whereas the 

    Example 1.7
     The time taken by train to cover 100km per hour is equal to the time 
    taken by it to cover the distance of 500km for 5 hours. Such as 100km/
     hr = 500km/5hrs.
     
    Example 1.8
     In the class with 20 men and 80 women, the total class size is 100, and 
    the proportion of men is 20/100 or 20%. The proportion of women is 
    80/100 or 80%. In both of these proportions the size of part of the class 
    is being related to the size of the entire class.
     Difference Between Ratio and Proportion
     To understand the concept of ratio and proportion, go through the 

    difference between ratio and proportion given here.

    Example 1.9
     The information on mortality from bird flu shows that  44 died and the other 
    79 lived could be expressed as a simple ratio, which compares the number who 
    died to the number who survived. 44/79 or 44:79 would be two ways of expressing 
    this simple ratio. The ratio of those who died relative to those who lived was 44 
    to 79.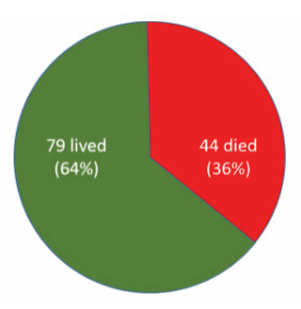

     Alternatively, we might want to focus on the proportion who lived. In 
    total, 123 people were infected, and 44 of these died. Therefore, the 
    proportion who died was 44/123, which could be expressed as a 
    decimal fraction (0.36) or as a percentage (36%). This proportion is 
    referred to as the “case-fatality” rate, although strictly speaking, it is a 
    proportion and not a rate.
     3. Rate: Rates are a special type of ratio that incorporate the dimension of 
    time into the denominator. Familiar examples include measurements 
    of speed (kilometers per hour. 

    Example 1.10
     If a car travels 24 kilometres in 2 hours, its average speed is a rate of 24 
    kilometres / 2 hours = 12 kilometres/hr.
     Note that some commonly used measurements of health outcomes are 
    referred to as “rates” even though they are actually proportions.
     
    For example:
     • A mortality rate is the proportion of deaths occurring over a span of 
    time in a population. 
    • An attack rate is the proportion of people developing an infectious 
    disease after exposure to a pathogen.
    • A case-fatality rate is the proportion of individuals who die after 
    developing a disease.
     Application of ratios, proportions and rates in nursing 
    Nurses use ratios, proportions and rates when administering medication. 
    1. Nurses need to be able to understand the doctor’s orders.  

    Example 1.11
     A doctor’s  order may be given as: 25 mcg/kg/min.  If the patient 
    weighs 52kg, how many milligrams should the patient receive in one 
    hour?  In order to do this, nurses must convert micrograms (mcg) to 
    milligrams (mg).  If 1mcg = 0.001mg, we can find the amount (in mg) 
    of 25mcg by setting up a proportion.
     2. Nurses use  proportions to Calculate Intravenous Infusion rates and drops per 
    minute (dpm), by considering the following:  
    • The total volume to be given, which is often written on the 
    prescription in mLs. 

    • The time over which the volume is to be given, often in minutes

    Example 1.12
     If 1500mLs of 0.9% sodium chloride fluid is to be given over 10 hours, 
    what is the infusion rate for delivery? If the IV administration set has a 
    drop factor of 20, what will you set the drop rate at?
     Solution :There are 2 parts to this question

     1) calculating the infusion rate (mL/hr) 


     If the drug is in solution (e.g. oral, IV, IM, SC) the correct dose to be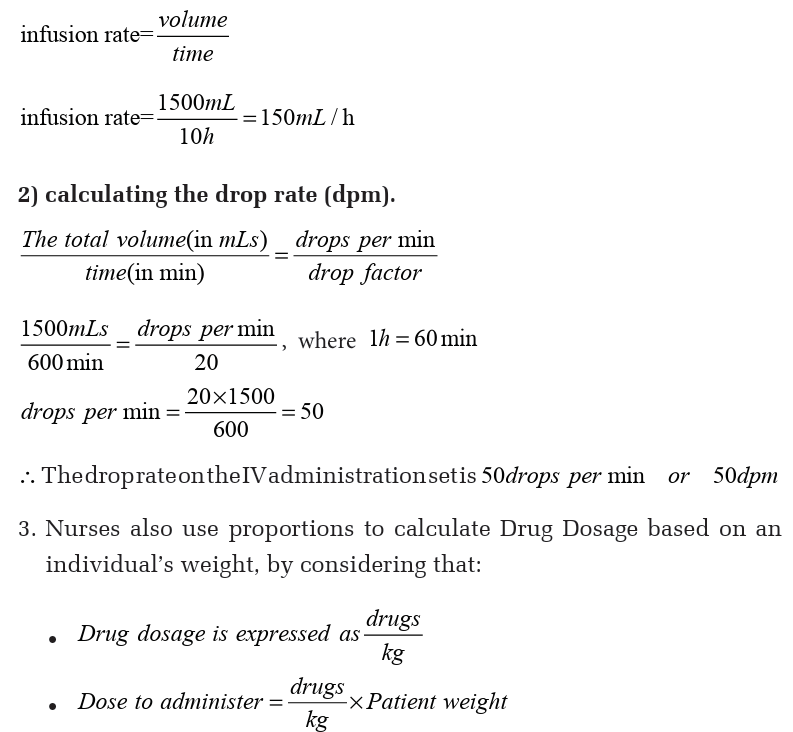 
    administered, may need to be drawn from a stock solution.  This is a 
    medication solution that contains a ratio of drug (either as solute or 
    solid) in a diluent (refresh these concepts in section 10 Dilutions using 

    the expression solute in diluent).


    Example 1.13

    Mr. Small weights 60kg. He has been ordered a drug with a dosage of 
    10 mg per kg. How much drug should be administered? If the drug 
    is available in a stock solution of 250mg/5mL, what volume of drug 
    solution should be administered? 
    Solution: There are two parts to this question 

    1) The dose of drug to give (in mg);


    Application Activity 1.5
     1. A first year, physiology subject has 36 males and 48 females, whereas 
    the clinical practice subject has 64 males and 80 females. You are 
    asked to work out which cohort has the largest male to female ratio.

    2. Yasmin is checking the IV fluid infusion on Mrs Cannon at the start 
    of the shift.  She sees from the fluid balance sheet that Mrs Cannon 
    has received 320 mL over the past 4 hours. Mrs Cannon is to receive 
    the full litre bag. How many hours would you expect it to take to 
    infuse the full litre?
     
    3. Apply your understanding of proportional thinking to solve the 
    following: 
    a) A patient is prescribed 150mg of soluble aspirin. We only have 
    300mg tablets on hand.  How    many tablets should be given? 
    b) A solution contains fluoxetine 20mg/5mL. How many milligrams 
    of fluoxetine are in 40mL of solution?
     c)   A stock has the strength of 5000units per mL. What volume 
    must be drawn up into an injection to give 6500units?  
    d) An intravenous line has been inserted in a patient. The total 
    volume to be given is 1200mL over 5hours at a drop factor of 
    15drops/mL. How many drops per minute will the patient 
    receive? 
    e)  Penicillin syrup contains 200mg of penicillin in 5mL of water. 
    If a patient requires 300mg of penicillin how much water will be 
    required to make the syrup?
     4. What fraction of H2 O2

     is hydrogen? Calculate it’s percentage.

    1.6. Absolute value and its properties

    Activity 1.6.1

    Draw a number line and state the number of units that are between;


    Absolute value of a number is the distance of that number from the
    original (zero point) on a number line. The symbol is used to denote

    the absolute value.


    Example 1.15

    Find x in the following


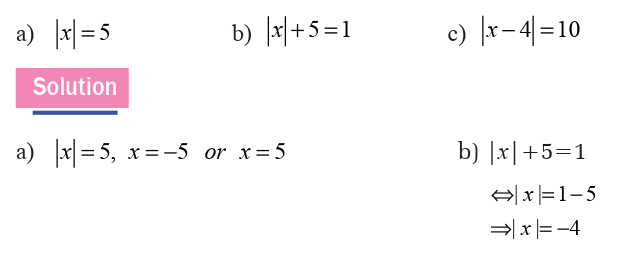
    There is no value of x since the absolute value of x must be a positive real number.



    Properties of the Absolute Value 

    Opposite numbers have equal absolute value. 

    1.7. Powers and radicals
     Powers in IR
     Activity 1.7.1
     Peter suggested that his allowance be changed. He wanted $2 
    the first week, with his allowance to be doubled each week. His 

    parent investigated the suggestion using this table

    1. Complete the table to find how many dollars Peter would be paid each 
    of the first five weeks.
     2. How much would Peter be paid the seventh week? The tenth week?

     3. Do you think his parent will agree with his suggestion? Explain.

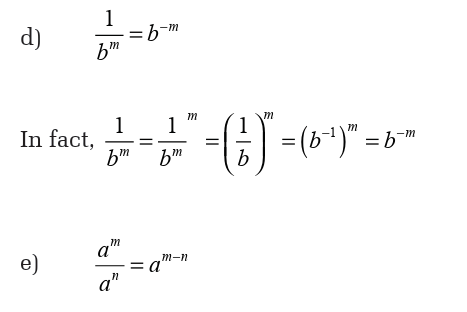
     These properties help us to simplify some powers.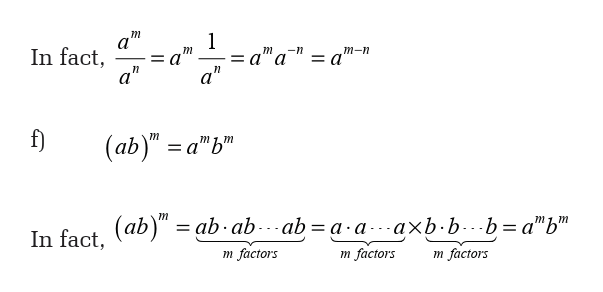
     There is no general way to simplify the sum of powers, even when the 
    powers have the same base. For instance,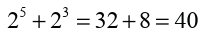 
     and 40 is 
    not an integer power of 2. But some products or ratios of powers can be 

    simplified using repeated multiplication model of an 


    1.A hummingbird has a mass of about 10-2 kg . Show that this mass is 0.01


    Radicals in real numbers
    Activity 1.7.2

    Evaluate the following powers



    Example 1.23




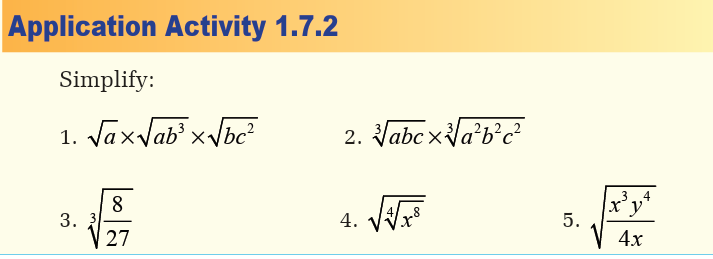
    Operations on radicals

    When adding or subtracting the radicals, we may need to simplify if we 
    have similar radicals. Similar radicals are the radicals with the same 

    indices and same bases. 


    Addition and subtraction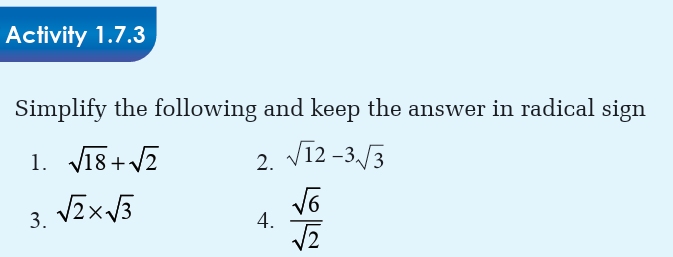
     When adding or subtracting the radicals we may need to simplify if we 
    have similar radicals. Similar radicals are the radicals with the same 

    indices and same bases.

    Rationalizing the denominator

    Activity 1.7.4

    Make the denominator of each of the following rational;

    Rationalizing is to convert a fraction with an irrational denominator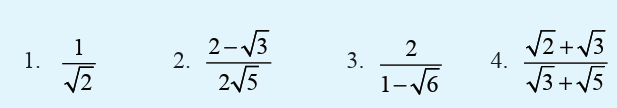 
    to a fraction with rational denominator. To do this, if the denominator 
    involves radicals, we multiply the numerator and denominator by the 

    conjugate of the denominator. 

    Example 1.27

    log (100) = ?

    We are required to find the power to which 10 must be raised to obtain 100





    Co-logarithm
     Co-logarithm, sometimes shortened to colog, of a number is the 
    logarithm of the reciprocal of that number, equal to the negative of the 

    logarithm of the number itself,

    4. Rationalizing is to convert a fraction with an irrational denominator 
    to a fraction with rational denominator. To do this, if the denominator 
    involves radicals we multiply the numerator and denominator by 

    the conjugate of the denominator. 

    5. The decimal logarithm of a positive real number x is defined to be 

    a real number y for which 10 must be raised to obtain x. We write 

    5. Contractors are tilling the bathroom floor in new house. The floor 
    measures 288 cm by 192 cm. They are using square tiles with sides 
    measuring 24 cm. How many tiles will they need?
     6. Esther’s little brother is playing with a set of collared blocks. Each 
    block has edges measuring 4 cm. What is the volume of one of the 
    blocks?
     7. Humans breathe about 15 breaths in a minute. The average breath at 
    rest contains 0.76 liter of air. About how many liters of air will you 
    breathe while at rest for 25 minutes?
     8. Density is the ratio of a substance’s mass to its volume. A volume of 
    20 cubic centimeters of gold has a mass of 386 grams. Express the 
    density of gold as a unit rate.
     9. A lion’s heart beats 12 times in 16seconds. How many times does a 

    lion’s heart beat in 60seconds?.

     a)How many people were tested negative?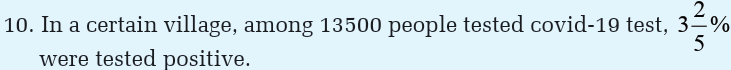

     b)How many people were tested positive?

    11.  Ingabire, Mugenzi and Gahima have jointly invested in buying and 
    selling of shares in the Rwanda stock exchange market. In one sale 
    as they invested different amount of money, they realised a gain of 
    1 080 000 Frw and intend to uniquely share it in the ratio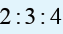 

    respectively. How much did Mugenzi get?

    Unit 2: Fundamentals of Trigonometry►