UNIT 1: SOUND WAVES
Key Unit Competence:Analyse the effects of sound waves in elastic medium
Introductory activity
What are the properties which explain mostly the behavior of sound?
1. a) Most people like to listen to music, but hardly anyone likes to listen
to noise. In your own view, how is musical sound different from noise?
b) A guitarist as shown in the figure above plays guitar. The sound is
made by the vibration of the guitar string and propagates as a wavethrough the air and reaches your ear.
i) Assuming you are near by the guitarist and your friend is behind you,
who can hear more sound? Explain your reasoning
ii) If another person playing flute comes in and plays it. Can you distinguish
sound from the flute from that of a guitar? How are the two soundsdifferent?
2. a) Now, while they are playing their instruments you keep moving away
and coming towards a point where they are playing the instruments.
Explain the variations of sound heard by you.
b) Do you think there would be any change in the sound if you(the
observer) and the players (the source) remained in the same position?
3. With scientific explanations explain why you may not be able tocommunicate well in a room where music is being played at a high tone.
1.1 PRODUCTION OF STATIONARY SOUND WAVES
Activity 1.1
Look at the Fig.1.2 and then answer the following questions.
1. The two students in the figure above are producing sound. In each case,
describe the method of production of sound.
2. Imagine that the student replaces the flute with a longer one, would the
sound produced remain the same?Explain you answer.
3. Do you think a guitar with longer string produces the same sound as
the one with a shorter string? Defend your answer using scientificexplanations.
1.1.1 Sound in pipes
The source of any sound is vibrating object. Almost any object can vibrate and hence
be a source of sound. For musical instruments, the source is set into vibration by
striking, plucking, bowing, or blowing. Standing waves (also known as stationary
waves are superposition of two waves moving in opposite directions, each having
the same amplitude and frequency) are produced and the source vibrates at its
natural resonant frequencies. The most widely used instruments that produce
sound waves make use of vibrating strings, such as the violin, guitar, and piano or
make use of vibrating columns of air, such as the flute, trumpet, and pipe organ.
They are called wind instruments.
We can create a standing wave:
• In a tube, which is open on both ends. The open end of a tube is approximately
a node in the pressure (or an antinode in the longitudinal displacement).
• In a tube, which is open on one end and closed on the other end. The closed
end of a tube is an antinode in the pressure (or a node in the longitudinal
displacement).
In both cases a pressure node is always a displacement antinode and vice versa.
A node is a point half way between the crest and the trough. The line that connects
the nodes is the nodal line. The nodal line shows the original position of the matter
carrying the wave.
Displacement node means that a very thin slice of the medium at the node does
not move (zero displacement). If you have a standing wave in a half-open tube,
there will be a displacement node (and a pressure antinode) at the closed end.
This is due to the fact that the molecules cannot move back and forth at the closed
end.In the open end you will, on the other hand, have a pressure node (and thus a
displacement antinode). This is due to the fact that the pressure at the end of thetube is equal to that of the surrounding air.
Pressure node does not mean that the pressure is low; it simply means that the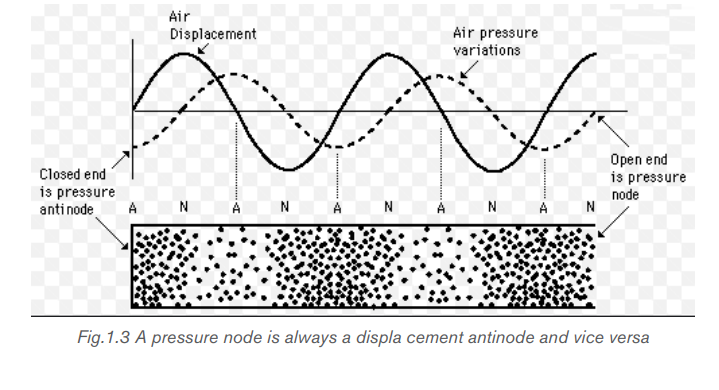
pressure is constant. Similarly, the pressure at the antinode is not “high”; it simplyhas the largest oscillations from low pressure to high pressure.
a. Tube of length L with two open ends
An open pipe is one which is open at both ends. The length of the pipe is thedistance between consecutive antinodes. But the distance between consecutive
The longest standing wave in a tube of length L with two open ends has displacement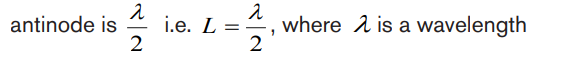
antinodes (pressure nodes) at both ends. It is called the fundamental.
Notes with higher frequencies than fundamental can be obtained from the pipe by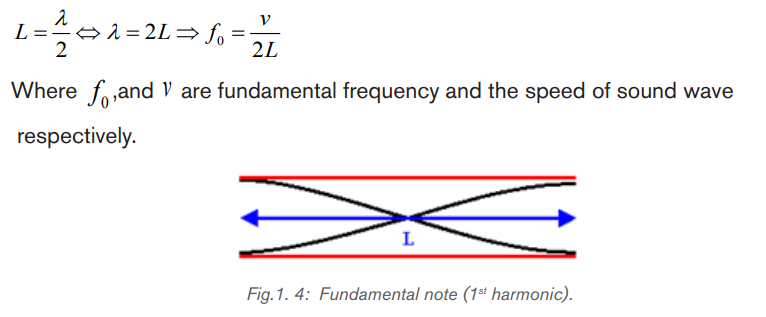
blowing harder. The stationary wave in the open pipe has always an antinode at
each end.
The next longest standing wave in a tube of length L with two open ends is the
second harmonic (first overtone). It also has displacement antinodes at eachend.
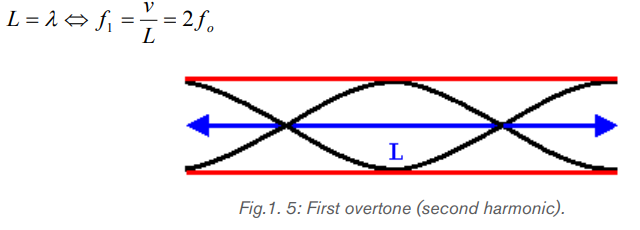
The second overtone is obtained from Fig. 1.6 and is the third harmonic.

Example 1.1

b. Tube of length L with one open end and one closed end.
The longest wavelength of standing wave in a tube of length L with one open
end and one closed end has a displacement antinode at the open end and adisplacement node at the closed end. This is the fundamental.

The next longest standing wave in a tube of length in a tube of length L with one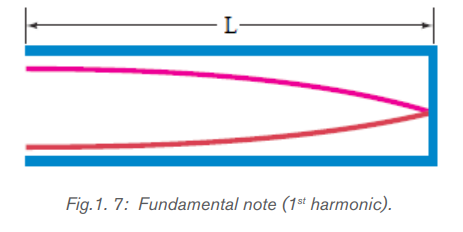
open end and one closed end is the third harmonic (second overtone). It alsohas a displacement antinode at one end and a node at the other.
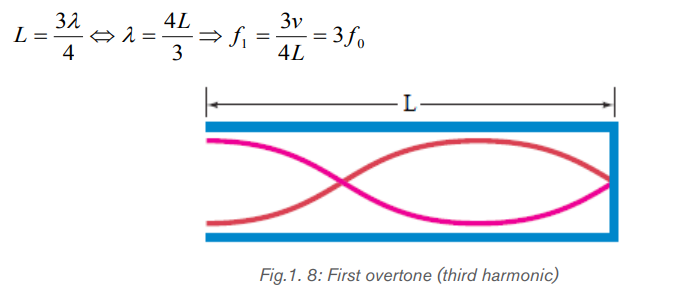
An odd-integer number of quarter wavelength has to fit into the tube of length L.

frequencies. Only odd harmonics of the fundamental are natural frequencies.
Example 1.2
A section of drainage culvert 1.23 m in length and makes a howling noise when
the wind blows.
a. Determine the frequencies of the first three harmonics of the culvert if it is
open at both ends. Take v = 343 m/s as the speed of sound in air.
b. What are the three lowest natural frequencies of the culvert if it is blocked
at one end?
c. For the culvert open at both ends, how many of the harmonics present fallwithin the normal human hearing range (20 Hz to 17 000 Hz)?

1.1.2 Vibrating strings
The string is a tightly stretched wire or length of gut. When it is struck, bowed or
plucked, progressive transverse waves travel to both ends, which are fixed, where
they are reflected to meet the incident waves. A stationary wave pattern is formed
for waves whose wavelengths fit into the length of the string, i.e. resonance occurs.
If you shake one end of a cord (slinky) and the other end is kept fixed, a continuous
wave will travel down to the fixed end and be reflected back, inverted. The
frequencies at which standing waves are produced are the natural frequencies
or resonant frequencies of the cord. A progressive sound wave (i.e. a longitudinal
wave) is produced in the surrounding air with frequency equal to that of the
stationary transverse wave on the string.
Now let consider a cord stretched between two supports that is plucked like a
guitar or violin string. Waves of a great variety of frequencies will travel in both
directions along the string, will be reflected at the ends, and will be travel back in
the opposite direction. The ends of the string, since they are fixed, will be nodes.
Consider a string of length L fixed at both ends, as shown in Fig.1.10. Standing
waves are set up in the string by a continuous superposition of wave incident on
and reflected from the ends.
Note that there is a boundary condition for the waves on the string. The ends of the
string, because they are fixed, must necessarily have zero displacement and are,therefore, nodes by definition.
Fig.1. 10 (a) A string of length L fixed at both ends. The normal modes of vibration form a harmonic
series: (b) the fundamental note; (c) First overtone; (d) the second overtone (Halliday, Resneck, &Walker, 2007).
Example 1.3
A piano string is 1.10 m long and has mass of 9 g.
a. How much tension must the string be under, if it is to vibrate at a fundamental
frequency of 131 Hz?b. What are the frequencies of the first four harmonics?

Resonance of sound
We have seen that a system such as a taut string is capable of oscillating in one or
more normal modes of oscillation. If a periodic force is applied to such a system,
the amplitude of the resulting motion is greater than normal when the frequency
of the applied force is equal to or nearly equal to one of the natural frequencies
of the system. This phenomenon is known as resonance. Although a block–
spring system or a simple pendulum has only one natural frequency, standing-wave
systems can have a whole set of natural frequencies.
Because oscillating systems exhibit large amplitude when driven at any of its natural
frequencies, these frequencies are often referred to as resonance frequencies.
Fig.1.11shows the response of an oscillating system to various driving frequencies,
where one of the resonance frequencies of the system is denoted by
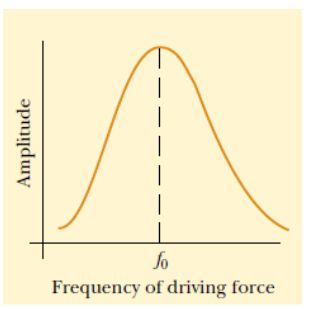
Fig.1. 11: Graph of the amplitude versus driving frequency for oscillating system. The amplitude is
a maximum at the resonance frequency. Note that the curve is not symmetric (Halliday, Resneck, &Walker, 2007)
A more spectacular example is a singer breaking a wine glass with her amplified
voice. A good-quality wine glass has normal-mode frequencies that you can hear
by tapping it.
If the singer emits a loud note with a frequency corresponding exactly to one of
these normal-mode frequencies, large-amplitude oscillations can build up andbreak the glass (Fig. 1.12)

Fig.1. 12 : Some singers can shatter a wine glass by maintaining a certain frequency of their voice
for seconds, (a) Standing-wave pattern in a vibrating wine glass. (b) A wine glass shattered by theamplified sound of a human voice
Beats and its phenomena
Beats occur when two sounds-say, two tuning forks- have nearly, but not exactly,
the same frequencies interfere with each other. A crest may meet a trough at
one instant in time resulting in destructive interference. However, at later time the
crest may meet a crest at the same point resulting in constructive interference. To
see how beats arise, consider two sound waves of equalamplitudes and slightlydifferent frequencies as shown on the figure below.
Fig.1. 13: Beats occur as a result of the superposition of two sound waves of slightly different
frequencies (Cutnell & Johnson, 2006).
In 1.00 s, the first source makes 50 vibrations whereas the second makes 60. We
now examine the waves at one point in space equidistant from the two sources.
The waveforms for each wave as a function of time, at a fixed position, are shown
on the top graph of Fig. 1.13; the red line represents the 50 Hz wave, and the blue
line represents the 60 Hz wave. The lower graph in Fig. 1.13 shows the sum of
the two waves as a function of time. At the time the two waves are in phase they
interfere constructively and at other time the two waves are completely out of phase
and interfere destructively. Thus, the resultant amplitude is large every 0.10 s and
drops periodically in between. This rising and falling of the intensity is what is heard
as beats. In this case the beats are 0.10 s apart. The beat frequency is equal tothe difference in frequencies of the two interfering waves.

The interference pattern varies in such a way that a listener hears an alternation
between loudness and softness. The variation from soft to loud and back to soft
is called a Beat. The phenomena of beats can be used to measure the unknownfrequency of a note.

Application activity 1.1
1. Is the wavelength of the fundamental standing wave in a tube open
at both ends greater than, equal to, or less than the wavelength of
the fundamental standing wave in a tube with one open end and one
closed end? Explain your answer.
2. You blow across the opening of a bottle to produce a sound. What
must be the approximate height of the bottle for the fundamental note
to be a middle C (with the wavelength of 1.29 m).
3. Two loudspeakers are separated by 2.5 m. A person stands at 3.0 m
from one and at 3.5 m from the other one. Assume a sound velocity of
343 m/s.
a. What is the minimum frequency to present destructive interference at
this point?
b. Calculate the other two frequencies that also produce destructive
interference.
4. How would you create a longitudinal wave in a stretched spring? Would
it be possible to create a transverse wave in that spring?
5. In mechanics, massless strings are often assumed. Why is this not a
good assumption when discussing waves on strings?
6. Draw the second harmonic (The second lowest tone it can make.) of
a one end fixed, one end open pipe. Calculate the frequency of this
mode if thepipe is 53.2 cm long, and the speed of sound in the pipe is
317 m/s.
7. Calculate the wavelengths below. The length given is the length of thewaveform in the picture bellow:
8. A guitar string is 64 cm long and has a fundamental Mi frequency of
330 Hz. When pressing in the first fret (nearest to the tuning keys) see
figure bellow the string is shortened in such a way that it plays a Fa
note having a frequency of 350 Hz. Calculate the distance betweenthis first fret and the nut necessary to get this effect.
9. Why is a pulse on a string considered to be transverse?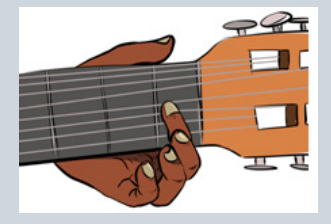
10. A guitar string has a total length of 90 cm and a mass of 3.6 g. From
the bridge to the nut there is a distance of 60 cm and the string has
a tension of 520 N. Calculate the fundamental frequency and the firsttwo overtones
1.2 CHARACTERISTICS AND PROPERTIES OF SOUND WAVES
Activity 1.2
Read the scenario below and answer the questions that follow.
On an interview for Physics placement in a certain school in Rwanda, Claudette
a S.6 leaver who had applied for the job was asked about sound waves
during the interview.
She was asked to state the properties of sound waves. Confidently, she
responded that the properties are reflection, refraction, diffraction and
interference. This was enough to make Claudette pass the first level of the
interview.
However, in the second step, she was required to discuss different media
in which sound waves can propagate. Claudette started discussing these
different media. What surprised the interviewer was Claudette’s ability to relate
sound waves to other kinds of waves stating that these waves behave thesame way when they pass from one medium to another.
Looking at Claudette’s face, the interviewer asked her to discuss the laws
governing reflection and refraction of sound waves. With a smile, she
started by saying that since sound waves have the same properties as for light;
these laws therefore do not change.
As she was attempting to state them, the interviewer stopped her and
congratulated her upon her confidence and bravery she showed in the room.
She was directly told that she was successful and she was given the job.
Claudette is now working as assistant S2 Physics Tutor and doubles as a
Physics laboratory attendant.
Questions
a. Explain the meaning of underlined terms used in the text above?
b. Do you think, it was 100% correct for Claudette to relate sound waves
to light waves? Explain?
c. There is where she was asked to discuss the different media in which
sound waves can propagate. Discuss these different media and talk
about speed of sound waves in the stated media.
d. In one of the paragraphs, Claudette said that the laws governing reflection
and refraction of sound waves were similar to those of light. Can you
explain these laws (Use diagrams where possible)
e. Assuming that you were an interviewer and the interview was out of 80.What mark would you award to Claudette? Why?
1.2.1 Properties of sound waves
Most of us start our lives by producing sound waves! We spend much of our life
surrounded by objects which produce sound waves. Most machines in use vibrate
and produce sound so the only sure way to silence them would be to put them in
vacuum where there would be no surrounding medium for the vibrating surfaces
of the machine to push against, hence no sound waves. Some physiologists
are concerned with how speech is produced, how speech impairment might be
corrected, how hearing loss can be alleviated.
Sound is associated with our sense of hearing and, therefore, with the physiology
of our ears that intercept the sound and the psychology of our brain which interprets
the sensations that reach our ears. Sound waves are longitudinal mechanical waves
that can travel through solids, liquids, or gases.
As the sound wave propagates, many interactions can occur, including reflection,
refraction, diffraction and interference. When a sound wave hits a surface, a part ofthe energy gets scattered while a part of it is absorbed.
a. Reflection of sound wave
Fixed end
First consider an elastic rope stretched from end to end. One end will be securely
attached to a pole on a lab bench while the other end will be held in the hand in
order to introduce pulses (single disturbance, on vibration) into the medium as
shown in Fig.1.14. Because the right end of the rope is attached to a pole (which is
attached to a lab bench), the last particle of the rope will be unable to move whena disturbance reaches it. This end of the rope is referred to as a fixed end.
Fig.1. 14 An elastic securely tied to a pole can be used to study the behavior
of waves at a fixed end
If a pulse is introduced at the left end of the rope, it will travel through the rope
towards the right end of the medium. This pulse is called the incident pulse since
it is incident towards (i.e., approaching) the boundary with the pole.
When the incident pulse reaches the boundary, two things occur:
• A portion of the energy carried by the pulse is reflected and returns towards
the left end of the rope. The disturbance that returns to the left after bouncing
off the pole is known as the reflected pulse.
• A portion of the energy carried by the pulse is transmitted to the pole, causing
the pole to vibrate.
When one observes the reflected pulse off the fixed end, there are several notable
observations. First the reflected pulse is inverted. That is, if an upward displaced
pulse is incident towards a fixed end boundary, it will reflect and return as adownward displaced pulse.
Similarly, if a downward displaced pulse is incident towards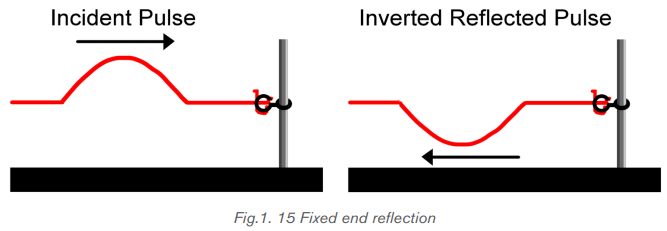
a fixed end boundary,
it will reflect and return as an upward displaced pulse.
The inversion of the reflected pulse can be explained by returning to our conceptions
of the nature of a mechanical wave. When a crest reaches the end of a medium
(“medium A”), the last particle of the medium A receives an upward displacement.
This particle is attached to the first particle of the other medium (“medium B”) on
the other side of the boundary. As the last particle of medium A pulls upwards on
the first particle of medium B, the first particle of medium B pulls downwards on the
last particle of medium A.
In general, Reflection leaves wavelength, speed, amplitude and frequencyunchanged.
Free End Reflection
Suppose a rope is attached to a ring that is loosely fit around the pole as in Fig.1.16.
Because the right end of the rope is no longer secured to the pole, the last particle
of the rope will be able to move when a disturbance reaches it. This end of the ropeis referred to as a free end.
Fig.1. 16 If the end of elastic rope not fastened to the pole then it will befree
to move up and down. This provides for the study of wave behavior at free end
When an upward displaced pulse is incident upon a free end, it returns as an
upward displaced pulse after reflection. And when a downward displaced pulse is
incident upon a free end, it returns as a downward displaced pulse after reflectionas in Fig.1.17. Inversion is not observed in free end reflection.
The reflection of sound waves can end up with any of the two phenomena either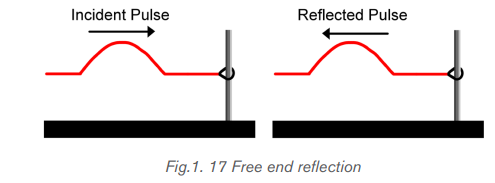
an echo or reverberation:
• Echo occurs when a reflected sound wave reaches the ear 0.1 s after we
hear the original sound. If the time elapsed between the arrivals of the two
sound waves is more than 0.1 s, then the sensation of the first sound will get
died out. An echo sounder or fathometer is a device used on a ship for thepurpose of measuring the depth of the sea.
In a small room the sound is also heard more than once, but the time differencesare so small that the sound just seems to loom. This is known as reverberation.
b. Refraction and Snell’s law and waves
Refraction of waves is the change in direction of waves as they pass from one
medium to another. The bending of waves is accompanied by the change in speed
and wavelength of the wave. So, if there is any change in media, the wave speed
changes. Sound waves travel with less velocity in cool air than they do in the warmer
air.
When a wave travels from deep water to shallow water in such a way that it meets
the boundary between the two depths straight on, no change in direction occurs.
On the other hand, if a wave meets the boundary at an angle, the direction of traveldoes change. This phenomenon is called refraction (Fig.1.18)
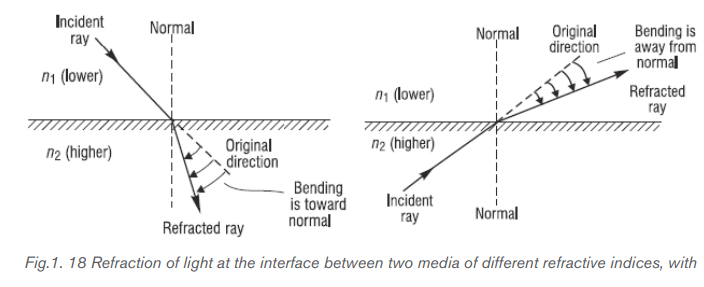
Snell’s law (also known as Snell–Descartes law or the law of refraction) is
a formula used to describe the relationship between the angles of incidence
and refraction, when referring to light or other waves passing through a boundary
between two different isotropic media, such as water, glass, or air.
Snell’s law states that the ratio of the sines of the angles of incidence and refraction
is equivalent to the ratio of phase velocities in the two media, or equivalent to thereciprocal of the ratio of the indices of refraction:

Where
Comparisons between the characteristics of the transmitted pulse and the reflected
pulse lead to the following observations.
• The transmitted pulse (in the less dense medium) is traveling faster than the
reflected pulse (in the denser medium).
• The transmitted pulse (in the less dense medium) has a larger wavelength
than the reflected pulse (in the denser medium).
• The speed and the wavelength of the reflected pulse are the same as thespeed and the wavelength of the incident pulse.
Because this is less than the incident angle of 30°, the refracted ray is bent
toward the normal, as expected. Its change in direction is called the angleof deviation and is given by

c. Diffraction
Diffraction is the name given to the phenomenon in which a wave spreads out as
it passes through a small aperture or around an obstacle. Diffraction patterns are
formed when the diffracted waves interfere with one another to produce light and
dark bands on a screen or piece of film. Diffraction patterns are most intense when
the size of the aperture or obstacle is comparable to the size of the wavelength of
the wave. Similar effects are observed when light waves travel through a medium
with a varying refractive index. Diffraction is due to the wave nature of light
When light passes through an opening it is observed to spread out. This is knownas diffraction and becomes more pronounced with narrower openings.
Diffraction occurs with all waves, including sound waves, water waves, and
electromagnetic waves such as visible light, x-rays and radio waves. Since diffraction
occurs for waves, but not for particles, it can serve as one means for distinguishingthe nature of light.
d. Interference and principle of Superposition
Interference occurs when two or more waves traveling through the same medium
overlap and combine together. Interference of incident and reflected waves isessential to the production of resonant standing waves.
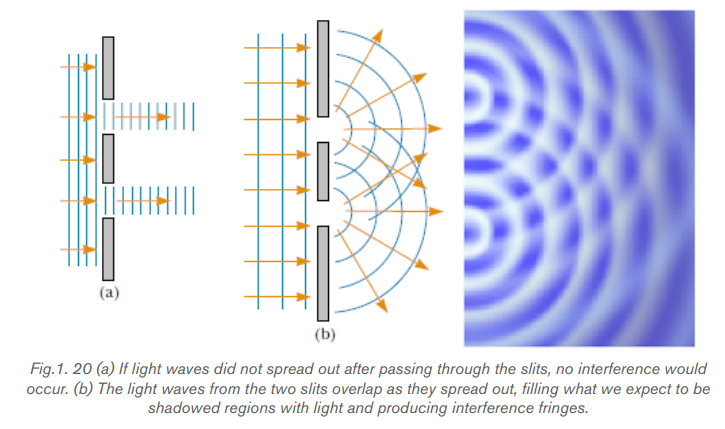
We can have constructive and destructive interference:
• If a person stands equidistant from two speakers which are playing the same
sound in phase, i.e. which are moving in and out together, then the two waves
arrive in phase after traveling the same distance. Crest meets crest and
trough meets trough at the location of the person. The amplitudes of the two
waves add and the sound is loudest here.
• If the two speakers play the same sound but are out of phase, i.e. one is
moving out while the other is moving in, and then the sound has a low volume
at the location of the person equidistant from the two speakers. This can
easily be demonstrated by switching the wires on one of the speakers. (This
is why you need to pay attention to the color of the wires when setting up your
stereo). Dead spots in an auditorium are sometimes produced by destructive
interference.
In general, the term “interference” refers to what happens when two or
more waves pass through the same region at the same time.
The principle of superposition
Combining the displacements of the separate pulses at each point to obtain the
actual displacement is an example of the principle of superposition: “When
two waves overlap, the actual displacement of any point on the string at any time
is obtained by adding the displacement the point would have if only the first wave
were present and the displacement it would have if only the second wave werepresent”.
Combining the displacements of the separate pulses at each point to obtain the
actual displacement is an example of the principle of superposition: “When
two waves overlap, the actual displacement of any point on the string at any time
is obtained by adding the displacement the point would have if only the first wave
were present and the displacement it would have if only the second wave werepresent”.
In other words, the wave function y(t, x) that describes the resulting motion in thissituation is obtained by adding the two wave functions for the two separate waves:
As we saw with transverse waves, when two waves meet, they create a third wave
that is a combination of the other two waves. This third wave is actually the sum of
the two waves at the points where they meet. The two original waves are still there
and will continue along their paths after passing through each other. After passingthe third wave no longer exists.

1.2.2 Characteristics of sound waves
Usually, the characteristics used to describe waves are period, frequency,
wavelength, and amplitude.
a. Frequency ranges
Any periodic motion has a frequency, which is the number of complete cycles in
a second and a period which is the time used to complete one cycle. While the
frequency is measured in Hertz (Hz), the period is measured in seconds (s). For a
wave, the frequency is the number of wave cycles that pass a point in a second. A
wave’s frequency equals the frequency of the vibrating source producing the wave.
Sound waves are classified into three categories that cover different frequency
ranges:
• Audible sound
Audible sound lies within the range of sensitivity of the human ear. They can
be generated in a variety of ways, such as musical instruments, human voices, or
loudspeakers. It is almost impossible to hear sounds outside the range of 20 Hz to
20 kHz. These are the limits of audibility for human beings but the range decreaseswith age.
Hearing is the perception of sound. The hearing mechanism involves some
interesting physics. The sound wave that impinges upon our ear is a pressure wave.
The ear is a transducer that converts sound waves into electrical nerve impulsesin a manner much more sophisticated than, but analogous to, a microphone.
• Infrasonic waves
Infrasonic waves have frequencies below the audible range. They are sound
waves with frequencies that are below 20 Hz limit.
Some animals such as elephants can use infrasonic waves to communicate
effectively with each other, even when they are separated by many kilometers. Their
large ears enable them to detect these low frequency sound waves which haverelatively long wavelengths.
Young bat-eared fox and Rhinoceros (Fig.1.21) also use infrasonic as low as 5 Hzto call one another. They have ears adapted for the detection of very weak sounds.
A number of animals are sensitive to infrasonic frequencies. It is believed by many
zoologists that this sensitivity in animals such as elephants may be helpful in
providing them with early warning of earthquakes and weather disturbances. It has
been suggested that the sensitivity of birds to infrasound aids their navigation and
even affects their migration.
• Ultrasonic waves
Ultrasonic waves have frequencies above the audible range. They are sound
waves whose frequencies are higher than 20 KHz. You may have used a “silent”
whistle to retrieve your dog. The ultrasonic sound emitted by that device is easily
heard by dogs, although humans cannot detect it at all. Ultrasonic waves are alsoused in medical imaging.
Some marine mammals, such as dolphin, whales, and porpoises use sound waves
to locate distant objects. In this process, called echolocation, a dolphin produces
a rapid train of short sound pulses that travel through the water, bounce off distant
objects, and reflect back to the dolphin. From these echoes, dolphins can determine
the size, shape, speed, and distance of their potential prey. Experiments have
shown that at distance of 114 m, a blindfolded dolphin can locate a stainless-steel
sphere with a diameter of 7.5 cm and can distinguish between a sheet of aluminum
and a sheet of copper. The Ultrasonic waves emitted by a dolphin enable it to seethrough bodies of other animals and people (Fig.1.22).
Skin muscles and fat are almost transparent to dolphins, so they see only a thin
outline of the body but the bones, teeth and gas-filled cavities are clearly apparent.
Physical evidence of cancers, tumors, heat attacks, and even emotional shake can
all be seen by dolphin. What is more interesting, the dolphin can reproduce the
sonic signals that paint the mental image of its surroundings, and thus the dolphin
probably communicates its experience to other dolphins. It needs no words or
symbol for fish, for example, but communicates an image of the real thing.
Dogs, cats and mice can hear ultrasound frequencies up to 450 000 Hz. Some
animals not only hear ultrasound but also use ultrasonic to see in dark. Bats also
use echo to navigate through air. Bats use ultrasonic with frequencies up to 100000 Hz to move around and hunt (Fig.1.23).
The waves reflect off objects and return the bat’s ears. The time it takes for the
sound waves to return tells the bat how far it is from obstacles or prey. The bat uses
the reflected sound waves to build up a picture of what lies ahead.
The process of imaging using Sonar (Sound Navigation and Ranging) is the same
as the echo-locating sonar of a submarine or a bat. The observer sends out a brief
pulse of ultrasound and waits for an echo. The pulse travels out, reflects off the
target and returns. The ultrasound machine uses pulses because the same device
acts as both transmitter and receiver.
Ultrasound has been used in a variety of clinical settings, including obstetrics and
gynecology, cardiology and cancer detection. The main advantage of ultrasound
is that certain structures can be observed without using radiation. Ultrasound can
also be done much faster than X-rays or other radiographic techniques.
Ultrasonic waves can be used to produce images of objects inside the body thus
Physicians use ultrasonic to observe fetuses. Ultrasound has frequencies too high
for you to hear. Echoes from ultrasound waves can show what is inside the body.Echo is a reflection of sound off the surface of an object.
In medicine, ultrasonic is used as a diagnostic tool, to destroy diseased tissue,
and to repair damaged tissue. Ultrasound examination of the heart is known as
echocardiography.
Many animals hear a much wider range of frequencies than human beings do. For
example, dog whistles vibrate at a higher frequency than the human ear can detect,
while evidence suggests that dolphins and whales communicate at frequencies
beyond human hearing (ultrasound) see Fig.1.25 below.(Cutnell & Johnson, 2006).
b. Wavelength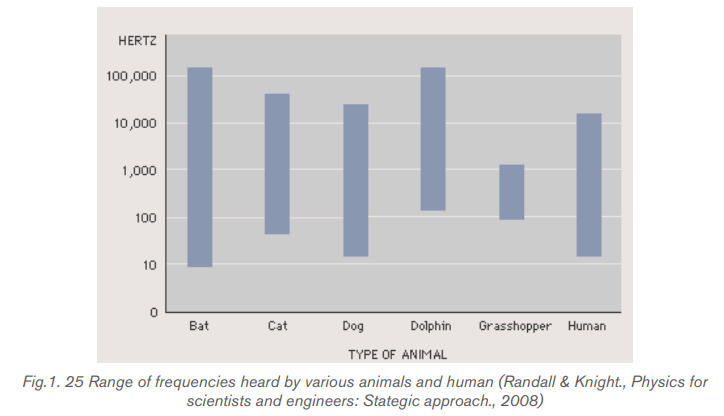
Wavelength is the distance covered by a wave in a period. It is represented by
the separation between a point on one wave and a similar point on the next cycle
of the wave. For a transverse wave, wavelength is measured between adjacent
crests or between adjacent troughs. For a longitudinal wave such as sound wave,
wavelength is the distance between adjacent compressions or rarefaction.
c. Speed of sound
For a periodic wave, the shape of the string at any instant is a repeating pattern. The
length of one complete wave pattern is the distance from one crest to the next or
from one trough to the next or from any point to the corresponding point on the next
repetition of the wave shape. We call this distance the wavelength of the wave,
denoted by the Greek letter lambda (λ).
The wave pattern travels with constant speed and advances a distance of onewavelength in a time interval of one period T. So, the wave speed is given by
where f is the frequency of the wave.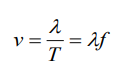
Sound travels faster in liquids and solids than in gases, since the particles in liquids
and solids are closer together and can respond more quickly to the motion of
their neighbors. As examples, the speed of sound is 331 m/s in air, 1500 m/s in
water and 5000 m/s in iron (though these mediums the seed of sound can changedepending on temperature and pressure). Sound does not travel in vacuum.




d. Amplitude
The amplitude of a wave is the maximum displacement of the medium from its rest
position. The amplitude of a transverse wave is the distance from the rest positionto a crest or a trough. The more energy a wave has, the greater is its amplitude.
Application activity 1.2
1. The correct statement about sound waves is that:
A. They are transverse waves
B. They can be polarized
C. They require material medium to propagate
2. Sound travels in
A. Air C. Water
B. Iron D. All of these
3. Two men talk on the moon. Assuming that the thin layer of gases on the
moon is negligible, which of the following is the right answer:
A. They hear each other with lower frequency
B. They hear each other with higher frequency
C. They can hear each other at such frequency
D. They cannot hear each other at all
4. Do you expect an echo to return to you more quickly on a hot day or a
cold day? Explain your answer.
A. Hot day.
B. Cold day.
C. Same on both days.
5. A sound wave is different than a light wave in that a sound wave is:
A. Produced by an oscillating object and a light wave is not.
B. Not capable of traveling through a vacuum.
C. Not capable of diffracting and a light wave is.
D. Capable of existing with a variety of frequencies and a light wave
has a single frequency.
6. A spider of mass 0.30 g waits in its web of negligible mass see Fig.
below. A slight movement causes the web to vibrate with a frequencyof about 15 Hz.
a. Estimate the value of the spring stiffness constant k for the web assuming
simple harmonic motion.
b. At what frequency would you expect the web to vibrate if an insect of
mass 0.10 g were trapped in addition to the spider?
7. Dolphins use sound waves to locate food. Experiments have shown
that a dolphin can detect a 7.5 cm target 110 m away, even in murky
water. For a bit of “dinner” at that distance, how much time passes
between the moment the dolphin emits a sound pulse and the moment
the dolphin hears its reflection and thereby detects the distant target?
8. By what factor would you have to multiply the tension in a stretched
string in order to double the wave speed? Explain your answer.
9. (a) The range of audible frequencies is from about 20 Hz to 20 000 Hz.
What is the range of the wavelengths of audible sound in air?
(b) The range of visible light extends from 400 nm to 700 nm. What is
the range of visible frequencies of light?
(c) Surgeons can remove brain tumors by using a cavitron ultrasonic
surgical aspirator, which produces sound waves of frequency 23
kHz. What is the wavelength of these waves in air?
(d) Sound having frequencies above the range of human hearing (about
20 000 Hz) is called ultrasound. Waves above this frequency can
be used to penetrate the body and to produce images by reflecting
from surfaces. In a typical ultrasound scan, the waves travel through
body tissue with a speed of 1500 m/s. For a good, detailed image,
the wavelength should be no more than 1.0 mm. What frequencysound is required for a good scan?
1.3 CHARACTERISTICS OF MUSICAL NOTES
Activity 1.3
The physical characteristics of a sound wave are directly related to the
perception of that sound by a listener.
1. What is the difference between the sound of whistle and that of drum?
2. Mutoni is playing the same notes on different musical instruments, can
you predict which musical instruments is played without seeing them?Explain your answers.
A musical note is produced by vibrations that are regular and repeating, i.e. by
periodic motion. Non-periodic motion results in noise which is not pleasant to the
ear. Many behaviors of musical note can be explained using a few characteristics:
intensity and loudness, frequency and pitch, and quality or timber
1.3.1. Pitch and frequency
The sound of a whistle is different from the sound of a drum. The whistle makes a
high sound. The drum makes a low sound. The highness or lowness of a sound is
called its pitch. The higher the frequency, the higher is the pitch. The frequency of
an audible sound wave determines how high or low we perceive the sound to be,
which is known as pitch.
Frequency refers to how often something happens or in our case, the number of
periodic, compression-rarefaction cycles that occur each second as a sound wave
moves through a medium and is measured in Hertz (Hz) or cycles/second. The term
pitch is used to describe our perception of frequencies within the range of human
hearing.
If a note of frequency 300 Hz and note of 600 Hz, are sounded by a siren, the
pitch of the higher note is recognized to be an upper octave of the lower note.
The musical interval between two notes is an upper octave if the ratio of their
frequencies is 2:1. It can be shown that the musical interval between two notes
depends on the ratio of their frequencies, and not on the actual frequencies.
Whether a sound is high-pitched or low-pitched depends on how fast something
vibrates. Fast vibrations make high-pitched sounds. Slow vibrations make low
pitched sounds.
Do not confuse the term pitch with frequency. Frequency is the physical
measurement of the number of oscillations per second. Pitch is a psychological
reaction to sound that enables a person to place the sound on a scale from high
to low, or from treble to bass. Thus, frequency is the stimulus and pitch is the response.
Although pitch is related mostly to frequency, they are not the same. A
phrase such as “the pitch of the sound” is incorrect because pitch is not a physicalproperty of the sound. The octave is a measure of musical frequency.
1.3.2 Intensity, amplitude and ear response
A police siren makes a loud sound. Whispering makes a soft sound. Whether a
sound is loud or soft depends on the force or power of the sound wave. Powerful
sound waves travel farther than weak sound waves. To talk to a friend across the
street you have to shout and send out powerful sound waves. Your friend would
never hear you if you whispered.
A unit called the decibel measures the power of sound waves. The sound waves
of a whisper are about 10 decibels. Loud music can have a level of 120 decibels
or more. Sounds above 140 decibels can actually make your ears hurt. The energy
carried by a sound wave is proportional to the square of its amplitude. The energy
passing in a unit area per unit time is called the intensity of the wave.

Sound intensity level
To the human ear the change in loudness when the power of a sound increases
from 0.1 W to 1.0 W is the same as when 1W to 10 W. The ear responds to the
ratio of the power and not to their difference.
We measure sound level intensity in terms of “decibels”. The unit bel is named afterthe inventor of the telephone, Alexander Graham Bell (1847–1922).
The decibel is a “relative unit” which is actually dimensionless, comparing a givensound to a standard intensity which represents the smallest audible sound:
The intensity of 0dB represents the softest audible sound (threshold of human
hearing), while 80 dB (i.e., moderately loud music) represents an intensity which isone hundred million times greater.
The physical characteristics of a sound wave are directly related to the perception
of that sound by a listener. For a given frequency the greater the pressure amplitude
of a sinusoidal sound wave, the greater the perceived loudness.
The loudness or softness of sound depends on the intensity of the sound wave
reaching the person concerned. Loudness is a subjective quantity unlike intensity.
Sound that is not wanted or unpleasant to the ear is called noise. High intensity
can damage hearing. The higher the intensity, the louder is the sound. Our ears,
however, do not respond linearly to the intensity. A wave that carries twice theenergy does not sound twice as loud.
Anatomy of human ear
The human ear is a remarkably sensitive detector of sound. Mechanical detectors
of sound can barely match the ear in detecting low intensity sounds. The ear has a
function of transforming the vibrational energy of waves into electrical signals that
are carried to the brain by ways of nerves as does a microphone.
The ear consists of three main parts: the outer ear, the middle ear and the inner ear.
In the outer ear, sounds waves from the outside travel down the ear canal to the
eardrum which vibrates in response to the colliding waves.The inner ear consists
of three small bones known as the hammer, anvil and stirrup which transfer the
vibrations of the eardrum to the inner ear at the oval window.
The function of the inner ear is to transduce vibration into nervous impulses. While
doing so, it also produces a frequency (or pitch) and intensity (or loudness) analysis
of the sound. Nerve fibres can fire at a rate of just under 200 times per second.
Sound level information is conveyed to the brain by the rate of nerve firing, for
example, by a group of nerves each firing at a rate at less than 200 pulses per
second. They can also fire in locked phase with acoustic signals up to about 5
kHz. At frequencies below 5 kHz, groups of nerve fibres firing in lock phase with
an acoustic signal convey information about frequency to the brain. Above about
5 kHz frequency information conveyed to the brain is based upon the
place of stimulation on the basilar membrane. As an aside, music translated
up into the frequency range above 5 kHz does not sound musical. (Hallowell, Davis;Richard,S., 1970)
This delicate system of levers, coupled with the relatively large area of the eardrum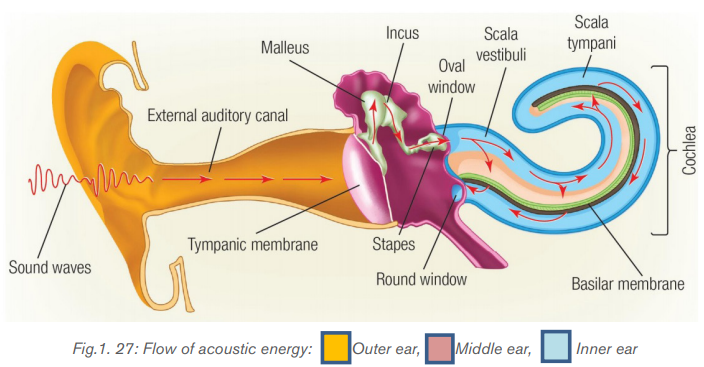
compared to the area of the oval window, results in pressure being amplified by
a factor of about 40. The inner ear consists of the semicircular canals, which are
important for controlling balance, and the liquid filled cochlea where the vibrationalenergy of sound waves is transformed into electrical energy and sent to the brain.
Logarithmic response of the ear versus intensity
The ear is not equally sensitive to all frequencies. To hear the same loudness for
sounds of different frequencies requires different intensities. Studies done overlarge numbers of people have produced the curves shown on Fig.1.28.
On this graph, each curve represents sounds that seemed to be equally loud. The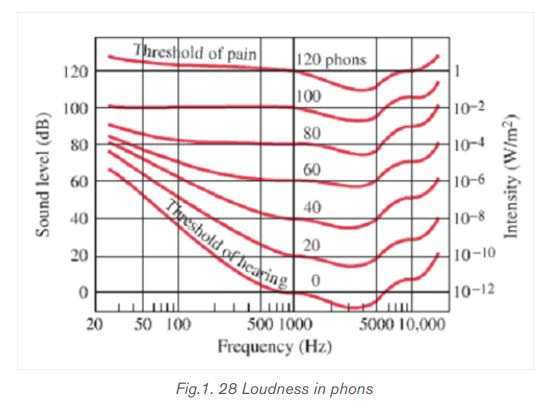
number labelling each curve represents the loudness level which is numerically
equal to the sound level in dB at 1000 Hz. The units are called phons.
Example: The curve labelled 40 represents sounds that are heard by an average
person to have the same loudness as 1000 Hz sound with a sound level of 40 dB.
From this 40 phon curve, we see that a 100 Hz tone must be at a level of about
62 dB to be perceived as loud as a 1000 Hz tone of only 40 dB.
Two aspects of any sound are immediately evident to human listener: loudness
and the pitch. Each refers to a sensation in the consciousness of the listener. But
to each of these subjective sensations there corresponds a physically measurable
quantity.
Loudness refers to the intensity in the sound wave. Intensity is related to the
energy transported by a wave per unit time across a unit area perpendicular to the
energy flow. Intensity is proportional to the square of the wave amplitude.
A unit called a phon is used to express loudness numerically. Phons differ from
decibels because the phon is a unit of loudness perception, whereas the decibel is
a unit of physical intensity. Fig.1.28 shows the relationship of loudness to intensity
(or intensity level) and frequency for persons with normal hearing. The curved lines
are equal-loudness curves. Each curve is labelled with its loudness in phons. Any
sound along a given curve is perceived as equally loud by the average person. The
curves were determined by having large numbers of people compare the loudness
of sounds at different frequencies and sound intensity levels. At a frequency of
1000 Hz, phons are taken to be numerically equal to decibels.
Because of this relationship between the subjective sensation of loudness and the
physically measurable quantity intensity, sound intensity levels are usually specified
on a logarithmic scale. The unit of this scale is a bel, after the inventor Alexander
Graham Bell.
1.3.3 Quality or timbre
If the same note is sounded on the violin and then on the piano, an untrained listener
can tell which instrument is being used, without seeing it. We would never mistake
a piano for flute. We say that the quality or timbre of note is different in each case.
The manner in which an instrument is played strongly influences the sound quality.
Two tones produced by different instruments might have the same fundamental
frequency (and thus the same pitch) but sound different because of different
harmonic content. The difference in sound is called tone color, quality, or timbre.A violin has a different timbre than a piano.
Application activity 1.3
1. Complete each of the following sentences by choosing the correct
term from the following words: loudness, pitch, sound quality, echoes,
intensity and noise
a. The ------------ of a sound wave depends on its amplitude
b. Reflected sound waves are called ---------------------------
c. Two different instruments playing the same note sound different because
of ------------------
2. Plane sound wave of frequency 100 Hz fall normally on a smooth wall.
At what distances from the wall will the air particles have:
a. Maximum amplitude of vibration
b. Minimum amplitude of vibration?
Give reasons for your answer. The speed of sound in air may be taken
as 340 m/s
3. A boy whistles a sound with the power of 4 0.5 10 W− × . What will be his
sound intensity at a distance of 5 m?
4. Calculate the intensity level equivalent to an intensity 1nW/m2
5. If the statement is true, write true. If it is false, change the underlined
word or words to make the statement true.
a. Intensity is mass per unit volume.
b. Loudness is how the ear perceives frequency
c. Music is a set of notes that are pleasing
6. The sound level of sound whose intensity is 10 2 I Wm 1.0 10 / − = × whatwill be the sound intensity level?
1.4 THE DOPPLER EFFECT AND ITS APPLICATIONS
Activity 1.4
1. People use sound for other things other than talking and making music.
In your own words, give more examples and explanations to support this
statement.
2. Imagine you are standing beside a road and a police car with its siren
turned on, drives by you. What do you notice about the heard sound?
3. In the second case, the same police car turned and comes towards you.
Comment on the heard sound4. Compare and contrast the sounds heard in case 2 and 3.
1.4.1 Doppler Effect
Doppler’s effect is the apparent variation in frequency of a wave due to the relative
motion of the source of the wave and the observer.
The effect takes its name from the Austrian Mathematician Christian Johann Doppler
(1803-1853), who first stated the physical principle in 1842. Doppler’s principle
explains why, if a source of sound of a constant pitch is moving toward an observer,
the sound seems higher in pitch, whereas if the source is moving away it seems
lower. This change in pitch can be heard by an observer listening to the whistle ofan express train from a station platform or another train.

Hence the frequency you hear is higher than the frequency emitted by the
approaching source.Example 1.10
If a source emits a sound of frequency 400 Hz when is at rest, then when the
source moves toward a fixed observer with a speed of 30 m/s, what frequency
does the observer hears knowing that the speed of a sound in air at roomtemperature is 343m/s?




The upper signs apply if source and/or observer move toward each other. The
lower signs apply if they are moving apart. The word toward is associated with
an increase in observed frequency. The words away from are associated with a
decrease in observed frequency.
Although the Doppler’s effect is most typically experienced with sound waves, it
is a phenomenon that is common to all waves. For example, the relative motion
of source and observer produces a frequency shift in light waves. The Doppler’s
effect is used in police radar systems to measure the speeds of motor vehicles.
Likewise, astronomers use the effect to determine the speeds of stars, galaxies,and other celestial objects relative to the Earth.
Example1.13
As an ambulance travels east down a highway at a speed of 33.5 m/s, its siren
emits sound at a frequency of 400 Hz. What frequency is heard by a person in a
car traveling west at 24.6 m/s
a. as the car approaches the ambulance and
b. as the car moves away from the ambulance?
c. Suppose the car is parked on the side of the highway as the ambulance
speeds by. What frequency does the person in the car hear as theambulance (i) approaches and (ii) recedes?

1.4.2 Uses of Doppler Effect
Astronomy
Doppler Effect is used to measure the speed at which stars and galaxies are
approaching or receding from us, in a mechanism named red shift or blue shift.
Redshift happens when light seen coming from an object that is moving away is
proportionally increased in wavelength, or shifted to the red end of the spectrum.
Vice versa occurs with blue shift. Since blue light has a higher frequency than red
light, the spectral lines of an approaching astronomical light source exhibit a blue
shift and those of a receding astronomical light source exhibits a redshift.
Medical imaging
In medicine, the Doppler Effect can be used to measure the direction and speed
of blood flow in arteries and veins. This is used in echocardiograms and medical
ultrasonography and is an effective tool in diagnosis of vascular problems.
Radar
The Doppler Effect is used to measure the velocity detected objects where a radar
beam is fired at a moving target. For example, the police use radar to detect a
speeding vehicle. Radio waves are fired using a radar gun at the moving vehicle.
The velocity is calculated using the difference between the emitted frequency and
the reflected frequency. In a similar way, Doppler radar is used by weather stationsto calculate factors like wind speed and intensity
Application activity 1.4
1. Choose the best answer: Bats can fly in the dark without hitting
anything because
A. They are flying mammals C. They are guided by ultrasonic waves
produced by them
B. Their night vision is going D. Of no scientific reason
2. Discuss application of sound waves in medicine and navigation
3. Explain how sonar is used to measure the depth of a sea
4. a. What is meant by Doppler Effect?
b. A police car sound a siren of 1000 Hz as it approaches a stationary
observer at a speed of 33.5 m/s. What is the apparent frequency of
the siren as heard by the observer if the speed of sound in air is 340
m/s.c. Discuss applications of the Doppler Effect.
Skills Lab 1
In this activity, you will design any musical instrument of your choice.
Procedures:
• Think of the instrument you wish to design. You may have two alternatives.
• Check whether the materials can be locally available in your area
• When you have all the required materials, start making it. You can find a
model instrument for reference.
• After you have designed your instrument, try to experiment (play it) to
check whether it is functioning. In case it is not functioning, try to design
it until it works
• When you are done, try to present it to the whole class in presence of
your tutor.
Note: You can ask a place at your school where you can keep your instrumentfor future use by either other students or tutors.
End of unit 1 assessment
For question 1 to 6, choose the letter of the best answer
1. Which of the following affects the frequency of wave?
A. Reflection C. Diffraction
B. Doppler Effect D. All of the above
2. Consider the following statements:
I) Recording of sound on tapes was first invented by Valdemar Poulsen.
II) Audio tapes have magnetic property.
III) The tapes may also be made of PVC (Polyvinyl-chloride)
2. Considering the above statements in question 2 choose the letter of the
best answer:
A. I, II, and III all are correct. C. I and II are correct, III is
wrong
B. I, II, and III all are wrong D. I and II are wrong, III is
correct
3. Nodes are
A. Positions of maximum displacement
B. Positions of no displacement
C. A position between no displacement and maximum displacement
D. None of these
4. Sound waves are:
A. Transverse waves characterized by the displacement of air molecules.
B. Longitudinal waves characterized by the displacement of air molecules.
C. Longitudinal waves characterized by pressure differences.
D. Both (B) and (C).
E. (A), (B), and (C).
5. In which of the following is the wavelength of the lowest vibration mode
the same as the length of the string or tube?
A. A string. D. An open tube.
B. A tube closed at one end. E. None of the above.
C. All of the above.
6. When a sound wave passes from air into water, what properties of the
wave will change?
A. Frequency. D. Wavelength.
B. Wave speed. E. Both frequency and wavelength.
C. Both wave speed and wavelength.
7. Does the phenomenon of wave interference apply only to sinusoidal
waves? Explain.
8. As oppositely moving pulses of the same shape (one upward, one
downward) on a string pass through each other, there is one instant at
which the string shows no displacement from the equilibrium position
at any point. Has the energy carried by the pulses disappeared at this
instant of time? If not, where is it?
9. Can two pulses traveling in opposite directions on the same string
reflect from each other? Explain.
10. When two waves interfere, can the amplitude of the resultant wave
be greater than the amplitude of any of the two original waves? Under
which conditions?
11. When two waves interfere constructively or destructively, is there any
gain or loss in energy? Explain.
12. Explain why your voice seems to sound better than usual when you
sing in the shower.
13. An airplane mechanic notices that the sound from a twin-engine aircraft
rapidly varies in loudness when both engines are running. What could
be causing this variation from loud to soft?
14. Explain how a musical instrument such as a piano may be tuned by
using the phenomenon of beats.
15. Fill in the gap
A. As a sound wave or water ripple travels out from its source, its ---------
----- decreases.
B. The vibrating air in a/an ----------------------------- has displacement
antinodes at both ends.
C. For a /an ……………., the fundamental corresponds to a wavelength
four times the length of the tube.
D. The ……………….. refers to the change in pitch of a sound due to the
motion either of the source or of the observer. If source and observerare
approaching each other, the perceived pitch is …….. If they are moving
apart, the perceived pitch is …………….
16. A bat, moving at 5.00 m/s, is chasing a flying insect. If the bat emits a
40.0 kHz chirp and receives back an echo at 40.4 kHz, at what speed
is the insect moving toward or away from the bat? (Take the speed of
sound in air to be v = 340 m/s.)
17. If you hear the horn of the car whose frequency is 216 Hz at a frequency
of 225 Hz, what is their velocity? Is it away from you or toward you? The
speed of sound is 343 m/s
18. You run at 12.5 m/s toward a stationary speaker that is emitting a
frequency of 518 Hz. What frequency do you hear? The speed of
sound is 343 m/s
19. If you are moving and you hear the frequency of the speaker at 557
Hz, what is your velocity? Is it away from or toward the speaker? Thespeed of sound is 343 m/s
20. Read the following text and answer the question
Researchers have known for decades that whales sing complicated songs.
Their songs can last for 30 min and a whale may repeat the song for two or
more hours. Songs can be heard at a distances of hundreds of kilometers.
There is evidence that whales use variations in the songs to tell other whales
about the location of food and predators. Only the male whales sing, which
has led some researchers to think that songs are also used to attract a male.
The whale songs may be threatened by noise pollution. In the past 50 years,
ocean noise has increased due to human activities. Goods are transported
across the ocean in larger ships than ever before. Large ships use bigger
engines. They produce low-frequency noise by stirring up air bubbles with their
propellers. Unfortunately, whales also use low-frequency sound in their songs,
perhaps because these sounds carry further than high-frequency sounds in
the ocean. Propeller noise from large ships is loud enough to interfere with
whale songs at a distance of 20 km.
Question: Are regulations needed to protect whales from noise?
In your own words, describe the major issue that needs to be resolved about
ocean noise pollution. List three arguments for those who think regulations
should require large ships to reduce noise pollution. List three arguments forthose who think regulations are not necessary.
