Integrated Science SME

Key Unit competence: Analyse and solve problems related to
                                               projectile and circular motion.

Introductory Activity 21
1. a) Throw a ball, a stone or any object upwards.
b) State what happens.
c) Hold a ball in your hands and release it to fall.
d) Is the motion of the ball same as in the first case?
e) Note down your observation.
f) Relate your observations for bodies moving linearly.

2. Observe the following image thereafter answer the question below

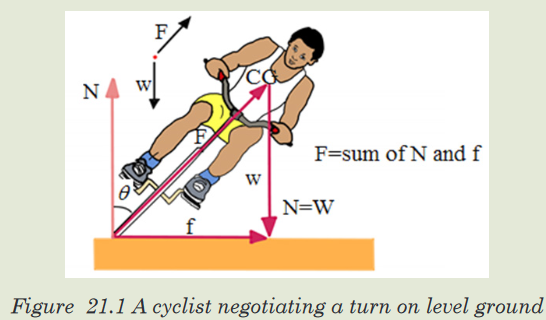
a) What happen for this bicyclist to turn on level ground easily?

21.1. Projectile Motion

Activity 21.1

1. a) Kick the football individually.
b) By observing, the flight of the ball state whether it will cover a
longer horizontaldistance when it is projected at a large angle or
a small angle.
c) Explain your observation and note down any key points in your
book.

2. Observe the image below and thereafter answer the next questions:

a) If the rifle is fired directly at the target in a horizontal direction, will
the bullet hit the center of the target?

b) Does the bullet fall during its flight?

Projectile motion is a predictable path traveled by an object that is influenced
only by the initial launch speed, launch angle, and the acceleration due to
gravity. You can try it out from where you’re sitting. Pick up an object, and
gently toss it up and away from you. It will rise as it flies away from you,
reach a maximum height, and then start falling down to the floor. Toss a few
more objects while you’re at it. As long as you’re not tossing pieces of paper
or feathers, the projectile paths should be similar

Airplanes and birds are not considered projectiles because they are self-
propelled. Neglecting air resistance, it is relatively easy to calculate the
height reached, the horizontal distance travelled, and the object’s velocity
at any point in time, given only the initial velocity and the angle at which the
projectile was propelled. The path taken is called a trajectory. We have three
cases: oblique projection, vertical projection and horizontal projection.

The best angle to kick the football, If I am kicking the ball really slow, a 45°
would be close to the best angle. At an angle of 45°, you get the best of both
horizontal velocity and time for the ball to be in the air.

A projectile, in other words, travels the farthest when it is launched at an
angle of 45 degrees.

The greatest distance is achieved using an angle close to 45° if the effects
of air resistance are negligible.

Key terms in projectile

• A projectile is any object that is given an initial velocity and then follows
a path determined entirely by gravitational acceleration. Regardless
of whether you›re launching a balloon, a baseball, or an arrow, all
projectiles follow a very predictable path, making them a great tool for
studying kinematics.

• Trajectory: The path of aprojectile in motion, a parabola upward and
across space.

• Maximum height:The highest vertical position along its trajectory. The
object is flying upwards before reaching the highest point and it’s falling
after that point. It means that at the highest point of projectile motion,
the vertical velocity is equal to 0 (Vy = 0).

• The horizontal range of a projectile:The distance along the horizontal
plane it would travel, before reaching the same vertical position as it
started from.

• Time of flight: is the amount of time spends in the air. If the ground from
which the projectile is launched is level, the time of flight only depends
on the initial velocity V0, the launch angle λ, and the acceleration due
to gravity.

• Angle of projection is the angle between the initial velocities of a body
from a horizontal plane through which the body is thrown.

Application activity 21.1

1. Make a research on other terms used in projectile motion
2. Draw an image of an object which can apply different terms used in
    projectile motion thereafter interpret it.

21.2. Applications of projectile motion

Activity 21.2

Task 1

1. Analyze the picture below and answer those questions:

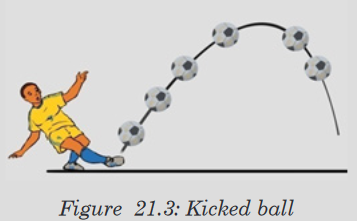
a) What is the cause turning back of this kicked ball?

b) Through your analysis, if the ball is kicked at 450 from horizontal
for first session and at 60⁰ from horizontal for second session.
What will happen? Explain your reason.

Task 2

You may have seen soldiers in the television news firing their rifles into the
air to celebrate some victory. The bullets travel as high speed projectiles
and, despite air resistance, return to Earth at high enough speeds to be
dangerous. Reports indicate that from time to time people are injured by
the returning bullets.

a) Explain your reasoning about the above statement

b) Plot a graph of the motion of rifles they flown

Task 3

At the instant horizontally pointed cannon is fired, a cannonball held at
the cannon’s side is released and drops to the ground. Which cannonball
strikes the ground first, the one fired from the cannon or the one dropped?

The first important area which comes to mind is ball games and sports.
Footballs are heavy enough to follow a nearly parabolic trajectory, without
spin, with the effect of spin often being spectacular. Footballers have to
develop a feel for such trajectories.

A cricket ball is small and dense enough to follow a nearly parabolic path,
and it is up to the batsman to judge this, in playing his shot. The fielder must
firstly get himself into the same plane as the flight, and then needs to judge

where to place himself. The symmetry of the flight means that when it comes
down to a catchable height, it will be moving at the same speed that it left
the bat.

With tennis and table tennis, the constant use of spin, even with lob shots,
makes parabolic trajectories less important. This is also true in games such
as golf, where spin predominates, and in rugby, where the shape of the ball
affects its motion.

Scoring from distance in basketball is an example of the pure judgement of
parabolic flight, and can only be mastered by constant practice.

There are the obvious throwing events, such as javelin, shot put and hammer,
where there is obviously pure projectile motion, but this is also the case
in jumping events, where the centre of mass of the body follows a purely
parabolic trajectory after take off.

Fundamentally, we can say that whenever anything moves freely, without
support, we have an example of projectile motion, and there are many that
are not mentioned, but perhaps we ought to end with satellites and space
stations. These orbit the earth in circles, but they are still in constant freefall,
and they are still technically projectiles, and an example of projectile motion.

21.2.1. Horizontal projection

Along Y-axis the object moves as in a free fall which means that the motion
is accelerated by g in the opposite direction of the axis. On the X-axis there
is no acceleration and the object moves as in a URM.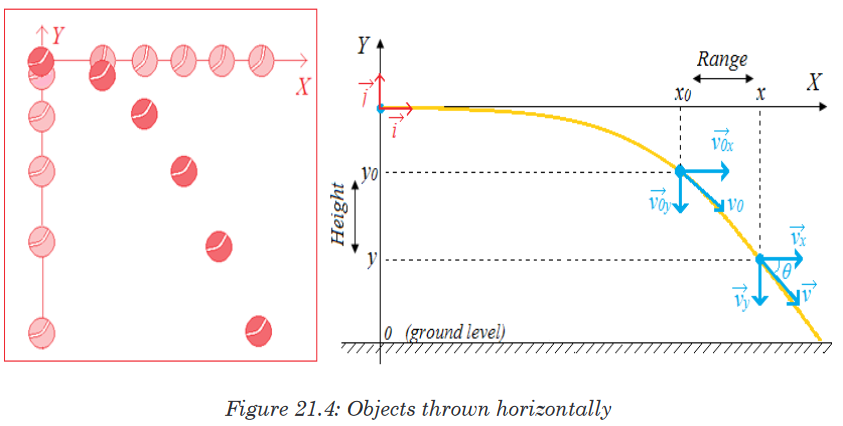

a. General condition

Velocity

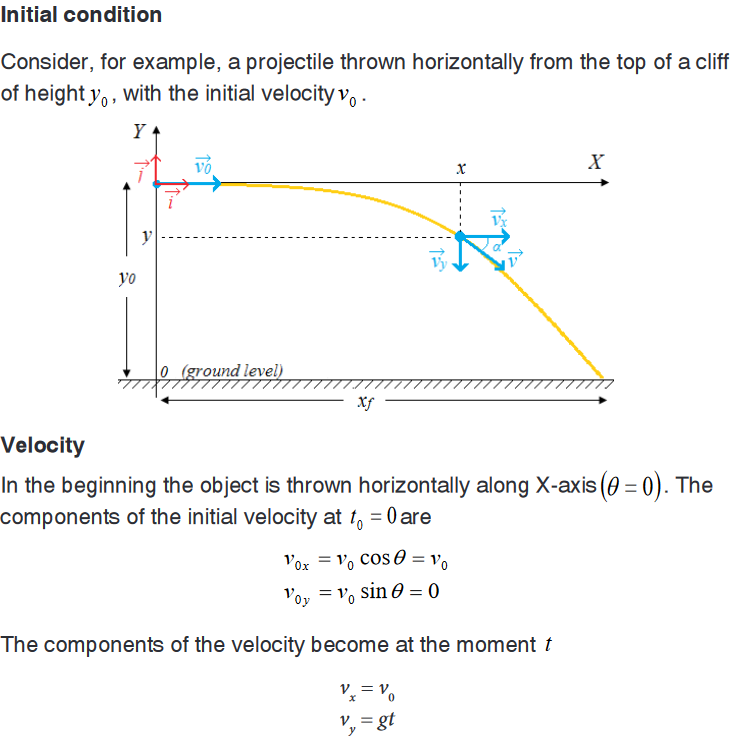
21.2. Motion of a projectile thrown obliquely
Now, we are going to examine the more general motion of object moving
through the air in two dimensions near the Earth’s surface, such as a golf
ball, athletes doing the long jump or high jump. Specifically, in the absence
of air resistance, there is no acceleration in the horizontal or x direction and
the object moves as in the URM. In the y direction, the object moves as in

the UDRM until when the object reaches the maximum height y_m . After, the
motion proceeds as when the projectile is thrown horizontally.

Consider now, a projectile fired obliquely with initial velocity  at an angle
θ above the horizontal axis.

a. General condition
When an object is fired obliquely, in the upward motion, it goes decelerating.
After reaching the maximum height, it goes downward accelerating. We
still can refer to the general conditions of the motion of a projectile thrown
horizontally

b. Initial condition
   • Position
The projectile coordinates at the moment t are

Note that the maximum height for a given initial velocity 0v will be reached
if the object is launched at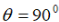  , which the motion of a projectile is thrown
vertically.

Motion duration

The motion of the object from the maximum height is similar to the motion
of a projectile thrown horizontally from the equivalent height .The time t_g
it takes the object to reach the ground from the maximum height is also
deduced similarly.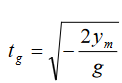

Then, the total duration of the motion will be the sum of the time to reach
the maximum height t_m and the time to reach the ground from the maximum
height t .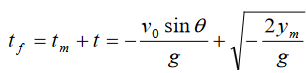

c. Oblique motion launched from the ground level

Motion duration

If the object is launched from the ground (y₀ =0) , it takes the same time to
reach the maximum height as to fall back to the ground.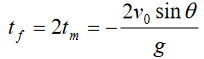

Range

We can find how far away the projectile hits the ground as we know that

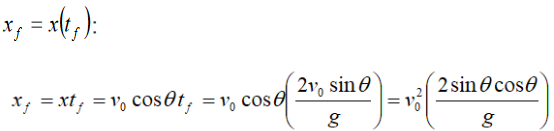
The maximum range, for a given initial velocity v₀ , is obtained when the sine
takes on its maximum value of 1, which occurs for  In this case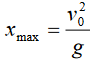

Notice: The magnitude of g is
Motion of projectiles thrown obliquely

The paths of projectiles launched at the same speed but at different
angles. The paths neglect air resistance. On the figure above the paths of
several projectiles all having the same initial speed but different projection
angles. The figure neglects the effects of air resistance, so the paths are all
parabolas. Notice that these projectiles reach different heights above the
ground. They also travel different horizontal distances, that is, they have
different horizontal ranges. The remarkable thing to note form the figure
above is that the same range is obtained for two different projection angles,
angles that add up to 90⁰.

For example, an object thrown into the air at an angle of 60⁰ will have the
same range as if it were thrown at 30⁰ with the same speed. Of course, for
the smaller angle the object remains in the air for a shorter time.

We have emphasized the special case of projectile motion for negligible air
resistance.

Example
A football is kicked at an angle Ɵ₀ = 37.00 with a velocity 20.0 m/s. calculate
    a). The maximum height,
    b). The time of travel before the football hits the ground,
    c). How far away it hits the ground.
    d). The velocity vector at the maximum height,
    e). The acceleration vector at the maximum height. Assume the ball
          leaves the foot at ground level, and ignore air resistance and rotation
          of the ball.

Solution

We resolve the initial velocity into its components
v_x0=v₀ cos37.0⁰ =(20.0 m⁄s)(0.799)=16.0 m⁄s
v_y0=v₀ sin37.0⁰ =(20.0 m⁄s)(0.602)=12.0 m⁄s

a). We consider a time interval that begins just after the football loses
contact with the foot until it reaches its maximum height. During this
time interval, the acceleration is g downward. At the maximum height,
the velocity is horizontal so, v_y=0 and this occurs at a time given by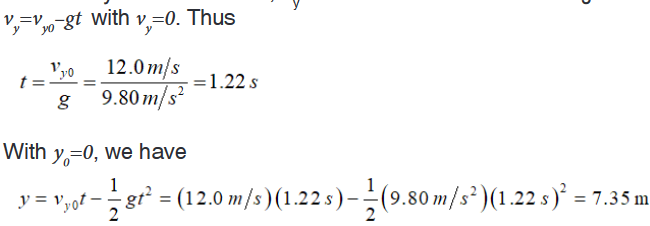

The maximum height is 7.35 m
b) To find the time interval it takes for the ball to return to the ground,
we consider a different time interval, starting at the moment the ball
leaves the foot (t=0, y₀ = 0) and ending just before the ball touches
the ground (y = 0).

This equation can be easily factored:

There are two solutions, t (which corresponds to the initial point, y0),
and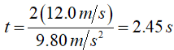

Which is the total travel time of the football.
c) The total distance traveled in the x-direction is found by:

d). At the highest point, there is no vertical component to the velocity. There
is only the horizontal component (which remains constant through the
flight), so

The acceleration vector is the same at the highest point as it is throughout
the flight, which is 9.80 m⁄s2 downward.

Application activity 21.2

1. There is more than one way to prove that the horizontal and vertical
components of a projectile’s motion are independent of each other.
Describe two or three ways that you could use to analyze the motion
of the two balls.

2. A projectile is launched at an angle into the air. Neglecting
air resistance, what is its vertical acceleration? Its horizontal
acceleration? At what point in its path does a projectile have
minimum speed?

3. A cannon ball is fired with an initial velocity of 100. m/s at an angle
of 45° above the horizontal. What maximum height will it reach and
how far will it fly horizontally?

21.3. Circular motion: Meaning and related key terms

Activity 21.3

Study carefully the motion of the ball shown below.

1. From your observation of below figure, how can a body move in that
circular path? Explain your reason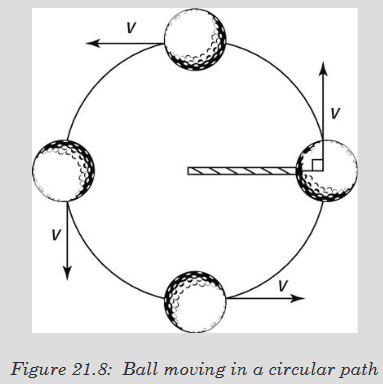

Circular motion: Movement of an object along the circumference of a circle,
or rotation along a circular path. It is a motion with constant velocity.

To indicate the angular position of a particle, or how far it has rotated we
specify the angle θ of a line joining the centre of the particle and its position
with respect to some reference line, such as the x axis. Consider an object
moving in a circle of radius r with a uniform speed v round a fixed point 0
as centre.

When an object rotates the angular displacement 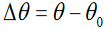, the average
angular velocity is defined as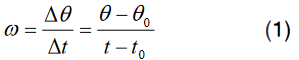

The linear displacement or the Arc of the object along the circle is

The linear average velocity

We define the instantaneous angular velocity as the very small angle θ∆ ,
through which the object turns in the very short time interval t∆ :

The instantaneous linear velocity

The angular velocity is generally specified in radian per second
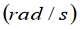
whereas the instantaneous linear velocity is expressed in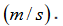

21.4.2. Periodic time and frequency

The period T is the time needed for the object to make one complete revolution.
During this time, the object travels a distance equal to the circumference of
the circle. The frequency f is referred to as the number of revolutions made
by an object in one second. The unit of frequency is Hertz.

The object’s angular speed is then represented by

21.4.3. The average angular acceleration

The average angular acceleration is defined as the change in angular velocity
divided by the time required to make this change:

The average linear acceleration

The instantaneous angular acceleration is

The instantaneous linear acceleration

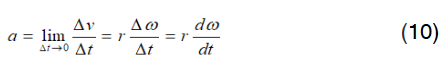
The angular acceleration is generally specified in radian per second
whereas the instantaneous linear acceleration is expressed in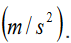

Application activity 21.4
1. A ball at the end of a string is revolving uniformly in a horizontal circle
of radius 2 meters at constant angular speed 10 rad/s. Determine the
magnitude of the linear velocity of a point located:
a) 0.5 meters from the center
b) 1 meter from the center
c) 2 meters from the center

2. The blades in a blender rotate at a rate of 5000 rpm. Determine the
magnitude of the linear velocity :
a) a point located 5 cm from the center
b) a point located 10 cm from the center

3. A point on the edge of a wheel 30 cm in radius, around a circle at
constant speed 10 meters/second.
What is the magnitude of the angular velocity?

4. The angular speed of wheel 20 cm in radian is 120 rpm. What is the
distance if the car travels in 10 seconds.

21.5. Acceleration in circular motion: Constant and
tangential acceleration

Activity 21.5

A car executing a turn, after a certain speed limit, a car will start drifting.

Why at that limitation of the speed the car start travelling? Explain your
reasoning

21.5.1. Tangential and Centripetal acceleration

In the circular motion, the tangential acceleration Ta always points in the
direction tangent to the circle and changes the rate of velocity in terms of
magnitude because their vectors are always in the same or opposite direction.
The tangential acceleration can be considered as the linear acceleration.

The centripetal acceleration (normal acceleration or radial acceleration) Na
changes the velocity in terms of direction and its vector is perpendicularly
directed inward the circle.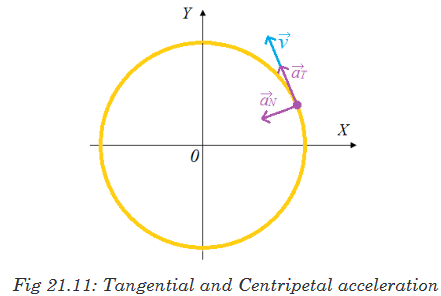

Since the velocity is constant, the tangential component of acceleration
doesn’t exist in UCM:

Consequently, the tangential component of the acceleration is also zero.
Only, the normal component of the acceleration exists in UCM. Thus, the
velocity v changes in direction but not in magnitude. The figure below
shows the representation of the angular velocityusing a distant reference
frame

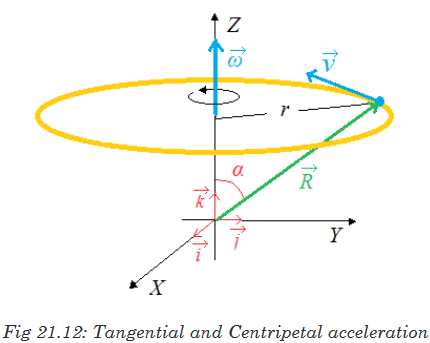
The centripetal component of the acceleration is directed along the radius.
From the above figure we can notice that

This relation indicates that the vector can be expressed in the vector form
by the equation:

It follows that

Introducing the equation (1) into (2)

The magnitude of the centripetal acceleration is given by

21.5.2. Acceleration in a non-uniform circular motion

Circular motion at a constant speed occurs when the acceleration of the object
is directed toward the centre of the circle (Only the centripetal component is
available). If the acceleration is not directed toward the centre but is at an
angle, as shown in figure below, the acceleration has two components; the
centripetal and the tangential component.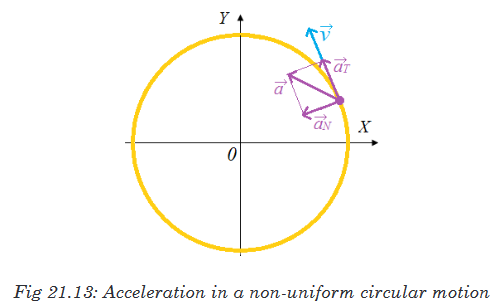

The tangential component of the acceleration is the rate that changes the
magnitude of the velocity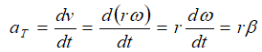

The centripetal acceleration arises from the change in direction of the velocity
and, as we have seen, is given by

If the tangential acceleration is in the direction of motion i.e. parallel to 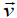, the
speed is increasing and if it is antiparallel to  is the speed is decreasing.

In either case, 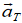 and 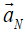are always perpendicular to each other; and their
directions change continually as the object moves along its circular path.
The total vector acceleration is the sum of these two: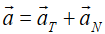

the magnitude of  at any moment is

21.5.3. Distance time graph of circular motion

When an object executes a circular motion of constant radius R, its projec-
tion on an axis executes a motion of amplitude a that repeats itself back
and forth, over the same path.

When M executes a uniform circular motion, its projection on X-axis executes
a back and forth motion between positions P and P’ about O.

Considering the displacement and the time, we find the following graph

Application activity 21.5

1. A ball is attached to a string that is 1.5m long. It is spun so that it
completes two full rotations every second. What is the centripetal
acceleration felt by the ball?

2. Imagine a car driving over a hill at a constant speed. Once the
car has reached the apex of the hill, what is the direction of the
acceleration?

21.6. Centripetal force

Activity 21.6

Observe the following figure and answer the question below:

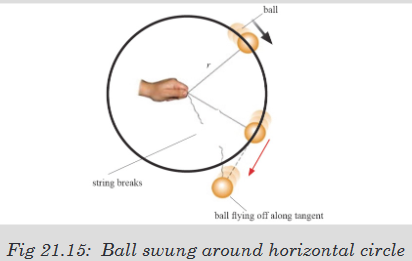
What would happen when a ball is attached to a string and is swung
round in horizontal circle? Explain your reasoning.

If you try to move in a circular path, you will finally notice that you keep
moving in a circle even when you try to stop. There is a force that keeps you
more in a circular path called centripetal force. Since a body moving in a
circle (or a circular arc) is accelerating, it follows

from Newton’s first law of motion that there must be force acting on it to
cause the acceleration.

This force, like the acceleration, will also be directed toward the centre and
is called the centripetal force. The value F of the centripetal force is given by

Newton’s second law, that is:

Wherem is the mass of the body and v is its speed in circular path of radius

R. If the angular velocity of the body is ω, we can also say, since V = Rω,

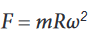
Application activity 21.6

1. A 3.0 kg mass is tied to a rope and swung in a horizontal circle. If the
velocity of the mass is 4.0 m/s and the radius of the circle is 0.75 m,
what is the centripetal force and centripetal acceleration of the mass?

2. A 200-gram ball, attached to the end of a cord, is revolved in a
horizontal circle with an angular speed of 5 rad s-1. If cord’s length is
60 cm, what is the centripetal force?

3. A student of mass 50kg decides to go on the ride. The coefficient of
static friction between the student and wall is 0.8. If the diameter of
the ride is 10m, what is the maximum period of the ride’s rotation that
will keep the student pinned to the wall once the floor drops? g=10m/s2

21.7. Applications of circular motion

Activity 21.7

Task 1

1. What is the difference between horizontal and vertical circular
motion?

2. Does gravity affect horizontal circular motion? Explain your reason

Task 2

a) Tie a thread of about 50cm on retort stand.
b) On a thread, tie a pendulum bob.
c) Displace the bob through a certain angle. What do you observe?
d) Release the bob to move through a certain angle so that it moves
in a horizontal circle.
e) Try to investigate forces acting in the bob.

Task 3

Observe the following image and answer the related questions

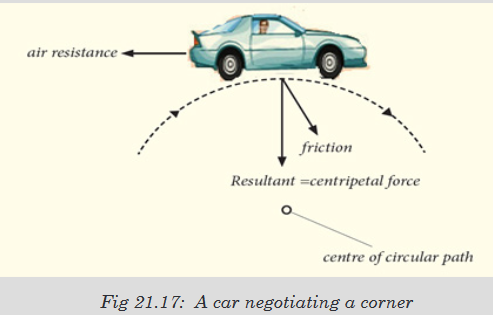
a) Explain the way the driver will use for not falling down at that
corner of the above figure

b) Identify different factors needed to travel properly in the corner

21.7.1. Vertical and horizontal circle

1. Vertical circle

Taking the approach that the ball moves in a vertical circle and is not
undergoing uniform circular motion, the radius is assumed constant, but the
speed v changes because of gravity. The free-body diagram is shown in the
figure below for the positions 1 and 2.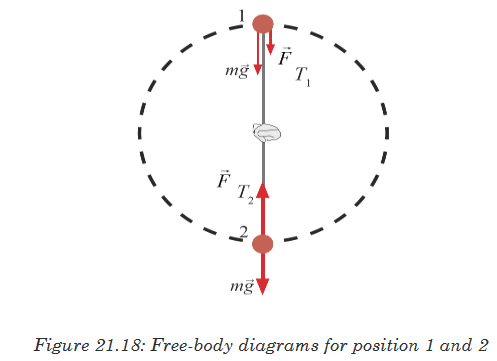

a) At the top (point 1), two forces act on the ball: the force of gravity and
the tension force the cord exerts at point 1. Both act downward and their
vector sum acts to give the ball its centripetal acceleration. We apply
Newton’s second law, for t a vertical direction, choosing downward as
positive since the acceleration is downward (toward the centre):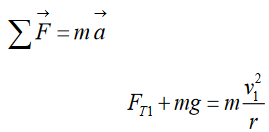

From this equation, we can see that the tension force F_T1 at point 1 will
get larger if V₁ (ball’s speed at top of circle) is made larger, as expected.
But we are asked for the minimum speed to keep the ball moving in a
circle.

The cord will remain taut as long as there is tension in it. But the tension
disappears (because V₁ is too small), the cord can go limp and the ball
will fall out of its circular path. Thus, the minimum speed will occur if F_T1
= 0, for which we have (minimum speed at top)

We solve for V₁:

This is the minimum speed at the top of the circle if the ball is to continue
moving in a circular path.

b) When the ball is at the bottom of the circle (point 2 in the figure 21.9), the
cord exerts its tension force upward, whereas the force of gravity, still
acts downward. So we apply Newton’s second law, this time choosing
upward as positive since the acceleration is upward (toward the centre):

We solve for

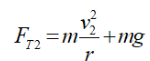
2. Horizontal circle

The second case is the case of a force on revolving ball (horizontal) which is:

Estimate the force a person must exert on a string attached to a ball to make
the ball revolve in a horizontal circle of radius r.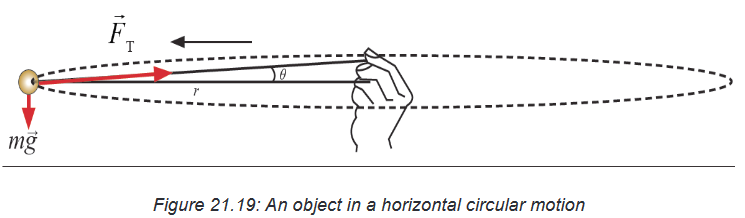

The forces acting on the ball are the force of gravity, downward, and the
tension that the string exerts toward the hand at the centre. The free-
body diagram for the ball is as shown in the figure 21.22. The ball’s weight
complicates matter and makes it a little difficult to revolve a ball with the cord
perfectly horizontal.

We assume the weight is small and put in the figure 21.22. Thus the tension
will act nearly horizontally and, in any case, provides the force necessary to
give the ball its centripetal acceleration. We apply Newton’s second law to
the radial direction ∑F=m_aN where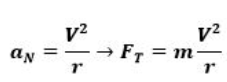

21.7.2. Conical pendulum

A small object of mass m is suspended from a string of length L. The object
revolves with constant speed v in a horizontal circle of radius r, as shown
in Figure 21.9.2. Because the string sweeps out the surface of a cone, the
system is known as a conical pendulum.

Let us find an expression for v.

To analyse the problem, begin by letting θ represent the angle between the
string and the vertical. In the free-body diagram shown, the force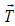 exerted
by the string is resolved into a vertical component and a horizontal
component acting toward the centre of revolution. Because the
object does not accelerate in the vertical direction,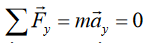 and the
upward vertical component of must balance the downward gravitational
force. Therefore;

Because the force providing the centripetal acceleration in this example is
the component , we can use the formula of centripetal acceleration to obtain

21.7.2. Conical pendulum

Where m and v are the mass and the speed respectively of the car and R is
the radius of the bend.

Also, the car is assumed to remain in the same horizontal plane and so has
no vertical acceleration, therefore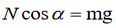

Hence by division:

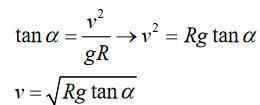
The equation shows that for a given radius of bend, the angle of banking is
only correct for one speed.

Example
A ball on the end of a string is revolved at a uniform rate in a vertical circle
of radius 72.0 cm, as shown in figure below. If its speed is 4.00 m/s and its
mass is 0.300 kg; calculate the tension in the string when the ball is

a). At the top of its path,
b). At the bottom of its path

Solution

a). Take positive to be downward. Write Newton’s 2nd law in the downward
direction.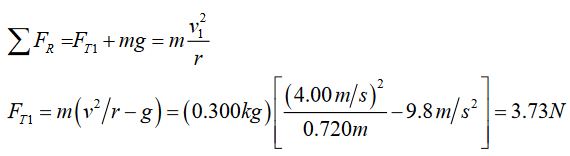

This a downward force, as expected.

b). Take positive to be upward. Write Newton’s 2nd law in the upward
direction.This is an upward force, as expected.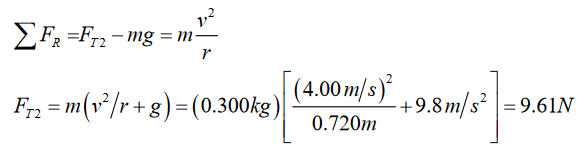

Application activity 21.7
1. Why do we give banking to curved roads?
2. A particle is revolving in a circle increasing its speed uniformly. Which
of following is constant? why? and why not? Explain the all three of
option.
a) Centripetal force b) Tangential acceleration c) Angular
acceleration
3. A steel ball of mass 0.5kg is suspended from a light inelastic string of
length 1m. The ball swings in a horizontal circle of radius 0.5 m. Find
i. The centripetal force and tension in the string.
ii. The angular Speed of the ball.
4. A student twirls a 75 gram weight at the end of a string in a horizontal
circle of radius 50 cm. If the speed of the weight is 7.0 m/s, what is
the tension in the string?

Skills lab 21

Go on youtube.com, watch video about “Trucks fail to Negotiate Dangerous
Bend in Road ”. It is a social issue which relationship with Circular motion.
1. What did you see on the video and what happen?
2. If you are engineer, how you will solve this problem?
3. Brainstorm with your classmates about the property needed to design a
    safety road by used scientific knowledge in Circular motion.

End unit assessment 21
1. At the instant a ball is thrown horizontally over a level range, a ball
    held at the side of the first is released and drops to the ground. If air
    resistance is neglected, which ball strikes the ground first?

2. Neglecting air resistance, if you throw a ball straight up with a speed
    of 20m/s, how fast will it be moving when you catch it?

3. A body describes a circumference of radius 2m and the motion is
    uniform. It does 2 rotations in 6s. If π² = 9.86, find the centripetal
    acceleration.

4. A moving body is in uniform circular motion. The radius of the
   circle is 25m. Assuming that the acceleration equals 9m/s², find the
   angular velocity.

5. How many rotations a wheel of 3.20m diameter does in one minute.
    Assuming that the linear speed is equal to 16m/s?

6. A ball at the end of a string is swinging in a horizontal circle of radius
    1.15m. The ball makes exactly 2.00 revolutions in a second. What is
    its centripetal acceleration?

7. The wheel of an engine of 4m diameter does 90 rotations per minute.
      Calculate:
h) The linear speed.
i) The angular speed.
j) The centripetal acceleration.

8. What is the angular velocity of the earth around its axis? What is the
     linear velocity of a point situated at the equator? The radius of the
     earth is supposed to be 6400km.