Integrated Science SME

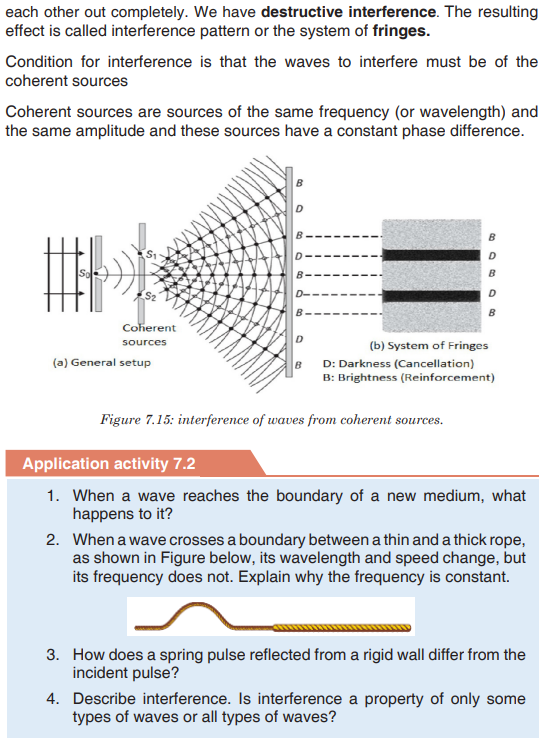
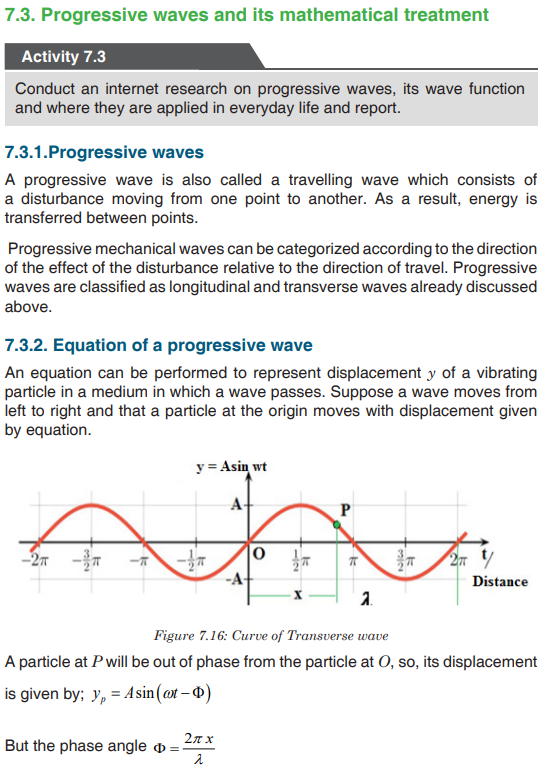
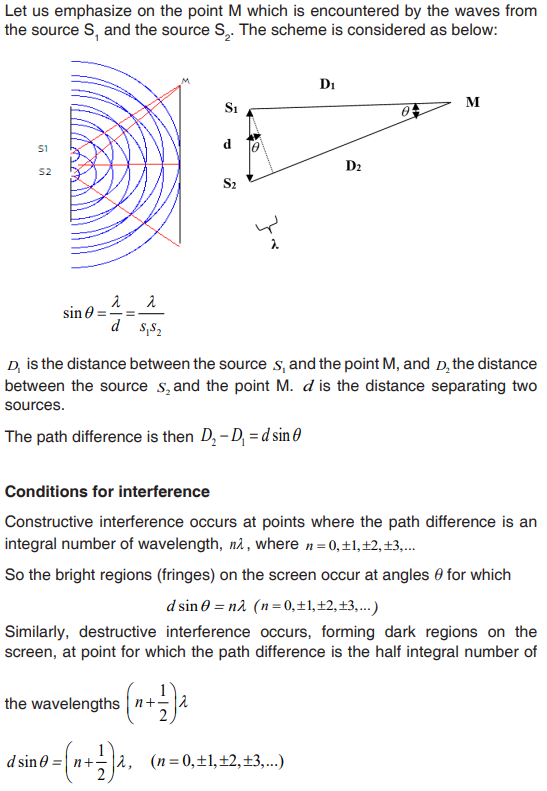
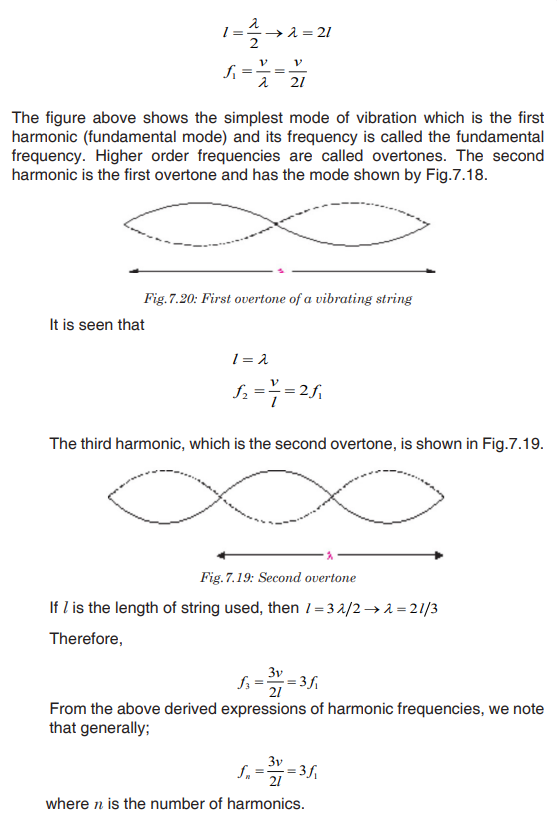
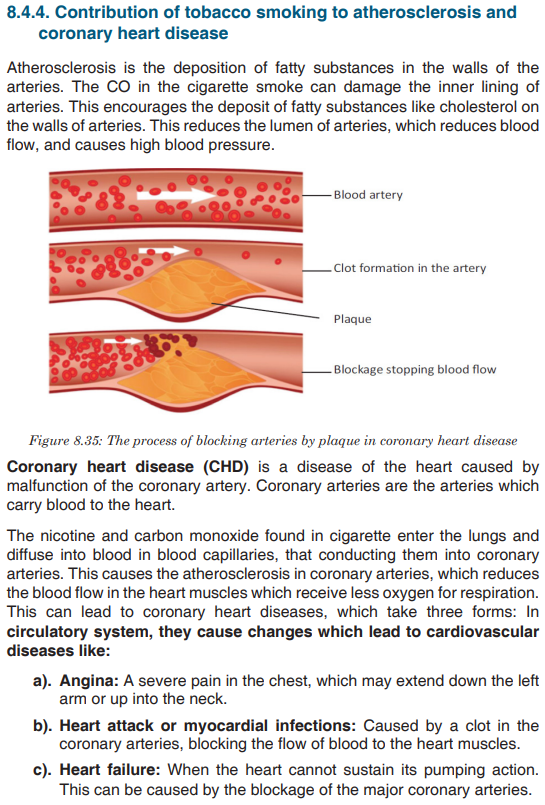
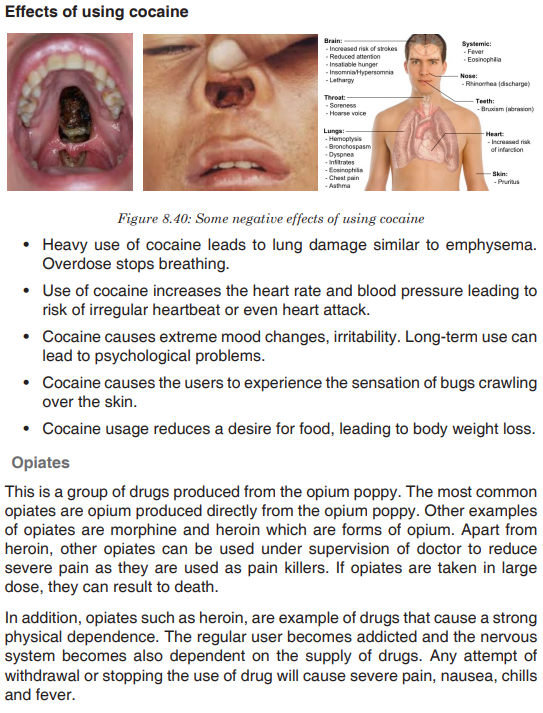
Topic outline

• 

  General

  • Announcements Forum
  • Social forum
  • Y1: Integrated Science SME File Uploaded 17/08/22, 09:33
  • Y1: Integrated Science SME TG File Uploaded 17/08/22, 09:35
• UNIT 1: THE CONCEPT OF INTEGRATED SCIENCE AND MEASUREMENTS OF PHYSICAL QUANTITIES

   

  Key Unit competence: Explain the concept of Integrated science and use accurately   
  

                                               different tools to measure physical quantities in sciences.

  Introductory Activity 1
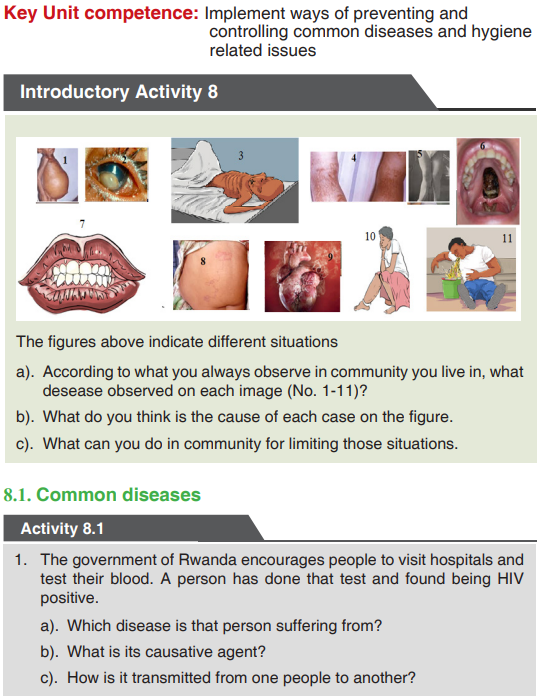
  Look carefully the following illustrations and answer the questions below:

  

  Questions:
  a). Describe the illustration A, B, C, D.
  b). Based on your knowledge from O-level, what are scientific concepts
  can you associate to each of those illustrations? Group the noted
  concepts in their science subject areas.
  c). Is there any one illustration in which you find application of many
  science subjects area? Justify your answer by providing other
  examples found in everyday life.
  d). Can you explain how and why every person should have integrated
  understanding of those science subject areas?
  e). What kind of physical quantities that can be measured in the
  illustration above? Suggest the names of the tools used in the
  illustration above?

  f). Outline other examples of physical quantities and the corresponding
  measuring tools
  g). What can be considered to select the best tool(s) to be used in
  measuring a given measurable quantity?

  1.1. Introduction to Integrated science

  
  Activity 1.1

  
  Task 1

  
  It is known that an Integrated Science course serves the purpose of
  unifying sciences in a whole one subject covering both the physical and
  life sciences. These courses are integrated in that the fields of science
  are not segmented. For example, in describing the physics of light, we
  show how this applies to the inner workings of our eyes, which, in turn, are
  sensitive to visible light in great part because of the chemical composition
  of our atmosphere.
  Use the paragraph above to answer the following questions:
  a). What does the term integrated science mean?
  b). Explain why Integrated Science is very important in finding
  appropriate solutions in various complex situations? Justify your
  answer based on the paragraph above and other examples
  observed in everyday life.

  Task 2
  

  Suppose you visited two industries and took the photos A and B below
  and saw that distinguished science subjects are involved in the process
  of production. Write a paragraph about your visit identifying how Physics,
  Biology and Chemistry are integrated in the process.

  
  

  

  
  

  1.1.1. Definition and rationale of Integrated science

  Human survival depends on knowledge through the exploration of the
  environment. Science provides knowledge while technology provides ways
  of using this knowledge. It is therefore very important to be aware of the
  global dimension of science needed in our lives in order to effectively deal
  with every day situation.
  The word “integrated” means “to restore the whole, to come together, to be
  a part of, to include.” Integrated science is a subject which incorporates
  the knowledge base of all the science fields, both physical and life sciences
  and these science fields are included in one subject as a whole “integrated
  science” in that the fields of science are not segmented. It is a subject
  which offers experiences which help people to develop an operational
  understanding of the structure of science that should enrich their lives and
  make them more responsible citizens in the society.
  Hence, integrated approach of learning science is appropriate as science
  knowledge is a tool to be used by every person to effectively deal with real
  world problems and life.
  For examples, when you are studying digestion process of animals, you will
  need the knowledge of chemical processes. Another example, in describing
  the physics of light, we show how this applies to the inner workings of our
  eyes, which, in turn, are sensitive to visible light in great part because of the
  chemical composition of our atmosphere.
  

  Aims of Integrated Science subject

  
  The overall aim of the integrated science subject is to enable students

  develop scientific literacy so that students can participate actively in the
  rapidly changing knowledge based society, prepare for further studies or
  careers in fields where the knowledge of science will be useful.
  However, the broad aims of integrated science subject are to enable students
  to:
  • Develop interest in and maintain a sense of wonder and curiosity about
  the natural and technological world;
  • Acquire a broad and general understanding of key science ideas and
  explanatory framework of science and appreciate how the ideas were
  developed and why they are valued;
  • Develop skills for making scientific inquiries;
  • Develop the ability to think scientifically, critically and creatively and
  to solve problems individually or collaboratively in science related
  contexts;
  • Use the language of science to communicate ideas and views on
  science – related issues;
  • Make informed decisions and judgments about science related issues;
  • Be aware of the social, ethnical, economic, environmental and
  technological implications of science and develop an attitude of
  responsible citizenship; and
  • Develop conceptual tools for thinking and making sense of the world.

  1.1.2. Interconnection between science subjects

  
  The purpose of science is to produce useful models of reality which are used
  to advance the development of technology, leading to better quality of life for
  human being and the environment around him or her.
  There are many branches of science and various ways of classifying them.
  One of the most common ways is to classify the branches into natural
  sciences, social sciences, and formal sciences.
  Natural sciences: the study of natural phenomena (including cosmological,
  geological, physical, chemical, and biological factors of the universe).
  Natural science can be divided into two main branches: physical science
  and life science (or biological science). Social sciences: the study of human
  behavior and societies. The social sciences include, but are not limited to:
  anthropology, archaeology, communication studies, economics, history,
  musicology, human geography, jurisprudence, linguistics, political science,
  psychology, public health, and sociology. Formal science is a branch of

  science studying formal language disciplines concerned with formal systems,
  such as logic, mathematics, statistics, theoretical computer science, artificial
  intelligence, information theory, game theory, systems theory, decision
  theory, and theoretical linguistics.

  Note:
  • Chemistry mainly deals with the study of matter’s properties and
  behaviors as well as reactions between them to produce new useful
  products. For a physicist to understand the working mechanism of
  chemical cells, help is sought from a chemist. On the other hand, the
  reasons behind the various colours observed in most of the chemical
  reactions are explained by a physicist.
  Petroleum products are dealt with by the chemist, but the transportation
  of such products make use of the principles of physics.
  • In Biology, the study of living cells and small insects by a biologist
  requires magnification. The concept of magnification using simple or
  compound microscope is a brain child of a physicist. A good physicist
  needs to have good health.

  1.1.3. Relationship between Integrated science with other subjects

  As science is about observation and experimentation of things in the physical
  and natural world, the relationship of Integrated science and other subjects
  might be explained in broader senses and will also predict much broader
  interconnections as applications of science are useful in human daily life.
  Below are some examples of relationship between Integrated science with
  other subjects:

  Science with Mathematics:

  
  A large number of scientific principles and rules are represented in the form of
  mathematical expressions, for which it is very necessary for person intending
  to get advanced study of science subjects to have sound mathematical basis.
  Without making use of mathematical expressions and rules, it is not possible
  to learn science in effective manner. Therefore, mathematics is considered
  to be sole language of science because of which real understanding of
  science is considered to be impossible without adequate knowledge of
  mathematics. Some of the useful mathematical tools which are generally
  used in the science are algebraic equations, geometrical formulas, graphs
  etc. For example, Astrology is an advanced branch of science in which it
  is predicted or enumerated that which planet revolves at which speed and
  when it will get appeared to the people of earth.

  Science with History:
  It sounds quite amazing that some kind of correlation can exist in between
  the science and history as earlier subject is practical in nature while nature
  of later subject is purely theoretical. However, it is possible to co-relate
  these subjects with each other. For example, in History, the determination of
  age fossils by historians and archaeologists use the principle developed by
  physicists. The medicine science lists the incidences which inspired various
  scientists to found out the medical remedies of various diseases.
  

  Science with Geography:
  Geography is the subject in which various concepts relating to earth on which
  we live are dealt with. Everything existing on earth, on different planets of the
  universe are also main subjects of geography. Which kind of crop should be
  sown in which kind of soils, how many kinds of rocks are found on the earth
  are some of the main topics which are covered by Geography. These topics
  are also covered by the subject of Science.
  In science, there are various concepts relating to the atmosphere and earth
  in which living and non-living beings. For this reason, temperature, wind
  directions and measurement of rainfall are conducted in the subject of
  science by making use of various apparatus. For example, in Geography,
  weather forecast, a geographer uses a barometer, wind gauge, etc. which
  are instruments developed by a physicist.
  Results obtained by the science in terms of climate and the manner in which
  it affects the human beings and earth are being interpreted by subject of
  Geography. The manner in which it is mentioned by the geography how
  soil gets produced through crushing process of rocks makes the subject a
  special branch of science.
  As there are various topics which are of common interest for geographers
  and scientists, it can be said that both of these subjects are very near to
  each other and complementary to each other.

  Science with Social Studies:
  Various evidences can be found in our life which can show the significant way
  in which life style of human beings have got affected by inclusion of scientific
  developments in their life. Today, there are various kinds of machines for
  performing different functions, about which primitive men even did not think.
  As a result of these machines, human life has become very easy and
  smooth and now we can accomplish complex functions within short period
  of time, which were considered to be very time consuming. Again, scientific
  

  
  

  researches have led to development of various medicines with the help of
  which physicians have found the remedies of various diseases, which were
  once considered to be incurable and were responsible for bringing about
  heavy loss of life in earlier times.

  Science with Physical education and sports:
  In games and sports, different instruments developed by physicists are used
  for accurate measurement of time, distance, mass and others.
  

  Application activity 1.1

  
  1. Write a paragraph to convince someone that science is related to
  other subjects. Use clear examples to support your arguments and
  reasoning.
  2. How can you describe the interconnections between science and
  technology, using at least three specific examples?

  1.2. Measurement of physical quantities

  
  Activity 1.2

  
  Task 1:

  
  Look around the place and identify possible physical quantities that can
  be measured? Explain the meaning of the physical quantities you have
  identified? Mention the SI units of the identified physical quantities?

  Task 2:
  It is possible to determine the nature and magnitude of the physical
  quantities that are measurable. Which of the following situations can be
  determined with the guidance of measurements? Support your answer
  with explanations and mention the physical quantity to be measured if
  possible.
  a). Love between a boy and girl.
  b). Size of the body
  c). Size of the garden?
  d). Amount occupied by water in a tank.
  

  
  

  1.2.1. Physical quantities and their measurements
  A quantity is any observable property or process in nature with which a
  number may be associated.
  A physical quantity is defined as a property of a material that can be quantified
  by measurement.
  Physical quantities are classified into fundamental and derived quantities.
  

  Fundamental physical quantities
  A quantity may be defined as any observable property or process in nature
  with which a number may be associated. This number is obtained by the
  operation of measurements. The number may be obtained directly by a single
  measurement or indirectly, say for example, by multiplying together two
  numbers obtained in separate operations of measurement. Fundamental
  quantities are those quantities that are not defined in terms of other quantities.
  In physics there are 7 fundamental quantities of measurements namely
  length, mass, time, temperature, electric current, amount of substance and
  luminous intensity.

  Derived physical quantities
  Quantities which are defined in terms of the fundamental quantities via a
  system of quantity equations are called derived quantities. Examples of
  derived quantities include area, volume, velocity, acceleration, density,
  weight and force.
  The SI units of derived quantities are obtained from equations using
  mathematical expressions
  Note that some derived units have been given special names. For example,
  force is measured in kg m/s2 and has been given a named unit called a
  newton (N).

  1.2.2. International system of units (SI)
  In order to measure any quantity, a standard unit (base unit) of reference
  is chosen. The standard unit chosen must be unchangeable, always
  reproducible and not subject to either the effect of aging and deterioration or
  possible destruction.
  In 1960, an international system of units was established. This system is
  called the International System of Units (SI).

  The International System of Units is an internationally agreed metric system
  of units of measurement. The value of a physical quantity is usually expressed
  as the product of a number and a unit.

  

  Name, Symbol and factor of metric prefixes in everyday use at workplace.SI
  prefixes used to form decimal multiples and submultiples of SI units (table 2
  below).

  

  Example for length
  • 10 mm= 1cm
  • 1m= 106μm
  • 1m=10-9Gm
  • 1m2=(1012pm)2=1024pm2

  Note: Numbers in the SI system are based on the number 10. Units in the SI
  system can therefore be multiplied or divided by 10 to form larger or smaller
  units.

  1.2.3. Measuring fundamental physical quantities
  
  

  Measuring length and distance
  

  We use different tools for measuring length: metre rule, ruler, tape measure,
  vernier caliper and the micrometer screw gauge based on the kind of length
  to measure. Straight distances that are less than one metre in length are
  generally measured using metre rules. Straight distances that are more than
  one metre in length are generally measured using tape measure.
  A tape measure or measuring tape is a flexible ruler and used to measure
  distance. A tape measure is in form of a strip of metal, plastic or cloth that has
  numbers marked on it as shown in figure below and is used for measuring.
  The instruments A and B in the figure 1.4. below represent examples of tape
  measures:
  

  

  It is a common measuring tool purposely designed to allow for a measure
  of great length to be easily carried out and permits one to measure around
  curves or corners. Surveyors use tape measures in lengths of over 100 m.
  Metre rules are graduated in millimetres (mm). Each division on the scale
  represents 1 mm unit (Fig 1.5. below).

   

  The direct way to measure length is by means of the straight edge of a ruler
  or metre ruler.

  The ruler is placed alongside the object to be measured, and the number of
  unit intervals of the ruler equal to the length of the object is then noted.

  Metre rule is used to measure lengths up to about 100 cm and has a
  sensitivity of 0.5 mm. Vernier calipers is an instrument used to measure
  outer dimensions of objects inside dimensions and depths.The figure 1.6
  shows the vernier calipers:

  

  We can measure outer dimensions of objects (using the main jaws), inside
  dimensions (using the smaller jaws at the top), and depths (using the stem).
  The vernier calipers have a main scale and a sliding vernier scale that can
  allow readings to the nearest 0.02 mm.

  To measure outer dimensions of an object, the object is placed between the
  jaws, which are then moved together until they secure the object.
  The screw clamp may then be tightened to ensure that the reading does not
  change while the scale is being read.

  The first significant figures are read immediately to the left of the zero of the
  vernier scale and the remaining digits are taken as the vernier scale division
  that lines up with any main scale division. The internal diameter of the test
  tube is given by ( MSR + (VC × LC) Whereby the main scale reading (MSR),
  the vernier coincidence (VC) and The smallest reading called the least count
  (LC) that can be read from vernier callipers is 1 mm – 0.9 mm = 0.1 mm or
  0.01 cm .

  The main scale called the vernier coincidence (VC) and multiplying it with
  the least count i.e 0.01 cm. Therefore, the external diameter of the cylindrical
  object is (MSR + (VC × LC)
  A micrometer screw gauge is an instrument for measuring very short length
  such as the diameters of wires, thin rods, and thickness of a paper.
  

  
  

  The micrometers have a pitch of 0.50 mm (two full turns are required to
  close the jaws by 1.00 mm). The rotating thimble is subdivided into 50 equal
  divisions. The thimble passes through a frame that carries a millimetre scale
  graduated to 0.5 mm. Thimble, which has a circular rotating scale that is
  calibrated from 0 to either 50 or 100 divisions. This scale is called the head
  scale (thimble scale). When the thimble is rotated, the spindle can move
  either forward or backwards. Ratchet which prevents the operator from
  exerting too much pressure on the object to be measured. The least count =
  0.01 mm. The micrometer screw gauge reading = MSR + (HSC × LC).
  When the pitch is 1 mm, the thimble has 100 divisions called head scale
  divisions. In this case each division represents 0.01 mm. This is the least
  count (LC) of this screw gauge.

  The thimble reading called the head scale coincidence (HSC) is the value of
  the mark on the thimble that coincides with the horizontal line on the sleeve.
  Main scale reading is taken by considering the reading of a mark on the fixed
  scale that is immediately before the sleeve enters the rim of the head scale.
  The jaws can be adjusted by rotating the thimble using the small ratchet
  knob. This includes a friction clutch which prevents too much tension being
  applied. The thimble must be rotated through two revolutions to open the
  jaws by 1 mm.

  In order to measure an object, the object is placed between the jaws and the
  thimble is rotated using the ratchet until the object is secured. The ratchet
  knob must be used to secure the object firmly between the jaws, otherwise
  the instrument could be damaged or give an inconsistent reading. The lock
  may be used to ensure that the thimble does not rotate while you take the
  reading.
  

  
  

  Measuring mass
  The mass of an object can be measured using a beam balance and a set
  of standard masses. It is noticed that the volume of the displaced water in
  measuring cylinder is equal to volume of an object lowered in the cylinder.
  There are many kinds of balances used for measuring mass illustrated below:

  

  Measuring time
  Time is measured using either analogue or digital watches and clocks
  and illustrated in figure below:
  

  

  Application activity 1.2
  1. Mention the appropriate instruments you would use to measure
  each of the following:
  a. The length of a football field.
  b. The mass of an object.
  c. The circumference of your waist.
  d. The time someone uses to cover a certain length.
  e. The diameter of a small ball.

  2. It is possible to read and record the readings using a scale of a
  vernier caliper in order to measure the external diameter of the rod.
  Steps followed in using vernier
  a. Place the object to be measured between the outside jaws as
  shown in the figure below. Slide the jaw until they touch the rod.

  

  b. Record the readings on the main scale and the vernier scale.
  The main scale reading is the mark on the main scale that is
  immediately before the zero mark of the vernier scale.

  c. Multiply the vernier scale reading by 0.01 cm.

  d. Add the main scale reading (in cm) and the vernier scale reading
  (in cm) to get the diameter of the rod.

  3. What is the diameter of the ball bearing shown in Figure below?

  

  4.
  a). What does S I Units stands for?
  b). Explain why it is correct to say that SI units are very important in
  measurements?
  c). Suppose you wish to know the length of a big garden. How do
  you get the length of your garden?

  d. Look at the following physical quantities: Mass, density, length,
  and time. Do all these quantities represent the fundamental
  quantities? Justify your decision by identifying the ones included
  in the category mentioned above.

  4. Look at the table below and try to complete it based on the skills
  gained in the previous activities done;

  

  5. Choose two physical quantities with which you are familiar. Imagine
  that you are skilled in physical quantities and its measurements.
  Explain briefly how the values of these quantities can be obtained?
  6. Express the following the indicated units and fill in blank spaces:
  a). 250 m in .....cm.
  b). 320 mg in ......g.
  c). 5μg in .........g.
  d). 7200 cm in .....m.
  e). 3 kg in ......... g.

  1.3. Dimensions of physical quantities

  Activity 1.3

  Given the formulas for the following derived quantities, try go get the
  dimensions of each quantity.
  a). velocity = displacement/time
  b). acceleration = change of velocity/time
  c). momentum = mass x velocity
  d). force = mass x acceleration
  e). work = force x displacement

  1.3.1. Introduction to dimensions of physical quantities

  The nature of physical quantity is described by nature of its dimensions.
  When we observe an object, the first thing we notice is the dimensions.
  In fact, we are also defined or observed with respect to our dimensions that
  is, height, weight, the amount of flesh. The dimension of a body means how
  it is relatable in terms of base quantities. When we define the dimension of a
  quantity, we generally define its identity and existence. It becomes clear that
  everything in the universe has dimension, thereby it has presence.

  Note: Dimensions are responsible in defining shape of an object.

  1.3.2. Definition of dimensions of physical quantities

  The dimension of a physical quantity is defined as the powers to which the
  fundamental quantities are raised in order to represent that quantity. The
  seven fundamental quantities are enclosed in square brackets [ ] to represent
  its dimensions.

  Examples of assigning dimensions to physical quantities

  Dimension of Length is described as [L], the dimension of time is described
  as [T], the dimension of mass is described as [M], the dimension of electric
  current is described as [A] and dimension of the amount of quantity can be
  described as [mol]. Adding further dimension of temperature is [K] and that
  dimension of luminous intensity is [Cd]
  Consider a physical quantity Q which depends on base quantities like length,
  mass, time, electric current, the amount of substance and temperature, when
  they are raised to powers a, b, c, d, e, and f. Then dimensions of physical
  quantity Q can be given as:
  [Q] = [LaMbTcAdmoleKf]
  It is mandatory for us to use [ ] in order to write dimension of a physical
  quantity. In real life, everything is written in terms of dimensions of mass,
  length and time. Look out few examples given below:

  1. The volume of a solid is given is the product of length, breadth and its
  height. Its dimension is given as:
  Volume = Length × Breadth × Height
  Volume = [L] × [L] × [L] (as length, breadth and height are lengths)
  Volume = [L]3

  As volume is dependent on mass and time, the powers of time and mass
  will be zero while expressing its dimensions i.e. [M]0 and [T]0
  The final dimension of volume will be [M]0[L]3[T]0 = [M0L3T0]

  2. In a similar manner, dimensions of area will be [M]0[L]2[T]0

  3. Speed of an object is distance covered by it in specific time and is given
  as:
  Speed = Distance/Time
  Dimension of Distance = [L]Dimension of Time = [T]Dimension of Speed = [L]/[T][Speed] = [L][T]-1 = [LT-1] = [M0LT-1]

  4. Acceleration of a body is defined as rate of change of velocity with
  respect to time, its dimensions are given as:
  Acceleration = Velocity / Time
  Dimension of velocity = [LT-1]Dimension of time = [T]Dimension of acceleration will be = [LT-1]/[T][Acceleration] = [LT-2] = [M0LT-2]

  

  5. Density of a body is defined as mass per unit volume, and its dimension

  is given as:
  Density = Mass / Volume
  Dimension of mass = [M]Dimension of volume = [L3]

  Dimension of density will be = [M] / [L3][Density] = [ML-3] or [ML-3T0]6. Force applied on a body is the product of acceleration and mass of
  the body
  Force = Mass × Acceleration
  Dimension of Mass = [M]Dimension of Acceleration = [LT-2]Dimension of Force will be = [M] × [LT-2][Force] = [MLT-2]

  1.3.3. Rules for writing dimensions of a physical quantity

  We follow certain rules while expression a physical quantity in terms of
  dimensions, they are as follows:
  • Dimensions are always enclosed in [ ] brackets
  • If the body is independent of any fundamental quantity, we take its
  power to be 0
  • When the dimensions are simplified we put all the fundamental
  quantities with their respective power in single [ ] brackets, for example
  as in velocity we write [L][T]-1 as [LT-1]• We always try to get derived quantities in terms of fundamental
  quantities while writing a dimension.
  • Laws of exponents are used while writing dimension of physical quantity
  so basic requirement is a must thing.
  • If the dimension is written as it is we take its power to be 1, which is an
  understood thing.
  • Plane angle and solid angle are dimensionless quantity that is they are
  independent of fundamental quantities.
  • Therefore, some of the examples of dimensions of physical quantities
  include the following:
  Force, [F] = [MLT-2]Velocity, [v] = [LT-1]Charge, (q) = [AT]

  Specific heat, (s) = [L2T2K-1]Gas constant, [R] = [ML2T-2K-1 mol-1]

  Benefits of Dimensions
  Before writing dimensions of a physical quantity, it is must know a thing to
  understand why do we need dimensions and what are benefits of writing a
  physical quantity. Benefits of describing a physical quantity are as follows:
  • Describing dimensions help in understanding the relation between
  physical quantities and its dependence on base or fundamental
  quantities, that is, how dimensions of a body rely on mass, time, length,
  temperature and others.
  • Dimensions are used in dimension analysis, where we use them to
  convert and interchange units.
  • Dimensions are used in predicting unknown formulae by just studying
  how a certain body depends on base quantities and up to which extent.
  • It makes measurement and study of physical quantities easier.
  • We are able to identify or observe a quantity just because of its
  dimensions.
  • Dimensions define objects and their existence.

  Limitations of Dimensions
  Besides being a useful quantity, there are many limitations of dimensions,
  which are as follows:
  • Dimensions can’t be used for trigonometric and exponential functions.
  • Dimensions never define exact form of a relation.
  • We can’t find values of certain constants in physical relations with the
  help of dimensions.
  • A dimensionally correct equation may not be the correct equation
  always.

  Dimension Table
  It consumes a lot of time while deriving dimensions of quantities. So in order
  to save time, we learn some basic dimensions of certain quantities like
  velocity, acceleration, and other related derived quantities.
  For Example, suppose you’re asked to find dimensions of Force and you
  remember dimension of acceleration is [LT-2], you can easily state that the
  dimension of force as [MLT-2] as force is the product of mass and acceleration
  of a body.
  The table below depicts dimensions of several derived quantities which one
  can use directly in problems of dimension analysis.

  

  Application activity 1.3
  1. i) What are four uses of dimensional analysis? Explain with one
  example for each.
  ii). What are three limitations of dimensional analysis in physics?
  2. Show that 2
  1 gt2 has the same dimensions of distance.
  3. What are the missing words in the following statements?
  a. The dimensions of velocity are ..................................... .
  b. The dimensions of force are ..........................................
  4. a) What does the term dimension mean in Physical quantities?
  b) Given the formulas for the following derived quantities, calculate the
  dimensions of each quantity.

  

  iii.Momentum = mass x velocity
  iv. Force = mass x acceleration
  v. Work = force x displacement
  21
  Skills lab 1
  Conduct a survey, collect and analyze data about when, where, and why
  people use different measuring instruments or devices and physical laws.
  To complete this project you must:
  • Develop a survey sheet about physical quantities, measuring
  instruments or devices, physical laws needed, appropriate SI units and
  metric prefixes used in everyday life.
  • Distribute your survey sheet to other student-teachers, family members
  and neighbors.
  • Compile and analyze your data.
  • Create a report to display your findings in your sheet.
  Plan it! To get started, think about the format and content of your survey
  sheet. Brainstorm what kinds of questions you will ask. Develop a plan for
  involving student-teachers in your class or other classes to gather more data.

  End unit assessment 1
  1. Differentiate a fundamental quantity and a derived quantity. Give one
  example of each and its corresponding SI units.
  2. Express the following in millimetres:
  (a) 2.7 m (b) 26.9 cm (c) 356 μm.
  3. What is the length of the glass rod shown in Figure below?

  

  4. Use the knowledge and skills gained from the previous concepts to
  complete the following sentences:
  a) A quantity may be defined as any ............................ in nature
  with which a number may be associated.
  b) Physical quantities are classified into ................ and
  ..................... quantities.
  c).................................are those quantities that are not defined
  in terms of other quantities.
  d) The value of a physical quantity is usually expressed as the
  product of a .....................and a ........................
  e) The SI units stands for ..............................................
  5. Kaneza conducted an experiment on the growth of plants and
  recorded the results in a table. He used four plants of the same type
  and size and measured their growth after one month.
  Table of results based on each plant type.

  

  
  

  
  

• UNIT 2: INTRODUCTION TO BIODIVERSITY

  Key Unit competence: Explain how biodiversity is threatened by
                                                 climate change and human activities.

  Introductory Activity 2
  Study the figure below and answer the asked questions:

  

  a). List all living things that are available in figure 2.1.
  b). Explain how each organism in the figure can be affected by
  another.
  c). Talk on how organisms in the figure can be affected by the
  physical environment in which they live.
  d). What would you suggest to study in this unit?

  2.1. Ecological terms: Species, Ecosystem, Niche,
  Population, Community and Biodiversity

  
  Activity 2.1

  
  Based on other biological concepts learnt in previous studies, give the
  meaning of the following ecological terms:
  a) Species b) Ecosystem c) Niche d) Population e) Community
  f) Biodiversity?

  Species is a group of closely related organisms which are capable of
  interbreeding to produce fertile offspring. Occasionally two organisms which
  are genetically closely related but not of the same species can interbreed
  to produce infertile offspring. For example, a cross between a donkey and
  a horse, produces a mule, which is infertile. Hence, a donkey and a horse
  do not belong in the same species. Another example includes lions and
  tigers belonging in different species. However, when a male tiger mates
  with a female lion they can have fertile offspring called tiglons, although the
  offspring of female tigers and male lions called ligers are not fertile. Note that
  normally tigers are forest dwellers and lions are plains dwellers and they are
  ecologically isolated. Breeding has only been observed in captivity.

  Ecological population is a group of individuals of the same species which live in a particular area at any given time.

  Ecological community consists of populations of different species which live in the same place at the same time, and interact with each other.

  A Habitat is a specific area or place in which an individual organism lives. When a habitat is very small it is regarded as a microhabitat.

  Within the habitat, an ecological niche is the status or the role of an
  organism in its habitat or the mode of life of an organism within its habitats.
  For example, insects are pollinating agents and preys of insectivores.Two
  important aspects of a species’ niche are the food it eats and how the food is obtained

  The picture below is of birds that occupy different niches. Each species eats a different type of food and obtains the food in a different way.Example: Each of these species of birds has a beak that suits it for its niche. For example, the long slender beak of the nectarivore allows it to sip liquid nectar from flowers. The short sturdy beak of the granivore allows it to crush hard, tough grains.

  

  In an environment, communities are influenced either by abiotic components, also called abiotic factors. These are the non-living physical aspects of the environment such as the sunlight, soil, temperature, wind, water, and air.
  Communities are also influenced by biotic components, or biotic factors.
  These are the living organisms in the environment.
  
  

  An ecosystem is a collection of all the organisms that live together in a
  particular place, together with their nonliving, or physical environment.
  A biome is a group of ecosystems that have the same climate and similar
  dominant communities.
  

  The biosphere is the whole of the earth’s surface, the sea and the air that is inhabited by living organisms. The highest level of organization is the entire biosphere.

  
  

  Biodiversity is defined as the full range of variety and variability within and among living organisms and the ecological complexes in which they occur. In other words, biodiversity is the variety of life. It refers to the totality of the species including the genetic variation represented in the species populations, across the full range of terrestrial organisms, including vertebrates and invertebrates, Protista, Bacteria and plants
  

  Importance of biodiversity
  Biodiversity contributes to ecosystem goods and services. The ecosystem goods and services include:
  • Provision of food, air, fire wood, medicines, energy, fresh water.
  • Nutrient cycling such carbon, water and nitrogen cycles by
  microorganisms and primary production by photosynthesis.
  • Cultural or aesthetic service recreation, ecotourism, cultural and
  religious inspiration.
  

  
  

  
  

  Threats of biodiversity
  The main causes of biodiversity loss can be attributed to the influence of
  human activities on ecosystems. Threats to biodiversity may include:
  

  a). Habitat loss and the degradation of the environment
  The habitat loss and the degradation of the environment occur in different ways.

  The most occurring, are tree cutting, agriculture and fires. These human
  activities lead to the alteration and loss of suitable habitats for biodiversity. As a consequence, there is a loss of plant species as well as the decrease in the animal species associated to this plant diversity.
  

  b). Introduction of invasive species and genetically modified organisms
  Species originating from a particular area are harmful to native species
  also called endemic species when they are introduced into new natural
  environments. They can lead to different forms of imbalance in the ecological equilibrium, so that endemic species may fail to compete with introduced species, and they may affect the abundance and distribution in natural habitat.

  c). Pollution
  Human activities such as excessive use of fertilizers, and increased pollutants from industries and domestic sewage affect biodiversity. They contribute to the alteration of the flow of energy, chemicals and physical constituents of the environment and hence species may die as a result of toxic accumulation.

  d). Overexploitation of natural resources
  Increased hunting, fishing, and farming in particular areas lead to the decrease and loss of biodiversity due to excessive and continuous harvesting without leaving enough time for the organisms to reproduce and stabilize in their natural habitat.
  

  e). Climate change
  This is a change in the pattern of weather, related changes in oceans, land surfaces and ice sheets due to global warming resulting from man’s activities. Increasing global temperatures have resulted into melting of icebergs raising sea levels and so flooding coastal areas eventually affecting the niche, and these may take the lives on many living things.
  

  Consequences of loss of biodiversity
  They are various consequences of loss of biodiversity that include:
  • Desertification, is thought by scientists to be a consequence of climate
  change, has been considered to be related to deforestation. Disrupting
  water cycles and soil structure results into less rainfall in an area.
  • Floods as a result of rising sea levels.
  • Habitat destruction for extensive farming, timber harvesting and
  infrastructure and settlement.
  • Decrease in food production as result of change in pattern of weather
  that affects productivity
  • Large scale deforestation has a negative effect on nutrient recycling
  and can accelerates soil erosion.
  • Diseases that come as effects of floods and malnutrition due to famine
  

  Identification of biodiversity
  Biodiversity can be categorized into three groups:
  • Genetic diversity: The combination of different genes found within
  a population of a single species, and the patterns of variation found
  within different populations of the same species. These variations are
  caused by the gene mutations or chromosomal mutations which create
  differences in individuals of the same species.

  • Species diversity:This is concerned with variation in number of
  species and their relative abundance in an area in which they inhabit.
  All species are different from each other. These could be structural
  differences, such as the difference between a mango tree and a cow.
  They could also be functional differences, such as the differences
  between bacteria that cause decay and those that help us to digest
  food. The variation in the relative abundance of species within a habitat
  may be caused by different factors, mainly environmental factors which
  can affect their rate of reproduction.

  • Ecosystem diversity: This is concerned with variations in ecosystems
  or habitats that occur within a region. Environmental factors like climate
  change may cause diversity of habitats or systems within a region.
  

  Application activity 2.1
  What do you understand by:
  a). Genetic diversity
  b). Species diversity
  c). Ecosystem diversity
  

  
  2.2. Determination of the distribution and abundance of
          organisms in an area
  
  

  Activity 2.2
  Observe the figures below, and relate the sampling technique with figure
  and discuss on methods used to determine distribution and abundance
  of organism in an area
  

  
  

  Biologists use different sampling techniques when they want to determine the distribution and abundance of organisms in area. The commonly used techniques are:

  a). Random sampling method
  A random sampling method is a sampling method where samples are taken from different positions within a habitat and those positions are chosen randomly. Random sampling in important to avoid the bias.
  

  b). Quadrat sampling method
  A quadrat is a square area that is marked using a pre-made square of
  plastic, or stakes and string and it can range in size. Different species and
  their numbers within the quadrat are counted. Counting is repeated many times in different places in the habitat to get an accurate representation of biodiversity.
  

  c). Frame quadrats
  Frame quadrats are small plot used to isolate a standard unit of area for
  the study of the distribution of an item over a large area. While originally
  

  
  

  
  

   
  

  
  

  
  

  g). Capture -recapture technique
  This method is useful for sampling non-fixed population and is suitable for animal such as fishes, birds, lizards and insects. A sample of the population to be studied is first captured and each individual is marked with a spot for identification. These are then released and given enough time to mix up with the rest of the members in the habitat. After a certain period of time, another sample is taken. During the mark-release-recapture technique, the total population can be estimated by the use of the formula:    n1xn2/n3

  where n1 is a number caught and marked in first sample, n2
   is a number caught in second sample n3 is a number in the second sample that had been marked.
  To understand this application, let us use the following example:
  A team of students used a sweep net to sample brown grasshoppers
  and each collect insect was marked with a very small spot of non-toxic
  waterproof paint and then they were released in the field. The next
  day, a second large sample was conducted and data were recorded
  as follows: number of caught and marked in first sample (n1
  ) = 247, number of caught in second sample (n2) = 269, and the number in the second sample that had been marked (n3) = 16. What is the number of estimated population? Solution: The estimated number:
  

  
  

  Application activity 2.2
  1. Explain the advantages of the random sampling techniques.
  2. Use suitable methods, such as frame quadrats, line transects, and
  belt transects, to assess the distribution and abundance of insect
  species in a school garden. Record your data and use the Simpson
  index of diversity (D) to calculate the diversity of collected insects.
  3. Suggest the benefits of using the following sampling techniques:
  a) Quadrats
  b) Transect
  c) Mark-capture-recapture
  4. State the conditions in which quadrats, transect and mark recapture
  are suitable sampling methods

  2.3. Spearman’s rank, Pearson’s linear correlation and Simpson’s Index of Diversity
  

  2.3.1. Spearman’s rank, Pearson’s linear correlation
  

  Activity 2.3.1
  

  A student reads a questionnaire and one question was difficult for him to answer. The question asked to explain the process of Spearman’s   ranking and Pearson’s linear correlation. As the one who is learning biology, assist him to answer correctly such question by doing research in different necessary resources and prepare complete related information in your exercise.
  

  To decide if there is an association between collected data, a correlation coefficient is calculated and plot scatter graph drawn in order to make a judgment. The strongest correlation is present for studied items when all the points lie on a straight line. In this case, there is linear correlation, and the correlation coefficient equals 1.
  

  If a given variable X increases so does another variable Y, the relationship is a positive correlation. If a variable X increases while the variable Y decreases, then the relationship is a negative correlation. A correlation coefficient of 0 means that there is no correlation at all. These correlation coefficients are ways to test a relationship observed and recorded to see if the variables are correlated and, if so, to find the strength of that correlation.
  

  
  

  a). Spearman’s rank correlation coefficient
  When collected data are not quantitative, but used an abundance scale or when the researcher is not sure if quantitative data are normally distributed. It might also be possible that a graph of results shows that the data are correlated, but not in a linear fashion. In this case, the Spearman’s rank correlation coefficient is used. It involves ranking the data recorded for each variable and assessing the difference between the ranks. You should always remember that correlation does not mean that changes in one variable cause changes in the other variable.
  

  b). Pearson’s correlation coefficient
  Pearson’s correlation coefficient can only be used where there might be
  a linear correlation and when there are collected quantitative data as
  measurements (for example, length, height, depth, and light intensity, mass) or counts (for example number of plant species in quadrats). The data must be normally distributed.

  
  

  Where:
  r is the correlation coefficient
  x is the number of species in a quadrat
  y is the number of species in the same quadrat
  n is the number of readings (From1 to n)
  x is the mean number of species
  ȳ is the mean number of species
  sx is the standard deviation for x
  sy is the standard deviation for y

  2.3.2. Simpson’s Index of Diversity (D)
  Activity 2.3.2

  Visit your smart classroom and download and analyze the videos that
  explains
  a). The purpose of calculating the Simpson diversity index.
  b). How to calculate Simpson index D, Simpson index of diversity
  and Simpson reciprocal index.
  

  The Simpson diversity index is among indices used to measure diversity. It is expressed in three related indices namely Simpson index, Simpson index of diversity and Simpson reciprocal index.
  a). Simpson index D
  Simpson index D can be expressed in two ways and takes into consideration the total number of organisms of a particular species and the total number of organisms of all species. It is calculated as follows:
  D =1-∑ (n/N) 2 with n: the total number of organisms of a particular species and N: the total number of organisms of all species. When the index equals or is nearby 0 there is an infinite diversity of considered species. When it equals or is nearby 1, this means that there is no diversity. The bigger the value of D, the lower the diversity and small is D, bigger is the diversity. 

  b). Simpson index of diversity 1 - D
  The value of this index also ranges between 0 and 1, but now, the greater the value, the greater the sample diversity. This makes more sense. In this case, the index represents the probability that two individuals randomly selected from a sample will belong to different species.
  

  c). Simpson reciprocal index 1 / D
  Another way of overcoming the problem of the counter-intuitive nature of Simpson’s index is to take the Simpson’s reciprocal index 1/D. The value of this index starts with 1 as the lowest possible figure. This figure would represent a community containing only one species. The higher the value, the greater the diversity.
  

  Example:
  1. In a woodland, a quadrat was sampled for ground vegetation. Data
  collected were recorded in the table 1.3.2. Find out the value of
  the Simpson index and draw the conclusion about the biological
  diversity of the sampled area.
  

  
  

  
  

  Putting the figures into the formula for Simpson’s Index and replace each
  letter by its respective value, the Simpson index shall be: D = 1 – 0.3511111= 0.648888889
  Based on the theory above, the quadrat presents a higher diversity because the value of D is nearby zero
  

  Application activity 2.3
  1. In which conditions results can you conclude that there is:
  a) A positive correlation?
  b) A negative correlation?
  c) Non-correlation.
  2. Explain the difference between species richness and species
  evenness
  3. Suggest what precautions you may need to take when measuring
  populations of aquatic animals or plants.
  4. explain why a habitat with high diversity tends to be more stable than
  one with lower diversity.
  5. In a survey of trees in a tropical forest, students identified five tree
  species (A to E). They counted the numbers of trees in an area
  100m×100m and found these results:
  
  

  
  

  Calculate the Simpson’s Index diversity for identified species
  and explain the advantage of using data on species diversity and
  abundance when calculating an index of diversity.

  6. The Simpson’s Index of diversity for vegetation in an open area
  inhabited by grasslands was 0.8. For a similar sized area of vegetation
  beneath some conifer trees it was 0.2. What do you conclude from
  these results?

  Skills lab 2
  Visit your school garden and sample into two areas A and B each with 25
  cm2 by using one of the sampling technics. Calculate the Simpson’s diversity index for the two samples, and indicate which one is more diverse than another. For each sample, consider 5 more abundant species only.
  

  End unit assessment 2
  1. Explain what is meant by a habitat.
  2. Make a list of all the habitats you can see in your school compound.
  3. Explain why we share so many of our genes with plants.
  4. Discuss the contribution of ecosystems to cultural traditions in
  Rwanda.
  5. Pollution is one of the causes of aquatic biodiversity loss:
  a) What do you understand by water pollution?
  b) Outline human activities that contribute to water pollution
  c) Discuss how polluted water affects aquatic living organisms?
  6. Relate desertification with biodiversity loss.
  7. Discuss on importances of biodiversity.
  8. Distinguish between:
  a) Community and population
  b) Ecological niche and habitat
  9. Describe the two main components of an ecosystem.
  10. Calculate the value of Simpson’s Diversity Index (D) for a single
  quadrate sample of ground vegetation in woodland from which
  the following sampling date was obtained, and conclude about the
  diversity of plants in the woodland:

  
  

  
  

  
  

  
  

  
  

  
  

• UNIT 3: INTRODUCTION TO CLASSIFICATION

  Key Unit competence: Apply the basic knowledge of classification
                                                to group living organisms in three domains
  Introductory Activity 3
  Observe organisms in the figure below and answer asked questions:

  

  3.1.Taxonomic hierarchy and Three domains of life:
  Archaea, Bacteria and Eukarya

  
  3.1.1.The taxonomic hierarchy
  
  

  Activity 3.1.1

  You are provided with cards written on a list of words such as continent,
  district, country, cell, province, sector, village and family.
  1. Arrange the above words in increasing size
  2. What is your opinion about the people of the same family and those
  in the whole country?
  3. Compare your arrangement in 1. above with possible groupings of
  organisms in biological taxonomic hierarchy.

  Taxonomy is the study of classification of living organisms in taxonomic
  levels called taxa (singular: taxon). In biological classification, these taxa
  form a hierarchy. Each kind of organism is assigned to its own species, and similar species are grouped into a genus (plural: genera). Similar genera are grouped into a family, families into an order, orders into a class, classes into a phylum (plural: phyla) and phyla into a kingdom. The hierarchy classification starts from the largest group, the domain.

  The eight taxonomic levels of classification are known as taxa (taxon in
  singular), these include: Domain, Kingdom, phylum, class, order, family, genus and species. As one moves down the taxonomic hierarchy, it follows that the number of individuals decreases but the number of common features increases.

  

  

  Application activity 3.1.1
  1. What are the three domains of living things?
  2. Discuss the ways in which a domain differs from a kingdom?

  3.1.2. Three domains: archaea, bacteria and eukarya
  Activity 3.1.2
  Visit the computer lab and search the characteristics archaea, bacteria
  and eukaryadomains and present them on manila paper.

  There are three domains used by biologists to divide organisms into three large groups based on their cell structure. The domain is the highest taxon in the hierarchy. The prokaryotes are divided between the domains Eubacteria and Archaebacteria, while all the eukaryotes are placed into the domain Eukarya.

  

  a). Domain Eubacteria
  Domain bacteria include prokaryotic organisms as their cells have no true nucleus.
  They are all microscopic that vary in size between 0.2 to 10 micrometers.
  The characteristic features of bacteria are:
  • Cells with no true nucleus
  • DNA exists in circular chromosome and does not have histone proteins
  associated with it.
  • No membrane-bound organelles (mitochondria, endoplasmic reticulum, Golgi body, chloroplasts)
  • Contain mesosomes as infolding of membrane and acts as sites for
  respiration as they lack mitochondria.
  • Ribosomes (70 S) are smaller than in eukaryotic cells
  • Cell wall is always present and contains peptidoglycans in place of
  cellulose
  • Cells divide by binary fission
  • Usually exist as single cells or colonies.

  

  b). Domain Archaea (Archaebacteria)
  This includes bacteria that live in extreme environments where few other
  organisms can survive, like in volcanic hot springs and black organic mud totally devoid of oxygen.

  They are classified according to the environments they live in:

  • Methanogenic bacteria that live in habitats deprived of oxygen and give
  off methane as a product of metabolism, for example those that live in
  the guts of ruminant animals.
  • Halophilic bacteria live only in salty conditions
  • Thermoacidophilic bacteria tolerate extreme acid and temperature that
  exceed boiling point of water and a pH below 2.

  c). Domain Eukarya
  All the organisms classified into this domain have cells with true nuclei and membrane-bound organelles. It includes the four remaining kingdoms: protists, fungi, plantae and Animalia. Their characteristic features are:
  • Cells with a nucleus and membrane-bounded organelles
  • linear DNA associated with histones arranged within a chromosome in
  the nucleus
  • Ribosomes (80S) in the cytosol are larger than in prokaryotes, while
  chloroplasts and mitochondria have small ribosomes (70S ribosomes),
  like those in prokaryotes.

  • Chloroplast and mitochondrial DNA is circular as in prokaryotes
  suggesting an evolutionary relationship between prokaryotes and
  eukaryotes
  • A great diversity of forms: unicellular, colonial and multicellular
  organisms
  • Cell division is by mitosis.
  • Many different ways of reproduction including asexually and sexually.

  Application activity 3.1.2
  1. What are the six kingdoms of living things as they are now identified?
  2. List three domains of living organisms.
  3. Which kingdoms include only prokaryotes? Which kingdoms include
  only heterotrophs?
  4. How do domains and kingdoms differ?
  5. Suppose that you discover a new single-celled organism which has
  a nucleus, mitochondria and a giant chloroplast. In which kingdom
  would you place it? What are your reasons?
  6. It is confirmed that: “Some bacteria can survive in extreme
  temperatures such as hot springs”. Justify this statement.

  3.2. Characteristic features of the kingdoms

  Activity 3.2
  Observe carefully the photo of organisms below and answer asked
  questions.

  

  1. Identify the characteristics of organism found on photo.

  2. Among other organisms you know, apart from that you are seeing on photo, search their characteristics and present them in your exercises book

  Living organisms are classified in five kingdoms namely Protoctista, Fungi, Plantae, Monera and Animalia.

  3.2.1. Characteristic features of the kingdom Protoctista

  This kingdom is made up of a very diverse range of eukaryotic organisms, which includes those that are often called protozoans and algae. Living things such as paramecium, amoeba, euglena, algae and plasmodia belong to the kingdom Protoctista.

  

  The characteristic features of protoctists are listed according to the different phyla due to their diverse range:
  • Rhizopus that have pseudopodia for locomotion. Example, amoeba.
  • Flagellates which are protoctista which move by using flagella. Example, Trypanosoma.
  • Sporozoans which are mainly parasitic organisms that reproduces by
  multiple fission. Example plasmodium.
  • Ciliates are protoctista which move with cilia. Example paramecium.
  • Euglenoid flagellates which are organisms with flagella but with a
  biochemistry quite distinct from that of flagellates. Example Euglena.
  • Green algae are photosynthetic protoctista with chlorophyll pigments.
  Example chlorella.

  • Red algae are photosynthetic protoctista with red pigment as well as
  chlorophyll. Example, chondrus
  • Brown algae which are photosynthetic protoctista with brown pigments
  as well as chlorophyll. Example Fucus and sea weed.

  3.2.2. Characteristic features of the kingdom fungi

  Fungi are all heterotrophic, obtaining energy and carbon from dead and
  decaying matter or by feeding as parasites on living organisms. There is a
  vast range in size from the microscopic yeasts to macroscopic fungi.

  

  Other characteristic features of fungi are:
  • Heterotrophic nutrition.
  • They use organic compounds made by other organisms as their source
  of energy and source of molecules for metabolism.
  • Reproduce asexually by means of spores and sexually by conjugation.
  • Simple body form, which may be unicellular or made up of long threads
  called hyphae (with or without cross walls).
  • Large fungi such as mushrooms produce large compacted masses of
  hyphae known as fruiting bodies to release spores.
  • Cells have cell walls made of chitin or other substances.

  3.2.3. Kingdom Plantae

  
  

  Plants are all multicellular photosynthetic organisms. They have complex
  bodies that are often highly branched both above and below the ground.
  Characteristic features of plants are:
  • Multicellular eukaryotes with cells that are differentiated to form tissues
  and organs.
  • Few specialized cells.
  • Cells have large and often permanent vacuoles for support with cell
  walls made of cellulose.
  • Most plants store carbohydrates as starch or sucrose.

  3.2.4. Kingdom Animalia

  Animals are multicellular organisms that are all heterotrophic with different methods of obtaining their food.
  

  
  

  
  

  Organisms in this kingdom have other additional features:
  • Different types of specialized cells.
  • Cells do not have chloroplasts and cannot photosynthesize (although
  some, such as coral polyps have photosynthetic protoctists living within
  their tissues).
  • Cell vacuoles are small and temporary (for example lysosomes and
  food vacuoles).
  • Cells do not have cell walls.
  • Communication is by the nervous system

  3.2.5. Kingdom Monera
  Organisms in this kingdom are unicellular, that do not have a nucleus. They are prokaryotic. They are the smallest and simplest organisms. Some of them stick together to form chains or clusters while others are single cells. The figure below shows a typical structure of a bacterial cell which contains all the main features of prokaryotes.
  Although some of them are harmful in causing human diseases, others are beneficial species that are essential to good health, as they are involved in food industry, medicine and in pharmacy.

  

  

  3.2.6.Common bacterial diseases in plants and animals
  
  

  Activity 3.2.6
  Suppose there is cholera outbreak in your village and the executive
  secretary invited you to sensitize people about preventive measures
  against cholera. Prepare a brief presentation for this purpose and include causes, mode of transmission and then preventive measures

  The bacteria that causes diseases are harmful to humans and other animals and are referred to as pathogenic bacteria. The body is a home to many millions of bacteria. Some are useful while others are harmful to humans. A bacterial disease is caused by entry of bacteria into a host which can grow and flourish in the host, causing harm to the host. Bacteria cause diseases like cholera, tuberculosis (TB), typhoid fever, pneumonia, tetanus, and diphtheria, and bacterial meningitis, tooth decay in humans and anthrax in cattle.

  

  

  

  3.2.7. Economic importance of bacteria
  Activity 3.2.7
  When an animal dies in a forest, it decays after a certain period of time.
  Once a farmer grows beans in the soil with such dead animal decay,
  beans grow well.
  1. What cause the dead animal to decay?
  2. Why the beans have grown well?
  Bacteria are economically important as these microorganisms are used by humans for many purposes and are harmful in causing disease and spoiling food. Bacteria are useful in many ways:

  a. Biotechnology
  Bacteria are used in biotechnology for example in the manufacturing
  industries. They are used to manufacture products such as ethanol, acetone, organic acid, enzymes, and perfumes. In the chemical industry, bacteria are most important in the production of pharmaceuticals. For example, Escherichia coli is used for commercial preparation of riboflavin and vitamin K.

  b. Genetic engineering
  Bactria are used in genetic engineering through the manipulation of genes, also called recombinant DNA technology. In this case, bacterial cells are transformed and used in production of commercially important products for example, production of human insulin used against diabetes.

  c. Decomposition of dead organisms
  In addition, bacteria are important in decomposition of dead organisms and animal wastes such as feces to form organic matter. This process improves soil fertility and plays an important role in mineral recycling in an ecosystem.

  d. Fibre retting
  Some bacteria including Clostridium butylicum are used to separate fibres in a process called retting. In this process, fibres are formed to make ropes and sacks.

  e. Nitrogen fixation
  Some other bacteria are used to fix nitrogen in form of nitrates into the soil. For example, Rhizobium bacteria which lives in root nodules of leguminous plants. Such bacteria help in improvement of soil fertility especially during nitrogen cycle.

  f. Digestion
  Some bacteria living in the gut of ruminant animals such as cattle, horses and other herbivores secrete cellulase, an enzyme that helps in the digestion of the cellulose of plant cell walls. Cellulose is the major source of energy for these animals. Another example is Escherichia coli that live in the human large intestine which synthesizes vitamin B and releases it for human use.

  g. Biological control
  Some bacteria are used as biological agents in biological pest control such as Bacillus thuringiensis (also called BT) instead of pesticides. Because of their specificity, these bacteria are regarded as environmentally friendly, with little effect on humans, wildlife, pollinators, or other beneficial insects.

  Application activity 3.2
  1. Discuss 4 characteristics for each among the five kingdoms
  2. What are the three methods that protists use to obtain food?
  3. Identify three characteristics of protists
  4. The following is a list of organisms belonging to various kingdoms:
  housefly (Musca domestica), maize (Zea mays), Frog (Rana spp),
  Bat and Eagle.
  a) Classify these organisms into their kingdoms.
  b) Name any two organisms that are not closely related and give a
  reason.
  5. How are fungi different from members of kingdom plantae?
  6. Mr. Green lives in one of the slums in a certain city. He prepares and
  sells chapattis on street. He is usually very clean, but one morning,
  he is late for work so he does not bother to wash his hands after
  visiting the toilet. That day he prepares 400 chapattis all of which are
  sold. Few hours later, his customer Sandra suffered from a disease
  with the following signs and symptoms: severe diarrhea, excessive
  loss of water leading to dehydration, and vomiting, after five days.
  Later, all his customers were rushed and admitted in hospital due to
  the same problem.
  a) Suggest the disease that Mr. Green’s customers were suffering
  from and what caused the disease?
  b) Name three other ways this disease might be spread around city.
  c) After reading this scenario, what message do you have for people
  who are like Mr. Green?
  d) Suppose you were the health officer for the area in town with such
  a problem. What steps would you take to prevent the disease
  from spreading further?
  e) House flies are described as vectors. Describe, how houseflies
  transmit diseases tohumans.
  7. Discuss 6 economic importances of bacteria.
  8. Explain how bacteria are used as biological control.

  3.3. Classification of viruses and their economic importance
  Activity 3.3
  Visit the internet and conduct a research to explain the following:
  a). The classification of viruses
  b). The economic importance of viruses.

  3.3.1. Classification of viruses
  Viruses can be classified according to:
  • Type of nucleic acid molecules they have. Most animal viruses contain
  RNA while plant viruses contain DNA.
  • Type of host cell: plant or animal viruses as they are specific to their hosts.
  • Presence or absence of the envelope: Plant viruses’ bacteriophage
  are no enveloped while animal viruses like HIV and influenza virus are
  enveloped.

  3.3.2.Characteristics of viruses
  Viruses are microorganisms whose structure is only visible with electron
  microscopes. A typical virus consists of DNA or RNA within a protective
  protein coat called capsid which provides protection. Viruses become active in metabolism only once insidethe host cell.When they infect cells, they use biochemical machinery and proteins of the host cellto copy their nucleic acids and to make proteins coats often leading to destructionof the host cells. The energy for these processes is provided by the ATP from the hostcell.

  Because viruses do not consist of cells, they also lack cell membranes,
  cytoplasm, ribosomes, and other cell organelles. Without these structures, they are unable to make proteins or even reproduce on their own. Instead, they must depend on a host cell to synthesize their proteins and to make copies of themselves. Viruses infect and live inside the cells of living organisms. They are also regarded as parasites since they depend entirely on living cells for their survival. Although viruses are not classified as living things, they share two important traits with living things: They have genetic material, and they can evolve.

  Application activity 3.3

  1. What is meant by the term virus?

  2. State the main components of a virus.

  3. Describe the two ways how viruses cause an infection

  4. Differentiate between a bacteriophage and a retrovirus?

  5. Do you think viruses should be considered as a form of life? Give reasons for your answer.

  3.4. Dichotomous keys for identification of organism
  

  Activity 3.4
  

  The figure below represents different types of plant leaves. Make a classification of these plants based on the external structure of the leaves.

  

  The dichotomous key is also called biological identification key. It is made up of a series of contrasting statements called leads indicated by the numbers 1, 2, 3…where each lead deals with a particular observable characteristic. The characteristics used in keys should be readily observable morphological features which may be either qualitative, such as shape of abdomen, nature of legs and color, or quantitative, such as number of antennae, number of pairs of legs and length of the antennae in case of arthropods. It is essential to note that size and color are often less considered to both can be influenced by the environment, the season, the age or state of the organism at the time of identification.

  3.4.1. Guidelines used in construction of a dichotomous key
  The following guidelines must be considered while constructing a dichotomous key.
  • Use morphological characteristics which are observable as much as
  possible such as leaf venation, nature of margin, apex, lamina and
  nature or length of the petiole (leaf stalk).
  • Start with a major characteristic that divide the organism or the specimen into two large groups such as the type of a leaf.
  • Select a single characteristic at a time and identify it using a number
  for example: simple leaf………go to 2, compound leaf………go to 5.
  This means that in 2 you will deal with only simple leaves and 5 only
  compound leaves.
  • Use similar forms of words for two contrasting statements for example
  at 2: leaf with parallel venation …………go to G and leaf with network
  venation ………go to 3.
  • The first statement should always be positive.
  • Avoid generalizations or overlapping variations, be specific and precise
  to the point.

  Example
  • Collect leaves from the following plants: cassava, avocado, jacaranda,
  cassia, hibiscus bean, maize or paspalum grass,
  • Label different leaves collected as, A, B, C, D, E, F and G
  • Observe and familiarize with the specimens before starting the
  experiment to minimize errors during the identification process
  • Make a table summarising the specimens and steps followed to identify
  each of them.
  • Construct a dichotomous key basing on the observable features
  (characteristics) and table of steps followed.
  Solution: The dichotomous key of specimens A, B, C, D, E, F and G.
  1a) Simple leaves ----------------------------------------------------------------go to 2
  b) Compound leaves ------------------------------------------------------------go to 5
  2 a) Parallel venation ------------------------------------------------------------G
   b) Network venation -----------------------------------------------------------go to 3

  3 a) Simple digitate ---------------------------------------------------------------------A
   b) Non simple digitate ---------------------------------------------------------go to 4
  4 a) Leaf with serrated margin ------------------------------------------------------E
   b) Leaf with smooth margin ---------------------------------------------------------B
  5 a) Leaf with three leaflets (compound trifoliate)------------------------------F
   b) Leaves with more than three leaflets -----------------------------------go to 6
  6 a) Pinnate leaf ------------------------------------------------------------------------D
  b) Bipinnate leaf ---------------------------------------------------------------------- C

  3.4.2. Common features used for identification of animals
  Animals are classified basing on the following features:
  • Locomotory structures such as legs, wings and fins
  • Antennae (presence, nature and number)
  • Presence or absence of eye and eye type
  • Number of body parts for example insects have three body parts
  • Body segments (nature and number)
  • Body surface structures such as fur, hair, feathers and scales
  • Feeding structures such as mouth parts in arthropods for example in
  insects
  • Type of skeleton present such as endoskeleton, exoskeleton and
  hydrostatic

  3.4.3. Common features used for identification of plants
  Plants can be classified basing on the following features:
  • The leaf structure such as: nature of apex, margin, venation, lamina
  and petiole
  • The flower structure including inflorescence type, flower shape and
  number of floral parts
  • The type of stem (woody, fleshy and herbaceous), shape (rectangular,
  cylindrical) and texture of the stem (smooth, spiny and thorny) …
  • The type of root system, tap root, storage root, fibrous roots…

  Precaution
  • Care must be taken while collecting and handling some organisms
  because some are poisonous, have thorns and others are able to sting
  • Collection of specimen should be done a day or few days before the
  experiment depending on nature of the experiment
  • Avoid and try to minimize where possible, uprooting, cutting down or
  plucking and pruning of plants as this may threaten the biodiversity as
  well as result into environmental degradation

  Application activity 3.4
  Read and interpret the dichotomous tree below and use it to answer the
  following questions.

  

  1. Specify the phylum of kingdom animalia represented by the above
  dichotomous tree? Give one observable reason to support your
  answer.
  2. According to this dichotomous tree, which characteristic feature was
  used to classify different insects?
  3. Which observable characteristic feature distinguishes between a
  spider and a mosquito?
  4. How does a millipede differ from a centipede?
  5. To which classes do a millipede and a centipede belong?
  6. Which class of arthropods is not represented on figure 2.12?

  Skills lab 3
  • Move around the school compound and select a small plant which you
  know the scientific name and the the taxonomic hieracrchy.
  • Place the plant between two sheets of newspaper and in between
  some heavy books. ...
  • When your plant is pressed, remove it from the newsprint and carefully
  glue it to the 11x16 paper. ...
  • Take your printer paper, cut a 3” x 4” piece of paper and glue this onto
  the bottom right corner of your herbarium sheet.
  • Label your work (Taxonomic hierarch, Sientific name, Local name,
  date and your name)

  End unit assessment 3
  1. Which one of the following living organisms belongs to Domain Bacteria?
  a). Euglena
  b). Vibrio cholerae
  c). Paramecium
  d). Moulds
  2. The group of classification where organisms resemble one another and are
  capable of interbreeding together to produce viable offspring is known as:
  a). Species
  b). Kingdom
  c). Genus
  d). Phylum
  3. Which one of the following is not a kingdom of living organisms?
  a). Monera
  b). Animalia
  c). Annelida
  d). Protoctista
  4. Which one of the following is a characteristic feature common to fish, reptiles
  and birds but absent in mammals?
  a). Possession of scales
  b). Has no limbs
  c). Possession of feathers
  d). Undergo internal fertilization
  5. Which one of the following statements about fish is not correct?
  a). Fish live both in water and on land and undergo external
  fertilization.
  b). Most fish have bones while others are cartilaginous
  c). Most fish have streamlined body, lateral line and swim bladder.
  d). Gills are organs for gaseous exchange in fish
  6. Which one of the following is not a characteristic of all insects?
  a). They have three body parts namely head, thorax and abdomen.
  b). They have three pairs of jointed legs attached on segment of the
  thorax.
  c). They have four pairs of jointed legs
  d). They have a pair of antennae attached on the head.
  7. The following are characteristics of all mammals except;
  a). They have mammary glands to secrete milk feed their young
  ones.
  b). Their skin is covered with hair.
  c). Undergo internal fertilization and internal development of the
  embryo.
  d). They have a pair of wings made up feathers.
  8. The point where the leaf joins the stem is called;
  a). Apex
  b). Margin
  c). Leaf base
  d). Lamina
  e). Length of petiole.
  9. Which of the following is less considered while identifying feature to
  construct
  a). dichotomous key of leaves?
  b). Nature of margin
  c). Nature of apex
  d). Size and color of leaf
  10. The following are characteristics of arachnids except;
  a). Four pairs of jointed legs
  b). Two body parts
  c). Three body parts
  d). Do not have wings
  11. Match the structures with the organisms which possess them.

  

  a). Which kingdoms are represented by the letters x and y?
  b). State one characteristic that organisms of x may share with:
  i. Prokaryotes
  ii. Fungi
  iii. Plantae
  13. What is the significance of classification of living organisms?

• UNIT 4: SOLUTIONS AND TITRATION

  Key Unit competence: To prepare standard solutions and use
                                                 them to determine concentration of other
                                                 solutions by method of titration.
  
  

  Introductory Activity 4
  Observe the photo below and attempt the questions that follow:

  

  1. For the bottle of beer 1, and that of Beer 2, we find on the bottle of its
  labels 5% alcohol and 6% alcohol respectively.
  a) Explain the meaning of 5% and 6% alcohol.
  b) 5% alcohol corresponds to which volume of alcohol of the total
  volume of 72cl of the bottle of beer 1.
  c) Calculate the volume of alcohol corresponding to 6% alcohol of
  the bottle of Beer 2 of the total volume of 65cl.
  2. On the label of the bottle of fruit juice we find that dilution is 1:5.
  Explain this ratio and explain also the purpose of diluting substances.

  4.1. Definition of standard solution and primary standard solution
  Activity 4.1
  1. Explain the concepts of:
  a) Solution
  b) concentration
  2. You are given a basic solution, NaOH (aq), and you are requested
  to determine its concentration. How could you proceed to know its
  concentration?

  A homogeneous mixture is known as a solution.
   An aqueous solution is a solution in which the solvent is water. Its
  concentration may be estimated in many ways.

  In analytical chemistry, a standard solution is a solution containing a
  precisely known concentration of an element or a substance and used to
  determine the unknown concentration of other solutions. A known weight of solute is dissolved to make a specific volume. It is prepared using a standard substance, such as a primary standard.

  Standardization is the process by which the concentration of a solution is determined by measuring accurately the volume of the solution required to react with an exactly known amount of a primary standard.

  A primary standard is defined as a substance or compound used to prepare standard solutions by actually weighing a known mass, dissolving it, and diluting to a definite volume.

  Or a substance, which is chemically stable in aqueous solution and its
  concentration remains constant with change in time such that it can be used to standardize other solutions.

  Some important examples of primary standard are;
  • Sodium Carbonate, Na2CO3
  • Potassium dichromate, K2Cr2O7
  • Benzoic acid, C6H5COOH
  • Oxalic acid, H2C2O4
  • Iodine, I2

  • Sodium oxalate, Na2C2O4
  • Butanoic acid, C3H7COOH
  • Sodium tetraborate, Borax, Na2B4O7
  • Potassium chloride, KCl
  • Arsenic(III)oxide, As2O3
  • Silver nitrate, AgNO3
  Standard solutions are normally used in titrations to determine unknown concentration of another substance.

  Application activity 4.1
  Differentiate between standard solution and primary standard solution

  4.2. Properties of a primary standard solution
  Activity 4.2
  1. Recall the concept of “primary standard solution”
  2. Do research and find out the role and characteristics of a good
  primary standard solution.

  A good primary standard solution meets the following criteria:
  • High level of purity
  • High stability
  • Be readily soluble in water
  • High equivalent weight (to reduce error from mass measurements)
  • Not hygroscopic (to reduce changes in mass in humid versus dry
  environments)
  • Non-toxic
  • Inexpensive and readily available
  • React instantaneously, stoichiometrically and irreversibly with other
  substances i.e. should not have interfering products during titration.
  • It should not get affected by carbon dioxide in air

  Molar concentrations are the most useful in chemical reaction calculations because they directly relate the moles of solute to the volume of solution. 

  The formula for molarity is:

  

  Application activity 4.2
  Discuss the properties of a good primary standard solution.

  4.3. Preparation of standard solutions
  Many of the reagents used in science are in the form of solutions which
  need to be purchased or prepared. For many purposes, the exact value of concentration is not critical; in other cases, the concentration of the solution and its method of preparation must be as accurate as possible.

  Thus, the preparation of solutions is one of the most fundamental tasks
  performed by a chemist.

  A solution may be prepared by two methods: dissolution method and
  dilution method.

  4.3.1. Preparation of standard solution by dissolution of solids
  Activity 4.3.1
  Some chemicals of high interest used in scientific laboratories, hospitals,
  pharmacies, are found in the form of solutions with precise concentration.
  1. What is the most common unit of the solution concentration?
  2. Using your knowledge in chemistry acquired so far and available
  resources identify the requirements and the procedure for the
  preparation of such solutions starting with solids.
  The most common unit of solution concentration is molarity (M).
  The molarity or molar concentration of a solution is defined as the number of moles of solute per one litre (mol/L) of solution.
  Molarity, therefore, is a ratio between moles of solute and litres of solution. To prepare laboratory solutions, usually a given volume and molarity are required. To determine molarity, the formula weight or molar mass of the solute is needed.

  When preparing a solution starting with a solid, the following steps may be followed:
  • Determine the mass in grams of one mole of solute, the molar mass,
  Mm.
  • Decide volume of solution required, in litres, V.
  • Decide molarity of solution required, M.
  • Calculate grams of solute required.

  In the preparation of solution, glasses, volumetric flask, pipette, droppers, glass rod, measuring cylinder, analytical balance, spatula, beakers, magnetic stirrer and other laboratory devices are used.

  The preparation of a solution by dissolution follows the steps illustrated by figure 4.1

  

  The following examples illustrate the calculations for preparing solutions.
  Examples:
  1. Describe in details how you can prepare the following solution: 50 mL of NaOH, 10%.
  Answer:
  Preliminary calculations
  10% means that in 100 mL of solution only 10 g are pure NaOH. So 50 mL
  of NaOH will be prepared by taking the mass of NaOH, dissolving it in water and making up to 50 ml. 

  

  Procedure
  • Weigh 5g of NaOH accurately using an analytical balance.
  • Carefully dissolve it in a beaker containing about 30mL of distilled water and stir using a glass rod or a magnetic stirrer till you get homogeneous mixture.
  • Transfer the solution and the washings in a 50 mL volumetric flask and
  mix.
  • Add more distilled water until the level is about 2 cm below the
  graduation mark on the volumetric flask.
  • Top up using distilled water from a dropper until the bottom of the
  meniscus is at the level of mark when viewed at eye level.
  • Stopper the flask and shake again to homogenise.
  • Label your solution: 10% NaOH; 50 mL
  • The solution prepared is 10% NaOH
  Usually, the minimum label requirements are: (1) Identity of contents (2).
  Concentration (3) Your name and (4) date of preparation.

  2. Describe in details the preparation of 250 cm3 of a 0.1M Na2CO3
  solution.

  Answer:
  Step 1: Preliminary calculations
  Calculate the amount of anhydrous sodium carbonate required to be
  dissolved in 250cm3 of solution. i.e:
  Molar mass of Na2CO3
  = (23 x 2) +12+ (16 x 3) = 106 g/mol
  Thus, 1 mole of Na2CO3 has a mass of 106 g.
  0.1mole of Na2CO3 solution will have a mass=106g/mol x 0.1mol =10.6 g.
  1000 cm3 of 0.1M Na2CO3 solution contains 10.6 g.

  
  Step 2: Procedure
  • Weigh 2.65g of sodium carbonate and carefully transfer in a beaker
  containing 150mL of distilled water.
  • Stir using a glass rod until complete dissolution.
  • Using a filter funnel, transfer the solution and the washings, in a 250
  mL volumetric flask.

  • Using a wash bottle, add more distilled water up to about 1cm of the
  graduation mark.
  • Using a dropper pipette, complete the volume the graduation mark.
  • Stopper the flask and shake to homogenise.
  • Label the solution.

  Application activity 4.3.1
  Give a detailed description, including calculations involved, for the
  preparation of the following solutions:
  a). 1L of a 0.01M KMnO4solution
  b). 250 mL oxalic acid 10g/L.

  4.3.2. Preparation of standard solution by dilution

  Activity 4.3.2
  Some chemicals of high interest used in scientific laboratories, hospitals,
  pharmacies, are found in the form of solutions with precise concentration.

  Some are obtained by dissolution of solids and others may be obtained
  by dilution of stock solution.
  1. What is meant by:
  a) stock solution? b) dilution?
  2. Do research to identify the requirements and the procedure for
  the preparation of such solutions starting with solutions or liquids.
  Apart from, dissolution method, we can prepare a solution by dilution from the stock solution. This consists of reducing the concentration of a concentrated stock solution to less concentrated

  A simple dilution is one in which a unit volume of material of interest (solute) is combined with an appropriate volume of a solvent to achieve the desired concentration.

  The dilution factor is the total number of unit volumes in which the solute is dissolved. For example a 1:5 dilution involve combining 1 unit of the solute and 4 unit volumes of the solvent.

  

  Thus, when preparing a solution starting with a solution or liquid reagent: When diluting more concentrated solutions,
  • Decide what volume (Vf) and molarity (Mf) the final solution should
  be.Volume can be expressed in liters or milliliters.
  • Determine molarity (Mi) of starting, more concentrated solution.
  • Calculate volume of starting solution (Vi) required using equation:
  MiVi= MfVf

  Where Mi and Mf are the initial and the final concentrations (or initial
  and final molar concentrations or initial and final molarities); Vi and Vf
   are the initial and the final volumes.

  Note: Vi must be in the same units as Vf.

  The following are the requirements: Graduated pipettes and /or micropipettes, volumetric flasks, Stoppers, Dropping pipettes, Stock solutions, Droppers, Distilled water.

  The preparation of a solution by diluting stock solutions follows the
  steps illustrated by figure 4.2

  

  Examples:
  1. Describe how you can prepare 1L of a 1M H2
  SO4 solution from the stock solution with the following specification: density (d) =1.84; percentage (P) by mass: 98%; Mw = 98 g/mol.

  Answer:
  Preliminary calculations
  The molarity of the stock solution may be calculated using the following
  relation.

  

  Hence the required volume of concentrated sulphuric acid to be pipetted is 54.35mL.

  Procedure:
  1) Using a graduated pipette or a burette, measure 54.35mL of
  concentrated H2SO4;
  2) Using a funnel, carefully transfer the concentrated acid into a 1L
  volumetric flask containing about 700mL of distilled water;
  3) Put a stopper and gently shake the mixture;
  4) Using a wash bottle, add more distilled water until the level is 1cm
  below the mark;
  5) Using a dropper pipette, make up to 1L dropwise;
  6) Stopper the volumetric flask and gently shake.
  7) Label the solution and specify the preparation date.

  The solution prepared is 1M H2SO4.
  2. Calculate the volume of 15M H2SO4 that would be required to prepare
  150cm3 of 2MH2SO4.

  

  Application activity 4.3.2
  Describe the preparation of 500mL 0.5M HCl solution from a stock
  solution of HCl with the following specifications.
  • Molar weight: 36.5g/mol
  • Percentage of HCl: 36% by mass
  • Density: 1.18g/mL

  4.4. Titration process focussing on precise measurements
  4.4.1. Simple acid-base titrations
  Activity 4.4.1
  1. Analyse the diagram below and answer the questions that follow

  

  b) Is it important in real life to perform operations illustrated by the
  above set up? Explain using at least two examples.
  c) What are the necessary requirements for such operations?
  2. You are provided with:
  S1: solution of HCl (aq) 0.1 M
  S2: solution of NaOH (aq)
  Materials: Burettes - Indicator (phenolphthalein) - pipettes - Washing
  bottles - Conical flasks - Beakers - Retort stands - Funnels

  Procedure
  a). Using a pipette, transfer 10 mL of S2 into a conical flask.
  b). Add three drops of phenolphthalein indicator and titrate it with S1
  from the burette.
  c). Repeat the titration until you obtain consistent values.
  d). Record your readings in the table below:

  

  Titration is a process used in volumetric analysis, in which a solution of one reactant of known concentration, of unknown concentration, the titrant, is added to a known volume of another reactant of unknown concentration, the titrand, until the reaction between the two is complete.
  The analyte (titrand) is the specie of interest in a titration i.e, the specie that is subjected to analysis.

  If a concentration and volume of the titrant is reacted with the analyte, it is possible to calculate the analyte’s concentration.

  The completion of the reaction is signalled by an indicator, i.e a substance that has distinctly different colours in acidic and basic media. E.g phenolphthalein.

  The point at which the indicator changes the colour and the titration is
  stopped is called end point.

  The equivalence point is the point, in a titration, at which the mole ratio of reactants is exactly equal to the mole ratio in the balanced chemical equation. The difference between the end point and equivalent point is called titration error.

  Because volume measurements play a key role in titration, it is also known as volumetric analysis. Usually it is the volume of the titrant required to react with a given quantity of an analyte that is precisely determined during a titration.

  Titrations can be classified by the type of reaction. Different types of titration reaction include acid-base titrations, redox titrations, complexometric titrations, etc. In our context we will deal with acid-base titrations.

  Acid-base titrations
  In an acid-base titration, a standard solution of a base is added to a known volume of an acid with unknown concentration or vice versa, until the end point is reached.

  At the equivalence point, the acid and the base that have reacted are in
  equivalent amounts.

  Therefore, naMbVb = nbMaVa,
  Where Ma=Molarity of acid; Mb =Molarity of the base
  Vb =Volume of base; nb = stoechiometric number of base
  Va =Volume of acid; na = stoechiometric number of acid
  Indicators and pH-meters can be used to determine the equivalence point.
  An acid-base titration needs an indicator which will change colour with the concentrations of hydrogen ions (H+).

  Choice of indicators in acid-base titrations
  When the technique of acid-base titration is extended to a wide variety of
  acidic and alkaline solution, care needs to be taken about the choice of
  indicator for any given reaction.

  The choice of an inappropriate indicator would lead to incorrect results, and it is therefore extremely important that the indicator is chosen carefully.
  The principle on which a choice of indicator is made concerns the strength of the acid or base involved in the reaction. Note that the strength of an acid or base is not to be confused with the concentration of its solution. Example of strong and weak acids and bases and choice of indicator are given in the Table below.

  

  The common equipments used in titration are:
  Burette
  Pipette
  Retort stand and clamp
  Dropper pipette
  pH-indicator/acid-base indicator
  White tile: used to see a colour change in the solution(a white paper can
  also be used)
  Conical flask (Erlenmeyer flask) or a beaker

  How to perform titrations?
  It is essential to be familiar with the use of pipette and burettes and how to handle them. The following points are useful in order to correctly perform a titration.
  1. The apparatus should be arranged as shown in the activity 4.4.1
  2. The burette tap is opened with the left hand and the right hand is
  used to shake the conical flask.
  3. The equivalence-point is reached when the indicator just changes
  permanently the colour.
  4. At the end-point, the level of the titrant is read on the burette.
  5. The titration is now repeated, three more times are recommended.
  Towards the end-point, the titrant is added dropwise to avoid
  overshooting.

  Notice: Before titration, check if the tip of the burette is filled with the titrant, and doesn’t contain bulb of air. If there is a bulb of air, a quick opening and closing of the tap will expel the air out of the burette.

  The results are summarised in a table as shown below:
  Burette readings should be written to two decimal places (for burette having precision up to hundredth)

  

  

  

  

  Procedure
  • Weigh accurately 1.0 g of sodium hydroxide pellets in a weighing
  boat and transfer into a 250cm3 volumetric flask.
  • Add a little distilled water and shake to dissolve.
  • Make up the solution to the mark with distilled water dropwise.
  • Label the solution FA2.
  • Pipette 20cm3 (or 25 cm3) of FA2 into a conical flask.
  • Add 2-3 drops of phenolphthalein indicator.
  • Titrate with FA1 from the burette.
  • Record your results in the spaces provided below.

  Specimen results
  Mass of weighing container + NaOH pellets = 11.30 g
  Mass of weighing container alone = 10.30 g
  Mass of NaOH pellets = 11.30 g – 10.30 g = 1.00 g
  Masses should be recorded to at least two decimal places (Table 11.4)
  Volume of pipette used = …………..

  

  Each value or entry in the table must be recorded or written to two decimal places.

  Different initial readings should be used. Initial reading in each experiment should be correctly subtracted from the final reading.

  Questions:
  a). Determine the values used to calculate average volume, and
  calculate the average volume of FA1 used.
  b). Write the equation of the reaction between NaOH and HCl
  c). Calculate the number of moles of FA1 used.
  d). Calculate the concentration of FA2 in mol.dm-3.
  e). Calculate the concentration of FA2 in g/L.

  

  

  

  

  

  

  What compound is represented by the picture above?
  What observable changes could be recorded if the substance was heated
  and how do you interpret those observations?
  When blue crystals of copper(II) is heated it becomes a white powder. This is due to the loss of water molecules attached to it. This water is known as water of crystallisation.

  Water of crystallisation is water present in definite proportions in some
  crystalline compounds.

  Many crystalline salts form hydrates containing 1, 2, 3, or more moles of
  water per mole of the compound and the water may be held in the crystal

  

  

  

  

  

  Skills lab 4
  You are asked to investigate the acidity content of aspirin tablets.
  Write a procedure including materials, set up and procedure you will use for that purpose.
  Your project will be performed either during evenings weekends. You will
  request from the school authorities to avail some materials for you.
  
  

  End unit assessment 4
  1. Explain the following terms: a. Standard solution b. Primary standard.
  2. Describe the characteristics of a primary standard.
  3. A solution is made by dissolving 5.00g of impure sodium hydroxide in
  water and making it up to 1dm3 of solution.25cm3 of this solution are neutralized by 30.0cm3 of hydrochloric acid of concentration 0.102M.
  Calculate the percentage purity of the sodium hydroxide.
  4. You are provided with a white powder containing a mixture of sodium
  carbonate and magnesium nitrate and 1M nitric acid. Make a solution
  using 10g of the powder and 47.3cm3 of water. You need 0.05dm3
  of the acid to fully react with the solution. What is the percentage
  composition of magnesium nitrate in the powder?

  

  

  

  

• UNIT 5: THE LENSES

  Key Unit competence: Interpret and solve problems solving in thin
                                                 lenses and glass prism

  Introductory Activity 5
  Observe the images below and answer the following questions

  

  a). Name image A,B,C and D and identify where they can be used in our
  daily life activities
  b). What is the effect of light on A, B, C and D?
  c). Analyze the phenomenon in figure C and write your observations in
  your notebook
  d). How the images are formed on each of the above figures? Explain.

  5.1. Types of lenses and their characteristics
  Activity 5.1
  1. Observe closely the lenses below and answer the asked questions:

  

  a). Predict the materials used to make the above lenses. Explain your
  answer
  b). How are the lenses different?
  c). Classify these lenses according to your observation and explain the
  criteria used to classify them.

  A lensis an optical device with perfect or approximate axial symmetry which transmits and refractslight, by converging or diverging the beam. Most lenses are spherical lenses: their two surfaces are parts of the surfaces of spheres. Lenses are classified by the curvature of the two optical surfaces.

  

  The lens which is thicker at the centre than at the edges is called a convex lens while the one which is thinner at its centre is known as a concave lens. The curved surface of the lens is called a meniscus. The lens in the human eye is thicker in the centre, and therefore it is a convex lens.

  The light rays from the ray box change the direction after passing through the lens. They are therefore refracted by the lens. Hence, lenses form images of objects by refracting light.

  You can see that the rays from the convex lens are getting closer and closer to a point. The rays are thus converging, and hence a convex lens is called a converging lens. You can also see that the refracted rays from the concave lens are spreading out. This kind of lens is called diverging lens. When light passes through a lens, refraction occurs at the two lens surfaces.

  Using Snell’s law and geometry, you can predict the paths of rays passing through lenses. To simplify such problems, assume that all refraction occurs on a plane, called the principal plane that passes through the center of the lens. This approximation, called the thin lens model, applies to all the lenses.

  

  

  5.2. Refraction of light through lenses

  
  Activity 5.2
  i. Hold a hand lens about 2 m from the window. Look through the lens.
  (CAUTION: Do not look at the sun).
  What do you see?
  ii. Move the lens farther away from your eye.
  What changes do you notice?
  iii. Now, hold the lens between the window and a white sheet of paper,
  but closer to paper.
  iv. Slowly move the lens away from the paper towards the window. Keep
  watching the paper.

  What do you see? What happens as you move the paper?

  Do you see that an inverted image of trees outside is formed on the
  paper? How do you think the image is formed?

  Lenses can be thought of as a series of tiny refracting prisms, each of
  which refracts light to produce an image. These prisms are near each other (truncated) and when they act together, they produce a bright image focused at a point.

  

  5.2.1. Ray diagrams and properties of images formed by lenses

  
  Notice that an image cannot be seen on the screen irrespective of the
  position of the object. The nature of the image formed by a convex lens depends on the position of the object along the principal axis of the lens.

  The principal focus of a lens plays an important part in the formation of
  an image by a lens since parallel rays from the object converge to it, and
  thus, we consider points F and 2F when describing the nature of the images formed by the lens.

  These images can be larger or smaller than the object or same size as the
  object. When an image is larger than the object, we say that it is magnified and when it is smaller, we say that it is diminished.

  Images which can be formed on the screen are Real images. Because light rays pass through these images, real images can be formed on the screen. All real images formed by the convex lens are inverted.

  To determine an image point, we need to consider only the three rays
  indicated if Fig 4, which uses an arrow (on the left) as the object, and a
  converging lens forming an image to the right. These rays, emanating from a single point on the object, are drawn as if the lens were infinitely thin, and we show only a single sharp bend at the centre line of the lens instead of refraction at each surface. These three rays are drawn as follows:

  

  The point where these three rays cross is the image point for that object
  point. Actually, any two of these rays will suffice to locate the image point, but drawing the third ray can serve as a check.

  5.2.2. Graphical determination of focal length of lenses
  If the lens is biconvex or plano-convex, a collimated parallel or diverging
  beam of light travelling through the lens will be converged to a spot behind the lens. In this case, the lens is called a converging lens.

  

  When an object is placed at a distance greater than the focal length from the lens, the image is real and inverted on the other side of the lens. When an object is placed at a distance equal to twice the focal length from the lens, the image is the same size as the object and inverted.

  

  A convex lens forms a virtual image that is upright and larger compared to the object when the object is located between the lens and the focal point.

  

  

  Concave lenses produce only virtual images that are upright and smaller
  compared to their objects.

  When an object is between F and the lens, there is no image formed on
  the screen. The image formed is not real and is only seen by removing the screen and placing an eye in its position. We say that it is a virtual image. For a virtual image, rays appear to come from its position.

  Unlike for a convex lens where the nature of the image depends on the
  position of the object, a concave lens gives only an upright, small, virtual
  image, and is situated between the principal focus and the lens for all
  positions of the object.

  Application activity 5.2
  1. Design an experiment to study images formed by convex lenses of
  various focal lengths. How does the focal length affect the position
  and size of the image produced?

  2. An object of length 5 cm is placed at a distance 25 cm in front of a
  lens of focal length 10 cm.

  Use a ray diagram to construct the image of this object and state its
  properties if the lens is:
  a). Converging or convex;
  b). Diverging or concave.

  5.3. The thin lens equations
  Activity 5.3
  Task 1:
  i. Place a converging lens on a table while facing a window.
  ii. Place a white screen behind the lens. Move the screen to and fro
  (forwards and backwards) until a sharp image of a distant object
  is seen on the screen.
  iii. Discuss and write down the observation in your notebook.
  iv. Measure the distance from the lens to the screen. What is this
  distance called?

  Task 2:
  v. Draw a ray diagram to determine the nature and position of the
  image of an object placed 10cm from a diverging lens of focal
  length 15cm.
  vi. Using the above information, find the nature and position of the
  image using a lens formula. (Assign f a negative sign during your
  substitution).
  What is the location of the image?

  5.3.1. Convex lens
  We now derive an equation that relates the image distance to the object
  distance and focal length of a thin lens. This equation will make the
  determination of image position quicker and more accurate than doing ray tracing. Let  be the object distance, the distance of the object from the center of the lens, and  the distance of the image from the center of the lens. And let  and  refer to the heights of object and image. Consider two rays shown in Figure below for a converging lens, assumed to be very thin.

  

  

  

  

  Will be valid for both converging and diverging lenses, and for all situations, if we use the following sign conventions:
  1. The focal length is positive for converging lenses and negative for
  diverging lenses.
  2. The object distance is positive if the object is on the side of the lens
  from which light is coming; otherwise, it is negative.
  3. The image distance is positive if the image is on the opposite side
  from where light is coming; if it is on the same side, it is negative.
  Equivalently, the image distance is positive for real image and
  negative for a virtual image.
  4. The height of the image, is positive if the image is upright, and
  negative if the image is inverted relative to the object. (ho is always
  taken as positive).

  5.3.3. Magnification
  The magnification, m, of a lens is defined as the ratio of the image height
  to object height. From the above figures and the sign conventions, we have

  

  for an upright image the magnification is positive, and for an inverted image the magnification is negative.

  5.3.4. The power of lenses
  Whenever a ray of light passes through a lens it bends except when it passes through the optical centre. The degree of convergence or divergence of a lens is expressed as power. A lens of short focal length deviates the rays more while a lens of large focal length deviates the rays less. Thus the power of a lens is defined as the reciprocal of its focal length.
  

  From sign convention 1, it follows that the power of converging lens, in
  diopters, is positive, whereas the power of a diverging lens is negative. A
  converging lens is sometimes referred to as positive lens, and a diverging
  lens as a negative lens.
  In case the lenses are combined

  

  Example 1
  An object is placed 32.0 cm from a convex lens that has a focal length of 8.0 cm.
  a). Where is the image?
  b). If the object is 3.0 cm high, how tall is the image?
  c). What is the orientation of the image?

  Solution
  1. Analyse and sketch the problem
  • Sketch the situation, locating the object and the lens.
  • Draw the two principal rays

  

  

  5.3.5. Lens maker formula
  The following assumptions are made for the derivation:
  • The lens is thin, so that distances measured from the poles of its
  surfaces can be taken as equal to the distances from the optical centre
  of the lens.
  • The aperture of the lens is small.
  • Object point is considered.
  • Incident and refracted rays make small angles.

  

  

  

  This equation gives the lens maker’s formula
  Note:
  • The lens maker’s formula indicates that a convex lens can behave like
  a diverging one if i t n > n i.e., if the lens is placed in a medium whose
  index is greater than the index of lens. Similarly a concave lens can be
  made convergent.
  • The lens maker’s formula can be derived for a concave lens in the
  same way.
  Sign convention states that real is positive while virtual is negative. This
  should be put under consideration when one is using the lens formula to
  solve problems.

  Application activity 5.3
  1. Compute the composition and focal length of the converging lens
  which will project the image lamp, magnified 4 times, upon a screen
  10.0 m from the lamp.
  2. A lens has a convex surface of radius 20 cm and a concave surface of
  radius 40 cm and is made of glass of refractive index 1.54. Compute
  the focal length and the power of the lens, and state whether it is a
  converging or a diverging lens.

  5.4. Defects of lenses, their corrections and applications of lenses
  Activity 5.4
  i. Place a white sheet of paper on a horizontal ground.
  ii. Hold a glass ruler above the paper so as to focus rays from the
  sun on to the paper.
  iii. Observe carefully the image formed on the sheet of paper.
  iv. Repeat the above with the convex lens. What have you observed?

  Aberration
  A lens made of a uniform glass with spherical surface cannot form a perfect image. The spherical aberration is prominent image defect for a point source on the optical axis of such a lens. It arises because all rays through the lens are not focused to a common point.

  The dependence of index of refraction of wavelength also causes the focal length, and thereby the image position, to depend on the color of the light. All simple lenses suffer from such chromatic aberration.

  There are several different types of aberration which can cause the image to be an imperfect replica of the object (spherical aberration, chromatic aberration, coma, field curvature, barrel, pincushion distortion, astigmatism, etc).

  Note that the image has coloured patches. This defect where by an image formed has coloured patches is called chromatic aberration. There are two kinds of defects; spherical aberration and chromatic aberration.

  5.4.1. Spherical aberration
  This arises in lenses of larger aperture when a wide beam of light incident on the lens, not all rays is brought to one focus.

  As a result, the image of the object becomes distorted. The defect is due to the fact that the focal length of the lens for rays far from the principal axis are less than for rays closer to a property of a spherical surface and as a result, they converge to a point closer to the lens.

  

  This defect can be minimized (reduced) by surrounding the lens with an
  aperture disc having a hole in the middle so that rays fall on the lens at a
  point closer to its principal axis. However, this reduces the brightness of the image since it reduces the amount of light energy passing through the lens.

  5.4.2. Chromatic aberration
  Chromatic aberration is caused by the dispersion of the lens material. Since, from the lens formulae, f is dependent upon n, it follows that different colours of light will be focused to different positions.

  

  Chromatic aberration can be minimised by using an achromatic doublet
  (or achromat) in which two materials with differing dispersion are bonded together to form a single lens.

  

  Application activity 5.4
  i. How spherical and chromatic aberration can be reduced?
  ii. If a plano-convex lens is used as objective lens in a telescope, how
  is its convex surface faced to minimize spherical aberration? Explain

  5.5. Refraction through prisms
  
  

  Activity 5.5
  1. Have you ever heard of a prism? How does it look like?
  2. Observe clearly the shapes of the glasses provided below and identify
  those with the shape of a prism.
  Explain your choices

  

  3. With the help of a teacher, touch, observe and identify the real shape
  of the prism.
  4. Examine the features of the one selected as a prism.

  5.5.1. Terms associated with refraction through prism
  In optics, a prism is transparent material like glass or plastic that refracts light. At least two of the flat surfaces must have an angle less than
  between them. The exact angle between the surfaces depends on the application.

  

  

  the edges and so bring the parallel rays to a focus.

  The truncated prisms of the diverging lens point the opposite way to those of the converging lens, and so a divergent beam is obtained when parallel rays are refracted by this lens because the deviation of the light is in the opposite direction.

  The middle part of the lens acts like a rectangular piece of glass and a ray
  incident to it strikes it normally, and thus passes un-deviated.

  Dispersion of light by a prism
  Dispersion of light is the separation of a beam of light into its constituent
  colours. This takes place when a light beam passes through a dispersive
  medium. A beam of white light incident on a prism splits into its constituent colours to form “a visible spectrum”consisted of colours violet, indigo, blue, green, yellow, orange and red.

  

  When a polychromatic light is incident on the first surface of the prism, each constituent colour gets refracted through a different angle. When these colours are incident on the second surface of the prism they are again refracted further.

  Application activity 5.5.1
  1. (i) Place a prism in the centre of a piece of paper so that its refracting
  surface is directly facing the windows in order to receive light from
  the sun.
  (ii) Place a white screen on the far side of the prism so that the
  refracted rays hit it.
  (iii) Observe what is formed on the screen.
  (iv) In brief, write in your notebook the observation.
  2. Do a research to find other terms associated to the refraction light
  through prism.

  5.5.2. Deviation by a prism and determination of refractive index
  
  

  Activity 5.5.2
  1. Have you ever heard of the word deviation? List down in your notebook at least two ways in which light can be deviated.
  2. You are provided with a glass prism of refracting angle , four
  optical pins, a white sheet of paper, a soft board and fixing pins.

  i. Place a prism on a white sheet of paper and mark its outline ABC.

  

  

  

  

  

  

  1. Deviation of light by a glass prism
  Light can be deviated by reflection and refraction. Since a prism refracts
  light, it therefore changes its direction.

  A prism deviates light on both faces. These deviations do not cancel out as in a parallel sided block where the emergent ray, although displaced, is parallel to the incident ray surface. The total deviation of a ray due to refraction at both faces of the prism is the sum of the deviation of the ray due to refraction at the first surface and its deviation at the second face.

  

  N.B: The deviation D for a small angle prism is D = A (n-1)
  The expression D = A (n – 1) shows that for a given angle A, all rays entering a small angle prism at small angles of incidence suffer the same deviation.

  2. Angle of minimum deviation
  From the variation figure below, there is one angle of incidence which gives a minimum deviation. The experiment shows that this minimum deviation occurs when the angle of emergence is exactly equal to the angle of incidence and the two internal angles of refraction are equal. At this value, a ray passes symmetrically through the prism and the ray inside the prism is perpendicular to the directing plane.

  

  3. Determination of refractive index n of a material of the prism
  A very convenient formula for refractive index, n, can be obtained in the minimum deviation case. The ray PQRS then passes symmetrically through the prism, and the angles made with the normal in the air and in the glass at Q, R respectively are equal. Suppose the angles are denoted by as shown. Then:
  

  

  And (The refracting angle); so,     

  

  4. Applications of total internal reflection of light by a prism
  Many optical instruments use right -angled prisms to reflect a beam of light through 90° or 180° (By total internal reflection) such as cameras, binoculars, periscope and telescope. One of the angles of right angled prism is 90°. When a ray of light strikes a face of prism perpendicular, it enters the prim without deviation and strikes the hypotenuse at an angle of 45°. Since the angle of incidence 45° is greater than critical angle of the glass which is 42°, the light is totally reflected by the prism through an angle of 90°. Two such prisms are used in periscope. The light is totally reflected by the prism by an angle of 180°. Two such prisms are used in binoculars.
  

  Application activity 5.5.2
  1. A ray of light is refracted through a 60 degree prism of ordinary glass
  making an incident of 35 degree with the normal i.e incident ray
  =35°.What will the angle of emergent ray and the angle of deviation
  measure?
  2. What are the conditions for minimum deviation when a ray of light
  passes through a prism?
  3. Show that the deviation produced by a small angled prism is
  independent with angle if incidence.

  Skills lab 5
  Determination of the focal length of a lens
  Apparatus required:
  1 torch bulb fitted in a bulb holder
  1 switch
  3 Torch cells
  2 Cell holders
  Connecting wires about 50cm long.
  Wire gauze
  Converging lens, of focal length 15cm.
  Lens holder,
  White screen
  Metter rule.
  Retort stand with its holding accessories.

  Instructions
  In this experiment you will determine the focal length of the converging lens provided.
  a). Mount the lens on the holder and place it facing a window
  b). Place the screen behind the lens and adjust the screen until a clear
  image of a distant object is obtained
  c). Measure and record the distance, x, between the lens and the screen.

  

  End unit assessment 5
  1. How does a convex lens work? Explain your reason
  2. What will happen when a light ray travelling in glass is incident on an
  air surface? Explain your answer
  3. What will happen When a light ray makes an angle of 900
   while entering a glass slab? Explain your reason
  4. What are factors responsible for the angle of deviation through prism
  depends?
  5. A beam of monochromatic light is incident at i = 50° on one face of an
  equilateral prism, the angle of emergence is 40°.Calculate the angle
  of minimum deviation.
  6. A 600 prism has a refractive index of 1.5. Calculate the angle of
  incidence for minimum deviation, the angle of emergence of light at
  maximum deviation and angle of maximum deviation.
  

  

• UNIT 6:SIMPLE AND COMPOUND OPTICAL INSTRUMENTS

  Key unit competence: Describe and use effectively simple and
                                                 compound optical instruments

  Introductory Activity 6

  
  

  1. After observing the above images, suggest the names of the available
  optical instruments.
  2. Compared to the above images, provide other optical instrument
  you know.
  3. Where do you think these instruments are used in our daily life
  activities?
  4. As a student teacher, what those instruments will help you in teaching
  and learning process?
  

  6.1. Introduction to optical instruments and their image formation
  
  

  Activity 6.1

  
  Task 1
  i. What objects (things) do you see in the classroom?
  ii. Move outside class and observe the kind of objects there, and write
  down at least five of them.
  iii. Look at the distant objects. Are you able to examine the objects in a
  more detailed manner? Do you think you can be able to see these
  objects at night?
  iv. When they are an eclipse, it’s recommended to use some devices to
  observe it.
  a). What are devices can you use to observe clearly that eclipse
  when it happened?
  b). How can you take a photo of that eclipse?

  TASK 2
  i. Hold a hand lens at above the word Rwanda at a distance of about
  4cm from the word.
  ii. Move the lens farther away slowly from the word while observing the
  word through the lens.
  iii. What changes do you notice after observing?
  iv. write your observation in your notebook.
  v. Compare the size of the word and the image of that word Rwanda.

  Task 3
  i. Have you ever heard or seen an instrument called a compound
  microscope? What is it used for?
  

  
  

  ii. Observe the above pictures carefully and discuss places where
  a compound microscope is used in daily life.
  iii. You are provided with two lenses of focal lengths 5cm and 10cm
  together with a half meter ruler and some plasticine.
  a). Arrange the lenses as shown in the figure below.
  

  
  

  b). Move the object until it appears in focus. What do you notice about the image? Is it distorted? Is it coloured differently in any way?`

  We use our eyes to see and view different objects. The eye cannot be used to view clearly these objects at night, and some distant objects or hidden objects. Objects which cannot be viewed by the eye can be focused using other instruments. All the instruments used to aid vision are called Optical instruments.

  When the lenses or mirrors or both are arranged in a way, the arrangement can be used to observe objects in a more detailed manner. The arrangement makes what we call a compound optical instrument. The compound instruments include a compound microscope, telescopes, prism binoculars etc.

  6.1.1. Image formation by a camera, simple and compound microscope

  1. Lens camera

  The image is upside down. The pin hole helps you to see the image of the object. This device is called a pin hole camera.

  We have already seen that when an object is beyond 2F of a thin converging lens, the image formed is smaller than the object.

  A camera consists of a light- tight box with a convex (converging) lens at one end and the film at the other end. It uses the convex lens to form a small, inverted, real image on the film at the back.
  

  
  

  The lens focuses light from the object onto a light sensitive film. It is moved to and fro so that a sharp image is formed on the film. In many cameras, this happens automatically. In cheaper cameras, the lens is fixed and the photographer moves forwards and backwards to focus the object.
  The diaphragm is a set of sliding plates between the lens and the film. It
  controls the aperture (diameter) of a hole through which light passes.

  In bright light, a small aperture is used to cut down the amount of light reaching the film and in dim light, a large hole is needed. Very large apertures give blurred images because of aberrations

  So the aperture has to be reduced to obtain clear images.

  In many cameras, the amount of light passing through the lens can be
  altered by an aperture control or stop of variable width. This size of the hole is marked in f – numbers i.e 1.4, 2, 2.8, 4,5.6, 8, 11, 16, 22, 32. Defined as
  

  Where is the focal length of the lens and D is the diameter of the lens
  opening.
  The smaller the f-number, the larger the aperture. An f-number of 4 means the diameter d of the aperture is ¼ the focal length, f of the lens. To widen the aperture, the f number should therefore be decreased.

  The aperture also controls the depth of field of the lens camera. The depth of field is a range of distances in which the camera can focus objects simultaneously. This depth of field is increased by reducing the aperture.
  This large depth of field ensures a large depth of focus. The depth of focus is the tiny distance the film plane can be moved to or from the lens without defocusing the image. A large depth of focus means that both near and far objects appear to be in focus at the same time which is obtained by a small hole in the diaphragm.

  The shutter controls the exposure time of the film. It opens and closes quickly to let a small amount of light into the camera.

  The exposure time affects the sharpness of the image. When the exposure time is short, the image is clear (sharp) but when it is long the image becomes blurred.

  The film: This is where the image is formed. It is kept in darkness until
  the shutter is opened. It is coated with light sensitive chemicals which are changed by the different shades and colours in the image. When the film is processed, these changes are fixed and the developed film is used to print the photograph.

  Note that a diminished image is always formed on the film and that the image of distant object is formed on a film at distance f from the lens. For near objects, the lens is moved further away from the film (closer to the object) to obtain a clear image. In this case, the film is at a distance greater than f of the lens.

  2. Simple Microscope (Magnifying Glass)
  The word Rwanda becomes larger and larger and finally disappears. This
  word gets larger because of the lens. We say that it is being magnified by
  the lens.

  Notice that the hair (fur) and other small holes on the skin are seen clearly.

  These parts of the skin are made bigger by the glass lens and this enables one to see them clearly. This lens which magnifies images is called a magnifying glass or a simple microscope.

  A magnifying glass consists of a thin converging lens and it is used to view very small organisms or parts of organisms which cannot be easily seen by the naked eye.

  It has to be held at the right distance between the eye and the object for the object to be in focus.A magnifying glass, the convex lens bends the parallel rays so that they converge and create a virtual image on your eyes’ retinas.

  Formation of images by a magnifying glass
  We have already seen that when an object is between the lens and its
  principal focus, the image formed is magnified and upright. So, a magnifying glass forms a virtual, upright, magnified image of an object placed between the lens and its principal focus.

  The image is at the least distance of vision since the eyes are not strained
  and the magnifying glass is said to be in normal adjustment.

  A microscope is in normal adjustment if the final image is formed at the near point, and it is not in normal adjustment if the final image is at infinity.
  

  
  

  3. The compound microscope and its images formation
  The compound microscope is used to detect small objects; is probably
  the most well-known and well-used research tool in biology. In daily life,
  microscopes are used in hospitals, in biology laboratories

  By arranging the lenses as above, you have actually made a compound
  microscope.

  We have already seen how a single lens (magnifying glass) can be used to
  magnify objects.

  However, to give a higher magnifying power, two lenses are needed. This
  arrangement of lenses makes a compound microscope. It produces a
  magnified inverted image of an object.
  

  A compound microscope is used to view very small organisms that cannot be seen using our naked eyes for example micro organisms.
  

  
  

  A compound microscope consists of two convex lenses of short focal lengths referred to as the objective and the eye piece. The objective is nearest to the object and the eye piece is nearest to the eye of the observer.

  The object to be viewed is placed just outside the focal point (at a distance just greater than the focal length) of the objective lens. This objective lens forms a real, magnified, inverted image at a point inside the principal focus of the eye piece.

  This image acts as an object for the eye piece and it produces a magnified virtual image. So the viewer, looking through the eye piece sees a magnified virtual image of a picture formed by the objective i.e of the real image.

  Image formation in a compound microscope
  

  
  

  Application activity 6.1
  1. In groups, discuss the differences and similarities between the lens
  camera and the human eye.

  2. (i) Make a paper box and carefully use a pin to make a tiny hole in the
  centre of the bottom of the paper box.
  (ii) Place a piece of wax paper on the open end of the box. Hold the
  paper in place with the rubber band.
  (iii) Turn off the room lights. Point the end of the box with a hole in a
  bright window.
  (iv) Look at the image formed on the wax paper. Which kind of image
  have you seen? Is it upside down or right side up. Is it smaller or
  larger than the actual object? What type of image is it?

  3. (i) Carefully place a magnifying glass above some prints on a piece
  of paper and adjust it until they are seen clearly.
  (ii) Make sure that you don’t feel any strain in the eye while you are
  observing.
  (iii) What do you think is the position of the image from the eye?
  Explain your reason
  (iv) Explain when the microscope can be in normal adjustment

  4. Research on other types of optical instrument and the formation of
  their images

  6.2. Magnifying power of optical instruments and its Calculation

  Activity 6.2

  
  1. What do you understand by the term magnification of an optical
  instrument?
  2. Research how to make a magnification of camera, projector,
  microscope and telescope.

  6.2.1. Magnifying power of a simple microscope
  We have already seen that the size of the image depends on the angle
  subtended by the object on the eye called the visual angle. Thus, the
  magnifying power depends on the visual angle.
  

  It is defined as the ratio of the angle subtended by the image to the lens to the angle subtended by the object at the near point N of the eye.
  

  
  

  We can write M in terms of the focal length by noting that θ = h N ( fig. 6.7
  (a)) and (Fig. 6.7 (b)), where h is the height of the object and we assume the angles are small so θ' and θ equal their sines and tangents. If the eye is relaxed (for least eye strain), the image will be at infinity and the object will be at infinity and the object will be precisely at the focal point.

  
  We see that the shorter the focal length of the lens, the greater the
  magnification.
  

  
  

  The magnification of a given lens can be increased a bit by moving the lens and adjusting your eye so that it focuses on the image at the eye’s near point. In this case, if your eye is very near the magnifier. Then the object distance is given by:

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

  
  

• UNIT 7: PROPAGATION OF MECHANICAL WAVES

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

• UNIT 8: COMMON DISEASES AND HYGIENE

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

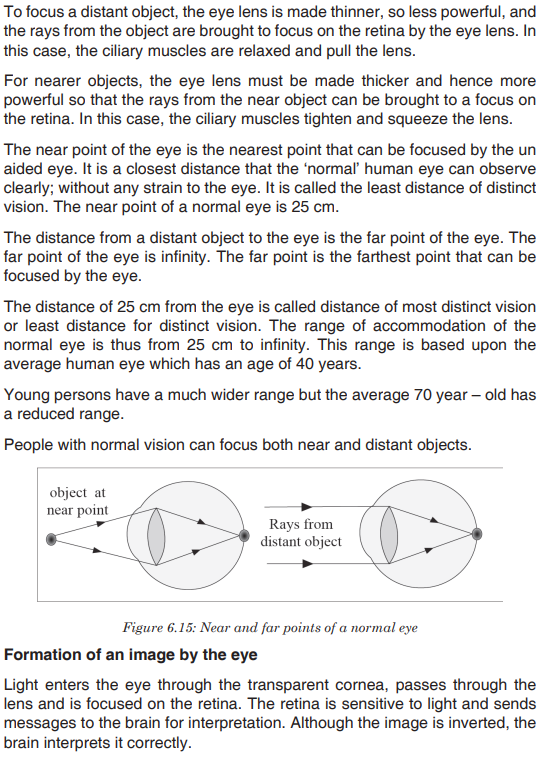
• UNIT 9: 239 MICROSCOPE AND CELL STRUCTURE

  Key Unit competence: Describe the structure and function of cells in an organism.

  Introductory Activity

  Observe the following images and answer the asked questions
  

  
  

  1. Name the illustrations in A) and B) above
  2. What are the use of illustrated materials in a)? Where are they used?
  3. Predict what you are going to learn in this unit
  

  9.1. Cell theory and microscopes

  Activity 9.1

  Carefully, analyze the following diagram and answer the related questions
  

  
  

  This is one of materials used in Biology.
  a). Have you ever seen and manipulate it?
  b). Observe the parts of the material, discuss and group them into the
  following:
  i. Supporting parts
  ii. Magnifying parts
  iii. Adjusting parts
  iv. Lighting parts
  c). Point out scientific activities that require the use of this material in
  biology.
  

  
  

  9.1.1. Cell theory
  Cytology is the study of the structure and function of cells. A Cell is the
  basic unit of life surrounded by a cell membrane and containing organelles.
  All living organisms are made of cells and nothing less than a cell can truly
  be said to be alive. The word cell comes from the Latin cellula, meaning
  a small room or cubicle, and was first used by Robert Hooke in his book
  Micrographia, published in 1665. Hooke was observing slides of cork taken
  from the bark of an Oak tree under the compound microscope. He decided
  that the slides were made up of a lot of many small chambers that he called
  cells that range in size are from 1μm – 1mm.
  Living organisms are classified into unicellular organisms made by only one
  cell, such as bacteria, whereas animals and plants are composed of many
  millions of cells built into tissues and organs. They are called multicellular
  organisms. In a multicellular organism, cells divide and thereafter they
  undergo differentiation or specialisation for specific functions.
  In biology, the historic scientific theory of cells is called cell theory. The cell
  theory states that all living organisms are made up of cells, and cells are the
  basic unit of structure function in all living organisms. The main principles
  of cell theory is that all known living organisms are made up of one or more
  cells, all cells come from pre-existing cells by division and cells contain the
  hereditary information that is passed from cell to cell during cell division.
  

  
  

  9.1.2. Microscopes: Compound-light microscope and Electron microscopes
  Microscopy is the technical field of using microscopes to view objects and
  areas of objects that cannot be seen with the naked eye. The microscope
  was created by Zacharias Janssen in the late 16th century Prior to the invention

  of the microscope, the details of objects on slides were
  limited. Single microscopes were similar to using a magnifying glass such as
  hand lens. The invention of the light microscope in the 17th century by Antony
  van Leeuwenhoek made cells visible for the first time and, for hundreds of
  years afterwards. Electron microscope invented in the 1930s enables the
  researchers to see very small organelles which cannot be seen by using
  light microscopes. The purpose of the use of a microscope is to magnify
  small objects such as cells or to magnify the fine details of a larger object in
  order to examine minute specimens that cannot be seen by the naked eye.
  

  a. Compound Light Microscope
  The optical microscope, often referred to as light microscope is a type of
  microscope which uses visible light and a system of lenses to magnify
  images of small samples.
  

  
  

  
  

  The parts of light microscope and their roles:
  • Base: Supports and stabilizes the microscope on the table or any other
  working place.
  • Light source: It is made by lamp or mirror which provides light for
  viewing the slide.
  • Stage: Is a platform used to hold the specimen in position during
  observation.
  • Stage clips: Are pliers used to fix and hold tightly the slide on stage.
  • Arm: Supports the body tube of microscope
  • Body tube: maintains the proper distance between the objective and
  ocular lenses
  

  • Arm: Used for holding when carrying the microscope and it holds the
  body tube which bears the lenses.
  • Coarse focus adjustment: Moves stage up and down a large amount
  for coarse focus
  • Fine focus adjustment: Moves stage up and down a tiny amount for
  fine focus
  • Objective lenses: Focuses and magnifies light coming through the slide
  • Revolving nosepiece: Rotates to allow use of different power objectives
  • Slide: Is a transparent pane on which a specimen is placed.
  • Eye piece/ocular lens: Magnifies image produced by objective lens
  • Condenser: It will gather the light from the illuminator and focus it on
  the specimen lying on the stage. The function of the condenser is to
  focus the light rays from the light source onto the specimen.
  • Iris diaphragm lever: This allows the amount of light passing through
  the condenser to be regulated to see the object.
  All parts of a microscope work together to magnify a specimen to be observed.
  Light from the source is focused on the specimen by the condenser lens. It
  then enters the objective lens, where it is magnified to produce a real image.
  The real image is magnified again by the ocular lens to produce a virtual
  image that is seen by the eye.
  

  Advantages and limitations of the light microscope
  Magnification: Most light microscopes can magnify a specimens up to a
  maximum of X1500.
  Resolution: It is the degree at which it is possible to distinguish clearly
  between two objects that are very close together. It is the smallest distance
  apart that two separate objects can be seen clearly as two objects. The
  resolution for the:
  • Human eye is 100μ.
  • Light microscope is 200 nm.
  • Electron microscope is 0.20 nm.
  The maximum resolution of the light microscope is 200 nm. This means
  that if two objects are closer together than 200 nm, they will be seen as
  one object. The light microscopes are used widely in education, laboratory
  analysis and research. But because they do not have high resolution, they
  cannot give detailed information about internal cell structure.
  

  Specimens: a wide range of specimens are viewed using the light microscope.
  These include: unicellular organisms, small sections from large plants and
  animals, and smear preparation of blood or cheek cells.
  Preparation of specimens for the light microscope
  A lot of biological materials are not coloured, so you cannot see details. Also,
  some material distorts when you try to cut it into thin sections. Preparation of
  slides to overcome these problems involves the following steps:
  a) Staining: Coloured stains are chemicals that bind on or in the specimens.
  This allows the specimens to be seen. Some stains bind to specific cell
  structures. For example, acetic orcein stains DNA dark red, while gentian
  violet stains bacterial cell walls.
  b) Sectioning: Specimens are embedded in wax, where thin sections are
  then cut without distorting the structure of the specimen. This is particularly
  useful for making sections of soft tissue, such as brain. Safety measures
  might be taken. Make sure that hands are washed with soap and warm
  water after the experiment. Use a disinfectant to wipe down all surfaces
  where bacteria mayhave been deposited for example. Be sure that some
  substances and animals might be harmful to the life.
  

  Measuring cells

  Cells and organelles can be measured with a microscope by means of an
  eyepiece called graticule. This is a transparent scale, usually having 100
  divisions (Figure 9.2, A). The eyepiece graticule is placed in the microscope
  eyepiece so that it can be seen at the same time as the object to be measured
  (Figure 9.2, B). At this figure (Figure 9.2, B), the cell lies between 40 and 60
  on the scale, so that it measures 20 eyepiece units in diameter (60- 40 = 20).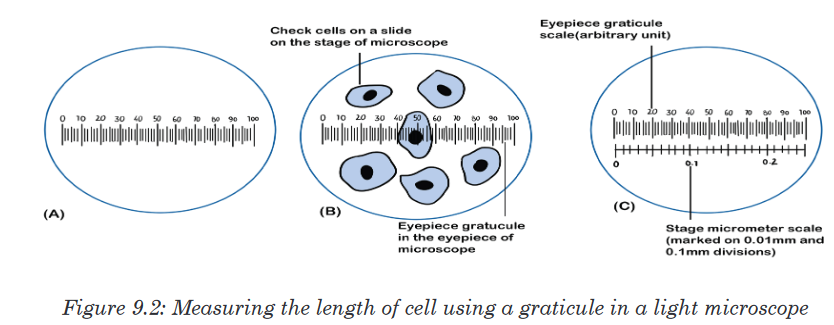
  

  
  

  
  

  Note that it is not possible to know the actual size of the eyepiece units
  until the eyepiece graticule scale is calibrated. To calibrate the eyepiece
  

  graticule scale, a miniature transparent ruler called a stage micrometre scale
  is placed on the microscope stage and is brought into focus. This scale may
  be fixed onto a glass slide or printed on a transparent film. It commonly
  has subdivisions of 0.1 and 0.01 mm. The images of the two scales can
  then be superimposed (Figure 9.2, C). If in the eyepiece graticule, 100 units
  

  measure 0.25 mm, the value of each eyepiece unit equals
  

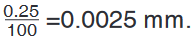
  By converting mm to μm, the value of eyepiece equals
  

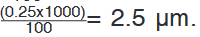
  The diameter of the cell shown superimposed (Figure 9.2, B) measures
  20 eyepiece units. Its actual diameter equals 20 × 2.5 μm = 50 μm. This
  diameter is greater than that of many human cells because the cell is a
  flattened epithelial cell.
  There is a relationship between the actual size, magnification and image
  size, where:
  Actual size = image size/ magnification.
  Magnification = image size/ actual size.
  Image size = Magnification x actual size.
  

  b. Electron microscope
  

  An electron microscopes use a beam of accelerated electrons as a source
  of illumination. Electron beams have a much smaller wave length of 0.004
  nm, 100 000 times shorter than light wavelength, and therefore have greater
  resolving powers and can produce higher effective magnifications than light
  microscopes. Electron microscopes are used to study the details of internal
  structures (the ultrastructure’s) of cells. Most modern TEMs can distinguish
  objects as small as 0.2nm. This means that they can produce clear images
  magnified up to 500,000 times greater than that of the human eye.
  There are two types of electron microscopes:
  • Transmission electron microscope (TEM).
  • Scanning electron microscope (SEM)
  

  i. Transmission electron microscope (TEM)

  
  

  
  

  • The electron beam passes through a very thin prepared sample.
  • Electrons pass through the denser parts of the sample less easily,
  so giving some contrast.
  • The final image produced is two-dimensional.
  • The magnification possible with a TEM is X500 000.
  

  ii. Scanning electron microscope (SEM)

  
  

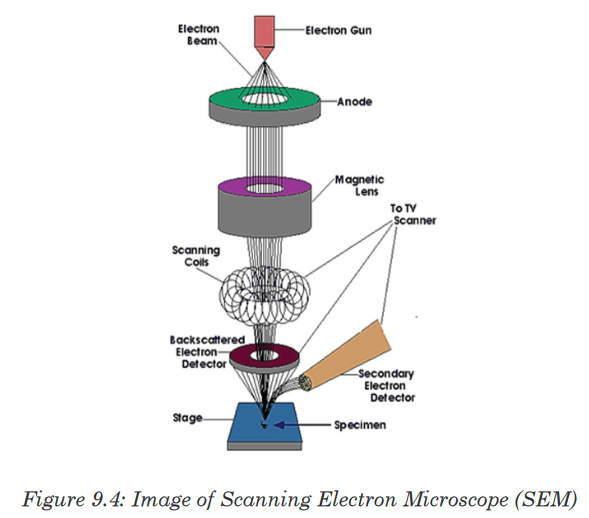
  • The electron beam is directed onto a sample. Electrons do not pass
  through the specimen.
  • They are bounced off the sample.
  • The final image produced is a three-dimensional.
  • The magnification possible with an SEM is about X100 000.
  

  Advantages and disadvantages of the electron microscope
  a. Advantages of electron microscope

  Light microscope has a higher resolution and are therefore able of a higher
  magnification estimated up to 2000 X more than in the light microscope.
  Electron microscopes therefore allow for the visualization of too small
  structures, such as cell organelles that would normally be not visible by
  optical microscopy. The SEM produces a 3D images that can reveal the
  detail of cellular and tissue arrangement. This is not possible by using light
  microscopes.
  

  
  

  b. Disadvantages of electron microscope

  Despite the advantages, electron microscope presents a number of
  disadvantages and limitations.
  • These type of microscope are extremely expensive and the maintenance
  costs are high.
  • Samples must be completely dry so that it is impossible to observe
  living specimens and moving specimens (they are dead).
  • It is not possible to observe colours because electrons do not possess
  a color. The image is only black-white images/ grey images.
  • The energy of the electron beam is very high, the sample is therefore
  exposed to high radiation, and therefore not able to live.
  • The space requirements are high, so that they may need a whole room.
  • Electron beams are deflected by molecules in air, so samples have to
  be placed in a vacuum.
  

  Application activity 9.1

  1. Make a comparison between light and electron microscope, highlighting
  the advantages and disadvantages for each type of microscope.
  2. Discuss the advantages and disadvantages (limitations) of an electron
  microscope.
  3. Calculate the magnification of an image measuring 50mm, while the
  object measures 5μm.
  

  4. If a nucleus measures 100mm on a diagram, with a magnification of
  X10 000, what is the actual size of the nucleus?
  5. Complete the table below:
  

  
  

  6. What is the importance of a light microscope?
  7. How can you apply microscope technique rules?
  8. Discuss the advantages and disadvantages of the types of electron
  microscopes in medicine and biology research.
  9. Make a comparative study between light and electron microscope
  focussing on the advantages of each type of microscope.
  

  9.2. Eukaryotic and Prokaryotic cells

  Activity 9.2

  With microscope, observe mounted slides of bacteria, and plant cells.
  Draw and label the parts that are common in both plant and bacterial
  specimens
  

  Eukaryotic cells contain membrane-bound organelles, including a true
  nucleus enclosed in a nuclear envelope. They include cells of: plants,
  animals, fungi and protoctista.
  

  
  

  
  Prokaryotes are organisms having cells with no true nuclear envelope.
  Prokaryotic cells do not contain a nucleus or any other membrane-bound
  organelle. Prokaryotes include bacteria and blue-green algae. They make
  up the monera kingdom.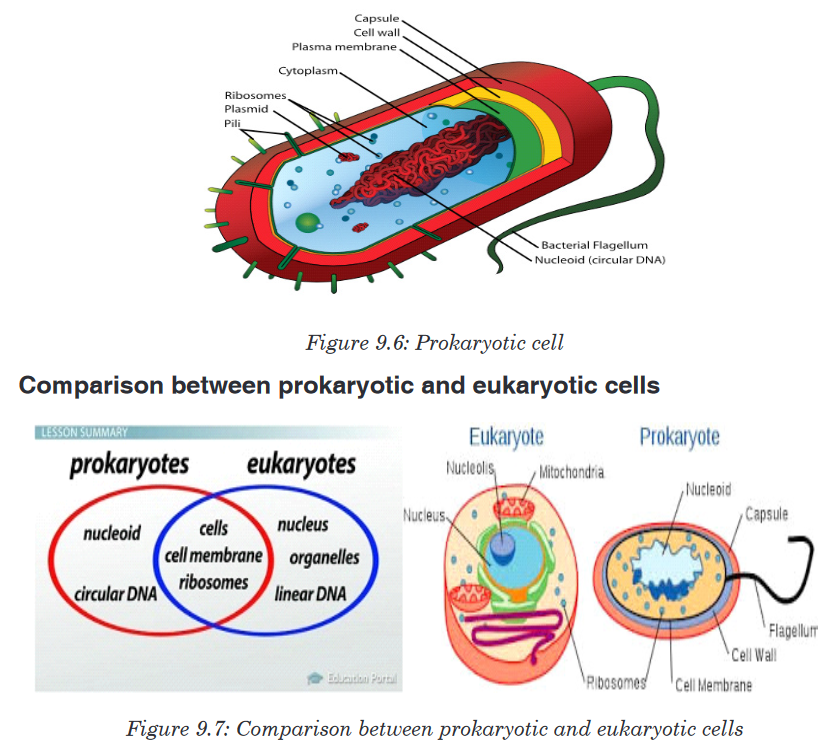
  

  
  

  
  

  
  

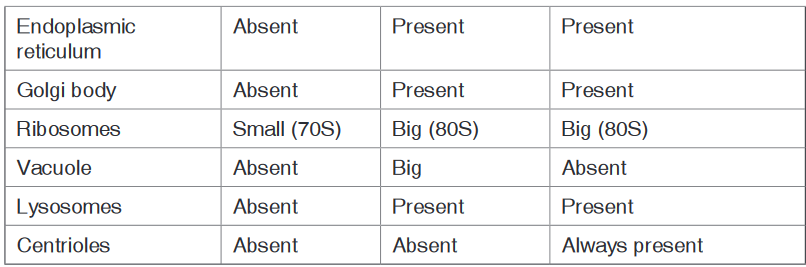
  Application activity 9.2

  1. Define a prokaryote and eukaryote.
  2. In a form of a table differentiate prokaryotic cells from eukaryotic cells.
  

  9.3. Plant and animal cells

  Activity 9.3

  Observe two electron photographs, one containing a plant cell another
  an animal cell.Record a description of their features, such as shape and
  internal parts.
  

  When viewed under light microscope, the most obvious features observed
  are the very large nucleus and a clear cytoplasm surrounded by a cell
  membrane. However, under electron microscope, it is possible to identify a
  range of organelles in plant and animal cells.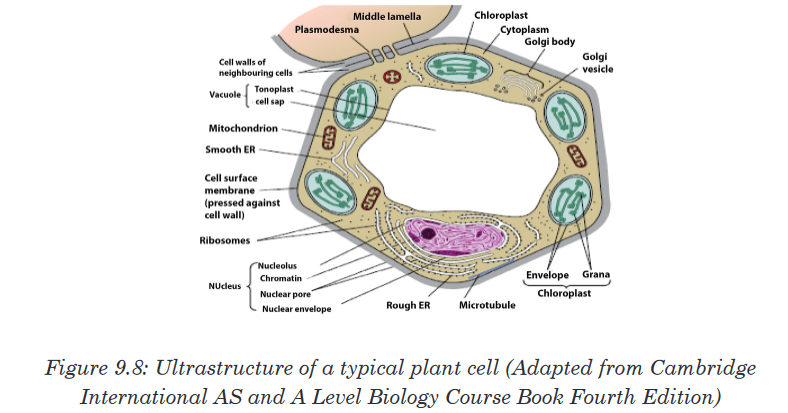
  

  
  

  
  

  Ultrastructure of a plant cell contains different parts like cell wall, cell
  membrane, cytoplasm with organelles. Organelles found in the cytoplasm of
  a plant cell include: chloroplast, mitochondria, Golgi apparatus, endoplasmic
  reticulum, ribosomes, big central vacuole, and the nucleus which contains
  chromosomes. The plant cell also has a regular shape, with a relatively
  bigger size than animal cell.
  

  
  

  
  

  Ultrastructure of an animal cell contains different parts like cell membrane,
  cytoplasm with organelles. Organelles found in the cytoplasm of an animal
  cell include: mitochondria, Golgi apparatus, endoplasmic reticulum,
  centrioles, ribosomes, small or absent vacuole, and the nucleus which
  contains chromosomes. The animal cell also has irregular shape, with a
  relatively smaller size than a plant cell.
  

  Application activity 9.3

  1. Describe the structure of:
  a). Animal cell and
  b). Plant cell
  

  9.4. Organelles and their functions

  Activity 9.4

  Under microscope, observe animal cell and plant cells. Explain the
  functions on all structures of both animal cell and plant cell.
  

  The previous sections described the structures of plant and animal cells.
  This unit will explain the function of each part of both animal cell and plant
  cell.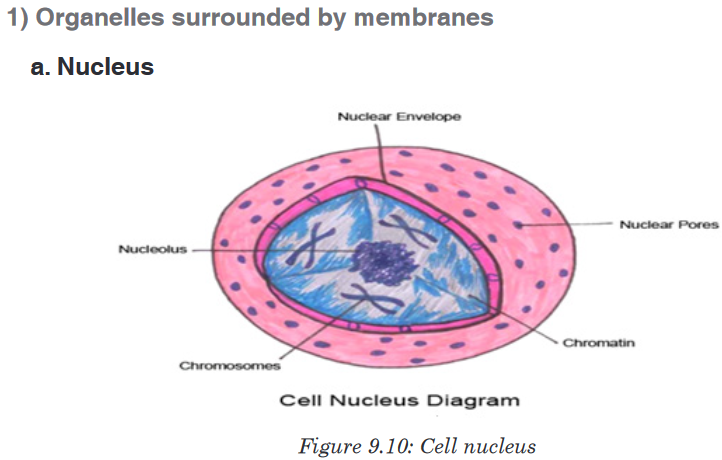
  

  
  

  
  

  The cell nucleus contains nearly all the cell’s DNA with the coded instructions
  for making proteins and other important molecules. The nucleus is surrounded
  by a double nuclear envelope, which allow materials to move into and out
  of the nucleus through nuclear pores. The granules found in the nucleus
  are called chromatin which consist of DNA bound to protein. When a cell
  divides, the chromatin condenses into chromosomes containing the genetic
  information that is passed from parents to their offspring. The nucleus
  contains a dense spherical structure called nucleolus in which assembly of
  ribosomes begins. The nucleus controls all activities of the cell.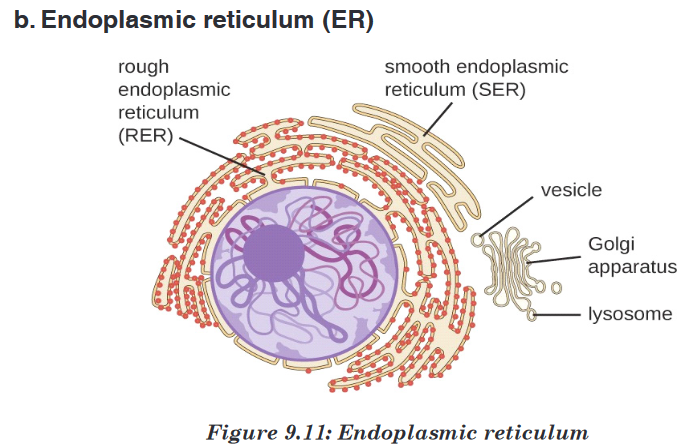
  

  
  

  The ER consists of a series of flattened membrane-bound sacs called
  cisternae. The rough ER is surrounded with ribosomes. The rough ER
  transports proteins made on attached ribosomes. The smooth ER does not
  have ribosomes, and it involves in making lipids that the cell needs.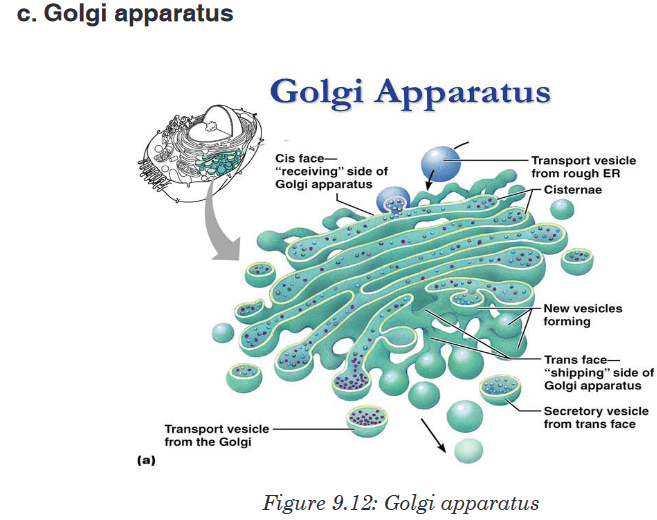
  

  
  

  The Golgi apparatus is a stack of membrane-bound, flattened sacs, which
  receives proteins from the ER and modify them. It may add sugar molecules
  to them. The Golgi apparatus then packages the modified substances into
  vesicles that can be transported to their final destinations throughout the cell
  or outside of the cell.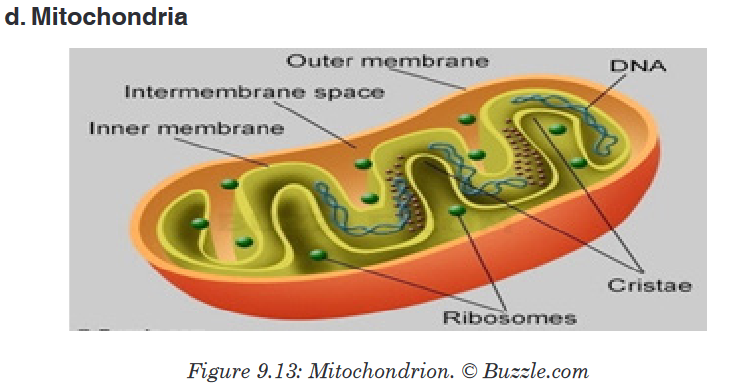
  

  
  

  Mitochondrion have two membranes separated by a fluid-filled space.
  The inner membrane is highly folded to form cristae. The central part of
  the mitochondrion is called matrix. The mitochondria are the site where the
  process of cell respiration takes place to produce Adenosine triphosphate
  (ATP), a universal energy carrier to be used in cell metabolism.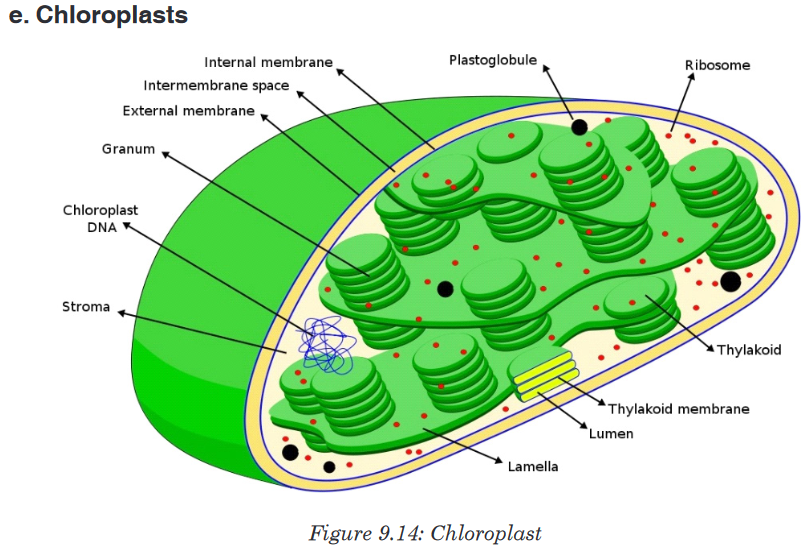
  

  
  

  Chloroplasts are the site of photosynthesis in plant cells. These are found in
  plant cells and in cells of some protoctists. They also have two membranes
  separated by a fluid-filled space. The inner membrane is continuous, with
  thylakoids. A stalk of thylakoids is called a granum (plural: grana). Chlorophyll
  molecules are present on the thylakoid membranes.
  

  
  

  These are spherical sacs surrounded by a single membrane. They contain
  powerful digestive enzymes. Their role is to break down materials such
  as white blood cells, and destroy invalid microorganisms. In acrosome,
  lysosomes help the sperm to penetrate the egg by breaking down the
  material surrounding the egg.
  

  
  

  Ribosomes are the site of protein synthesis in the cell. Some are in cytoplasm;
  others are bound to ER. Ribosomes consist of two major components (two
  subunits): the small ribosomal subunit, which reads the RNA, and the large
  subunit, which joins amino acids to form a polypeptide chain. Each subunit
  

  is composed of one or more ribosomal RNA (rRNA) molecules and a variety
  of ribosomal proteins (r-protein). Ribosomes act as an assembly line where
  coded information (mRNA) from the nucleus is used to assemble proteins
  from amino acids. Cells that are more active in protein synthesis are often
  packed with ribosomes.
  

  
  

  Centrioles are small tubes of protein fibres (microtubules), which are
  involved in animal cell division. They form fibres, known as spindle, which
  move chromosomes during nuclear division.
  

  
  

  A vacuole is a saclike structure that is used to store materials such as water,
  salts, proteins, and carbohydrates. In many plant cells there is a single, and
  large central vacuole filled with liquid. The pressure of central vacuole in
  this cells makes it possible for plants to support heavy structures such as
  leaves and flowers. Some animals and some unicellular organisms contain
  contractile vacuoles which contract rhythmically to pump excess water out
  of the cell.
  

  
  

  Cytoskeleton is a network of protein filaments that helps the cell to maintain
  its shape. It is also involved in in movement. The main components of
  cytoskeleton are microfilaments made of a protein called actin, microtubules
  made of a protein called tubulins, and intermediate filaments.
  Definitely, a cell has many organelles with different functions and work
  together for the survival of the cell.The structure of the cell membrane is
  based on fluid mosaic model. The term fluid mosaic is used to describe
  the molecular arrangements in membranes. The main features of the fluid
  mosaic model are:
  • A bilayer of phospholipid molecules forming the basic structure.
  • Many protein molecules floating in the phospholipid bilayer. Some are
  free, others are bound to other components or to structures within the
  cell.
  • Some extrinsic proteins are partially embedded in the bilayer on the
  inside or the outside face while other intrinsic proteins are completely
  spanning the bilayer.
  

  
  

  The basic structure of phospholipids has two parts: hydrophilic part which
  means water loving and which consists of the phosphate head, and
  hydrophobic part which means water hating and which consist of fatty acids.
  If phospholipid molecules are completely surrounded by water, a bilayer can
  form phosphate heads on each side of the bilayer stick into water, while the
  hydrophobic fatty acid tails point towards each other.
  Types of protein found in the cell membrane
  Various types of proteins are found in the cell membrane. They include:
  • Carrier proteins: They fix or attach molecules and facilitate them to
  cross through the cell membrane by active transport.
  • Channel proteins: they act as pores by pumping substances and allow
  facilitated diffusion.
  • Receptors: They act as receptors of enzymes and neurotransmitters
  • Glycoproteins: They act as receptor proteins which recognize the
  substance to pass through the membrane
  • Integrated proteins: They define the shape of the cell
  • Immune proteins (antigens): found in the membrane on the red blood
  cell, they recognize the antibodies.
  Roles of different components of cell membrane
  a). Cholesterol
  • Gives the membranes of some eukaryotic cells the mechanical stability.
  • It fits between fatty acid tails and helps make the barrier more complete,
  so substances like water molecules and ions cannot pass easily and
  directly through the membrane.
  b). Channel proteins
  • Allow the movement of some substances across the membrane.
  • Large molecules like glucose enter and leave the cell using these
  protein channels.
  c). Carrier proteins
  • Actively move some substances across the cell membrane. For
  example, magnesium and other mineral ions are actively pumped into
  the roots hair cells from the surrounding soil.
  • Nitrate ions are actively transported into xylem vessels of plants
  d). Receptor sites
  • Allow hormones to bind with the cell so that a cell response can be
  carried out.
  

  • Glycoproteins and glycolipids may be involved in cells signaling that
  they are self to allow recognition by the immune system.
  • Some hormone receptors are glycoprotein and some are glycolipid.
  e). Enzymes and coenzymes
  • Some reactions including metabolic processes in photosynthesis take
  place in membranes of chloroplasts.
  • Some stages of respiration take place in membranes of mitochondria,
  where Enzymes and coenzymes may be bound to these membranes.
  • The more membrane there is, the more enzymes and coenzymes it
  can hold and this helps to explain why mitochondrial inner membranes
  are folded to form cristae, and why chloroplasts contain many stacks of
  membranes called thylakoids.
  Properties of the cell membrane
  • It is mainly made of lipids, proteins and carbohydrates.
  • It is semi-permeable or partially permeable and allow some substances
  to pass through but prevents others to cross depending on their size,
  charges and polarity.
  • It is positively charged outside and negatively charged inside and has
  a hydrophilic pole and a hydrophobic pole
  • It is a bilayer, sensitive, flexible, has inorganic ions and its proteins
  and lipids may be mobile and contains different types of enzymes and
  coenzymes.
  • It is perforated of pores and recognizes chemicals messengers
  including hormones and neurotransmitters.
  Functions of a cell membrane
  • The cell membrane acts as a selective barrier at the surface of the cell,
  and controls the exchange between the cell and its environment.
  • The membrane proteins act as pores where chemicals pass through.
  • Glycocalyx including glycoprotein and glycolipid are involved in the cell
  protection, the process by which cell adhesions are brought about and
  also in the uptake and entry of selected substances.
  Comparison between animal and plant cell
  By referring to the diagrams which show the structure of animal cell and
  plant cell, similarities and differences between animal cell and plant cell can
  be identified.
  

  Similarities between animal cell and plant cell
  • Both animal and plant cells have a cell membrane, a cytoplasm and a
  nucleus.
  • Both animal and plant cells have a true nucleus bounded by an
  envelope.
  • Both animal and plant cells have mitochondria, Golgi apparatus,
  Reticulum endoplasmic, lysosome, big ribosomes (80S), peroxisome,
  microtubules.
  • The protoplasm is enveloped by a bounding cell membrane called
  plasmalemma.
  • The protoplasm is composed of a dense round structure called nucleus
  which is surrounded by a less dense jelly-like cytoplasm.
  • The cytoplasm contains numerous organelles such as mitochondria,
  Golgi bodies, secretory vacuoles, endoplasmic reticulum.
  • Mitochondria appear as very small darkly staining, rod-like structures.
  • Golgi bodies are semi-transparent irregular, and membrane bound
  structures.
  • Vacuoles contain secretions, food- particles, or decomposing organic
  substances.
  • Chemically, both plant and animal cells are made up of water (80-90%),
  proteins (7-13%), lipids (1-2%), carbohydrates (1-1.5%) and inorganic
  salts.
  • The cytoplasmic organelles are suspended in a semi-fluid jelly matrix
  called cytosol.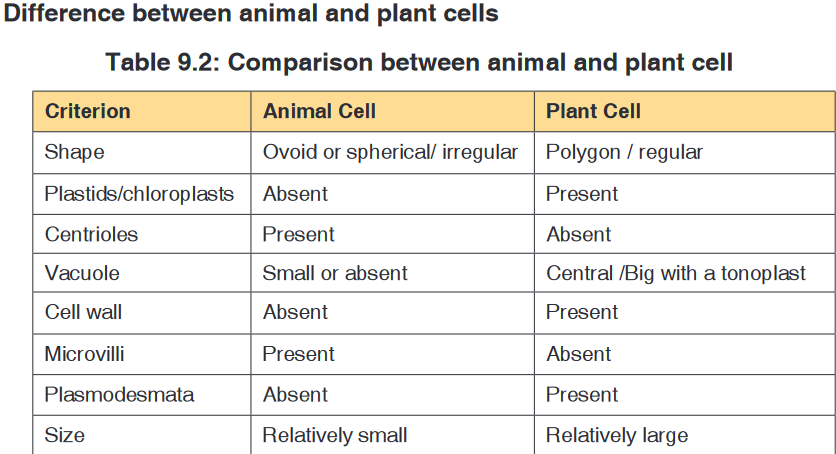
  

  
  

  Application activity 9.4

  1. What is meant by the fluid mosaic model of the cell membrane?
  2. State the properties of the cell membrane.
  3. Discuss at least 4 types of the proteins in the cell membrane and their
  roles.
  4. What does partially permeable membrane mean?
  5. Explain why muscle cells contain a lot of mitochondria, whereas most
  fat storage cells do not.
  6. What kind of information is contained in chromosomes?
  7. You examine an unknown cell under the microscope and discover
  that the cell contains chloroplasts. What type of organism could you
  decide that the cell came from?
  8. The diagram below shows the structures which would be visible in a
  plant cell examined under an electron microscope.
  

  
  

  a). Identify the parts labelled in this plant cell and:
  b). State one function for A,B, C, E,D,G, F, and H
  9. Explain two functions of the cytoskeleton?
  10. What structures do both animal and plant cells have in common?
  11. Answer by true or false:
  a). All organelles of a cell are well seen through a compound light
  microscope.
  b). Chloroplasts are found in both animal and plant cells.
  c). Mitochondria are found only in animal cells.
  

  9.5. Specialized cells

  
  

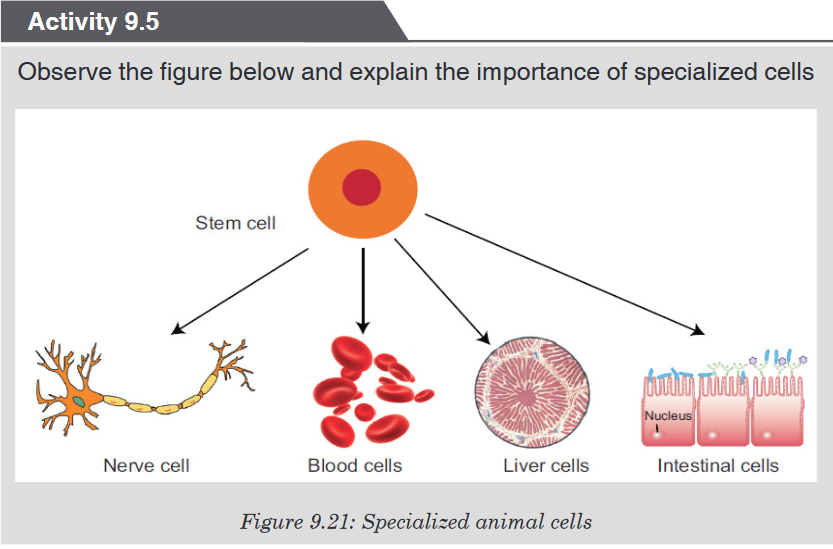
  9.5.1. Specialized animal cells and their functions

  Differentiation refers to the changes occurring in cells of a multicellular
  organism so that each different type of cell becomes specialised to perform
  a specific function.
  

  
  

  All blood cells are produced from undifferentiated stem cells in the bone
  marrow but the cells destined to become erythrocytes (red blood cells)
  lose their nucleus, mitochondria, Golgi apparatus and rough endoplasmic
  reticulum. They are packed full of the protein called haemoglobin. The shape
  

  of this cells change so that they become biconcave discs, and they are then
  able to transport Oxygen in the body.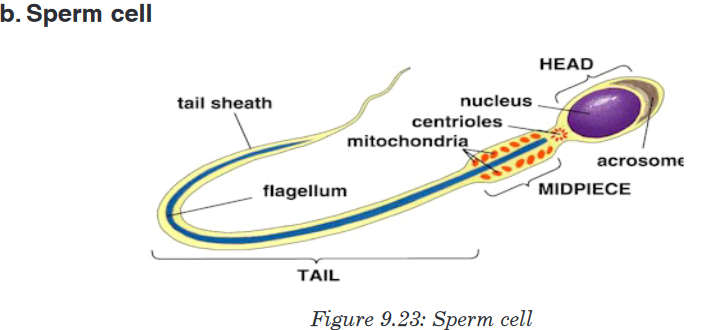
  

  
  

  Sperm cells are specialized to fertilize the egg. Its specialization involves
  many changes in shape and organelles content.
  By shape, the sperm cells are very small, long and thin to help them to move
  easily, and they have a flagellum which helps them to move up the uterine
  tract towards the egg.
  By organelles content, sperm cells contain numerous mitochondria
  which generate much energy for their movement. Their acrosome releases
  specialized lysosomes contains many enzymes on the outside of the egg.
  These enzymes lyse the wall of the egg, and facilitate the sperm nucleus to
  penetrate easily. In content, the sperm cell nucleus contains the half number
  of chromosomes of the germ cell in order to fulfil its role as a gamete of
  fertilizing the egg.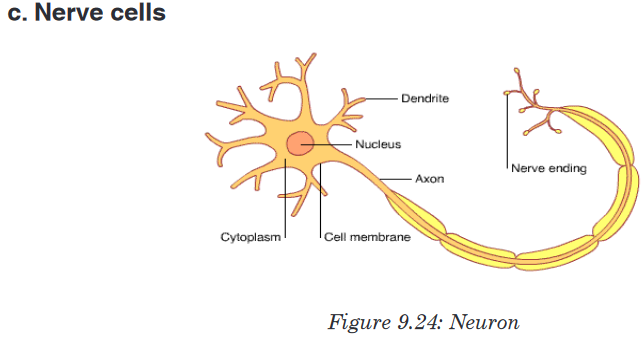
  

  
  

  Nerve cells also known as a neuron are specialized cells to carry nervous
  information in the body. It is an electrically excitable cell that receives,
  processes, and transmits information through electrical and chemical
  signals. These signals between neurons occur via specialized connections
  called synapses. Specialized animal cells have different functions. Some of
  them are summarized in the following table.

  

  

  9.5.2. Specialized plant cells and their functions

  
  

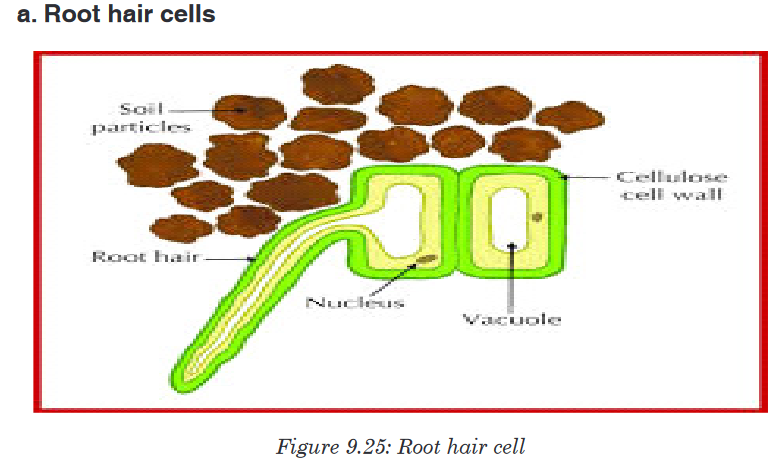
  The root hair cells have hair-like projection from their surface out into the
  soil. This increase the surface area of root available to absorb water and
  minerals from the soil. Root hairs are tip-growing cells that originate from
  epidermal cells called trichoblasts. Their role is to extend the surface area of
  the root to facilitate absorption of mineral nutrients and water.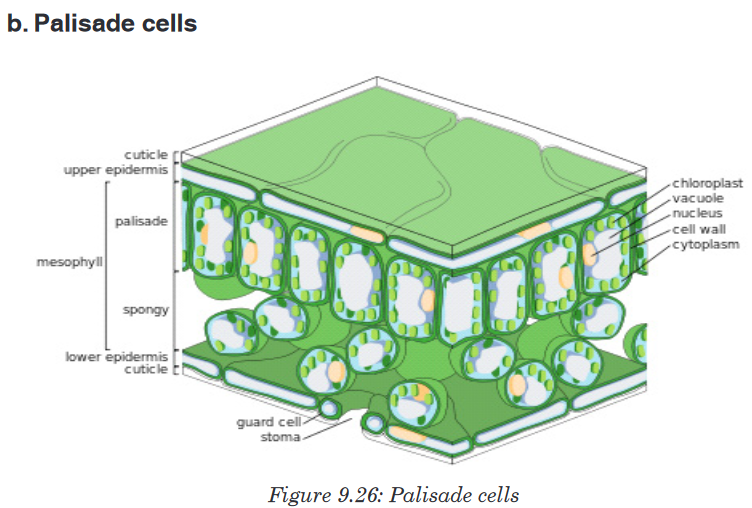
  

  
  

  Palisade cells are plant cells located in leaves, right below the epidermis
  and cuticle. They are vertically elongated, a different shape from the spongy
  

  mesophyll cells beneath them in the leaf. Their big number of chloroplasts
  allow them to absorb a major portion of the light energy used by the leaf in
  the process of photosynthesis.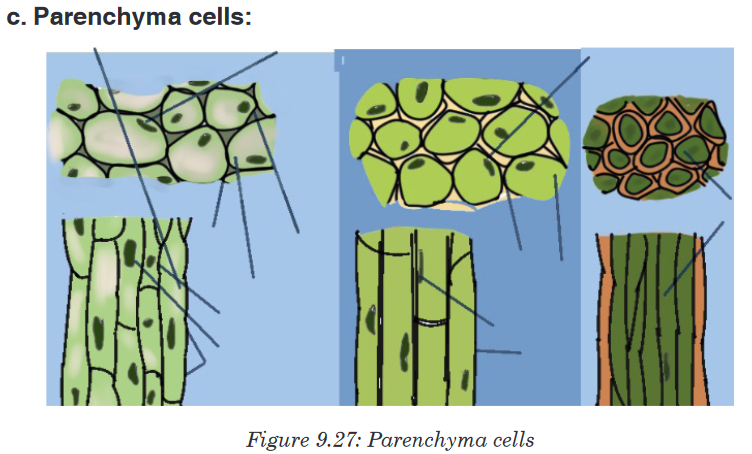
  

  
  

  Parenchyma cells are alive at maturity. They have function in storage,
  photosynthesis, and as the bulk of ground and vascular tissues. Palisade
  parenchyma cells are elongated cells located in many leaves just below the
  epidermis. Parenchyma is composed of relatively simple, undifferentiated
  parenchyma cells. In most plants, metabolic activity such as respiration,
  digestion, and photosynthesis occurs in these cells because they retain their
  protoplasts (the cytoplasm, nucleus, and cell organelles) that carry out these
  functions. Parenchyma cells are capable of cell division, even after they have
  differentiated into the mature form.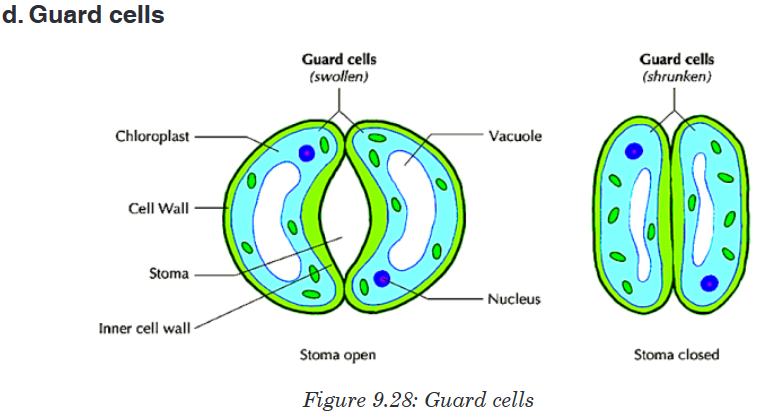
  

  
  

  Guard cells are cells surrounding each stoma. They help to regulate the
  rate of transpiration by opening and closing the stomata. Guard cells are
  specialized cells in the epidermis of leaves, stems and other organs that
  are used to control gas exchange. They are produced in pairs with a gap
  between them that forms a stomatal pore.
  

  Application activity 9.5

  1. Explain why differentiation to produce erythrocytes involves a change
  in shape.
  2. Red blood cells cannot divide as they have no nucleus. State two
  other biological processes that red blood cells cannot carry out.
  3. Describe how the following are specialized for their roles:
  a) Neutrophil
  b) Sperm cell
  c) Root hair cell
  4. Explain why photosynthesis is carried out in palisade mesophyll more
  than in spongy mesophyll.
  5. In what kinds of organisms’ cell specialization is a pronounced
  characteristic?
  6. Using what you know about the ways muscles move, predict which
  organelles would be most common in muscle cells.
  7. Discuss the advantages of cell specialization for living things
  

  Skills lab 9

  Take tissue cells from a rabbit and from a young leaf of a sweet potato.
  Prepare the slides containing those tissues. Observe them under the light
  microscope, and draw their structures on the paper and present to the class.
  

  End unit assessment 9

  Section A. Multiple choice questions
  1. Which organelle converts the chemical energy in food into a form that
  cells can use?
  a) Chromosome
  b) Chloroplast
  c) Nucleus
  d) Mitochondrion
  

  2. The cell membranes are constructed mainly of:
  a) Carbohydrate gates
  b) Protein pumps
  c) Lipid bilayer
  d) Free-moving proteins
  3. In many cells, the structure that controls the cell’s activities is the:
  a) Nucleus
  b) Nucleolus
  c) Cell membrane
  d) Organelle
  4. Despite differences in size and shape, all cells have cytoplasm and a
  a) Cell wall
  b) Cell membrane
  c) Mitochondria
  d) Nucleus
  5. If a cell of an organism contains a nucleus, the organism is a (an)
  a) Plant
  b) Eukaryote
  c) Animal
  d) Prokaryote
  6. Match each part of the cell to its correct statement:
  

  
  

  Section B: Questions with short answers
  1. How does a cell membrane differ from a cell wall?
  2. Name the structures that animal and plant cells have in common,
  those found in only plant cells, and those found only in animal cells.
  

  3. List:
  a) Three organelles each lacking a boundary membrane
  b) Three organelles each bounded by a single membrane
  c) Three organelles each bounded by two membranes (an envelope)
  4. Identify each cell structure or organelle from its description below.
  a) Manufactures lysosomes and ribosomes
  b) Site of protein synthesis
  c) Can bud off vesicles which form the Golgi body
  d) Can transport newly synthesized protein round the cell
  e) Manufactures ATP in animal and plant cells
  f) Controls the activity of the cell, because it contains the DNA
  g) Carries out photosynthesis
  h) Can act as a starting point for the growth of spindle microtubules
  during cell division
  i) Contains chromatin
  j) Partially permeable barrier only about 7 nm thick
  k) Organelle about 25 nm in diameter
  l) Which two organelles other than the nucleus contain their own
  DNA?
  Section C: Essay questions
  1. Describe the structure and function of the cell membrane and cell wall.
  2. Describe the basic structure of the cell membrane.
  3. Explain two common characteristics of chloroplasts and mitochondria.
  Consider both function and membrane structure.
  4. The diagram below shows the structure of a liver cell as seen using an
  electron microscope.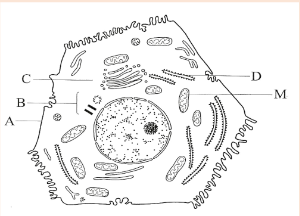
  

  
  

  a) Name the parts labelled A, B, C and D.
  b) The magnification of the diagram above is 12 000. Calculate the
  actual length of the mitochondrion labelled M, giving your answer
  in μm. Show your working.
  c) Explain the advantage to have a division of labor between different
  cells in the body.
  5. The diagram below shows the structure of a cell membrane. Observe
  carefully the diagram and answer the questions that follows:
  

  
  

  a) Name parts labelled A – D and give the function of the part B.
  b) State four factors that can affect diffusion across the cell membrane.
  6. What types of molecule are likely to be involved in?
  a) Cell signalling and recognition?
  b) Allowing small charged molecules to pass through the cell
  membrane?
  7. What is the difference between rough and smooth endoplasmic
  reticulum?
  8. The photograph in the figure below shows an organelle of the living
  cell.
  

  
  

  a). Name this organelle.
  b). What is the function of this organelle?
  

• UNIT 10:CELL AND NUCLEAR DIVISION

  Key Unit competence: Describe the stages of the cell cycle and

  explain the significance of cell and nuclear

  division in organisms

  Introductory Activity 10

  Observe the figure 10.1 of the house built in bricks below. The bricks came from the valley where they are made, and then have been used to build this house.
  
  
  Figure 10.1: A house in bricks
  1.    Is it possible to build a house like this by using only one brick?
  2.    Link the analogous example of building a house by using bricks with growth of and increasing in size of a human body from the body size of a one day new baby to the body size of 35 years person.
  3.    Is it possible for the body of a person to be made by only one cell?
  4.    Where are cells which make the human body come from?
  5.    How are they produced?

  10.1.   Cell cycle

  Activity 10.1

  The male and female gametes fuse to form a zygote and after the zygote goes through different phases and a baby is born.visit your smart classroom, and discuss more information about the main phases of the cell cycle.

  The cell cycle is a series of events of cellular growth and division that has

  five phases such as:

  •      The first growth phase (G₁),

  •      The synthesis phase (S),

  •      The second growth phase (G₂),

  •      Mitosis (M),

  •      Cytokinesis.

  The three first phases (G1, S, and G2) of the cell cycle collectively are known as interphase (the phase between two mitotic divisions).

   

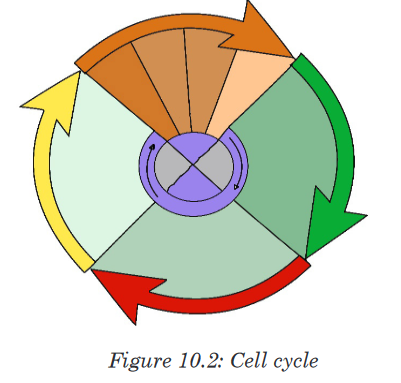
  During the cell cycle, the cell grows, grows its DNA and divides into two
  daughter cells.
  10.1.1. The first growth phase (G1)
  During this phase, a cell undergoes rapid growth and the cell performs its
  routine functions. The cell spends most of its life in the G1 phase. If the cell
  is not dividing, it remains in this phase. The time taken for the completion of
  G1 phase varies among species and the type of cells. But on an average, it
  takes around 11 hours for the completion of this phase.

  10.1.2. The synthesis phase (S)
  DNA synthesis or DNA replication takes place in this phase. The S phase
  takes around 8 hours to complete.
  10.1.3. The second growth phase (G2)
  It is the short period in which the cell continues to grow, making proteins
  and manufacturing many organelles necessary for cell division. This phase
  serves as an intermediate between the synthesis phase and the mitotic
  phase. It takes around four hours to complete
  10.1.4. Mitosis
  This is the phase of nuclear division in which one nucleus divides through
  four phases (prophase, metaphase, anaphase and telophase) and becomes
  two nuclei.
  10.1.5. Cytokinesis
  In this phase, the cytoplasm divides in half, producing two daughter cells,
  each containing a complete set of genetic material.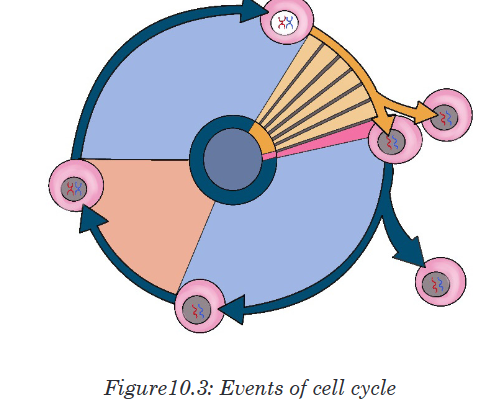

  

  Application activity 10.1

  1. What do you understand by the cell cycle?
  2. Describe all phases of the cell cycle.
  3. Predict what may happen if the cytokinesis does not take place in the
  succession of cell cycle.

  10. 2. Mitosis and Meiosis: Stages and results
  Activity 10.2
  Many of schools in Rwanda have the smart classrooms. Visit your school
  smart classroom and download a video showing the phases of mitosis
  and meiosisand present them on manila papers.
  10.2.1. Mitosis
  Mitosis is a type of cell division that produces two daughter cells having the
  same number and kind of chromosomes as the mother cell. It takes place
  only in eukaryotes, where the nuclear division (karyokinesis) occurs. This
  phase takes around 1 hour to complete. The mitotic cell division is more
  rapid at the meristematic region of plant and root tip as it is the growing
  region of the plant. The mitotic phase is divided into four steps that include
  Prophase, Metaphase, Anaphase and Telophase.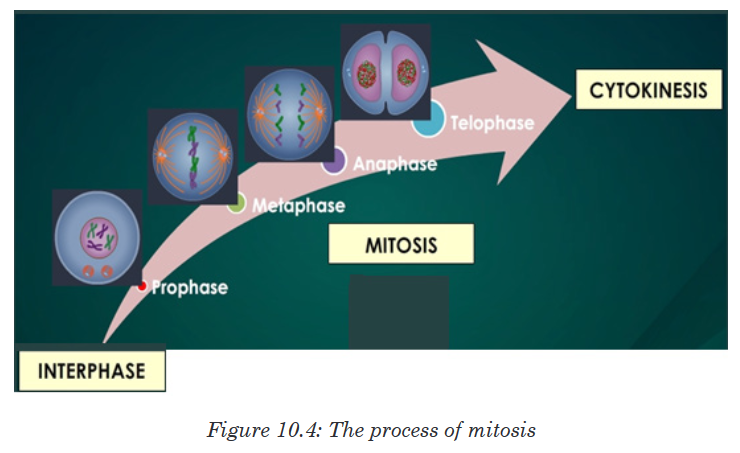

  

  a. Prophase
  Prophase is the first and longest phase of mitosis. During prophase:
  • The DNA and histone proteins coils up into visible chromosomes, each
  made up of two sister chromatids held together by the centromere.
  • The nucleus disappears as the nuclear envelope and nucleolus break
  apart.
  • The centrioles begin to move to opposite ends, or poles, of the cell.
  • As the centrioles migrate, the fiber-like spindle begins to elongate

  between the centrioles. In plant cells, the spindle forms without
  centrioles. The spindle plays an essential role moving chromosomes
  and in the separation of sister chromatids.

  

  b. Metaphase
  During metaphase, the spindle which attaches to the centromere of each
  chromosome helps the chromosomes to line up at the center of the cell by
  forming the equatorial plate also known as the metaphase plate. Each sister
  chromatid is attached to a separate spindle fiber, with one fiber extending to
  one pole, and the other fiber extending to the other pole.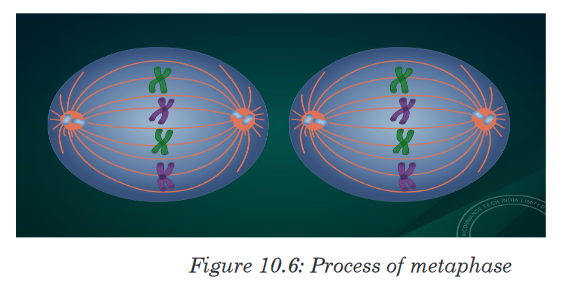

  

  c. Anaphase
  During Anaphase:
  • Centromeres divide,
  • The sister chromatids separate and pulled apart by the shortening of
  the spindles,
  • One sister chromatid moves to one pole of the cell, and the other sister
  chromatid moves to the opposite pole, (sister chromatids take the name
  of chromosomes as soon as they separate).
  • At the end of anaphase, each pole of the cell has a complete set of
  chromosomes, identical to the amount of DNA at the beginning of G1
  of the cell cycle.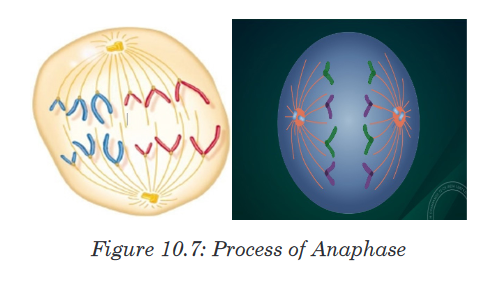

  

  d. Telophase
  During telophase which is the opposite of prophase:
  • The spindle disappears,
  • Formation of two nuclei,
  • The nuclear envelopes surround the two nuclei.

  

  e. Cytokinesis
  During this phase, the cytoplasm divides in half, producing two daughter
  cells, each containing a complete set of genetic material as the mother cell.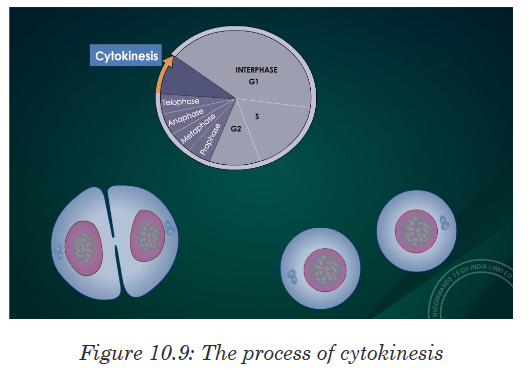

   

  Table 10.2: A table showing phases of cell cycle with one important
  event at each phase

   

   10.2.2. Meiosis
  In sexual reproduction, meiosis produces haploid gametes that fuse together
  during fertilization to produce a diploid zygote. Meiosis involves two divisions
  without an interphase in between, starting with one diploid cell and generating
  four haploid cells. Each division, named meiosis I and meiosis II, has four
  stages: prophase, metaphase, anaphase, and telophase.

  
  
  

  During meiosis the number of chromosomes is reduced from a diploid number
  (2n) to a haploid number . During fertilization, haploid gametes come
  together to form a diploid zygote, and the original number of chromosomes
  (2n) is restored.
  Eight stages of meiosis are summarized below:
  1. Prophase I
  Prophase I is very similar to prophase of mitosis, but with one very
  significant difference. In prophase I, the nuclear envelope breaks down, the
  chromosomes condense, and the centrioles begin to migrate to opposite
  poles of the cell, with the spindle fibers growing between them.
  During this time, the homologous chromosomes form pairs. These
  homologous chromosomes line up gene-for-gene down their entire length,
  allowing the crossing-over to occur.
  This process permits the exchange of genetic material between maternal
  and paternal chromosomes. Thus, crossing-over results in genetic
  recombination by producing a new mixture of genetic material. This is an
  important step in creating genetic variation.
  2. Metaphase I
  In metaphase I, the 23 pairs of homologous chromosomes line up along
  the equator of the cell.
  3. Anaphase I
  During anaphase I the spindle fibers shorten, and the homologous
  chromosome pairs are separated from each other. One chromosome from
  each pair moves toward one pole, with the other moving toward the other
  pole, resulting in a nucleus with 23 chromosomes at one pole and the
  other 23 at the other pole. The sister chromatids remain attached at the
  centromere.
  4. Telophase I
  he spindle fibers disappear and the nucleus reforms. This is quickly
  followed by cytokinesis and the formation of two haploid cells, each with
  a unique combination of chromosomes, some from the father and the rest
  from the mother.
  After cytokinesis, both cells immediately enter meiosis II, without
  replication of the DNA. Meiosis I is described as reductional division as it
  reduces by half the number of chromosomes of the mother cell. Meiosis II
  is equational division, and it occurs like a normal mitosis, separating the
  sister chromatids from each other.
  
  

  5. Prophase II
  Once again the nuclear membrane breaks down, and the spindle begins
  to reform as the centrioles move to opposite sides of the cell.
  6. Metaphase II

  The 23 chromosomes, each made out of two sister chromatids, occupy
  the equator of the cell.
  7. Anaphase II
  The centromere divides and sister chromatids are separated and move to
  opposite poles of the cell. As the chromatids separate, each is known as a
  chromosome. Anaphase II results in a cell with 23 chromosomes at each
  end of the cell; each chromosome contains half as much genetic material
  as at the start of anaphase II.
  8. Telophase II
  The nucleus reforms and the spindle fibers break down. Each cell
  undergoes cytokinesis, producing four haploid cells, each with a unique
  combination of genes and chromosomes.

  
  
  

  
  

  
  
  

  
  
  

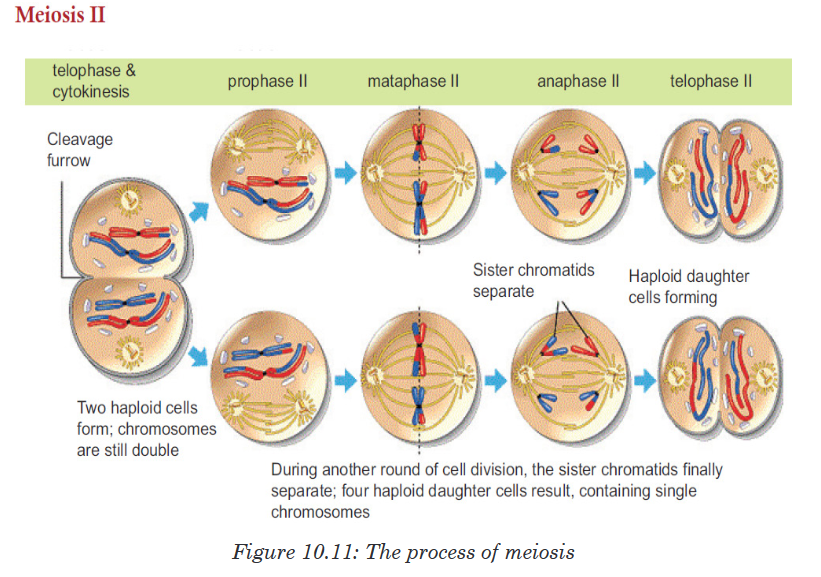
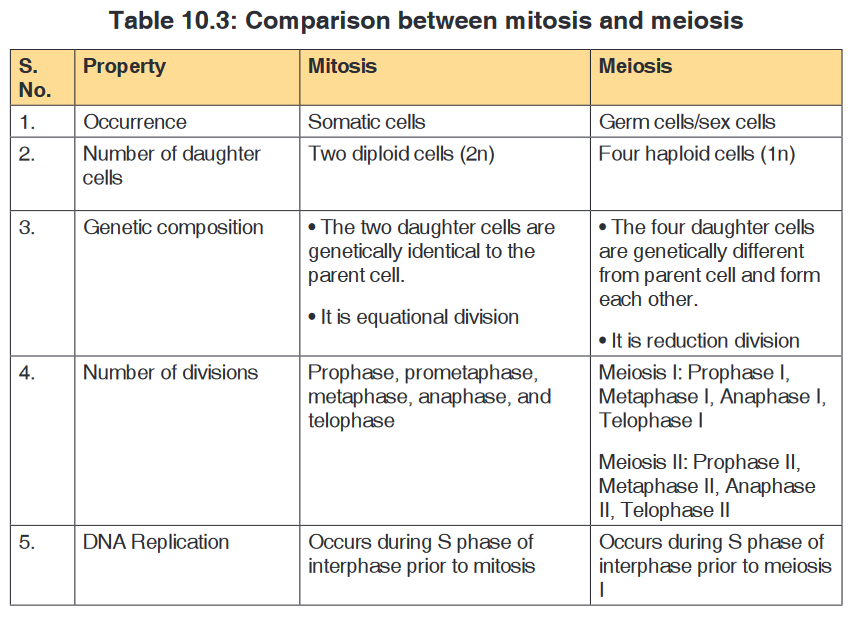
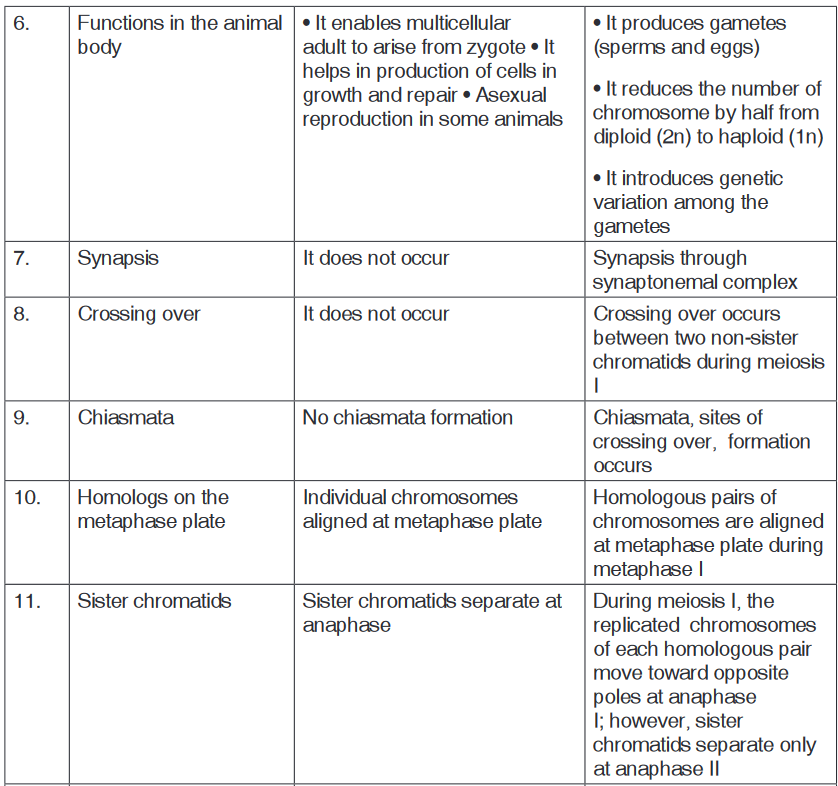
  Haploid and diploid conditions of the cell
  During the formation of gametes, the number of chromosomesis reduced
  by half, and returned to the full amount when the two gametes fuse during
  fertilization. The cells of human beings, most animals and many plants
  (except for their gametes) are diploid abbreviated as 2n. They contain two
  sets of chromosomes in their nuclei. The haploid cells have only one set of
  
  

  chromosomes, abbreviated as n. Ploidy is a term referring to the number of
  sets of chromosomes.
  Organisms with more than two sets of chromosomes are termed polyploidy.
  Chromosomes that carry the same genes are termed homologous
  chromosomes. Meiosis is a special type of nuclear division which segregates
  one copy of each homologous chromosome into each new “gamete”. Mitosis
  maintains the cell’s original ploidy level (for example, one diploid 2n cell
  producing two diploid 2n cells; one haploid n cell producing two haploid
  n cells; etc.). Meiosis, on the other hand, reduces the number of sets of
  chromosomes by half, so that when gametic recombination fertilization
  occurs the ploidy of the parents will be re-established.
  Two successive nuclear divisions occur, Meiosis I (Reduction) and Meiosis II
  (Division). Meiosis produces 4 haploid cells. Mitosis produces 2 diploid cells.
  The old name for meiosis was reduction/ division. Meiosis I reduces the
  ploidy level from 2n to n (reduction) while Meiosis II divides the remaining set
  of chromosomes in a mitosis-like process (division). Most of the differences
  between the processes occur during Meiosis I.
  
  

  
  

  Application activity 10.2
  
  

  1. Give two reasons why cells divide.
  2. As a cell increases in size, which increases more rapidly, its surface
  area or its volume?
  3. Describe what happens during each of the four phases of mitosis.
  4. How is cytokinesis in plant cells similar to cytokinesis in animal cell?
  5. The diagram shows meiosis in an animal cell.
  
  

  a). What is the diploid number of chromosomes in this cell?
  b). Where do you think this cell could be found in an animal?
  c). What is the stage of cell division shown at B? Give a reason for
  your choice.
  
  

  
  
  

  10.3. Mitosis and Meiosis roles in living organisms

  Activity 10.3

  Observe figures below and explain the significance of mitosis in living
  organisms.
  
  

  The Significance of Mitosis in Cell Replacement and Tissue Repair by
  Stem Cells
  a). Mitosis allows growth: The number of cells within an organism
  increases by mitosis and this is the basis of growth in multicellular cells.
  b). Mitosis allows to repairing and cell replacement: Replacement of
  cells and tissues also involves mitosis. Cells are constantly dying and
  are being replaced, for example, in the skin
  c). Mitosis is involved in asexual reproduction: a single parent cell
  divides into two genetically identical offspring.
  
  

  d). Mitosis allows genetic stability by producing two nuclei which have
  the same number of chromosomes as the parent cell.
  e). Regeneration: Some animals are able to regenerate whole parts of
  the body, such as legs in crustacean and arms in starfish. Production
  of the new cells involves mitosis.
  
  

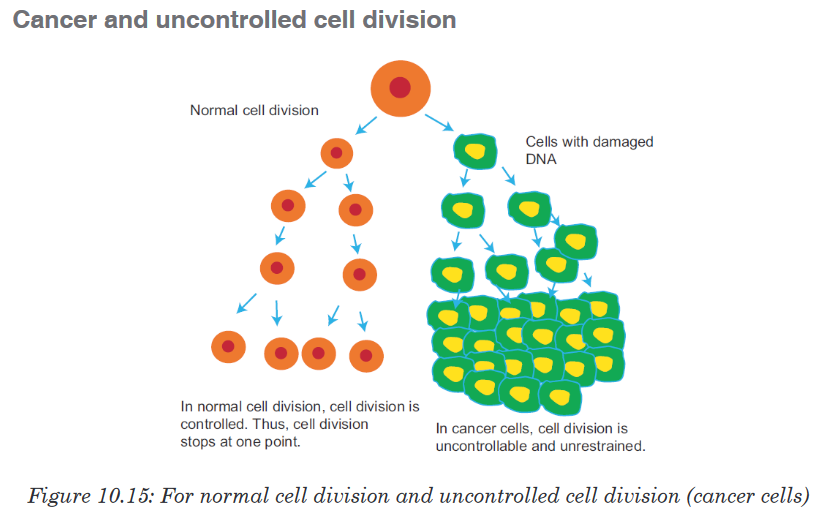
  Many cancers result from uncontrolled cell division, when the regulation of
  the cycle is lost. Cancerous cells divide much more rapidly than healthy
  cells. These cells use the blood and nutrients that other cells need and they
  can stress the environment of the healthy cells. As cancerous cells do not
  provide any useful function to the organism, they are extremely harmful. If
  cancerous cells are allowed to grow uncontrolled, they will kill the host
  organism.
  
  

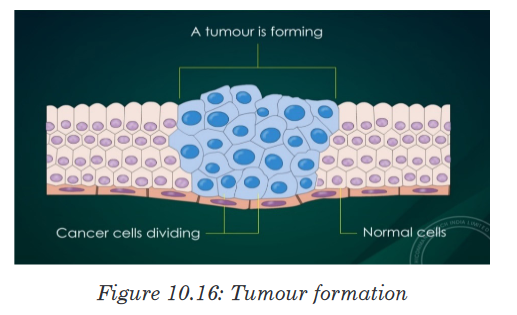
  The problem begins when a single cell in a tissue undergoes transformation,
  the process that convertsa normal cell to a cancer cell. The body’s immune
  system normally recognizes a transformed cell asan abnormal and destroys
  it.
  However, if the cell escapes immune system, it may proliferate to form
  atumor (a mass of abnormal cells within an otherwise normal tissue). There
  are three types of tumors: benign tumors, malignant tumors and metastasis.
  
  

  
  i. Benign tumor: It is a lump of the abnormal cells that remains at the
  original site. Most benign tumors do not cause seriousproblems and
  can be removed by surgery.
  ii. Malignant tumors: These are abnormal cells that have become
  invasive enough to impair with the functions of one or more organs.
  An individual with a malignant tumor is said to have cancer.
  iii. Metastasis: Cancer cells may also separate from the original tumor,
  enter the blood and lymph vessels, and invade other parts of the
  body, where they proliferate to form more tumors. This spread of
  cancer cells beyond their original site is called metastasis.
  Many cancers can be inherited, such as breast cancer, others are triggered
  by viral infections, tobacco smoke (e.g. lung cancer) and radiations (e.g.
  skin cancer). All cancers have one thing in common: the control over the cell
  cycle has broken down.
  Significance of Meiosis
  a. Cells undergo Reduction Division Prior to Sexual Reproduction
  Generally, a cycle of reproduction consists of meiosis and fertilization. Before
  sexual reproduction occurs, gametes undergo meiosis and produce haploid
  cells. Thus during sexual reproduction, one haploid (1n) gamete comes from
  the paternal side and another haploid (1n) gamete comes from the maternal
  side; then, they both fuse to form a zygote, which is diploid (2n). The fusion
  of gametes to form zygote or new cell is called as fertilization or syngamy.
  If meiosis does not occur before sexual reproduction, the chromosome
  number would double up with each fertilization. And after few generations,
  the number of chromosomes in each cell would become impossibly large.
  For example, in humans, in just 10 generations, the 46 chromosomes would
  increase to about 47104 (46 × 210).

  b. Role and Significance of Meiosis in Producing Gametes
  Gametogenesis is a biological process by which diploid cells undergo cell
  division and differentiation to form mature haploid gametes. It occurs through
  meiosis. In humans, the male gamete (sperm) is produced by a process
  called spermatogenesis and the female gamete (egg) is produced by a
  process called oogenesis through meiotic division. Here gametes function
  takes place soon after meiosis but in plants it happens after gametophyte
  formation sexual reproduction of plants starts with spore formation.
  Sporophyte is a diploids generation of flowering plant where haploid spores
  are produced by meiosis which in turns undergoes mitosis to form multi-
  celled haploid gametophytes. These haploid gametophytes differentiate to

  produce gametes—sperm and egg cells. Similarly, embryo sac is formed
  by reduction division. Each of the cells of embryo sac is haploid. Two of the
  nuclei fuse to produce diploid nucleus.

  c. The Role of Meiosis in Reproduction of Plants
  Generally, plants reproducing sexually have life cycle consisting of two
  phases
  • A multicellular gametophyte or haploid stage:
  It is a haploid stage with n chromosomes. It alternates with a multicellular
  sporophyte stage.
  • A multicellular sporophyte or diploid stage:
  It is a diploid stage with 2n chromosomes, made up of n pairs. A mature
  sporophyte produces spores by meiosis, a process which reduces the
  number of chromosomes from 2n to 1n.
  Alternation of generations (also known as mutagenesis) refers to the
  occurrence in the plant life cycle of both a multicellular diploid organism
  (sporophyte) and a multicellular haploid organism (gametophyte), each giving
  rise to the other. This is in contrast to animals, in which the only multicellular
  phase is the diploid organism (such as the human man or woman), whereas
  the haploid phase is a single egg or sperm cell. In bryophytes (mosses and
  liverworts), the dominant generation is haploid, so that the gametophyte
  comprises the main plant. On the contrary, in trichophytes (vascular plants),
  the diploid generation is dominant and the sporophyte comprises the main
  plant.

  d. Independent Assortment of Chromosomes
  Specifically, at metaphase I, each homologous pair of chromosomes
  positioned independently of the other pairs. As a result, each homologous
  pair sorts out its maternal and paternal homologue into daughter cells
  independently of every other pair. This act of separating homologous pairs
  independently is called independent assortment. The random orientation
  of homologous pairs of chromosomes due to independent assortment in
  meiosis I (metaphase) increases genetic variation in organisms.

  e. Crossing Over and Random Fertilization
  During crossing over, DNA segments of the two parents-paternal and
  maternal are combined into a single chromosome producing recombinant
  chromosomes, which are non-identical with their sister chromatids.
  In humans, an average of one to three crossing over events occurs per
  
  

  chromosome pair, depending on the position of their centromeres and on
  the size of the chromosome. Thus, crossing over is an important event of
  meiosis that brings genetic variation in sexual life cycles.
  Besides independent assortment and crossing over, the random fertilization
  during sexual reproduction also increases genetic variation in organisms.
  During random fertilization, the male gamete and female gamete fuse to
  form zygote. The most interesting thing is that this zygote has the possibility
  of about 70 trillion diploid combinations. The number 70 trillion comes from
  possible combinations of male and female gametes which are 223 × 223 = 70
  trillion. The possibility of this enormous number of combinations makes each
  and every one of us unique physically and genetically.
  
  f. Non-disjunction of Chromosomes
  Proper separation of chromosomes during meiosis is essential for the
  normal growth in humans. Any set of chromosomes that do not separate
  properly during meiosis results in improper separation of chromosomes or
  non-disjunction, which is a serious issue in human genetics. Non-disjunction
  is a condition in which the homologues or sister chromatids fail to separate
  properly during meiosis. It can lead to the gain or loss of chromosome, a
  condition called as aneuploidy. Example: Down syndrome is an autosomal
  trisomy. It is also called as trisomy 21, where non-disjunction results in an
  embryo with three copies of chromosome 21 instead of the usual two copies of
  chromosome 21. The origin of trisomics condition is through non-disjunction
  of chromosome 21 during meiosis. Failure of paired homologues to separate
  during either anaphase I or II may lead to gametes with 23 + 1 chromosome
  composition instead of the normal 23 gamete chromosome composition.
  Therefore, instead of 46 normal chromosomes, Down syndrome patient will
  have 47 chromosomes with three copies of chromosome 21 instead of the
  normal 2 copies. It was first discovered by John Langdon Down. The chance
  of occurrence is one infant in every 800 live births.
  
  

  The most common symptoms of Down syndrome or trisomy 21 are:
  • They are short.
  • They may also have protruding, furrowed tongues, which causes the
  mouth to remain partially open.
  • They are mentally retarded.
  • They have a prominent epicanthic fold in the corner of each eye; and
  typical flat face and round head.
  • Usually, there is a wide gap between the first and the second digits on
  their feet.
  
  

  
  
  

  Organisms and the significance of cell division
  a. Spindle fibres formation
  Spindle fibres are microtubules that move chromosomes during cell division.
  They are found in eukaryotic cells. Spindle fibres move chromosomes during
  mitosis and meiosis to ensure that each daughter cell gets the correct number
  of chromosomes. The spindle apparatus consists of spindle fibres, motor
  proteins, chromosomes, and, in some cells, structures called asters (which
  are star-shaped structures form around each pair of centrioles during mitosis.
  They help to manipulate chromosomes during cell division to ensure that
  each daughter cell has the appropriate complement of chromosomes).
  In animal cells, spindle fibres are produced from cylindrical microtubules
  called centrioles. Centrioles are separated by asters to generate spindle
  fibres during the cell cycle. Centrioles are located in a region of the cell
  known as the centrosome.
  
  

  
  

  Synapsis
  In prophase I, homologous chromosomes become closely associated in
  synapsis. Synapsis includes the formation of an elaborate structure called
  the synaptonemal complex, consisting of homologous chromosomes paired
  closely along a lattice or zipper-like structure of proteins between them.
  The components of synaptonemal complex include a meiosis-specific form
  of cohesion that helps the two homologous chromosomes to be closely
  associated along their length.

  
  

  Some events that occur along with synapsis are:
  • The nuclear envelope breaks down.
  • Two pairs of centrosome migrate to opposite poles.
  • Spindle fibres formation occurs.
  
  Bivalents
  These arethe two homologous chromosomes attached at chiasmata. The
  homologous chromosomes consist of two sister chromatids each.
  
  Chiasma formation and movement of chromosomes.
  Chiasmata is the region of crossing over between two homologous
  chromosomes during prophase I of meiosis. At the chiasmata, homologous
  chromosomes exchange genes, allowing genetic information from both the
  paternal and maternal chromatids to be exchanged, and a recombination
  of paternal and maternal genes can be passed down to the progeny. This
  process is important in diploid organisms to ensure variation in the progeny.
  
  

  
  
  

  
  
  

  
  
  

  Process of chiasmata formation
  At prophase I of meiosis, after the homologous chromosomes pair up in
  the process called synapsis, the non-sister chromatids overlap, forming an
  X-shape. They then exchange their alleles at the point of crossing over. The
  X-shape the homologous pair together until the cell progresses to anaphase.
  
  

  
  

  Movement of chromosomes
  In early Prophase I, chromosomes change their size and become short and
  thick. This is the first movement they make during meiosis
  In late Prophase I, homologous chromosomes become fully shortened and
  thickened lie side by side (in a process called synapsis).
  In metaphase I, Pairs of homologous chromosomes migrate to the equatorial
  plane of the cell. Each chromosome moves independently of all the others
  and the phenomenon is called independent assortment.
  During anaphase I, the homologous chromosomes separate and begin to
  move to the opposite poles of the cell, pulled by the shrinking spindle fibers.
  In telophase I, the movement of the homologous chromosomes to the poles
  is completed.
  During Prophase II chromosomes again become thicker and shorter begin
  to move to the equatorial plane of the cell. Spindle fibers once again begin
  to form at the poles.
  During metaphase II the chromosomes become aligned on the equatorial
  plane and spindle fibers attach to the centromeres.
  In anaphase II, the centromeres divide, separating the sister chromatids,
  that move to the opposite poles due to the spindle fibers pulling.
  In telophase II, the movement of the chromosomes to the poles is completed
  and the spindle disappears.
  
  

  
  
  

  Application activity 10.3
  
  

  
  1. Discuss possible functions of mitosis in living organisms.
  2. Appreciate the role of cyclins in the process of cell cycle.
  3. Describe the process of tumor formation.
  4. Describe the three types of tumors.
  
  

  
  

  Skills lab 10

  Use microscope to compare the sizes of the similar cells in larger and small
  plants. For example, you might compare the leaf cells of grass to the leaf
  cells of a tree. Be sure you use the same magnification when comparing the
  sizes of the cells. Do the same from the small and large animal e.g. from frog
  and from human.
  
  

  
  

  Are the cells of small plants larger or smaller than those of the larger plants?
  Are the cells of the small animal larger or smaller than those of larger animal?
  Make a general statement that compares the number and the sizes of cells
  in small organisms to those in large organisms.
  
  

  
  
  

  End unit assessment 10
  
  

  I. Choose whether the following statements are True (T) or False (F)
  1. A typical cell spends most of its time in interphase.
  2. Mitosis is a process where a single cell divides into three identical
  daughter cells.
  3. Cytokinesis is a division of cytoplasm.
  4. The process of mitosis is basically divided into 5 phases.
  5. Meiosis is divided into three stages: Meiosis I, Meiosis II and Meiosis
  III.
  6. The unrestrained, uncontrolled growth of cells in human beings results
  into a disease called cancer.
  7. Cancer occurs due to failure in controlling cell division.
  8. Proper separation of chromosomes during meiosis is not essential for
  the normal growth in humans.
  9. The life span of blood cells ranges from less than one day to a few
  months.
  
  

  II. Multiple Choice Questions
  1. In telophase, the nuclear envelope re-forms around the........... set of
  haploid daughter chromosomes.
  (a) one (b) two (c) three (d) four
  2. ............................... is a condition in which the homologues or sister
  chromatids fail to separate properly during meiosis.
  (a) Disjunction (b) Non-disjunction (c) Down syndrome
  (d) None of these
  3. Which of the event is correct in anaphase
  (a) Sister chromatids separate and give rise to daughter chromosomes.
  (b) Chromosomes are aligned at metaphase plate.
  (c) Cytokinesis starts occurring.
  (d) Chromosomes begin to uncoil.
  4. One round of oogenesis produces
  (a) One egg (b) Two eggs (c) Three eggs (d) Four eggs
  5. In mitosis, which of the following occurs?
  (a) Chiasmata formation (b) DNA replication (c) Synapsis
  (d) None of these
  
  
  

  III. Long Answer Type Questions
  1. Describe the main stages of cell cycle.
  2. In your own words, explain what is meant by homologous pairs of
  chromosomes.
  3. In your own words, describe the process of mitosis.
  4. In your own words, describe the process of meiosis.
  5. Outline the significance of mitosis in cell replacement and tissue
  repair by stem cells.
  6. In your own words, explain how uncontrolled cell division can result in
  the formation of a tumor.
  7. What is the need for reduction prior to fertilization in sexual
  reproduction?
  8. In your own words, explain the importance of effective cell division.

  9. Outline the role of meiosis in gametogenesis in humans and in the
  formation of pollen grain and embryo sacs in flowering plants.
  10. Explain how crossing over and random assortment of homologous
  chromosomes during meiosis and random fusion of gametes at
  fertilization leads to genetic variation, including the expression of rare
  recessive alleles.
  11. Analyze the following diagram and answer the questions below:
  
  

  a) Identify the stage of cell division shown in the figure.
  b) Label the structures marked as (1), (2), (3) and (4).
  c) Which type of cell is involved in this division?
  d) What will happen if the structure marked (3) is not formed?
  12. How can you correlate the spread of HIV virus with the process
  of Mitosis? Knowing the viral disease and its spread.
  
  

   

   

  
  
• UNIT 11: AUTOTROPHIC NUTRITION

  Key Unit competence: Describe the process of photosynthesis
  and explain the various environmental
  factors that influence the rate of
  photosynthesis

  Introductory Activity 11

  Read the passage below and then answer questions that follow.
  Vital process that makes up our life
  The life is all about autotrophic nutrition. There is a number of reactions
  that take place during the autotrophic nutrition but all are simpled
  summarised by the saying inorganic matters are transformed into organic
  matters. And as said in physics, the energy is neither created nor lost but
  only transformed from one form to another, the process of autotrophic
  nutrition transforms light energy into chemical energy. But, opposite to
  most of metabolic reactions which produce harmful waste products, the
  waste product from photosynthesis is useful for life. So, no autotrophic
  nutrition, no life either.
  1. Suggest a name to autotrophic nutrition
  2. Which waste product from autotrophic nutrition is useful for life?
  3. Do you agree that no autotrophic nutrition, no life either? Why?
  4. The overall equation of autotrophic nutrition should be written as:
  

  
  

  5. What requirements are missing on the above equation?
  6. What factors can affect the rate of autotrophic nutrition.
  

  11.1. Types of autotrophic nutrition

  Activity 11.1

  Do a research on different types of autotrophic nutrition and present them
  on manila paper.
  

  Autotrophic nutrition is a process by which living organisms make their own
  food. This process is carried out by photoautotrophs like green plants, green
  algae and green bacteria; and chemoautotrophs. Living organisms which
  make their own food are called autotrophs, while others, including humans,
  which cannot make their own food but depend on autotrophs are called
  heterotrophs.
  

  
  

  There are two types of autotrophic nutrition such as chemoautotrophic and
  photoautotrophic nutrition.
  

  
  

  Chemoautotrophic nutrition
  It is an autotrophic nutrition where organisms (mainly bacteria) get energy
  from oxidation of chemicals, mainly inorganic substances like hydrogen
  sulphide and ammonia.
  

  
  

  Photoautotrophic nutrition
  It is an autotrophic nutrition where organisms get energy from sunlight and
  convert it into sugars. Green plants and some bacteria like green Sulphur
  bacteria can make their own food from simple inorganic substances by a
  process called photosynthesis. Photosynthesis is a process by which,
  autotrophs make their own food by using inorganic substances in presence
  of light energy and chlorophyll.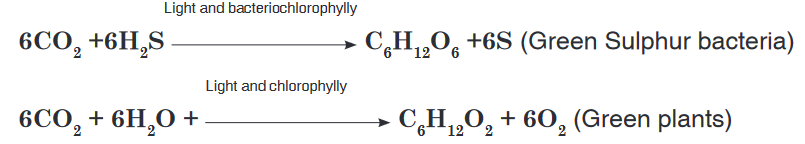
  

  
  

  Application activity 11.1

  1. Define Photosynthesis
  2. Differentiate:
  a) Autotrophs and heterotrophs.
  b) Chemoautotrophs and photoautotrophs.
  3. Animals’ life depends on plants. Defend this statement by providing
  two convincing reasons.
  

  11.2. Structure of the chloroplast and Adaptations for
  photosynthesis

  Activity 11.2

  With a compound microscope and well prepared slides of plant cell
  • Observe the slides under the compound microscopes, and draw the
  structure of chloroplast.
  • Search and relate the structure of chloroplast with the process of
  photosynthesis.
  

  In eukaryotes photosynthesis takes place in chloroplasts. A chloroplast
  contains many sets of disc like sacs called thylakoids, which are arranged
  in stacks known as grana. Each granum looks like a stack of coins where
  each coin being a thylakoid. In the thylakoid, proteins are organized with the
  chlorophyll and other pigments into clusters known as photosystems. The
  

  photosystems are the light-collecting units of the chloroplast.
  The function of thylakoids is to hold the chlorophyll molecules in a suitable
  position for trapping the maximum amount of light. A typical chloroplast
  contains approximatively 60 grana, each consisting of about 50 thylakoids.
  The space outside the thylakoid membranes are made by watery matrix
  called stroma. The stroma contains enzymes responsible for photosynthesis.
  

  
  

  
  

  Note: Photosynthetic prokaryotes have no chloroplasts, but thylakoids often
  occur as extensions of the plasma membrane and are arranged around the
  periphery of the prokaryotic cell.
  

  The structure of chlorophyll
  The chlorophyll molecule is made of atoms of Carbon and Nitrogen joined
  in a complex porphyrin ring containing an atom of Magnesium in the center
  of the ring. The chlorophyll also has long hydrophobic carbon tail of 20
  carbon atoms (phytol) which hold it in the thylakoid membrane. In short, the
  chlorophyll consists of a porphyrin ring and a phytol tail.
  The chlorophyll a differs from the chlorophyll b in that: the porphyrin of the
  chlorophyll a has the methyl group as a functional group, which is
  replaced by an aldehyde group (-CHO) for chlorophyll b.
  

  
  

  
  The difference between the chlorophyll a and the chlorophyll b shifts the
  wavelength of light absorbed and reflected by chlorophyll b, so that the
  chlorophyll b is yellow-green, whereas the chlorophyll a is bright-green.
  

  Adaptations for photosynthesis
  By considering both external and internal structures of the leaf, we can
  recognize several adaptations for photosynthesis.
  Adaptation of leaf for photosynthesis considering to its internal structure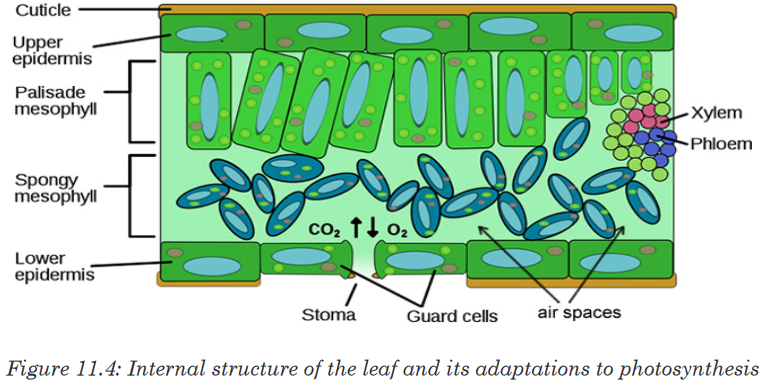
  

  
  

  
  

  Note: When stomata are opened, the rate of photosynthesis may be 10
  to 20 times as fast as the maximum rate of respiration. If the stomata are
  closed, photosynthesis still can continue, using CO2 produced during cell
  respiration. The equilibrium can be reached between photosynthesis and
  cell respiration.
  Photosynthesis uses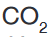 From respiration, and respiration uses Oxygen
  from photosynthesis. However, the rate of photosynthesis under these
  circumstances will be much slower than when an external source of
  

  is available. The stomata cannot remain closed indefinitely, they have to be
  open in order to maintain transpiration of the plant.
  Adaptation of leaf for photosynthesis considering its external structure
  

  
  

  • Leaves are thin and flat, this facilitate absorption of the maximum
  amount of light.
  

  • The cuticle is transparent to allow absorption of light into tissues.
  • Presence of a waxy substance on the cuticle to prevent excessive
  water loss from photosynthetic tissues.
  • Presence of the midrib and veins containing vascular tissues like: the
  Xylem which brings water and minerals from soil to photosynthetic
  tissues, and Phloem which carry away manufactured organic food from
  photosynthetic tissues to other parts (translocation).
  • Having the leaf stalk which holds the lamina in a good position to
  receive the maximum amount of the light.
  

  Application activity 11.2

  1. Describe the structure of a chloroplast.
  2. Explain adaptations of both thylakoid and stroma for their functions.
  3. Relate the internal structure of the leaf with the process of
  photosynthesis
  

  11.3. Absorption, action spectra and other carbon dioxide
  fixation pathways

  Activity 11.3

  1. Is it possible for a plant to grow without solar light? Justify your answer.
  2. Why do plants have different colours? Justify each color of plant
  observed in environment.
  

  In addition to water and 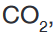photosynthesis requires light and chlorophyll.
  The chlorophyll pigment is found in the chloroplasts. The light that our eyes
  perceive as white light is a mixture of different wavelengths. Most of them are
  visible to our eyes and make up the visible spectrum. Our eyes see different
  wavelengths of visible spectrum as different colors (violet, blue, green, yellow,
  orange and red) except indigo which is not visible to our eyes. Plants absorb
  the light energy by using molecules called pigments such as: chlorophyll
  a, chlorophyll b, carotene (orange), xanthophyll (yellow) and phaeophytin
  (grey) but chlorophyll a is the principle pigment in photosynthesis.
  

  The chlorophyll absorbs light very well in blue-violet and red regions of visible
  spectrum. However, chlorophyll does not absorb well the green light, instead
  it allows the green light to be reflected. That is why young leaves and other
  parts of the plants containing large amount of chlorophyll appear green.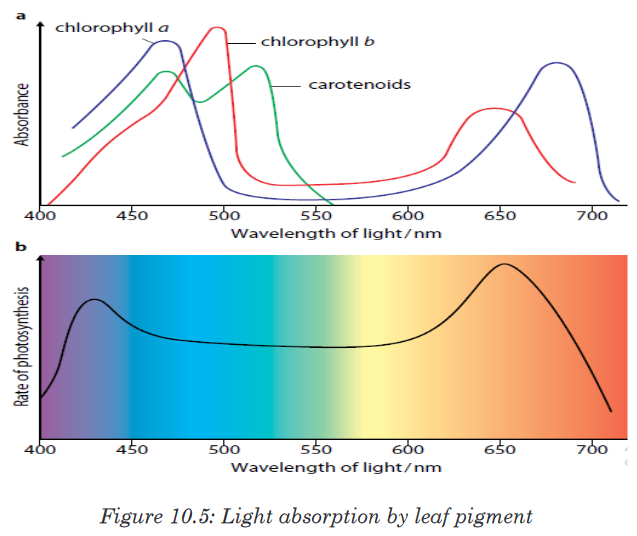
  

  
  

  The chlorophyll a as a principle and abundant pigment, it is directly involved
  in light reactions of photosynthesis. Other pigments (chlorophyll b, carotene,
  xanthophyll and phaeophytin) are accessory pigments. They absorb light
  colours that chlorophyll a cannot absorb, and this enables plants to capture
  more energy from light.
  The amount of energy that the pigment can absorb from the light, depends
  on its intensity and its wavelengths. So, the greater the intensity of light, the
  greater amount of energy will be absorbed by the pigment in a given time.
  The process of photosynthesis occurs through two main stages such as:
  • The light-dependent reactions: which take place in thylakoids, and
  • The light-independent reactions (Calvin cycle): which take place in
  stroma.
  

  a) The light-dependent reactions
  They require light energy and occur in thylakoids. They produce Oxygen gas
  and convert ADP and NADP+ into ATP and NADPH.
  The light-dependent reactions involve the following steps:
  Step 1: Photosynthesis begins when the chlorophyll a in photosystem II
  absorbs light at different wavelengths of light.
  • When the light energy hits the chlorophyll a, the light energy is absorbed
  by its electrons, by raising their energy level.
  

  • These electrons with high potential energy (electrons with sufficient
  quantum energy) are passed to the electron-transport chain.
  • Excited electrons are taken up by an electron acceptor (NADP+:
  oxidized Nicotinamide Adenine Dinucleotide Phosphate), and pass
  along electron transfer chain from photosystem II to the photosystem I.
  (Note: The photosystems are the light-collecting units of the chloroplast).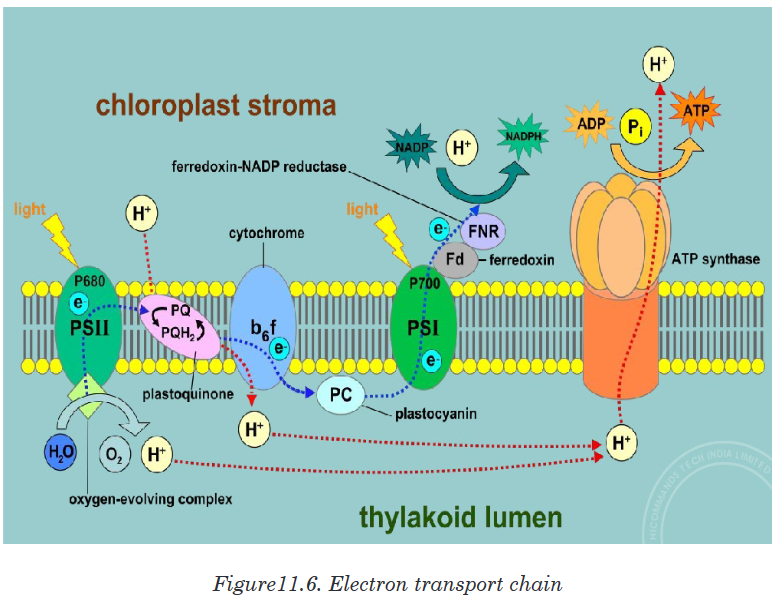
  

  
  

  Step 2: Enzymes in thylakoids and light absorbed by photosystem II are
  used to break down a water molecule into energized electrons, hydrogen
  ions H+, and Oxygen.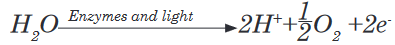
  

  
  

  • Oxygen produced is released to be used by living things in respiration.
  • Electrons and H+ from photolysis of water are used to reduce NADP+
  to NADPH (Reduced Nicotinamide Adenine Dinucleotide Phosphate).
  • The light-dependent reactions also allow generation of ATP (Adenosine
  Triphosphate) by adding inorganic phosphate to   (Adenosine
  Diphosphate):
  

  
  

  Generally, the light-dependent reactions use light energy, ADP, Pi, NADP+
  and water to produce ATP, NADPH and Oxygen. Or simply:

  
  

  Both ATP and NADPH are energy carriers which provide energy to sugars
  (energy containing sugars) in Light-independent reactions.

  Step 3: The fixation of Pi to ADP+ to form ATP is called photophosphorylation.
  Photophosphorylation can be done into two processes: cyclic
  photophosphorylation, and non-cyclic photophosphorylation.
  i) Cyclic photophosphorylation
  It involves only photosystem I and not photosystem II. There is no
  production of NADPH and no release of Oxygen. When the light hits
  the chlorophyll in PSI, the light-excited electron leaves the molecule.
  This light-excited electron is taken up by an electron acceptor which
  passes it along an electron transfer chain (a series of electron carriers)
  until it returns to the chlorophyll molecule that it left (cyclic process).
  As an excited electron moves along an electron transfer chain, it loses
  energy which will be used for the synthesis of ATP from ADP+ and
  inorganic phosphate in the process called chemiosmosis. Electron
  carriers can vary, but the principle include the cytochromes.
  ii) Non-cyclic photophosphorylation
  It is the main route of ATP synthesis. It is done in the following steps:
  • When the photosystem II (in chlorophyll) absorbs light, an electron is
  excited to a higher energy level and captured by the primary electron
  acceptor.
  • Enzymes extract electrons from a water molecule replacing each
  electron that the chlorophyll molecule lost when absorbed light
  energy. This reaction dissociates a water molecule into hydrogen
  ions (2H+) and Oxygen which is released for animals’ respiration.
  • Excited electron moves from the primary electron acceptor of
  photosystem II to photosystem I, via an electron transport chain.
  • When excited electron moves from the primary electron acceptor of
  photosystem II to photosystem I, via an electron transport chain its
  energy level lowers. The energy removed is used to synthesize ATP
  from ADP and in a process called: Non-cyclic phosphorylation.
  

  The hydrogen ions (2H+) produced from dissociation of water
  molecule combines with NADP+ to form NADPH₂.
  

  • Both ATP and NADPH2 will be used in the light-independent reactions
  (Calvin cycle) for synthesis of sugars.
  

  
  

  The significance of the cyclic phosphorylation
  Non-cyclic photophosphorylation produces ATP and NADPH in equal
  quantities, but the Calvin cycle consumes more ATP than NADPH. The
  concentration of NADPH in a chloroplast may determine which pathway
  (cyclic versus non-cyclic) electrons pass through.
  If a chloroplast runs low on ATP for the Calvin cycle, NADPH will accumulate
  as the cycle slows down. The rise of NADPH may stimulate a shift from non-
  cyclic (which produces ATP only) to cyclic electron pathway until ATP supply
  catches with the demand.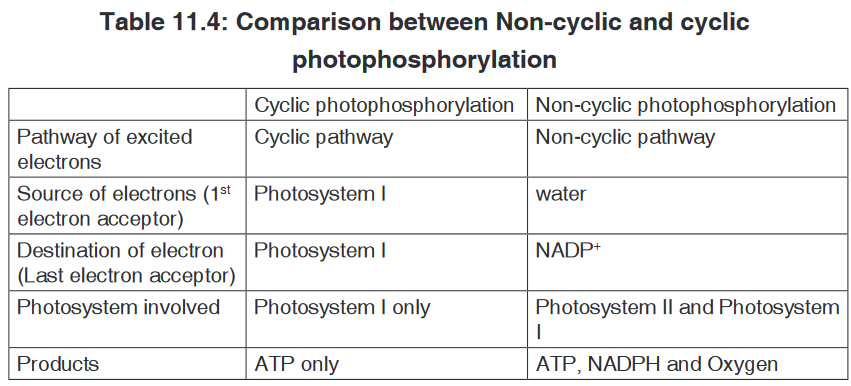
  

  
  

  b) The light-independent reactions (Calvin cycle)
  The light-independent reactions occur in stroma, and consist of reducing
  CO2 into sugars by using ATP and NADPH both coming from light-dependent
  reactions in thylakoids. The Calvin cycle involves three main stages such as:
  • Carbon fixation in form of CO₂.
  • Carbon reduction from CO₂ to glucose.
  • Regeneration of RuBP.

  Step 1: Carbon fixation (Carboxylation) in form of CO2
  The Calvin cycle begins with a 5-Carbon sugar phosphate called
  Riburose-1, 5 biphosphate (RuBP) which fixes the CO₂ from air. This
  reaction is catalyzed by an enzyme called RuBPcarboxylase-oxygenase
  (RUBISCO), which makes up about 30% of the total protein of the leaf, so
  it is probably one of the most common proteins on the Earth.
  The combination of RuBP and CO2 results in a theoretic 6-carbon
  compound which is highly unstable. It immediately splits into two
  molecules of 3-carbon known as phosphoglyceric acid (PGA) or glycerate
  3-phosphate, or 3-phosphoglycelate.
  

  Step 2: Carbon reduction from CO₂ to glucose
  With energy from ATP and reducing power from NADPH, the
  phosphoglyceric acid is reduced into 3carbon molecules known as
  glyceraldehyde-3-phosphate or phosphoglyceraldehyde (PGAL).
  

  Each molecule of PGA receives an additional phosphate group from
  ATP, becoming 1, 3-biphosphoglycerate, and a pair of electrons and H+
  from NADPH reduces the carboxyl group of 3-phosphoglycerate to the
  aldehyde group of PGAL which stores more potential energy.
  

  ATP gives one phosphate group becoming ADP+, and NADPH gives H+
  and electrons to become NADP+. Both ADP+, and NADP+ will be used
  again in light-dependent reactions.
  

  With 6 turns of Calvin cycle, the plant cell fixes 6CO₂ molecules which
  are used to synthesize 2 molecules of PGAL which leave the cycle and
  combine to make one molecule of glucose or fructose. This glucose can
  be converted into:

  • Sucrose: When Oxygen combined with fructose. It is a form by which
  carbohydrates are transported in plants.
  • Polysaccharides like starch for energy storage, and cellulose for
  structural support.
  

  • Amino acids when combined with nitrates,
  • Nucleic acids when Oxygen combined with phosphates, and
  • Lipids.
  

  
  

  Step 3: Regeneration of RuBP
  The remaining ten 3-carbon molecules (PGAL) are converted back into six
  5-carbon molecules, ready to fix other CO2 molecules for the next cycle. The
  light-independent reactions can be summarized as: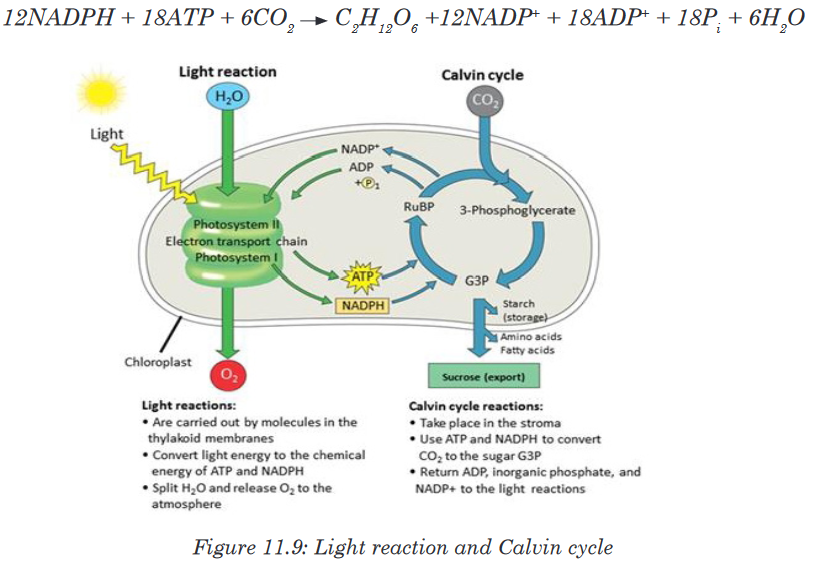
  

  
  

  
  

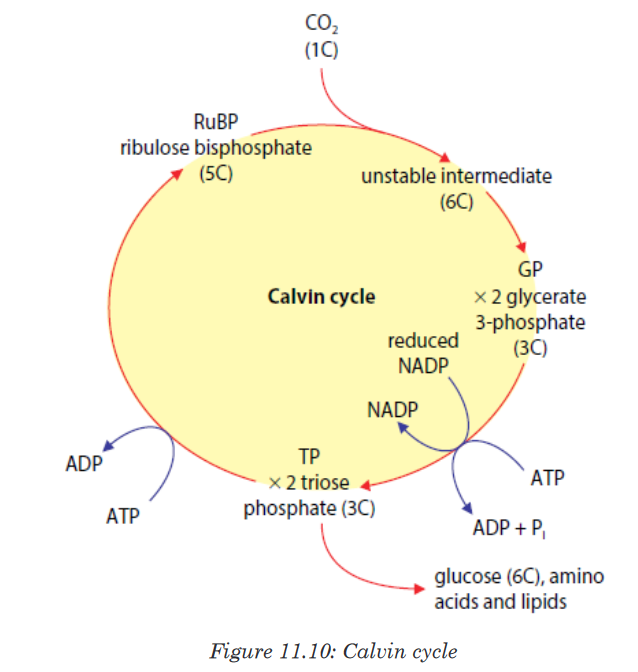
  Other carbon dioxide fixation pathways (C4 CAM)
  The most common pathway combines one molecule of CO₂ with a 5-carbon
  sugar called ribulose biphosphate (RuBP). The enzyme which catalyzes
  this reaction (nicknamed “Rubisco”) is the most abundant enzyme on earth!
  The resulting 6-carbon molecule is unstable, so it immediately splits into
  two 3-carbon molecules. The 3 carbon compound which is the first stable
  molecule of this pathway gives this largest group of plants the name “C-3
  plants”.

  Dry air, hot temperatures, and bright sunlight slow the C-3 pathway for
  carbon fixation. This is because stomata, which normally allow CO₂ to enter
  and O₂ to leave, must close to prevent loss of water vapor. Closed stomata
  lead to a shortage of CO₂. Two alternative pathways for carbon fixation
  demonstrate biochemical adaptations to differing environments. Plants such
  as corn solve the problem by using a separate compartment to fix CO₂.
  

  Here CO₂ combines with a 3-carbon molecule, resulting in a 4-carbon
  molecule. Because the first stable organic molecule has four carbons, this
  adaptation has the name C-4. Shuttled away from the initial fixation site, the
  

  4-carbon molecule is actually broken back down into CO2, and when enough
  accumulates, Rubisco fixes it a second time!
  

  In some temperate plants such as wheat, rice, potato and bean only Calvin
  cycle occurs. Such plants are called C-3 plants. While in some other plants
  dual carboxylation takes place: (1) carboxylation of phosphoenol pyruvate
  (PEP) and (2) carboxylation of RuBP. Such plants are called C-4 plants e.g.
  maize, sugar cane and sorghum. In these, the first product formed during
  carbon dioxide fixation is a four carbon compound oxalo acetic acid (OAA).
  C-4 plants have special type of leaf anatomy called Kranz Anatomy. They
  have special large cells around vascular bundles called bundle sheath cells.
  These are characterized by having large number of chloroplasts, thick walls
  and no intercellular spaces. The shape, size and arrangement of thylakoids
  in chloroplasts are also different in bundle sheath cell as compared to
  mesophyll cell chloroplasts.
  

  The pathway followed by C-4 plants is called C-4 cycle or Hatch and Slack
  pathway. This was discovered by Hatch and Slack in sugar cane. The
  primary CO₂ acceptor is a 3-carbon molecule phosphoenol pyruvate (PEP).
  The reaction is catalyzed by PEP carboxylase or PEP case in mesophyll cell
  chloroplast. It forms 4-carbon compounds like OAA, malic acid or aspartate,
  which are transported to the bundle sheath cells. In bundle sheath cells,
  these acids are broken down to release CO₂ and 3-carbon molecule. The
  3-carbon molecule is transported back to mesophyll cells and converted to
  PEP again, while CO₂ enters into C-3 cycle to form sugars. C-4 plants are
  more efficient than C-3 plants as in C-4 plants, photosynthesis can occur at
  low concentration CO₂ and photorespiration is negligible or absent.
  

  Cacti and succulent (water-storing) plants such as the jade plant avoid water
  loss by fixing CO₂ only at night. These plants close their stomata during the
  day and open them only in the cooler and more humid nighttime hours. Leaf
  structure differs slightly from that of C-4 plants, but the fixation pathways are
  similar. The family of plants in which this pathway was discovered gives the
  pathway its name, Crassulacean Acid Metabolism, or CAM. All carbon
  fixation pathways lead to the Calvin cycle to build sugar.
  

  The CAM pathway is similar to the C4 pathway in that carbon dioxide is
  first incorporated into organic intermediates before it enters the Calvin cycle.
  The difference is that in C4 plants, the initial steps of carbon fixation are
  separated structurally from the Calvin cycle whereas in CAM plants, the two
  steps occur at separate times.
  

  The CAM pathway and the C4 pathway compared:

  
  

  
  

  
  

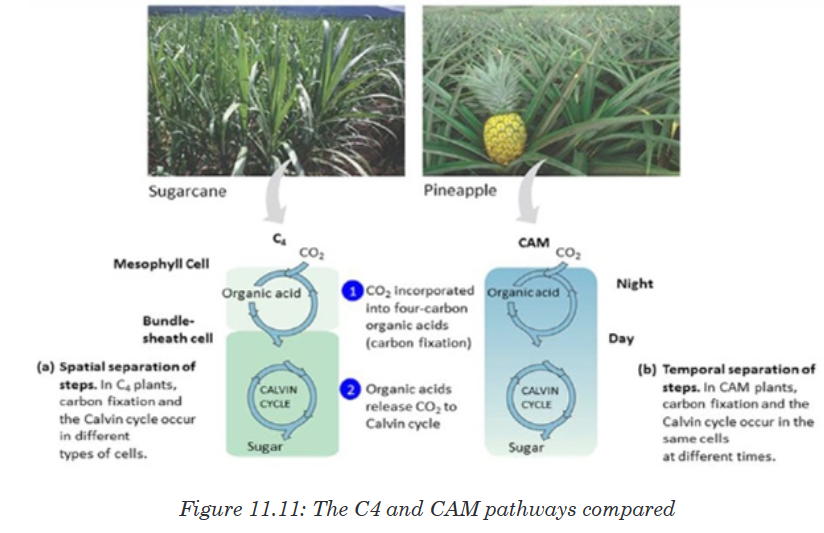
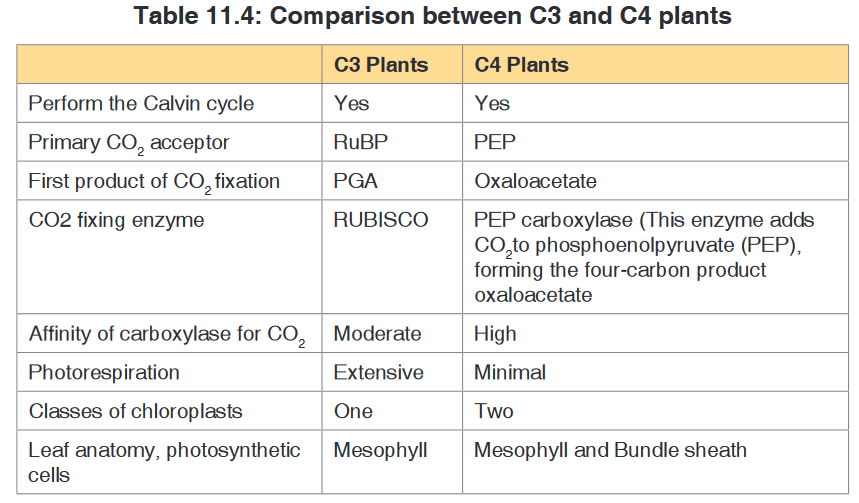
  Photorespiration
  In most plants, initial fixation of carbon occurs via Rubisco, the Calvin cycle
  enzyme that adds CO₂ to ribulose biphosphate. Such plants are called C3
  plants because the first organic product is a three carbon organic compound,
  PGA. These plants produce less food when their stomata close on hot and
  dry days.
  The declining level of CO₂ in the leaf starves the Calvin cycle. Making matter
  worse, Rubisco can accept O2 in place of CO₂. As O₂ concentration overtakes
  CO2 concentration within the air space, Rubisco adds O₂ instead of CO₂. The
  product splits and one piece, a two-carbon compound is exported from the
  chloroplast. Mitochondria then break the two-carbon molecule into CO₂.
  

  
  

  
  The process is called photorespiration because it occurs in presence of
  light (photo) and consumes O₂ (respiration). However, unlike normal cellular
  respiration, photorespiration generates no ATP, and unlike photosynthesis,
  photorespiration generates no food. In fact, photorespiration decreases
  photosynthetic output by using material from the Calvin cycle.
  

  Application activity 11.3

  1. Why are light and chlorophyll needed for photosynthesis?
  2. Describe the relationship between the chlorophyll and the color of
  plants.
  3. How well would a plant grow under pure yellow light? Explain your
  answer.
  4. Appreciate the presence of accessory pigments in leaves for the
  process of photosynthesis.
  5. differentiate the light-dependent stage and light-independent stage of
  photosynthesis.
  6. Distinguish the cyclic and non-cyclic photophosphorylation.
  7. Explain the stages of the Calvin cycle.
  8. Appreciate the significance of the cyclic phosphorylation.
  9. In a tabular form, compare the process of photosynthesis in C₃ and
  C₄ plants.
  10. What do you understand by photorespiration?
  

  11.4. Rate of photosynthesis: limiting factors of
  photosynthesis

  Activity 11.4

  By using prior knowledge, what do you think should influence the
  photosynthesis process in plants?
  

  The photosynthesis rate varies with the species but also varies within
  individuals for a same species; this varies under the influence of certain
  external factors which are: the temperature, CO2 concentration in the
  atmosphere, light intensity and soil humidity.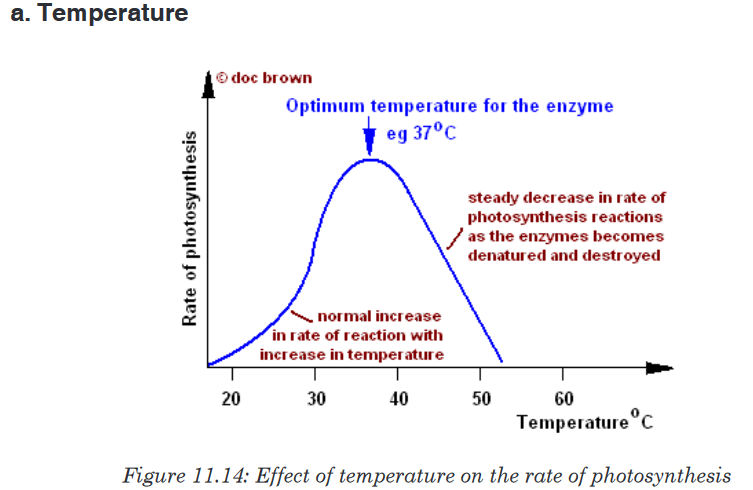
  

  
  

  Photosynthesis is low at 0˚C, certain alpine plants do photosynthesis at has
  less -15˚C.
  

  Photosynthesis presents an optimum towards 35 to 40 ˚C, then it decreases
  and is cancelled at around 50˚C.
  

  b. CO2 concentration in the atmosphere
  

  
  

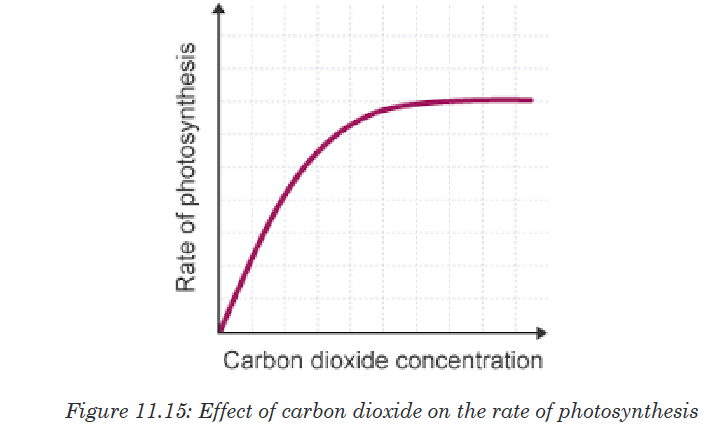
  The photosynthetic rate is zero in place lacking CO₂, it increases with the
  increase concentration of CO₂ in the atmosphere and reaches an optimum
  ranging between 5 and 8%CO₂ concentration.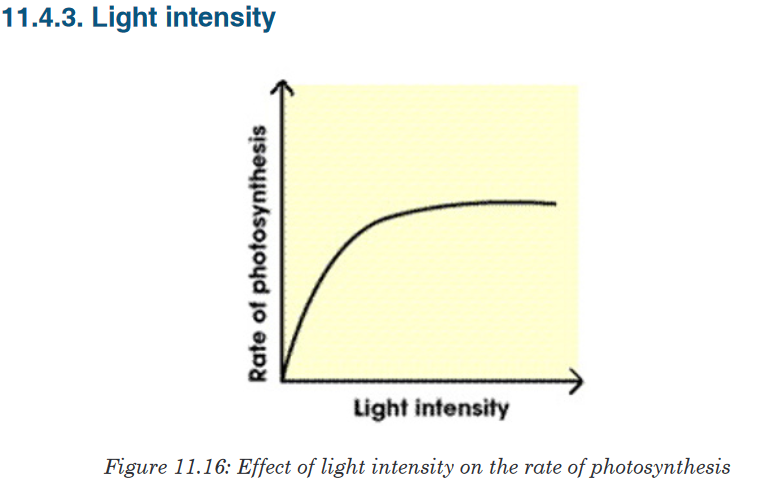
  

  
  

  The photosynthesis rate is low during night, it increases when the light
  intensity increases but the optimum varies according to the plants.
  

  11.4.4. Availability of water for the plant
  The photosynthesis rate is low when the soil is dry, it increases when the
  content of water increases for the terrestrial plants, and for the aquatic plants
  it remains constant as long as they are fixed in water.
  

  Note: The limiting factors work together to influence the rate of photosynthesis
  

  
  

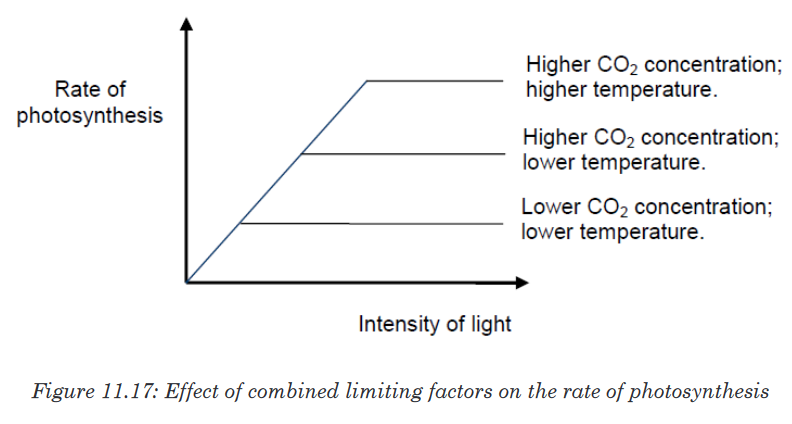
  Application activity 11.4
  1. Use the graphs to explain how the limiting factors below may influence
  the rate of photosynthesis:
  a) Temperature
  b) Light intensity
  c) Concentration of CO₂ in air.
  2. A student who studies Biology talked to his Biology group members
  that:
  a) “In Rwanda, the rate of photosynthesis is generally lower at 5:30
  AM than it is at 12:30 PM, during a sunny day”. Defend him by
  providing two convincing reasons.
  He also said that:
  b) “The rate of photosynthesis is generally higher in Rwanda during
  the sunny day than in Sahara Desert”. Defend him with a convincing
  reason.
  

  11.5. Importance of autotrophic nutrition and Tests for
  starch in terrestrial plants and for oxygen in aquatic
  plants

  Activity 11.5

  Describe the following topic: Animals depend on Plants, rather than
  plants depend on animals
  

  A. Importance of autotrophic nutrition
  Autotrophic nutrition is a process by which living organisms (autotrophs:
  photoautotrophs and chemoautotrophs) make their own food. The
  autotrophism is very essential as it allows production of Oxygen and food
  for not only themselves but also for heterotrophs. The roles of autotrophic
  nutrition include:

  • Independence of green plants from other living organisms to the
  nutrition point of view
  This importance relates to their capacity for synthesizing organic molecules
  from glucose produced by CO2 and water, this completely make them
  independents of the other living organisms to the nutrition point of view.
  

  • Energy storage
  The autotrophs like green plants, by the process of photosynthesis
  synthesize certain substances like: the cellulose, starch… which are
  variables sources of energy.

  • Production of O2 for the living organisms’ respiration
  The oxygen produced by the photosynthesis is necessary for the living
  organisms’ respiration. Thus without photosynthesis, no oxygen; without
  oxygen no respiration; without respiration no life on Earth.

  • Cleaning the atmosphere
  Photoautotrophs absorb carbon dioxide from surrounding air, and release
  Oxygen (produced by photosynthesis) in atmosphere.

  • Formation of Ozone layer
  Ozone layer is a thick layer in the atmosphere which is formed Ozone
  molecule (O3). Oxygen atoms which make ozone molecule are produced
  by photosynthesis. Ozone layer protects the Earth from high solar
  radiations, and this allows the existence of the life on the Earth.
  Synthesis of the organic substances: food for the heterotrophs (animal
  and mushrooms): The organic substances produced by photosynthesis
  are the food for the heterotrophs which are unable to synthesize these
  substances by their own means.

  B. Tests for starch in terrestrial plants
  The process of photosynthesis results in production of Oxygen and Organic
  substances like simple sugars, double sugars starch, amino acids among
  other. It is evident that, if someone need to be sure that photosynthesis has
  occurred, he can simple test for the presence of some of those substances
  produced by photosynthesis.

  Materials and substances needed to test for the presence of starch in
  terrestrial plants
  Bunsen burner, tripod stand, wire gauze,forceps, the petri dish, test tube
  holder, 250 cm3 beaker, dropping pipette, boiling tube, a water bath, leaf
  to be tested (hibiscus leaves are excellent),90% ethanol,cold water, iodine/
  potassium iodide solution.

  The process of testing for starch in a leaf
  1. Prepare a water bath; heat the water to boiling point and keep it boiling.
  2. Detach a leaf from a dicotyledonous plant that has been exposed to
  sunlight for at least three hours.
  

  3. With forceps, hold the leaf in boiling water for about 10 seconds. This will
  kill the cells, stop all chemical reactions and allow alcohol and iodine to
  penetrate the leaf more easily, and will removes the waxy cuticle which
  prevents entry of iodine/potassium iodide solution, will also denatures
  enzymes, particularly those which convert starch to glucose e.g. diastase.
  Boiling arrests all chemical reactions, since enzymes which catalyse the
  reactions are denatured. Denatured enzymes have altered or destroyed
  active sites due to heat, pH, and ionic concentration.
  4. Extinguish the Bunsen burner.
  5. Half fill a test tube with ethanol (ethyl alcohol).
  6. With forceps, place the leaf in the alcohol.
  7. Place the test tube containing ethanol and the leaf into the hot water.
  The ethanol will boil and dissolve out the chlorophyll in the leaf. When
  the leaf is nearly colorless, remove it from the ethanol with forceps and
  wash it in cold water. This will soften the leaf by replacing water removed
  by the ethanol.
  8. Place the softened leaf in a Petri dish and, using a dropping pipette,
  cover it with iodine solution. Leave for 3 minutes.
  9. If the colour of the leave turns blue-black, it means that it contains starch,
  and therefore photosynthesis has occurred in the leave. If no color
  change (Iodine Solution remains brown), starch is not present.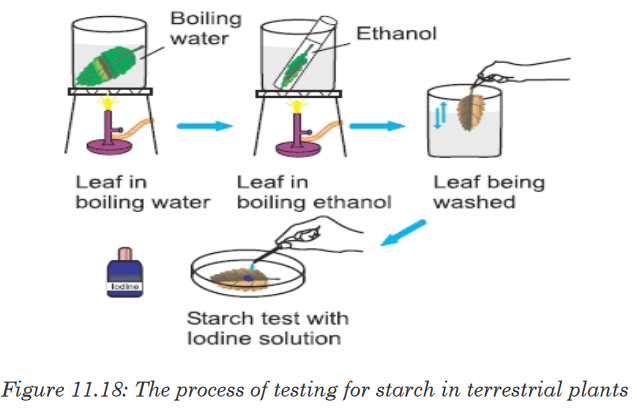
  

  
  

  We can also measure the process of photosynthesis via the production of
  oxygen, or by using the Audus apparatus to measure the amount of gas
  evolved over a period of time. Oxygen can be measured by counting bubbles
  evolved from pondweed. If you illuminate a plant (Presume you are using an
  aquatic/water plant) it will produce oxygen. You can put the plant under a
  

  funnel and collect the bubbles in an upturned test tube. If the gas is collected
  fresh, it will relight a glowing splint. You can also use Elodea, but we find
  Cabomba more reliable. Put the weed in a solution of NaHCO₃ solution. You
  can then investigate the amount of gas produced at different distances from
  a lamp.
  

  
  

  Application activity 11.5
  1. Which products of photosynthesis may be present but not revealed
  by the iodine test?
  2. Write down the steps to follow during testing for starch in terrestrial
  plant.
  3. Appreciate the necessity of boiling the leaf to be used in testing for
  starch in plants.
  4. Summarize the process of testing for Oxygen in aquatic plants.
  5. Explain why the leaf which is nearly colorless, should first be washed
  in cold water.
  6. Summarize the importances of photosynthesis to the living organisms.
  

  Skills lab 11
  
  

  Evidence of photosynthesis
  
  

  Materials: Large clear plastic cup, sodium bicarbonate solution (baking
  soda), aquatic filamentous green algae, large test tube, retor stand.
  
  

  Procedure:
  • Fill three large clear plastic cups with water and 3g or 6g of sodium
  bicarbonate as shown below:
  

  • Place aquatic green algae in three large test tubes. Fill the tube with
  water or sodium bicarbonate solution in the cup. Caution: handle the
  test tube carefully.
  • Hold your thumb over the mouth of the test tube. Turn the tube over,
  and lower it to the bottom of the cup. Make sure there is no air trapped
  in the tube.
  • Fix each setup in a stand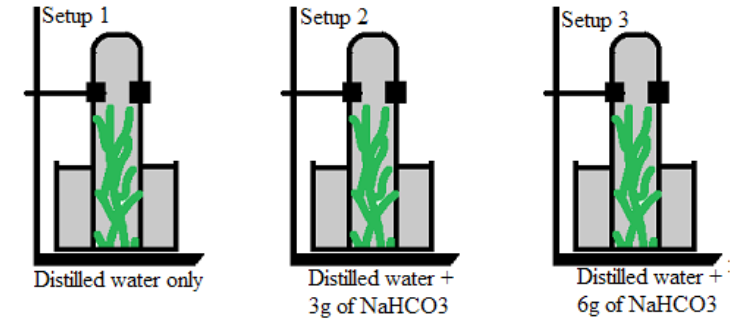
  

  
  

  • Place your setups in bright light.
  • After at least 20 minutes, record your observations and draw a
  conclusion.
  

  
  

  End unit assessment 11
  I. Choose whether the given statements are True (T) or False (F)
  1. Organisms that are heterotrophic can make their own food.
  2. Photosynthesis has two stages - light reaction and dark reaction.
  3. CAM cycle includes triple carboxylation.
  4. A pigment is a material that changes colour of reflected or transmitted
  light.
  5. Within leaves, chloroplasts are responsible for respiration.
  

  II. Multiple Choice Questions
  1. Green plants does not require which of the following for photosynthesis?
  (a) Sunlight   (b) CO₂   (c) O₂   (d) Water
  

  2. C-4 cycle occurs in
  (a) Wheat (b) Rice (c) Sugar cane (d) All of the above
  3. Autotrophs are commonly called producers because they
  (a) Produce young plants
  (b) Produce CO₂ from light energy
  (c) Produce sugars from chemical energy
  (d) Produce water from light energy
  

  III. Long Answer Type Questions
  1. State and explain the types of autotrophic nutrition.
  2. Relate the structure of a chloroplast with its function and structure of
  leaf in photosynthesis.
  3. State the pigments involved in light absorption.
  4. Outline the three main stages of Calvin cycle.
  5. Compare anatomy of C4 and CAM plants.
  6. Differentiate between C4, CAM and C3 plants during carbon dioxide
  fixation.
  7. Investigate the effect of light intensity on the rate of photosynthesis.
  The chart below shows the sequence of events that takes place in
  the light dependent reactions.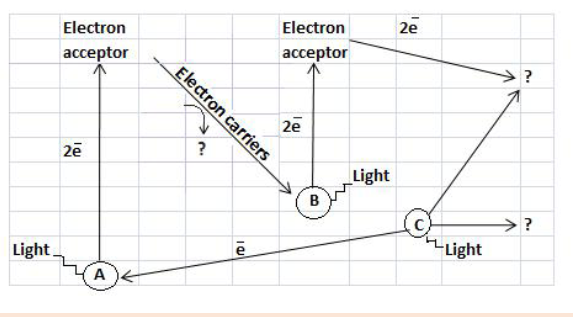
  

  
  

  a) Identify the point A and B
  b) What process is taking place at C?
  c) What are the products of the light dependent reaction? (They are
  indicated by? on the diagram).
  

  8. The diagram below summarizes the movement of materials into and
  out of chloroplast. Identify the substances moved, indicated by labels
  A-D.

  
  

  9. The diagram below represents the CALVIN’S Cycle also known as
  the light independent reactions of the photosynthesis.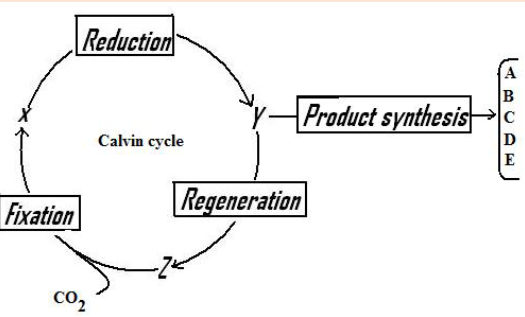
  

  
  

  a). Name substances X, Y and Z.
  b). (i) State any two steps of the Calvin cycle which are endothermic.
  (ii) State the source of the energy consumed in these two steps.
  c). Why is it said that the reduction is the most important step of the
  Calvin cycle?
  d). Name any two products represented by A, B, C, D or E.
  

  
  

• UNIT 12: THE CHEMICAL BASIS OF LIFE

  Key Unit competence: Explain the use of biological molecules in
  living organism.

  Introductory Activity 12
  

  
  

  Analyze all foods in the figure above and answer the questions below:
  a). Among the foods observed in figure, plan a list for your menu for
  breakfast, lunch and supper. Justify your choices.
  b). Are there foods you missed on the list which you prefer to eat?
  Why?
  c). List the nutrients our body gains from different food and justify
  why all are needed.
  

  12.1. Biological molecules
  

  Activity 12.1
  1. Discuss chemical elements, sub-units of different types of
  carbohydrates, lipids and proteins.
  2. What do you know about the function of water to living organisms?
  

  12.1.1. The chemical elements that make up carbohydrates,
  lipids and proteins

  a. Carbohydrates
  Carbohydrates comprise a large group of organic compounds which contain
  carbon, hydrogen and oxygen. The word carbohydrate indicates that these
  organic compounds are hydrates of carbon. Their general formula is
  .In carbohydrates the ration hydrogen-oxygen is usually 2:1.
  Carbohydrates are divided into three groups including the monosaccharide
  (single sugars), disaccharides (double sugars) and polysaccharides (many
  sugars). The most common monosaccharide of carbohydrates is glucose
  with molecular formula C6 H12 O6 .
  Lipids
  Lipids are a broad group of naturally occurring molecules which include
  waxes, sterols, fat soluble vitamins (such as vitamins A, D, E and K),
  monoglycerides, diglycerides, triglycerides, Phospholipids and others.
  Lipids are made by carbon, hydrogen and oxygen, but the amount of oxygen
  in lipids is much smaller than in carbohydrates.
  Lipids are grouped into fats which are solid at room temperature and oils
  which are liquid at room temperature.
  

  b. Proteins
  Proteins are organic compounds of large molecular mass. For example,
  the hemoglobin has a molecular mass of 64500. In addition to carbon,
  hydrogen and oxygen, proteins always contain nitrogen, usually Sulphur and
  sometimes phosphorus.
  

  c. Water
  Living organisms contain between 60% and 90% of water, the remaining
  being the dry mass. Water is made up of only two elements, Hydrogen and
  Oxygen.
  

  The function of water is defined by its physical and chemical properties that
  differ from those of most liquids and make it effective in supporting life.
  

  12.1.2. The sub-units that make up biological molecules
  a. Sub-units of Carbohydrates
  In carbohydrates the following three categories are identified:
  Monosaccharides , disaccharides and polysaccharides.

  i. Monosaccharides
  Monosaccharides are the smallest subunits and are made up of single
  sugar molecules. Monosaccharides are the sugars like galactose, fructose
  and glucose with a general formula C₆ H₁₂ O₆ , and these typically take on
  a ring-shaped structure.

  All monosaccharides are reducing sugars capable of acting as a reducing
  agents because they have a free aldehyde group or a free ketone group.
  

  Sources of Monosaccharides:
  • Glucose: Fruits and vegetables are natural sources of glucose. It’s also
  commonly found in syrups, candy, honey, sports drinks, and desserts.
  • Fructose: The primary natural dietary source of fructose is fruit, which
  is why fructose is commonly referred to as fruit sugar.
  • Galactose: The main dietary source of galactose is lactose, the sugar
  in milk and milk products, such as cheese, butter, and yogurt.

  ii. Oligosaccharides
  These are complex carbohydrate chains made up of two to twenty
  simple sugars joined together with a covalent bond. The most common
  oligosaccharide is the disaccharide, and examples of this include sucrose,
  maltose and lactose whose general formula is C₁₂ H₂₂ O₁₁ .

  A disaccharide is the sugar formed when two monosaccharides are joined
  by glycosidic bond. Like monosaccharides, disaccharides are soluble in
  water, have sweet taste, and they are reducing sugars because they are
  able to reduce Copper II Sulfate of benedict solution directly by heating
  into copper II oxide except sucrose which is non-reducing sugar which are
  unable to reduce the copper ions in Benedict’s solution.

  This makes the color of Benedict’s solution to persist when this sugar is
  boiled with it.

  Sucrose is made up of two monosaccharides: Glucose and fructose
  Maltose is made up of two monosaccharides: Glucose and glucose
  Lactose is made up of two monosaccharides: Glucose and galactose
  

  In maltose ring, the two ring of glucose are bonded by the -1, 4-glycosidic
  bond while in sucrose the glucose and fructose are bonded by -1,
  2-glycosidic bond.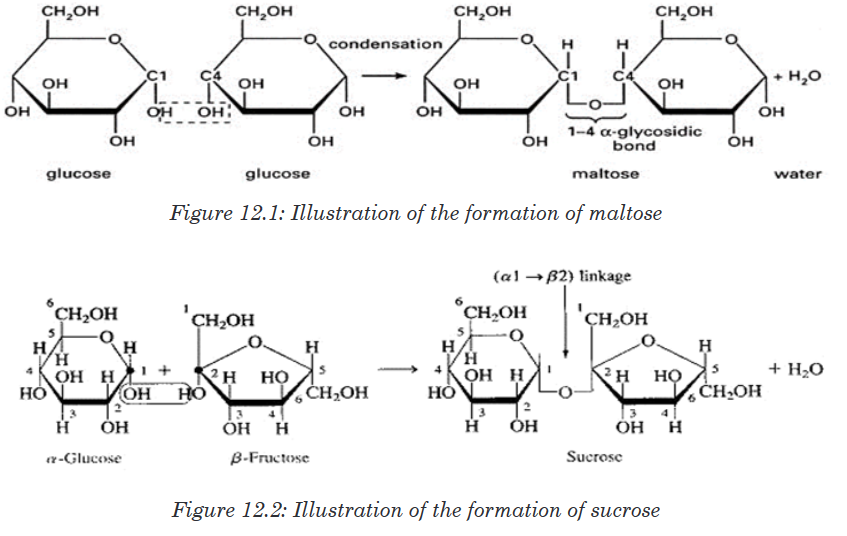
  

  
  

  
  

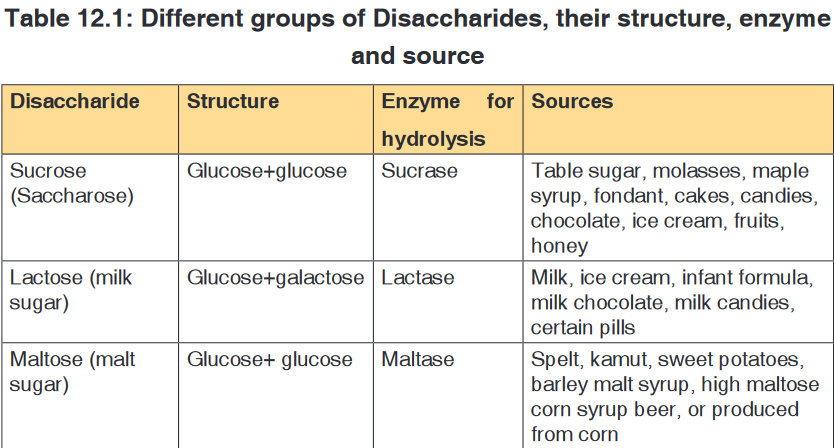
  iii. Polysaccharides
  These are known for their ability to store energy and are made up of long
  chains of glucose sugars. The most common polysaccharides are starch
  (sugar of plant tissues), glycogen (glucose in the human liver and muscles),
  cellulose (structural polysaccharide in plants; which acts as a dietary fiber
  

  when consumed), chitin (sugar found in exoskeleton of arthropods) and
  peptidoglycan (sugar found in the bacteria cell membrane).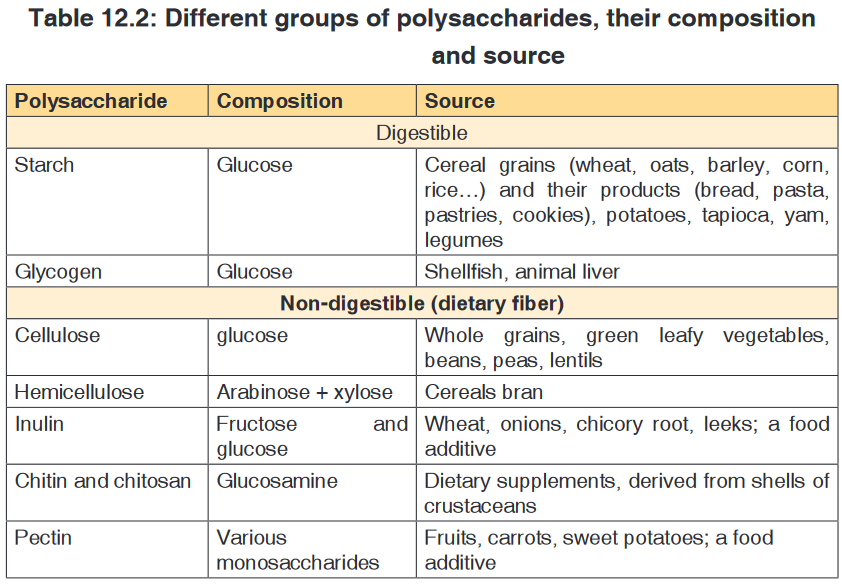
  

  
  

  b. Sub-units of Proteins
  These are also referred to as macro-nutrients. The protein are also called
  body- building food.

  The protein molecules are made up of small units called amino acids joined
  together like links in a chain.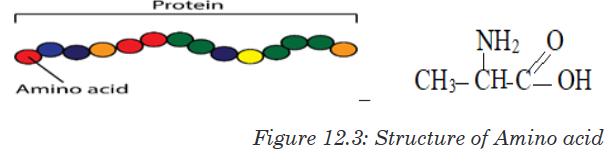
  

  
  

  There are 21 different amino acids and each has its own chemical name.
  Different proteins are made when different numbers and types of amino acids
  combine through a covalent peptide bond. Proteins are therefore known as
  polypeptides.
  Examples of proteins
  a). Collagen, myosin and elastin found in meat,
  b). Caseinogen, lactalbumin, lacto globulin found in milk,

  c). Avalbumin, mucin and liporitellin found in eggs,
  d). Zein found in maize
  

  The 21 different amino acids found in protein are:
  Arginine, Serine,Selenocysteine, Leusine, Histidine,Threonine, Glycine,
  Methionine, Lysine, Asparagine, Proline, Phenylalanine, Aspartic acid,
  Glutamine, Alanine, Tyrosine, Glutamic acid, Cysteine,Valine, Tryptophan,
  Isoleucine.
  They are used to repair, to build, to maintain our bodies; to make muscles
  and to make breast milk during lactation period. The proteins are classified
  into two categories: animal or complete proteins and plant proteins or
  incomplete proteins.
  

  c. Sub-units of lipids
  Lipids are made by two components namely glycerol and fatty acids. The
  chemical formula for glycerol is C₃ H₈ O₃ .
  

  Structural formula of glycerolis
  

  
  

  
  

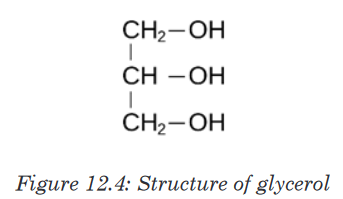
  Sources and classification of lipids
  Fats and oils are obtained from both the plants and animals. And fat is
  present in food either as visible fat or invisible fat.

  Visible fat is the one that is easily seen or detected in food for example; fat
  in meat, butter, margarine, lard, suet and cooking fat and oil.
  

  
  

  
  Invisible fat is the part of food that is not easily seen for example fat with
  in lean meat, egg yolk, flesh of oily fish, groundnuts, soya beans, avocado
  and fat found in prepared foods, for example, pastry, cakes, biscuits, French
  fries, pancakes, croquettes.
  

  
  

  Lipids are of different types as it is summarized in the following table.

  
  

  The following are three main types of lipids: Triglycerides, phospholipids and
  steroids:
  • Triglycerides: These are lipids that are obtained from cooking oils,
  butter and animal fat. They are made up with: one molecule of glycerol
  and three molecules of fatty acids bonded together by Ester bonds.
  The triglycerides play the role like storing energy they have thermal
  insulation and protective properties

  
  

  • Sterols: These are lipids that include steroid hormones like testosterone
  and oestrogen, cholesterol that is formed four carbon-based rings and
  it helps in regulation of fluid and strength of the cell membrane.

  • Phospholipids: They are made up of one molecule of glycerol, two
  molecules of fatty acids and one phosphate group. The phospholipids
  form a molecule that is part hydrophobic, part hydrophilic, ideal for
  basis of cell surface membranes
  

  
  

  Functions of lipids
  • Fats are a source of energy. They supply energy to the body more than
  carbohydrates and proteins.
  • Fat surrounds and protects important organs of the body such as
  the kidney and the heart, however too much fat around the organs is
  dangerous as it slows down their functioning.
  

  • Fat forms an insulating layer beneath the skin to help keep us warm
  by preserving body heat and it also protects the skeleton and organs.
  • Fat provides a source of fat soluble vitamins A, D, E and K in the body.
  • Fat is a reserve of energy for long term storage and can be used if
  energy intake is restricted.
  • Fat in foods provides texture and flavour in foods and it helps to make
  it palatable.

  Food containing fat provides a feeling of satiety or fullness after a meal as
  fat is digested slowly.

  12.1.3. The structure of proteins and their function

  Activity 12.1.3
  1. From the books make a research on proteins and answer to the
  following questions:
  a). What are different structures of proteins?
  b). Differentiate globular proteins and fibrous proteins.
  2. Take a plastic cord, create the bulk on it and suppose that those are
  monomers of a long chain of polymer (the whole cord), heat it using
  a Bunsen burner or another source of fire. Discuss the change that
  takes place.
  

  Proteins are organic compounds of large molecular mass ranging up to
  40,000,000 for some viral proteins but more typically several thousand. For
  example, the hemoglobin has a molecular mass of 64,500. Proteins are
  polymers of amino acids and they are not truly soluble in water, but form
  colloidal suspensions. In addition to carbon, hydrogen and oxygen, proteins
  always contain nitrogen, usually Sulphur and sometimes phosphorus.
  Whereas there are relatively few carbohydrates and fats, the number of
  proteins is limitless. Coined by a Dutch chemist Mulder the word protein
  etymologically means “of the first importance” due to the fundamental role
  they play in living cells.

  a. Amino acids
  Amino acids are group of over a hundred chemicals of which around 20
  commonly occur in proteins. They always contain a basic group, the amine
  group (-NH2) and an acid group (-COOH) together with -R group side chain
  (Figure 12.14). All the amino acid differs one to another by the structure of
  their side chain.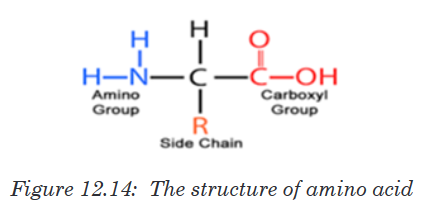
  

  
  

  Amino acids are divided into two categories including essential amino acid
  and non-essential amino acid. Essential amino acids are those amino acids
  which cannot be synthesized by the body. They include isoleucine, leucine,
  lysine, methionine, phenylalanine, threonine, tryptophan, valine, arginine
  and histidine. Non –essential amino acids are synthesized by the organism.
  They include alanine, asparagine, aspartic acid, cysteine, glutamine,
  glutamic acid, glycine, proline, serine and tyrosine. The simplest amino acid
  is glycine with H as -R group (Figure 12.15. a). The other one is Alanine with
  –CH3 as -R group (Figure 12.15.b). All 20 amino acids can be found in diet
  from animals such as meat, eggs, milk, fish…but diet from plant lack one or
  two essential amino acids such plant are beans, soy beans…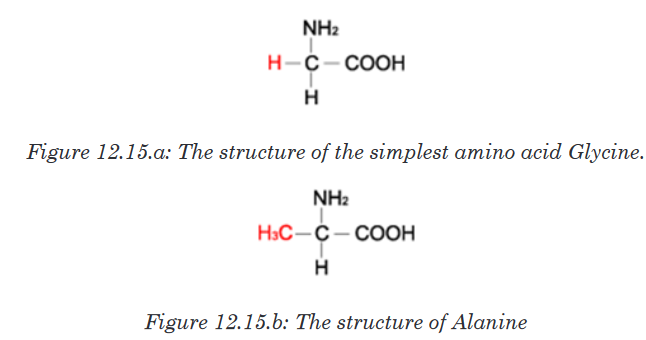

  
  

  When an amino acid is exposed to basic solution, it is deprotonated (release
  of a proton H+) to became negative carboxylate COO -while in acid solution
  it is protonated (gains of a proton H+) to became ammonium positive ion
  -NH3 +(Figure 12.16.a and Figure 12.16.b).

  
  

  
  

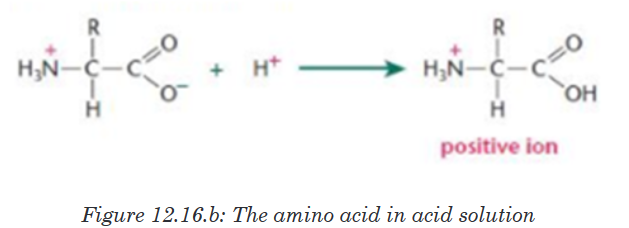
  At a physiological pH, usually around 7, the amino acid exists as ZWITTERION
  (from German means hermaphrodite) it is a molecule with two different
  charges (positive and negative) at the same time (Figure 12.17).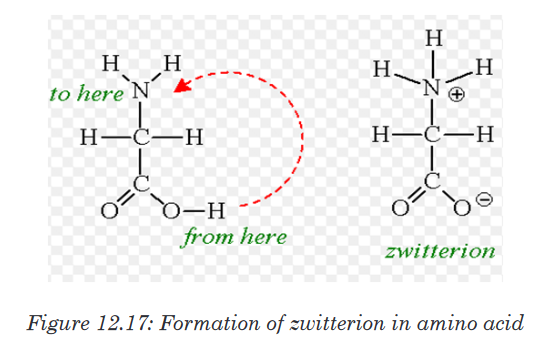

  
  

  b. Formation and breakage of peptide bond
  The formation of peptide bond follows the same pattern as the formation
  of glycosidic bond in carbohydrates and ester bond in fats. A condensation
  reaction occurs between the amino group of one amino acid and the carboxyl
  group of another, to form a dipeptide (Figure 12.18).
  

  
  

  A peptide bond is formed between two amino acids to form a dipeptide
  molecule, if three amino acids are assembled together it is a tripeptide, four
  amino acids form a tetrapeptide and so on. A long chain of amino acid it is
  called a polypeptide. The polypeptide chain or oligopeptide comprise more
  than 50 amino acids joined together by a peptide bond.
  

  During digestion, proteins are hydrolyzed and give their monomer amino
  acids small molecules that can be diffused in the wall of intestine to the
  organism. In hydrolysis the peptide bond break down by the addition of a
  water molecule (Figure 12.19).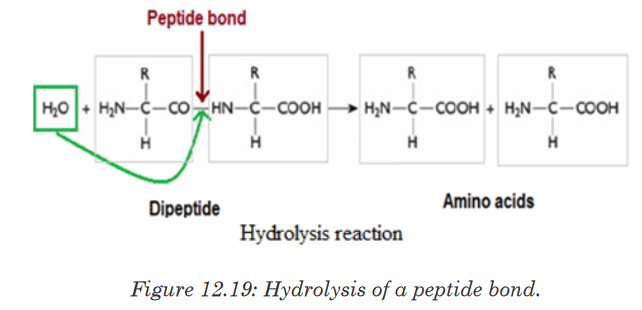
  

  
  

  c. Structure and denaturation of proteins
  The long chain of polypeptide can take different form according to its
  molecular weight and the types of bond that hold together atoms and
  molecules, those form are described as primary, secondary, tertiary and
  quaternary structure. A human has tens of thousands of different proteins,
  each with a specific structure and function. Proteins in fact are the most
  structurally sophisticated molecules known. Consistent with their diverse
  functions, they vary extensively in structure, each type of protein having a
  unique three-dimensional shape.
  

  Structure of proteins
  i. Primary structure of proteins
  Primary structure of a protein is the sequence of amino acid in a linear shape,
  the amino acid are joined together with the peptide bond.The alteration of
  this linear sequence (change of the shape) can inhibit the proper function
  of the protein as well as the function of the protein depending on its three
  dimensional shape.
  

  
  

  ii. Secondary structure of proteins
  The regular arrangement of amino acids in primary structure can induce
  the interaction of the back bone of the polypeptide chain (side chain) by
  hydrogen bonds. Those side chains are coiled and folded in the patterns
  that contribute to the protein’s overall shape. One such secondary structure
  is α-helix and sometime β-pleated sheet.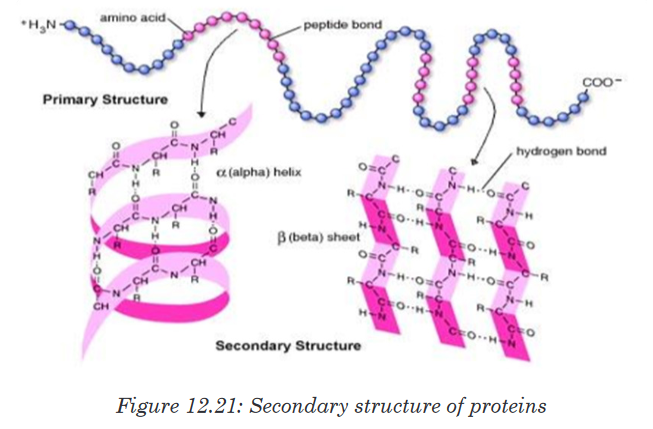

  
  

  iii. Tertiary structure of proteins
  In addition to hydrogen and peptide bond in primary and secondary structure,
  the tertiary structure of protein has other types of interaction called hydrophobic
  interaction. Once the amino acid side chains are close together, Van der
  Waals interactions hold it together, and their stability depends on ionic bond
  between positively and negatively charged R groups. The cumulative effect
  of those week interactions reinforced with the covalent bonds called disulfide
  bridges (-S-S) give the protein a unique shape.
  

  
  

  iv. Quaternary structure of proteins
  Quaternary structure involves different polypeptide chains into one functional
  three dimensional molecules. For example, the protein that bind oxygen in
  red blood cells (Hemoglobin) is made by four polypeptide subunits, two of
  the same kind (α chains) and two of another kind (β chains). Both α and β
  sub-units primarily are α helical secondary structure with anon polypeptide
  chain iron that binds oxygen called Haeme.
  

  
  

  Globular proteinsuch as haemoglobin and enzymes are soluble in water.
  In coiling, the hydrophobic R group is dressed toward the inside while the
  hydrophilic is addressed toward the outside. The opposite is observed in
  fibrous protein such as collagen and keratin which are insoluble in water.
  Such protein may contain another group of compound which is not an amino
  acid called prosthetic group for example the iron (haeme) is prosthetic group
  in haemoglobin, magnesium in green pigment of plant (chlorophyll) is also a
  prosthetic group.
  

  Protein denaturation
  Protein denaturation is a mechanism by which quaternary, tertiary and
  secondary structure of protein changes their shape due to external stress
  called agent or factor of denaturation. Protein denaturation may be temporary
  or permanent due to a variety of factors. The agent of denaturation may
  include heat, changes in pH, Ultra Violet (UV°) rays, high salt concentration
  and heavy metals. Cooked egg is an example of a denatured protein due to
  the heat. This also explains why excessively high fever disease is fatal to the
  organism because protein in the blood denature at high temperature. The
  agents of denaturation will denature protein causing the loose of its shape
  and hence its ability to function.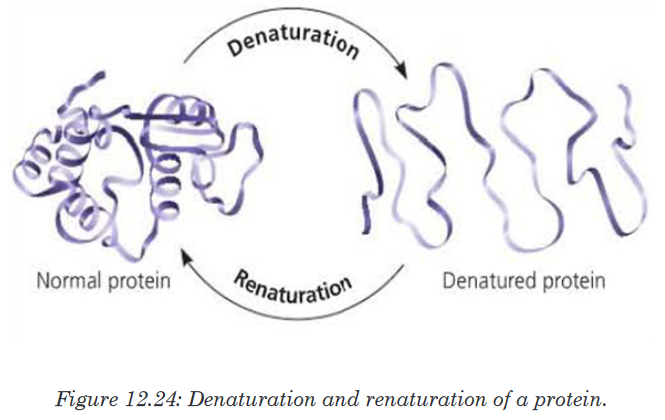
  

  
  

  d. Functions of proteins.
  • Proteins such as lipase, pepsin and protease act as enzymes as they
  play a crucial role in biochemical reaction where they act as catalysts.
  • Proteins play an important role in coordination and sensitivity (hormones
  and pigments).
  

  • Proteins have a transport functions. Example: Haemoglobin transport
  oxygen
  • Proteins in the cell membrane facilitate the transport of substance
  across the cell membrane.
  • Proteins provide a mechanical support and strength.
  • Proteins such as myosin and actin are involved in movement.
  • Proteins play the role of defense of the organisms. Example: Antibodies
  are proteins

  12.1.4. Molecular structure and functions of polysaccharides,
  glycogen and cellulose
  

  Activity 12.1.4
  1. Based on the meaning of monosaccharide, what is the meaning of
  polysaccharide?

  2. Classify the following compound into polysaccharide, monosaccharide
  and disaccharide
  a). Glucose, fructose and galactose
  b). Lactose, sucrose, and maltose
  c). Starch, cellulose and glycogen

  3. Use glucose to form any polysaccharide of your choice

  In the same way that two monosaccharides may combine in pairs to give
  a disaccharide, many monosaccharides may combine by condensation
  reactions to form a polysaccharide. The number of monosaccharides that
  combine is variable and the chain produced may be branched or unbranched.
  Polysaccharide are many but the most known are starch, glycogen and
  cellulose.
  

  a. Starch
  Starch is made up of two components: amylose and amylopectin. Amylose
  is a linear unbranched polymer of 200 to 1500 α-glucose units in a repeated
  sequence of α-1,4-glucosidic bonds. The amylose chain coils into helix held
  by hydrogen bonds formed between hydroxyl groups. A more compact shape
  is formed. The amylose helices are entangled in the branches of amylopectin
  to form a complex compact three dimensional starch molecule.

  Amylopectin is a branched polymer of 200 to 200,000 α-glucose units per
  starch molecule. The linear chains of α-glucose units are held together by
  α-1,4-glucosidic bonds. Branches occur at intervals of approximately 25 to 30
  

  where α-1,6-glucosidic bonds occur. Starch grains are found in chloroplast,
  potato tubers, cereals and legumes. Starch is insoluble in cold water. It is
  digested by salivary amylase and pancreatic amylase into maltose and the
  latter is hydrolyzed by maltase enzyme to form glucose. Therefore, diabetic
  people should avoid tubers since they are rich in starch which in turn gives
  glucose.
  

  
  

  b. Glycogen
  Glycogen is often called animal starch because it is a major polysaccharide
  storage material in animals and fungi. The brain and other tissues require
  constant supply of blood glucose for survival. Some tissues particularly the
  liver and skeletal muscles store glycogen in the form that can be rapidly
  mobilized to form glucose. Like starch, glycogen is made up of α-glucose
  and exists as granules. It is similar to amylopectin in structure but it has
  shorter chains (10-20glucose unit) and is more highly branched.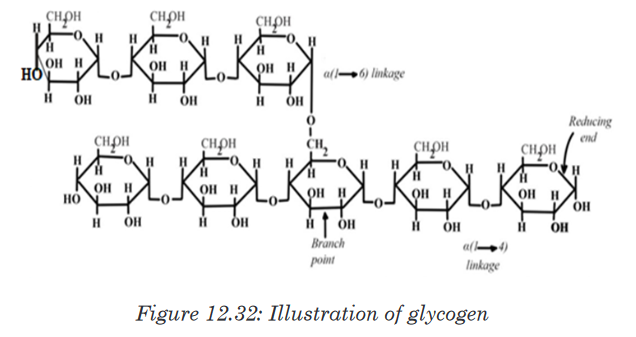
  

  
  

  c. Cellulose
  Cellulose is the structural polysaccharide in plant cell wall. It is found in
  vegetables and fruits but cannot be hydrolyzed by enzymes in the human
  digestive system. Cellulose is composed of long unbranched chains of up
  to 10,000 β-glucose units linked by β-1,4-glucosidic bonds. Each β-glucose
  unit is related to the next by a rotation of 180°C with OH groups projecting
  outwards on either side of the chain.

  Cellulose chains run parallel to one another. Unlike amylopectin and
  glycogen molecules, there are no side chains (no branch) in the cellulose.
  This allows the linear chains to lie close together. Many H-bonds are formed
  between the OH groups of adjacent chains. The chains group together to
  form microfibrils arranged in larger bundles of macrofibrils. The fibrils give
  the plant cell their high tensile strength and rigidity. The layers of fibrils are
  permeable to water and solutes.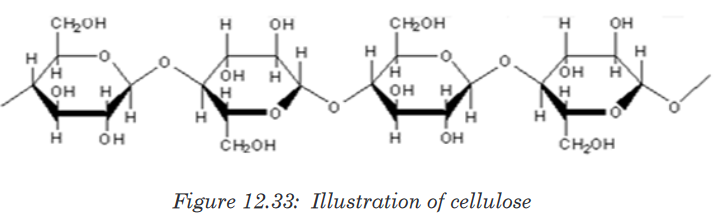
  

  
  

  12.1.5. Isomerism of monosaccharide and formation of
  glycosidic bond
  Monosaccharides are group of sweet and soluble crystalline molecules of
  relatively low molecular mass. They are named with the suffix –ose. The
  general formula for a monosaccharide is (CH₂ O) , with n the number of
  carbon atoms. The simplest monosaccharide has n=3 and it is a triose
  sugar. When n = 5, this is a pentose sugar, and when n = 6, this is a hexose
  sugar. The two common pentose sugars are ribose and deoxyribose, while
  the most known hexose is glucose. Its molecular formula is C6H12O6. It is
  the most important simple sugar in human metabolism called simple sugar
  or monosaccharide because it is one of the smallest units which has the
  characteristics of this class of carbohydrates.

  a. Isomerism and ring formation
  Monosaccharides can exist as isomers. The isomer is defined as each of
  two or more compounds with the same formula but a different arrangement
  of atoms in the molecule and different properties. The isomer can also be
  each of two or more atomic nuclei that have the same atomic number and
  

  the same mass number but different energy states. For example, glucose,
  fructose and galactose share the same molecular formula which is C6H12O6
  however they differ by their structural formulae as follow:
  

  
  

  One important aspect of the structure of pentoses and hexoses is that the
  chain of carbon atoms is long enough to close up on itself and form a more
  stable ring structure. This can be illustrated using glucose as an example.
  When glucose forms a ring, carbon atom number 1 joins to the oxygen on
  carbon atom number 5.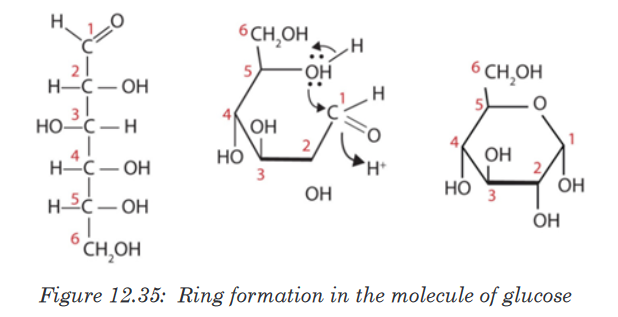
  

  
  

  All hexoses sugars can exist as straight-chain structures but they tend to
  form ring structures. Glucose, fructose, galactose can exist in ring structures.
  

  
  

  Ring monosaccharides are said to be alpha (α) if the -OH group located
  on carbon 1 is below the ring and beta (β) when the -OH group is above
  the ring. The molecule of glucose for example can exist as alpha and beta
  glucose denoted by α-glucose and β-glucose.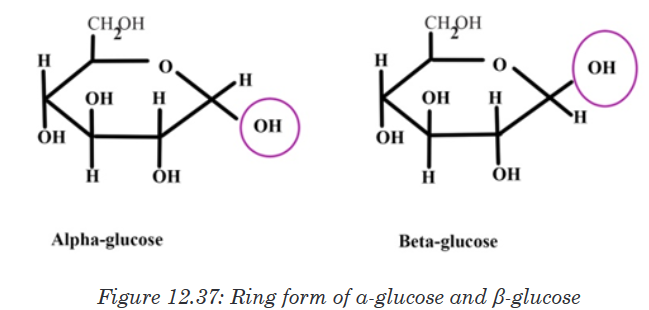
  

  
  

  b. Formation and breakdown of glycosidic bonds
  Monosaccharides may combine together in pairs to give a disaccharide
  (double-sugar). The union involves the loss of a single molecule of water
  and is therefore a condensation reaction. The bond which is formed is
  called a glycosidic bond. It is usually formed between carbon atom1of one
  monosaccharide and carbon atom 4 of the other, hence it is called a -1, 4-
  glycosidic bond. Any two monosaccharides may be linked together to form a
  disaccharide of which maltose, sucrose and lactose are the most common.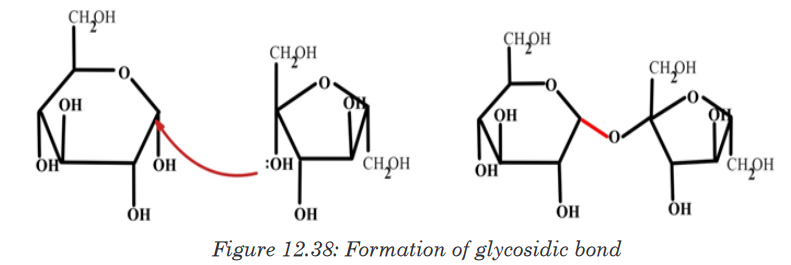
  

  
  

  The addition of water under suitable conditions is necessary if the disaccharide
  is to be split into its constituent monosaccharide. This is called hydrolysis
  water-breakdown or more accurately, breakdown by water.
  

  Application activity 12.1

  1. Provided with different kinds of biological molecules such as
  carbohydrates, proteins, lipids, make a table to show their food source
  you always take and suggest their functions.
  2. Explain what is meant the essential amino acids
  3. Describe the formation of a peptide bond?
  4. Alanine is an amino acid with -CH3 as a side chain. Writes its structural
  formulae.
  5. Most of the plant lacks one or more of the essential amino acids
  needed by the body explain how a vegetarian can obtain the essential
  amino acids.
  6. What are the structures of proteins?
  7. How do we call the bond in a dipeptide?
  8. What type of reaction is involved in the formation of glucose from
  starch?
  9. Use the type of reaction above to form glucose from sucrose molecule
  10. Describe how the glycosidic bond is formed.
  11. Describe the major types of starch
  

  12.2. Test for the presence of different biological molecules
  in variety of context

  Activity 12.2
  You are given solutions containing different food stuffs including maize
  flour, vegetable cooking oil, and egg white sugar cane liquid and passion
  fruit. Using prior knowledge of biological molecules to suggest the type of
  biological molecule in each one of them. Suggest the chemical tests used
  to identify each of the molecules.
  

  2.2.1. Test for carbohydrates
  Activity 12.2.1
  Materials required:
  Starch powder, Irish potatoes juice, prepared porridge, Iodine solution,
  beakers, droppers, source of heat and test tubes

  A.Test for starch
  Procedure
  • Mix 1g of starch powder with 100ml of water
  • Boil the mixture while stirring; then cool the solution
  • Boil the mixture while stirring; then cool the solution
  • Put 2ml of starch solution in a test tube labeled 1, 2ml of Irish potato
  juice in a test tube labeled 2 and 2ml of prepared porridge in a test
  tube labeled 3
  • In each test tube put 2 drops of Iodine solution and shake
  • Record your observation and draw a conclusion

  B.Test for reducing sugar
  Requirements:
  Glucose powder, beaker and test tube, Benedict solution, Bunsen burner,
  droppers.
  Procedure:
  • In the beaker mix 1cm3 of water and 1g of glucose powder.
  • Pour the prepared solution of glucose in a test tube and
  • Add 2ml of benedict’s solution and heat
  • Record your observation.

  Biological molecules are grouped into organic molecules including
  carbohydrates, proteins, lipids, nucleic acids and vitamins. They also contain
  inorganic molecules such as minerals and water. The first four organic
  molecules are called macromolecules because they are required in organism
  in large quantity. Carbohydrates including starch, reducing and non-reducing
  sugars appear in this category and are the main energy producers in the
  organisms. Others, including lipids and proteins are needed for building
  organisms while vitamins protect the organisms against diseases.
  

  We need to ensure that what we take from diet have all required biological
  molecules.
  a. Test for starch
  Carbohydrates such as starch are tested by mixing a sample with 2-4 drops
  of iodine or Lugol’s solution. If the sample contains starch the solution
  will turn from a yellow to brown color to a dark purple/dark blue (Figure
  12.10). The color change is due to a chemical reaction between the large
  carbohydrate molecule and the iodine ions. If the sample does not contain
  starch the solution remains yellow-brown.
  

  
  

  b. Testing for reducing and non-reducing sugar
  The presence of reducing sugar can be tested by using benedict reagent.
  Benedict solution has copper ions that have a light blue color. When this
  solution is heated in the presence of simple reducing sugars such as
  glucose, the blue color of copper ions changes from a light green color to
  rusty orange-brown color (Figure 12.11).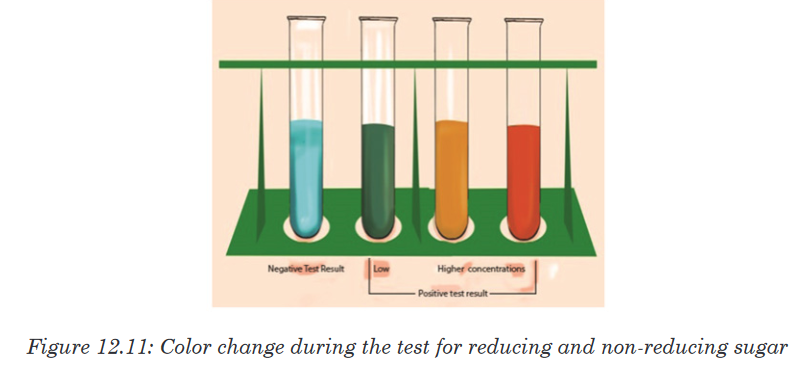
  

  
  

  If the color of Benedict reagent persists, the sugar tested is not a reducing
  sugar. Note that there is no special reagent to test for non-reducing sugar, but
  by the addition of HCl, non-reducing sugars can be hydrolyzed to reducing
  sugars. To test the presence of reducing sugars, a solution of sodium
  hydroxide is needed to neutralize the acidity because Benedict reagent
  works better in neutral solution.

  12.2.2. Test for proteins
  
  

  Activity 12.2.2
  Requirements
  Milk, eggs, soybeans, test tubes, beakers, mortar for crushing beans, 1%
  NaOH or 1% KOH solution, 0.1M of CuSO4 solution and Millon’s reagent.
  
  

  Procedure
  • Extract the white fluid from an egg (albumen)
  • Prepare an extra of soya bean and 10ml of fresh milk
  • Put 2ml of albumen solution in a test tube labelled A1 and 2ml in A2
  • Put 2ml of milk solution in a test tube labelled B1 and 2ml in B2
  • Put 2ml of soya bean solution in a test tube labelled C1 and 2ml in
  C2
  • Put 1ml of KOH or NaOH solution in each of the test tubes A1, B1,
  and C1. Shake the mixture and add 1ml of CuSO4 solution in each
  (A1, B1, and C1) test tube
  • Put 1ml of Millon’s reagent in each of test tubes (A2, B2, and C2).
  Shake the mixture and thereafter boil the three test tubes (A2, B2,
  and C2).
  • Record and interpret your observations.
  

  The Biuret reagent is used to test for the presence of proteins. It contains
  copper ions with blue characteristic color. During the copper ions react with
  protein molecules and causes the biuret solution to turn from a light blue
  color to purple if proteins are present.

  
  

  The test can also be done by using Millon’s reagent, which in the presence
  of proteins, the Millon reagent changes from colorless to pink.
  

  12.2.3. Test for lipids

  Activity 12.2.3

  Laboratory experiments
  Use olive oil to carry out the following experiments
  To 2 cm³ of olive oil in the test tube:
  • Add 5 cm³ of ethanol followed by 5 drops of water.
  • Shake the mixture and record your observation.
  To another test tube containing 2 cm³ of olive oil:
  • Add 5 drops of Sudan III solution
  • Shake thoroughly and examine the mixture in the test tube after few
  minute and record your observations
  

  The presence of lipids can be determined using Sudan III indicator, which is
  fat-loving molecules that are colored. During the test for a solution containing
  lipids, two results are likely to be found: there is either the separation of
  layers indicating the levels of water and lipid, or the dye migrates toward
  one of the layers. If the mixtures are all water soluble, the conclusion is that
  the lipids are not present. In this case, the Sudan III indicator will form small
  micelles/droplets and disperse throughout the solution.
  

  A positive result indicates the lipid layers sitting on top of the water layer with
  a red-orange color. When using ethanol for testing lipids the presence of the
  color changes from colorless to milky (emulsion test).
  

  
  

  12.2.4. Test for vitamin C (Ascorbic Acid)

  Activity 12.2.4

  Squeeze the orange fruits to extract the juice and carry out the following
  test.
  

  
  

  Vitamin C is tested by using DCPIP (Dichlophenol Indophenol). Its positive
  (presence of vitamin C) test decolorizes DCPIP, while the negative (absence
  of vitamin C) test is indicated by the persistence blue color of DCPIP.
  

  12.3. The structure of DNA

  Activity 12.3

  1. Discuss the following in the class.
  Nucleotide sequences make DNA, and DNA makes you. If DNA is
  a double stranded structure, how do the two strands in DNA join or
  stick together to form double stranded structure?
  Make a report on it and present to the class.
  

  A basic unit nucleotide of DNA (Deoxyribo Nucleic Acid) is made up of
  pentose sugar(Deoxyribose) , a nitrogenous base, and a phosphate sugar.
  However, a combination of only a pentose sugar and nitrogenous base,
  without phosphate group, is called nucleoside.
  

  Pentose sugar + Nitrogenous base + Phosphate group =Nucleotide
  

  Pentose sugar + Nitrogenous base=Nucleoside
  

  In DNA, bases are covalently bonded to the 1’ carbon of the pentose sugar.
  The purine and pyrimidines bases attached to pentose sugar from different
  positions of their nitrogen bases. Purine bases use the 9th position of nitrogen
  to attach with 1’ carbon of pentose sugar, while pyrimidine bases use the 1st
  position of nitrogen to attach with 1’ carbon of pentose sugar.
  

  In both DNA, the phosphate group (PO42–) attaches to the 5’ carbon of
  pentose sugar. Thus, by attaching phosphate group to a nucleoside yields a
  nucleoside phosphate or nucleotide. The complex of deoxyribose, nitrogenous
  base and phosphate group is called DNA nucleotide (a deoxyribonucleotide).
  

  
  

  Phosphodiester Bond formation
  Two nucleotides are covalently joined together by a bond called
  phosphodiester bond. In phosphodiester bond, the phosphate group, which
  is attached on 5’ of one nucleotide, forms a bond with the 3’ carbon of another
  nucleotide. In this way, many phosphodiester bonds are formed between
  sugar and phosphate groups. The repeated sugar-phosphate-sugar-
  phosphate backbone is a strong one. Because of this strong backbone, DNA
  is a stable structure.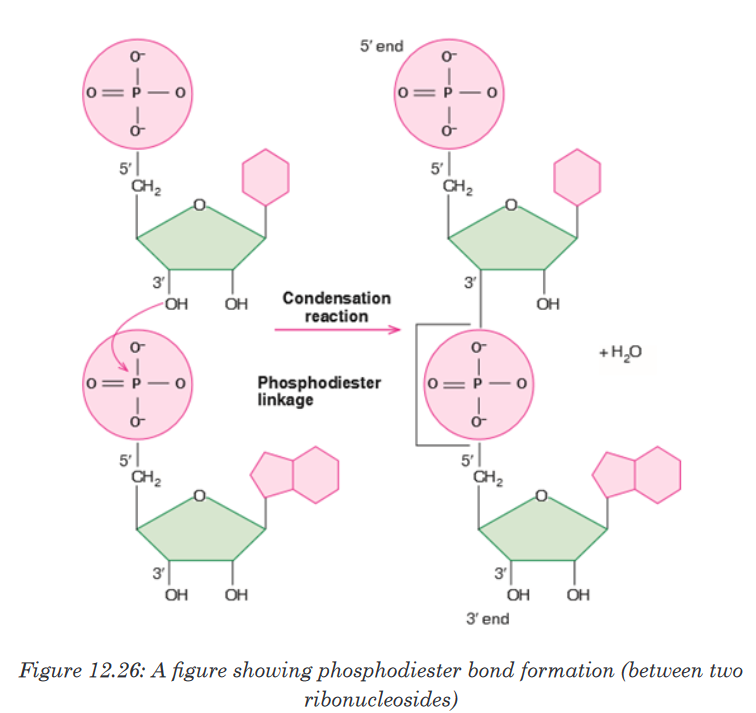
  

  
  

  In 1953, James D. Watson, an American molecular biologist, and Francis
  H.C.Crick, a British molecular biologist, proposed a model for the physical
  and chemical structure of the DNA molecule. Today, their model is known
  as double helix model of DNA or simply the Structure of DNA. The main
  features of Watson and Crick double helix model of DNA are:

  1. Two polynucleotide chains wind around each other in a right-hand
  double helix.

  2. The two polynucleotide chains run side-by-side in an antiparallel fashion.
  This means that one strand of DNA will orient itself in a 5’ -3’ direction,
  whereas, the other strand will orient itself alongside the first one in a 3’-5’
  direction. In this way, the two strands are oriented in opposite directions

  3. On one hand, the sugar-phosphate backbones lie outside of the double
  helix. On the other hand, the bases orient themselves toward the central
  axis of the double helix structure. The bases of one strand are bonded
  with the bases of the other strand of double helix by hydrogen bonds.
  These bonds are weak chemical bonds. Since hydrogen bonds are
  relatively weak bonds, the two strands can be easily separated by heating
  

  the DNA. The bonding of these bases in the double helical structure
  follows the Chargaff’s base pairing rules. For example—Adenine (A) will
  form a hydrogen bond with Thymine (T). Similarly, Guanine (G) will form
  a hydrogen bond with Cytosine (C). This specific base paring is called
  complementary base pairing.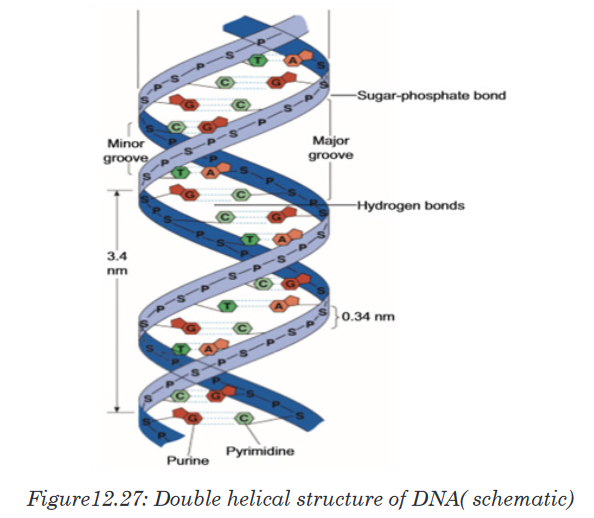
  

  
  

  
  

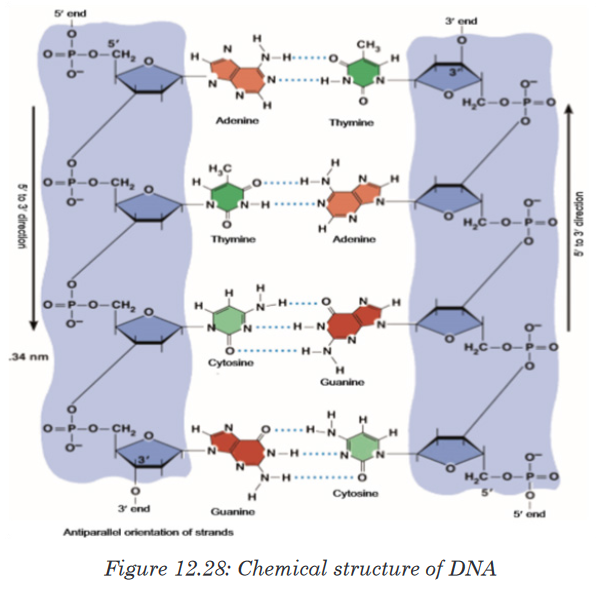
  4. The distance between adjacent bases is 0.34 nm in the DNA helix. A
  complete turn of the helix takes 3.4 nm. One complete turn, which is
  360° turn, accommodates 10 base pairs (bp). And the diameter of the
  helix is 2 nm.

  5. There are major and minor grooves in the double helix. The two sugar-
  phosphate backbones of the double helix are not equally spaced from
  one another along the helical axis, because of the way the base bind with
  each other. As a result, there is an unequal size of grooves between the
  backbones. The wider groove is called major groove; rich in chemical
  information. The narrower groove is called minor groove; less rich in
  chemical information.

  DNA is also Described as a Twisted Ladder Structure

  A typical ladder has two long wooden or metal side strands or pieces between
  which a series of rungs or bars are set in suitable distances. In the structure
  of DNA, the pentose sugars and phosphate groups make up the “long two
  side strands or pieces” of a typical ladder. And the A-T and G-C base pairs
  which are bonded by hydrogen bonds make up the

  “rungs or bars”of a typical ladder. But unlike a typical ladder which is straight,
  the two strands of DNA are twisted into spiral. Scientists call this a double
  helix. DNA also folds and coils itself into more complex shapes. The coiled
  shape makes it very small. In fact, it is small enough to easily fit inside any
  of our cells. If a DNA from a cell is unfolded, it would stretch out to a length
  of about six feet. The structural twisted nature of DNA has been attributed to
  enhance its stability and strength. Thus, for these simple similarities with a
  typical ladder, DNA is also referred as a twisted ladder structure.
  

  
  

  Application activity 12.3
  i. Watson and Crick proposed the model of ....................................
  ii. Enzyme ..................................... maintains the length of telomere.
  iii. ...................................... can be used to cure cancer.
  iv. .................................. bonds are seen in both DNA and RNA.
  v. ...................................... directs synthesis of proteins in the body
  

  12.4. Water and Enzymes

  Activity 12.4.a

  You are provided with three groups of enzymes: Group A Group B Group
  C Enzymes Maltase and lactase Dehydrogenase and oxidase Pepsin
  and renin
  

  
  

  Make a research to find out:
  a). Specific role of each of the six enzymes mentioned above
  b). Criterion followed to name enzymes of group A, B and C respectively
  

  Activity 12.4.b
  1. What is the medium of reaction in the organisms?
  2. If two people are boiling the same quantity of cooking oil and
  water, which one could evaporate first? Explain your choice.
  

  12.4.1. Water
  Living organisms contain between 60% and 90% of water, the remaining
  being the dry mass. The scientist accepts that life originates from water
  and most of animals live in water. The function of water is defined by its
  properties mainly: Its physical properties, solvent properties, heat capacity,
  surface tension and freezing points. The physical and chemical properties of
  water differ from those of most other liquids but make it uniquely effective in
  supporting living activities.
  

  a). Physical properties of water
  Water has the high boiling point (100°C) compared to other liquid due to the
  hydrogen bond that exists among molecules of water. This help the water to
  exist on the surface in a liquid state otherwise it would evaporate.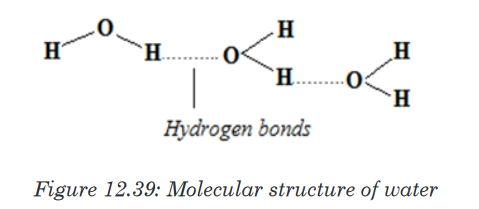
  

  
  

  Table 12.4: Biological significance of the physical properties of water

  
  

  
  

  
  

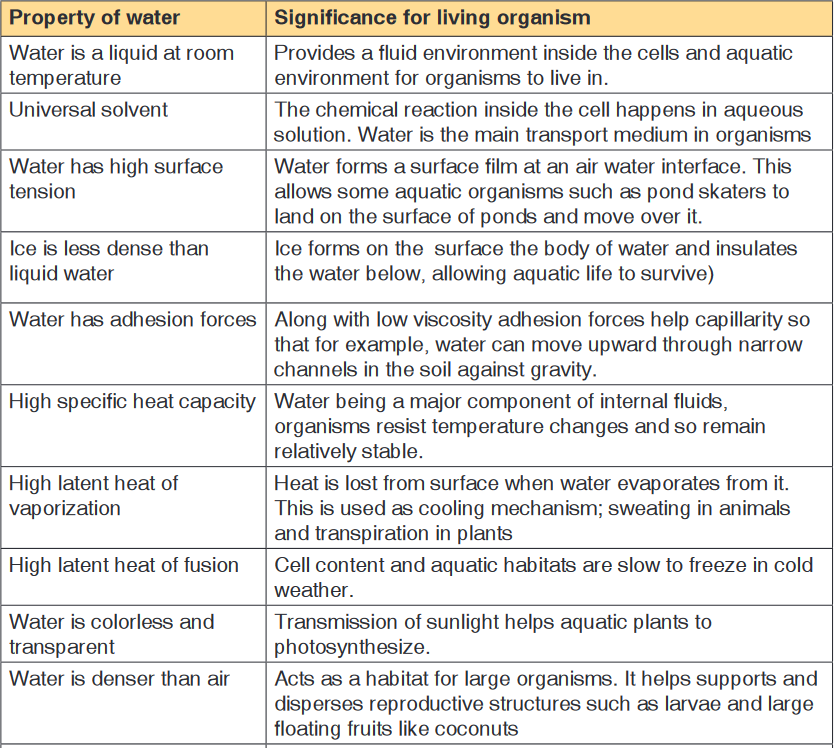
  b. Solvent properties of water
  Water is a polar molecule due to its chemical arrangement of hydrogen
  and oxygen atom in asymmetric shape instead of being linear. Most of the
  substance that are transported in the blood is dissolved in the plasma, the
  fluid part of the blood. Water occupies around 92% of the constituents of
  plasma. Thus the oxygen atom has a positive charge and hydrogen atom
  net positive charges. This is of great importance because all negative and
  positive ions are attracted by water. Therefore, water is a good solvent
  because the ionic solids and polar molecules are dissolved in it.
  

  
  

  c. Heat capacity and latent heat of vaporization
  Large changes of heat results in a comparatively small rise in water
  temperature this explain why water has a high heat capacity compared to
  other liquid. The high heat capacity is defined as the amount of heat required
  to raise the temperature of 1gram to 10C.The high thermal capacity of water
  make the ideal environment for life in plant and animals because it helps in
  maintaining the temperature even if there will be environmental fluctuations
  in temperature. The biological importance of this is that the range of
  temperatures in which biochemical processes can proceed is narrow.
  

  The latent heat of vaporization is a measure of heat energy needed to cause
  the evaporation of a liquid, which means to change from water liquid to
  water vapor. During vaporization the energy transferred to water molecules
  correspond to the loss of energy in the surroundings which therefore cool
  down. During sweating and transpiration living organisms use vaporization
  to cool down.
  

  i. Surface tension
  The surface tension of water results from its polar nature, and is defined
  as the ability of the external surface of the liquid to resist to external force
  due to cohesive nature of its molecules. The high surface tension of
  water and the cohesion force play a vital role in capillarity thus help the
  transport of substance in vessels (tracheid of plant) to the stems and to
  fulfill the blood in the cardiovascular vessels. Water being the second liquid
  with high surface tension after mercury its surface tension is lowered by
  the dissolution of ions and molecules and tend to collect at the interface
  between its liquid phase and other.

  ii. Freezing points
  Oppositely to other liquid water expand as it freezes, under 40 C
  temperatures the hydrogen bond becomes more rigid but more open.
  This explains why the solid water (ice) is less dense than the liquid water
  and why the ice floats over water rather than sinking. When the bodies of
  water freeze the ice float over the liquid act as an insulator and prevent
  water below it from freezing. This protects the aquatic organisms so that
  they can survive the winter.
  

  
  

  d. Functions of water
  • Turgidity of plant cell which increase their size is due to the availability
  of water.
  • The transport of substances (minerals, nutrients in plant and animals)
  is done in water.
  • Excretion of waste product
  • Support for hydrostatic skeleton.
  

  • Temperature regulation in plant and animals(transpiration)
  • Seed germination by breaking down the seed coat
  • Medium for biochemical reaction.

  12.4.2. Enzymes, their characteristics and actions
  

  Activity 12.4.2a
  

  You are provided with three groups of enzymes:
  

  
  

  Make a research from text book or internet to find out:
  a). What is the specific role of each of the six enzymes mentioned
  above?
  b). What criterion was followed to name enzymes of group A, B and C
  respectively?

  a. Criteria for naming enzymes
  Enzymes are biological catalyst produced by a living organism to control
  the speed of specific biochemical reactions (metabolism) by reducing its
  activation energy.

  First of all, Individual enzymes are named by adding -ase to the name
  of the substrate with which they react. The enzyme that controls urea
  decomposition is called urease; those that control protein hydrolyses are
  known as proteases.

  A second way of naming enzymes refers to the enzyme commission number
  (EC number) which is a numerical classification scheme for enzymes based
  on the chemical reactions they catalyse.

  As a system of enzyme nomenclature, every EC number is associated
  with a recommended name for the respective enzyme catalysing a specific
  reaction. They include:

  • Oxidoreductases catalyse redox reactions by the transfer of hydrogen,
  oxygen or electrons from one molecule to another. Example: Oxidase
  catalyses the addition of oxygen to hydrogen to form water.

  • Glucose + oxygen glucose oxidase (→Oxidase )gluconic acid +water

  • Hydrolase catalyses the hydrolysis of a substrate by the addition of
  water.

  • Sucrose + water (→Hydrolase )glucose+ fructose

  • Ligases catalyze reactions in which new chemical bonds are formed
  and use ATP as energy source.

  • Amino acid + tRNA (→(ligase) )amino acid-tRNA complex.

  • Transferases catalyze group transfer reactions. The transfer occurs
  from one molecule that will be the donor to another molecule that will
  be the acceptor. Most of the time, the donor is a cofactor that is charged
  with the group about to be transferred. Example: Hexokinase used in
  glycolysis.

  • Lyases catalyze reactions where functional groups are added to break
  double bonds in molecules or the reverse where double bonds are
  formed by the removal of functional groups. For example: Fructose
  bisphosphate aldolase used in converting fructose 1,6-bisphospate to
  G3P and DHAP by cutting C-C bond.

  • Isomerases catalyze reactions that transfer functional groups within a
  molecule so that isomeric forms are produced. These enzymes allow
  for structural or geometric changes within a compound. Sometime the
  interconverstion is carried out by an intramolecular oxidoreduction.
  In this case, one molecule is both the hydrogen acceptor and donor,
  so there’s no oxidized product. The lack of a oxidized product is the
  reason this enzyme falls under this classification. The subclasses are
  created under this category by the type of isomerism. For example:
  phosphoglucose isomerase for converting glucose 6-phosphate to
  fructose 6-phosphate. Moving chemical group inside same substrate.
  

  A third way of naming enzymes is by their specific names e.g. trypsin and
  pepsin are proteases. Pepsin, trypsin, and some other enzymes possess, in
  addition, the peculiar property known as autocatalysis, which permits them
  to cause their own formation from an inert precursor called zymogen.
  

  b. Characteristics of enzymes

  Activity 12.4.2b

  Requirement:

  Three test tubes, match box, about 1g of liver, 1g of sands, 1% H₂ O₂ and
  MnO2 powder.
  Procedure:
  • Label three test tubes A, B and C respectively.
  • Put about 0.1 g of MnO2 powder in test tube A and 1g of liver in
  tube B and 0.1g of sand in tube C.
  

  • Pour 5 ml of H2O2 (hydrogen peroxide) in each tube. What do you
  observe?
  • Place a glowing splint in the mouth parts of each test tube. What do
  you observe?
  Questions
  1. Explain your observations.
  2. Write down the chemical equation of the reaction taking place in
  tube A and B
  3. Carry out your further research to find out the characteristics of
  enzymes

  
  

  The following are main characteristics of enzymes
  1. Enzymes are protein in nature: all enzymes are made up of proteins.

  2. Enzymes are affected by temperature. They work best at specific
  temperatures; for example, enzymes found in human bodies work best
  at 37oC. This is called the optimum temperature.

  • Very low temperatures inactivate enzymes. Therefore enzymes are
  not able to catalyse reactions temperatures beyond the optimum
  temperature denature enzymes. The structure of the protein molecule
  is destroyed by heat.

  3. Enzymes work best at specific pH. Different enzymes have a given
  specific pH at which they act best.
  This pH is called optimum pH. Some enzymes work best at low pH (acidic
  medium) while others work best at high pH (alkaline medium).
  

  Most enzymes in the human body for instance work best at neutral or
  slightly alkaline pH. Examples are: lipases, peptidases and amylase. A
  few enzymes like pepsin that digests proteins in the stomach works best
  at an acidic pH of 2.

  4. Enzymes remain unchanged after catalysing a reaction. Enzymes
  are catalysts and can therefore be used over and over again in small
  amounts without being changed.
  

  5. Enzymes catalyse reversible reactions. This means that they can change
  a substrate into products and the products back to the original substrate.
  

  
  

  6. Enzymes are substrate-specific. This means that an enzyme can only
  catalyse one reaction involving aparticular substrate. This is because
  they have active sites which can only fit to a particular substrate whose
  shape complements the active site. For example, pepsin works on
  proteins but not on fats or starch.

  7. Enzymes work rapidly. Enzymes work very fast in converting substrates
  into products. The fastest known enzyme is catalase, which is found in
  both animal and plant tissues.

  8. Enzymes are efficient. This is best described by the fact that:
  • They are required in very small amounts.
  • They are not used up in a reaction and can therefore be used
  repeatedly.

  9. Enzymes are globular proteins.

  10. Enzymes lower the activation energy (Ea) required for reactions to take
  place. In many chemical reactions, the substrate will not be converted to
  a product unless it is temporarily given some extra energy. This energy
  is called activation energy i.e. the minimum energy required the make a
  reaction take place.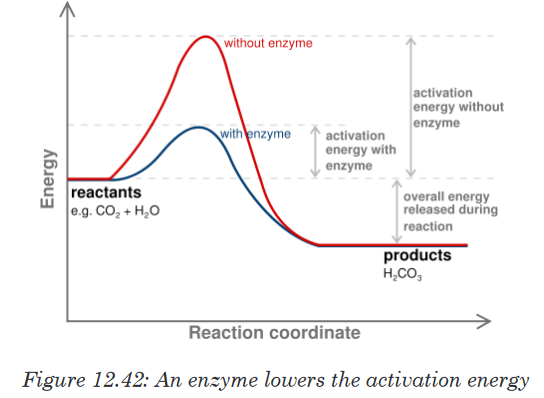
  

  
  

  An enzyme provides a reaction surface for a reaction to take place. This
  is normally a hollow or cleft in the enzyme which is called the active site,
  but it is normally hydrophobic in nature rather than hydrophilic. An enzyme
  provides a reaction surface and a hydrophilic environment for the reaction
  to take place.

  A very small amount of enzymes is needed to react with a large amount of
  substrate. The turnover number of an enzyme is the number or reactions
  an enzyme molecule can catalyse in one second. Enzymes have a high
  

  turnover number e.g. the turnover number of catalase is 200,000 i.e. one
  molecule of enzyme catalase can catalyse the breakdown of about 200,000
  molecules of hydrogen peroxide per second into water and oxygen at body
  temperature.

  A cofactor is the best general term to describe the non-protein substances
  required by an enzyme to function properly. This term covers both organic
  molecules and metal ions. A co-enzyme is an organic molecule that acts as
  a cofactor. A prosthetic group is a cofactor that is covalently bound to the
  enzyme.
  

  12.4.3. Factors affecting enzyme action

  Activity 12.4.3

  You will need
  Eight test tubes containing 2 cm3 starch solution, amylase solution, and
  cold water (ice) water bath, iodine solution, HCl solution, and droppers
  Procedure:
  1. Label your test tubes A-D as follows:
  

  
  

  2. Add 1 cm³ of starch solution to each test tube

  3. Keep tube A and B in cold (ice) and tube C and D in the water bath
  at 350C for 5 minutes.

  4. Add 1 cm³ of 1M HCl on test tubes B and D, then shake the mixture
  to stir.

  5. Add 1 cm³ of amylase solution on each test tube. Shake and therefore
  keep A and B in cold and C and D in water bath for 10 minutes.

  6. Take a sample from each tube and mix it with one drop of iodine.
  Use a different tile for each test tube. Record and interpret your
  observation and then draw a conclusion.

  Enzymes activities can be limited by a number of factors such as the
  temperature, the pH, the concentration of the substrate or the enzyme itself
  and the presence of inhibitors.
  

  i. Temperature
  At zero temperature, the enzyme cannot work because it is inactivated. At
  low temperatures, an enzyme-controlled reaction occurs very slowly.

  The molecules in solution move slowly and take a longer time to bind to
  active sites. Increasing temperature increases the kinetic energy of the
  reactants. As the reactant molecules move faster, they increase the number
  of collisions of molecules to form enzyme-substrate complex.

  At optimum temperature, the rate of reaction is at maximum. The enzyme is
  still in active state. The optimum temperature varies with different enzymes.
  The optimum temperature for enzymes in the human body is about 37^oC.
  When the temperature exceeds the optimum level, the enzyme is denatured.

  The effect is irreversible. However, some species are thermophilic that is
  they better work at high temperatures; others are thermophobic, that is they
  better work at low temperatures. For example, some thermophilic algae and
  bacteria can survive in hot springs of 60^oC.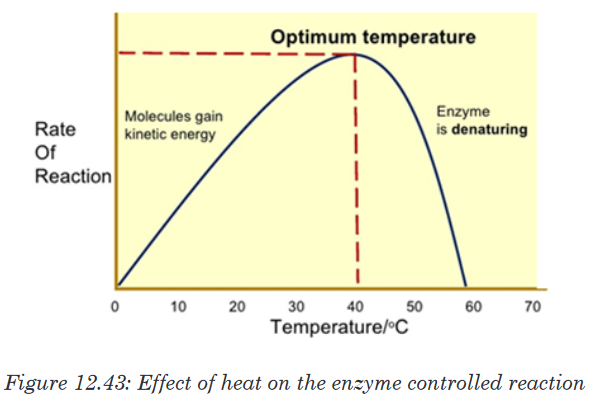
  

  
  

  The rate doubles for each 10°C rise in temperature between 0°C and 40°C.
  The temperature coefficient Q10 is the number which indicates the effect of
  rising the temperature by 10°C on the enzyme-controlled reaction. The Q10
  is defined as the increase in the rate of a reaction or a physiological process
  for a 10°C rise in temperature. It is calculated as the ratio between rate of
  reaction occurring at (X + l0)°C and the rate of reaction at X °C. The Q10 at
  a given temperature x can be calculated from: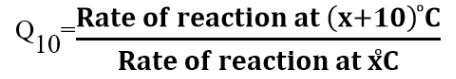
  

  
  

  Worked out example
  The rate of an enzyme-controlled reaction has been recorded at different
  temperatures as follows:
  

  
  

  This means that the rate of the reaction doubles if the temperature is raised
  from 30oC to 40oC

  Be aware that not all enzymes have an optimum temperature of 40°C. Some
  bacteria and algae living in hot springs (e.g. Amashyuza in Rubavu) are
  able to tolerate very high temperatures. Enzymes from such organisms are
  proving useful in various industrial applications.
  

  ii. The pH
  Most enzymes are effective only within a narrow pH range. The optimum pH
  is the pH at which the maximum rate of reaction occurs. Below or above the
  optimum pH the H+ or OH- ions react with functional groups of amino acids
  in the enzyme which loses its tertiary structure and become natured.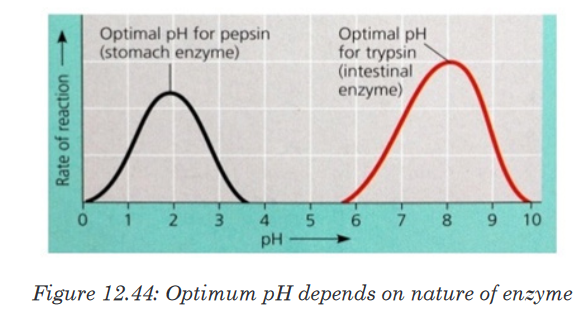
  

  
  

  Different enzymes have different pH optima (look in the table).
  

  
  

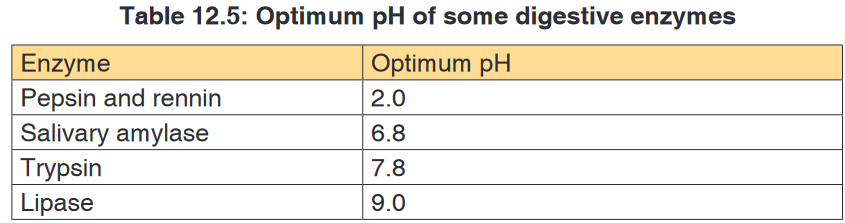
  iii. Enzyme concentration
  The rate of an enzyme-catalyzed reaction is directly proportional to the
  concentration of the enzyme if substrates are present in excess concentration
  and no other factors are limiting.
  

  
  

  iv. Substrate concentration
  At low substrate concentration, the rate of an enzyme reaction increases with
  increasing substrate concentration. The active site of an enzyme molecule
  can only bind with a certain number of substrate molecules at a given time.
  At high substrate concentration, there is saturation of active sites and the
  velocity of the reaction reaches the maximum rate.
  

  
  

  v. Inhibitors
  The inhibitors are chemicals or substances that prevent the action of an
  enzyme. An inhibitor binds to an enzyme and then decreases or stops its
  activity. There are three types of inhibitors:
  a). Competitive inhibitors are molecules that have the similar shape
  as the substrate. They are competing with the substrate to the active
  site of the enzyme e.g. O2 compete with CO2 for the site of RuBP-
  carboxylase.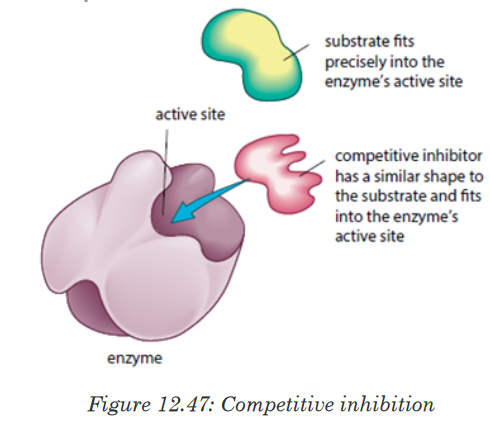
  

  
  

  b). Non-competitive inhibitors are molecules that can be fixed to the
  other part of enzyme (not to the active site) so that they change the
  shape of active site, due to this the substrate cannot bind to the
  active sit of the enzyme.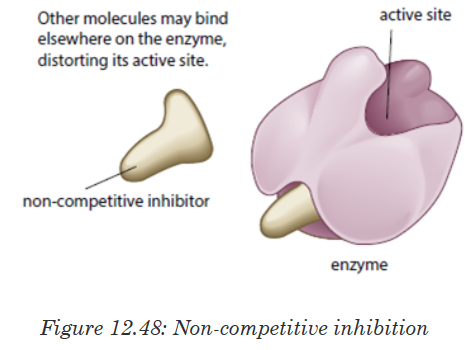
  

  
  

  c). End product inhibitor or Allosteric inhibitor or Allostery.
  This is a chain enzymatic metabolic pathway where the final end product acts
  as an allosteric reversible inhibitor for the first, the second or the third step
  in the metabolic pathway. The shape of an allosteric enzyme is altered by
  the binding of the end product to an allosteric site. This decreases enzymatic
  activity. By acting as allosteric inhibitors of enzymes in an earlier metabolic
  pathway, the metabolites can help to regulate metabolism according to the
  needs of organisms. This is an example of negative feedback.
  

  This often happen when few enzymes are working on a large number
  of substrate e.g. ATP is an end-product inhibitor of the enzyme PFK
  (Phosphofructokinase) in glycolysis during cell respiration. The end-product
  inhibitor leads to a negative feedback.
  

  
  

  The products of enzyme-catalysed reactions are often involved in the
  feedback control of those enzymes. Glucose-1-phosphate is the product
  formed from this enzyme-catalysed reaction. As its concentration increases,
  it increasingly inhibits the enzyme.
  

  Note: Reversible and irreversible inhibition
  Competitive inhibitor is reversible inhibitor as it binds temporarily to the
  active site. It can be overcome by increasing the relative concentration of
  the substrate. Some non-competitive inhibitors are reversible, that is, if the
  inhibitor binds temporarily and loosely to the allosteric site. Some inhibitors
  have very tightly, often, by forming covalent bonds with enzyme.

  The nerve gas DIPF (DiIsopropylPhosphoFluoridate) is an irreversible
  inhibitor. It binds permanently with enzyme acetylcholisterase, altering
  its shape. The enzyme cannot bind with and break down its substrate
  acetylcholine (neurotransmitter). Acetylcholine molecules accumulate in the
  synaptic cleft.

  Nerve impulses cannot be stopped causing continuous muscle contraction.
  This leads to convulsions, paralysis and eventually death.
  

  Many pesticides such as organophosphate pesticides act as irreversible
  enzyme inhibitors. Exposure to pesticides can produce harmful effects to
  the nervous and muscular systems of humans. Heavy metal ions such as
  Pb2+, Hg2+, Ag+, As+ and iodine-containing compounds which combine
  permanently with sulphydryl groups in the active site or other parts of the
  enzyme cause inactivation of enzyme.
  

  This usually disrupts disulphide bridges and cause denaturation of the
  enzyme.
  

  12.4.4. Importance of enzymes in living organisms
  

  Activity 12.4.4
  Elaborate your ideas about the need for different enzymes in living
  organisms.

  Without enzymes, most of the biochemical reactions in living cells at body
  temperature would occur very slowly at not at all. Enzyme can only catalyze
  reactions in which the substrate shape fits that of its active site
  

  There are thousands upon thousands of metabolic reactions that happen
  in the body that require enzymes to speed up their rate of reaction, or will
  never happen. Enzymes are very specific, so nearly each of these chemical
  reactions has its own enzyme to increase its rate of reaction. In addition, the
  organism has several areas that differ from one another by the pH. Therefore,
  the acid medium requires enzymes that work at low pH while other media
  are alkaline and therefore require enzymes that work at high pH. In addition
  to digestion, enzymes are known to catalyze about 4,000 other chemical
  reactions in your body. For example, enzymes are needed to copy genetic
  material before your cells divide.
  

  Enzymes are also needed to generate energy molecules called ATP, move

  fluid and nutrients around the insides of cells and pump waste material out
  of cells. Most enzymes work best at normal body temperature – about 98
  degrees Fahrenheit – and in an alkaline environment. As such, high fevers
  and over-acidity reduce the effectiveness of most enzymes. Some enzymes
  need co-factors or co-enzymes to work properly.
  

  12.4.5. Mode of action of enzymes
  

  Activity 12.4.5
  
  

  There are two main hypotheses that explain the more of action of an
  enzyme on its substrate: the lock and key hypothesis and the induced-fit
  hypothesis. Carry out a research to find the relevance of each.
  

  Enzymes do not change but substrates are converted to products. A substrate
  is a molecule upon which an enzyme acts. In the case of a single substrate,
  the substrate binds with the enzyme active site to form an enzyme-substrate
  complex. Thereafter the substrate is transformed into one or more products,
  which are then released from the active site.
  

  This process is summarized as follows:
  

  
  

  Whereby: E = enzyme, S = substrate(s), ES = Complex Enzyme-Substrate
  and P= product (s). There are two main hypotheses explaining the mechanism
  of enzyme action:
  

  a. The lock and key hypothesis by Emil Fischer
  In this hypothesis the substrate is the key and enzyme is the lock. In otherwise
  the active site is exactly complementary to the shape of the substrate.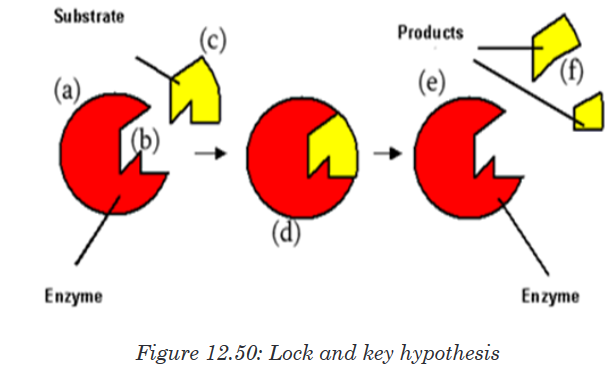
  

  
  

  
  

  b. The induced-fit hypothesis by Daniel Koshland
  The induced-fit hypothesis is a modified version of the lock and key hypothesis
  and is more widely accepted hypothesis. In this hypothesis, the active site
  is flexible and is not exactly complementary to the shape of the substrate.
  

  An enzyme collides with the substrate molecule.The substrate binds to the
  active site. The bindings induce a slight change in the shape of the enzyme
  to enclose the substrate making the fit more precise. The active site now
  becomes fully complementary with the substrate as the substrate binds to
  the enzyme.
  

  
  

  Application activity 12.4
  1. Fill the blank with appropriate terms: Enzymes are
  biological ____________________ produced by
  ___________________________ cells. Enzymes reduce the
  amount of ____________________ energy required for reactions
  to occur. They consist of globular ____________________ with
  _______________________ structure.
  2. Answer the following questions:
  a). What is the main role of enzymes?
  b). What would happen if there are no enzymes in the cell? State any
  four properties of enzymes.

  Skills lab 12

  Test the components of the food and beverages produced by different
  companies in our country. Here, you will need to use the knowledge of food
  test techniques.test techniques.
  

  End unit assessment 12
  1. Biological molecules are divided into (Choose the correct answer):
  a). Organic molecules and inorganic molecules
  b). Carbohydrates and starch
  c). Lipids, carbohydrates and water
  d). Carbohydrates, food and potatoes
  2. Name the reagents that are used to test for the following food
  substances
  a). Lipids
  b). Starch
  c). Reducing sugar
  3. Some drops of fresh pineapple fruit juice are added drop by drop to
  DCPIP solution. The deep blue color of the DCPIP quickly fades.
  a). Explain why the blue colour disappeared?
  b). What is the importance of this food substance to the human body?
  4. Write the formula of a monosaccharide with 3 atoms of carbon
  5. Compare the structure of fat(triglycerides)and the phospholipids
  6. Give two examples of how carbohydrates are used in the body.
  7. The formula for a hexose is C₆H₁₂O₆ or (CH₂O)6. What would be the
  formula of?
  

  a). Triose
  b). Pentose
  8. Distinguish between:
  a). Alpha glucose and beta glucose
  b). Glycogen and cellulose
  c). Amylopectin and amylose
  9. The drug can cleave the covalent bond between two sulfur atoms
  of non-adjacent amino acids. Which level of protein can be affected
  the most if the drug is mixed with primary, secondary, tertiary and
  quaternary structure of proteins.
  10. State the property of water that allows each of the following to take
  place. In each case, explain its importance:
  

  a). The cooling of skin during sweating
  b). The transport of glucose and ions in a mammal
  c). Much smaller temperature fluctuations in lakes and oceans than
  in terrestrial (land-based) habitats.
  11. Construct the table that organize the following terms and label the
  columns and rows.
  Phosphodiester linkages Monosaccharide polypeptides
  Peptide bonds Nucleotides Triacylglycerol
  Glycosidic linkages Amino acids Polynucleotides
  Ester linkages fatty acids Polysaccharides
  12. Explain what happen during protein denaturation?
  13. Enzymes are biocatalysts.
  a). What is the meaning of the following terms elated to enzyme
  activity?
  i. Catalyst
  ii. Activation energy
  iii. Lock and key
  iv. Q10
  b). Why are there hundreds of different enzymes in a cell?
  c). How do enzymes reduce the activation energy of a reaction?
  14. Enzyme activity is related to a number of factors.
  a). Explain why enzymes work faster at high temperatures
  b). Describe what happens to the enzyme structure if the temperature
  is raised well above the optimum temperature.
  c). How are enzymes affected by pH?
  d). Why do different enzymes have a different optimum pH?
  e). What is the difference between a reversible and irreversible
  enzyme inhibitor?

  15. Some bacteria and algae can survive in the boiling waters of hot
  springs. Enzymes from these organisms are used in industrial
  processes. Why are these enzymes useful?
  

  16. The following set data show the effect of temperature on the
  completion time of an enzyme reaction.
  

  
  

  a). Plot the data on a graph
  b). What is the optimum temperature of this reaction?
  c). Describe the shape of the graph between 10 and 400 C
  d). Calculate the rate of increase between 20 and 300 C.
  

  
  

• UNIT 13:KIRCHHOFF’S LAWS IN ELECTRIC CIRCUITS

  Key unit competence: Interpret and solve problems in electric
                                                  circuits using Kirchhoff’s laws

  Introductory Activity 13

  
  

  Look at the illustration given above.
  a). What type of devices available in the illustration above?
  b). Can you suggest the names of the available devices in the illustration
  above?
  c). Is there any complete circuit in the illustration above?
  d). What kind of electrical circuits identified in the illustration above?
  

  e). Have you ever used or connected these electrical components
  somewhere? If yes, what were the difficulties in handling these
  electrical components in circuit construction?
  f). What can be considered to select the best electrical device(s) to be
  used in electrical circuit construction?
  g). What can be put in recognition to minimize risks when connecting
  these electrical components in the circuit?
  

  13.1. Simple electric circuits and its construction
  

  Activity 13.1
  Observe the following diagram and answer the next questions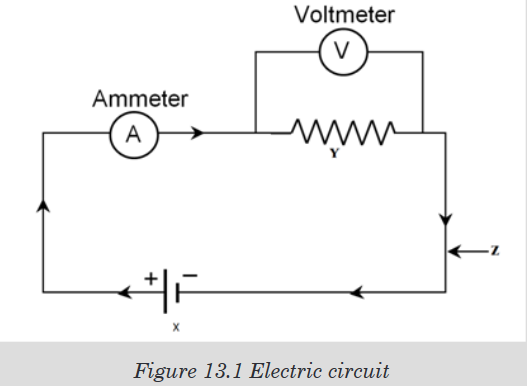
  

  
  

  a). Explain the role of part X, Y, Z
  b). Give any example of device that is represented by X and Y.
  c). Are ammeters and voltmeters necessary in creation of simple electric
  circuit? Explain.
  d). Give other necessary devices in simple electrical circuit.
  

  13.1.1. Electric circuit components, devices and their symbols
  In electric circuit diagrams, we represent the actual components with
  symbols. Table below shows some of the components, their symbols and
  definition that are used in electric circuit diagrams.
  

  
  

  
  

  
  

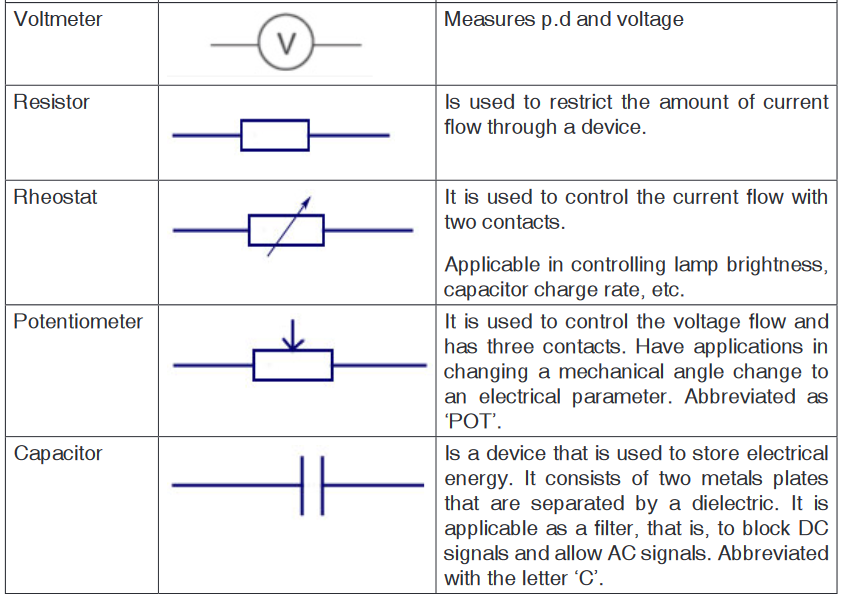
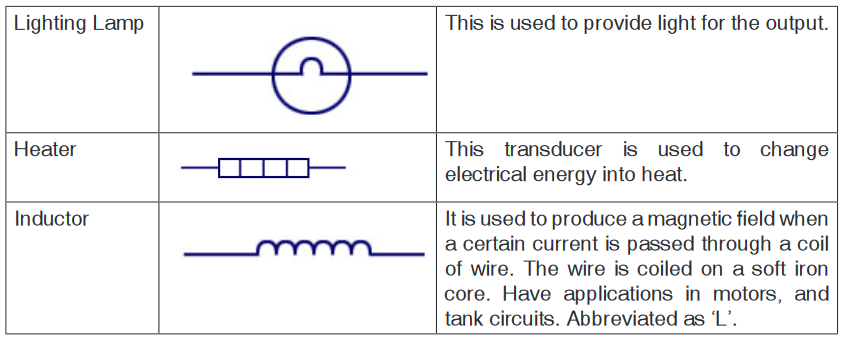
  13.1.2. Sample arrangement of electric components in a simple
  electric circuit
  Remember the cell provides electrical energy needed to light the bulb. The
  bulb converts electrical energy into light and heat energy.
  

  A cell is a kind of a ‘pump’ which provides electrical energy needed to drive
  charges along a complete path formed by the wire through the bulb switch
  and back again to the cell.
  

  When the switch is open, the bulb does not light. This is called an open
  circuit. When the bulb lights the circuit is called closed circuit.
  

  In a series circuit, the current is the same at all points; it is not used up. In a
  parallel circuit the total current equals the sum of the currents in the separate
  branches.
  

  Schematic diagram and its corresponding illustrations:
  

  
  

  
  

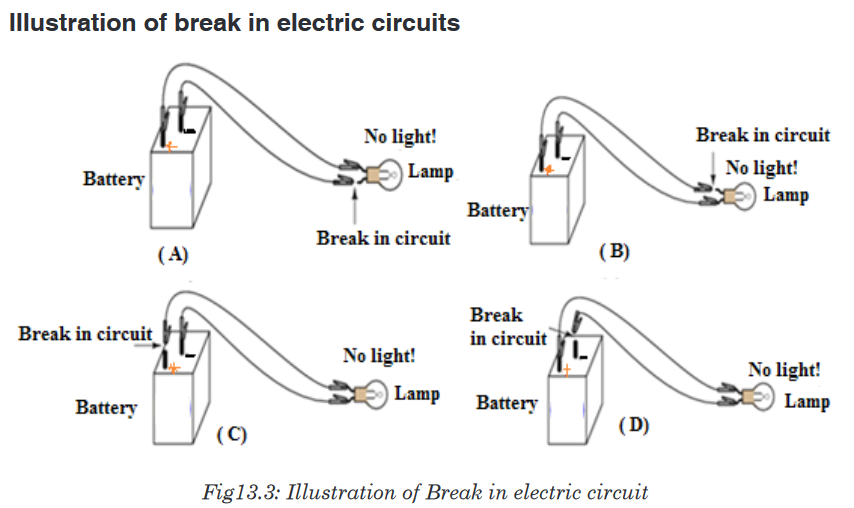
  Application activity 13.1
  1. Define the term electric circuit.
  2. Draw a diagram for a simple circuit using preferable electric
  components.
  3. What is an open circuit?
  4. The following are some symbols of electric components.
  

  
  

  a). Name the electric components represented by these symbol.
  b). Using these symbols, draw a simple circuit diagram.
  

  13.2. Measurement of electric current and voltage in a
  simple electric circuit
  

  Application activity 13.2
  Interpret the scale on the figure below for an analogue ammeter that
  measures current in the range 0 – 1 A, or 0 – 5 A. Determine the reading
  of the Ammeter.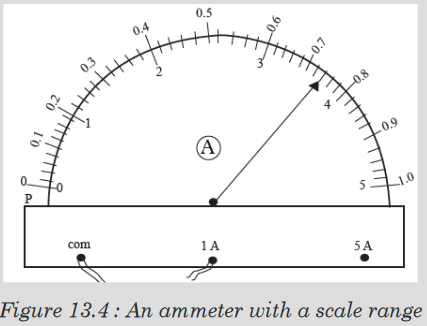
  

  
  

  Measurement of electric current
  Ammeter has two positive terminals and one negative terminal. Fig. (a)
  Shows an analogue ammeter and (b) shows a digital ammeter.
  

  
  

  An analogue ammeter may have more than one scale (Fig.(a)). The
  magnitude of the current determines the scale to be used. Smaller currents
  are measured in milliamperes (mA) and microamperes ( A).
  1 mA = 1/ 1 000 A = 1 x10^-3 A, 1μ A = 1 10^-6 A.
  

  How to use an ammeter to measure current in a circuit

  Reading an analogue ammeter
  
  

  Figure below shows the scale on an analogue ammeter that measures
  current in the range 0 – 1 A, or 0 – 5 A.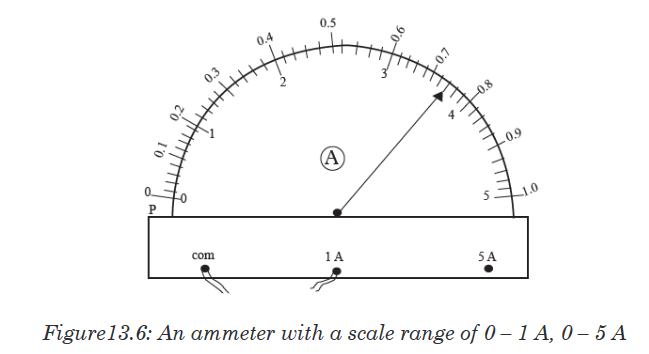
  

  
  

  When connected to the 1 A terminal, the upper scale running from 0 - 1 A
  should be used.
  

  We determine the current represented by each smallest division on the
  upper scale
  

  as follows:
  5 divisions correspond to........... 0.1 A
  1 division corresponds to .................................. 0.1/5A = 0.02 A
  In Figure 13.6, the pointer is on the second mark after the 0.7 mark, hence
  the ammeter reading is:
  0.7 A + (2 divisions × 0.02 A) = 0.7A + 0.04 A = 0.74 A
  

  Potential difference (p.d)

  Potential difference is defined as the work done in moving one coulomb
  of charge from one point to the other in an electrical circuit. The SI unit of
  potential difference is the volt (V).
  

  In the electric circuit, the electrons move towards the positive terminal of the
  battery. The battery lifts the electrons up through an electrical height. This
  electrical height is called a potential.
  

  The positive and the negative terminals have a difference in potential. The
  potential difference is also known as the voltage.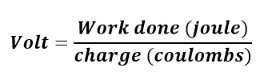
  

  
  

  1 volt is therefore defined as the energy needed to move one coulomb of
  charge from one point to another.

  Measurement of voltage

  Figure 13.7(a) shows analog voltmeter and (b) shows digital voltmeter the
  symbol for a voltmeter. A voltmeter is used to measure voltage across a
  device in an electric circuit.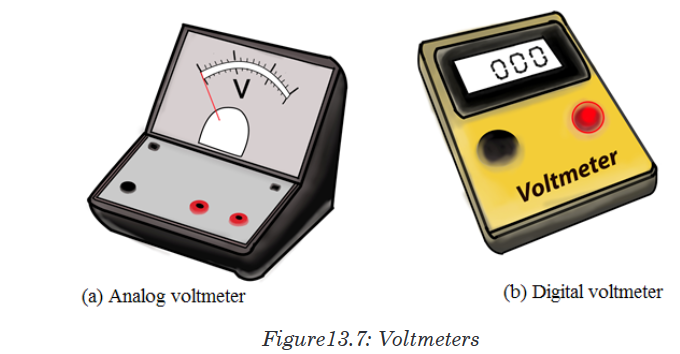
  

  
  

  The positive terminal of voltmeter is connected to the wire from the positive
  terminal of the cells and the negative terminal to the wire leading to negative
  terminal. A voltmeter is always parallel to the device whose voltage is to be
  measured.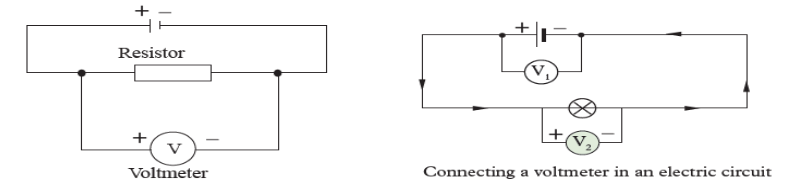
  

  
  

  Voltmeters have uniform scales calibrated in volts or mill-volts. The most
  used scales have a range of 0 – 5 V and 0 – 1.5 V. Figure below shows a
  scale of a voltmeter.
  

  
  

  Application activity 13.2
  1. Define the term potential difference and state its SI units.
  2. Name the instrument used to measure voltage.
  3. Define a volt.
  4. In a circuit, 5 joules are used to drive 2 coulombs of charge across a
  bulb in a simple circuit. Find the potential difference across the bulb?
  5. Name the instrument used to measure potential difference.
  6. Two cells, A and B connected in parallel are in series with a bulb as
  shown in Figure below.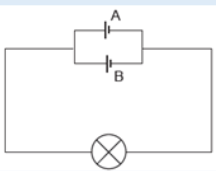
  

  
  

  Figure13.8: Circuit with parallel cells

  Copy the diagram and show where the:
  a). Ammeter should be connected in order to measure the current
  through cell A.
  b). Voltmeter should be connected to measure the potential difference
  across both the bulb and cell B.

  13.3. Different sources of electric current

  Activity 13.3
  Search on internet about different sources of electric current and answer
  the following questions.

  a). What is a source of electric current?
  b). What is another name of electric source of energy?
  c). List some of electric sources you have found.
  d). On the picture below are some sources of electric energy:
  

  
  

  • Name them and tell what the common role they have.

  • Tell what energy is changed in electric energy for each device.

  There are several different devices that can supply the voltage necessary to
  generate an electric current. The two most common sources are generators
  and electrolytic cells.
  

  Generators use mechanical energy, such as water pouring through a dam or
  the motion of a turbine driven by steam, to produce electricity. The electric
  outlets on the walls of homes and other buildings, from which electricity to
  operate lights and appliances is drawn, are connected to giant generators
  located in electric power stations. Each outlet contains two terminals. The
  voltage between the terminals drives an electric current through the appliance
  that is plugged into the outlet.
  

  Generator electrolytic cells use chemical energy to produce electricity.
  Chemical reactions within an electrolytic cell produce a potential difference
  between the cell’s terminals. An electric battery consists of a cell or group of
  cells connected together.
  

  There are many sources of electric current other than mechanical generators
  and electrolytic cells. Fuel cells or engines, for example, produce electricity
  through chemical reactions. Unlike electrolytic cells, however, fuel cells do
  not store chemicals and therefore must be constantly refilled.
  

  Certain sources of electric current operate on the principle that some metals
  hold onto their electrons more strongly than other metals do. Platinum, for
  example, holds its electrons less strongly than aluminum does. If a strip of
  

  platinum and a strip of aluminum are pressed together under the proper
  conditions, some electrons will flow from the platinum to the aluminum. As
  the aluminum gains electrons and becomes negative, the platinum loses
  electrons and becomes positive.
  

  The strength with which a metal holds its electrons varies with temperature.
  If two strips of different metals are joined and the joint heated, electrons will
  pass from one strip to the other. Electricity produced directly by heating is
  called thermoelectricity.
  

  Some substances emit electrons when they are struck by light. Electricity
  produced in this way is called photo-electricity. When pressure is applied
  to certain crystals, a potential difference develops across them. Electricity
  thus produced is called piezoelectricity. Some microphones work on this
  principle.
  

  Notice: An electric generator is a device which is used to produce electric
  energy, which can be stored in batteries or can be directly supplied to the
  homes, shops, offices, etc. Electric generators work on the principle of
  electromagnetic induction. A conductor coil (a copper coil tightly wound
  onto a metal core) is rotated rapidly between the poles of a horseshoe type
  magnet. A conductor coil (a copper coil tightly wound onto a metal core) is
  rotated rapidly between the poles of a horseshoe type magnet. The conductor
  coil along with its core is known as an armature. The armature is connected
  to a shaft of a mechanical energy source such as a motor and rotated. The
  mechanical energy required can be provided by engines operating on fuels
  such as diesel, petrol, natural gas, etc. or via renewable energy sources
  such as a wind turbine, water turbine, solar-powered turbine. When the coil
  rotates, it cuts the magnetic field which lies between the two poles of the
  magnet. The magnetic field will interfere with the electrons in the conductor
  to induce a flow of electric current inside it.
  

  Application activity 13.3
  1. Sources of electric current are also known as electric generators.
  Explain electric generators.
  2. What is an engine? Compare engine to batteries.
  3. Compare and contrast battery from dry cells
  4. Research on differences between piezoelectricity and thermoelectricity.
  5. Research on differences between renewable and non- renewable
  form of energy sources.
  

  13.4. Connection of electrical current source and resistors
  Activity 13.4

  Task1: Series circuits
  

  Provided materials: Battery cells, three torch light bulbs and conducting
  wires
  

  Technical procedure:

  • Arrange the battery cells as shown in figure below.
  • Connect all the two bulbs in series and switch on.
  • Remove one bulb and discuss your observations.
  • Arrange the circuit to have two bulbs, and then to have one bulb
  and discuss the observation.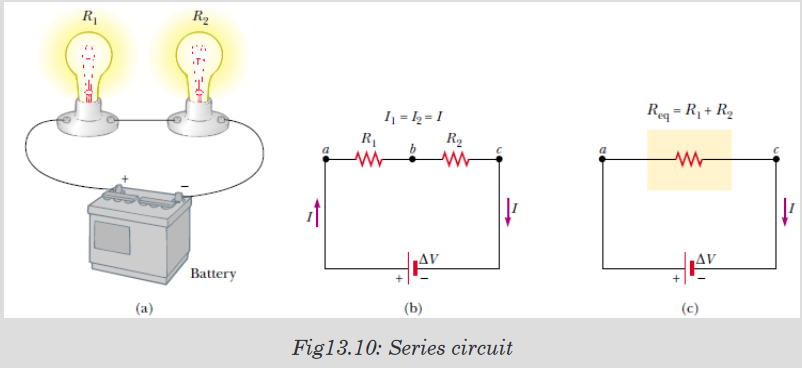
  

  
  

  Use your observations to answer the following questions:
  1. What happens in the circuit with three bulbs when one bulb is
  removed?
  2. What happens when the circuit has two bulbs?
  3. What happens when the circuit has one bulb only?
  

  Task 2: Parallel circuits
  Materials: Battery cells, two torch light bulbs and conducting wires

  Technical procedure:
  • Arrange the battery cells as shown in figure 13.11.
  

  • Connect all the three bulbs in parallel and switch on.
  • Remove one bulb and discuss your observations.
  • Remove the second bulb and discuss your observations.
  

  
  

  Use your observation to answer to questions below:
  1. What happens in the circuit with two bulbs when one bulb is removed?
  2. What happens when the circuit has two bulbs?
  3. What happens when the circuit has one bulb only?

  Circuits consisting of just one battery and one load resistance are very
  simple to analyze, but they are not often found in practical applications.
  Usually, we find circuits where more than two components are connected
  together. There are two basic ways in which to connect more than two circuit
  components: series and parallel.

  13.4.1. Resistors in series
  The defining characteristic of a series circuit is that there is only one path for
  electrons to flow. Consider three resistors R₁, R₂ and R₃ connected in series
  across a battery of potential difference V. Across the resistors the potential
  difference drops are V₁, V₂ and V₃ but the current flow I is constant due to
  the same amount of charges flowing across each resistor.
  

  
  

  13.4.2. Resistors in parallel
  The defining characteristic of a parallel circuit is that all components are
  connected between the same set of electrically common points and the
  resistors form more than one continuous path for electrons to flow.
  

  Assume three resistors of resistance R₁, R₂ and R₃ connected in parallel
  across a battery of potential difference V. The potential difference across
  each resistor is the same and is equal to the potential difference V across
  the battery, but the current flow splits into three parts I₁, I₂ and I₃ due to the
  separation of charges.
  

  
  

  
  

  
  

  
  

  Household circuits are always wires so that the lights and appliances are
  connected in parallel. This way each device operated independently of
  the others, so if one is turned off the others remain on. This also had the
  advantage that the voltage supplied to each element is the same.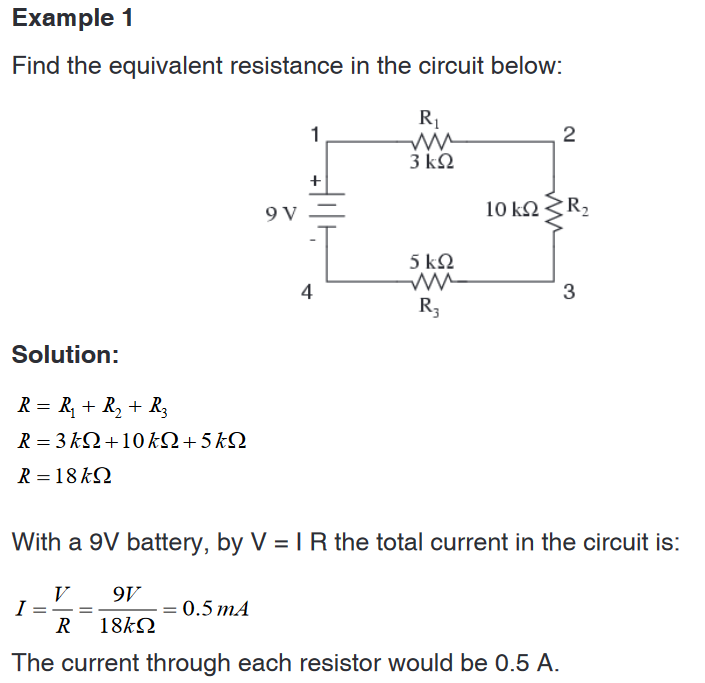
  

  
  

  
  

  Example 2
  A parallel circuit is shown in the figure below. In this case the current supplied
  by the battery splits up, and the amount going through each resistor depends
  on the resistance.
  

  From the figure below, if the values of the three resistors are
  

  
  

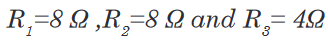
  Determine the total resistance of the circuit.

  
  

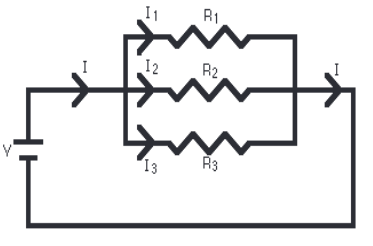
  Solution
  The total resistance R is found by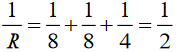
  

  This gives that R=2Ω
  

  With a 10 V battery, by V = I R the total current in the circuit is:
  

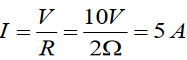
  The individual currents can also be found using 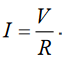The voltage across
  each resistor is 10 V, so: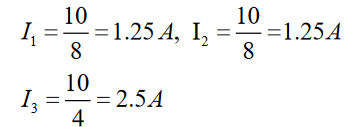
  

  
  

  Note that the currents add together to 5A, the total current.
  

  Example 3
  Interpret the circuit below and determine the total resistance of the circuit.
  

  
  

  Solution
  Here we can use the shorter product over sum equation as we only have two
  parallel resistors.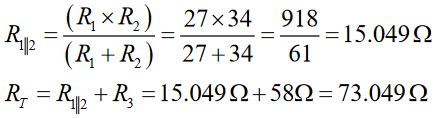
  

  
  

  Application activity 13.4
  1. Use the concept of equivalent resistance to determine the unknown
  resistance of the identified resistor that would make the circuit’s
  equivalent.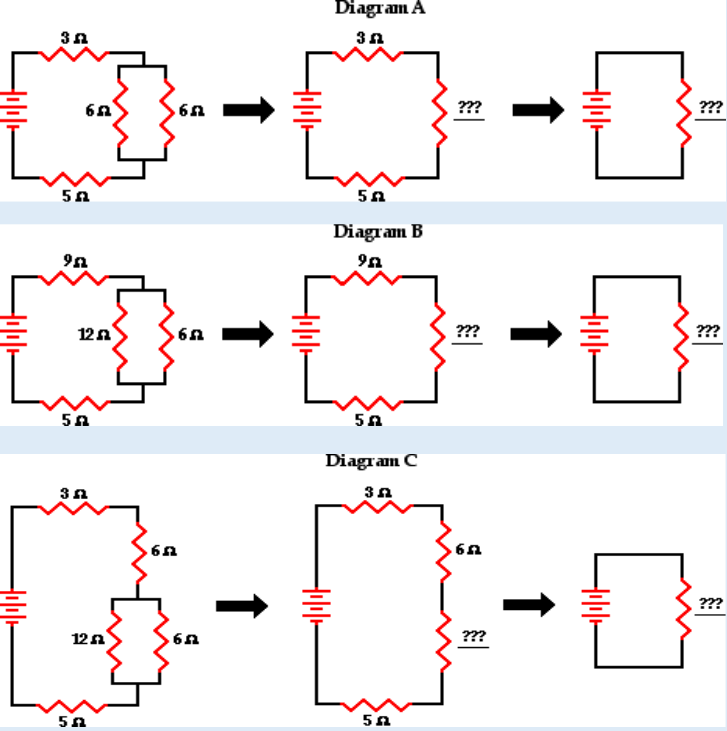
  

  
  

  
  

  2. A parallel pair of resistance of value of Ω3 and Ω6 are together
  connected in series with another resistor of value Ω4 and a battery
  of e.m.f. 18 V as shown on the fig. (a) below. Calculate the current
  through each resistor.
  Calculate the current through each resistor.
  

  
  

  3. (a) Find the equivalent resistance between points a and b in Figure
  below. (b) A potential difference of 34.0 V is applied between points a
  and b. Calculate the current in each resistor.
  

  
  

  4. Use your understanding of equivalent resistance to complete the
  following statements:

  i. Two 3Ω resistors placed in series would provide a resistance
  which is equivalent to one ___ Ω resistor.

  ii. Three 3Ω resistors placed in series would provide a resistance
  which is equivalent to one ___ Ω resistor.
  iii. Three 5Ω resistors placed in series would provide a resistance
  which is equivalent to one ___ Ω resistor.
  iv. Three resistors with resistance values of 2Ω , 4Ω and 6Ω are
  placed in series. These would provide a resistance which is
  equivalent to one ___ Ω resistor.
  v. Three resistors with resistance values of 5Ω , 6Ω and 7Ω are
  placed in series. These would provide a resistance which is
  equivalent to one _____ Ω resistor.
  vi. Three resistors with resistance values of 12Ω, 3Ω and 21Ω are
  placed in series. These would provide a resistance which is
  equivalent to one _____ Ω resistor.

  5. As the number of resistors in a series circuit increases, the overall
  resistance __________ (increases, decreases, remains the same)
  and the current in the circuit __________ (increases, decreases,
  remains the same).

  6. Imagine that we add a third resistor in series with the first two. Does
  the current in the battery (a) increase, (b) decrease, or (c) remain
  the same? Does the terminal voltage of the battery (d) increase, (e)
  decrease, or (f) remain the same?

  7. Imagine that we add a third resistor in parallel with the first two. Does
  the current in the battery (a) increase, (b) decrease, or (c) remain
  the same? Does the terminal voltage of the battery (d) increase, (e)
  decrease, or (f) remain the same?
  

  13.5. Kirchhoff’s laws and its applications in solving
  problems in electric circuits
  

  Activity 13.5
  A single-loop circuit contains two resistors and two batteries, as shown
  in the following figure (neglect the internal resistances of the batteries).
  a). Find the current in the circuit.
  b). What power is delivered to each resistor? What power is delivered
  by the 12V battery?
  

  
  

  13.5.1. Kirchhoff’s laws
  Simple circuits can be analyzed using the expression V = IR and the rules for
  series and parallel combinations of resistors. Very often, however, it is not
  possible to reduce a circuit to a single loop.
  

  The procedure for analyzing more complex circuits is greatly simplified if
  we use two principles called Kirchhoff’s rules developed by the German
  Physicist Gustav Robert Kirchhoff (1824-1887).
  

  First, here are two terms that we will use often. A junction in a circuit is a
  point where three or more conductors meet. Junctions are also called nodes
  of branch points. A loop is any closed conducting path.
  

  In figure 13.13 below, the points a and b are junctions, but points c and d are
  not. The curved lines show some possible loops in this circuits.
  

  
  

  i.e The sum of the currents entering the junction must equal the sum of the
  currents leaving the junction.
  

  Kirchhoff’s loop rule: The algebraic sum of the potential differences in any
  loop, including those associated with emfs and those of resistive elements,
  must equal zero. That is,
  

  Kirchhoff’s first rule is a statement of conservation of electric charge. All
  charges that enter a given point in a circuit must leave that point because
  charge cannot build up at a point.
  

  Kirchhoff’s second rule follows from the law of conservation of energy.
  

  The sum of the increases in energy as the charge passes through some
  circuit elements must equal the sum of the decreases in energy as it passes
  through other elements. The potential energy decreases whenever the
  charge moves through a potential drop –IR across a resistor or whenever it
  moves in the reverse direction through a sourceof emf. The potential energy
  increases whenever the charge passes through abattery from the negative
  terminal to the positive terminal.
  

  When applying Kirchhoff’s second rule in practice, we imagine traveling
  around the loop and consider changes in electric potential, rather than the
  changes in potential energy.
  

  Problem solving strategy
  Junction rule: Assign symbols and directions to the currents in the various
  junctions. If you guess the wrong direction for a current it does not matter.
  The end result will be a negative answer for that current and the magnitude
  will be correct.
  

  Loop rule: You must choose a direction for moving around the loop. As you
  move around the loop the voltage drops and increases should be recorded
  according to the rules (a-d) below.

  a). If a resistor is traversed in the direction of the current, the change in
  potential across the resistor is –IR.
  b). If a resistor is traversed in the direction opposite the current, the
  change in potential across the resistor is +IR.
  c). If a source of emf is traversed in the direction of the emf (from – to +)
  the change in potential is .
  d). If a source of emf is traversed opposite the direction of the emf (from
  + to –) the change in potential is .
  

  
  

  
  

  
  

  
  

  
  

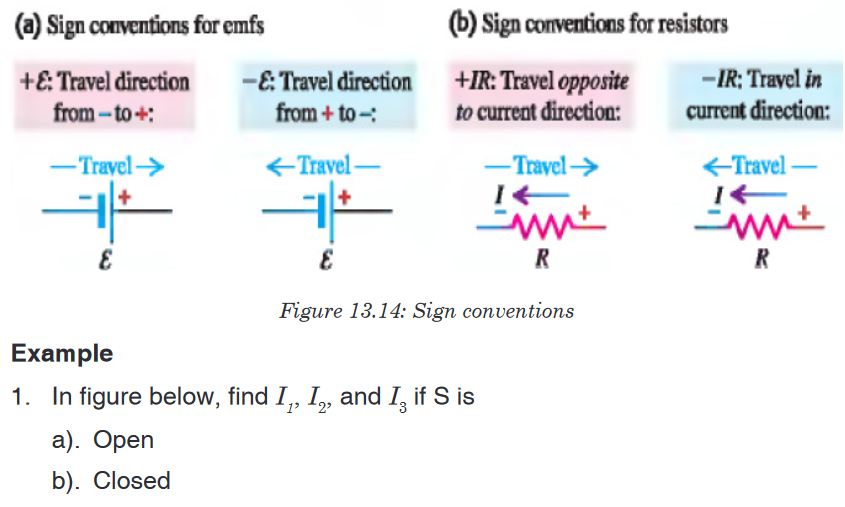
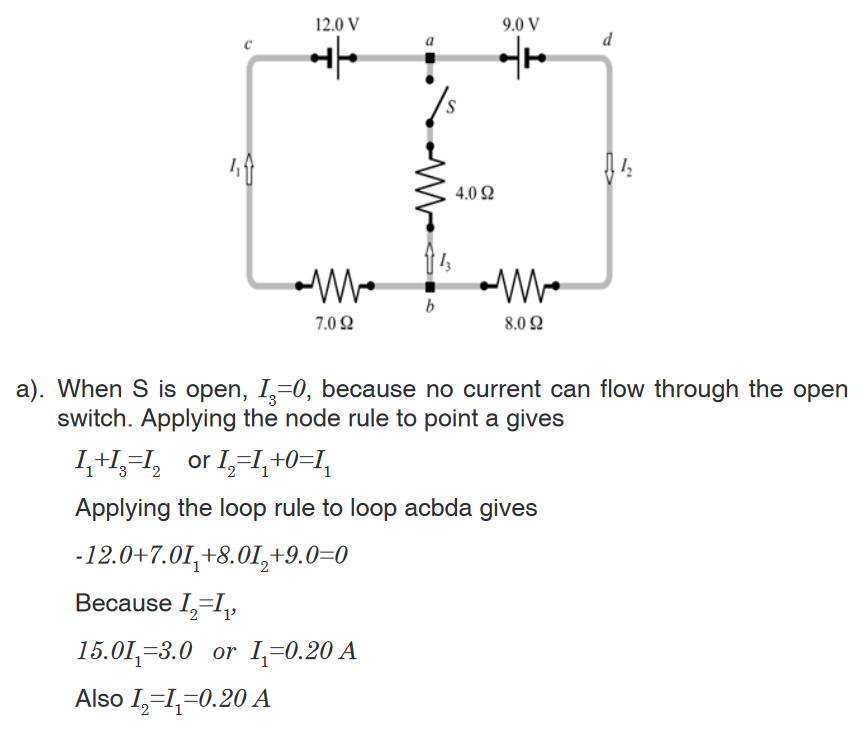
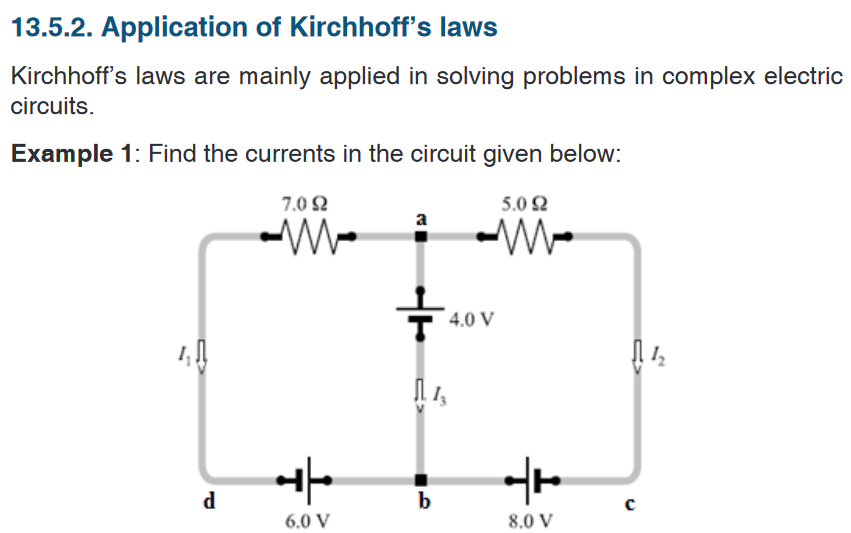
  Solution
  This circuit cannot be reduced further because it contains no resistors in
  simple series or parallel combinations. We therefore revert to Kirchhoff’s
  rules. If the currents had not been labeled and shown by arrows, we would
  do that first. No special care needed to be taken in assigning the current
  directions, since those chosen incorrectly will simply give negative numerical
  values.
  

  We apply the node rule to node b in the figure above.
  

  Current into b = Current out of b.
  

  
  

  The minus sign tells us that I₃ is opposite in direction to that shown in the
  figure.
  

  Example 2: The circuit shown in figure below contains two batteries, each
  with an emf and an internal resistance, and two resistors. Find (a) the current
  in the circuit (magnitude and direction); (b) the terminal voltage V_ab of the
  16.0 V battery; (c) the potential difference V_ac of a with respect to point c.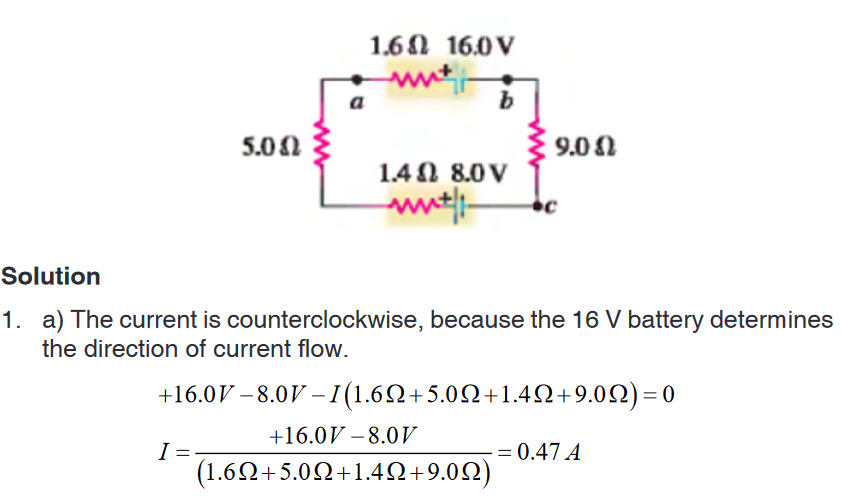
  

  
  

  
  

  Example 3: In figure below, the battery has an internal resistance of 0.7Ω.
  Find:
            i. The current drawn from battery,
           ii. The current in each 15 Ω resistor,
           iii. The terminal voltage of the battery.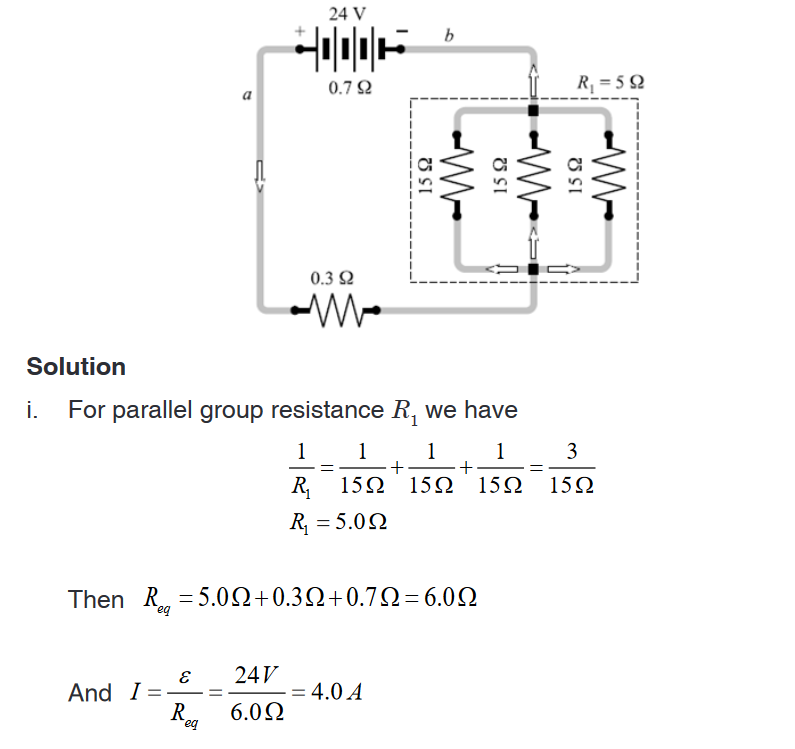
  

  
  

  
  

  Application activity 13.5
  In the circuit below, each cell has e.m.f of 1.5 V and zero internal
  resistance. Each resistor has a resistance of 10 Ω. There are currents I₁
  and I₂ in the branches as shown.
  

  
  

  a). Use Kirchhoff’s first law to write down an expression for the current in
  BE, in terms of I₁ and I₂
  b). Use Kirchhoff’s first law to write down equations for the circuit loops
  i) ABEFA ; ii) CBEDC
  

  Skills lab 13
  Conduct a survey to find out how people construct electric circuits and apply
  Kirchhoff’s laws in analysis of complex electric circuits before installation
  process.
  

  Collect and analyze data about when, where, and why people use Kirchhoff’s
  laws in dealing with complex electric circuits.
  

  To complete this project you must
  

  • Develop a survey sheet about electric components, demonstration of
  Kirchhoff’s laws and complex electric circuit.
  • Distribute your survey sheet to other student-teachers, family members
  and neighbors.
  • Compile and analyze your data.
  • Create a report to display your findings in your sheet.
  

  Plan it! To get started, think about the format and content of your survey
  sheet. Brainstorm what kinds of questions you will ask. Develop a plan for
  involving student-teachers in your class or other classes to gather more data.
  

  End unit assessment 13
  1. State Kirchhoff Current Law and Kirchhoff Voltage Law.
  2. Distinguish between electric sources of currents from receptors.
  3. Find the current across the 10V battery
  

  
  

  4. The figure below shows four resistors connected in a circuit with a
  battery.Which of the following correctly ranks the potential difference,
  across the four resistors?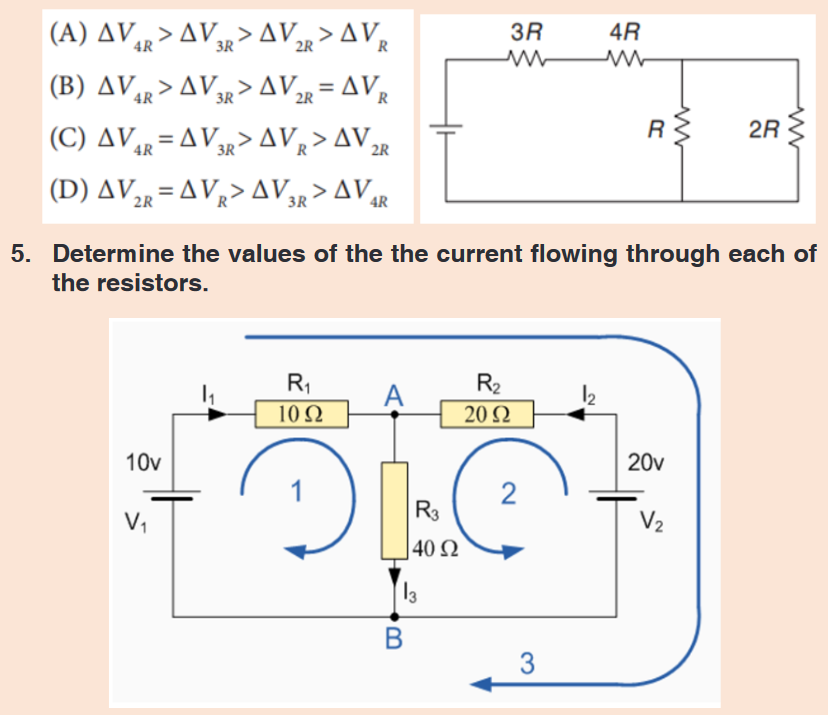
  

  
  

  
  

  
  

• UNIT 14: ASEXUAL AND SEXUAL REPRODUCTION IN PLANTS

  Key Unit competence: Describe modes of reproduction in plants
                                                and apply various methods of asexual and
                                                Sexual reproduction as means of increasing
                                                crop yield.

  Introductory Activity 14
  A.
  The kingdom Plantae comprises about 260,000 known species including
  flowering and non-flowering plants. All plants have a general organization
  which includes vegetative and reproductive organs. Plants reproduce
  through different ways. Use the books and other source of information to
  do the following:

  1. Write on how lower organisms such unicellular plant and another like
  cassava, sugar cane and apple reproduce.

  2. Describe the techniques used by people to grow Irish potatoes,
  cassava and bananas.

  3. Describe each of the following methods of asexual reproduction:
  fragmentation, budding and spore formation.

  B.
  1. Observe the following pictures and suggest what is going on.

  2. How are the pictures below related to reproduction in flowering plants.

  

  14.1. Comparison between sexual and asexual reproduction

  Application activity 14.1

  
  Observe the figures below taken from environment and answer the
  following questions.

  

  a). Name the figure A and B.
  b). Where the smallest (young ones) of banana come from?
  c). How the young bananas have been reproduced?
  d). How the young one of goat has been reproduced?
  e). Compare the modes of reproduction of banana plant and a goat.

  Asexual Reproduction

  
  Prokaryote like bacteria and unicellular organisms reproduce asexually by
  cell division or binary fission of the parent cell. This is a type of reproduction
  done by a single organism without production of gametes. It usually results
  in the production of identical offspring, the only genetic variation arising as a
  result of random mutation among the individuals.

  Sexual Reproduction
  Sexual reproduction is a type of reproduction in which two parents are
  involved, each capable of producing gametes. It is essentially cellular in
  nature which involves the fertilization of one haploid gamete with another,
  producing a new diploid cell called the zygote. The union of structurally
  similar physiologically different gametes is called isogamy. This is found
  only in lower forms such as Protozoa. The following is summary table of
  difference between asexual and sexual reproduction.

  

  Application activity 14.1
  1. Distinguish sexual and asexual reproduction.

  14.2. Asexual reproduction in plants

  
  14.2.1. Asexual reproduction and its methods

  
  Activity 14.2.1.a
  Brainstorm on asexual reproduction in lower organisms and write reports
  as an out-of-class activity.
  There are five common modes of asexual reproduction: fission, budding,
  vegetative reproduction, spore formation and fragmentation.

  1. Fission
  An important form of fission is binary fission. In binary fission, the parent
  organism is replaced by two daughter organisms, because it literally divides
  in two. Organisms, prokaryotes, and eukaryotes (such as unicellular fungi),
  reproduce asexually through binary fission; most of these are also capable
  of sexual reproduction. Another type of fission is multiple fission that is
  advantageous to the plant life cycle. Multiple fission at the cellular level
  occurs in many algae. The nucleus of the parent cell divides several times by
  mitosis, producing several nuclei. The cytoplasm then separates, creating
  multiple daughter cells.

  2. Budding
  Some cells split via budding resulting in a ‘mother’ and ‘daughter’ cell. The
  offspring organism is smaller than the parent. Budding is also known on a
  multicellular level.

  3. Vegetative reproduction
  Vegetative reproduction is a type of asexual reproduction found in plants
  where new individuals are formed without the production of seeds or spores
  by meiosis or syngamy. Examples of vegetative reproduction include the
  formation of miniaturized plants called plantlets on specialized leaves (for
  example in kalanchoe) and some produce new plants out of rhizomes or
  stolon (for example in strawberry). Other plants reproduce by forming bulbs
  or tubers (for example tulip bulbs and dahlia tubers). Some plants produce
  adventitious shoots and suckers that form along their lateral roots.
  Plants that reproduce vegetative may form a clonal colony, where all the
  individuals are clones, and the clones may cover a large area.

  4. Spore formation
  Many multicellular organisms form spores during their biological life cycle in
  a process called sporogenesis. Plants and many algae on the other hand
  undergo sporic meiosis where meiosis leads to the formation of haploid
  spores rather than gametes. These spores grow into multicellular individuals
  (called gametophytes in the case of plants) without a fertilization event. Then
  in the plant life cycle. Fungi and some algae can also utilize true asexual
  spore formation, which involves mitosis giving rise to reproductive cells
  called mitospores that develop into a new organism after dispersal.
  

  Activity 14.2.1.b
  Demonstration of asexual reproduction by fragmentation in algae

  Requirements
  Glass beakers of 500ml, Scalpel, Forceps, Pins, Spatula, Weighing
  balance, Labels, Artificial, fertilizers, Clear river water and Spirogyra
  (algae).

  Procedure
  1. Label five beakers of the same size as A, B, C, D and E. Pour water
  in each beaker. Weigh several measures of artificial fertilizers of 1 g
  each.
  2. Transfer 1g of fertilizer to beaker A, then 2g to beaker B, 3g to beaker
  C, 4g to beaker D Then lastly put 5g of fertilizers to beaker E. Note
  the concentration of fertilizers is increasing from A- E.
  3. Using forceps pick spirogyra and put it on a tile. Add several drops
  of water to avoid drying. Tease off a piece of spirogyra using a pin.
  Cut that piece into 5 fragments of the same length and transfer each
  piece into the beaker.
  4. Stand the beakers in a place where they can receive adequate sunlight
  for the seven days. On the next day start to examine the fragments in
  each beaker every day and record any observable changes such the
  increase in size of the spirogyra.
  Draw a table as this shown here and record your observation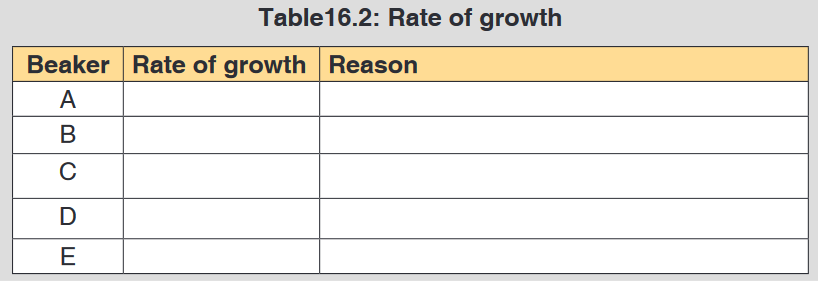
  

  
  

  5. Fragmentation
  Fragmentation is a form of asexual reproduction where a new organism
  grows from a fragment of the parent. Each fragment develops into a mature,
  fully grown individual. Fragmentation is seen in many organisms such as
  fungi, and plants. Some plants have specialized structures for reproduction
  via fragmentation, such as gemma in liverworts. Most lichens, which are a
  

  symbiotic union of a fungus and photosynthetic algae, reproduce through
  fragmentation to ensure that new individuals contain both symbionts. These
  fragments can take the form of soredia, dust-like particles consisting of
  fungal hyphen wrapped around photobiont cells.
  

  
  

  Application activity 14.2.1
  1. Write on the types of asexual reproduction.
  2. Explain the term fragmentation and give one example of plant which
  reproduces by using this type of asexual reproduction.
  

  14.2.2. Advantages and disadvantages of asexual reproduction

  Activity 14.2.2

  Make discussion on asexual reproduction in lower organisms and higher
  plants, outlining advantages and disadvantages.
  

  a. Advantages of asexual reproduction
  • As it occurs by mitosis,the offspring are genetically identical not only
  to their parents but also amongst themselves. This is advantageous,
  for example in agriculture where successive generations of plant retain
  the desired qualities or high yield of flowers, fruits and cereals.
  • It is faster as it does not involve stages such development of gonads,
  gamete formation, fertilization, fruit and seed formation and their
  dispersal. So plant can be rapidly propagated vegetatively using
  cuttings, bulbs, offsets and other parts.
  

  b. Disadvantages of asexual reproduction
  • It is suited to the environments that are generally stable in terms of
  humidity, soil, temperature and light. If there is a drastic change in the
  environment, the individuals may not be able to cope with the change
  and so gradually die off.

  • It can lead to overcrowding of the individuals plants around the parent
  plant and this can lead to excessive competition for soil nutrients, light
  and moisture. The new individuals will therefore become weak and
  only a few may survive.

  Application activity 14.2.2
  Explain the advantages and disadvantages of asexual reproduction.

  14.2.3. Vegetative and artificial propagation in flowering plants
  

  Activity 14.2.3

  Demonstration of asexual reproduction in plants by cuttings
  

  Requirements
  Growth medium or moist soil, sweet potatoes vines, elephant grass,
  sugarcane or cassava stems, secateurs/sharp knife and rooting hormone.
  

  Procedure
  1. Collect clean and healthy stems from cassava, sugarcane or potato
  plants.
  2. Using a secateurs/sharp knife, cut the stem of either cassava,
  sugarcane or sweet potato stems into suitable sizes.
  3. Place them in either suitable medium of growth or apply rooting
  hormone if available or plant them in moist soil in the school garden.
  4. Leave the set up for about 13 days, and then observe the development
  of roots and leaves at nodes.
  Draw and record what you will observe after 13 days on the development
  of roots and leaves at nodes.
  

  Artificial vegetative propagation is the deliberate production of new plants
  from parts of old plants by humans. This can be done by following three
  methods: Cutting, layering, and grafting.
  

  a. Cutting
  This is simple procedure in which part of the plant is removed by cutting and
  placed in a suitable medium for grow. The part of the plant which is removed
  by cutting it from the parent plant is called a ‘cutting’. In this method one-
  year-old stem of root is cut from a distance of 20 to 30 cm. and is buried in
  the moist soil in natural position. After sometime, roots develop from this
  cutting and it grows into a new plant. This method is commonly used in rose
  and sugar cane. Care is taken that nodes which were lower in parent plant
  (morphologically) are put in the soil, while the morphologically higher nodes
  are kept up. Adventitious roots are given off at the lower nodes.
  

  
  

  b. Layering
  This method of vegetative propagation is used in those plants whose soft
  branches occur near the ground such as jasmine plant. In this method, a
  branch of the plant which is near to the ground is pulled towards the ground
  and a part of this branch is covered with moist soil leaving the tip of this
  branch above the ground. After sometime, roots develop from that part of
  the branch which was buried in the soil. This branch is then cut of along with
  the roots from the parent plant and develops into a new plant. This method
  of asexual reproduction is also used in the production of plants such as
  Bougainvillea, jasmine, guava, strawberries, lemon, China rose etc.
  

  
  

  c. Grafting
  In this method of vegetative propagation the stems of two different plants are
  joined together so as to produce a new plant containing the characters of
  both plants. Out of the two plants one plant has a strong root system while
  the other has a better flower or fruit yield. The plant of which the root system
  is taken is called ‘stock’, while the other plant of which the shoot is selected
  is known as ‘scion’ or ‘graft’. These two stems i.e. the stock and the scion
  are fitted together by making slanting cuts in them and bound tightly with a
  piece of cloth and is covered with a polythene sheet.
  

  While joining the scion with the stock care should be taken that the diameter
  of the stock and scion chosen for grafting should be equal. Scion gets the
  mineral and water from the soil through the stock and develops branches
  and produce fruits. This method of propagation is used in mango, apple,
  banana, pear, grape, pineapple and peach.
  

  
  

  Vegetative and artificial reproduction in flowering plants
  The reproductive part of the plant is a flower. The union of male and female
  gametes to form a zygote is called fertilization. The transfer of pollen grains
  from the anther to the stigma of the same flower or the different flower is
  called pollination. In nature, plants reproduce asexually in a variety of ways.
  The vegetative reproductive parts in flowering plant are stem, branches, and
  leaves and they have the following characteristics:
  

  Characteristics of the stem
  • Stem develops from the plumule of embryo.
  • Stem is generally the ascending part of the plant axis.
  • It bears a terminal bud for growth in length.
  • The stem is differentiated into nodes and internodes. The stem nodes
  possess dissimilar appendages called leaves.
  

  • The young stem is green and capable of performing photosynthesis.
  • In the mature state it bears flowers and fruits. Leaves and stem
  branches develop exogenously.
  • Stem exposes leaves, flowers and fruits to their most suitable position
  in the aerial environment for optimum function, Hair, if present, is
  commonly multicellula.
  • Stems are usually positively phototropic, negatively geotropic and
  negatively hydrotropic.

  Characteristics of the leaf
  • It is dissimilar lateral flattened outgrowth of the stem.
  • The leaf is exogenous in origin.
  • It is borne on the stem in the region of a node.
  • An axillary bud is often present in the axil of the leaf.
  • Leaf has limited growth. An apical bud or a regular growing point is
  absent.
  • The leaf base may possess two lateral outgrowths called stipules.
  • A leaf is differentiated into three parts: leaf base, petiole and lamina.
  • The lamina possesses prominent vascular strands called veins.
  • It is green and specialized to perform photosynthesis.
  • Leaf bears abundant stomata for exchange of gases and it is the major
  seat of transpiration.
  

  Characteristics of the branches
  A branch or tree branch is a woody structural member connected to but not
  part of the central trunk of a tree. Large branches are known as boughs
  and small branches are known as twigs. Due to a broad range of species of
  trees, branches and twigs can be found in many different shapes and sizes.
  

  Application activity 14.2.3
  1. Discuss on the methods of artificial vegetative propagation.
  2. Cassava produces flowers, fruits and seeds. Why people prefer to
  grow cassava by cutting rather than using seed?
  

  14.2.4. Application of artificial propagation in growing improved
  varieties of plants

  Activity 14.2.4

  Using addition resources to your textbook available in your school such
  as the books from the school library and search further information from
  the internet. Discuss on application of artificial propagation in growing
  improved varieties of plants.

  Artificial vegetative propagation is usually used in agriculture for the
  propagation (or reproduction) of those plants which produce either very few
  seeds or do not produce viable seeds. Some examples of such plants which
  are reproduced by artificial vegetative propagation methods are: Banana,
  Pineapple, Orange, Grape, Rose, etc.

  Vegetative propagation of particular cultivars that have desirable
  characteristics is very common practice. Reasons for preferring vegetative
  rather than sexual means of reproduction vary, but commonly include greater
  ease and speed of propagation of certain plants, such as many perennial root
  crops and vines. Another major attraction is that the resulting plant amounts
  to a clone of the parent plant and accordingly is of a more predictable quality
  than most seedlings. However, as can be seen in many variegated plants,
  this does not always apply, because many plants actually are chimeras and
  cuttings might reflect the attributes of only one or some of the parent cell
  lines.

  Man-made methods of vegetative reproduction are usually enhancements
  of natural processes, but they range from rooting cuttings to grafting and
  artificial propagation by laboratory tissue culture. In horticulture, a “cutting”
  is a piece that has been cut off from a mother plant and then caused to
  grow into a whole plant. A popular use of grafting is to produce fruit trees,
  sometimes with more than one variety of the same fruit species growing from
  the same stem. Rootstocks for fruit trees are either seedlings or propagated
  by layering.
  

  
  

  Application activity 14.2.4
  1. Describe the methods of artificial vegetative propagation.
  2. Elaborate on the characteristics of vegetative reproductive parts
  in a flowering plant
  3. Explain the application of artificial propagation in growing
  improved varieties of plants.
  

  14.3. Sexual reproduction in plants
  

  14.3.1. Alternation of generation in bryophytes and
  pteridophytes

  Activity 14.3.1
  Visit library and computer lab and search the comparison of the lifecycles
  of mosses and ferns and present them on Manilla paper.
  

  The life cycle of an organism is the progressive sequence of changes
  which an organism goes through from the moment of fertilization to death.
  During its life cycle, the organism produces new generations of individuals
  which repeat continuously the process. New generations are produced by
  reproduction, which may be sexual or asexual. The life cycle involves the
  mitosis and meiosis. In this lesson, we will make concern on how meiosis
  can affect the life cycle of living organisms.
  

  The life cycle is seen in seaweeds, mosses ferns and their relatives. Their
  life cycles start with the sexually mature adult plants. Since they produce
  gametes, they are called the gametophytes (gamete plants). These are
  haploid, as they produce eggs and sperms. The egg and sperm fuse to
  produce a diploid zygote, but this does not develop directly into a new
  gametophyte. Instead it grows (by mitotic divisions) into another plant which
  is quite distinct from the gametophyte called sporophyte (spore plant).The
  function of sporophyte is to produce spores.In bryophytes, the sporophyte
  depends on gametophyte for nourishment. As spores are formed by meiosis,
  they are haploid. When the later are dispersed by wind on suitable soil,
  they germinate and grow by mitosis into gametophytes, which then repeat
  the sequence of life cycle. Ferns and mosses consist of two distinct plants:
  haploid gametophyte and diploid sporophyte, which alternate each other
  within the life cycle. This phenomenon is known as alternation of generation.
  

  So, Alternation of generation is a phenomenon in the plant life cycle in which
  a diploid stage a sporophyte alternates with a haploid stage of gametophyte.
  

  The importance of alternation of generation to organisms
  • Spores produced can survive hash conditions and only germinate
  when conditions are favorable.
  • It ensures rapid multiplication of the plant species as spores are usually
  produced in vast numbers.
  • Interdependence between the gametophyte and sporophyte
  generations ensure that both generations exist at any given time. This
  prevents extinction of the plant species.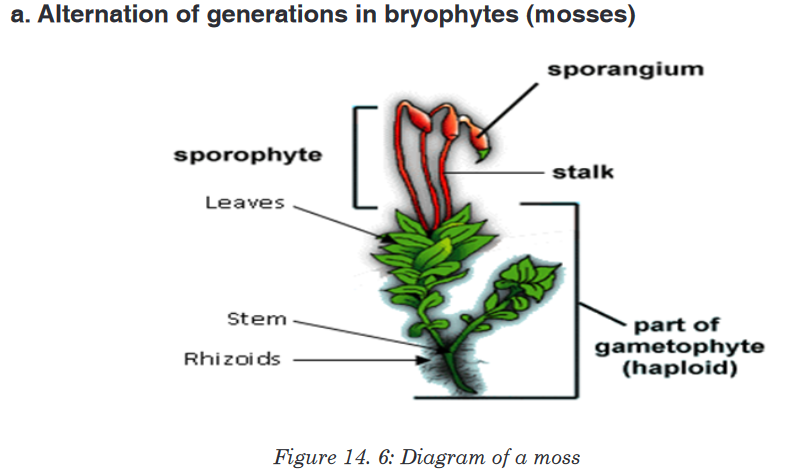
  

  
  

  The life cycle in mosses involves alternation of generations between the
  diploid (2n)sporophyte and haploid gametophyte. In bryophytes, the
  gametophyte is adominant stage of the life cycle, while the sporophyte is
  dependent on gametophyte for supplying water and nutrients. Gametes are
  formed in special reproductive organs at the tips of gametophytes.Sperms
  are produced in antheridia (singular: antheridium), and eggs in archegonia
  (singular: archegonium). Some species produce both sperms and eggs on
  the same plant, whereas others produce sperms and eggs on separate
  plants.
  

  During fertilization which requires water, the sperms released from antheridia
  fuse with the eggs and form a diploid (2n) zygote. The zygote grows into
  the sporophyte. Sporophyte is a long stalk ending in a capsule in which
  haploid spores are formed by meiosis. When spores become mature
  

  
  enough, the capsule bursts and spores are scattered by wind. Under suitable
  conditions, spores then germinate by forming underground filaments called
  protonemata (singular: protonema). Small buds produced by protonemata
  give rise to new gametophyte plants which can start the cycle again.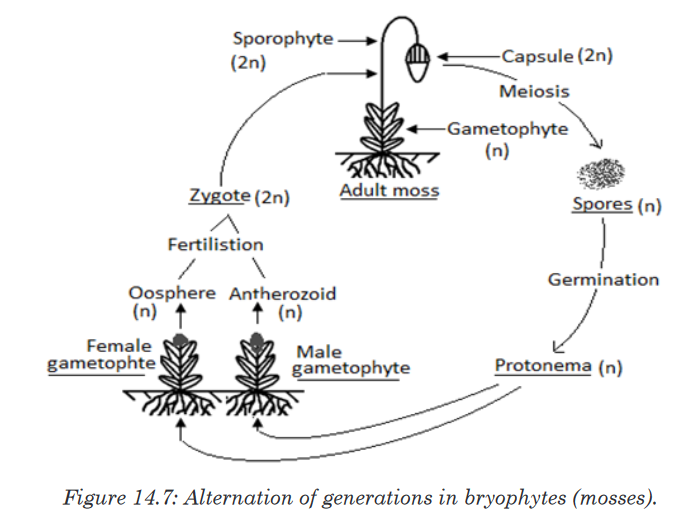
  

  
  

  Bryophytes grow in habitats where water is available constantly because for
  fertilization to occur, the sperm of bryophyte must swim to an egg. Without
  water, this movement is impossible. Because of this dependence on water
  for reproduction, bryophytes must live in habitats where water is available at
  least part of the year.

  b. Alternation of generations in pteridophytes (ferns)

  Pteridophytes also exhibit alternation of generations. Ferns are formed
  of true roots, stem and leaves (fronds) with vascular tissues. They have
  lignified tissues. The horizontal underground stem is called rhizome which
  bears adventitious roots. The leafy plant is a sporophyte. Mature leaves
  commonly called fronds bearing yellow or orange masses of sporangia
  which are grouped into the structures called sori (singular: sorus) on their
  lower side.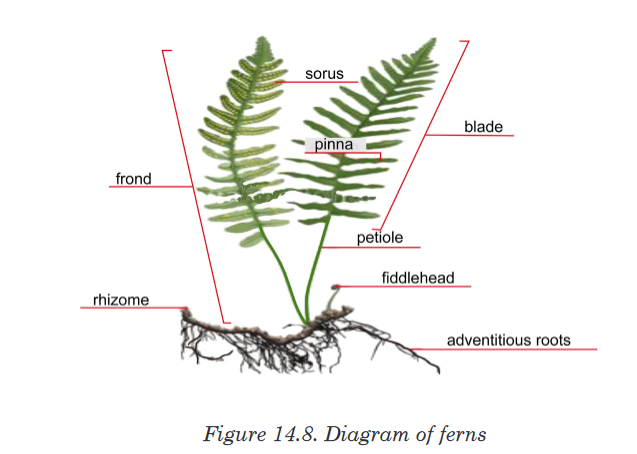
  

  
  

  Ferns have a life cycle in which the diploid (2n) sporophyte is the dominant
  generation, large (some fern trees can have 7 m of height), and differentiated
  into leaf, stem and roots with vascular tissues, while the haploid gametophyte
  (prothallus) is very simple with few millimeters. In ferns, the sporophyte
  produces haploid spores by meiosis. This is done on the underside of the
  leaf called frond, in sporangia (singular: sporangium). Sporangia are grouped
  into sori (singular: sorus).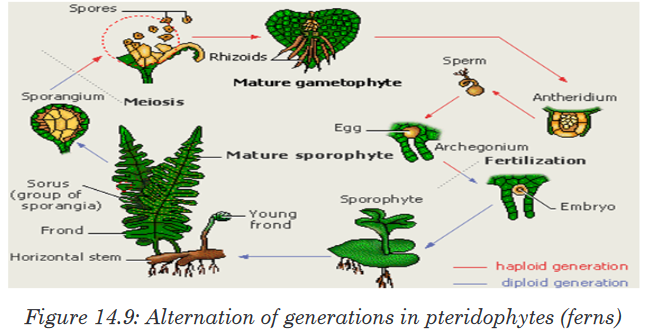
  

  
  

  When spores are mature enough, the sporangia burst and spores are
  released on ground. If conditions are favorable, spores germinate and grow
  into the haploid heart-shaped gametophytes , which grows independently
  of sporophyte. Antheridia and archegonia found underside of gametophyte
  produce sperms and eggs respectively. During fertilization, sperms swim
  towards eggs and fuse together to form diploid zygotes, which grow and
  develop into new sporophytes. As sporophyte grows, the gametophyte dries
  and dies.
  

  
  

  Application activity 14.3
  1. Explain the meaning of the term alternation of generation.
  2. How is water essential in the life cycle of a bryophyte?
  3. What is the archegonium and antheridium?
  4. How are these structures important in the life cycle of a moss plant?
  5. What is the dominant stage of the fern life cycle?
  6. Explain the relationship of the fern gametophyte and sporophyte.
  7. Compare the gametophyte and sporophyte stages of the plant cycle.
  Which is haploid? Which is diploid?
  8. How do bryophytes reproduce asexually?
  

  14.3.2. Types, structure and functions of flowers
  

  Activity 14.3.2
  
  

  Collect different forms of flowers from the school compound or around the
  school, such as hibiscus, morning glory, sweet potato, or maize flower (or
  any type of flower in your community not necessarily the ones mentioned
  here)
  1. Observe and describe the structures of collected flowers.
  2. How do collected flowers differ externally?
  3. Cut one of the flowers into two halves, draw and label one half of
  flower.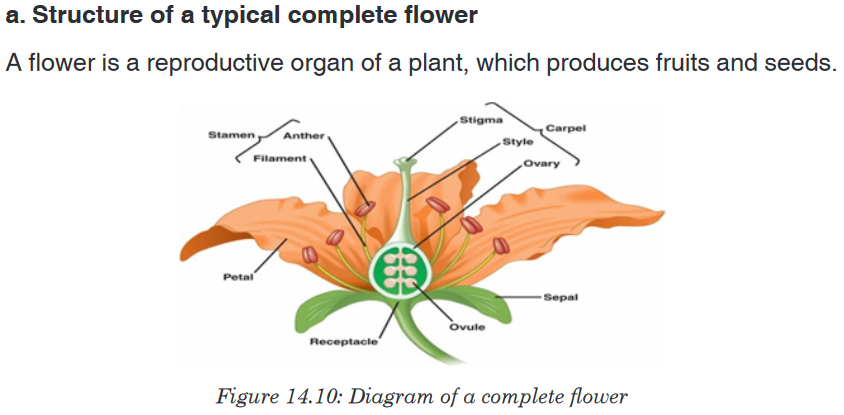
  

  
  

  
  

  A typical hermaphrodite or bisexual flower contains the following parts:
  • Pedicel: It is the stalk which attaches the flower on the main floral axis.

  • Receptacle: It is the swollen part at the end of the stalk where other
  parts of the flower are attached.

  • The calyx: It is the set of sepals, generally having green colour. They
  protect the internal parts of the flower. In some plants, the sepals are
  coloured and are called petaloids.

  • The corolla: It is the set of petals, with different colours and nectar
  glands that produce sugary substances which participate in attraction of
  pollinating agents. In some plants, the petals are green and are called
  sepaloids. Both calyx and corolla are collectively called perianth. They
  are called floral envelope or accessory organs as they do not participate
  directly in reproduction, or in formation of fruits and seeds, they all insure
  the protection of internal parts of the flower.

  • Androecium: It is the male reproductive organs of the flower. It consists
  of many stamens. A stamen consists of: the filament which supports
  anther, and anther which contains the pollen grains or male gametes.

  • Gynoecium/pistil: It is the female reproductive organ. It consists of
  many carpels, and each carpel is made of: stigma (plural: stigmata),
  style and ovary with ovules.

  a). The stigma: Receive pollen grains from anther during pollination.
  b). Style: Supports the stigma in a good position to receive pollen grains.
  c). Ovary: A sac where ovules are produced. Ovules become seeds
  after fertilisation.
  

  b. Types of flowers
  1. According to absence of some reproductive parts of the flower, we can
  distinguish:

  i. Unisexual flower: A flower that consists of one type of reproductive
  organ. This can be staminate: unisexual male (with androecium
  only), or carpellate: unisexual female (with gynoecium only). E.g.
  flower of papaya.

  ii. Bisexual or hermaphrodite flower: A fl ower with the two
  reproductive organs. It contains both male and female reproductive
  organs (androecium and gynoecium). E.g. flowers of beans.
  Dioecious plants are plants that have male flowers and female flowers
  on separate plants (e.g. papaya/pawpaw) while monoecious plants
  are plants that have both male and female flowers on the same plant
  (e.g. maize).

  2. According to the position of ovary in the point of insertion of calyx, corolla
  and stamen, we can distinguish:
  i. A flower with inferior ovary: It is when the ovary is located below
  the point of insertion of calyx, corolla and stamens.

  ii. A flower with superior ovary: It is when the ovary is located over
  the point of insertion of calyx, corolla and stamens.

  iii. The semi-infer or semi-super flower: When ovary is neither infer
  nor super but in the middle of receptacle which is hollowed.
  • When sepals are joined together, the flowers are called gamosepal,
  and where are not joined together, the flower is called dialysepal.
  • When petals are joined together, the flowers are called gamopetal,
  and when are not joined together, the flower is called dialypetal.
  When they are absent, the flower is called apetal.

  3. According to the shape and symmetry of the flower, we can distinguish:

  i. Zygomorphic or irregular flower: A flower with a bilateral symmetry.
  The flower cannot be divided into two similar halves. E.g. flowers of
  beans, cassia.

  ii. Actinomorphic or regular flower: A flower with a radial symmetry.
  The flower can be divided into two or more planes to produce similar
  halves. E.g. flowers of coffee, orange.
  

  4. Dichogany: It is when male and female organs of the flower mature at
  different times. We can distinguish:

  • Protandry: When stamens mature before pistil.

  • Protogyny: When pistil matures before stamen.

  5. Inflorescence is when two or more flowers borne on a common stalk.
  

  c. Representation of the number and characteristics of a flower
  There are two ways by which we can present the number and characteristics
  of different parts of the flower. These ways include: floral diagram and floral
  formula.
  

  Floral formula
  The fl oral formula indicates the number and characteristics of different
  floral organs. It varies from one flower to another. By convention, there are
  standard symbols that are used to represent different parts of the flower and
  their characteristics:

  K: for calyx, K5: calyx with five free sepals, K(5): calyx with five fused sepals.

  C: for corolla, C5: corolla with five free petals, C(5): corolla with five fused
  petals.

  P: for perianth, P4: four free tepals, P(4): four fused tepals, P2+2: four tepals
  in two whorls of three each.

  A: for Androecium or stamen, A5: androecium with five free stamens, A(5):
  five fused stamens, A5+5: ten stamens in two whorls of five each, A0:
  stamens absent, A∞: stamens indefinite in number, A(9)+1: androecium of
  10 stamens nine fused together and one free.

  G: for pistil or gynoecium, G₂: two free carpels, G₂: two fused carpels, G0:
  carpels absent, G₂: Bicarpellary, syncarpous semi-inferior ovary.

  Representation of the symmetry of flower:
  Փ: zygomorphic or irregular
  : Actinomorphic or regular flower.
  Representation of sex of the flower: ♂: staminate flower, ♀: pistillate
  flower,
  

  
  Bisexual flower
  The floral formula is specific to each species of plant.
  

  Examples
  Write a floral formula of coffee having
  • The bilateral symmetry
  • Hermaphrodite flower
  • 1 calyx with 5 fused sepals
  • 1 corolla with 5 petals
  • 5 fused stamens
  • 1 pistil with 2 carpels each one with infer ovary of 2 chambers

  Answer: (5S)+ (5P) +(5A)+ 2C-2 or K(5) + C(5) + A(5) + G-2(2)
  Write a floral formula of Irish potato having
  • 5 free sepals
  • 5 free petals
  • 5 free stamens
  • 2 fused carpels with 2 chambers having many ovules
  • 1 infer ovary
  • Bisexual flower
  • Radial symmetry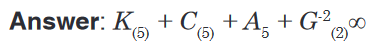
  

  
  

  Application activity 14.3.2
  1. What are the male and female structures of a flower?
  2. How might be an advantage for a plant to have many flowers together
  in a single structure?
  3. Where does the female gametophyte develop?
  4. Describe the flower and how it is involved in reproduction.
  

  14.3.3. Pollination and double fertilisation in flowering plants

  Activity 14.3.3

  Visit a computer lab, download and describe the videos of the process
  of double fertilization in flowering plants, and search more information to
  identify different pollinating agents

  1. Pollination
  Pollination is transfer of pollen grains from anther to the stigma.

  a). Types of pollination: There are two types of pollination such as: self-
  pollination and cross-pollination.

  i. Self-pollination: It is the transfer of pollen grains from anther to the
  stigma of the same flower, or of different flowers but of the same
  plants. It involves one plant. E.g. flowers of maize and beans.

  ii. Cross-pollination: It is the transfer of pollen grains from anther to
  the stigma of the flower of another plants. It involves two plants. E.g.
  flowers of pawpaw.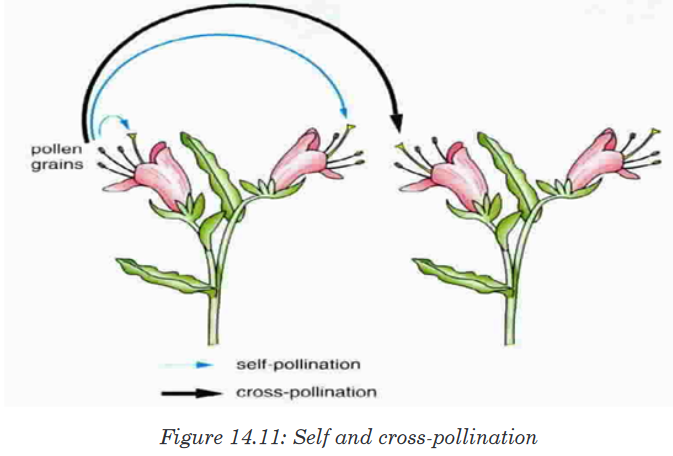
  

  
  

  b). Main Pollinating agents
  Flower structure is closely related with the way they are pollinated. This
  means that flowers are adapted to specific agents or mode of pollination.
  The common agents of pollination are: insects (entomophily), wind
  (anemophily), water (hydrophily), humans (anthropophily), and birds
  (ornithophily).
  

  Characteristics of insect-pollinated flowers (entomophilous flowers)
  • Flowers produce the nectar to attract pollinators.
  • Flowers have large brightly coloured corolla to attract pollinators.
  • Production of scents to attract pollinators.
  • The surface of the stigma should be sticky to hold pollen grains.
  • Pollen grains are sticky and rough enough to remain on the surface of
  stigma.

  Characteristics of wind-pollinated flowers (enemophilous flowers)
  • The flowers have large stigma to hold pollen grains.
  • The surface of the stigma should be sticky to hold pollen grains.
  • Pollen grains are rough enough to remain on the surface of stigma.
  • The flowers are or are not brightly-colored.
  • They have or do not have scent.
  • They do or do not secrete nectar.
  • They produce large quantities of pollen grains, as much of them never
  reach the stigmas.

  2. Double fertilization and events after fertilization in flowering plants
  Double fertilization is a complex fertilization mechanism of flowering plants
  (angiosperms). This process involves the joining of a female gametophyte
  (megagametophyte, also called the embryo sac) with two male gametes
  (sperm).
  

  a. Development of pollen grains and plant ovules
  i. Development of pollen grains

  The pollen grains are produced in the anthers while the ovules are produced
  in the ovary.
  

  Pollen grains
  Each anther has four pollen sacs which contain many diploid microspore
  mother cells that undergo meiosis to form four microspores each. At first,
  the four microspores remain together as tetrads. The nucleus of each
  microspore then divides by mitosis, forming a generative nucleus and a
  tube or vegetative nucleus. At this point, the content of the pollen grain
  may be considered as the male gametophyte. A two-layered wall forms
  

  around each pollen grain. The outer wall, the exine is thick and sculptured.
  The inner wall, the intine is thin and smooth. There are many pores or
  apertures in the wall through which a pollen tube may emerge.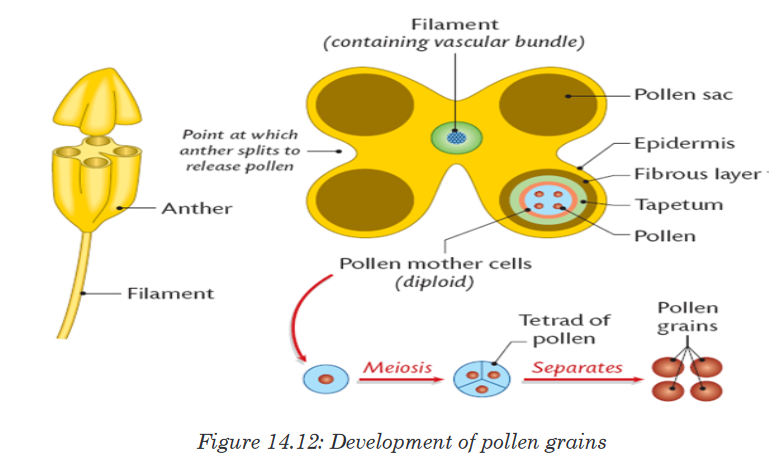

  

  ii. Development of Plant ovule
  Each ovule is attached to the ovary wall by a short stalk called funicle. The
  main tissue in the ovule is the nucellus which is enclosed and protected by
  the integuments.

  At one end of the ovule, there is a small pore called micropyle. A single
  diploid megaspore mother cell in the nucellus undergoes meiosis,
  producing four megaspores. Three of the four megaspores degenerate,
  while the remaining cell, called the embryo sac, grows to many times its
  original size. The nucleus of the embryo sac divides mitotically three times,
  resulting in eight haploid nuclei which are arranged in groups of four nuclei
  at the two poles. At this point, the contents of the embryo sac may be
  regarded at the female gametophyte.

  One nucleus from each pole migrates to the centre of the embryo sac.
  These two nuclei are called polar nuclei, and they fuse to form a single
  diploid nucleus. Meanwhile, cell walls form around the remaining six nuclei
  and they form the synergids, antipodals and the egg (ovum). Only the egg
  functions as the female gamete.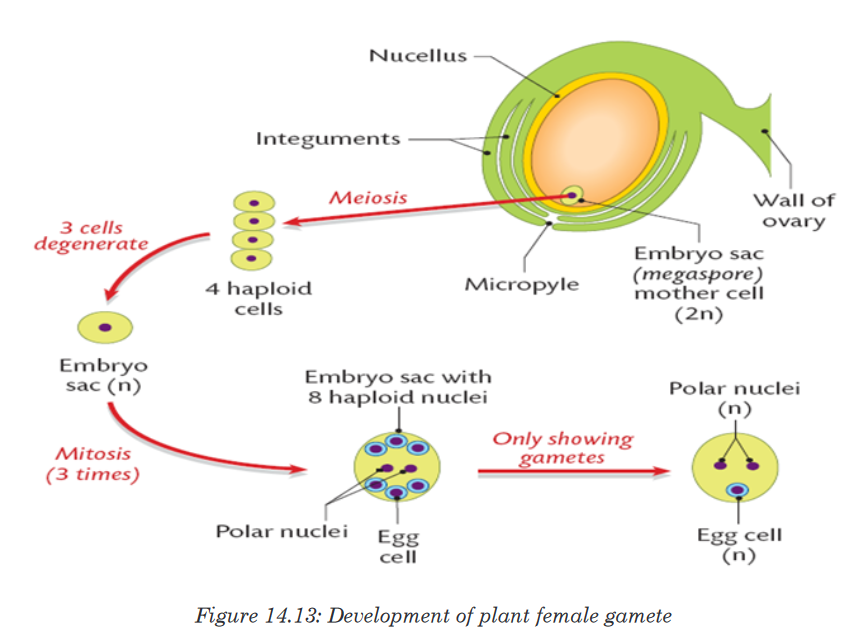

  

  In summary, the pollen grain contains two haploid nuclei: one called
  generative nucleus, and the other the tube nucleus.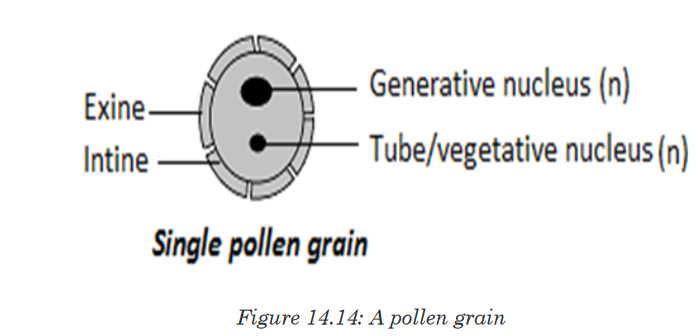

  

  On the other hand, the ovule or embryonic sac contains eight nuclei:
  • Three antipodal nuclei/cells at one end
  • Two polar nuclei/cells in the middle of ovule
  • Two synergids (non-functional nuclei)
  • One big egg cell.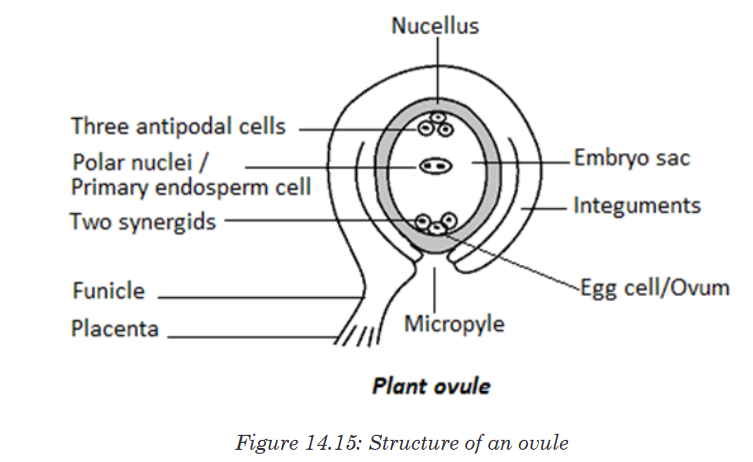

  

  The process of double fertilization
  Double fertilization begins when a pollen grain adheres to the stigma of the
  carpel, the female reproductive structure of a flower.

  The pollen grain then takes in moisture and begins to germinate, forming a
  pollen tube that extends down toward the ovary through the style.

  The growth of the pollen tube is controlled by the pollen tube nucleus. In
  the pollen tube, the generative nucleus divides mitotically into two haploid
  nuclei which are the male gamete nuclei. These follow behind the tube
  nucleus as the pollen tube grows down the style towards the ovule. The
  tip of the pollen tube then enters the ovary and penetrates through the
  micropyle opening, releasing the two sperms in the megagametophyte or
  ovule.

  The tube nucleus degenerates, leaving a clear passage for the entry of
  male nuclei. One nucleus fertilizes the egg cell to form a diploid zygote
  (2N), which will grow into a new plant embryo; the other fuses with polar
  nuclei to form a triploid nucleus (3N), which will grow into a food-rich tissue
  known as endosperm, which nourishes the seedling as it grows.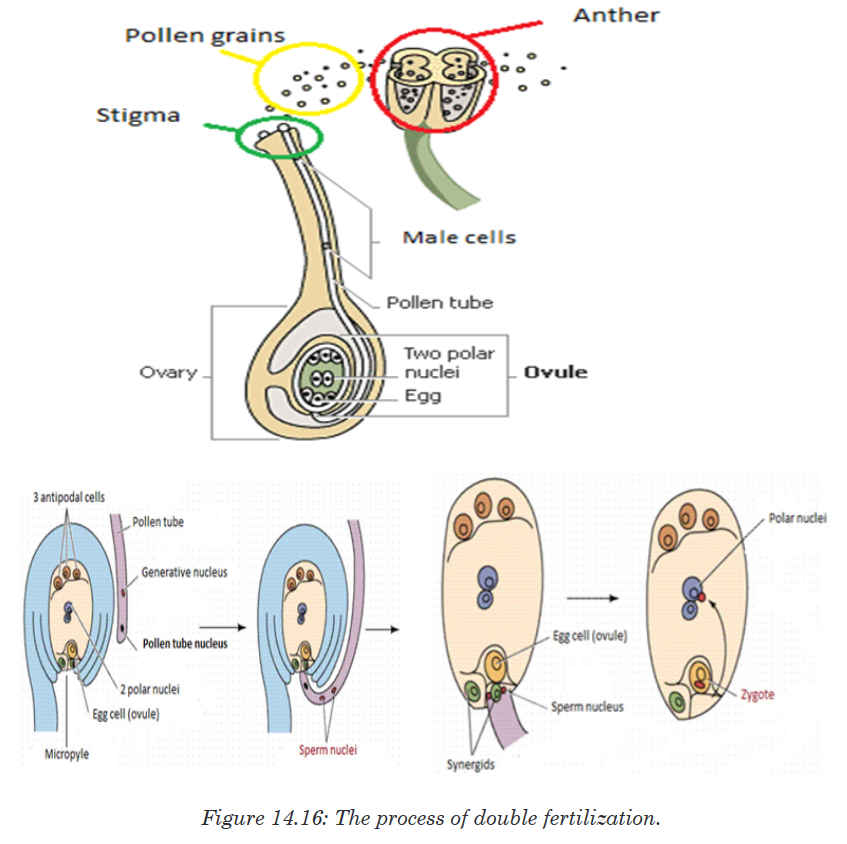

  

  This process is described as double fertilisation and is typical of
  angiosperms. If there is more than one ovule in the ovary, each must be
  fertilised by separate pollen grain and hence the fruit will have many seeds
  genetically different from each other.

  3. Events in a flower after fertilization
  After fertilisation, the calyx, corolla, stamens and style may wither gradually
  and fall off, but in some flowers the calyx may persist. The ovule forms the
  seed, the two integuments of the ovule will form the seed coat, and the ovary
  will develop into fruit, with the ovary wall forming the pericarp (fruit wall).
  The diploid zygote undergoes cell division to form the embryo, the triploid
  primary endosperm nucleus develops into endosperm, a store used by the
  developing embryo. This persists in endospermic seeds of monocotyledons.

  
  The micropyle persists as a small hole in the seed coat through which water
  is absorbed during germination.

  

  Application activity 14.3.3
  1. Are angiosperms typically wind or animal pollinated? How does this
  process occur?
  2. What is meant by the term endosperm?
  3. How are brightly coloured petals advantageous to the plant?
  4. What do you understand by the term double fertilization?
  5. What happens to the antipodal cells and synergids cells after
  fertilization?

  14.3.4. Structures and types of fruits and seeds

  Activity 14.3.4

  
  Observe slides containing micrographs of different fruits and seeds.
  According to their characteristics:
  1. Differentiate fruits.
  2. Draw and show a structure of seed as seen on microscope

  Below are some examples of fruits:

  

  

  A fruit is a structure formed from the ovary of a flower, usually after the
  ovules have been fertilized. In nature, a fruit is normally produced only after
  fertilization of ovules has taken place, but in many plants, largely cultivated
  varieties such as seedless citrus fruits, grapes, bananas, and cucumbers,
  fruit matures without fertilization, a process known as parthenocarpy. Ovules
  within fertilized ovaries develop to produce seeds. In unfertilized varieties,
  seeds fail to develop, and the ovules remain with their original size.

  A fruit consists of two main parts; pericarp (fruit wall) and the seed. The
  pericarp has three layers: epicarp or exocarp (outermost), mesocarpe
  (middle) and endocarp (inner).

  

  The fruit can have a dry pericarp or fleshy pericarp. The fruits with fleshy
  pericarp include: berry and drupe. Drupe is a fleshy fruit with only one seed,
  E. g. avocado.

  

  Berry is a fleshy fruit having many seeds inside of it. E.g. tomatoes, orange,
  and pawpaw.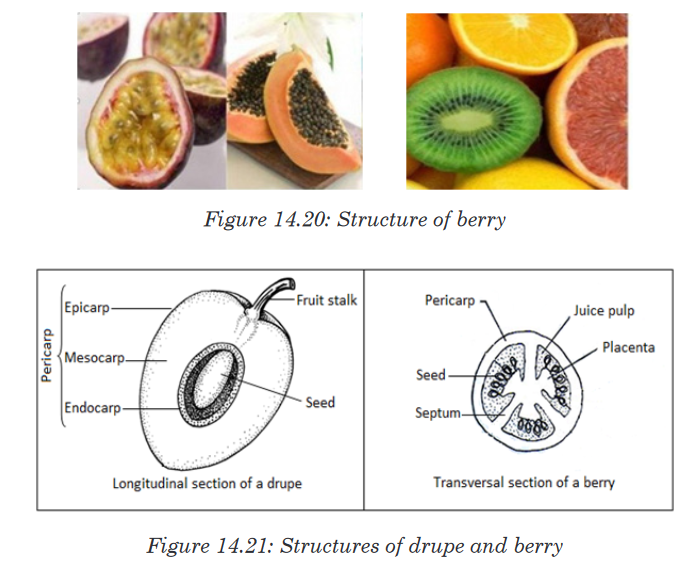

  

  The fruits with dry pericarp include indehiscent fruit or dehiscent fruit.
  Indehiscentfruits do not open. Seeds remain inside of the fruits. E.g. fruits of
  coconuts. Dehiscent fruits open and release seeds. These include: dehiscent
  fruits with one carpel, and those with many carpels. Dehiscent fruits with one
  carpel include; those which open along one side, e.g. follicle; and those
  which open along both sides, e.g. legume (beans).

  Fruits of eucalyptus are exam of dehiscent fruits with many carpels.

  

  The major function of a fruit is the protection of developing seeds. In many
  plants, the fruit also aids in seed distribution (dispersal).

  Food value
  Fruits are eaten raw or cooked, dried, canned, or preserved. Carbohydrates,
  including starches and sugars, constitute the principal nutritional material.
  Citrus fruits, tomatoes, and strawberries are primary sources of vitamin C,
  and most fruits contain considerable quantities of vitamin A and vitamin B.
  In general, fruits contain little protein or fat. Exceptions are avocados, nuts,
  and olives, which contain large quantities of fat, and grains and legumes,
  which contain considerable protein.

  A seed is an embryonic plant enclosed in a protective outer covering. The
  formation of the seed is part of the process of reproduction in seed plants,
  the spermatophytes, including the gymnosperm and angiosperm plants.
  Seeds are the product of the ripened ovule, after fertilization by pollen and
  some growth within the mother plant. The embryo is developed from the
  zygote and the seed coat from the integuments of the ovule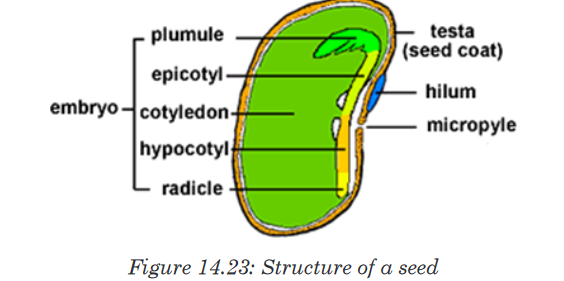

  

  The main components of the embryo are:A seed is made up of a seed coat
  (testa), one or two cotyledons and an embryonic axis. The embryonic axis is
  made up of a plumule, an epicotyl, a hypocotyl and a radical. A seed which
  has one seed-leaf is described as monocotyledonous, and one which has
  two, as dicotyledonous. Maize is monocotyledonous seed while bean is a
  dicotyledonous seed.

  • The cotyledons, the seed leaves, attached to the embryonic axis. There
  may be one (Monocotyledons), or two (Dicotyledons). The cotyledons
  are also the source of nutrients in the non-endospermic Dicotyledons,
  in this case they replace the endosperm, and are thick and leathery. In
  endospermic seeds the cotyledons are thin and papery.

  • The epicotyl, the embryonic axis above the point of attachment of the
  cotyledon(s).

  • The plumule, the tip of the epicotyl, and has a feathery appearance due
  to the presence of young leaf primordia at the apex, and will become
  the shoot upon germination.

  • The hypocotyl, the embryonic axis below the point of attachment of
  the cotyledon(s), connecting the epicotyl and the radicle, being the
  stem-root transition zone.

  • The radicle, the basal tip of the hypocotyl, grows into the primary root.
  Monocotyledonous plants have two additional structures in the form of
  sheaths. The plumule is covered with a coleoptile that forms the first leaf
  while the radicle is covered with a coleorhiza that connects to the primary
  root and adventitiousroots form from the sides. Here the hypocotyl is a
  rudimentary axis between radicle and plumule.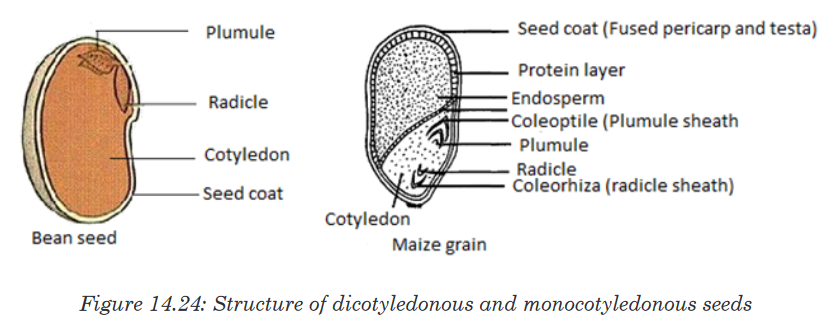

  

  Application activity 14.3.4
  1. Describe the structure of a drupe
  2. Differentiate between a drupe and a berry
  3. What would happen to the fruit if ovules in the flower did not develop?
  4. Compare the typical structure of seeds that are dispersed by animals
  to those dispersed by wind and water.

  14.3.5. Fruits and seeds dispersal with their adaptations

  Activity 14.3.5
  A man visited a lake and he found around the lake some grown plants of
  maize, beans and other variety plants meanwhile nobody has cultivated
  any seed or fruit. Suggest ways of those variety of (plants) have been
  reached on that lake.

  Dispersal of fruits and seeds is the scattering of fruits and seeds from their
  mother plants. They are four methods of seeds and fruits dispersal such as:
  1. Dispersal by Wind
  2. Dispersal by Water
  3. Dispersal by Animals and
  4. Mechanical Dispersal.
  
  

  Seeds disperses by wind or water are typically lightweight, allowing them
  to be carried in air or to float on the surface of water. The wind carries also
  small seeds that have wing-like structure. Seeds dispersed by animals
  are typically contained in sweet, nutritious flesh fruits. They can be carried
  externally on their feet, fur, feathers, or beaks.

  Those seeds with hooks or sticky substances rely on the chance that they will
  attach themselves to a passing animal. Other seeds are eaten by animals
  and passed out in the faeces.

  
  With mechanical Dispersal: All dehiscent fruits scatter the seeds when
  they burst. This dehiscence is accompanied by the expression of great force
  in many fruits so that seeds are jerked a considerable distance away from
  the mother plant. Such fruits are called explosive fruits.

  These seeds will germinate where the faeces will be deposited. The dispersal
  of seeds is important for the survival of the plant species because:

  • It minimises overcrowding of plants growing around the parent plant
  that could then result in too much competition for nutrients and light;

  • It allows the plant species to colonise new habitats which can offer
  suitable conditions.

  Application activity 14.3.5
  1. Why is it adaptive for some seeds to remain dormant before they
  germinate?
  2. The seeds of a bishop pine germinate only after they have undergone
  a forest fire. Evaluate the significance of this structural adaptation.
  3. Evaluate the importance of seed dispersal.

  Skills lab 14
  After studies, and completion of this unit 14, student-teachers will use the
  acquired knowledge to increase the crop productivity using different modes
  of vegetative and artificial propagation. They will also improve the quality of
  fruit plants by using forexample grafting method.

  End unit assessment 14

  PART A

  A. Multiple choice questions (choose the best answers)
  1. In cutting method of vegetative propagation, cuttings are mainly taken
  from
  a). Leaves of parent plant.
  b). Roots or stems of parent plant.
  c). Shoots of parent plant.
  d). Buds of parent plant.

  2. Artificial methods of vegetative propagation includes
  a). Cloning
  b). Grafting
  c). Cuttings
  d). Both b and c

  3. Example of plant in which vegetative propagation is occurred by
  leaves is called __________
  a). Cannabis
  b). Chrysanthemum
  c). Bryophyllum
  d). Brassica

  4. Which of the following is NOT an advantage of asexual reproduction?
  a). Rapid reproduction.
  b). High genetic diversity.
  c). No need for a mate.
  d). Low resource investment in offspring.

  B. PART B
  1. Answer by true or false.
  a). Mosses have life cycles that depend on water for reproduction.
  b). In ferns the gametophyte depends on sporophyte.
  c). In mosses the sporophyte dominates over the gametophyte.
  d). Seeds that are dispersed by animals are not contained in a flesh-
  sweet tissue.
  e). During pollination, pollen grains move from stigma to anther.

  2. Chose the letter that best answers the question or complete the
  statement.
  a). Which of the following is not part of a flower?
  i. Stamens
  ii. Petals
  iii. Carpels
  iv. Stem
  v. Sepals.
  b). Which flower structure that includes all the others listed below?
  i. Stigma
  ii. Carpel
  iii. Ovary
  iv. Style
  v. Ovule
  c). The thickened ovary wall of a plant may join with other parts of the
  flower stem to become the _______________
  i. Cotyledon
  ii. Fruit
  iii. Endosperm
  iv. Seed
  d). In angiosperms the structures that produce the male gametophyte
  are called the _______________
  i. Pollen tubes
  ii. Stigma
  iii. Anthers
  iv. Sepals

  e). The small, multicellular structures by which liverworts reproduce
  asexually are ______________
  i. Archegonia
  ii. Gemmae
  iii. Protonema
  iv. Rhizoids

  f). The small, multicellular structures by which liverworts reproduce
  asexually are __________________
  i. Archegonia
  ii. Gemmae
  iii. Protonema
  iv. Rhizoids

  g). In angiosperms, the mature seed is surrounded by a __________
  i. Flower
  ii. Fruit
  iii. Cotyledon
  iv. Cone

  h). The leaves of ferns are called ______________
  i. Spores
  ii. Fronds
  iii. Sori
  iv. Rhizomes

  i). The most recognizable stage of a moss is the _____________
  i. Gametophyte
  ii. Archegonium
  iii. Protonema
  iv. Sporophyte

  3. Which are more likely to be dispersed by animals- the seeds of
  angiosperms or the spores of a fern? Explain your reasoning.

  4. Pollination is a process that occurs only in seed plants. What process
  in seedless plants is analogous to pollination?

  5. What is the dominant stage of the ferns life cycle? Explain the
  relationship of the fern gametophyte and sporophyte.

  6. How is water essential in the life cycle of a bryophyte?

  7. What characteristic of bryophytes is responsible for their small size?
  Explain.

  8. Briefly explain why a seed may remain dormant even when the
  environmental conditions are favorable for germination.

  9. Describe the relationship between the gametophyte and sporophyte
  in mosses.

  10. During the lifecycle of a moss, what environmental conditions are
  necessary for fertilization to occur?

  11. Describe the dominant stage in the lifecycle of a fern.

  12. Propose a hypothesis to explain why angiosperms have become the
  dominant type of plant on the earth.

  13. Moss plants are small. Ferns can grow as tall as small tree. Explain
  why this is so. How does your answer illustrate a major characteristic
  of the plant kingdom?

  14. Study the structure of the seed below.

  

  a). Name the parts labelled by: A, B and C

  b). What is the importance of the part C for a growing seedling?

  15. Many flowers have bright patterns of coloration that directly surround
  the reproductive structures. Evaluate the importance of those bright-
  coloured patterns to plants.

  16. What is the function of endosperm?

  17. Some plants form flowers that produce stamens but no carpels. Could
  fruit form on one of these flowers? Explain your answer.

  18. Distinguish between pollination and fertilization.

  19. Give names of letters from A to J, and explain the function of the parts
  represented by: B, G, and E.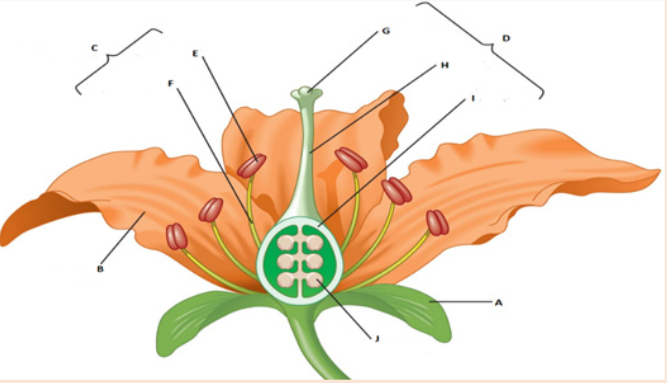

  

  20. Explain why the relationship between bees and flowers is described
  as mutually beneficial.

  21. What is the main advantage of cross-pollination?

  22. Why are the stamens of wind-pollinated plants and insect-pollinated
  plants different?

  23. Differentiate wind-pollinated flowers from insect-pollinated flowers.

  24. Give one example of a plant that uses each of the following dispersal
  mechanism:

  a). An explosive device which works by being inflated with water.
  b). A winged seed lifted by air currents.
  c). A buoyant seed carried by sea currents.
  d). A gluey substance which sticks the seed to an animal.

• UNIT 15: STRUCTURE OF AN ATOM AND MASS SPECTRUM

  Key Unit competence: Interpret simple mass spectra and use
                                                them to calculate R.A.M. of different
                                                 elements.

  Introductory Activity
  The presentations A, B, and C below show three atomic nuclei of different
  elements. Study the presentations carefully and answer the questions
  below.

  

  1. How many blue and red spheres do you see in each of the diagrams
  above?
  2. What do the three diagrams A, B, and C have in common?
  3. Based on your knowledge concerning atomic structure, what do you
  think that
  d) the blue spheres represent?
  e) the red spheres represent? Provide explanations.
  4.Using the information obtained in question (3) write the atomic symbol
  for each of the diagrams.
  5.Are there some other particle(s) missing from the above diagrams? If
  yes name the particle(s).
  6.What could you obtain if the atom is broken down?

  15.1. The constituents of an atom, their properties and the
  outline of their discovery

  Activity 15.1

  
  1. Regardless of some exceptions, all atoms are composed of the same
  components. True or False? If this statement is true why do different
  atoms have different chemical properties?

  2. The contributions of Joseph John Thomson and Ernest Rutherford
  led the way to today’s understanding of the structure of the atom. Use
  available resources to figure out:

  c) the contribution of each of them.
  d) the modern view of the structure of the atom?
  e) the role of each particle in an atom.

  Atoms are the basic units of elements and compounds. In ordinary chemical
  reactions, atoms retain their identity. An atom is the smallest identifiable unit
  of an element. There are about 91 different naturally occurring elements. In
  addition, scientists have succeeded in making over 20 synthetic elements
  (elements not found in nature but produced in Laboratories of Research
  Centres).

  An element is defined as a substance that cannot be broken down by ordinary
  chemical methods in simpler substances. Some examples of elements
  include hydrogen (H), helium (He), potassium (K), carbon (C), and mercury
  (Hg). In an element, all atoms have the same number of protons or electrons
  although the number of neutrons can vary. A substance made of only one
  type of atom is also called element or elemental substance, for example:
  hydrogen (H₂), chlorine (Cl₂), sodium (Na). Elements are the basic building
  blocks of more complex matter.

  A compound is a matter or substance formed by the combination of two or
  more different elements in fixed ratios. Consider, Hydrogen peroxide (H₂O₂)
  is a compound composed of two elements, hydrogen and oxygen, in a fixed
  ratio (2:2).

  1. Discovery of the atom constituents
  The oldest description of matter in science was advanced by the Greek
  philosopher Democritus in 400BC.

  He suggested that matter can be divided into small particles up to an ultimate
  particle that cannot any more be divided, and called that particle atom. Atoms
  came from the Greek word atomos meaning indivisible.

  The work of Dalton and other scientists such as Avogadro, etc., contributed
  more so that chemistry was beginning to be understood. They proposed new
  concept of atom, and from that moment scientists started to think about the
  nature of the atom.

  In 1808 Dalton published A New System of Chemical Philosophy, in which he
  presented his theory of atoms:

  Dalton’s Atomic Theory
  a). Each element is made up of tiny particles called atoms.

  b). The atoms of a given element are identical; the atoms of different
  elements are different in some fundamental way(s).

  c). Chemical compounds are formed when atoms of different elements
  combine with each other. A given compound always has the same
  relative numbers and types of atoms.

  d). Chemical reactions involve reorganization of the atoms—changes
  in the way they are bound together. The atoms themselves are not
  changed in a chemical reaction.

  

  2. Discovery of Electrons and Thomson’s Atomic Model
  In 1897 J. J. Thomson (1856–1940) and other scientists conducted several
  experiments, and found that atoms are divisible. They conducted experiments
  with gas discharge tubes. A gas discharge tube is shown in Figure 15.2.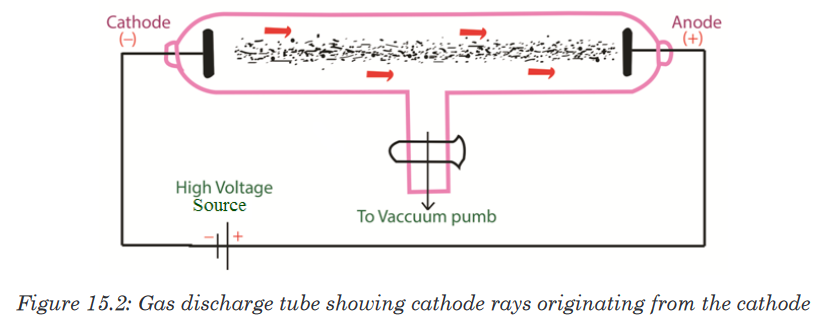

  

  The gas discharge tube is an evacuated glass tube and has two electrodes,
  a cathode (negative electrode) and an anode (positive electrode). The
  electrodes are connected to a high voltage source. Inside the tube, an
  electric discharge occurs between the electrodes.

  The discharge or ‘rays’ originate from the cathode and move toward the
  anode, and hence are called cathode rays. Using luminescent techniques,
  the cathode rays are made visible and it was found that these rays are
  deflected away from negatively charged plates. The scientist J. J. Thomson
  concluded that the cathode rays consist of negatively charged particles, and
  he called them electrons.

  Thomson postulated that an atom consisted of a diffuse cloud of positive
  charge with the negative electrons embedded randomly in it. This model,
  shown in Figure 15.3, is often called the plum pudding model because the
  electrons are like raisins dispersed in a pudding (the positive charge cloud),
  as in plum pudding.

  

  In 1909 Robert Millikan (1868–1953) conducted the famous charged oil
  drop experiment and came to several conclusions: He found the magnitude
  of the charge of an electron equal to -1.602x10-19C. From the charge-to-
  mass ratio(e/m) determined by Thomson, the mass of an electron was also
  calculated.

  

  3. Discovery of Protons and Rutherford’s Atomic Model
  In 1886 Eugene Goldstein (1850–1930) observed that a cathode-ray tube
  also generates a stream of positively charged particles that move towards
  the cathode. These were called canal rays because they were observed
  occasionally to pass through a channel, or “canal,” drilled in the negative
  electrode (Figure 15.4). These positive rays, or positive ions, are created
  when the gaseous atoms in the tube lose electrons. Positive ions are formed
  by the process.

  

  Different elements give positive ions with different e/m ratios. The regularity
  of the e/m values for different ions led to the idea that there is a subatomic
  particle with one unit of positive charge, called the proton. The proton is a
  fundamental particle with a charge equal in magnitude but opposite in sign to
  the charge on the electron. Its mass is almost 1836 times that of the electron.

  

  Figure 15.4: A cathode-ray tube with a different design and with a perforated cathode
  

  The proton was observed by Ernest Rutherford and James Chadwick in
  1919 as a particle that is emitted by bombardment of certain atoms with
  α-particles.

  

  Rutherford reasoned that if Thomson’s model were accurate, the massive
  α-particles should crash through the thin foil like cannonballs through gauze,
  as shown in Figure 15.6(a). He expected α-particles to travel through the
  foil with, at the most, very minor deflections in their paths. The results of the
  experiment were very different from those Rutherford anticipated. Although
  most of the α- particles passed straight through, many of the particles were
  deflected at large angles, as shown in Figure 15.6(b), and some were reflected,
  never hitting the detector. This outcome was a great surprise to Rutherford.
  Rutherford knew from these results that the plum pudding model for the
  atom could not be correct. The large deflections of the α-particles could be
  caused only by a centre of concentrated positive charge that contains most
  of the atom’s mass, as illustrated in Figure 15.6(b). Most of the α-particles
  pass directly through the foil because the atom is mostly empty space. The
  deflected α-particles are those that had a “close encounter” with the massive
  positive centre of the atom, and the few reflected α-particles are those that
  made a “direct hit” on the much more massive positive centre.

  In Rutherford’s mind these results could be explained only in terms of a
  nuclear atom—an atom with a dense centre of positive charge (the nucleus)
  with electrons moving around the nucleus at a distance that is large relative
  to the nuclear radius.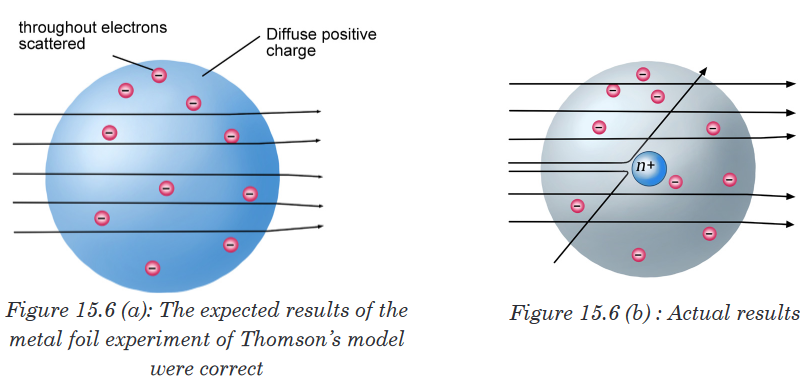

  

  4. Discovery of Neutrons
  In spite of the success of Rutherford and his co-workers in explaining atomic
  structure, one major problem remained unsolved.

  If the hydrogen contains one proton and the helium atom contains two
  protons, the relative atomic mass of helium should be twice that of hydrogen.
  However, the relative atomic mass of helium is four and not two.

  This question was answered by the discovery of James Chadwick, English
  physicist who showed the origin of the extra mass of helium by bombarding
  a beryllium foil with alpha particles. (See figure 15.7).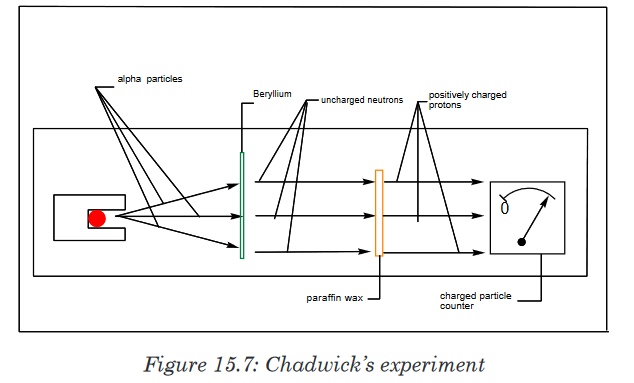

  

  In the presence of beryllium, the alpha particles are not detected; but they
  displace uncharged particles from the nuclei of beryllium atoms. These
  uncharged particles cannot be detected by a charged counter of particles.

  However, those uncharged particles can displace positively charged
  particles from another substance. They were called neutrons. The mass of
  the neutron is slightly greater than that of proton.

  Figure 15.8 shows the location of the elementary particles (protons, neutrons,
  and electrons) in an atom. There are other subatomic particles, but the
  electron, the proton, and the neutron are the three fundamental components
  of the atom that are important in chemistry.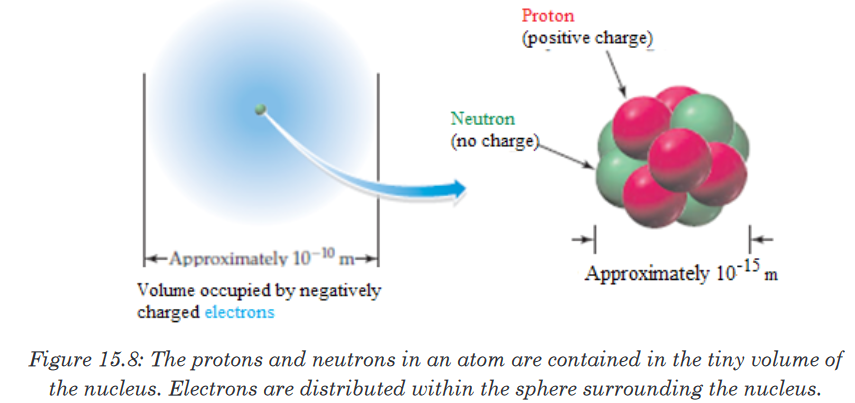

  

  As a result of the experiments described above, it is found that atoms
  consist of very small, very dense nuclei surrounded by clouds of electrons at
  relatively great distances from the nuclei. All nuclei contain protons; nuclei of
  all atoms except the common form of hydrogen also contain neutrons.

  5. Properties of sub-atomic particles

  
  Protons and neutrons are collectively known as nucleons. Both protons and
  neutrons have a mass almost equal to that of hydrogen atom. The neutron
  has no charge whereas the proton carries one positive charge. The electron
  with one negative charge occupies the space outside the nucleus.

  The following table summarizes the relative masses, the relative charges
  and the position within the atom of these sub-atomic particles.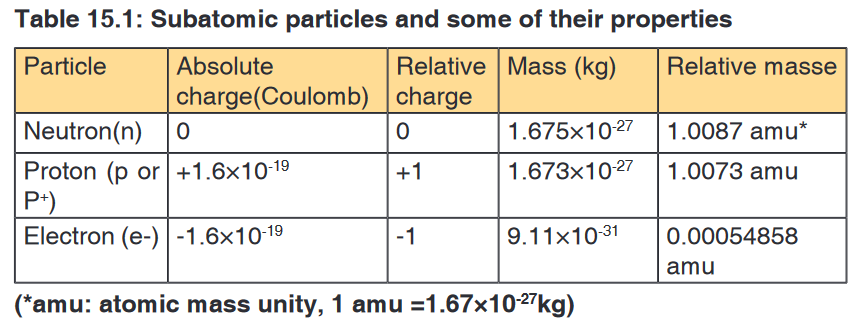

  

  Application activity 15.1
  1. In an experiment, it was found that the total charge on an oil drop was
  5.93 × 10^-18 C. How many negative charges does the drop contain?

  2. All atoms of the elements contain three fundamental particles. True
  or false? Give an example to support your answer.

  3. Compare the atom constituents
  d) in terms of their relative masses
  e) in terms of their relative charges

  4. Using the periodic table as a guide, specify the number of protons and
  electrons in a neutral atom of each of these elements.
  a). Carbon (C) b). Calcium (Ca) c).Chlorine (Cl) d). Chromium (Cr)

  15.2. Concept of atomic number, mass number, isotopic
  mass and relative atomic mass

  
  Activity 15.2

  
  Atoms of the same element may exhibit some physical properties like
  mass, density, velocity. Is the statement true or false? Use available
  textbooks and suggest an appropriate explanation?

  The atomic number or proton number, Z, denotes the number of protons in
  an atom’s nucleus. It corresponds to the order of the element in the periodic
  table.

  The mass number or nucleon number, A, denotes the total number of protons
  and neutrons in an atom.

  Mass number = number of protons + number of neutrons
                               = atomic number + neutron number

  
  The number of neutrons can be obtained by subtracting the atomic number
  from the mass number.

  Chemists use the following shorthand to represent an atom. The mass
  number is shown as a superscript (top number) and the atomic number is
  shown as a subscript (bottom number) beside the symbol of the element.

  By convention, the atomic number is usually written to the left subscript of
  the elemental notation, and the mass number to the left superscript of the
  elemental notation as represented by the example below, where X represents
  any element symbol.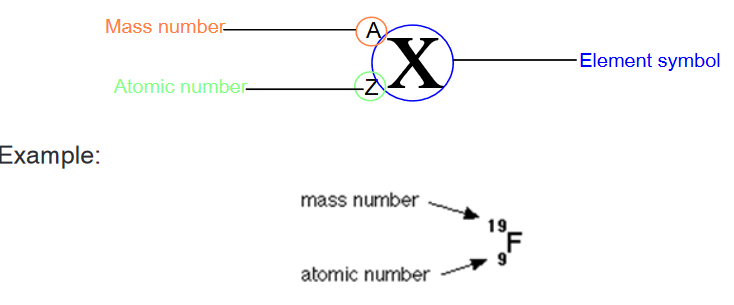

  

  Some atoms of the same element have the same atomic number, but different
  mass numbers. This means a different number of neutrons. Such atoms are
  called isotopes of the element. They are nuclides of the same element.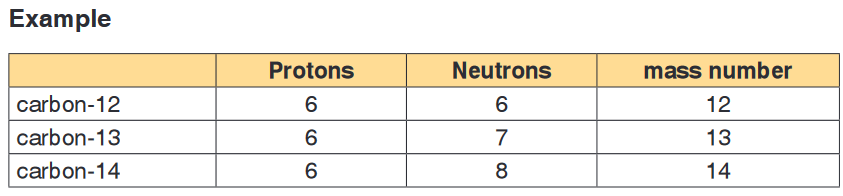

  

  Isotopes of an element have the same chemical properties because they
  have the same number of electrons.

  When elements react, it is the electrons that are involved in the reactions.

  This means that the isotopes of an element cannot be differentiated by
  chemical reactions.

  Because isotopes of an element have different numbers of neutrons,
  they have different masses, and isotopes have slightly different physical
  properties.

  The mass of a single isotope is its isotopic mass. The relative isotopic mass
  of an isotope is the relative mass of that isotope compared with the isotope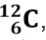

  which is given a mass of 12.00 units (12.00 atomic mass units). That is,
  relative isotopic mass relates to the relative atomic mass scale on which one
  isotope of the carbon element, carbon-12 is taken as the reference standard
  for atomic masses and is given a relative mass of 12 units, precisely 12
  atomic mass units (a.m.u).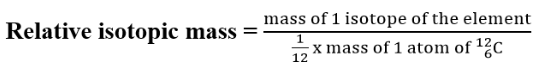

  
  Atomic mass unit (a.m.u) is a unit of mass used to express “relative atomic
  masses”. It is 1/12 of the mass of the isotope of carbon-12 and is equal to
  1.66054x10^-27kg.
  

  The relative isotopic masses of all other atoms are obtained by comparison
  with the mass of a carbon-12 atom.
  

  On that scale, the relative atomic mass of a proton and that of a neutron are
  both very close to one unit (1.0074 and 1.0089 units respectively). Since
  the relative mass of an electron is negligible (0.0005units), it follows that all
  isotopic masses will be close to whole numbers.
  

  However relative atomic masses of elements are not close to whole numbers
  because natural occurring elements are often mixtures of isotopes.
  

  Application activity 15.2
  1. How do you call the members of each of the following pairs? Explain.
  

  
  

  2. Write, using the periodic table, the correct symbols to identify an atom
  that contains
  a). 4 protons, 4 electrons, and 5 neutrons;
  b). 23 protons, 23 electrons, and 28 neutrons;
  c). 54 protons, 54 electrons, and 70 neutrons; and
  d). 31 protons, 31 electrons, and 38 neutrons.

  3. Use the list of the words given below to fill in the blank spaces. Each
  word will be used once.
  Atomic number, Mass number, protons, Electrons, Isotopes, neutron
  a). The atomic number tells you how many ___________________
  and ____________________ are in an atom.
  b). ____________________ is the number written as subscript on
  the left of the atomic symbol.
  c). The total number of protons and neutrons in an atom is called
  the ____________.
  d). Atoms with the same number of protons but different number of
  neutrons are called ________________.
  e). The subatomic particle that has no charge is called a
  

  15.3. Calculations of the relative atomic masses of elements
  

  Activity 15.3

  Using textbooks and internet connection, explain the concept of relative
  mass and attempt to solve the problems below.
  1. Argon has three naturally occurring isotopes: argon-36, argon-38,
  and argon-40. Based on argon’s reported relative atomic mass from
  the periodic table, which isotope do you think is the most abundant in
  nature? Explain
  

  
  

  The Relative atomic mass, symbolized as R.A.M (Ar), is defined as the
  average of the relative isotopic masses of the different isotopes weighted in
  the proportions in which they naturally occur.
  

  Thus, the different isotopic masses of the same elements and the percentage
  abundance of each isotope of an element must be known in order to
  accurately calculate the relative atomic mass of an element.
  

  Notice: Remember that mass number is not the same as the relative atomic
  mass or isotopic mass! The mass number is the total number of protons and
  neutrons while relative atomic mass is the average of the isotopic masses.
  

  
  

  By applying the same formula, the relative abundance of the isotopes may be
  calculated knowing the relative atomic mass of the element and the atomic
  masses of the respective isotopes.

  
  

  Application activity 15.3
  

  1. Three isotopes of magnesium occur in nature. Their abundances and
  masses, determined by mass spectrometry, are listed in the following
  table. Use this information to calculate the relative atomic mass of
  magnesium.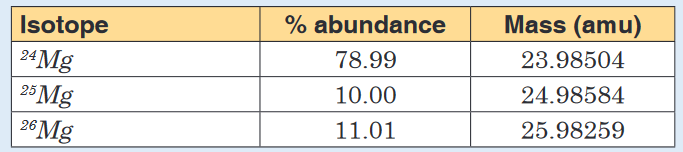
  

  
  

  2. The atomic weight of gallium is 69.72 amu. The masses of the
  naturally occurring Isotopes are 68.9257 amu for ⁶⁹Ga and 70.9249
  amu for ⁷¹Ga. Calculate the percent abundance of each isotope.
  

  3. Natural occurring lead contains 1.55% lead-204, 23.6% lead-206,
  22.6% lead-205 and 52.3% lead -208. Calculate the relative atomic
  mass of lead.
  

  4. The table below shows the mass number and the percentage
  abundances of the isotopes of an element X
  

  
  

  e) Calculate the relative atomic mass of X
  f) Identify the element X.
  15.4. Mass spectrometer

  15.4.1. Description and functioning of its components
  

  Activity 15.4.1

  1. Recall the concept of relative atomic mass of an element.

  2. Do research and identify the name of an instrument used to
  estimate the mass and proportions of the isotopes that make up
  a given element. How does it work?

  The mass spectrometer is an instrument that separates positive gaseous
  atoms and molecules according to their mass-charge ratio and that records
  the resulting mass spectrum.
  

  In the mass spectrometer, atoms and molecules are converted into ions. The
  ions are separated as a result of the deflection which occurs in a magnetic
  and electric field.
  

  The basic components of a mass spectrometer are: vaporisation chamber
  (to produce gaseous atoms or molecules), ionization chamber (to produce
  positive ions), accelerating chamber (to accelerate the positive ions to a high
  and constant velocity), magnetic field (to separate positive ions of different
  m/z ratios), detector (to detect the number and m/z ratio of the positive ions)
  and the recorder (to plot the mass spectrum of the sample).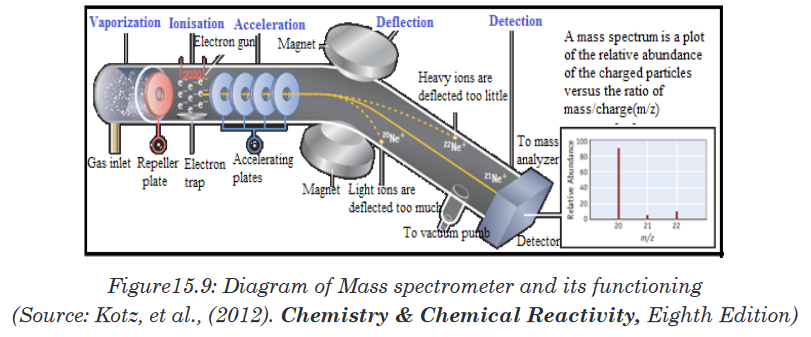
  

  
  

  A mass spectrometer works in five main stages, namely vaporization,
  ionization, acceleration, deflection, and detection to produce the mass
  spectrum.
  

  Stage 1: Vaporization
  At the beginning, the test sample is heated until it becomes vapour and is
  introduced as a vapour into the ionization chamber. When a sample is a solid
  with low vapour pressure, it can directly be introduced into the ionization
  chamber.
  

  Stage 2: Ionisation
  The vaporized sample passes into the ionization chamber (with a positive
  voltage of about 10,000 volts). The electrically heated metal coil gives
  off electrons which are attracted to the electron trap which is a positively
  charged plate.
  

  The particles in the sample (atoms or molecules) are therefore bombarded
  with a stream of electrons (electrons gun), and some of the collisions are
  energetic enough to knock one or more electrons out of the sample particles
  to make positive ions. Mass spectrometers always work with positive ions.
  

  Most of the positive ions formed will carry a charge of +1 because it is much
  more difficult to remove further electrons from an already positive ion.
  

  Most of the sample molecules are not ionized at all but are continuously
  drawn off by vacuum pumps which are connected to the ionization chamber.
  Some of the molecules are converted to negative ions through the absorption
  of electrons.
  

  Stage 3: Acceleration
  The positive ions are accelerated by an electric field so that they move
  rapidly through the machine at high and constant velocity.
  

  Stage 4: Deflection
  The ions are then deflected by a magnetic field according to their masses
  and charges ratio. Different ions are deflected by the magnetic field at
  different extents. The extent to which the beam of ions is deflected depends
  on four factors:
  

  1. The magnitude of the accelerating voltage (electric field strength).
  Higher voltages result in beams of more rapidly moving particles to
  be deflected less than the beams of the more slowly moving particles
  produced by lower voltages.

  2. Magnetic field strength. Stronger fields deflect a given beam more
  than weaker fields.

  3. Masses of the particles. Because of their inertia, heavier particles
  are deflected less than lighter particles that carry the same charge.

  4. Charges on the particles. Particles with higher charges interact
  more strongly with magnetic fields and are thus deflected more than
  particles of equal mass with smaller charges

  The two last factors (mass of the ion and charge on the ion) are combined
  into the mass/charge ratio. Mass/charge ratio is given the symbol m/z (or
  sometimes m/e).

  For example, if an ion had a mass of 28 and a charge of 1+, its mass/charge
  ratio would be 28. An ion with a mass of 56 and a charge of 2+ would also
  have a mass/charge ratio of 28.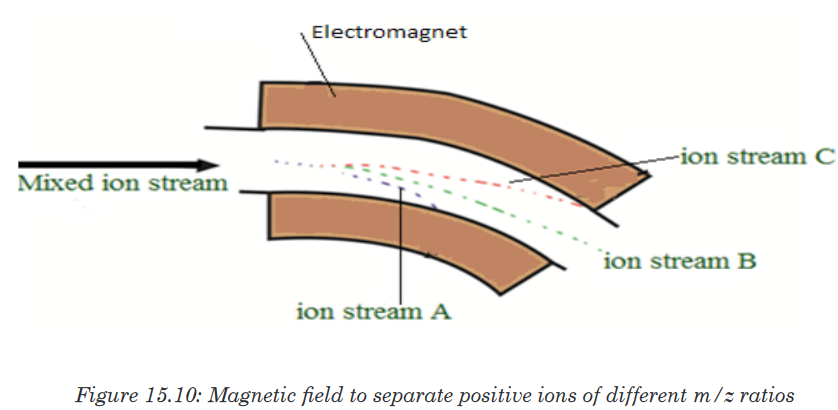
  

  
  

  In the figure 15.10 above, ion stream A is most deflected: it will contain ions
  with the smallest mass/charge ratio. Ion stream C is the least deflected: it
  contains ions with the greatest mass/charge ratio. Assuming 1+ ions, stream
  A has the lightest ions, stream B the next lightest and stream C the heaviest.
  Lighter ions are going to be more deflected than heavy ones.
  

  Stage 5: Detection

  The beam of ions passing through the machine is detected electrically. As
  they pass out of the magnetic field, ions are detected by an ion detector,
  which records the position of the ions on the screen and the number of ions
  that hit the screen at each position. These two pieces of information are
  used to produce a mass spectrum for the sample.
  

  A flow of electrons in the wire is detected as an electric current, which can
  be amplified and recorded. The more ions arriving, the greater the current.
  

  Detecting the other ions
  How might the other ions be detected (those in streams A and C which have
  been lost in the machine)?
  

  Remember that stream A was most deflected. To bring them on to the
  detector, you would need to deflect them less by using a smaller magnetic
  field.
  

  To bring those with a larger m/z value (the heavier ions if the charge is +1) to
  the detector you would have to deflect them more by using a larger magnetic
  field.
  

  If you vary the magnetic field, you can bring each ion stream in turn on
  the detector to produce a current which is proportional to the number of
  ions arriving. The mass of each ion being detected is related to the size
  of the magnetic field used to bring it on to the detector. The machine can
  be calibrated to record current (which is a measure of the number of ions)
  against m/z directly. The mass is measured on the 12C scale.
  

  Note: The ¹²C scale is a scale on which the 12C isotope weighs exactly 12
  units.

  Recorder
  The detector of a typical instrument consists of a counter, which produces
  a current that is proportional to the number of ions, which strike it. Using of
  electron multiplier circuits, this current can be measured so accurately that
  the current caused by just one ion striking the detector can be measured.
  The signal from the detector is fed to a recorder, which produces the mass
  spectrum. In modern instruments, the output of the detector is fed through
  an interface to a computer. The computer can store the data, provide the
  output in both tabular and graphic forms, and compare the data to standard
  spectra, which are contained in spectra libraries also stored in the computer.
  

  The following figure is an example of a mass spectrum of unknown element
  that has 2 isotopes.
  

  
  

  Application activity 15.4.1
  1. Use the list of the words given below to fill in the blank spaces. Each
  word will be used once.
  

  Vaporization chamber, mass spectrum, velocity, ionization, deflection,
  detector, acceleration
  

  A sample of the element is placed in the _________ chamber where
  it is converted into gaseous atoms. The gaseous atoms are ionized
  by bombardment of high energy electrons emitted by a hot cathode
  to become positive ions (in practice, the voltage in the ________
  chamber is set in such a way that only one electron is removed from
  each atom). The positive ions (with different masses) are then going
  faster to a high and constant _________by two negatively charged
  plates: the process is called_________. The positive ions are then
  deviated by the magnet field. This process is called ____________
  (ions with smaller mass will be deflected more than the heavier ones).
  These ions are then detected by the ion _________. The information
  is fed into a computer which prints out the________ of the element.
  

  2. The correct order for the basic features of a mass spectrometer is...
  a) acceleration, deflection, detection, ionization
  b) ionisation, acceleration, deflection, detection
  c) acceleration, ionisation, deflection, detection
  d) acceleration, deflection, ionisation, detection
  

  3. Which one of the following statements about ionisation in a mass
  spectrometer is incorrect?

  a) gaseous atoms are ionised by bombarding them with high energy
  electrons
  

  b) atoms are ionised so they can be accelerated

  c) atoms are ionised so they can be deflected

  d) it doesn’t matter how much energy you use to ionise the atoms

  4. The path of ions after deflection depends on...
  a) only the mass of the ion
  b) only the charge on the ion
  c) both the charge and the mass of the ion
  d) neither the charge nor the mass of the ion

  5. Which of the following species will be deflected to the greatest extent?
  

  
  

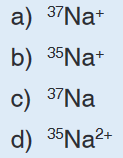
  6. Which of the following separates the ions according to their mass-to-
  charge?
  a) Ion source
  b) Detector
  c) Magnetic sector
  d) Electric sector

  15.4.2. Interpretation of mass spectra and uses of the mass
  spectrometer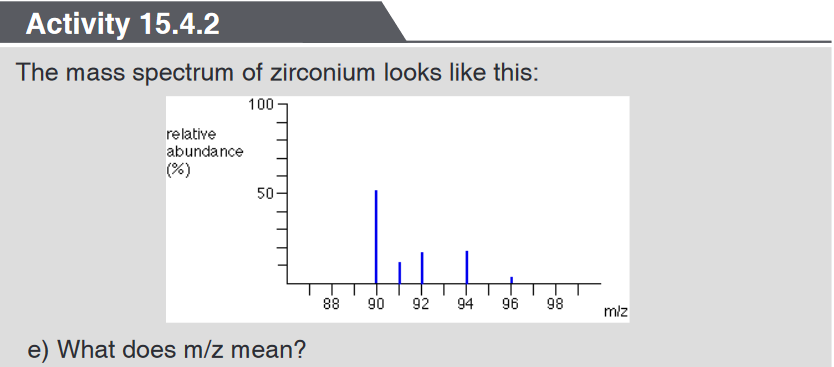
  

  
  

  f) Explain as fully as possible what the mass spectrum shows about
  zirconium. (You are not required to read actual values from the relative
  abundance axis.)

  g) The spectrum shows lines for 1+ ions. If there were also peaks for 2+
  ions, where would you expect to find them, and what would you predict
  about their heights relative to the 1+ peaks?

  The mass spectrum of an element shows how you can find out the masses
  and relative abundances of the various isotopes of the element and use that
  information to calculate the relative atomic mass of the element.
  

  Example 1: The mass spectrum of boron
  

  
  

  The mass spectrum of boron may be used to know the number of boron
  isotopes and their relative abundances.
  

  The two peaks in the mass spectrum shows that there are 2 isotopes of
  boron with relative isotopic masses of 10 and 11 on the 12C scale.
  

  The relative size of the peaks gives you a direct measure of the relative
  abundances of the isotopes. The tallest peak is often given an arbitrary
  height of 100 but you may find all sorts of other scales used; it doesn’t
  matter. You can find the relative abundances by measuring the lines on the
  stick diagram.
  

  In this case, the two isotopes (with their relative abundances) are:
  

  
  

  
  

  The mass spectrum of zirconium may be used to know the number of
  zirconium isotopes and their relative abundances
  

  The five peaks in the mass spectrum show that there are five isotopes of
  zirconium with relative isotopic masses of 90, 91, 92, 94 and 96 on the ¹²C
  scale.
  

  This time, the relative abundances are given as percentages. Again you can
  find these relative abundances by measuring the lines on the stick diagram.
  In this case, the five isotopes (with their relative percentage abundances)
  are:
  

  
  

  Example 3: The mass spectrum of chlorine
  

  Chlorine is taken as typical of elements with more than one atom per molecule.
  Chlorine has two isotopes, ³⁵Cl and ³⁷Cl, in the approximate ratio of 3 atoms
  of ³⁵Cl to 1 atom of ³⁷Cl. You might suppose that the mass spectrum would
  look like this:
  

  
  

  But it is not true. The problem is that chlorine consists of molecules, not
  individual atoms. When chlorine is passed into the ionization chamber, an
  electron is knocked off the molecule to give a molecular ion, Cl₂+. These
  ions won’t be particularly stable, and some will fall apart to give a chlorine
  atom and a Cl+ ion. The term for this is fragmentation.
  

  
  

  If the Cl atom formed isn’t then ionized in the ionization chamber, it simply
  gets lost in the machine (neither accelerated nor deflected).
  

  The Cl+ ions will pass through the machine and will give lines at 35 and 37,
  depending on the isotope and you would get exactly the pattern in the last
  diagram. The problem is that you will also record lines for the unfragmented
  Cl₂+ ions.
  

  At the end the spectrum will show peaks due to ionized atoms, Cl+ at 35, and
  37, and ionized molecule Cl₂
  + at 70, 72, 74 as in the figure 15.12 below.
  

  
  

  Relative atomic masses can be calculated using the information from the
  mass spectrum.
  

  Example 1: The mass spectrum of boron is given below:
  

  Determine the relative atomic mass of boron
  

  From the mass spectrum given, we have123 typical atoms of boron (sum of
  relative abundances). 23 of these would be ¹⁰B and 100 would be ¹¹B.
  

  The total mass of these would be (23 x 10) + (100 x 11) = 1330
  

  The average mass of these 123 atoms would be 1330 / 123 = 10.8 (to 3
  significant figures).
  

  10.8 is the relative atomic mass of boron.
  

  Example 2: The figure below represents the mass spectrum of zirconium
  

  
  

  
  Suppose you had 100 typical atoms of zirconium (sum of relative abundances).
  51.5 of these would be ⁹⁰Zr, 11.2 would be ⁹¹Zr and so on. The total mass of
  these 100 typical atoms would be
  

  (51.5 x 90) + (11.2 x 91) + (17.1 x 92) + (17.4 x 94) + (2.8 x 96) = 9131.8
  

  The weighted average mass of these 100 atoms would be 9131.8 / 100 =
  91.3 (to 3 significant figures).
  

  91.3 is the relative atomic mass of zirconium.

  
  

  b) How many isotopes does magnesium possess
  c) Estimate the isotopic mass of each of the magnesium isotopes
  d) Estimate the relative abundance for each of the isotopes of
  magnesium

  2. Which of the following is not done through mass spectrometry?
  e) Calculating the isotopic abundance of elements
  f) Investigating the elemental composition of planets
  g) Confirming the presence of O-H and C=O in organic compounds
  h) Calculating the molecular mass of organic compounds

  3. When a pure, gaseous sample of element X is introduced in a mass
  spectrometer, four mononuclear, singly charged ions are detected as
  shown in the spectrum below.
  

  
  

  i) Describe the process by which the gaseous sample of X is converted
  into ions in a mass spectrometer.

  j) What adjustment is made to the operating system in order to direct
  the different ions, in turn, onto, the detector of a mass spectrometer?

  k) What is the number of isotopes of element X? Justify your answer.

  l) Use the data from the spectrum above to calculate the relative atomic
  mass of X.

  m)Identify the element X.

  Skills lab 15
  

  When atoms of any element are subjected to high voltages, cathode rays
  are emitted and are the same for all elements.
  

  During your free time, write an essay about all other radiations that may be
  emitted by atoms specifying the conditions under which they can be emitted
  and their properties. In your essay, you have to point out the benefits and
  the disadvantages of those radiations to humans and their environment.
  

  End unit assessment 15
  I. Multiple choice questions
  1. Which of the following is true regarding a typical atom?
  a) Neutrons and electrons have the same mass.
  b) The mass of neutrons is much less than that of electrons.
  c) Neutrons and protons together make the nucleus electrically
  neutral.
  d) Protons are more massive than electrons

  2. Which of the following statements is(are) true? For the false
  statements, correct them.
  a) All particles in the nucleus of an atom are charged.
  b) The atom is best described as a uniform sphere of matter in which
  electrons are embedded.
  c) The mass of the nucleus is only a very small fraction of the mass
  of the entire atom.
  d) The volume of the nucleus is only a very small fraction of the total
  volume of the atom.
  e) The number of neutrons in a neutral atom must equal the number
  of electrons.

  3. Each of the following statements is true, but Dalton might have
  had trouble explaining some of them with his atomic theory. Give
  explanations for the following statements.
  a) Atoms can be broken down into smaller particles.
  b) One sample of lithium hydride is 87.4% lithium by mass, while
  another sample of lithium hydride is 74.9% lithium by mass.
  However, the two samples have the same chemical properties

  4. In mass spectrometer, the sample that has to be analyzed is
  bombarded with which of the following?
  a) Protons
  b) Electrons
  c) Neutrons
  d) Alpha particles
  

  5. Mass spectrometer separates ions on the basis of which of the
  following?
  a) Mass
  b) Charge
  c) Molecular weight
  d) Mass to charge ratio

  6. In a mass spectrometer, the ions are sorted out in which of the following
  ways?
  a) By accelerating them through electric field.
  b) By accelerating them through magnetic field.
  c) By accelerating them through electric and magnetic field.
  d) By applying a high voltage.

  7. The procedure for mass spectroscopy starts with which of the following
  processes?
  a) The sample is bombarded by electron beam.
  b) The ions are separated by passing them into electric and magnetic
  field.
  c) The sample is converted into gaseous state.
  d) The ions are detected.

  8. Which of the following ions pass through the slit and reach the collecting
  plate?
  a) Negative ions of all masses.
  b) Positive ions of all masses.
  c) Negative ions of specific mass.
  d) Positive ions of specific mass.

  9. Which of the following statements is not true about mass spectrometry?
  a) Impurities of masses different from the one being analyzed
  interferes with the result.
  b) It has great sensitivity.
  c) It is suitable for data storage.
  d) It is suitable for library retrieval.
  

  10. In a mass spectrometer, the sample gas is introduced into the highly
  evacuated spectrometer tube and it is ionised by the electron beam.
  a) True
  b) False

  II. Short and long answer questions
  11. What are the three fundamental particles from which atoms are built?
  What are their electric charges? Which of these particles constitute
  the nucleus of an atom? Which is the least massive particle of the
  fundamental particles?

  12. Verify that the atomic weight of lithium is 6.94, given the following
  information:
  ⁶Li, mass = 6.015121 u; percent abundance = 7.50%
  ⁷Li, mass = 7.016003 u; percent abundance = 92.50%

  13. The diagram below shows the main parts of a mass spectrometer.
  

  
  

  a) Describe the different steps involved in taking a mass spectrum of a
  sample
  i. Which two properties of the ions determine how much they are
  deflected by the magnetic field? What effect does each of these
  properties have on the extent of deflection?
  ii. Of the three different ion streams in the diagram above, why is
  the ion stream C least deflected?
  iii. What would you have to do to focus the ion stream C on the
  detector?

  b) Why is it important that there is a vacuum in the instrument?

  c) Describe briefly how the detector works.
  

  14.
  (a) A mass spectrum of a sample of indium shows two peaks at m/z
  = 113 and m/z = 115. The relative atomic mass of indium is 114.5.
  Calculate the relative abundances of these two isotopes.
  

  (b)The mass spectrum of the sample of magnesium contains three
  peaks with the mass-to-charge rations and relative intensities
  shown below
  i. Explain why magnesium gives three peaks in mass spectrum?
  

  
  

  ii. Use the information in the table above to calculate the accurate
  value for the relative atomic mass of magnesium

  15. There exists 3 isotopes of oxygen that occur naturally with atomic mass

  16, 17 and 18 with abundance 99.1% ; 0.89% and 0.01% respectively.
  Given that oxygen occurs naturally as diatomic molecule,
  a) Predict the number of peaks that will be observed on the screen
  of mass spectrometer.
  b) Show the molecular ions that are responsible of these peaks.
  

• UNIT 16: ELECTRON CONFIGURATIONS OF ATOMS AND IONS

  Key Unit competence: Relate Bohr’s model of the atom with
                                                hydrogen spectrum and energy levels, and
                                                interpret graphical information in relation to
                                                ionization energy of elements.

  Introductory Activity 16
  Observe the images below and answer the questions asked.

  

  1. What can you see on the image above?
  2. What type of motion is performed by the people on the image?
  3. How does their potential energy change?

  16.1. Bohr’s atomic model: Concept of energy levels and
  spectra

  
  Activity 16.1
  1. Describe the Rutherford atomic structure?
  2. What improvements have been brought by Bohr to the Rutherford
  atomic structure
  3. Establish a relationship between the Bohr’s atomic model and
  the illustration in the introductory activity.

  16.1.1 Bohr’s atomic model

  From the observations in introductory activity 16, the potential energy of
  a person walking up ramp increases in uniform and continuous manner
  whereas potential energy of person walking up steps increases in stepwise
  and quantized manner. This can be explained by the values of energy
  which are continuous for the person walking up ramp while they are discrete
  (discontinued) for the person walkingup steps (Figures (a) and b of the
  introductory activity).

  A model is a simplified representation used to explain the workings of a real
  world system or event. A model is useful because it helps you understand
  what’s observed in nature. It’s not unusual to have more than one model
  represent and help people understand a particular topic.

  There are two models of atomic structure in use today: the Bohr model and
  the quantum mechanical model. Of these two models, the Bohr model is
  simpler and relatively easy to understand.

  Have you ever bought colour crystals for your fireplace — to make flames of
  different colours? Or have you ever watched fireworks and wondered where
  the colours came from?

  Colour comes from different elements. If you sprinkle table salt on a fire, you
  get a yellow colour. Salts that contain copper give a greenish-blue flame.
  And if you look at the flames through a spectroscope, an instrument that
  uses a prism to break up light into its various components, you see a number
  of lines of various colours. Those distinct lines of colour make up a line
  spectrum.

  Niels Bohr, a Danish scientist, explained this line spectrum while developing
  a model for the atom:

  • The Bohr model shows that the electrons in atoms are in orbits of
  differing energy around the nucleus (think of planets orbiting around
  the sun).

  • Bohr used the term energy levels (or shells) to describe these
  orbits of differing energy. He said that the energy of an electron
  is quantized, meaning electrons can have one energy level or another
  but nothing in between.

  • The energy level an electron normally occupies is called its ground
  state. But it can move to a higher-energy, less-stable level, or shell, by
  absorbing energy. This higher-energy, less-stable state is called the
  electron’s excited state.

  • After it is done being excited, the electron can return to its original
  ground state by releasing the energy it has absorbed, as shown in
  the diagram below.
  

  
  • Sometimes the energy released by electrons occupies the portion of
  the electromagnetic spectrum (the range of wavelengths of energy)
  that humans detect as visible light. Slight variations in the amount of
  the energy are seen as light of different colours.

  The energy change is accompanied by absorption of radiation energy of
  E=E₂ E₁ = h v where, h is a constant called ‘Planck’s constant’ and v is the
  frequency of radiation absorbed or emitted.
  

  The value of h is 6.626 x 10^-34 J.s. The absorption and emission of light due
  to electron jumps are measured by use of spectrometers.
  

  Bohr found that the closer an electron is to the nucleus, the less energy it
  needs, but the farther away it is, the more energy it needs. So Bohr numbered
  the electron’s energy levels.
  

  The higher the energy-level number, the farther away the electron is from
  the nucleus and the higher the energy.
  

  Bohr also found that the various energy levels can hold differing numbers of
  electrons: energy level 1 may hold up to 2 electrons, energy level 2 may hold
  up to 8 electrons, and so on.
  

  Weakness of Bohr’s Model
  The Bohr model works well for very simple atoms such as hydrogen (which
  has 1 electron) but not for more complex atoms. Although the Bohr model
  is still used today, especially in elementary textbooks, a more sophisticated
  (and complex) model (the quantum mechanical model) is used much more
  frequently.
  

  16.2.2. Absorption and emission spectra and energy associated

  1. Atomic spectrum

  The atomic spectrum is the range of characteristic frequencies or
  electromagnetic radiations that are readily absorbed and emitted by an atom.
  

  A spectrum obtained from a glowing source is called an emission spectrum.
  When white light is passed through a prism we see a myriad of colours
  – specifically what we term to be a rainbow. This dispersion of white light
  demonstrates that white light contains all the wavelengths of colour and is
  thus considered to be continuous. Each colour blends into the next with
  no discontinuity.
  

  When elements are vaporized and then thermally excited, they emit light;
  however, this light was not in the form of a continuous spectrum as was
  observed with white light. Instead, a discrete line spectrum was seen when
  the light was passed through a narrow slit. A series of fine lines of different
  colours separated by large black spaces was observed. The wavelengths of
  those lines are characteristic of the element producing them – thus, elements
  can be identified based on the spectral line data that they produce.
  

  Typically, we can examine the visible line spectra produced by an element
  in lab – using electricity, tubes filled with elements in the gaseous state and
  a spectroscope or diffraction grating which separates the light emitted by the
  gas into its components.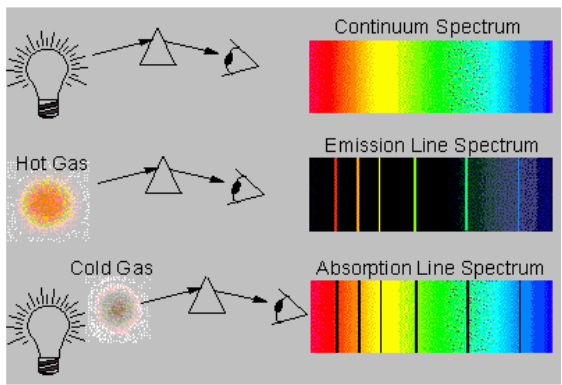
  

  
  

  2. Emission and absorption spectra
  Emission is the ability of a substance to give off light, when it interacts
  with heat. Absorption is the opposite of emission, where energy, light or
  

  radiation is absorbed by the electrons of a particular matter.
  Emission and absorption spectra are techniques that are used in chemistry
  and physics. Spectroscopy is the interaction of radiation and matter. Using
  spectroscopy, a scientist can figure out the composition of a certain matter.
  This is really beneficial, of dealing with unknown substances. Emission
  spectra and absorption spectra are different from each other but still related.
  

  a. Emission spectrum

  Every substances reacts differently when it interacts with light. The material
  starts off with being in the ground state, where all molecules are stable and
  settled. However when heat, energy or light is applied to a substance, some
  of the molecules transition into a higher energy state or an excited state.
  During this state the molecules are unstable and try to emit the energy
  in order to reach the state of equilibrium. The molecules emit energy
  in the form of photons or light. The difference between the substance in
  ground state and excited state is then used to determine the emission level
  of the substance.
  

  Each element or substances has a unique emission level or the amount
  of energy it radiates; this helps the scientists identify elements in unknown
  substances. The emission of an element is recorded on an emission
  spectrum or atomic spectrum. The emittance of an object measures
  how much light is emitted by it. The amount of emission of an object varies
  depending on the spectroscopic composition of the object and temperature.
  The frequencies on an emission spectrum are recorded in light
  frequencies, where the colour of the light determines the frequency.
  

  
  

  b. Absorption spectrum
  Absorption is the ability of a matter or electron to absorb light or radiation
  which makes them transition into a higher energy state. Absorption is
  used to determine the absorption level of certain objects and their ability to
  retain heat.
  

  Absorption spectrum is the plotting of the energy that is absorbed by
  an element or substance. Absorption can be plotted in a wavelength,
  frequency or wave number. There are two types of absorption: atomic
  absorption spectra and molecular absorption spectra.
  

  Absorption is used to determine the presence of a particular substance
  in a sample, or the quantity of the present substance in the sample. They
  are also used in molecular and atomic physics, astronomical spectroscopy
  and remote sensing. Absorption is primarily determined by the atomic and
  molecular composition of the material. They can also depend on temperature,
  electromagnetic field, interaction between the molecules of the sample,
  crystal structure in solids and temperature.
  

  In order to determine the absorption level of a substance, a beam of
  radiation is directed at the sample and the absence of light that is
  reflected through the object can be used to calculate the absorption.
  The absorption spectrum is usually light coloured, with dark bands that
  run through it. These dark bands are used to determine the absorption of
  the object.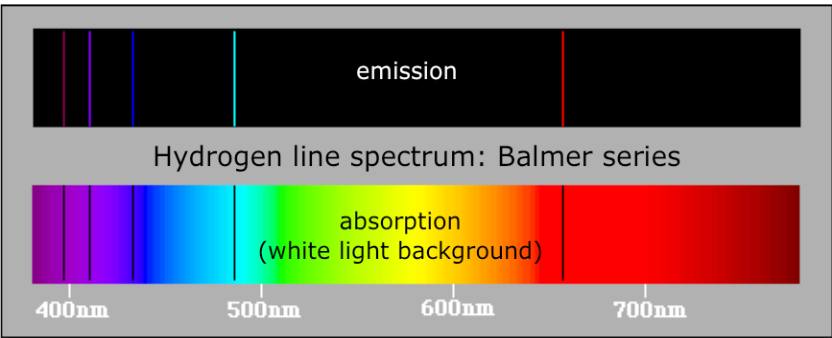
  

  
  

  
  

  
  

  
  

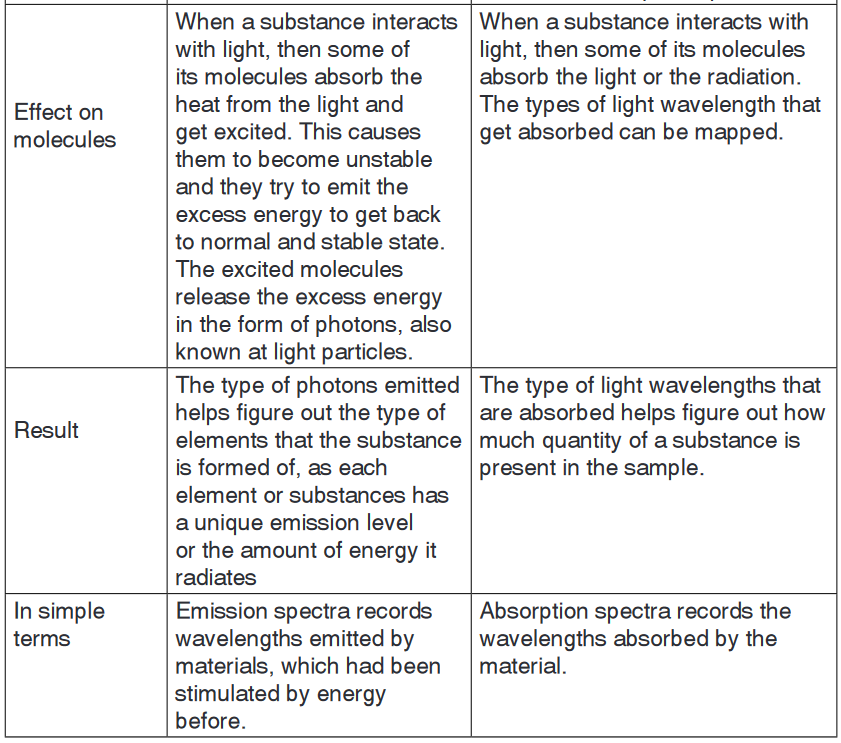
  Application activity 16.1
  1. Find out two more examples that you can use to illustrate the
  concept of quantization.

  2. Discuss the main weakness of:
  c) Rutherford’s nuclear atom.
  d) Bohr’s atomic model.

  16.2. Hydrogen spectrum and spectral line series

  Activity 16.2

  Look at the picture of neon tube light below and do research about how
  this neon tube light works to produce light and present your findings.
  

  
  

  Bohr’s atomic model allows explaining the emission spectra of atoms. This
  happens when excited electrons lose energy in form of electromagnetic ra-
  diation and fall to lower energy levels.
  

  The wave-particle nature of the light

  Light as a wave

  The light is a wave-like phenomenon as shown in Figure 16.1.
  

  It is characterized by its wave length, generally symbolized by the Greek
  letter lambda, λ, and its frequency, represented by the Greek letter nu, ν.
  

  As shown in the Figure 16.1 below, the wavelength represents the distance
  between two successive summits/peaks (or two successive troughs).
  

  The frequency represents the number of complete wavelengths made by the
  light per second, also called cycles per second.
  

  Visible light is composed by different visible lights with different λ and ν.
  

  But all those lights have the same speed, the speed of light, which, in a
  vacuum, is equal to: 3.00x10⁸m/s; although different types of light have
  different λ and ν, they move at the same speed c. This results in the relation
  

  between the speed of light and its wavelengthand frequency: c = νλ
  

  From this relation, and since c is constant, we can conclude that:
  

  • Light with long wavelength has low frequency, whereas

  • Light with short wavelength has high frequency.

  Let’s take an example to illustrate: light1 has λ1 equal to 10⁵m whereas light₂
  has λ₂ equal to 10^-5m. After 1 second, both would have travelled 3.00x10⁸m,
  the speed of light, but their frequencies will be different:
  

  
  

  Hence energy in the light is proportional to its frequency; the higher the
  frequency of the light, the higher is its energy and vice-versa.
  

  The different colours of the visible light differ by their wavelength as shown
  in the Figure 16.2
  

  
  

  As illustrated in Figure 16.2 below, the right side of the spectrum consists of
  high-energy, high-frequency and short wavelength radiations. Conversely,
  the left side consists of low-energy,low-frequency and long wavelength
  radiations.
  

  
  

  When an electron is excited or de-excited, the energy absorbed or emitted
  corresponds to the difference of energy, ΔE, between the final energy level
  of the electron, E₂, and the starting energy level of the electron,
  

  E₁: E₂ – E₁ =ΔE = hν. ΔE is positive when E₂>E₁, this is the case of absorption
  and excitation of electron; on the other hand ΔE may be negative when
  E₂<E₁, in case of emission and de-excitation of electron.
  

  Figure 16.3 below shows the different series of emission spectra of hydrogen.
  As you can see, the difference between those series is the final energy level
  where the electron fall after de-excitation.
  

  The series have been named according to the scientists who discovered
  them. Ionization of an atom or loss of an electron corresponds to excitation
  of an electron to the level n=∞.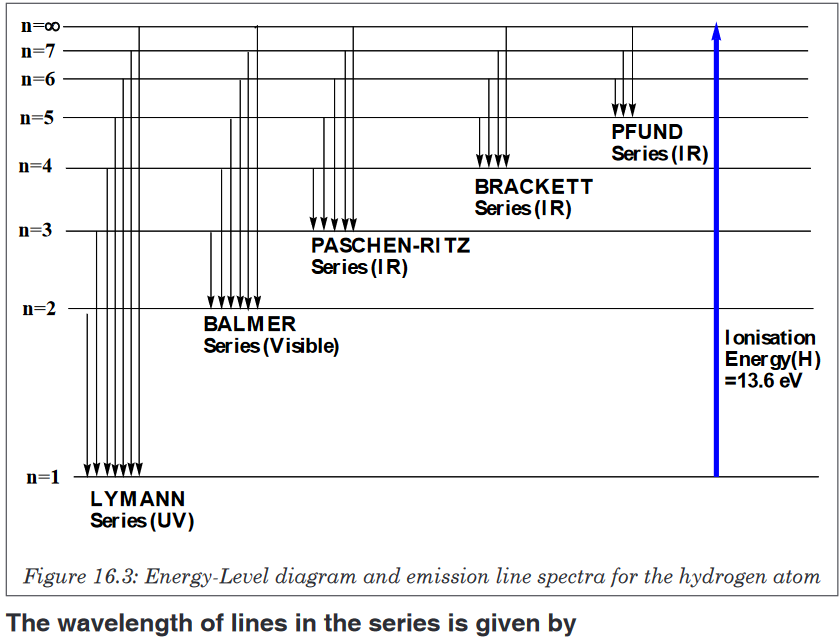
  

  
  

  
  

  Examples
  1. Find the wavelength and frequency in Balmer series associated with a
  drop of an electron from the fourth orbit.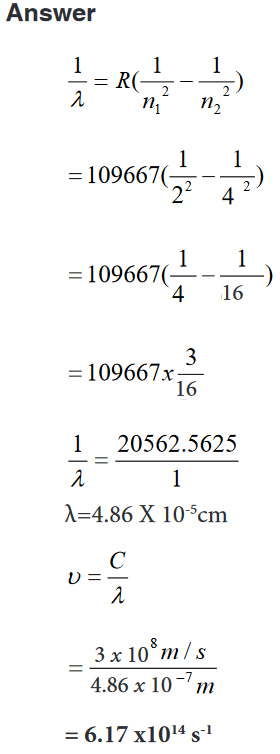
  

  
  

  2. Find the wave length, frequency and energy of the third line in the
  Lyman series.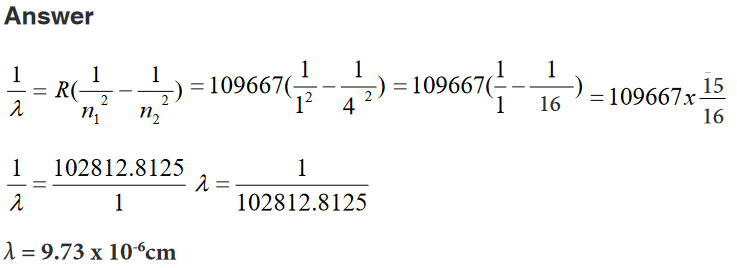
  

  
  

  
  

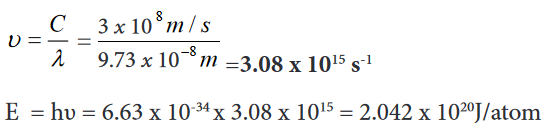
  Application activity 16.2
  1. What is the meaning of infinity level in the hydrogen spectral lines?
  

  2. Given a transition of an electron from n=5 to n=2. Calculate
  c) Energy
  d) Frequency
  e) Wavelength
  

  3. What is the wavelength (in nanometres) of a photon emitted during
  a transition from the ni = 5 state to the nf = 2 state in the hydrogen
  atom?
  

  16.3. Quantum theory of the atom
  Activity 16.3
  1. Recall the Bohr’s model of an atom.

  2. What were the limitations of that model?

  3. What improvements other scientists have brought to that model?
  

  In 1913, physicist Niels Bohr described as an atom as a small, positively
  charged nucleus surrounded by electrons that travel in circular orbits around
  the nucleus—similar in structure to the solar system, but with attraction
  provided by electrostatic forces rather than gravity. An electron must absorb
  or emit specific amounts of energy to transition between these fixed orbits.
  

  1. Despite its success in accounting for spectral lines of the H atom, the
  Bohr model failed to predict the spectrum of any other element. The
  model worked well for one-electron species, but not for atoms or ions
  with more than one electron.
  

  2. According to Bohr, the circular orbits in which electrons revolve are
  planar.
  

  3. Bohr’s theory fails to account for Zeeman Effect and Stark Effect.
  

  4. Bohr assumes that the electron revolves around the nucleus in circular
  orbits at fixed distance from the nucleus and with a fixed velocity.
  

  In 1926, Erwin Schrödinger used this idea to develop a mathematical
  model of the atom how electrons move in wave form, and developed the
  Schrodinger equation which describes how the quantum state of a system
  changes with time.
  

  This was the beginning of Quantum Mechanics (or Quantum Theory). A
  consequence of using waveforms to describe particles is that it is impossible
  to obtain precise values for both the position and velocity of a particle at the
  same time. This became known as the “uncertainty principle” formulated
  by Werner Heisenberg in 1926. This model was able to explain observations
  of atomic behaviour that previous models could not. Afterwards the planetary
  model of the atom was discarded in favour of one that described atomic
  orbital zones around the nucleus where a given electron is most likely to be
  observed.
  

  Thus, the quantum mechanical model is based on mathematics. Although it
  is more difficult to understand than the Bohr model, it can be used to explain
  observations made on complex atoms.
  

  Max Planck proposed that energy emitted is not done so in a continuous
  manner but is given off in small packets which he called quanta. He
  determined that an atom can emit only certain amounts of energy and
  therefore they must contain certain quantities of energy and that those are
  fixed. Thus, the energy of an atom is quantized. The change in the atom’s
  energy results from the gain or loss of one or more packets of energy. Planck
  derived an equation to explain this quantized form of energy (as opposed to
  the idea that energy emitted was continuous)
  

            
  

  where h = Planck’s constant = 6.626 x 10^-34 J•s and ν = frequency (as above)
  

  According to quantum theory, energy is always emitted in integral multiples
  of hν; (hν, 2 hν, 3 hν . . .), but never, for example, 1.67 hν or 4.98 hν. At the
  time Planck presented his theory, he could not explain why energies should
  be fixed or quantized in this manner.
  

  Therefore, despite the fact that Planck thought that energy was quantized,
  physicists continued to think of energy as travelling in waves. Energy as
  waves, however, could not explain the photoelectric effect. The quantum
  mechanical model is based on quantum theory, which says matter also
  has properties associated with waves. According to quantum theory, it is
  impossible to know the exact position and momentum of an electron at the
  same time. This is known as the Uncertainty Principle.

  The quantum mechanical model of the atom uses complex shapes of
  orbitals(sometimes called electron clouds), volumes of space in which there
  is likely to be an electron. So, this model is based on probability rather than
  certainty.
  

  The existence of discrete atomic energy levels is retained from Bohr’s model
  in the current atomic model.
  

  The allowed wave-like motion of the electron leads to an atom with certain
  fixed energy states much like Bohr assumed. The electron’s exact location
  cannot be determined.
  

  Solutions of Schrödinger’s wave equation are functions that describe atomic
  orbitals.
  

  Each function describes a fixed-energy state the electron can occupy and
  gives the probability of finding it in a given 3-dimensional space.
  

  Applying wave mathematics to the electron wave, Erwin Schrödinger derived
  an equation that is the basis for the quantum-mechanical model of hydrogen
  atom.
  

  This probability can be shown pictorially by means of an electron probability
  density diagram, or simply, an electron density diagram.
  

  Electron probability density in the H atom ground state.
  

  
  

  The distinction between atomic orbital and probability of the electron being
  at a distance r from the nucleus.
  

  The probability of the electron being far from the nucleus is very small, but
  not zero.
  

  
  

  The maximum radial probability for the ground-state of H atom appears at
  (0.529 Å, or 5.29 x 10 ^–10 m), the same as 1st Bohr orbit.
  

  The electron spends most of its time at the same distance that the Bohr
  model predicted it spent all of its time. Each atomic orbital, has a distinctive
  radial probability distribution and probability contour diagram.
  

  Four numbers, called quantum numbers, were introduced to describe the
  characteristics of electrons and their orbitals:

  Principal quantum number: n
  Angular momentum quantum number: ℓ
  Magnetic quantum number: m_ℓ
  Spin quantum number: m_s

  Application activity 16.3

  Discuss the improvements brought by the quantum theory in the
  understanding of the atomic structure
  

  16.3.1. Quantum numbers for energy levels, sub-energy levels
  and orbitals

  Activity 16.3.1

  1. Explain the difference between orbit and orbitals.

  2. The energy of both orbit and orbital is determined by a number n
  known as principal quantum number. Explain.

  3. An electron in an orbital is even described by other quantum numbers.
  What are they?

  4. Do research to precise the relationship between these quantum
  numbers, their role in the description of electrons in orbitals and their
  number in each energy level.

  We have seen the weakness and critics against the atomic Bohr’s model.
  In order to answer the questions not answered by that model, other atomic
  models were proposed. One of those models is the Quantum model that
  has been developed by the Australian physicist Erwin Schrödinger (1887-
  1961). The model is based on a mathematical equation called Schrödinger
  equation. This model is based on the following assumptions or hypotheses:
  

  An electron is in continuous movement around the nucleus but cannot be
  localized with precision; only the high probability of finding it in a certain
  region around the nucleus can be known.
  

  The region where the probability of finding electron is high, at more than
  95%, is called “orbital”; in other words, the orbital is the volume or the space
  (three-dimensional) around the nucleus where there is a high probability of
  finding the electron.
  

  Without going into the mathematical development of the Schrödinger
  equation, we can say that the energy of the electron depends on the orbital
  where it is located. And an atomic orbital is described by a certain number of
  “quantum numbers” according to the solution of Schrodinger equation, i.e. 3
  whole numbers:
  

  1. The principal quantum number is a positive integer which varies
  from 1 to ∞. The principal quantum number indicates the energy level in
  an atom where electrons can be located: the higher the n value, the higher
  the energy level. An electron in energy level n=1 has lowest energy in
  an atom. The principal quantum number, n, has been traditionally given
  names by the letters: K (n=1), L (n=2), M (n=3), N (n=4), O (n=5), P
  (n=6).
  

  In the Bohr’s atomic model, K, L, M, … were used to represent different
  orbits or shells of electrons. Later on, the term shell sometimes is used to
  describe a group of orbitals with the same principal quantum number. The
  term subshell describes a group of orbitals with the same principal and
  second quantum number. The maximum number of orbitals and electrons
  that can be found in an energy level n are n² and 2n², respectively (Table
  16.2). The maximum number of sub shells in an energy level n equals n.
  

  In summary:
  

  n = principal quantum number; all orbitals with same n are in the same shell.
  l = secondary (azimuthal) quantum number; divides shells into subshells.
  ml = magnetic quantum number; divides subshells into individual orbitals.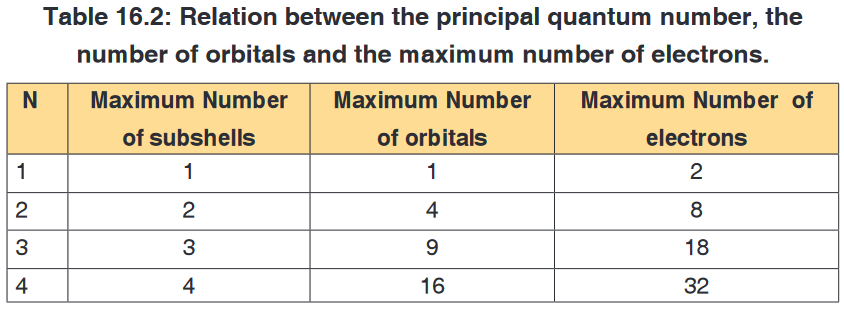
  

  
  

  2. The angular momentum quantum number (l)
  The second quantum number is the angular quantum number represented
  by the letter, l: it is an integer which can take any value from zero or higher
  but less than n-1, i.e. equal to: 0, 1, 2, 3,….up to n-1. For example if n= 1, l
  is equal to 0, if n = 2, l can be 0, 1.
  

  It is also called secondary or azimuthal quantum number. It indicates the
  shape of the orbital and is sometimes called the orbital shape quantum
  number. By tradition, those different shapes of orbitals have been given
  names or letter symbols: l = 0 = s, l =1 = p, l = 2 = d, l=3 = f
  

  3. Magnetic quantum number (ml)
  The magnetic quantum number describes the spatial orientation of the
  orbital. It is an integer that varies from -l to +l. For example if: l = 0, ml can
  only be 0; if l = 1, ml = -1, 0, +1; if l=2, ml = -2, -1, 0, 1, 2. As you can see
  for each value of l there are (2l+ 1) values of ml corresponding to (2l + 1)
  orientations under the influence of magnetic field.
  

  It is called the magnetic quantum number because the effect of different
  orientations of orbitals was first observed in the presence of a magnetic field.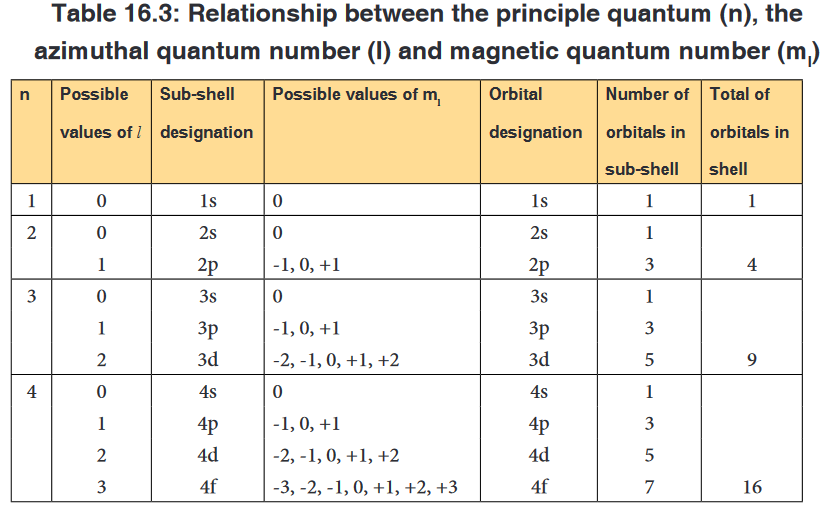
  

  
  

  The table 16.3 shows that, apart s sub-level that has only one orbital, other
  sub-levels have a certain number of different orbitals; those orbitals have the
  same energy but differ in their specific orientations. Example p orbitals are 3
  with different orientations: p_xp_yp_z.

  4. The spin quantum number (m_s)

  The fourth quantum number is the spin quantum number, represented by
  the symbol ms. It describes the spin of an electron that occupies a particular
  orbital. The electron behaves as a spinning magnet. The spin quantum
  number is the property of the electron, not the orbital.
  

  This number describes the spinning direction of the electron in a magnetic
  field. The direction could be either clockwise or counter clockwise. The
  electron behaves as if it were spinning about its axis, thereby generating a
  magnetic field whose direction depends on the direction of the spin. The two
  directions for the magnetic field correspond to the two possible values for the
  spin quantum number, m_s (S).
  

  Only two values are possible: ms = +1/2 and -1/2 as shown in the Figure 16.4
  below.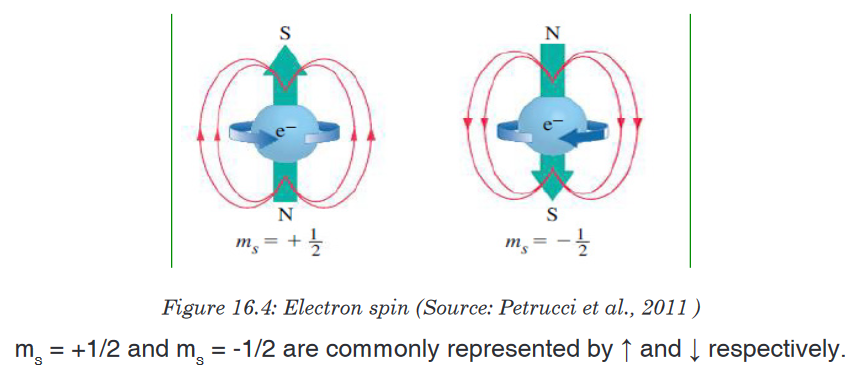
  

  
  

  In conclusion an electron in any given atom is described by 4 quantum
  numbers: (i) three quantum numbers which describe the orbital where the
  electron is located: n, l and ml and (ii) one quantum number describing the
  spin of the electron, m_s.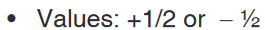
  

  
  

  • Electrons will spin opposite each other in the same orbital
  

  
  

  16.3.2. Number and shape of “s” and “p” orbitals

  Activity 16.3.2

  1. Explain the terms orbital and quantum numbers.
  2. How the terms explained in 1. above are related?
  3. Do research and point out the possible shapes assigned to s and
  p orbitals.

  An orbital is a region of space around the nucleus in which there is a great
  chance (high probability) to find an electron. It is described by three quantum
  numbers.
  

  These quantum numbers describe the size, shape, and orientation in space
  of the orbitals on an atom.

  The principal quantum number (n) describes the size of the orbital.
  The angular quantum number (l) describes the shape of the orbital.
  The magnetic quantum number (ml), describes the spatial orientation of
  a particular orbital.

  All electrons that have the same value for n (the principal quantum number)
  are in the same shell. Within a shell (same n), all electrons that share the
  same value for l( the angular momentum quantum number, or orbital shape)
  are in the same subshell. The electrons in subshell have same principal
  quantum number, same azimuthal quantum number and differ in magnetic
  and spinquantum number. When electrons share the same n, l, and m, they
  are said to be in the same orbital. That is, they have the same energy level,
  shape, and orientation. The electrons in the same orbital differ only in spin
  quantum number.
  

  Chemists describe the shell and subshell in which an orbital belongs with a
  two-character code such as 2p or 4f. The first character indicates the shell
  (n = 2 or n = 4). The second character identifies the subshell. By convention,
  the following lowercase letters are used to indicate different subshells.
  

  
  

  The number of subshells in a shell is equal to the principal quantum number
  for the shell. For example the n = 3 shell, contains three subshells: the 3s,
  3p, and 3d orbitals.
  

  There is only one orbital in the n = 1 shell because there is only one way in
  which a sphere can be oriented in space. The only allowed combination of
  quantum numbers for which n = 1 is the following.
  

  
  

  There is only one orbital in the 2s subshell. But, there are three orbitals in the
  2p subshell because there are three directions in which a p orbital can point.
  One of these orbitals is oriented along the X axis, another along the Y axis,
  and the third along the Z axis of a coordinate system, as shown in the figure
  below. These orbitals are therefore known as the 2p_x, 2p_y, and 2p_z orbitals.
  

  The number of orbitals in a shell is the square of the principal quantum
  number: 1² = 1, 2² = 4, 3² = 9. There is one orbital in an s subshell (l = 0),
  three orbitals in a p subshell (l = 1), and five orbitals in a d subshell (l = 2).
  The number of orbitals in a subshell is therefore 2(l) + 1.
  

  Orbitals have shapes that are best described as spherical (l = 0), polar (l =
  1), or cloverleaf (l = 2).

  Shapes of “s” and “p” orbitals
  

  
  

  
  

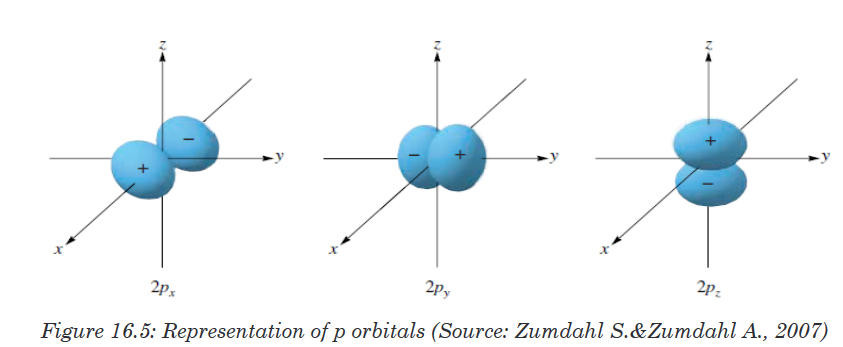
  Application activity 16.3.2
  1. Determine the number of orbitals that can exist at energy level
  corresponding to n=1, 2, 3.
  2. Outline diagrams representing the s and p orbitals.
  

  16.4. Electronic configuration of atoms and ions
  

  16.4. 1. Rules governing the electronic configurations

  Activity 16.4.1

  1. Using your knowledge acquired so far in chemistry, define the term
  electron configuration.
  2. How this concept can apply to the quantum theory of the atomic
  structure?
  3. Using available resources, figure out the rules that dictate the
  electronic configuration.

  The electron configuration is the distribution of electrons of an atom in its
  atomic orbitals. The electronic configuration of an atom is governed by three
  main rules including Aufbau principle, Pauli Exclusion Principle and Hund’s
  rule.

  1. Pauli Exclusion Principle

  No two electrons in the same atom can have the same set of the four quantum
  numbers. If two electrons have the same values of n, l, ml, they must have
  

  different values of ms. Then, since only two values of msare allowed, an
  orbital can hold only two electrons, and they must have opposite spins.
  

  2. Hund’s rule
  Electrons occupy all the orbitals of a given sublevel singly before pairing
  begins.
  

  Spins of electrons in different incomplete orbitals are parallel in the ground
  state. The most stable arrangement of electrons in the subshells is the one
  with the greatest number of parallel spins.
  

  That is, the most stable arrangement for electrons in orbitals of equal
  energy (degenerate) is where the number of electrons with the same spin is
  maximized • Example: Carbon - 6 electrons
  

  For example, for an element with atomic number equal to 6, the electronic
  configuration is:1s²2s²2p_x¹p_y¹p_z0

  When building the electronic configuration of elements, the above principles
  are applied. writing the principal quantum number in Arabic number, followed
  by the orbitals immediately followed by the number of electrons in the orbital
  as superscript.
  

  An atom X: 1s²: has only two electrons in s orbital at the 1^st energy level

  An atom Y: 1s²2s²2p³: has electrons in 2 levels of energy: level n=1, and level
  n= 2. In level 1, it has 2 electrons in s orbital. In level 2, it has 2 electrons in
  s orbital and 3 electrons in p orbitals.
  

  Figure 2.8 is a useful and simple aid for keeping track of the order in which
  electrons are first filled for each atomic orbital. The different orbitals are filled
  in the order 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f,
  6d, 7p.
  

  Notice that as energy levels increase starting from n=3, 4s orbital is filled
  before 3d, 5s before 4d, etc… as shown in the diagram below. But when
  ionized, 4s electrons are ionized before 3d, and 5s before 4d.
  

  3. Aufbau Principle

  The Aufbau principle or build up principle or construction principle state that
  “Electrons fill lower energy orbitals (closer to the nucleus) before they fill
  higher energy ones”.
  

  
  

  Orbitals in atomic ground state electron configuration are filled in order of
  increasing n+l. For equal n+l values, the orbital with the lower n is most
  often filled first.
  

  Examples:
  Using, s, p, d, f notation, write the electronic configuration for elements of
  atomic numbers: 16, 23, 37
  

  
  

  The s, p, d and f notation uses numbers to designate a principal shell and
  the letters to identify a subshell; a superscript number indicates the number
  of electrons in a designated subshell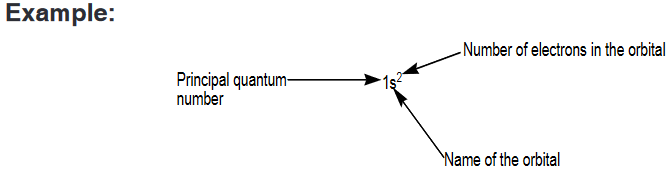
  

  
  

  Note that 1s² is read “one s two,” not “one s squared.”
  

  Application activity 16.4.1.a
  1. Using the spdf notation, build the electronic configuration of the
  following atoms: ₁H, ₃Li, ₅B, ₁₁Na, ₁₈Ar,₁₉K, ₂₁Sc, ₂₄Cr, ₂₆Fe, ₂₉Cu
  

  Expanded notation
  Expanded notation is another method of writing the s, p, d and f notation.
  The method uses the same concept as s, p, d and f notation except that
  each individual orbital of a sub-level having many orbitals is represented
  with a subscript letter indicating the orientation of the orbital. This applies for
  p, d, and f orbitals.
  

  Considering that p-orbital has three components p_x, p_y, and p_z, the expanded
  electronic configuration of some elements is given hereafter.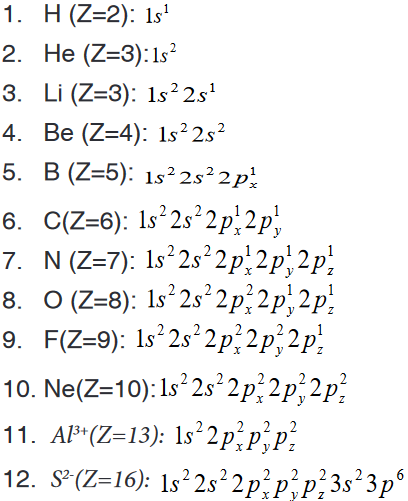
  

  
  

  Application activity 16.4.1.b
  Write the expanded electronic configuration for each of the following
  atom/ions.
  

  S(z=16), P^3-(z=15), Mg²⁺(z=12)

  Orbital box representation
  An orbital box representation consists of a box for each orbital in a given
  energy level, grouped by sublevel, with an arrow indicating an electron and
  its spin.
  

  Note that two electrons in the same orbital have necessarily opposite spins
  as indicated in the examples below.
  

  The table 16.4 shows the electronic configuration of some elements using
  orbital box representation and applying Hund’s rule.
  Examples
  

  
  

  N.B:An orbital box representation doesn’t show the real form of the orbital;
  the forms of the different orbitals are shown in Figures 16.4, 16.5 and 16.6
  above.

  Table 16.4: Electronic configuration using orbital box representation
  

  
  

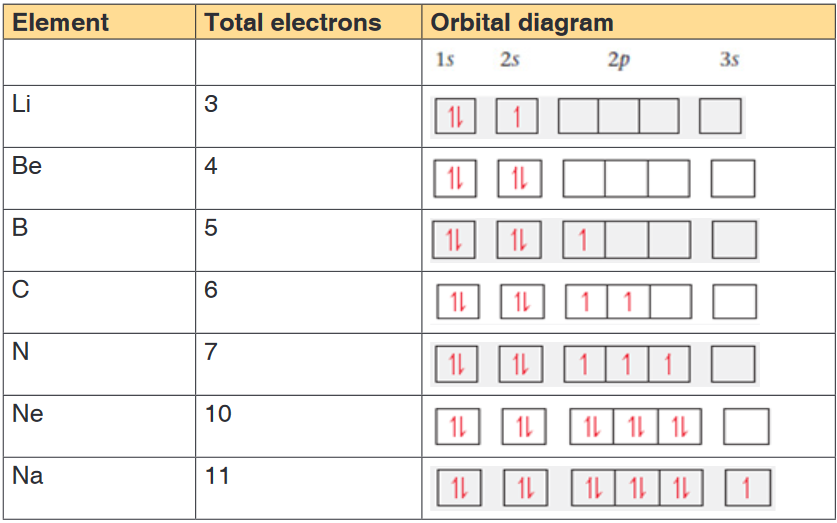
  Application activity 16.4.1.c
  Using boxes to represent orbitals, draw the electronic configuration of
  N^3- (z=7), Ti⁴⁺(z=22), Mg²⁺(z=12), Ar(z=18)
  Identify the isoelectronic species that are present.
  

  Noble Gas Notation or condensed electron configuration

  All noble gases have completely filled subshells and can be used as a
  shorthand way of writing electron configurations for subsequent atoms.
  

  When using this method, the following steps are respected.
  a). Identify the noble gas whose electronic configuration is included in

  that of the concerned element.

  b). Write the chemical symbol of the identified noble gas within square
  brackets. We call this the noble gas core.

  c). Add electrons beyond the noble gas core. Note that electrons that
  are added to the electronic level of the highest principal quantum
  number (the outermost level or valence shell) are called valence
  electrons.

  Example: Given the electronic configurations of the noble gases Ne and Ar,
  one can write the electronic configuration of some elements in
  noble gas notation of some elements as:
  

  
  

  Application activity 16.4.1.d
  Using the noble gas notation, write the electronic configuration of the
  following atoms/ions.
  a). Ge (Z=32)
  b). S (Z=16)
  c). Co²⁺ (Z=27)
  d). Br- (Z=35)
  e). Sr (Z=38)

  16.4.2. Electronic configuration and stability

  Activity 16.4.2

  State the Hund’s rule and explain how the rule is important in the
  understanding of the behaviour of an element.

  Hund’s rule states that electrons first occupy the similar energy orbitals
  that are empty before occupying those which are half-full. This is especially
  helpful when determining unpaired electrons. The Aufbau process denotes
  the method of “building up” each sub-shell before moving on to the next;
  

  Almost all the elements follow the same trend for writing electronic
  configuration.
  

  Sometimes electron configurations of certain elements appear to violate the
  rules that govern the electron configuration.
  

  For example, the electron configuration of chromium is [Ar]3d⁵4s¹rather
  than the [Ar]3d⁴4s²configuration we might have expected.
  

  Similarly, the configuration of copper is [Ar]3d ¹⁰4s¹instead of [Ar]3d⁹4s².
  

  This anomalous behaviour is largely a consequence of the closeness of the
  3d and 4s orbital energies.

  The orbitals in which the sub-shell is exactly half-filled or completely filled
  are more stable because of the symmetrical distribution of electrons.

  Application activity 16.4.2
  1. Write the electronic structure of the following chemical species.
  K (Z=19), Ne (Z=10), Al³⁺ (Z=13), Cl (Z=17), O^2- (Z=16)

  2. a) Write the electronic configuration for each of the following pairs
  of ions. State the more stable ion in gaseous state and explain your
  choice.

  i. Cu+ and Cu²⁺  (ii) Fe²⁺and  Fe³⁺
  

  b) Using information in question (a) specify the species from each pair
  has a more stable electronic configuration. Explain.

  16.5. Relationship between ionization energy, energy levels
  and factors influencing ionization energy

  16.5.1. The graphs of ionization energy versus the number of
  electrons removed
  

  Activity 16.5.1
  1. Write the electronic configuration of the following elements/ions, use
  s, p, d, …) Sodium, magnesium, magnesium ion (Mg²⁺), aluminium,
  aluminium ion (Al³⁺), oxide ion (O^2-).

  2. Identify the common feature of ions in (1) and why do they have such
  feature.

  3. Suggest what happened to aluminium atom when it changed to
  aluminium ion (Al³⁺).

  4. Identify the group and the period of aluminium, sodium and oxygen
  atom.

  Concept of Ionization energy
  The ionization energy is a measure of the energy needed for an atom, in
  gaseous state, to lose an electron and become positive ion.
  

  The first ionisation energy is the energy required to remove one electron from
  an atom in its gaseous state. The example below shows how to represent
  the successive ionization energies of an atom M.

  First ionisation energy: M(g) →M⁺(g) + e^-
  

  Second ionisation energy and n^th ionisation energy: Two or more
  electrons can be removed and we have successive ionization energies.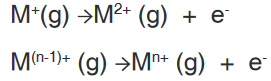
  

  
  

  The ionization energy is usually expressed in kilojoules per mole (kJ.mol-1).
  This energy is required to overcome the attractive force between the nucleus
  and the electron and then remove the electron. Theoretically there are as
  many successive ionisation energies as there are electrons in the original
  atom. In figure 2.9, someone can make an interpretation of successive
  ionization energies of an atom.

  • Successive ionisation energies for an element increase, since the
  remaining electrons are pulled closer to the nucleus and are more
  tightly held.

  • Evidence for the arrangements of electrons in shells of different
  energies is provided by values of successive ionisation energies for
  elements.

  • The figure below shows a graph of the logarithm of the ionisation
  energy required for the removal of one electron after another from the
  potassium atom.

  • A logarithmic scale is used in order to give a condensed graph, since
  there is a large range in values of successive ionisation energies.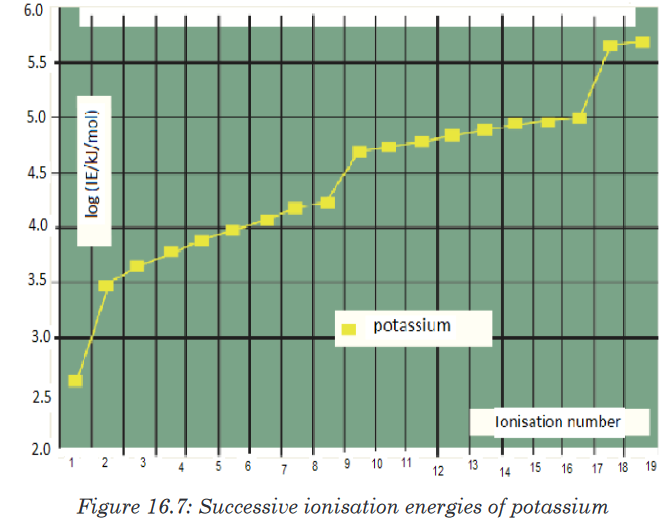
  

  
  

  • The graph that has four parts shows three breaks. These three breaks
  are evidence of principal energy level.
  • The first break occurs after the first electron has been removed from
  the forth energy level (n = 4). The second breaks after the ninth electron
  has been removed from the third energy level (n = 3).
  • The third break occurs after the 17th electron is removed from a second
  energy level.
  • The two electrons with the highest ionisation energy are close to the
  nucleus and form the n = 1 shell.
  

  Application activity 16.5.1

  1. What is meant by the term first ionisation energy?
  2. Explain why helium has the highest first ionisation of all the elements.
  3. Explain why the first ionisation energy of sodium is less than that of
  neon, but the second ionisation energy of sodium is greater than the
  second ionisation energy of neon.
  4. Sketch a graph to show the successive ionisation energies for
  aluminium. What does the shape of your graph tells you about the
  electron configuration of aluminium?
  

  16.5.2. Interpretation of a graph of first ionization energy versus
  the atomic numbers of elements.

  Activity 16.5.2

  Using the s, p, d, f notation, predict the electronic configurations of the
  first twenty elements.
  

  Use the established electronic configurations to predict the trends in the
  first ionisation energy values for the elements above.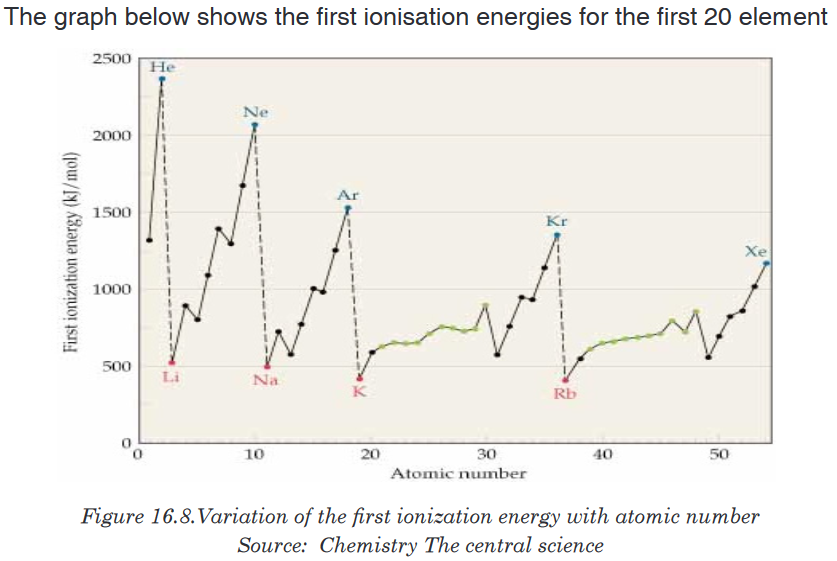
  

  
  

  Note that the noble gases have high ionization energies, whereas the alkali
  metals and alkaline earth metals have low ionization energies.
  

  Note also that, apart from small irregularities, the first ionization energies of
  elements in a period increase with increasing atomic number.
  

  Application activity 16.5.2

  1. Write an equation to illustrate the process which occurs during the
  first ionization of neon.

  2. Explain why the value of the first ionization energy of magnesium is
  higher than that of sodium.

  3. Write an equation to illustrate the process occurring when the second
  ionization energy of magnesium is measured.

  4. The Ne atom and the Mg²⁺ ion have the same number of electrons.
  Give two reasons why the first ionization energy of neon is lower than
  the third ionization energy of magnesium.

  5. Explain why the first ionization of aluminum is smaller than that of
  magnesium greater than the first ionization energy of magnesium.
  

  16.5.3. Factors influencing the magnitude of ionization energy

  Activity 16.5.3

  1. Why is the first ionisation of neon higher than that of fluorine?

  2. Explain why the first ionisation energy of potassium is lower than that
  of sodium?

  The ionization energy is a physical property of elements that can be influenced
  by some factors:
  

  1. Size of atom
  The atomic size is the distance between the nucleus and valence shell.
  As the number of energy levels (shells) increases, the force of attraction
  between nucleus and valence electron decreases. Therefore, the valence
  electrons are loosely held to the nucleus and lower energy is required to
  remove them, i.e. ionization energy decreases with increase in atomic size
  and vice versa. This is what happens when you go down a Group.
  

  2. Nuclear charge
  The nuclear charge is the total charge of all the protons in the nucleus. As
  the nuclear charge increases, the force of attraction between nucleus and
  valence electrons on the same valence energy level increases and hence
  makes it difficult to remove an electron from the valence shell. The higher
  the nuclear charge, the higher the ionization energy. This is what happens
  when you cross a period from left to right.

  3. Screening effect or Shielding effect
  The Screening effect or Shielding effect is due to the presence of inner
  electrons which have a screening or shielding effect against the attraction
  of the nucleus towards the outermost electrons. The electrons present in
  inner shells between the nucleus and the valence shell reduce the attraction
  between nucleus and the outermost electrons. This shielding effect
  increases with the increasing number of inner electrons. A strong Shielding
  effect makes it easier to remove an external electron and hence lowers the
  ionization energy.

  4. Electronic Configuration
  Electronic configuration plays an important role in determining the value
  of ionization energy. Atoms having stable configuration (i.e. fully filled or
  half filled) have least tendency to lose electrons and hence have high of
  ionization energy values.
  

  Application activity 16.5.3
  1. Why is the first ionization energy of krypton lower than the first
  ionization energy of argon?
  

  2. Explain why the value of the first ionization energy of sulphur is
  lower than that of phosphorus.
  

  3. Explain why the third ionisation energy of magnesium is very
  much larger than the second ionisation energy of magnesium.
  

  Skills lab 16
  Absorption and emission spectra are like finger prints. Assume that you
  have to market some goods using advertising lamps that can emit light with
  at least 10 alternating colours. Write paper specifying the chemical elements
  that may be involved in the production of these advertising lamps.
  

  End unit assessment 16
  1. Which of the following is the correct representation of the ground-
  state electron configuration of molybdenum? Explain what is wrong
  with each of the others.
  

  
  

  2. Which of the following electron configurations are correct and which
  ones are wrong? Explain.
  

  
  

  3. Photosynthesis uses 660 nm light to convert CO₂ and H₂O into
  glucose and O₂. Calculate the frequency of this light.

  4. Which of the following orbital designations are incorrect: 1s, 1p, 7d,
  9s, 3f, 4f, 2d?

  5. The data encoded on CDs, DVDs, and Blu-ray discs is read by lasers.
  What is the wavelength in nanometres and the energy in joules of the
  following lasers?
  CD laser, v = 3.85 x 10¹⁴ Hz
  DVD laser, v = 4.62 x 10¹⁴ Hz
  Blu-ray laser, v = 7.41 x 10¹⁴ Hz

  6. Concerning the concept of energy levels and orbitals,
  a) How many subshells are found in n=3?
  b) What are the names of the orbitals in n=3?
  c) How many orbitals have the values n=4 and l=3?
  d) How many orbitals have the values n=3, l=2 and ml= −2?
  e) What is the total number of orbitals in the level n=4?

  7. A hypothetical electromagnetic wave is pictured here. What is the
  wavelength of this radiation?
  

  
  

  8. Consider the following waves representing electromagnetic radiation:
  

  
  

  a) Which wave has the longer wavelength?
  b) Calculate the wavelengths of the two radiations
  c) Which wave has the higher frequency and larger photon energy?

  9.Order the orbitals for a multielectron atom in each of the following lists
  according to increasing energy:
  a). 5p, 5d
  b). 4s, 3d
  c). 6s, 4d

  10. According to the Aufbau principle, which orbital is filled immediately
  after each of the following in a multielectron atom?
  a) 4s
  b) 3d
  c) 5f
  d) 5p

  11. According to the Aufbau principle, which orbital is filled immediately
  before each of the following?
  a) 3p
  b) 4p
  c) 4f
  d) 5d

  12. The ground-state electron configurations listed here are incorrect.
  Explain what mistakes have been made in each and write the correct
  electron configurations.
  

  
  

  13. Four possible electron configurations for a nitrogen atom are shown
  below, but only one represents the correct configuration for a
  nitrogen atom in its ground state. Which one is the correct electron
  configuration? Which configurations violate the Pauli Exclusion
  Principle? Which configurations violate Hund’s rule?
  

  
  

  14. Explain the variation in the ionization energies of carbon, as displayed
  in this graph.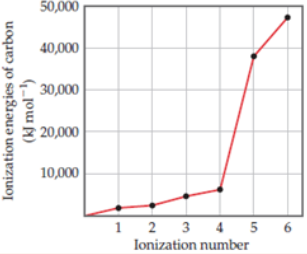
  

  
  

  15. The first seven ionization energies of an element W are shown below
  

  
  

  What factors determine the magnitude of the first ionization energy

  16. The following table shows the ionisation energies ( in kJ mol-1) of the
  five elements lettered A, B, C, D and E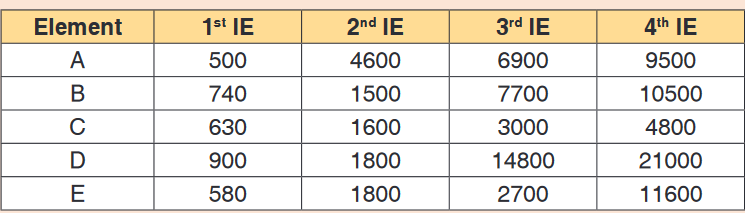
  

  
  

  a) Which of these elements is most likely to form an ion with a
  charge of 1+? Give reasons for your answer.

  b) Which two of the elements are in the same group of the periodic
  table? Which group do they belong to?

  c) In which group of the periodic table is element E likely to occur?
  Give reasons for your answer.

  d) Which element would require the least energy to convert one
  mole of gaseous atoms into ions carrying two positive charges?
  

• UNIT 17: IONIC AND METALLIC BONDS

  Key Unit competence: Describe how properties of ionic
                                                compounds and metals are related to the
                                                nature of their bonding

  Introductory Activity
  Consider the following figures and answer the related questions

  

  1. Figure 1 shows materials commonly used at home. If you reflect back
  around your house/home you will see hundreds of objects made from
  different kinds of materials.
  a) Observe the objects (in picture) and classify them according to
  the materials they are made of.
  b) Have you ever wondered why the manufacturers choose the
  material they did for each item?
  c) Why are frying saucepans made of metals and dishes, cups and
  plates often made of glass and ceramic?
  d) Could dishes be made of metal? And saucepans made of
  ceramic and glass?

  2. Figure 17.1 (b) shows the electric conductivity of distilled water,
  solid table salt and a solution of a table salt respectively.
  a) Use the diagrams A, B and C to explain the observations from
  the set up.
  i. No light is given out by bulb in A
  ii. No light is given out by bulb in B
  iii. Light is given out in C
  b) Suppose that you have a 30 cm bar made of table salt. Suggest
  the change, if there is any, that can occur and deduce the
  property related, when this salt bar is:
  i. Dropped from a table of 1 m high to the floor
  ii. Immersed in water found in a water bath.
  iii. Dry heated to 100^oC

  17.1. Explanations of why atoms of elements form bonds

  Activity 17.1

  
  Consider Chlorine (Cl, Z = 17) and Argon (Ar, 18) atoms of the elements
  of Period 3 in the Periodic Table.
  d) Which of these atoms is more reactive?
  e) Suggest the reasons for your answer in (a) in terms of the
  electronegativity and electronic structure.
  f) Choose, between Chlorine and Argon, which one has lower energy
  potential.

  The atoms of most elements form chemical bonds because the atoms become
  more stable when bonded together. Electric forces attract neighboring atoms
  to each other, making them stick together.

  In atoms, electrons are arranged into complex layers called shells. For most
  atoms, the outermost shell is incomplete, and the atom shares electrons with
  other atoms to fill the shell.

  The type of chemical bond maximizes the stability of the atoms that form it.

  An ionic bond, where one atom essentially donates an electron to another,
  forms when one atom becomes stable by losing its outer electrons and the
  other atoms become stable (usually by filling its valence shell) by gaining the
  electrons.

  Covalent bonds form when sharing atoms results in the highest stability.

  Other types of bonds besides ionic and covalent chemical bonds exist, too.

  Atoms with incomplete shells are said to have high potential energy;
  atoms whose outer shells arefull have low potential energy. In nature,
  objects with high potential energy “seek” a lower energy, becoming more
  stable as a result. Atoms form chemical bonds to achieve lower potential
  energy.

  Application activity 17.1

  Explain why atoms of elements form bonds

  17.2. Gain of stability by losing and gaining electrons

  Activity 17.2

  
  Observe the electronic configuration of the following atoms in groups and
  discuss the following questions.

  

  a) How many electrons does sodium have on its outer most shell?
  i. How many electrons does Sodium need to be stable?
  ii. What is the easiest way for Sodium to be stable?

  b) How many electrons does Chlorine have on its outer most shell?
  i. How many electrons does Chlorine need missing to get stability?
  ii. What is the easiest for Chlorine to be stable?

  c) Does Neon need more electrons to be stable? If Yes why? If no
  why?

  Like people always relate and connect to others depending on their values,
  interests and goals so does unstable atoms. They combine together to
  achieve stability. We know that noble gases are the most stable elements in
  the periodic table. They have a filled outer electron energy level.

  When an atom loses, gains, or shares electrons through bonding to achieve
  a filled outer electron energy level, the resulting compound is often more
  stable than individual separate atoms.

  • Neutral sodium has one valence electron. When it loses this electron
  to chlorine, the resulting Na+ cation has an outermost electron energy
  level that contains eight electrons. It is isoelectronic (same electronic
  configuration) with the noble gas neon.

  • On the other hand, chlorine has an outer electron energy level that
  contains seven electrons. When chlorine gains sodium’s electron, it
  becomes an anion that is isoelectronic with the noble gas argon. The
  fact that atoms need to form bonds with other atoms by loosing or
  gaining electrons to attain stability is called the octet rule; this means
  to have 8 electrons at the outermost shell.

  It is easiest to apply the “Octet Rule” to predict whether two atoms will form
  bonds and how many bonds they will form. Most atoms need 8 electrons
  to complete their outer shell. So, an atom that has 2 outer electrons will
  often form a chemical bond with an atom that lacks two electrons to be
  “complete”. The octet rule states that elements gain or lose electrons to
  attain an electron configuration of the nearest noble gas. Octet comes from
  Latin language meaning “eight”.

  Note that the “Duet Rule” is also applied. The noble gas HELIUM has two
  electrons (a doublet) in its outer shell, which is very stable. Hydrogen only
  needs one additional electron to attain this stable configuration, while lithium
  needs to lose one.

  Low atomic weight elements (the first twenty elements) are most likely to
  adhere to the Octet Rule. For example,

  • A sodium atom has one lone electron in its outer shell.

  • A chlorine atom, in contrast, is short one electron to fill its outer shell.

  • Sodium readily donates (looses) its outer electron (forming the Na+ ion,
  since it then has one more proton than it has electrons), while chlorine
  readily accepts (gains) a donated electrons(making the Cl- ion, since
  chlorine is stable when it has one more electron than it has protons).

  • Sodium and chlorine form an ionic bond with each other, to form table
  salt or sodium chloride.

  Application activity 17.2

  
  d) State the following Rule?
  i. Octet Rule
  ii. Duet Rule

  b) Answer to the following questions
  i. Does sodium need to gain electron than chlorine? (Yes or No)
  ii. Explain the target of sodium when it is seeking to lose electron
  and chlorine to gain electron.

  c) Which of the following is stable? Explain why?
  i. Na⁺ ii. Na iii.Cl iv.Cl^-

  17.3. Ionic bonding

  Activity 17.3

  In the Ordinary Level, you learnt that there exist three main types of
  chemical bonding namely, covalent, ionic and metallic.

  b) Recall the definition of the ionic bond.

  c) State the properties of a table salt and use it to generalize the
  properties of ionic compounds. (Appearance, Solubility in water and
  in petrol, Temperature required to melt, Electrical conductivity of solid
  and aqueous solution)

  17.3.1. Concept of ionic bonding
  The ionic bond is formed by complete transfer of electrons from one to
  the other, being a metal atom and the other a non-metal atom.

  Due to the atoms are neutral:

  • When an atom gives up an electron, it is positively charged, forming
  what is called a positive ion or cation. The positive charge of a
  monovalent cation is equal in magnitude but opposite to that of the
  electron (1,602 x 10-19 C) sign.

  • If an atom captures one electron, it will be negatively charged, thereby
  forming a negative ion or anion. The negative charge of a monovalent
  anion is therefore the same as the electron.

  When two counter-ions have been formed, i.e. a cation and an anion, they
  attract each other through electrostatic forces, and so, they can form a
  stable molecule.

  These electrostatic attractive forces (sometimes called Coulomb
  forces) are therefore responsible for the formation of ionic compounds.

  Suppose the simple case of sodium chloride or common salt. The sodium
  atom (Z = 11) has a single (unpaired) electron in orbital 3s, somewhat
  isolated from other pairs; while in the chlorine atom, there is also a single
  (unpaired) electron, but in this case it is in the 3p_z orbital, other 3s, 3p_x and
  3p_y orbitals are being inhabited by respective pairs of electrons.

  The alone electron passes from sodium to chlorine; which, besides forming
  a pair with the electron in 3p_z orbital, it will be found surrounded by other
  couples.

  All the atoms of the alkali (group 1) metals have an external electronic
  configuration type ns¹, i.e., with a single electron in the outermost orbit. This
  electron, which is often called valence electron is quite far from the core
  (the nucleus), which is separated also by the other electrons, called internal
  (electrons), which largely core-shielding attraction on said valence electron.

  So, it is quite easy to remove this electron, for which a little energy is spent.
  This is why the ionization energy, which, for the alkali metals, is very small.

  When an alkali metal atom has been easily removed its valence electron,
  however, it is difficult to remove a second electron, as their ionization
  energy is very high. Therefore, the alkali metal cations are relatively easily
  monovalent (M⁺).

  For the group 13 elements (B, Al, Ga, In, Tl), it costs much energy to remove
  valence electrons, which, in this case, are the type ns2np1, so it is difficult.
  Hence, they form trivalent cations, except heavier atom of Tl that can form
  in certain cases, monovalent cation.

  The elements of groups 14, 15, 16 and 17 of the Periodic Table, as well as
  the noble gases (group 18), the ionization energy is increasing, so it is very
  difficult for these elements to form positive ions.

  • Only the heaviest elements of group 14, tin and lead, form, in some
  cases, divalent cations (loss of two of the valence electrons np²). The
  rest of the elements of these groups form covalent bonds or negative
  ions.

  • The atoms of group 17 elements of the Periodic Table (halogens) have
  an outer electron configuration ns²np⁵, that is, they lack one electron
  to complete the p orbitals and thus to form the electron configuration

  of noble gas that follows in the same period. Therefore, it is easy to
  understand that if one of these atoms is joined by a new electron; a more
  stable configuration is obtained, shedding energy in this process. This
  energy is called electron affinity, which for the halogens is high. These
  elements will form in a relatively easily way, monovalent anions.

  • These anions have no tendency to take a second electron, so it would
  have to stand, alone in an outermost orbit, without the nucleus exercised
  about it any attractive force. Halogens form only monovalent anions.

  • Atoms of oxygen family elements (group 16 of the Periodic Table) are
  missing two electrons to complete the external orbitals np and acquire
  the noble gas configuration. Therefore, these elements tend to form
  divalent ions, although in this process the energy balance is slightly
  negative.

  • Nitrogen family elements (group 15 of the periodic table are hardly
  trivalent anion; while carbon group (group 14) is almost impossible
  the form tetravalent anions. Therefore, the compounds of the nitrogen
  family are largely covalent part and those of carbon family are typically
  covalent.

  17.3.2. Ionic bond formation

  Once the oppositely charged ions form when electrons are transferred from
  one atom to another, they are attracted by their positive and negative
  charges (by electrostatic forces) and form an ionic compound. Ionic bonds
  are also formed when there is a large electronegativity difference between
  two atoms. This difference causes an unequal sharing of electrons such that
  one atom completely loses one or more electrons and the other atom
  gains one or more electrons. For example, in the creation of an ionic bond
  between a metal atom, sodium (electronegativity = 0.93) and a non-metal,
  fluorine (electronegativity = 3.98).

  Let us take a look of how sodium and fluorine bond to form sodium
  fluoride.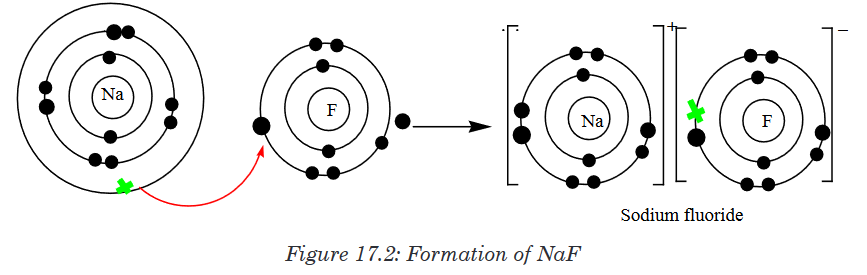

  
  

  The curved arrow between sodium and fluorine atoms represents the
  transfer of an electron from a sodium atom to a fluorine atom to form
  oppositely charged ions. These two ions are strongly attracted to each
  other because of their opposite charges. A bond is now formed and the
  resulting compound is called Sodium fluoride
  

  Another example of ionic bonding formation is the formation of magnesium
  oxide.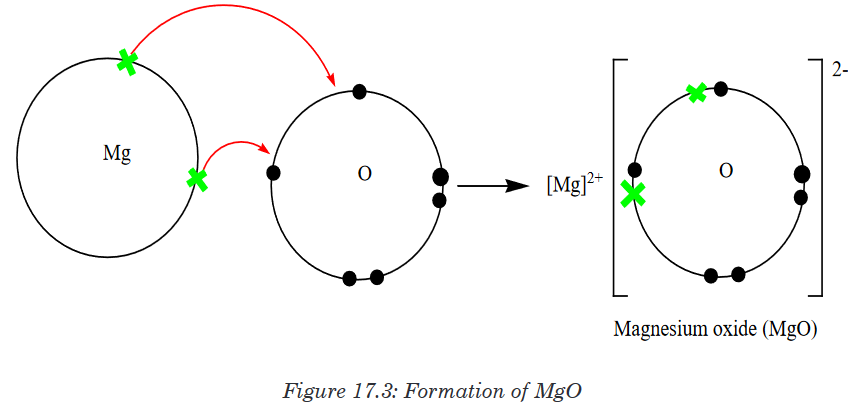
  

  
  

  17.3.3. Properties of ionic compounds
  Here are the properties shared by the ionic compounds. Notice that the
  properties of ionic compounds relate to how strongly the positive and
  negative ions attract each other in an ionic bond.
  

  1. They have high melting points and high boiling points
  

  In an ionic lattice, there are many strong electrostatic attractions between
  oppositely charged ions. We therefore expect that ionic solids will have
  high melting points. On melting although the regular lattice is broken down,
  there will still be significant attractions between the ions in the liquid. This
  should result in high boiling points also.
  

  The factors which affect the melting point of an ionic compound are:
  

  • The charge on the ions of ionic compound: “The greater the charge,
  the greater the electrostatic attraction, the stronger the ionic bond, the
  higher the melting point.”

  For example, Melting Point of NaCl is 801 ^oC and that of MgO is
  2,800 ^oC.
  

  • The size of the ions of ionic compound: “Smaller ions can pack
  closer together than larger ions so the electrostatic attraction is greater,
  the ionic bond is stronger, the melting point is higher.” For example,
  Melting Point of NaF is 992 ^oC and that of CsF is 2,800 ^oC.
  

  2. Most ionic compounds are soluble in water
  This is because the electrostatic forces of the polar water molecules are
  stronger than the electrostatic forces keeping the ions together. When an
  ionic compound like NaCl is added to water, water molecules attract the
  positive and negative salt ions. Water molecules surround each ion and move
  the ions apart from each other. The separated ions dissolve in water. There
  are several exceptions, however, where the electrostatic forces between the
  ions in an ionic compound are strong enough that the water molecules cannot
  separate them. Despite these few limitations, water’s ability to dissolve ionic
  compounds is one of the major reasons it is so vital to life on Earth. Ionic
  compounds are generally insoluble in non-polar solvents like kerosene.
  

  3. They are hard and brittle
  Ionic crystals are hard because the positive and negative ions are strongly
  attracted to each other and difficult to separate, however, ionic solids are
  brittle.
  

  When a stress is applied to the ionic lattice, the layers shift slightly. The layers
  are arranged so that each cation is surrounded by anions in the lattice. If the
  layers shift then ions of the same charge will be brought closer together. Ions
  of the same charge will repel each other, so the lattice structure breaks down
  into smaller pieces.
  

  4. They conduct electricity when molten or dissolved in water
  In order for a substance to conduct electricity, it must contain mobile particles
  capable of carrying charge.
  

  • Solid ionic compounds do not conduct electricity because the ions
  (charged particles) are locked into a rigid lattice or array. The ions
  cannot move out of the lattice, so the solid cannot conduct electricity.
  

  • When is molten, the ions are free to move out of the lattice structure.
  

  – Cations (positive ions) move towards the negative electrode
  (cathode): M+ + e- → M
  

  – Anions (negative ions) move towards the positive electrode (anode):
  X- → X + e-
  

  • When the ionic compound is dissolved in water to form an aqueous
  solution, the ions are released from the lattice structure and are free
  to move so the solution conducts electricity just like the molten (liquid)
  ionic compound.
  

  5. They form crystals
  Ionic compounds form crystal lattices rather than amorphous solids. Although
  molecular compounds form crystals, they frequently take other forms but
  molecular crystals typically are softer than ionic crystals. At an atomic level,
  an ionic crystal is a regular structure, with the cation and anion alternating
  with each other and forming a three-dimensional structure based largely on
  the smaller ion evenly filling in the gaps between the larger ion.
  

  Application activity 17.3
  

  1. The diagram below represents a part of the structure of sodium
  chloride. The ionic charge is shown on the centre of only one of the
  ions.
  

  
  

  a) On the diagram, mark the charges on the four negative ions.

  b) What change occurs to the motion of the ions in sodium chloride
  when it is heated from room temperature to a temperature below
  its melting point?

  c) Sodium chloride can be formed by reacting sodium with chlorine.
  A chloride ion has one more electron than a chlorine atom. In
  the formation of sodium chloride, from where does this electron
  come?

  2. Draw diagrams to illustrate the formation of ionic compounds in the
  following substances:
  a) Calcium chloride
  b) Sodium peroxide
  c) Iron (III) chloride
  d) Sodium sulphide

  3. Solid sodium chloride and solid magnesium oxide are both held
  together by ionic (electrovalent) bonds.

  a) Using s, p and d notation write down the symbol for and the
  electronic configuration of (i) a sodium ion; (ii) a chloride ion; (iii)
  a magnesium ion; (iv) an oxide ion.
  

  b) Explain what holds sodium and chloride ions together in the solid
  crystal

  c) Sodium chloride melts at 1074 K; magnesium oxide melts at 3125
  K. Both have identical structures. Why is there such a difference in
  their melting points?

  17.4. Metallic bonding

  Activity 17.4

  1. Give three examples of substances which are malleable, ductile,
  good conductor of heat and electricity, and having a characteristic
  luster. Here you can use a dictionary or other searching tools to find
  the meaning for any unfamiliar word.

  2. Suggest another property, apart from those given, of the substances
  you have given in (1).

  3. Choose from the examples given in (1), one which is most common
  and well known.

  a) This substance is seen to be composed by atoms of one element.
  Which one?

  b) Use a labeled drawing to show the internal structure of that kind
  of substance.

  A metallic bond is a type of chemical bond formed between positively charged
  atoms in which the free electrons are shared among a lattice of cations. In
  contrast, covalent and ionic bonds form between two discrete (separate)
  atoms.
  

  Metallic bonding is the main type of chemical bonds that forms between
  metal atoms (pure metals and alloys and some metalloids). A metal is a
  lattice of positive metal ‘ions’ in a ‘sea’ of delocalised electrons.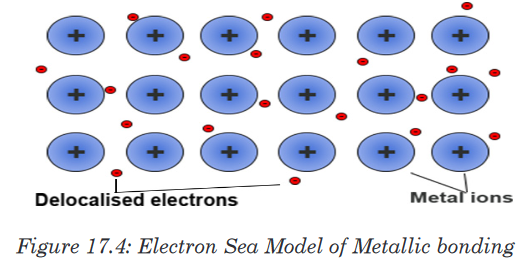
  

  
  

  17.4.1. How metallic bonds work
  The outer energy levels of metal atoms (the s and p orbitals) overlap. At least
  one of the valence electrons participating in a metallic bond is not shared
  with a neighbor atom, nor is it lost to form an ion. Instead, the electrons form
  what may be termed an “electron sea” in which valence electrons are free
  to move from one atom to another. Metallic bonding refers to the interaction
  between the delocalised electrons and the metal nuclei.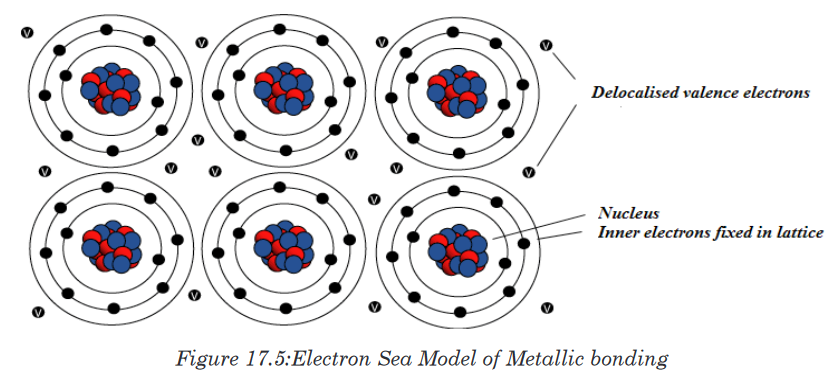
  

  
  

  The electron sea model is an oversimplification of metallic bonding.
  Calculations based on electronic band structure or density functions are
  more accurate. Metallic bonding may be seen as a consequence of a
  material having many more delocalized energy states than it has delocalized
  electrons (electron deficiency), so localized unpaired electrons may become
  delocalized and mobile. The electrons can change energy states and move
  throughout a lattice in any direction.
  

  Bonding can also take the form of metallic cluster formation, in which
  delocalized electrons flow around localized cores. Bond formation depends
  heavily on conditions. For example, hydrogen is a metal under high pressure!
  As pressure is reduced, bonding changes from metallic to non-polar covalent.
  

  17.4.2. Physical properties of metals
  Because electrons are delocalized around positively-charged nuclei, metallic
  bonding explains many properties of metals.
  

  1. Electrical Conductivity
  Most metals are excellent electrical conductors because the electrons in the
  electron sea are free to move and carry charge. For example, electric wires
  in our homes are made of aluminium and copper. They are good conductor
  

  of electricity. Electricity flows most easily through gold, silver, copper and
  aluminium. Gold and silver are used for fine electrical contacts in computers.
  

  2. Thermal Conductivity
  Metals conduct heatbecause the free electrons are able to transfer energy
  away from the heat source and because vibrations of atoms (phonons) move
  through a solid metal as a wave. Cooking utensils and water boilers are also
  made of iron, copper and aluminium, because they are good conductors of
  heat.
  

  3. Ductility
  Metalstend to be ductile or able to be drawn into thin wires because local
  bonds between atoms can be easily broken and also reformed. Single atoms
  or entire sheets of them can slide past each other and reform bonds. Wires
  are mainly made from copper, aluminium, iron and magnesium.
  

  4. Malleability
  Metals are often malleable or capable of being molded or pounded into a
  shape, again because bonds between atoms readily break and reform. This
  ability to bend or be shaped without breaking occurs because the electrons
  simply slide over each other instead of separating. The binding force between
  metals is non-directional, so drawing or shaping a metal is less likely to
  fracture it. Electrons in a crystal may be replaced by others. Gold and Silver
  metals are the most malleable metals. They can be hammered into very fine
  sheets. Thin aluminium foils are widely used for safe wrapping of medicines,
  chocolates and food material.
  

  5. Metallic Luster
  Metals tend to be shiny or display metallic luster. They are opaque once a
  certain minimum thickness is achieved.
  

  The electron sea reflects photons off the smooth surface therefore there is an
  upper frequency limit to the light that can be reflected. Silver is a very good
  reflector. It reflects about 90% of the light falling on it. All modern mirrors
  contain a thin coating of metals. Due to their shiny appearance they can be
  used in jewellery and decorations.
  

  Application activity 17.4
  

  1. Magnesium has a higher melting and boiling point than sodium. This
  can be explained in terms of the electronic structures, the packing,
  and the atomic radii of the two elements.
  

  a) Explain why each of these three things causes the magnesium
  melting and boiling points to be higher.

  b) Explain why metals are good conductors of electricity.

  c) Explain why metals are also good conductors of heat.

  2. Pure metals are usually malleable and ductile.
  a) Explain what those two words mean.

  b) If a metal is subjected to a small stress, it will return to its original
  shape when the stress is removed. However, when it is subjected to
  a larger stress, it may change shape permanently. Explain, with the
  help of simple diagrams why there is a different result depending on
  the size of the stress.

  c) When a piece of metal is worked by a blacksmith, it is heated to a high
  temperature in a furnace to make it easier to shape. After working
  it with a hammer, it needs to be re-heated because it becomes too
  difficult to work. Explain what is going on in terms of the structure of
  the metal.

  d) Why is brass harder than either of its component metals, copper
  and zinc?

  Skills lab 17

  Experiment to demonstrate the malleability and ductility of metals
  Materials: Wires, nails, hammer, piece of cloth.
  

  Procedure:
  1. Wrap the material to be test in a heavy plastic or cloth to avoid pieces
  flying from the material.

  2. Place the material on a flat hard surface

  3. Use a harmer to pound the material flat

  4. Record your observations as malleable or non-malleable.
  

  End unit assessment 17

  1. State whether the following statement is True or False. Justify
  your answer. “Sodium Chloride has a higher melting point than
  Magnesium Oxide”.

  2. Why are ionic compounds brittle?

  3. Why do ionic compounds have high melting points?

  4. What happens when an electric current is passed through a solution
  of an ionic compound?

  5. This question is about metallic bonding.
  a) Describe the bonding that is present in metals.
  b) Explain how the bonding and structure lead to the typical metallic
  properties of electrical conductivity and malleability.
  c) Suggest a reason why aluminium is a better conductor of
  electricity than magnesium.

  6. Silver and sodium chloride melt at similar temperatures. Give two
  physical properties of silver which are different from those of sodium
  chloride and, in each case, give one reason why the property of
  silver is different from that of sodium chloride.

  7. This question is about calcium oxide (CaO).
  a) Describe the nature and strength of the bonding in solid calcium
  oxide.
  b) Use the kinetic theory to describe the changes that take place
  as calcium oxide is heated from 25°C to a temperature above its
  melting point.
  c) State two properties of calcium oxide that depend on its bonding.
  

  
  

• UNIT 18: VARIATION IN TRENDS OF THE PHYSICAL PROPERTIES

  Key Unit competence: Use atomic structure and electronic
                                                 configuration to explain the trends in the
                                                physical properties of the elements.

  Introductory Activity 18
  An extended family is a family that extends beyond the nuclear family,
  consisting of parents like father, mother, their children, aunts, uncles,
  grandparents and cousins. They all live in the same household. It is easily
  to see characteristics that qualify as physical traits include hair color and
  type, attached earlobes, adorable freckles, eye color and hairline among
  family members.

  Think about this activity in order to understand well and answer the
  following questions.

  1. Have you ever noticed physical similarities between relatives at a
  family reunion?

  2. What do physical characteristics indicate among the family
  members?

  3. What are the physical characteristics that may be possessed by the
  same family members?

  18.1. Historical background of the Periodic Table

  
  Activity 18.1

  
  Use textbooks and internet connection and point out the main steps in
  the development of the periodic table.

  Scientists have always been searching for patterns and similarities in the
  properties and reactions of substances.

  For a long time chemists look at ways of dividing up the two big group,
  metallic and non-metallic elements into smaller sub-groups. They grouped
  together very reactive metals like lithium, sodium and potassium, slightly

  less reactive metals such as calcium, strontium and barium and very reactive
  non-metals like chlorine, bromine and iodine.

  Some elements were discovered which had properties in between metallic
  and non-metallic. These elements were described as metalloids (e.g. silicon).

  • In 1669, Hennig Brand a German merchant and amateur alchemist
  invented the Philosopher’s Stone; an object that supposedly could turn
  metals into pure gold. He heated residues from boiled urine, and a liquid
  dropped out and burst into flames. He also discovered phosphorus.

  • In 1680 Robert Boyle also discovered phosphorus without knowing
  about Henning Brand’ discovery.

  • In 1809, curiously 47 elements were discovered and named, and
  scientists began to design their atomic structures based on their
  characteristics.

  • In 1829, Johann Dobereiner classified some elements into groups of
  three, which he called triads.
  The elements in a triad had similar chemical properties and orderly
  physical properties.

  • Examples of triads : Cl, Br, I and Ca, Sr, Ba

  • Dobereiner showed that when the three elements in each triad were
  written in order of atomic mass, the middle element had properties in
  between those of the other two.

  • In 1863, John Newlands (1838 - 1898) suggested that elements be
  arranged in “octaves” because he noticed (after arranging the elements
  in order of increasing atomic mass) that certain properties repeated
  every 8th element. (Law of Octaves).His law of octaves failed beyond
  the element calcium.

  • In 1869, Dimitri Mendeleev based on John Newlands’ ideas started
  the development of elements organized into the periodic table. The
  arrangement of chemical elements were done by using atomic mass
  as the key characteristic to decide where each element belonged in his
  table. The elements were arranged in rows and columns. He predicted
  the discovery of other elements, and left spaces open in his periodic
  table for them.

  • At the same time, Lothar Meyer published his own periodic table with
  elements organized by increasing atomic mass.

  • In 1886, French physicist Antoine Becquerel first discovered
  radioactivity. During the same period of 1886, Ernest Rutherford named
  three types of radiation; alpha, beta and gamma rays.

  • In 1886, Marie and Pierre Curie started working on the radioactivity
  and they discovered radium and polonium. They discovered that beta
  particles were negatively charged.

  
  

  • In 1895, Lord Rayleigh discovered a new gaseous element named
  argon which proved to be chemically inert. This element did not fit any
  of the known periodic groups.

  
  

  • In 1898, William Ramsay suggested that argon be placed into the
  periodic table between chlorine and potassium in a family with helium,
  despite the fact that argon’s atomic weight was greater than that of
  potassium. This group was termed the “zero” group due to the zero
  valency of the elements. Ramsey accurately predicted the future
  discovery and properties neon.
  
  

  • In 1913, Henry Moseley worked on X-rays and determined the actual
  nuclear charge (atomic number) of the elements. He has rearranged
  the elements in order of increasing atomic number.
  
  

  • In 1897 English physicist J. J. Thomson discovered small negatively
  charged particles in an atom and named them as electrons; John
  Sealy Townsend and Robert A. Millikan investigated the electrons and
  determined their exact charge and mass.
  
  

  • In 1900, Antoine Becquerel discovered that electrons and beta particles
  as identified by the Curies are the same thing.
  
  

  • In 1903, Ernest Rutherford proclaimed that radioactivity is initiated by
  the atoms which are broken down.
  
  

  • In 1911, Ernest Rutherford and Hans Geiger discovered that electrons
  are moving around the nucleus of an atom.
  
  

  • In 1913, Niels Bohr suggested that electrons move around a nucleus
  in discreete energy levels called orbits. He observed also that light is
  emitted or absorbed when electrons transit from one orbit to another.
  
  

  • In 1914, Rutherford identified protons in the atomic nucleus. He also
  transformed a nitrogen atom into an oxygen atom for the first time.
  English physicist Henry Moseley provided atomic numbers, based on
  the number of electrons in an atom, rather than based on atomic mass.
  
  

  • In 1932 James Chadwick discovered neutrons, and isotopes were
  identified. This was the complete basis for the periodic table. In that
  same year Englishman Cockroft and the Irishman Walton first split an
  atom by bombarding lithium in a particle accelerator, changing it to two
  helium nuclei.The last major changes to the periodic table give rise
  from Glenn Seaborg’s work in the middle of the 20th Century. In 1940,

  he discovered plutonium and all the transuranic elements from 94 to
  102.
  

  
  

  • In 1944, Glenn T. Seaborg discovered 10 new elements and moved

  out 14 elements of the main body of the periodic table to their current
  location below the lanthanide series. These elements were known as
  Actinides series.
  

  
  

  • In 1951, Seaborg was awarded the Nobel Prize in chemistry for his

  work. Element 106 has been named seaborgium (Sg) in his honor.
  

  
  

  • Presently, 118 elements are in the modern Periodic Table.

  Although Dimitri Mendeleev is often considered as the “father” of the periodic
  table, however the work of many scientists contributed to its present form.
  

  The representation of a modern Periodic Table of Elements is shown below.

  
  

  

  The elements also belong to the families (chemical families). These elements
  have similar physical and chemical properties exist among the families and
  the periods of the periodic table.

  
  

  Application activity 18.1

  
  The periodic table is an important tool used in chemistry:
  1. Why scientists have developed a classification of chemical
  elements?

  
  

  2. Explain why the elements are classified in groups and periods of
  the periodic table

  
  

  3. Choose one element of Group 1 and one of group 17 and make
  their electronic configurations using orbitals.

  
  

  18.2. Comparison of Mendeleev’s table with the modern
  Periodic Table

  
  

  Activity 18.2
  

  
  

  1. Look at the modern periodic table and write down four things it tells
  you.
  

  
  

  2. Explain the gaps found in the Mendeleev periodic table compared
  to the modern one?
  

  
  

  3. How many elements does the modern periodic table contain?
  The periodic table is the arrangement of chemical elements according to their
  chemical and physical properties. The modern periodic table was created
  after a series of different versions of the periodic table. The Russian Chemist/
  Professor Dmitri Mendeleev was the first to come up with a structure for
  the periodic table with columns and rows. This feature is the main building
  block for the modern periodic table as well. The columns in the periodic
  table are called groups or families, and they group together elements with
  similar properties. The rows in the periodic table are called periods, and they
  represent sets of elements that get repeated due the possession of similar
  properties. The main difference between Mendeleev and Modern Periodic
  Table are shown in the Table 18.1.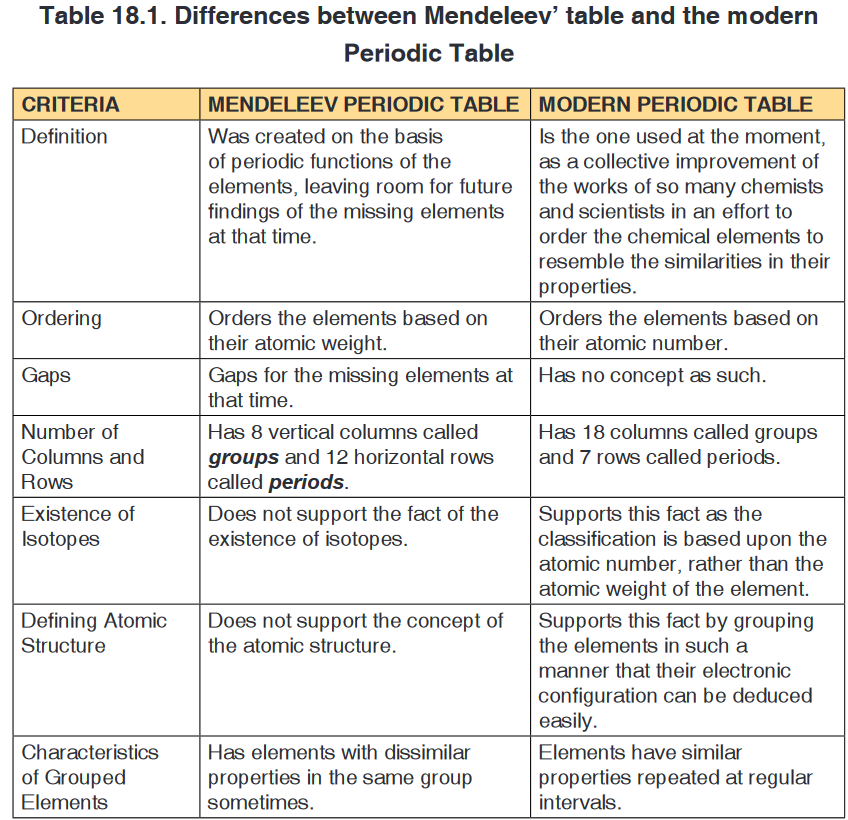

  
  

  

  
  

  Application activity 18.2

  
  1. Discuss the similarities and differences of Mendeleev’s table and
  modern periodic Table.

  
  

  2. How were the positions of cobalt and nickel resolved in the modern
  periodic table?

  
  

  18.3. Location of the elements in the Periodic Table based
  on the electronic configuration

  
  

  Activity 18.3

  
  1. Based on knowledge gained in the previous years:
  a) Represent the electronic configuration of the elements 25X and
  11Y.
  b) Discuss the information given by the number of electrons in
  the last orbitals of the above element about their position in the
  periodic table?
  c) Explain the period and the group of the periodic table in which
  the above elements are located.
  

  
  

  2. Is it possible to have an element with atomic number 1.5 between
  hydrogen and helium?
  

  
  

  18.3.1. Major Divisions of the Periodic Table
  

  
  

  The periodic table is a tabular of the chemical elements organized on the basis
  of their atomic numbers, electron configurations, and chemical properties.
  

  
  

  In the periodic table, the elements are organized by periods and groups.
  The period relates to the principal energy level which is being filled by
  electrons. Elements with the same number of valence electrons are put in
  the same group, such as the halogens and the noble gases. The chemical
  properties of an atom relate directly to the number of valence electrons, and
  the periodic table is a road map among those properties such that chemical
  properties can be deduced by the position of an element on the table. The
  electrons in the outermost or valence shell are especially important because
  they participate in forming chemical bonds.
  

  
  

  18.3.2. Location of elements in modern Periodic Table using

  
  

  examples
  

  
  

  In the periodic table, the elements are located based on groups and periods.
  

  
  

  a. Finding Period of Elements
  

  
  

  Period of the element is equal to highest energy level of electrons or principal
  quantum number. Look at following examples for better understanding;

  

  

  

  Which one(s) of the following statements are correct, which one(s)
  are false for these elements.
  a) X is alkaline metal
  b) Z is halogens
  c) U is lanthanide
  d) T is noble gas
  2. Explain the major parts of the periodic table?
  

  
  

  18.4. Classification of the elements into blocks (s, p, d,
  f-block)

  
  

  Activity 18.4

  
  1. Using the s p d f notation write condensed electronic configuration for
  the following elements. Al (Z = 13), K (Z = 19), Sr (Z = 38) and Fe (Z
  = 26). Br(Z = 35), Zr(Z = 40), Nd(Z = 60) ,Yb (Z= 70)
  

  
  

  2. For each element, identify the last subshell that is occupied by
  electrons and draw adequate conclusions.
  

  
  

  The long form of periodic table can be divided into four main blocks. These
  are: s- block, p- block, d- block, and f-block.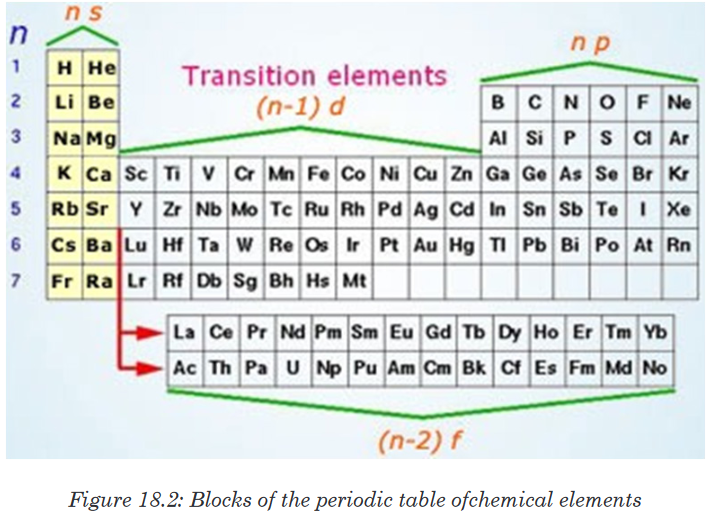

  

  1. s-Block Elements
  The elements in which the last electron enters the s-subshell of their
  outermost energy level are called s-block elements.
  

  
  

  This block is situated at extreme left of the periodic table. It contains elements
  of groups 1 and 2.
  

  
  

  Their general configuration is ns1-2, where n represents the outermost shell.
  

  
  

  The elements of group 1 are called alkali metals whereas the elements of
  group 2 are called alkaline earth metals.
  

  
  

  2. p-Block Elements
  The elements in which the last electron enters the p-sub-shell of their
  outermost energy level are called p-block elements.
  

  
  

  The general configuration of their outermost shell is ns2 np1-4. The only
  exception is helium (ls2). Strictly, helium belongs to the s-block but its
  positioning in the p-block along with other group 18 elements is justified
  because it has completely filled valence shell (1s2) and as a result, exhibits
  properties characteristic of other noble gases. This block is situated at the
  extreme right of the periodic table and contains elements of groups 13, 14,
  15, 16, 17 and 18 of the periodic table.
  

  
  

  Most of these elements are non-metals, some are metalloids and a few
  others are heavy elements which exhibit metallic character.

  
  

  The non-metallic character increases as we move from left to right across a
  period and metallic character increases as we go down the group.
  

  
  

  3. d-Block Elements
  The elements in which the last electron enters the d-subshell of the
  penultimate energy level are called d-block elements.
  

  
  

  Their general valence shell configuration is (n-1) d^1-10 ns^1-2, where n represents
  the outermost energy level. d-block contains three complete rows of ten
  elements in each. The fourth row is incomplete.
  

  
  

  The three rows are called first, second and third transition series. They
  involve the filling of 3d, 4d and 5d orbitals respectively. The d-block contains
  elements of groups 3 to 12 of the periodic table.
  

  
  

  4. f-Block Elements
  The elements in which the last electron enters the f-sublevel of the anti-
  penultimate (third to the outermost shell) shell are called f-block elements.
  

  
  

  Their general configuration is (n–2)f^1-14 (n–1) d^0-1 ns², where n represents the
  outermost shell.
  

  
  

  They consist of two series of elements placed at the bottom of the periodic
  table.
  

  
  

  The elements of first series follow lanthanum (⁵⁷La) and are called
  lanthanides. The elements of second series follow actinium (⁸⁹Ac) and are
  called actinides. Actinide elements are radioactive.
  

  
  

  Many of them have been made only in nanogram quantities or even less by
  nuclear reactions. Chemistry of the actinides is complicated and is not fully
  studied.
  

  
  

  Briefly, in the periodic table, elements are divided into:
  

  
  

  • The s-block (contains reactive metals of Group 1A (1) and 2A (2)),
  • The p-block (contains metals and non metals of Group 3A (13)
  through 8A (18)),
  • The d-block (contains transition metals Group 3B (3) through Group
  2B (12)), and
  • The f-block (contains lanthanide and actinide series or inner
  transition metals).

  
  

  Application activity 18.4
  1. a) How many blocks into which chemical elements are classified and
  how are they named?

  b) What is the criterion used for this classification?
  

  
  

  2. Which block of elements will tend to form: positive ions? Negative
  ions?
  

  
  

  3. Give any two examples of elements of s block, p block, d block and
  f block.
  

  
  

  4. Why d-block elements are called transition elements?
  

  
  

  5. Why f-block elements are called inner transition elements?
  

  
  

  18.5. Factors that influence the change of each physical
  property of the elements across a period and down a
  group

  
  

  Activity 18.5
  

  
  

  The elements in the periodic table display many trends which can be
  used to predict their physical properties.
  

  
  

  Use available resources and explain three of the factors that you think
  can influence the physical properties of elements in the periodic table.
  

  
  

  In the Periodic Table, there are a number of physical properties that are not
  really “similar” as it was previously defined, but are more trend-like. This
  means is that as you move down a group or across a period, you will see a
  trend-like variation in the properties.
  

  
  

  The actual trends that are observed with the physical properties have to do
  with the following factors:
  1. The number of protons in the nucleus (called the nuclear charge).
  2. The number of electrons held between the nucleus and its outermost
  electrons (called the shielding effect).
  

  
  

  Explanation:
  Electrons in inner levels or shells tend to shield outer electrons from the full
  nuclear charge, which is reduced to effective nuclear charge (Z_eff).

  
  

  Electrons are held in an atom or ion by the electrostatic attraction between
  the positively charged nucleus and the negatively charged electrons. In multi-
  electron species, the electrons do not experience the full positive charge of
  the nucleus due to shielding by electrons which lie between the electron of
  interest and the nucleus. The amount of positive charge that actually acts on
  an electron is called the effective nuclear charge.
  

  
  

  Electrons that have a greater penetration shield others more effectively. For
  example, electrons in level n = 1 shield those in level n = 2 very effectively,
  and those in n = 1 and n = 2 shield electrons in level n = 3. Electrons at the
  same level, but in different sublevels, also shield other electrons to some
  extent. The extent of penetration and shielding effect is in the order:
  

  
  

  s>p>d>f.
  

  
  

  The effective nuclear charge (Z_eff) greatly influence atomic properties. In
  general,
  

  
  

  • Z_eff increases significantly across a period (left-to-right)
  • Z_effincreases slightly down a group.
  

  
  

  Application activity 18.5

  
  

  Periodic Table Trends are influenced by the following factors:
  a) Size of the atom
  b) Nuclear charge
  c) Shielding effect
  Which of them affect the variation of physical properties in a group, in a
  period?

  
  

  18.6. Variation of the physical properties down the group
  and across the period

  
  

  Activity 18.6

  
  Analyze the table about the molar ionization energy values for some
  elements and answers the questions that follow.
  1. How is the variation of these values if you consider elements in the
  same
  a) period?

  b) group?
  Using available resources including internet, attempt to give a
  plausible explanation to the trend observed.
  

  
  

  2. Analyze the trends of others physical properties and try to find each
  time appropriate reasons for those trends.
  

  
  

  Periodic trends are specific patterns that are present in the periodic table
  that illustrate different aspects of a certain element, including its size and its
  electronic properties.
  

  
  

  Major periodic trends include: atomic radius, electronegativity, ionisation
  energy, electron affinity, melting point, density, metallic character.
  Periodic trends, arising from the arrangement of the periodic table, provide
  chemists with an invaluable tool to quickly predict an element’s properties.
  These trends exist because of the similar atomic structure of the elements
  within their respective group families or periods, and because of the periodic
  nature of the elements.
  

  
  

  The elements in the periodic table are arranged in order of increasing atomic
  number. All of these elements display several other trends and we can
  use the periodic table to predict their physical properties. There are many
  noticeable patterns in the physical and chemical properties of elements as
  we descend in a group or move across a period in the Periodic Table.
  

  
  

  18.6.1. Atomic radius
  The atomic radius is the distance from the centre of the nucleus to the
  outermost shell of an atom when it is in the ground state.
  

  
  

  The covalent radius is one-half the distance between the two nuclei of
  identical atoms that are joined together by a single covalent bond.
  

  
  

  The metallic radius is one-half the distance between the nuclei of two atoms
  in contact in the crystalline solid metal.
  

  
  

  A cation is an atom that has lost one of its outer electrons. Cations have a
  smaller radius than the atom that they were formed from.
  

  
  

  An anion is an atom that has gained an outer electron. Anions have a greater
  radius than the atom that they were formed from.
  

  
  

  Going across a period, the atomic radius decreases. This is caused by the
  increase in the number of protons and electrons across a period. One proton
  has a greater effect than one electron; thus, electrons are pulled towards the
  nucleus, resulting in a smaller radius.

  
  

  Atomic radius increases down the group. This is caused by electron
  shielding. The valence electrons occupy higher levels due to the increasing
  quantum number . As a result, the valence electrons are further away
  from the nucleus as ‘n’ increases. Electron shielding prevents these outer
  electrons from being attracted to the nucleus; thus, they are loosely held,
  and the resulting atomic radius is large.
  

  
  

  18.6.2. Electronegativity
  Electronegativity is a measure of the relative ability of an atom to attract
  the pair of electrons in a covalent bond. Two factors help to determine the
  electronegativity value of an element:
  • The size of the nuclear charge
  • The size of the atom
  

  
  

  Going across a period, the electronegativity value increases: as the nuclear
  charge increases, the size of the atom decreases and hence there is a greater
  attraction between the nucleus and the pair of electrons in a covalent bond.
  

  
  

  Going down a group, the electronegativity value decreases. The effect of the
  increase in the nuclear charge is less than the increase in atomic radius and
  the shielding of the inner electrons.
  

  
  

  Important exceptions of the above rules include the noble gases,
  lanthanides and actinides. The noble gases possess a complete valence
  shell and do not usually attract electrons. The lanthanides and actinides
  possess more complicated chemistry that does not generally follow any
  trends. Therefore, noble gases, lanthanides, and actinides do not have
  electronegativity values.
  

  
  

  As for the transition metals, although they have electronegativity values,
  there is little variance among them across the period and up and down a
  group. This is because their metallic properties affect their ability to attract
  electrons as easily as the other elements.
  

  
  

  According to these two general trends, the most electronegative element is
  fluorine, with 3.98 Pauling units.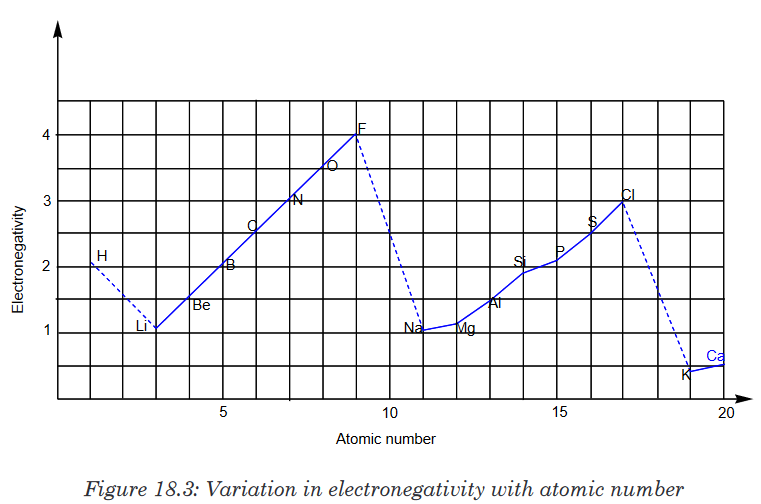

  

  
  

  18.6.3.Ionization energy (I.E)
  Ionisation energy is the minimum energy (in kJ/mol) required to remove one
  mole of electrons from one mole of gaseous atom in the ground state.
  

  
  

  In general, going across a period, the ionisation energy increases because
  the nuclear charge increases and hence electrons are more strongly attracted
  to the nucleus.
  

  
  

  In general, the second ionisation energy of an element is always greater than
  the first ionisation. This is explained as follows: every time you remove an
  electron from an atom, the remaining electrons are more strongly attracted
  by the nucleus and it requires more energy to remove other electrons from
  the atom.
  

  
  

  Hence: 1^st IE < 2^nd IE < 3^rd IE
  

  
  

  Ionisation energy of rare gases or any species with an octet electronic
  structure show very high IE because the electron is being removed from a
  very stable electronic structure.
  

  
  

  Down a group, the ionisation energy decreases because the electron which is
  removed is further from the nucleus. The nuclear charge also increases, but
  the extra inner electrons reduce the effect of the nuclear charge by shielding
  the outer electrons from the nucleus.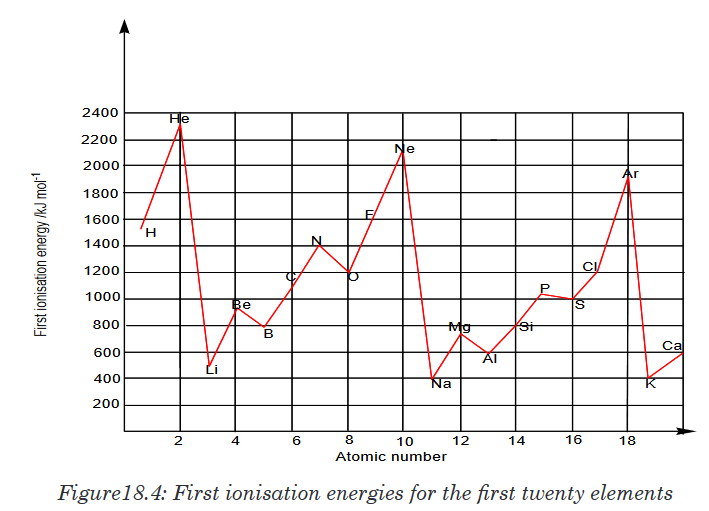

  
  

  

  18.6.4. Electron affinity
  As the name suggests, electron affinityis the ability of an atom to accept
  an electron. Unlike electronegativity, electron affinity is a quantitative
  measurement of the energy change that occurs when an electron is added
  to a neutral gas atom. The more negative the electron affinity value, the
  higher an atom’s affinity for electrons.
  

  
  

  That is the electron affinity (E.A.) is the energy change that occurs when an
  electron is added to a gaseous atom.
  

  
  

  It can be either positive or negative value. The greater the negative value,
  the more stable the anion is.
  

  
  

  The electron affinity is positive: X(g)+e⁻→X⁻+ Energy (Exothermic)
  

  
  

  The electron affinity is negative:X(g)+e⁻ + Energy → X⁻ (Endothermic)
  

  
  

  Electron affinity increases from left to right within a period. This is caused by
  the decrease in atomic radius. Moving from left to right across a period, atoms
  become smaller as the forces of attraction become stronger. This causes the
  electron to move closer to the nucleus, thus increasing the electron affinity
  from left to right across a period.
  

  
  

  Electron affinity decreases from top to bottom within a group. This is
  caused by the increase in atomic radius. With a larger distance between the
  negatively-charged electron and the positively-charged nucleus, the force of
  attraction is relatively weaker. Therefore, electron affinity decreases.

  
  

  18.6.5. The melting points and boiling points

  
  Trends can be a bit complicated due to significant structural change from
  one element to another in the same group.
  

  
  

  For groups 1 and 2, the melting and boiling points decrease down the
  group. As the atomic radius increases, the strength of the metallic bonding
  decreases.
  

  
  

  For groups 7/17(halogens) and 18/0(noble gases), the melting and boiling
  points increase down the group, as the molecule becomes bigger with more
  electrons, the Van der Waals forces increase.
  

  
  

  Across a period, melting and boiling points depend upon the structure and
  the bonding in the elements.

  

  Sodium, magnesium and aluminium are metals. The strength of the metallic
  bonding depends upon the number of delocalised electrons in the metal
  structure. The melting point increases from sodium to aluminium.
  

  
  

  Silicon exists as a giant covalent structure. Each silicon atom is covalently
  bonded to four other silicon atoms in a tetrahedral structure (similar to
  diamond). A great number of covalent bonds have to be broken to break up
  the giant structure.
  

  
  

  Phosphorus, sulphur and chlorine are all simple molecular species.
  Phosphorus consists of P₄ molecules; sulphur consists of S₈ molecules;
  chlorine consists of Cl₂ molecules. The strength of the Van der Waals forces
  increases as the size of the molecule increases.
  

  
  

  Argon exists as isolated atoms (it is monatomic) with weak van der Waals
  forces between atoms.
  

  
  

  The illustrations below show the variation of melting and boiling point for
  some elements of the periodic table (Figures 18.13 and 18.14).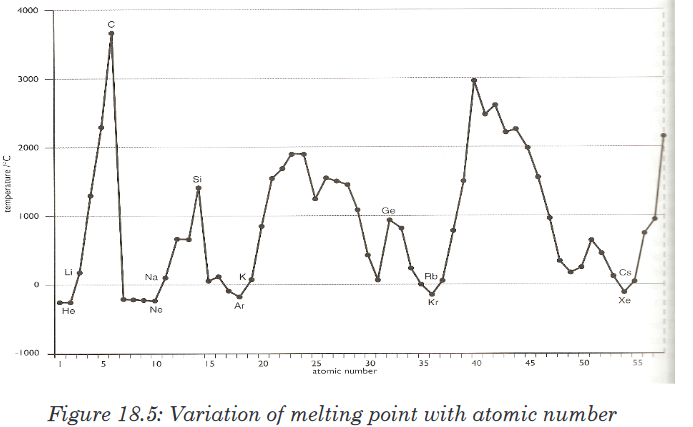

  

  

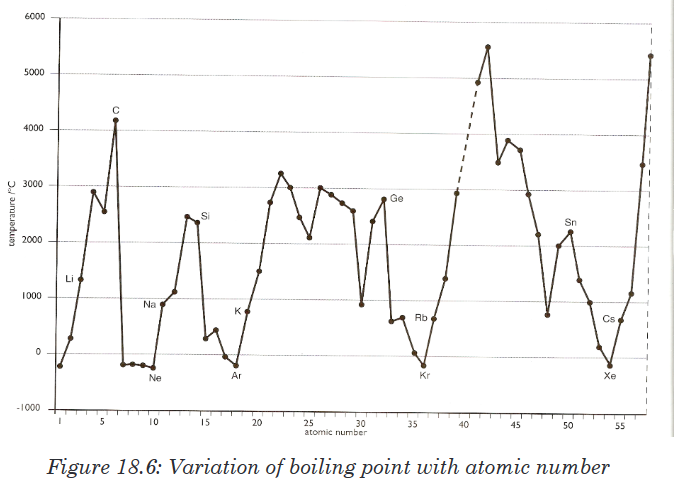  18.6.6. The density
  The density of a substance is its mass per unit volume, usually in g/cm3.
  The density is a basic physical property of a homogeneous substance; it
  is an intensive property, which means it depends only on the substance’s
  composition and does not vary with size or amount.
  

  
  

  The trends in density of elements can be observed in groups and periods
  of the periodic table. In general in any period of the table, the density first
  increases from group 1 to a maximum in the centre of the period because the

  mass increases while the size decreases, and then the density decreases
  again towards group 18 because of the nature of bonds.
  

  
  

  Going down a group gives an overall increase in density because even
  though the volume increases down the group, the mass increases more.
  

  
  

  The variation of density with atomic number is shown in the Figure 18.7.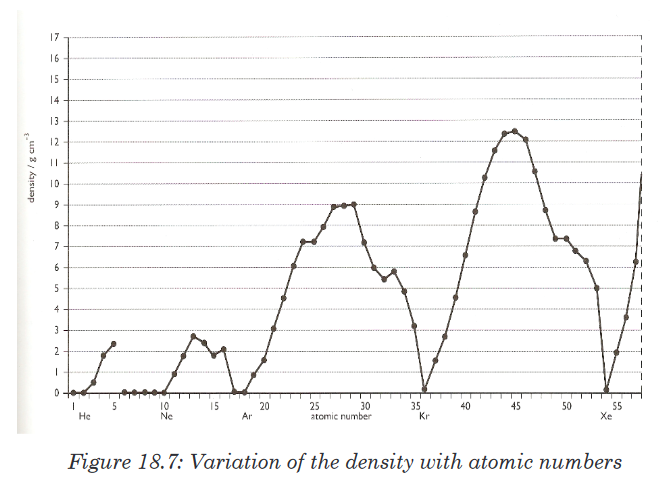

  

  18.6.7. Electrical and thermal conductivity
  The electrical conductivity is the ability of a substance to conduct an electric
  current.
  

  
  

  Across a period, the conductivity increases as the number of delocalised
  electrons increases and then decreases as the metallic character decreases
  because electrons
  

  
  

  within the covalent bonds are held much more tightly in these elements than
  in metals.
  

  
  

  Down a group, the conductivity increases. The delocalised electrons become
  less attracted by the nuclei.
  

  
  

  18.6.8. Electropositivity or Metallic character
  Electropositivity or Metallic character refers to the level of reactivity of a
  metal. Metals tend to lose electrons in chemical reactions, as indicated by
  their low ionization energies.
  

  
  

  Metals are located in the left and lower three-quarters of the periodic table,
  and tend to lose electrons to non-metals. Non-metals are located in the upper
  

  
  

  right quarter of the table, and tend to gain electrons from metal. Metalloids
  are located in the region between the other two classes and have properties.
  

  
  

  Metallic character is strongest for the elements in the leftmost part of the
  periodic table and tends to decrease as we move to the right of any period.
  

  
  

  Within any group of the representative elements, the metallic character
  increases progressively going down.
  

  
  

  Application activity 18.6
  1. Explain why:
  a) the atomic radius decreases across a period.
  b) electronegativity decreases down a group.
  c) Electron affinity increases across a period
  

  
  

  2. Describe and explain the trend in:
  a) Melting point
  b) metallic character
  i. Across a period       (ii) down the group
  

  
  

  3. Why is it always the case that the 2^nd ionisation energy is larger than
  the 1st I.E, the 3^rd larger than the second I.E and so on?
  

  
  

  4. In each of the following pairs, indicate which one of the two species is
  

  5. The first and second ionization energies of K are 419 kJ/mol and 3052
  kJ/mol, and those of Ca are590 kJ/mol and 1145 kJ/mol, respectively.
  Compare their values and comment on the differences
  

  
  

  Skills lab 18
  Consider an element with these properties and answer the questions that
  follow.
  

  
  

  • Reacts mildly with 6 M HCl.
  • Does not react with base or with water at room temperature.
  • Has a good electrical conductivity.
  • Is relatively cheap.

  
  

  1. What element has these properties?

  
  

  2. If this element undergoes combustion in air, write a balanced chemical
  equation for the reaction.
  

  
  

  3. How much energy would it take (in kJ) to melt 1 kg of this element?
  

  
  

  4. Plot a graph of the electrical conductivity for all elements in the group
  that includes this element. Is this element the best choice in its group
  for an electrical conductor? Explain.
  

  
  

  5. Would this element make a good copper replacement for wiring in a
  house? Explain why or why not.
  

  
  

  End unit assessment 18
  1. What were the limitations of Newland’s classification?
  2. The following are coded groups/families of the representative
  elements of the periodic table (first 4 periods, s, p blocks only). The
  groups are in number of particular order. Use the hints below to
  identify the group and place of three elements of each group in their
  correct location in the periodic table: AOU, BVW, CKM, DLQ, ENT,
  FIJ, GPY, and HRS.

  

  Hints
  A has only one electron in p subshell
  B is more electronegative than V
  C has a larger atomic radius than both M and W
  D has electronic configuration ending in p5
  E is one of the most reactive metals
  F has a smaller ionization energy than J
  G has only 1 energy level with any electrons
  H has one more proton than O and is in the same period as O

  I is the largest alkaline earth metal
  J has one more proton than E
  K has electron configuration ending in p3
  L has more filled energy levels than D
  M is larger than K
  N has the largest radius in its family
  O is smaller than F but in the same energy level as F
  P is smaller than Y
  Q is the most reactive non-metal
  R has the highest electronegativity in its family
  T has the lowest density in its family
  U more easily loses electrons (think about ionization energy) than
  either A or O
  V has only 4 electrons in a p-subshell
  W has 3 completely filled energy levels
  Y has the lowest ionization energy in its family.
  

  
  

  3. Justify the following statements:
  a) The first ionization energy of nitrogen is higher than that of oxygen
  even though nuclear charge of nitrogen is less compared to
  oxygen.
  b) Noble gases are having high ionization energies.
  

  
  

  4. Explain why:
  a) Alkali metals (group 1 elements) are not found free in nature.
  b) Atomic radius of gallium is smaller than that of aluminium.(Z of Al
  = 13, Z of Ga = 31)
  

  
  

  5. Arrange these elements in order of decreasing atomic size; sulphur,
  chlorine, aluminium and sodium. Does your arrangement demonstrate
  a group or a periodic trend?
  

  
  

  6. List these ions in order of increasing ionic radius: N^3-, Na⁺, F-, Mg²⁺, O^2-

  
  

  
  
• UNIT 19: COVALENT BOND AND MOLECULAR STRUCTURES

  

  As you can see from the picture above, Oxygen is the big buff creature
  with the tattoo of “O” on its arm. The little bunny represents a Hydrogen
  atom. The blue and red bow tied in the middle of the rope, pulled by the
  two creatures represents the shared pair of electrons, a single bond.

  Because the Hydrogen atom is weaker, the shared pair of electrons will be
  pulled closer to the Oxygen atom.
  

  1. Suggest the measure used in Chemistry to describe the strength
  dedicated to oxygen, the stronger.
  

  2. Suppose that the rope being pulled represents a single covalent bond.
  The electron contributed by hydrogen, the weaker, will be transferred
  to oxygen the stronger. If not, why?
  

  3. Suppose again that we have two oxygens. They have the same
  strengths. What will happen to the pulled rope, or the shared pair of
  electrons?
  

  4. Suggest a reason why, from the figure, one oxygen needed sharing
  with two hydrogens to form water.
  

  5. Conclude about the possible types of covalent bonds.
  

  19.1. Theories on the formation of covalent bond
  

  Activity 19.1
  1. Referring to the types of bonding already known, let us base on the
  electrovalent (ionic) bonding. Suppose that potassium metal and
  chlorine atom combine to form potassium chloride. Recall that each
  of those atoms engages in that bonding to get stability. How atoms
  in electrovalent bonding get the stability?
  

  2. In covalent bonding, the same purpose remains but each atom
  contributes the same number of electrons to share in bonding. This
  is achieved by atoms of equal or close electronegativities.
  

  a) Draw the diagram to show the outer Bohr energy level for each
  of the following: Hydrogen (Z = 1), chlorine (Z = 17), potassium
  (Z = 19) and nitrogen (Z = 7).
  

  b) Basing on the information given, construct the H2, Cl2 and NH3
  molecules by only showing the electrons on the outermost shell.
  Be informed that only the unpaired (single) electrons need to
  participate in the bonding. The paired ones are stable.
  

  The sharing of pair of electrons between two atoms is referred to as a
  covalent bond. Normally, each atom that is participating in the covalent
  bond formation, contributes equal number of electrons to form pair(s) of
  electrons. The pair of electrons shared between the atoms is also known as
  bond pair.

  The bond pair is strongly attracted by the nuclei of two atoms and thus by
  reducing the potential energy of them. This is the driving force of formation of
  covalent bond, which stabilizes the two atoms.
  

  If two atoms share only one bond pair, that bond is referred to as a single
  bond. If two bond pairs are shared, that is known as a double bond. Likewise,
  a triple bond is formed when the atoms share three bond pairs.
  

  A covalent bond is formed between two atoms when their electronegativity
  difference is less than 1.7 on Pauling’s scale. Usually it is formed between
  two non-metals. For example;
  

  • H₂ molecule: The electronegativity difference is zero.
  • Cl₂ molecule: The electronegativity difference is zero.
  • Hydrogen chloride (HCl): The electronegativity difference between
  them is 3.5 - 2.1 = 1.4.
  • Ammonia (NH₃): The electronegativity difference between them is
  3.0 - 2.1 = 0.9.
  • H₂O molecule: The electronegativity difference between them is
  3.5 - 2.1 = 1.4.
  

  To explain the formation of covalent bond, a simple qualitative model was
  developed by Gilbert Newton Lewis in 1916.
  

  According to this model:
  • Octet rule:The inert gas atoms with 8 electrons in their outer shell
  (also known as valence shell) are highly stable. The Helium atom with

  2 electrons in its outer shell is also stable.
  

  • Hence every atom tries to get nearest inert gas configuration by sharing
  electrons.
  • The bond formed due to sharing of electrons is otherwise known as a
  covalent bond.
  • Only the electrons in the valence shell are contributed for sharing.
  The inner electrons, which are also known as core electrons do not
  participate in the bond formation.
  • In the formation of covalent bond between two atoms, each atom
  contributes its valence electrons to form pair(s) of electrons, which in
  turn is/are shared by both of them.

  • Due to sharing of electrons, each atom gets nearest inert gas
  configuration.

  • Covalency: The number of electrons contributed by the atom of an
  element in the formation of covalent compound is known as covalency
  of that element.

  • In Lewis dot model, the electrons in the valence shell of the atom
  are shown as dots around it.

  19.1.1. Lewis structures using octet rule

  Lewis structures (also known as Dot and cross structures, Lewis dot diagrams,
  Lewis dot formulas, Lewis dot structures, and electron-dot structures) are
  diagrams that show the bonding between atoms of a molecule and the
  lone pairs of electrons that may exist in the molecule. A Lewis structure
  can be drawn for any covalently bonded molecule, as well as coordination
  compounds.
  

  The Lewis Structure was named after Gilbert Newton Lewis, who introduced
  it in his 1916 article “The Atom and the Molecule”.
  

  Lewis structures extend the concept of the electron dot diagram by adding
  lines between atoms to represent shared pairs in a chemical bond.
  

  Lewis structures show each atom and its position in the structure of the
  molecule using its chemical symbol. Lines are drawn between atoms that
  are bonded to one another (pairs of dots canbe used instead of lines).
  Excess electrons that form lone pairs are represented as pairs of dots, and
  are placed next to the atoms.

  How to draw Lewis Structures
  Let us use the nitrate ion (NO₃-) as a typical example. An outline of how to
  determine the “best” Lewis structure for NO₃- is given below:

  1. Determine the total number of valence electrons in a molecule.

  

  2. Draw a skeleton for the molecule which connects all atoms using
  only single bonds. In simple molecules, the atom with the most
  available sites for bonding is usually placed central. The number of
  bonding sites is determined by considering the number of valence
  electrons and the ability of an atom to expand its octet.

  As you become better, you will be able to recognize that certain groups
  of atoms prefer to bond together in a certain way!

  

  3. Of the 24 valence electrons in NO₃-, 6 were required to make the
  skeleton. Consider the remaining 18 electrons and place them so
  as to fill the octets of as many atoms as possible (start with
  the most electronegative atoms first then proceed to the more
  electropositive atoms).

  

  4. Are the octets of all the atoms filled? If not then fill the remaining
  octets by making multiple bonds (make a lone pair of electrons,
  located on a more electronegative atom, into a bonding pair of
  electrons that is shared with the atom that is electron deficient).

  

  5. Check that you have the lowest formal charges (F.C.) possible for
  all the atoms, without violating the octet rule; F.C. = (valence e-) - (1/2
  bonding e-) - (lone electrons).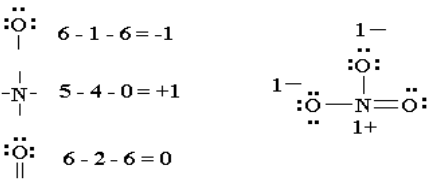

  

  6. Thus the Lewis structure of NO₃- ion can be written in the following
  ways: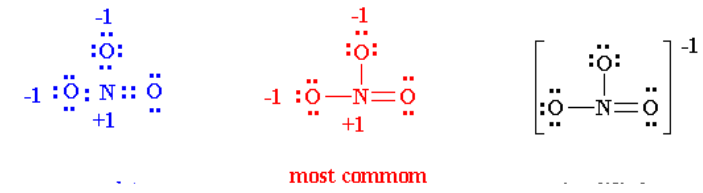

  

  19.1.2. Lewis structures of unusual compounds that do not obey
  Octet Rule
  

  There are three general ways in which the octet rule breaks down:
  • Molecules with an odd number of electrons
  • Molecules in which an atom has less than an octet
  • Molecules in which an atom has more than an octet
  

  1. Odd number of electrons
  Consider the example of the Lewis structure for the molecule nitrous oxide
  (NO):
  • Total electrons: 6 + 5 = 11
  • Bonding structure: 

  
  

  • Octet on “outer” element:

  

  • Remainder of electrons (11-8 = 3) on “central” atom:

  

  There are currently 5 valence electrons around the nitrogen. A double bond
  would place 7 around the nitrogen, and a triple bond would place 9 around
  the nitrogen. We appear unable to get an octet around each atom.
  

  2. Less than an octet (most often encountered with elements of Boron
  and Beryllium)
  

  Consider the example of the Lewis structure for boron trifluoride (BF₃):
  • Add electrons (3 x 7) + 3 = 24
  • Draw connectivities

  

  • Add octets to outer atoms:

  

  • Add extra electrons (24 – 24 = 0) to central atom:

  

  • Does central electron have octet? No, it has 6 electrons. Add a multiple
  bond (double bond) to see if central atom can achieve an octet:

  

  The central Boron now has an octet (there would be three resonance Lewis
  structures).
  

  However, in this structure with a double bond the fluorine atom is sharing
  extra electrons with the boron.
  

  The fluorine would have a positive ‘+’ partial charge, and the boron a
  negative ‘-’ partial charge, this is inconsistent with the electronegativities
  of fluorine and boron. Thus, the structure of BF₃ with single bonds, and 6
  valence electrons around the central boron is the most likely structure.
  

  BF₃ reacts strongly with compounds which have an unshared (lone) pair
  of electrons which can be used to form a bond with the boron. Example:
  Reaction of BF₃ with ammonia.

  

  
  3. More than an octet (most common example of exceptions to the
  Octet Rule)
  PCl₅ is a legitimate compound, whereas NCl₅ is not.

  

  Expanded valence shells are observed only for elements in period 3 (i.e.
  n=3) and beyond.
  

  The ‘octet’ rule is based upon available ns and np-orbitals for valence
  electrons (2 electrons in the s orbitals, and 6 in the p orbitals). Beginning
  with the n=3 principle quantum number, the d-orbitals become available
  (l=2).
  

  “The orbital diagram for the valence shell of phosphorous is:

  

  “Third period elements occasionally exceed the octet rule by using their
  empty d-orbitals to accommodate additional electrons.”
  

  Size is also an important consideration: “The larger the central atom, the larger
  the number of electrons which can surround it”. Expanded valence shells
  occur most often when the central atom is bonded to small electronegative
  atoms, such as F, Cl and O.
  

  Example: Draw the Lewis structure for ICl₄-
  • Count up the valence electrons: 7 + (4 x 7) + 1 = 36 electrons
  • Draw the connectivities:

  

  • Add octet of electrons to outer atoms:

  

  • Add extra electrons (36-32=4) to central atom:

  

  The ICl₄- ion thus has 12 valence electrons around the central Iodine (in the
  5d orbitals)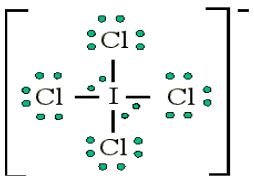

  

  Other examples include: PCl5 and SF6
  

  Application activity 19.1
  1. Make a clear definition of the covalent bond.
  2. For each of the following, write the electron configuration and
  choose one which violates the Octet Rule?

  

  19.2. Coordinate or dative covalent bond

  Activity 19.2

  
  The covalent bonding refers to the sharing of electrons to form a bond
  pair. There is a special type of covalence where the electrons shared are
  given by only one of the bonding atoms.
  

  This special type of covalent bonding is described to be “dative”.
  

  Formulate a succinct definition of the “dative covalent bond”.
  

  A dative covalent bond, or coordinate bond is a type of covalent bonding
  (i.e., electron sharing) where the shared electron pair(s) are completely
  provided by one of the participants in the union, and not by contributions
  from the two of them.
  

  The contributors of these shared electrons are either neutral molecules
  which contain lone pair(s) of electrons on one of their atoms, or negatively
  charged groups (radicals) with free electrons to donate. Examples of these
  are: H₂O, NH₃ and CN⁻.
  

  Examples of coordinate bonding:
  In the reaction between ammonia and hydrogen chloride a coordinate bond
  takes place forming solid ammonium chloride.
                                 NH₃ + HCl → NH₄Cl
  In this reaction the hydrogen ion from the hydrogen chloride leaves its
  electrons and gets transferred to the lone pair of electrons on the ammonia
  molecule forming ammonium ions (NH₄+). This is known as a coordinate
  bonding.
  

  Seeing that the hydrogen has left its electrons, the chloride will therefore
  have a negative charge while the ammonium will have a positive charge.
  The diagram below shows the reaction: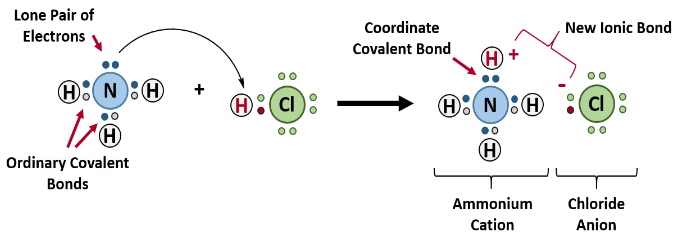

  

  Figure 19.2: Reaction of ammonia with hydrogen chloride
  

  Note: The complete compounds eventually formed comprises of the three
  types of bonding, i.e., covalent, co-ordinate and electrovalent. In NH₄Cl:
  Formation of NH3 (covalency); formation of NH₄+ (co-ordinate or dative
  bonding); and formation of NH₄Cl (electrovalency).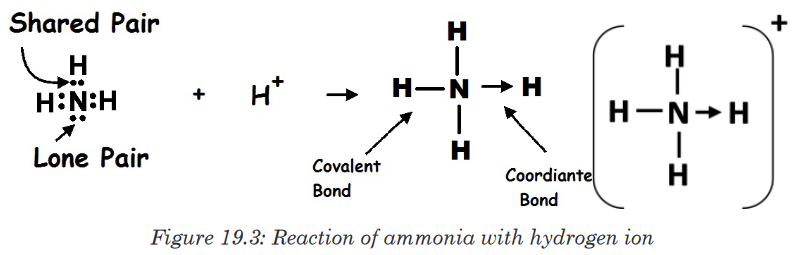

  

  Dative covalent bonds are represented on drawings as an “arrow”, which
  usually points from the atom donating the lone pair to the atom accepting it.
  

  Another example would be the reaction between ammonia and boron
  trifluoride. Boron trifluoride is said to be electron deficient meaning it has
  3 pairs of electrons at its bonding level but it is capable of having four pairs.
  In this reaction the ammonia is used to supply this extra lone pair.
  

  A coordinate bond is formed where the lone pair from the nitrogen moves
  toward the boron. The end containing the nitrogen will therefore become
  more positive while the boron end will become more negative because it has
  received electrons.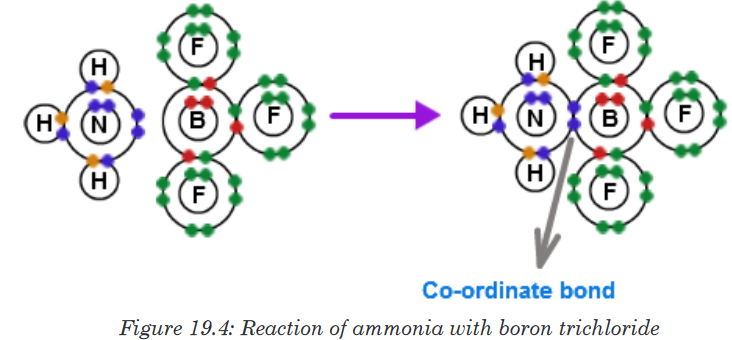

  

  Application activity 19.2
  1. Give the difference and the similarity between a dative covalent
  bond and the normal covalent bond.

  2. An aluminium chloride molecule reacts with a chloride ion to form
  the AlCl₄− ion.

  a) Name the type of bond formed in this reaction.
  b) Explain how this type of bond is formed in the AlCl₄− ion.

  3. Co-ordinate bonding can be described as dative covalency.
  a) In this context, what is the meaning of each of the terms covalency
  and dative?
  b) Write an equation for a reaction in which a co-ordinate bond is
  formed.
  

  19.3. Overlap of atomic orbitals to form covalent bonds

  Activity 19.3

  
  There are different theories describing the formation of a covalent bond.
  For your own, basing on the knowledge of the composition of the atom,
  formulate a paragraph which describe how two neutral atoms can be
  bound together to form a covalent bond (Include the way there will be
  attracted or repelled and what make them to remain together)
  

  Covalent bonding occurs when atoms share electrons (Lewis Model),
  concentrating electron density between nuclei. The build-up of electron
  density between two nuclei occurs when a valence atomic orbital of one
  atom merges with that of another atom (Valence Bond Theory).
  

  The orbitals share a region of space, i.e. they overlap. The overlap of orbitals
  allows two electrons of opposite spin to share the common space between
  the nuclei, forming a covalent bond.
  

  The simplest case to consider is the hydrogen molecule, H2. When we say
  that the two electrons from each of the hydrogen atoms are shared to form
  a covalent bond between the two atoms, what we mean in Valence Bond
  Theory terms is that the two spherical 1s orbitals overlap, allowing the two
  electrons to form a pair within the two overlapping orbitals.

  

  These two electrons are now attracted to the positive charge of both of the
  hydrogen nuclei, with the result that they serve as a sort of “chemical glue”
  holding the two nuclei together.
  

  How far apart are the two nuclei? That is a very important issue to consider.
  • If they are too far apart, their respective 1s-orbitals cannot overlap,
  and thus no covalent bond can form - they are still just two separate
  hydrogen atoms.
  

  • As they move closer and closer together, orbital overlap begins to
  occur, and a bond begins to form. This lowers the potential energy of the
  system, as new, attractive positive-negative electrostatic interactions
  become possible between the nucleus of one atom and the electron
  of the second. However, something else is happening at the same
  time: as the atoms get closer, the repulsive positive-positive interaction
  between the two nuclei also begins to increase.
  

  • When the two nuclei are‘too close’, we have a very unstable, high-
  energy situation.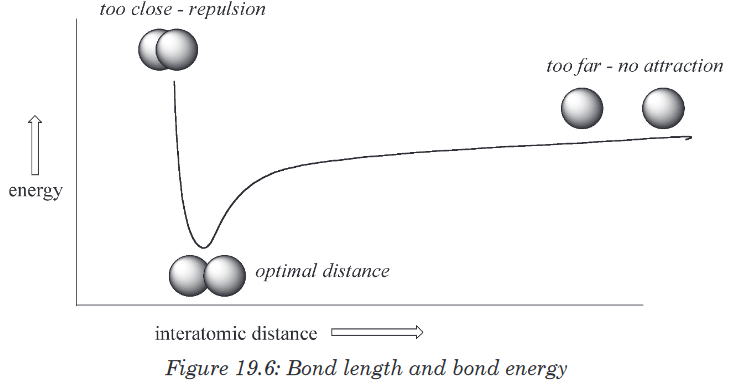

  

  There is a defined optimal distance between the nuclei in which the potential
  energy is at a minimum, meaning that the combined attractive and repulsive
  forces add up to the greatest overall attractive force. This optimal inter-
  nuclear distance is the bond length. For the H2 molecule, this distance is
  74x10^-12 meters, or 0.74 Å (Å means angstrom, or 10^-10 meters).

  Likewise, the difference in potential energy between the lowest state (at
  the optimal inter-nuclear distance) and the state where the two atoms are
  completely separated is called the bond energy. For the hydrogen molecule,
  this energy is equal to about 104 kcal/mol.
  

  Every covalent bond in a given molecule has a characteristic length and
  strength. Most covalent bonds in organic molecules range in strength from
  just under 100 kcal/mol (for a carbon-hydrogen bond in ethane, for example)
  up to nearly 200 kcal/mol.
  

  Application activity 19.3
  1. Explain the following terms:
  a) Bond length
  b) Bond energy
  2. Account for the Valence Bond Theory.
  3. Describe how the Lewis and Valence Bond Theories complement
  each other in explaining the formation of a covalent bond.
  

  19.4. The concept of valence bond theory and formation of
  (σ) and (π) bonds
  
  

  Activity 19.4
  

  1. Recall and draw the shapes of s-orbital and p-orbital.
  2. Using drawing, try to show different possible combinations of those
  orbitals overlapping.
  

  Earlier we saw that covalent bonding requires the sharing of electrons
  between two atoms, so that each atom can complete its valence shell. But
  how does this sharing process occur? Remember that we can only estimate
  the likelihood of finding an electron in a certain area as a probability. In
  chemistry, valence bond (VB) theory is one of two basic theories—along
  with molecular orbital (MO) theory—that use quantum mechanics to explain
  chemical bonding.
  

  According to this theory, a covalent bond is formed when two orbitals overlap
  (share the same space) to produce a new combined orbital containing two
  electrons of opposite spin.

  The valence bond theory was proposed by Heitler and London to explain
  the formation of covalent bond quantitatively using Quantum Mechanics.
  Later on, Linus Pauling improved this theory by introducing the concept of
  hybridization.
  

  The main postulates of this theory are as follows:
  

  • A covalent bond is formed by the overlapping of two half filled valence
  atomic orbitals of two different atoms.
  • The electrons in the overlapping orbitals get paired and confined
  between the nuclei of two atoms.
  • The electron density between two bonded atoms increases due to
  overlapping. This confers stability to the molecule.
  • Greater the extent of overlapping, stronger is the bond formed.
  • The direction of the covalent bond is along the region of overlapping of
  the atomic orbitals i.e., covalent bond is directional.
  • There are two types of covalent bonds based on the pattern of
  overlapping as follows:
  

  i. σ-bond: The covalent bond formed due to overlapping of atomic
  orbital along the inter nucleus axis is called σ-bond. It is a stronger
  bond and cylindrically symmetrical. Depending on the types of
  orbitals overlapping, the σ-bond is divided into following types:
  σ_s-s bond

  ii. π-bond: The covalent bond formed by sidewise overlapping of
  atomic orbitals is called π- bond. In this bond, the electron density
  is present above and below the inter-nuclear axis. It is relatively a
  weaker bond since the electrons are not strongly attracted by the
  nuclei of bonding atoms.
  

  
  

  Note: The ‘s’ orbitals can only form σ-bonds, whereas the p, d& f orbitals can
  form both σ and π-bonds.

  Examples:Formation of covalent bonds in oxygen and hydrogen chloride
  molecules.
  1. O₂ molecule:
  • The electronic configuration of O in the ground state is
  

  
  

  • The half filled 2p_y orbitals of two oxygen atoms overlap along the
  inter-nuclear axis and form σ_p-p bond.
  • The remaining half filled 2p_z orbitals overlap laterally to form a π_p-p
  bond.
  • Thus a double bond (one σ_p-p and one π_p-p) is formed between two
  oxygen atoms.
  

  
  

  
  

  • The half filled 1s orbital of hydrogen overlap with the half filled 3p_z
  atomic orbital of chlorine atom along the inter-nuclear axis to form a
  σ_s-p bond.
  

  
  

  Need for modification of valence bond theory
  The old version of Valence Bond Theory is limited to diatomic (like N2) and
  binary (like HCl) molecules only. It could not explain the structures and bond
  angles of molecules with more than three atoms. For example: It could not
  explain the structures and bond angles of H₂O, NH₃ etc.
  

  However, in order to explain the structures and bond angles of these
  molecules, Linus Pauling modified the Valence Bond Theory using
  hybridization concept.
  

  Note: Both types of overlapping orbitals can be related to bond order.
  • Single bonds have one sigma bond,
  • Double bonds consist of one σ and one π-bond,
  • Triple bonds contain one σ and two π-bonds.
  

  Application activity 19.4
  1. In chemistry, valence bond (VB) theory is one of two basic theories—
  along with molecular orbital (MO) theory—that use quantum
  mechanics to explain chemical bonding. In one sentence, describe
  how the covalent bond is formed, according to this theory.
  

  2. Explain why the Valence Bond Theory needed to be modified.
  

  3. Describe the types of covalent bond basing on the pattern of
  overlapping.
  

  19.5. Hybridisation and its types

  Activity 19.5

  Just as animals can be cross bred to form hybrids (having the
  characteristics of each of the intermixed animal), atomic orbitals also can
  be intermixed. Make a research to formulate a definition of hybridization
  and state the common types of hybridization of the atomic orbitals.
  

  19.5.1. Definition of hybridisation
  The concept hybridization involves the “cross breeding” of atomic orbitals
  to create “new” orbitals. Hence the use of the term “hybrid”: Think of a
  hybrid animal which is a cross breed of two species.
  

  Hybridization is the process of “intermixing of atomic orbitals of nearly same
  energies to form same number of identical and degenerate (having equivalent
  energies) new type of orbitals”. Orbitals which are formed in hybridization
  process are called hybrid orbitals.
  

  During hybridization, the atomic orbitals with different characteristics are
  mixed with each other. Hence there is no meaning of hybridization between
  same type of orbitals i.e., mixing of two ‘s’ orbitals or two ‘p’ orbitals is not
  called hybridization. However orbital of ‘s’ type can mix with the orbitals of
  ‘p’ type or of ‘d’ type.
  

  Keep in mind that only the orbitals of nearer energy values can participate in
  the hybridization. Based on the type and number of orbitals, the hybridization
  can be subdivided into following types.
  

  19.5.2. Types of hybridization

  1. sp-Hybridization
  Intermixing of one ‘s’ and one ‘p’ orbitals of almost equal energy to give two
  identical and degenerate hybrid orbitals is called ‘sp’ hybridization.
  These two sp-hybrid orbitals are arranged linearly at by making 180o of
  angle.
  They possess 50% ‘s’ and 50% ‘p’ character.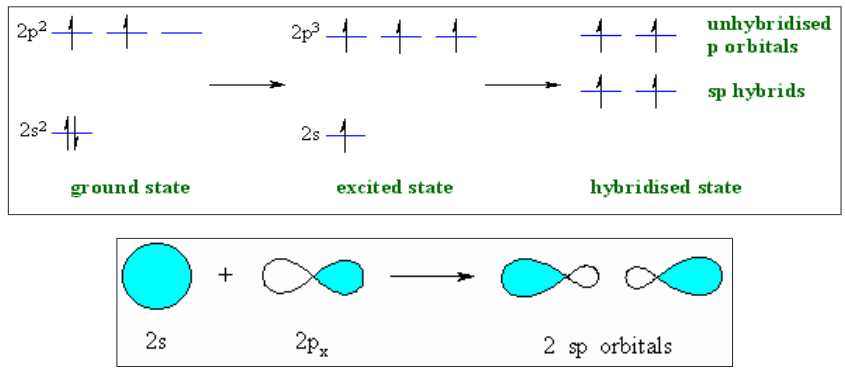
  

  
  

  2. sp²-Hybridization
  Intermixing of one ‘s’ and two ‘p’ orbitals of almost equal energy to give
  three identical and degenerate hybrid orbitals is known as sp² hybridization.
  The three sp2 hybrid orbitals are oriented in trigonal planar symmetry at
  angles of 120^o to each other.

  The sp² hybrid orbitals have 33.3% ‘s’ character and 66.6% ‘p’ character.
  

  
  

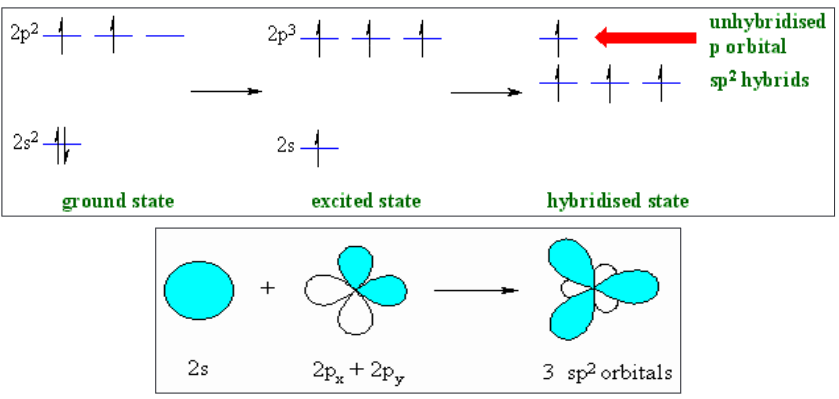
  3. sp³-Hybridization
  In sp³ hybridization, one ‘s’ and three ‘p’ orbitals of almost equal energy
  intermix to give four identical and degenerate hybrid orbitals.
  

  These four sp³ hybrid orbitals are oriented in tetrahedral symmetry with
  109^o28’ angle with each other.
  

  The sp³ hybrid orbitals have 25% ‘s’ character and 75% ‘p’ character.
  

  
  

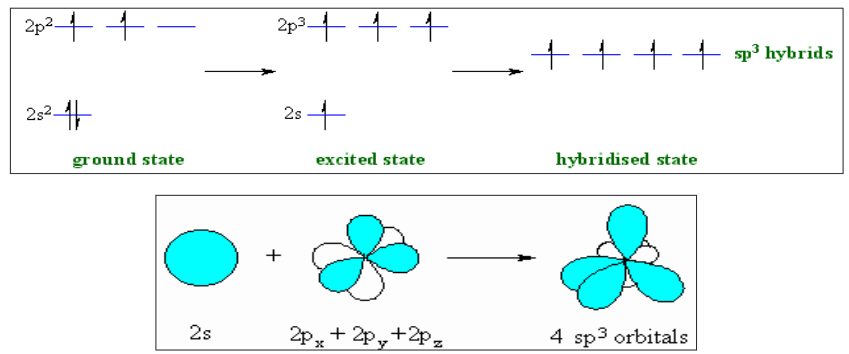
  4. sp³d-Hybridization
  In sp³d hybridization, one ‘s’, three ‘p’ and one ‘d’ orbitals of almost equal
  energy intermix to give five identical and degenerate hybrid orbitals, which
  are arranged in trigonal bipyramidal symmetry.
  

  Among them, three are arranged in trigonal plane and the remaining two
  orbitals are present above and below the trigonal plane at right angles.
  

  The five sp³d hybrid orbitals have 20% ‘s’, 60% ‘p’ and 20% ‘d’ characters.
  

  
  

  5. sp³d²-Hybridization
  Intermixing of one ‘s’, three ‘p’ and two ‘d’ orbitals of almost same
  energy by giving six identical and degenerate hybrid orbitals is called
  sp³d² hybridization.
  

  These six sp³d² orbitals are arranged in octahedral symmetry by making 90o
  angles to each other. This arrangement can be visualized as four orbitals
  arranged in a square plane and the remaining two are oriented above and
  below this plane perpendicularly.
  

  
  

  Conditions for the hybridization
  • Orbitals of same element should take part in the hybridization.
  • There should be minimum difference between the orbitals undergoing
  hybridization.
  

  Characteristics of Hybridization
  • During hybridization the number of hybrid orbitals formed is equal to
  the number of atomic orbitals involved in hybridization.
  • Hybrid orbitals form more stable and stronger bonds than pure atomic
  orbitals.
  • Hybridization does not take place in isolated atoms and possible in
  those atoms which are prior to participate in chemical bonding.
  

  Application activity 19.5
  1. What is meant by hybridization?
  2. Use a table to state five types of the common types of hybridization
  and for each; give the name of the shape and bond angles they
  present.
  

  19.6. VSEPR theory

  Activity 19.6

  Find out the ball and stick molecular models in the laboratory and try to
  construct the following molecules: H₂O, HCl, CH₄, CO₂ and NH₃
  • For each of the molecule constructed, try to draw it in your exercise
  book as it appears.
  

  
  

  In order to predictthe geometry of molecules, Nyholm and Gillespie
  developed a qualitative model known as Valence Shell Electron Pair
  Repulsion Theory (VSEPR Theory). The basic assumptions of this theory
  are summarized below.
  

  1. The electron pairs in the valence shell around the central atom of a
  molecule repel each other and tend to orient in space so as to minimize
  the repulsions and maximize the distance between them.
  

  2. There are two types of valence shell electron pairs namely, (i) Bond
  pairs and (ii) Lone pairs.
  

  • Bond pairs are shared by two atoms and are attracted by two nuclei.
  Hence they occupy less space and cause less repulsion. It is also
  called “sharing pair”.
  

  • Lone pairs are not involved in bond formation and are in attraction with
  only one nucleus. Hence they occupy more space. As a result, the lone
  pairs cause more repulsion.
  The order of repulsion between different types of electron pairs is as
  follows:
  

  Lone pair - Lone pair > Lone Pair - Bond pair > Bond pair - Bond pair
  

  Note: The bond pairs are usually represented by a solid line, whereas
  

               the lone pairs are represented by a lobe with two electrons.
  3. In VSEPR theory, the multiple bonds are treated as if they were single
  bonds. The electron pairs in multiple bonds are treated collectively
  as a single super pair. The repulsion caused by bonds increases with
  increase in the number of bonded pairs between two atoms i.e., a triple
  bond causes more repulsion than a double bond which in turn causes
  more repulsion than a single bond.
  

  4. The shape of a molecule can be predicted from the number and type
  of valence shell electron pairs around the central atom. When the
  valence shell of central atom contains only bond pairs, the molecule
  assumes symmetrical geometry due to even repulsions between them.
  However the symmetry is distorted when there are also lone pairs along
  with bond pairs due to uneven repulsion forces.
  

  5. Primary & Secondary effects on bond angle and shape:
  

  i. The bond angle decreases due to the presence of lone pairs, which
  cause more repulsion on the bond pairs and as a result the bond
  pairs tend to come closer.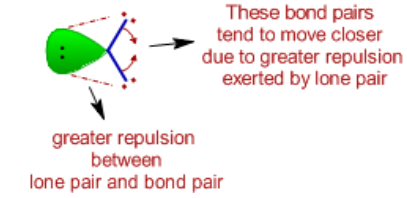
  

  
  

  ii. The repulsion between electron pairs increases with increase
  in electronegativity of central atom and hence the bond angle
  increases. The bond pairs are closer and thus by shortening the
  distance between them, which in turn increases the repulsion. Hence
  the bonds tend to move away from each other.
  

  
  

  However the bond angle decreases when the electronegativities of
  ligand atoms are more than that of central atom. There is increase
  in the distance between bond pairs since they are now closer to
  ligand atoms. Due to this, they tend to move closer resulting in the
  decrease in bond angle.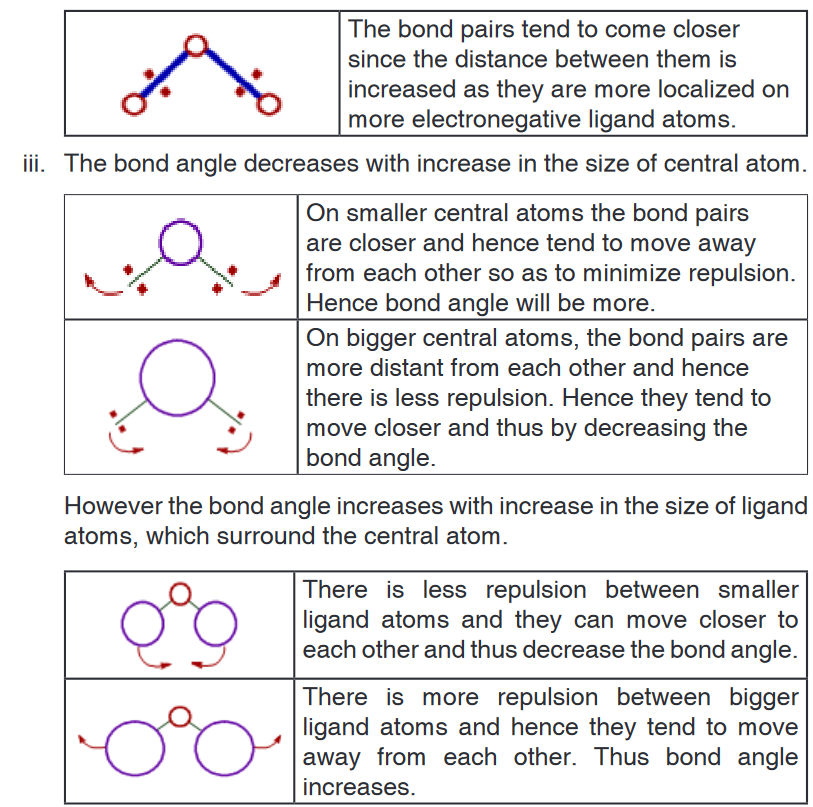
  

  
  

  iv. The bond angles are also changed when multiple bonds are present.
  It is due to uneven repulsions.
  

  6. When there are two or more resonance structures, the VSEPR theory is
  applicable to any of such contributing structure.
  

  The shape of molecule and also the approximate bond angles can be
  predicted from the number and type of electron pairs in the valence shell of
  central atom as tabulated below.
  

  In the following table the molecule is represented by “AXE” notation, where
  A = Central atom
  X = Ligand atom bonded to the central atom either by a single bond or
  by multiple bond; indicating a bond pair.
  E = Lone pai
  

  Note:
  • The sum of number of ligand atoms (X) and number of lone pairs (E) is
  also known as steric number.
  • The bond pairs are shown as green colored thick lines, whereas the
  lone pairs are shown as point charges using green colored lobes.
  

  
  

  
  

  
  

  
  

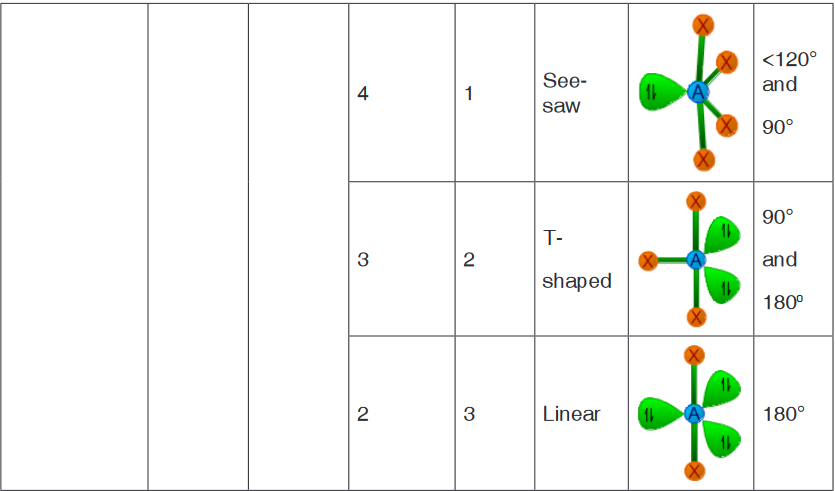
  Determination of shape of a molecule
  • The first step in determination of shape of a molecule is to write the
  Lewis dot structure of the molecule.
  

  • Then find out the number of bond pairs and lone pairs in the valence
  shell of central atom.
  

  • While counting the number of bond pairs, treat multiple bonds as if
  they were single bonds. Thus electron pairs in multiple bonds are to be
  treated collectively as a single super pair.
  

  • Use the above table to predict the shape of molecule based on steric
  number and the number of bond pairs and lone pairs.
  

  The following table shows some examples for each type of shapes:
  

  
  

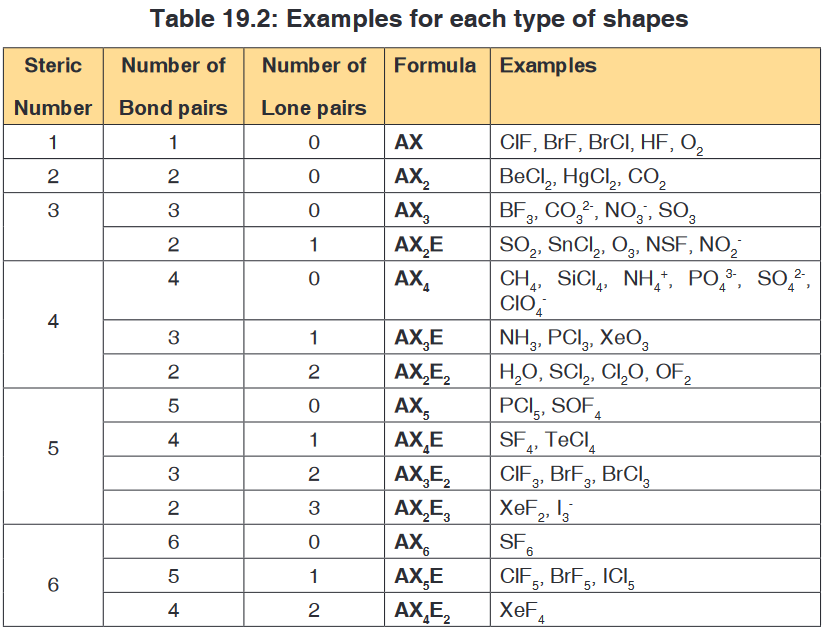
  Worked examples
  1. Methane (CH₄)
  • The Lewis structure of methane molecule is:
  

  
  

  • There are 4 bond pairs around the central carbon atom in its valence
  shell. Hence it has tetrahedral shape with 109^o28’ of bond angles.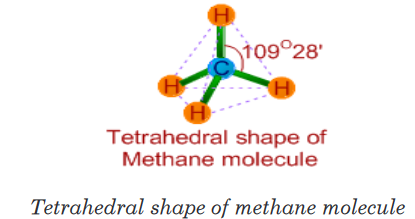
  

  
  

  2. Ammonia (PCl₃)
  • The Lewis structure of ammonia indicates there are three bond pairs
  and one lone pair around the central nitrogen atom.
  

  
  

  • Since the steric number is 4, its structure is based on tetrahedral
  geometry. However, its shape is pyramidal with a lone pair on nitrogen
  atom.

  • The bond angle is decreased from 109^o28’ to 107^o48’ due to repulsion
  caused by lone pair on the bond pairs.
  

  
  

  3. Water (H₂O)
  • It is evident from the Lewis structure of water molecule; there are two
  bond pairs and two lone pairs in the valence shell of oxygen. Hence
  its structure is based on tetrahedral geometry. However its shape is
  angular with two lone pairs on oxygen.
  

  
  

  • The bond angle is decreased to 104o28’ due to repulsions caused by
  lone pairs on bond pairs. It can be noted that the bond angle decreases
  with increase in the number of lone pairs on the central atom.
  

  4. Formaldehyde (HCHO)
  There are three bond pairs around the central carbon atom. The double
  bond between C and O is considered as a single super pair. Hence the
  shape of the molecule is trigonal planar and the bond angles are expected
  to be equal to 120^o.
  

  However, the C=O exerts more repulsion on the C-H bond pairs. Hence the
  <H-C-H bond angle will be less than 120o and the <H-C-O is greater than
  120^o.
  

  
  

  Application activity 19.6
  1. There are two types of valence shell electron pairs such as Bond
  pairs and Lone pairs.
  a) State and explain these electron pairs.
  b) Show the increasing order of repulsion between different types
  of electron pairs.
  

  2. Questions about covalent bonding.
  a) Sketch the shapes of each of the following molecules, showing
  any lone pairs of electrons. In each case, state the bond angle(s)
  present in the molecule and name the shape.
  

  
  

  b) State the types of intermolecular force which exist, in the liquid
  state, between pairs of BF₃ molecules and between pairs of NF₃
  molecules.
  c) Name the type of bond which you would expect to be formed
  between a molecule of BF₃ and a molecule of NF₃. Explain how
  this bond is able to form.
  

  3. The following diagram shows a hydrogen peroxide molecule.
  

  
  

  a) On the diagram above, draw the lone pairs, in appropriate positions,
  on the oxygen atoms.
  

  b) Indicate, on the diagram, the magnitude of one of the bond angles.
  

  c) When considering electron pair repulsions in molecules, why does a
  lone pair of electrons repel more strongly than a bonding pair?
  

  4. Phosphorus and nitrogen are in Group V of the Periodic Table and both
  elements form hydrides. Phosphine, PH₃, reacts to form phosphonium
  ions, , in a similar way to that by which ammonia, NH₃, forms ammonium
  ions,
  

  a) Give the name of the type of bond formed when phosphine reacts
  with an H+ion. Explain how this bond is formed.
  

  b) Draw the shapes, including any lone pairs of electrons, of a phosphine
  molecule and of a phosphonium ion. Give the name of the shape
  of the phosphine molecule and state the bond angle found in the
  phosphonium ion.
  

  5. The shape of the molecule BCl₃ and that of the unstable molecule CCl₂
  are shown below.
  

  
  

  a) Why is each bond angle exactly 120° in BCl₃?
  b) Predict the bond angle in CCl2 and explain why this angle is different
  from that in BCl₃
  c) Give the name which describes the shape of molecules having bond
  angles of 109° 28’.
  Give an example of one such molecule.
  6. The shape of the XeF₄ molecule is shown below.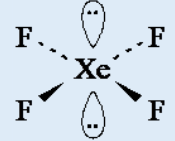
  

  
  

  a) State the bond angle in XeF₄
  

  b) Suggest why the lone pairs of electrons are opposite each other in
  this molecule.
  

  c) Name the shape of this molecule, given that the shape describes
  the positions of the Xe and F atoms only.
  

  7. Copy and complete the following table:
  

  
  

  8. Boron, nitrogen and oxygen form fluorides with molecular formulae
  BF₃,NF3 and OF₂

  a) Draw the shape of each molecule showing the position of lone pairs
  if any.
  

  b) Give the bond angle in each case, explaining your reasons.
  

  19.7. Polarity of the covalent bond in relation to difference
              in electronegativity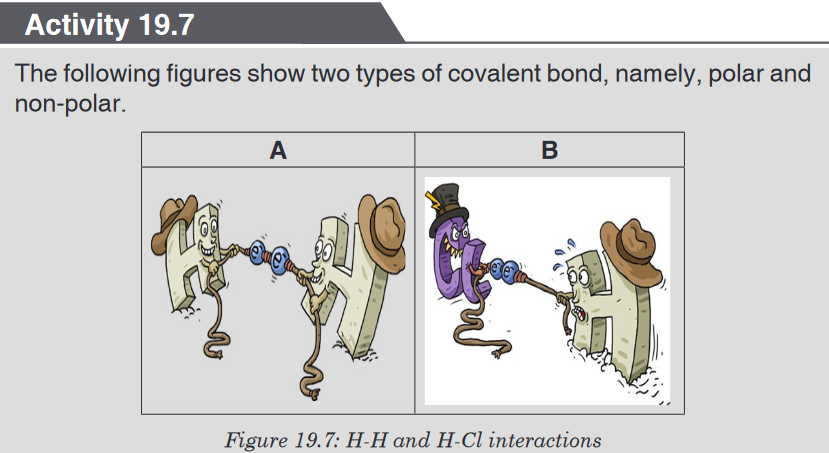
  

  
  

  1. Covalent bond is formed between two atoms with similar or close
  ability to attract electrons towards themselves, and this is the reason
  why they share electrons without being transferred.
  

  a) What is the name of the measure used to compare that ability?
  

  b) When the strengths of both atoms are equal, the covalent bond
  will be non-polar. Is figure A represents the polar or non-polar
  bond? Why?
  

  c) Look at the figure B. The atom, in the zone with more electrons,
  will have a partial negative charge. In which zone can we label the
  partial negative charges?
  

  2. Experiment to study the behaviour of water on the charged species.
  • Fill a burette with water.
  • Open the tap and bring a charged ebonite rod close to the stream of
  water running from the jet.
  • Observe the direction of water and using a drawing, note the change,
  if there is any.
  

  A quantity termed ‘electronegativity’ is used to determine the polarity of
  the covalent bond; whether a given bond will be non-polar covalent, polar
  covalent, or ionic.
  

  Electronegativity is defined as the ability of an atom in a particular molecule to
  attract electrons to itself (the greater the value, the greater the attractiveness
  for electrons).
  

  Fluorine is the most electronegative element (electronegativity = 4.0), the
  least electronegative is Caesium (electronegativity = 0.7).
  

  The bond pair is equally shared in between two atoms when the
  electronegativity difference between them is zero or nearer to zero. In this
  case, neither of the atoms gets excess of electron density and hence carry no
  charge. This is called non-polar covalent bond.
  

  However, when there is a considerable difference in the electronegativity,
  the bond pair is no longer shared equally between the atoms. It is shifted
  slightly towards the atom with higher electronegativity by creating partial
  negative charge (represented by δ-) over it, whereas, the atom with less
  electronegativity gets partial positive charge (represented by δ+). This type
  of bond is also referred to as polar covalent bond.
  

  We can use the difference in electronegativitybetween two atoms to gauge
  the polarity of the bonding between them.
  

  In F₂ the electrons areshared equally between the atoms, the bond is non-
  polar covalent.
  

  In HF the fluorine atom has greater electronegativity than the hydrogen
  atom. The sharing of electrons in HF is unequal: the fluorine atom attracts
  electron density away from the hydrogen (the bond is thus a polar covalent
  bond). The H-F bond can thus be represented as: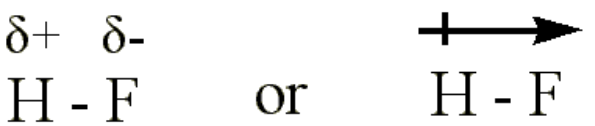
  

  
  

  The ‘⁺’ and ‘^-’ symbols indicate partial positive and negative charge
  respectively.
  

  The arrow indicates the “pull” of electrons off the hydrogen and towards the
  more electronegative atom, fluorine.
  

  In LiF the much greater relative electronegativity of the fluorine atom
  completely strips the electron from the lithium and the result is an ionic bond
  (no sharing of the electron).
  

  Note:The following is the general thumb rule for predicting the type of bond
  based upon electronegativity differences:
  • If the electronegativities are equal (i.e. if the electronegativity difference
  is 0), the bond is non-polar covalent.
  

  • If the difference in electronegativities between the two atoms is greater
  than 0, but less than 2.0, the bond is polar covalent.
  

  • If the difference in electronegativities between the two atoms is 2.0, or
  greater, the bond is ionic.
  

  Using the examples used above, we can predict the type of bond as follows:
  

  
  

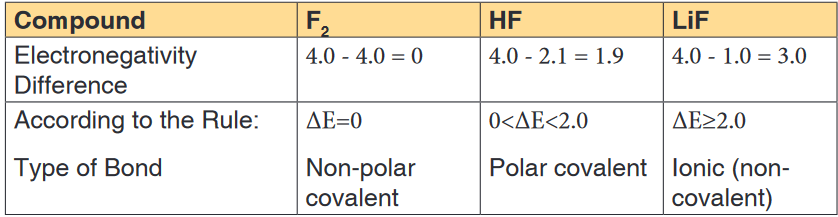
  Note: A non-polar molecule is one in which the electrons are distributed
  more symmetrically and thus does not have an abundance of charges at
  the opposite sides. The charges all cancel out each other. Examples of non-
  polar molecules include diatomic molecules, CH4, CO2, C2H4, cyclohexene,
  CCl4, etc.
  

  Application activity 19.7

  1. State what is meant by the term polar bond.
  

  2. Sulphuric acid is a liquid that can be represented by the formula
  drawn below.
  

  3. The two substances CS2 and HCN have linear molecules but CS2
  molecules are non-polar while HCN molecules are polar; explain why
  these molecules have different polarities. Support your explanation
  with appropriate diagrams.
  

  4. A negatively charged rod was brought near a jet of water running
  out from a burette. The jet of water was deflected as shown:
  

  
  

  a) With reference to the structure of water, explain why the jet of
  water was deflected.

  b) State the effect on the jet of water if the negatively charged rod is
  replaced by a positively charged rod. Explain your answer.

  c) If hexane is used instead of water and a negatively charged rod
  is brought near the liquid jet, would the liquid jet be deflected?
  Explain your answer.
  

  19.8. Physical properties of covalent structures
  

  Activity 19.8
  
  

  1. You are provided with the following chemical compounds: PH3,
  CO₂, H₂O and SiO₂, Cl₂, Br₂ and I₂ and graphite.
  a) Classify them into solid, liquid and gas.
  b) What type of bond which held together atoms in the given
  compounds they have in common?
  c) Deduce from (b) the name describing all those compounds.
  

  d) Some of them have very high melting points. Suggest the reason
  for this.
  

  2. State some points that you know about diamond.
  Covalent bonds involve the sharing of electrons so that all atoms have “full
  outer shells”. Sometimes in a Covalent Bond, both shared electrons come
  from the same atom. This is known as a Dative Covalent Bond. This often
  results in the formation of charged molecules.
  Covalently bonded substances fall into two main types:
  • Simple molecular structures
  • Giant covalent structures.
  

  19.8.1. Simple molecular structures
  Substances composed of relatively small covalently bonded structures are
  called Simple Molecular Structures. These contain only a few atoms held
  together by strong covalent bonds and can be further categorised into two
  types: Individual (which are usually gases like carbon dioxide) and molecular
  (which are usually solids like iodine).
  

  The physical properties
  
  

  1. Low melting and boiling points
  Simple Molecular Structures tend to have low melting and boiling points
  since the forces between molecules (intermolecular forces, which are van
  der Waals forces) are quite weak. Little energy is required to separate
  the molecules.
  

  2. Poor electrical conductivity
  There are no charged particles (ions or electrons) delocalized throughout
  the molecular crystal lattice to conduct electricity. They cannot conduct
  electricity in either the solid or molten state.
  

  3. Solubility

  They tend to be quite insoluble in water, but this depends on how
  polarized the molecule is. The more polar the molecules, the more water
  molecules will be attracted to them (some may dissolve in water as a
  result of forming hydrogen bonds with it). Molecular crystals tend to
  dissolve in non-polar solvents such as alcohol.
  

  4. Soft and low density

  Van der Waals forces are weak and non-directional. The lattice is readily
  destroyed and the crystals are soft and have low density.
  

  19.8.2. Giant covalent structures

  Sometimes covalently bonded structures can form giant networks, known as
  Giant Covalent Structures or Macromolecular Structures.
  

  Giant covalent structures contain very many atoms, each joined to adjacent
  atoms by covalent bonds. The atoms are usually arranged into giant regular
  lattices - extremely strong structures because of the many bonds involved.
  

  Properties of giant covalent structures

  • Very high melting points. This is because a lot of strong covalent
  bonds must be broken. Graphite, for example, has a melting point of
  more than 3,600°C.
  • Variable electrical conductivity. Diamond does not conduct electricity,
  whereas graphite contains free electrons so it does conduct electricity.
  Silicon is a semi-conductor – it is midway between non-conductive and
  conductive.
  

  1. Physical properties of diamond
  Diamond is a form (allotrope) of carbon in which each carbon atom is
  joined to four other carbon atoms, forming a giant covalent structure. As
  a result, diamond is very hard and has a high melting point. It does not
  conduct electricity. Diamond is tetrahedral face-centered cubic.
  

  
  

  The physical properties of diamond are outlined below.
  

  • It has a very high melting point (almost 4,000°C). Very strong
  carbon-carbon covalent bonds have to be broken throughout the
  structure before melting occurs.
  

  • It is very hard. This is again due to the need to break very strong
  covalent bonds operating in 3-dimensions.
  

  • It does not conduct electricity. All the electrons are held tightly
  between the atoms, and are not free to move.
  

  • It is insoluble in water and organic solvents. There are no possible
  attractions which could occur between solvent molecules and carbon
  atoms which could outweigh the attractions between the covalently
  bound carbon atoms.
  

  2. Physical properties of graphite
  Graphite is another form (allotrope) of carbon in which the carbon atoms
  form layers. These layers can slide over each other, so graphite is much
  softer than diamond. Each carbon atom in a layer is joined to only three
  other carbon atoms in hexagonal rings.
  

  
  

  The physical properties of graphite are oulined below.

  • It has a high melting point, similar to that of diamond. In order to
  melt graphite, it isn’t enough to loosen one sheet from another. You
  have to break the covalent bonding throughout the whole structure.
  

  • It has a soft, slippery feel, and is used in pencils and as a dry
  lubricant for things like locks. You can think of graphite rather
  like a pack of cards - each card is strong, but the cards will slide
  over each other, or even fall off the pack altogether. When you use
  a pencil, sheets are rubbed off and stick to the paper.
  

  • It has a lower density than diamond. This is because of the
  relatively large amount of space that is “wasted” between the sheets.
  

  • It is insoluble in water and organic solvents - for the same reason
  that diamond is insoluble. Attractions between solvent molecules
  and carbon atoms will never be strong enough to overcome the
  strong covalent bonds in graphite.
  

  • It conducts electricity. The delocalised electrons are free to move
  throughout the sheets. If a piece of graphite is connected into a
  circuit, electrons can fall off one end of the sheet and be replaced
  with new ones at the other end.
  

  3. Physical properties of silicon dioxide
  Silica, which is found in sand, has a similar structure to diamond. It is
  also hard and has a high melting point, but contains silicon and oxygen
  atoms, instead of carbon atoms. Silica or SiO2 is tetrahedral. The fact
  that it is a semi-conductor makes it immensely useful in the electronics
  industry: most transistors are made of silica.
  

  
  

  The physical properties of diamond are oulined below.
  

  • It has a high melting point - varying depending on what the particular
  structure is (remember that the structure given is only one of three
  possible structures), but around 1700°C. Very strong silicon-oxygen
  covalent bonds have to be broken throughout the structure before
  melting occurs.
  

  • It is hard. This is due to the need to break the very strong covalent
  bonds.
  

  • It does not conduct electricity. There are not any delocalised
  electrons. All the electrons are held tightly between the atoms, and
  aren’t free to move.
  

  • It is insoluble in water and organic solvents. There are no possible
  attractions which could occur between solvent molecules and the
  silicon or oxygen atoms which could overcome the covalent bonds in
  the giant structure.
  
  

  Application activity 19.8
  1. What is meant by the statement that “the electrons in diamond are
  localized, whereas graphite has delocalised electrons”.
  

  2. Which electrons in graphite are delocalised? How do they affect the
  properties of graphite?
  

  3. Why is it easy to rub away carbon atoms from graphite?
  

  4. Why is graphite used as lubricant?
  

  5. Diamond and graphite are both forms of carbon.
  • Diamond is able to scratch almost all other substances, whereas
  graphite may be used as a lubricant.
  • Diamond and graphite both have high melting points.
  a) Explain each of these properties of diamond and graphite in
  terms of structure and bonding.
  b) Give one other difference in the properties of diamond and
  graphite.
  

  6. Iodine and diamond are both crystalline solids at room temperature.
  a) Identify one similarity in the bonding, and one difference in the
  structures, of these two solids.
  b) Explain why these two solids have very different melting points.
  

  7. Silicon dioxide has a macromolecular structure. Draw a diagram
  to show the arrangement of atoms around a silicon atom in silicon
  dioxide. Give the name of the shape of this arrangement of atoms
  and state the bond angle.

  19.9. Intermolecular forces

  Activity 19.9
  

  Experiment: To investigate boiling point and to determine the
  relation between boiling point and intermolecular forces.
  

  Apparatus

  • Water, cooking oil (sunflower oil), Glycerine, nail polish remover,
  methylated spirits
  • Test-tubes and a beaker
  • Hot plate
  

  Method

  Methylated spirits and nail polish remover are highly flammable. They
  will easily catch fire if left near an open flame. For this reason they must
  be heated in a water bath. This experiment must be performed in a well
  ventilated room.
  

  • Place about 20 mL of each substance given in separate test-tubes.
  

  • Half-fill the beaker with water and place on the hot plate.
  

  • Place the test-tubes in the beaker.
  

  • Observe how long each substance takes to boil. As soon as a
  substance boils, remove it from the water bath.
  

  Results and questions
  

  1. Write down the order in which the substances boiled, starting with
  the substance that boiled first and ending with the substance that
  boiled last.
  

  2. Suggest the explanation for the above order.

  Now let us talk about the intermolecular forces that exist between molecules.
  Intermolecular forces are much weaker than the intramolecular forces of
  attraction but are important because they determine the physical properties
  of molecules like their boiling point, melting point, density, and enthalpies of
  fusion and vaporization.
  

  19.9.1. Definition, types and origin of intermolecular forces
  Intermolecular forces are the forces between molecules forces that bind
  them together.
  

  Intermolecular forces are like the glue that holds molecules together. There
  are strong and weak forces; the stronger the force, the more energy is
  required to break those molecules apart from each other.
  

  Intermolecular forces include (listed from weakest to strongest):
  • Van der Waals dispersion forces
  • Van der Waals dipole-dipole interactions
  • Hydrogen bonding
  

  So, if two molecules are only connected using van der Waals dispersion
  forces, then it would require very little energy to break those molecules apart
  from each other. On the other hand, if two molecules are connected using
  ionic bonds, it takes a whole lot more energy to break those two apart.
  

  1. Van der Waals Dispersion Forces
  Van der Waals dispersion forces, also called London forces, occur
  due to instantaneous dipoles. At any given moment the electrons in a
  molecule or atom may not be evenly distributed around the molecule.
  If more electrons are on the left side of the molecule than on the right
  side, then there will be a slight (partial) negative charge on the left side
  of the molecule. The side with fewer electrons will have a slight (partial)
  positive charge.
  

  These momentary, partial, positive and negative charges are attracted
  to each other (like the positive and negative ends on a magnet). This
  causes momentary bonds between molecules. We can already see why
  these bonds would be so weak, because they only last for a little while.
  

  Van der Waals dispersion forces increase as the atomic size increases.
  This means that larger molecules will feel more force, thus increasing
  the intermolecular forces. So if we have two molecules that are exactly
  the same except that one is bigger than the other (such as methane and
  ethane), then the intermolecular forces of the bigger one will be stronger
  than for the smaller one.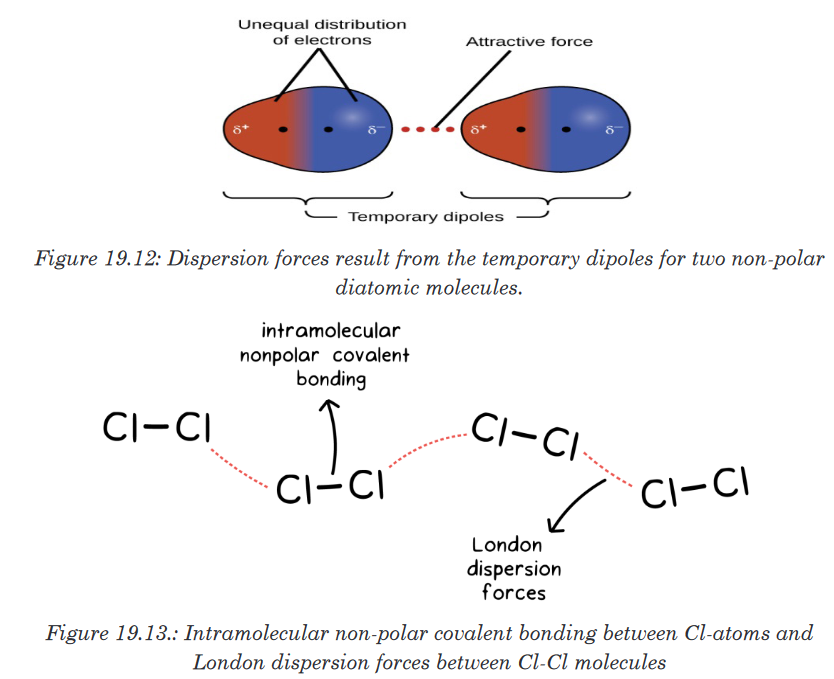
  

  
  

  2. Van der Waals Dipole-Dipole Interactions

  A partial positive charge and a partial negative charge can be created
  between two atoms when there is a difference in electronegativity. These
  interactions are called van der Waals dipole-dipole interactions.
  

  For example, carbon is less electronegative than oxygen, creating a
  partial positive on carbon and a partial negative on oxygen. The dipole
  interactions are stronger than the dispersion forces because the oxygen
  will almost always have slightly more electrons than the carbon, instead
  of constantly changing. There still is not a full negative charge on the
  oxygen, or a full positive charge on the carbon. But the partial positive and
  negative charges are still enough to attract opposite charges together.
  

  The higher the difference in electronegativity, the strong the dipole-
  dipole interactions will be. So compounds with a higher electronegativity
  difference will have strong intermolecular forces.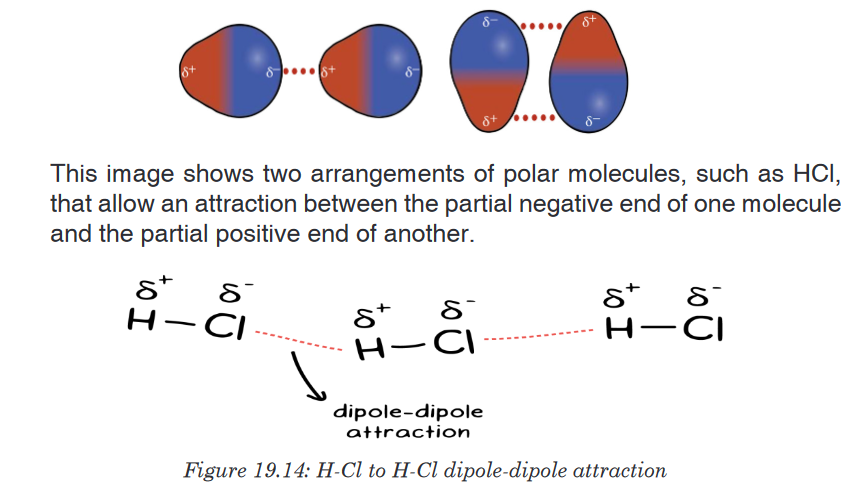
  

  
  

  3. Hydrogen bonding
  This is a special kind of dipole-dipole interaction that occurs between
  a hydrogen atom bonded to a high electronegative atom, specifically
  either an oxygen, nitrogen, or fluorine atom. The partially positive end of
  hydrogen is attracted to the partially negative end of the oxygen, nitrogen,
  or fluorine of another molecule. A hydrogen bond is usually represented
  as a dotted line between the hydrogen and the unshared electron pair of
  the other electronegative atom.
  

  Hydrogen bonding is a relatively strong force of attraction between
  molecules, and considerable energy is required to break hydrogen
  bonds. This explains the exceptionally high boiling points and melting
  points of compounds like water and hydrogen fluoride.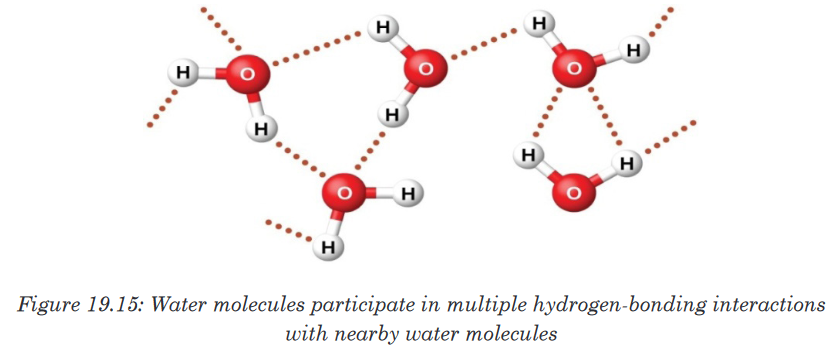
  

  
  

  
  

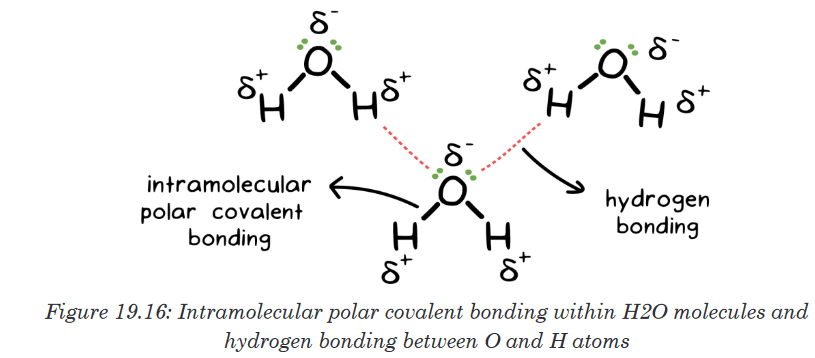
  19.9.2. Effect of intramolecular forces on physical properties of
  certain molecules

  Intermolecular forces control how well molecules stick together. This affects
  many of the measurable physical properties of substances:
  

  • Melting and Boiling Points
  – If molecules stick together more, they will be tougher to break apart
  – Stronger intermolecular forces → higher melting and boiling points
  

  • Viscosity
  – Viscosity is a measure of how well substances flow.
  – Stronger intermolecular forces → higher viscosity.
  

  • Surface Tension
  – Surface tension is a measure of the toughness of the surface of a
  liquid
  – Stronger intermolecular forces → higher surface tension.
  

  • Vapour Pressure
  – This is a small amount of gas that is found above all liquids.
  – Stronger intermolecular forces → Lower vapour pressure.
  

  Note: If you are asked to rank molecules in order of melting point, boiling
  point, viscosity, surface tension or vapour pressure, what they are actually
  asking is for you to rank them by strength of intermolecular forces (either
  increasing or decreasing).Here is the strategy for this:
  

  • Look for molecules with hydrogen bonding. They will have the
  strongest intermolecular forces.
  

  • Look for molecules with dipoles. These will have the next strongest
  intermolecular forces.
  

  • Larger molecules will have stronger London dispersion forces.
  These are the weakest intermolecular forces but will often be the
  deciding factor in multiple choice questions.
  

  If we use this trend to predict the boiling points for the lightest hydride for
  each group, we would expect NH3 to boil at about −120 °C, H₂O to boil at
  about −80 °C, and HF to boil at about −110 °C. However, when we measure
  the boiling points for these compounds, we find that they are dramatically
  higher than the trends would predict, as shown in the figure below. The
  stark contrast between our naïve predictions and reality provides compelling
  evidence for the strength of hydrogen bonding.
  

  
  

  These exhibit anomalously high boiling points due to hydrogen bonding.
  Hydrogen bonding is important in many chemical and biological processes.
  It is responsible for water’s unique solvent capabilities. Hydrogen bonds

  hold complementary strands of DNA together, and they are responsible
  for determining the three-dimensional structure of folded proteins including
  enzymes and antibodies.
                               1. An Example: Water
  Since oxygen is more electronegative than hydrogen, oxygen pulls the
  shared electrons more closely to itself. This gives the oxygen atom a slightly
  more negative charge than either of the hydrogen atoms. This imbalance is
  called a dipole, causing the water molecule to have a positive and negative
  side, almost like a tiny magnet. Water molecules align so the hydrogen on
  one molecule will face the oxygen on another molecule. This gives water a
  greater viscosity and also allows water to dissolve other molecules that have
  either a slightly positive or negative charge.
  

                          2. Protein Folding
  Protein structure is partially determined by hydrogen bonding. Hydrogen
  bonds can occur between a hydrogen on an amine and an electronegative
  element, such as oxygen on another residue. As a protein folds into place, a
  series of hydrogen bond “zips” the molecule together, holding it in a specific
  three-dimensional form that gives the protein its particular function.
                         3. DNA
  Hydrogen bonds hold complementary strands of DNA together. Nucleotides
  pair precisely based on the position of available hydrogen bond donors
  (available, slightly positive hydrogens) and hydrogen bond acceptors
  (electronegative oxygens). The nucleotide thymine has one donor and one
  acceptor site that pairs perfectly with the nucleotide adenine’s complementary
  acceptor and donor site. Cytosine pairs perfectly with guanine through three
  hydrogen bonds.
  

  Application activity 19.9

  1. Define the following and give an example of each:
  a) Dispersion force
  b) Dipole-dipole attraction
  c) Hydrogen bond
  2. The table below shows the boiling points of some other hydrogen
  halides.
  

  
  

  a) Explain the trend in the boiling points of the hydrogen halides from
  HCl to HI.

  b) Give one reason why the boiling point of HF is higher than that of
  all the other hydrogen halides.

  3. The types of intermolecular forces in a substance are identical whether
  it is a solid, a liquid, or a gas. Why then does a substance change
  phase from a gas to a liquid or to a solid?

  4. Why do the boiling points of the noble gases increase in the order He
  < Ne < Ar < Kr < Xe?

  5. Neon and HF have approximately the same molecular masses. Explain
  why the boiling points of Neon and HF differ.

  6. Arrange each of the following sets of compounds in order of increasing
  boiling point temperature:
  a) HCl, H₂O, SiH₄
  b) F₂, Cl₂, Br₂
  c) CH₄, C₂H₆, C₃H₈
  d) O₂, NO, N₂
  

  7. The molecular mass of butanol, C₄H₉OH, is 74.14; that of ethylene
  glycol, CH₂(OH)CH₂OH, is 62.08, yet their boiling points are 117.2 °C
  and 174 °C, respectively. Explain the reason for the difference.
  

  8. On the basis of intermolecular attractions, explain the differences in
  the boiling points of n–butane (−1 °C) and chloroethane (12 °C), which
  have similar molar masses.
  

  9. On the basis of dipole moments and/or hydrogen bonding, explain in
  a qualitative way the differences in the boiling points of acetone (56.2
  °C) and 1-propanol (97.4 °C), which have similar molar masses.
  

  10. The melting point of H₂O(s) is 0 °C. Would you expect the melting
  point of H₂S(s) to be −85 °C, 0 °C, or 185 °C? Explain your answer.
  

  11. Explain why a hydrogen bond between two water molecules is weaker
  than a hydrogen bond between two hydrogen fluoride molecules.
  

  12. Under certain conditions, molecules of acetic acid, CH₃COOH, form
  “dimers,” pairs of acetic acid molecules held together by strong
  intermolecular attractions:
  

  
  

  Draw a dimer of acetic acid, showing how two CH₃COOH molecules
  are held together, and stating the type of intermolecular force that is
  responsible.
  

  13. Proteins are chains of amino acids that can form in a variety of
  arrangements, one of which is a helix. What kind of intermolecular
  force is responsible for holding the protein strand in this shape? On
  the protein image, show the locations of the intermolecular forces that
  hold the protein together:
  

  
  

  14. Identify the intermolecular forces present in the following solids:
  a) CH₃CH₂OH
  b) CH₃CH₂CH₃
  c) CH₃CH₂Cl
  15. Explain why non-polar molecules usually have much lower surface
  tension than polar ones.
  

  
  

  1. Pour water into a small jar that has a tight-fitting lid until the jar is about
  a third full.

  2. Add an equal amount of vegetable oil to the jar. Cover the jar tightly.

  3. Shake the jar vigorously for 20 seconds. Observe the contents.

  4. Allow the jar to sit undisturbed for 1 minute. Observe again.

  5. Remove the top and add 3 drops of liquid detergent.

  6. Cover the jar and repeat Steps 3 and 4.
  a) Based on your observations, write an operational definition of
  detergent.
  b) How might your observations relate to chemical bonds in the
  detergent, oil and water molecules?
  c) Demonstrate the action of soaps and detergents to your family.
  d) Pour some vegetable oil on a clean cloth and show how a detergent
  solution can wash the oil away better than water alone can.
  e) Explain to your family the features of soap and detergent molecules
  in terms of their chemical bonds.

  End unit assessment 19

  1. Which of the following statements is false about VSEPR theory?
  a) The geometry of a molecule is determined by the number of
  electron groups on the central atom.
  b) The geometry of the electron groups is determined by minimizing
  repulsions between them.
  c) A lone pair, a single bond, a double bond, a triple bond and a
  single electron - each of these is counted as a single electron
  group.
  d) Bond angles may depart from the idealized angles because lone
  pairs of electrons take up less space than bond pairs.
  e) The number of electron groups can be determined from the Lewis
  structure of the molecule.
  

  2. Choose the best answer. The correct dot formulation for nitrogen
  trichloride has:
  a) 3 N-Cl bonds and 10 lone pairs of electrons.
  b) 3 N=Cl bonds and 6 lone pairs of electrons.
  

  c) 1 N-Cl bond, 2 N=Cl bonds and 7 lone pairs of electrons.
  d) 2 N-Cl bonds, 1 N=Cl bond and 8 lone pairs of electrons.
  e) 3 N-Cl bonds and 9 lone pairs of electrons.
  3. Choose the molecule that is incorrectly matched with the electronic
  geometry about the central atom.
  a) CF4 - tetrahedral
  b) BeBr2 - linear
  c) H2O - tetrahedral
  d) NH3 - tetrahedral
  e) PF3 - pyramidal
  4. Choose the correct answer. A π(pi) bond is the result of the
  a) Overlap of two s orbitals.
  b) Overlap of an s and a p orbital.
  c) Overlap of two p orbitals along their axes.
  d) Sidewise overlap of two parallel p orbitals.
  e) Sidewise overlap of two s orbitals.
  

  5. Choose the missing answer. The F-S-F bond angles in SF6 are ______.
  a) 109^o28’
  b) 120^o only
  c) 90^o and 120^o
  

  6. Draw a complete line-bond or electron-dot formula for acetic acid and
  then decide which statement is incorrect.
  a) One carbon is described by sp2 hybridization.
  b) The molecule contains only one πbond.
  c) The molecule contains four lone pairs of valence electrons.
  d) One carbon is described by sp3 hybridization.
  e) Both oxygens are described by sp3 hybridization.
  

  7. The equation below shows the reaction between boron trifluoride and
  a fluoride ion. BF₃ + F− → BF₄−
  

  a) Draw diagrams to show the shape of the BF3 molecule and the
  shape of the BF₄− ion. In each case, name the shape. Account for
  the shape of the BF4− ion and state the bond angle present.
  

  b) In terms of the electrons involved, explain how the bond between
  the BF₃ molecule and the F− ion is formed. Name the type of bond
  formed in this reaction.

  8. Draw the shape of a molecule of BeCl2and the shape of a molecule of
  Cl₂O. Show any lone pairs of electrons on the central atom. Name the
  shape of each molecule.

  9. Ammonia, NH₃, reacts with sodium to form sodium amide, NaNH₂, and
  hydrogen.

  a) Draw the shape of an ammonia molecule and that of an amide
  ion, NH₂−. In each case show any lone pairs of electrons.
  b) State the bond angle found in an ammonia molecule.
  c) Explain why the bond angle in an amide ion is smaller than that in
  an ammonia molecule.
  

  10. The table below shows the electronegativity values of some elements.
  

  
  

  a) Explain why the O–H bond in a methanol molecule is polar.
  

  b) The boiling point of methanol is +65 °C; the boiling point of oxygen is
  –183 °C. Methanol and oxygen each have a Mr value of 32. Explain,
  in terms of the intermolecular forces present in each case, why the
  boiling point of methanol is much higher than that of oxygen.
  

  12. The table below gives the boiling points, Tb, of some hydrogen halides.
  

  
  

  a) By referring to the types of intermolecular force involved, explain why
  energy must be supplied in order to boil liquid hydrogen chloride.
  b) Explain why the boiling point of hydrogen bromide lies between
  those of hydrogen chloride and hydrogen iodide.
  c) Explain why the boiling point of hydrogen fluoride is higher than that
  of hydrogen chloride.
  d) Draw a sketch to illustrate how two molecules of hydrogen fluoride
  interact in liquid hydrogen fluoride.

  13. Figure below shows some data concerned with halogens.
  

  
  

  a) Define the term electronegativity.
  b) Explain the trend in boiling points from hydrogen chloride to hydrogen
  iodide.
  c) Explain why hydrogen fluoride does not fit this trend.

  14. The oxygen atoms in the sulphate ion surround the sulphur in a regular
  tetrahedral shape.
  a) Write the formula of the ion.
  b) State the O–S–O. bond angle.

  15. (a) State one feature which molecules must have in order for hydrogen
  bonding to occur between them.
  b) Give the name of the type of intermolecular bonding present in
  hydrogen sulphide, H₂S, and explain why hydrogen bonding does
  not occur.
  c) Account for the much lower boiling point of H₂S (–61 °C) compared
  with that of water (100 °C).

  16. Protein molecules are composed of sequences of amino acid molecules
  that have joined together, with the elimination of water, to form long
  chains. Part of a protein chain is represented by the graphical formula
  given below.
  

  
  

  Explain the formation of hydrogen bonding between protein molecules.
  17. The diagram below shows how a water molecule interacts with a
  hydrogen fluoride molecule.

  
  

  a) What is the value of the bond angle in a single molecule of water?
  b) Explain your answer to part (a) by using the concept of electron
  pair repulsion.
  c) Name the type of interaction between a water molecule and a
  hydrogen fluoride molecule shown in the diagram above.
  d) Explain the origin of the + charge shown on the hydrogen atom in
  the diagram.
  e) When water interacts with hydrogen fluoride, the value of the bond
  angle in water changes slightly. Predict how the angle is different
  from that in a single molecule of water and explain your answer.

  18. Phosphorus exists in several different forms, two of which are white
  phosphorus and red phosphorus. White phosphorus consists of
  P4molecules, and melts at 44°C. Red phosphorus is macromolecular,
  and has a melting point above 550°C.
  a) Explain what is meant by the term macromolecular.
  b) By considering the structure and bonding present in these two
  forms of phosphorus, explain why their melting points are so
  different.
  

• UNIT 20:MOMENTS AND EQUILIBRIUM OF BODIES

  Key Unit Competence: Explain the principle of moments and
                                                 apply it to the equilibrium of a body.

  Introductory Activity 20
  Study the diagrams (a), ( b) and (c) below:

  
  1. Referring to pictures (a) and (b), name the tools used.
  2. What happens when force is applied:
  i. At the end of the tool used?
  ii. In the middle of the tool used?
  3. Referring to (c) that shows two children balancing on a seesaw.
  i. If they have different weights can they balance? Explain
  ii. If they have the same weight do they balance? Explain

  20.1. Vector and scalar quantities
  
  

  Activity 20.1
  
  

  Task 1

  Try to stand in a line behind one another. Push your friend.
  i. What happens to your friend?
  ii. How do you feel?
  iii. What if in the process one stops pushing, what would happen?
  
  

  Task 2

  
  

  Most quantities measured in science (Physics) are classified as either Scalar
  or vector.
  

  A scalar quantity is a physical quantity that is defined by only magnitude
  (size).
  

  Examples of scalar quantities are volume, mass, speed, and time intervals.
  The rules of ordinary arithmetic are used to manipulate scalar quantities.
  

  A vector quantity is a quantity with both magnitude and direction.
  

  Example of vector quantity: velocity, acceleration, force, weight, electric
  field, displacement and pressure.
  

  20.1.1. Force as vector and moment of a force about a point
  

  Force as vector

  The force is vector quantity. We can think of force as that which causes an
  object to accelerate. What happens when several forces act simultaneously
  on an object? In this case, the object accelerates only if the net force acting
  on it is not equal to zero.
  

  The net force acting on an object is defined as the vector sum of all forces
  acting on the object. (We sometimes refer to the net force as the total force,
  the resultant force, or the unbalanced force.)
  

  Moment of a force or torque
  

  
  

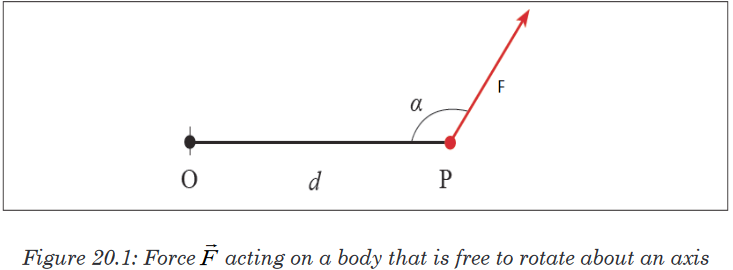
  This figure shows a force 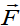 acting on a body that is free to rotate about an
  axis. The force is applied at the point P whose position is defined by the
  vector
  

  The direction of and make an angle α with each other.
  

  We define the torque acting on the body from:τ=F×d sinα

  The perpendicular distance of the line of action of the force from the axis of
  rotation is called the moment arm of the force.
  

  The S.I unit of torque is Newton-metre [N m] or metre-newton [m N]

  20.1.2. Principles of moment

  The principle of moments states that” when in equilibrium the total sum of
  the anticlockwise moment is equal to the total sum of the clockwise moment.”
  When a system is stable or balance it is said to be in equilibrium as all the
  forces acting on the system cancel each other out. In equilibrium:
  Total anticlockwise moment = Total clockwise moment
  The principle can be explained by considering two people on a seesaw.
  

  
  

  Moments acting on a seesaw
  

  Both people exert a downward force on the seesaw due to their weights.
  

  Person A’s weight is trying to turn the seesaw anticlockwise with person B’s
  weight is trying to turn the seesaw clockwise.
  

  
  

  
  

  
  

  Application activity 20.1
  
  

  1. Complete the following paragraph using the following words: forces,
  unbalanced , accelerating, slower, balanced, resultant, faster, stay
  still, and decelerating.
  A ball will stay still if the forces on it are __________. If the forces
  on it are unbalanced, the ball will get ______ or ______. The overall
  force is called the __________ force. If something gets faster, we say
  it is __________.
  

  2. A beam of negligible weight is horizontal in equilibrium, with forces
  acting upon it, as shown in the diagram.
  Calculate the value of the weights R and W.
  

  
  

  20.2. Types of equilibrium: stable, unstable and neutral
  

  Activity 20.2
  
  

  i. Displace the desk. What happens when you withdraw the force you
  applied?
  

  ii. Place a bottle on a table so that it rests on its horizontal surface.
  Displace or roll it. What happens?
  

  iii. Place a knife edge on a table resting on its tip. Give it a small
  displacement. What happens to it?
  

  iv. From the observations made, how do you conclude?
  

  Equilibrium has many different meanings, depending on what subject
  (chemistry or physics) or what topic (energy or forces). Dealing with energy,
  there are three types of equilibrium.
  

  A body is in either Stable, Unstable or in neutral equilibrium depending how
  it behaves when subjected to a small displacement.
  

  Stable is when any sort of movement will raise the object’s centre of gravity.
  When objects in stable equilibrium are moved, they have a tendency to fall
  back to their original position. For instance, a skateboarder at the bottom, in
  the middle, of a ramp. Either way the skateboarder moves, his/her potential
  energy will increase because he/she will be rising in height. The boarder will
  also roll back to the bottom of the ramp if he/she doesn’t exert any sort of
  energy to maintain the new position.
  

  When a body returns to its original position on being slightly disturbed,
  it is said to be in stable equilibrium.
  Unstableis when any sort of movement will lower the object’s centre of gravity.
  When such objects are moved, they cannot return to their original position
  without some exertion of energy. For instance, when a coin is placed on its
  side, it exhibits unstable equilibrium. Any sort of push will cause the coin to
  fall flat, lowering its centre of mass. The coin will not return to its side unless
  someone picks it up and resets it.
  

  If the position of a body is disturbed and the body does not return to its
  original position, it is in unstable equilibrium.

  Neutral is when any sort of movement does not affect the object’s centre of
  gravity. For instance, a ball on a table exhibits neutral equilibrium. If the ball
  rolls, the centre of mass stays at the same height and thus it maintains the
  same equilibrium.
  

  A body is said to be in neutral equilibrium if it moves to a new position
  when it is disturbed.
  

  Let us consider a cone to understand these states.
  

  
  

  From whatever we have done, we can conclude and say that a body is
  stable when:
  

  1. The object’s base is broad.
  2. The centre of gravity is as low as possible.
  3. The vertical line drawn from the centre of gravity should fall within
  the base. Lowering the centre of gravity of an object is important for
  stability.
  

  Application activity 20.2

  Figure below shows a cone. Explain how to lay it on a flat table so that it is
  in (a) stable equilibrium, (b) unstable equilibrium, (c) neutral equilibrium.
  

  
  

  20.3. Condition for equilibrium of a body about an axis and
              Stevinus proof
  

  Activity 20.3
  
  

  As a class, let us move outside. With the help of a teacher outside the
  class:
  a). Are you seeing any object outside?
  b). Are they stationary or in motion?
  c). If at rest, what causes them to be at rest?
  

  20.3.1. Condition for equilibrium of a body about an axis

  Objects in daily life have at least one force acting on them (gravity). If they
  are at rest, then there must be other forces acting on them as well so that
  the net force is zero. A book at rest on a table, for example, has two forces
  acting on it, the downward force of gravity and the normal force the table
  exerts upward on it.
  

  
  

  Since the net force on the book is zero, the upward force exerted by the
  table on the book must be equal in magnitude to the force of gravity acting
  downward on the book. Such an object is said to be in equilibrium (Latin
  for “equal forces” or “balance”) under the action of these two forces. The two
  conditions for equilibrium of a rigid object under the action of coplanar forces
  are:

  1. The first or force condition: the vector sum of all forces acting on
  the body must be zero: Where the plane of the coplanar forces is
  taken to be the xy-plane. We must remember that if a particular
  force component points along the negative x or y axis, it must have
  a negative sign.
  

  
  

  
  

  2. The second or torque condition: take an axis perpendicular to the
  plane of the coplanar forces. Call the torques that tend to cause
  clockwise rotation about the axis negative, and counterclockwise
  torques positive; then the sum of all the torques acting on the object
  must be zero: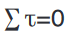
  

  
  

  20.3.2. Stevinus proof

  Stevinus (sometimes called Stevin) proof of the law of equilibrium on an
  inclined plane known as the “Epitaph of Stevinus”.
  

  He derived the condition for the balance of forces on inclined planes using
  a diagram with a “wreath” containing evenly spaced round masses resting
  on the planes of a triangular prism (see the illustration on the figure). He
  concluded that the weights required were proportional to the lengths of the
  sides on which they rested assuming the third side was horizontal and that
  the effect of a weight was reduced in a similar manner.
  

  It’s implicit that the reduction factor is the height of the triangle divided by
  the side (the sine of the angle of the side with respect to the horizontal). The
  proof diagram of this concept is known as the “Epitaph of Stevinus”.
  

  
  

  20.3.3. Free –Body Diagrams (FBD)
  
  

  In physics and engineering, a free body diagram (force diagram, or FBD)
  is a graphical illustration used to visualize the applied forces, movements,
  and resulting reactions on a body in a given condition. They depict a body
  or connected bodies with all the applied forces and moments, and reactions,
  which act on the body (ies).
  

  In educational environment, learning to draw a free body diagram is an
  important step in understanding certain topics in physics, such as statics,
  dynamics and other forms of classical mechanics.
  

  Free body diagrams consist of:

  • A simplified version of body (often a dot or a box)
  

  • Forces shown as a straight arrows pointing in the direction they act on
  the body
  

  • Moments shown as curved arrows pointing in the direction they act on
  the body
  

  • Coordinate system
  

  • Frequently reaction to applied forces are shown with hash marks
    through the stem of the arrow.
  

  A number of forces and moments shown in a free body diagram depends on
  the specific problem and the assumptions made; common assumptions are
  neglecting air resistance, friction and assuming rigid bodies.
  

  In statics all forces and moments must balance to zero; the physical
  interpretation of this is that if the forces and moments do not sum to zero the
  body is accelerating and the principle of statics do not apply. In dynamics the
  resultant forces and moments can be non-zero.

  Example: Motion on a horizontal plane with frictional force
  

  FBD

  
  

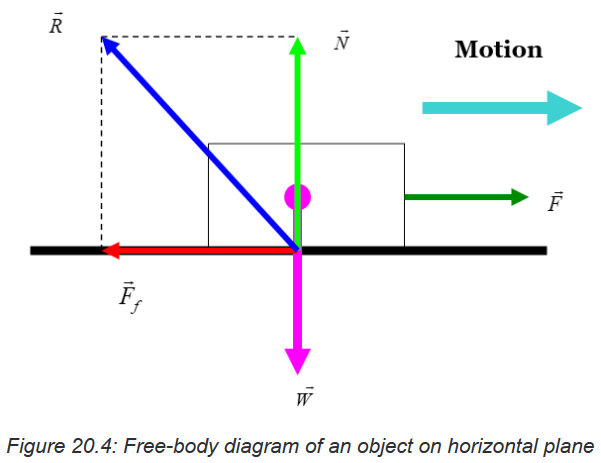
  Example 20.1: Forces on a beam and supports.
  

  A uniform 1500-kg beam, 20.0 m long, supports a 15,000-kg printing press
  5.0 m from the right support column (Figure below). Calculate the force on
  each of the vertical support columns.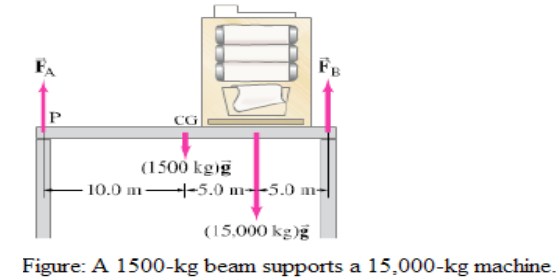
  

  
  

  
  

  APPROACH
  
  

  We analyze the forces on a beam (the force the beam exerts on each column
  is equal and opposite to the force exerted by the column on the beam). We
  label these forces and in the figure. The weight of the beam itself acts at its
  center of gravity, 10.0 m from either end. We choose a convenient axis for
  writing the torque equation: the point of application of (labeled P), so will no
  enter the equation (its lever arm will be zero) and we will have an equation
  in only one unknown, .
  

  
  

  Our next example involves a beam that is attached to a wall by a hinge and
  is supported by a cable or cord. It is important to remember that flexible
  cable can support a force only along its length. (if there were a component
  of force perpendicular to the cable, it would bend because it is flexible.) But
  for a rigid device, such as the hinge in figure below, the force can be in any
  direction and we can know the direction only after solving the problem. The
  hinge is assumed small and smooth, so it can exert no internal torque (about
  its center) on the beam.
  

  Application activity 20.3

  1. A uniform beam, 2.20 m long with mass m=25.0 kg, is mounted by
  a hinge on a wall as shown in figure below. The beam is held in
  horizontal position by a cable that makes an angle ?=30.0⁰as shown.
  The beam supports a sign of mass M=28.0 kg suspended from its
  end.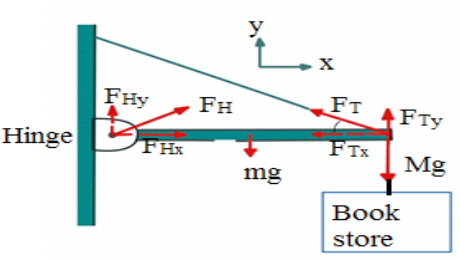
  

  
  

  Determine the components of the force (→ F _H ) that the hinge exerts on
  the beam, and the tension F_T in supporting cable.
  

  
  2.   A 5.0-m-long ladder leans against a wall at a point 4.0 m above a
        cement floor as shown in figure below. The ladder is uniform and has
        mass m=12.0 kg. Assuming the wall is frictionless (but the floor is not),
        determine the forces exerted on the ladder by the floor and by the wall.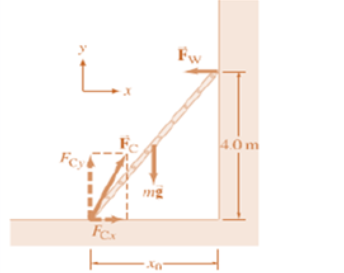
  

  
  

  20.4. Forces and moments in equilibrium

  Activity 20.4
  • Try to lift your seat alone.
  • How do you feel?
  • Tell your friend to help you and you lift it together
  • Are you feeling the same way as before when you were alone?
  • What if your friend pulls in opposite direction to that of your force?
     What would happen?
  

  20.4.1. Forces in equilibrium
  

  When all the forces that act upon an object are balanced, then the object is
  said to be in a state of equilibrium. The forces are considered to be balanced
  if the rightward forces are balanced by leftward forces and the upward forces
  are balanced by the downward forces. This however does not necessarily
  mean that all the forces are equal to each other.
  

  There are two cases of equilibrium that are often encountered; the first case
  deals with an object subjected to only two forces, and the second case is
  concerned with an object subjected to three force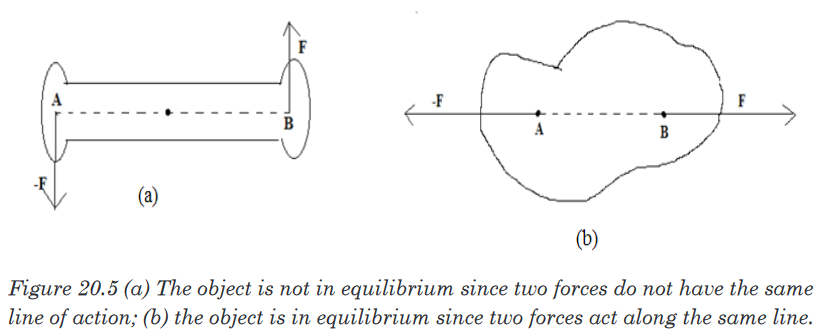
  

  
  

  Case I: if an object is subjected to two forces, the object is in equilibrium if
  and only if the two forces are equal in magnitude, opposite in direction and
  have the same line of action.
  

  Figure (a) shows a situation in which the object is not in equilibrium because
  the two forces are not along the same line. Note that the torque about any
  axis such as one through A is not zero. Which violet the second condition of
  equilibrium.
  

  Figure (b), the object is in equilibrium because the forces have the same line
  of action. In this situation, it is easy to see that the net torque about any axis
  is zero.
  

  Case II: If an object subjected to three forces is in equilibrium, the line of
  action of the three forces must intersect at a common point; that is the force
  must be concurrent. One exception to this rule is the situation in which none
  of the lines of action intersect. In this situation, the forces must be parallel.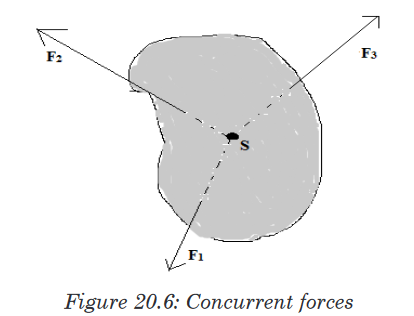
  

  
  

  If three forces act on an object that is in equilibrium, their lines of action must
  intersect at a point S (or they must be parallel).
  

  
  

  20.4.2. Couples and Torques

  There are many examples in practice where two forces, acting together,
  exert a moment or turning effect on some object. As a very simple case,
  suppose two strings are tied to a wheel at X,Y and two equal and opposite
  forces, F, are exerted tangentially to the wheel, figure below. If the wheel is
  pivoted at its centre, O, it begins to rotate about O in anticlockwise direction.
  The total moment about O is then
  

  
  

  Two equal and opposite forces whose lines of action do not coincide are said
  to form a couple. The two forces always has a turning effect, or moment,
  called a torque, which is given by
  

  since XY is perpendicular to each of the forces F in figure below,
  

  The moving coil or armature in electric motor is made to spin round by a
  couple. When it is working, two parallel and equal forces, in opposite
  directions, act on opposite sides of the coil and produce a torque on it.
  

  In figure(ii), a wheel W is rotated about its center O by a tangential force F
  at A on one side. To find the whole effect of F on the wheel, we can put two
  other forces F at O which are parallel to F at A but opposite in direction. This
  does not disturb the mechanics because the two forces at O would cancel
  and leave F at A. But the upward force F at O and the opposite parallel force
  F at A form a couple of moment . This is actually the moment of F at A.
  

  In addition, however, we are left with the downward force at O. so when F is
  applied to A to turn the wheel, it produces a couple plus an equal force F at
  O, the centre of the wheel.
  

  
  

  20.4.3. Equilibrium of Coplanar forces
  Forces in equilibrium mean that they are balanced.
  

  Coplanar forces act in the same plane. Two balanced forces are equal in
  magnitude but opposite in direction to the other.
  

  Parallelogram of forces
  

  A force is a vector quantity. So it can be represented in size and direction by
  a straight line drawn to scale. The sum or resultant of two forces and can
  be added by one of two vector methods.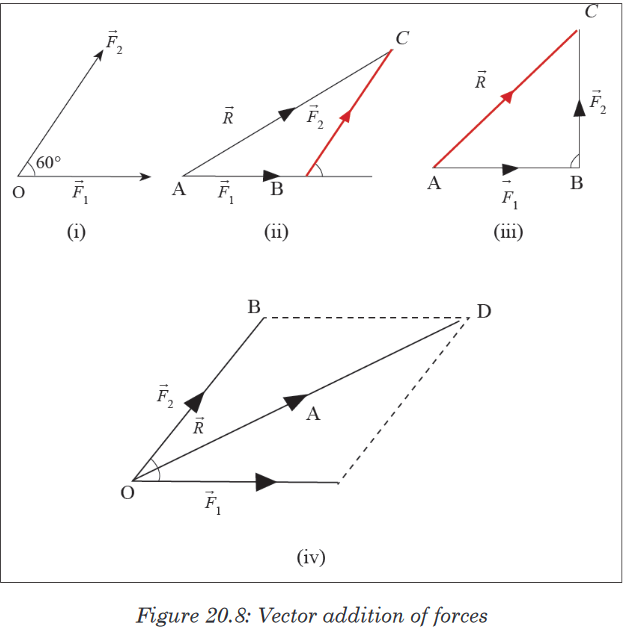
  

  
  

  If three forces are in equilibrium, they can be represented in magnitude and
  direction by the three sides of a triangle taken in order. This is called the
  triangle of forces theorem. This result can be extended to many forces in
  equilibrium.
  

  20.4.4. Equilibrium of moments of force

  We consider the equilibrium of an object like a horizontal bar. In the lab it
  will be a meter stick. Equilibrium means that it does not have translation
  (motion in which all points on the body move with the same vector velocity)
  or rotation.
  

  We can define the rotation by choosing any point on the body, calling that
  point the “axis”, and considering rotation about that axis.
  

  There may be several forces acting on the body, and each force acts at
  certain point. In the diagram, acts at point and acts at point; A is the axis.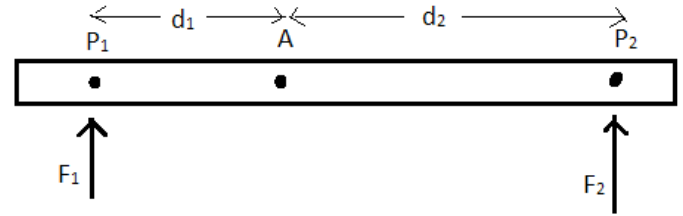
  

  
  

  We consider only forces that act up or down. The distance from point where
  the force acts to the axis is called the moment arm, and in the diagram. The
  product of the force times the moment arm is called the torque (also called
  the moment), and is represented by a Greek letter tau
  

  Torque also has a sign: it is positive (by convention) if it tends to rotate
  the object in counterclockwise direction around the axis. It is negative if it
  tends to rotate the object in a clockwise direction around the axis. In the
  diagram the torque due to is positive and the torque to is negative. The
  forces themselves have signs. We may take forces positive if directed up,
  and negative down.
  

  The conditions for equilibrium are then stated simply: the sum of all forces
  must be zero, and the sum of all torques must be zero. One particular force
  requires further consideration: the weight of the bar. The weight (force of
  earth’s gravity) does not act at a point, but acts at all points along the object.
  However, for the purposes of determining equilibrium, the weight can be
  considered to be concentrated at a single point, called the center of mass.
  Thus a bar supported by two upward forces, and held in equilibrium, looks
  like the figure below.
  

  
  

  Since the axis, for problem-solving purposes, can be chosen anywhere along
  the bar, it is convenient to choose it at the point where one of the forces acts.
  Then the moment arm of that force will be equal to zero, and so that force
  will not come into torque equation. For example, we may choose the axis to
  be at the center of mass.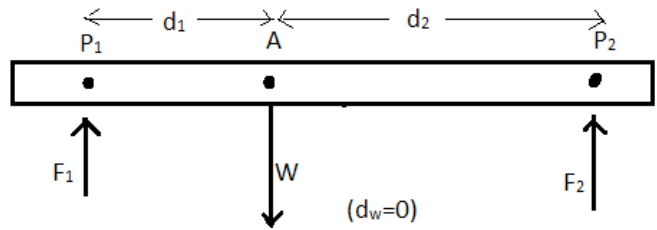
  

  
  

  
  

  
  

  Application activity 20.4
  
  

  Determine the mass of the object using the principle of moments.
  Apparatus required
  • 1 uniform meter rule
  • A knife edge
  • Unknown mass
  

  
  

  Instructions
  
  

  Follow these steps to determine the mass M of the provided body (meter
  ruler).
  

  a) Weigh the meter ruler provided to obtain its mass, M. Balance the
  meter ruler on a knife edge. Read Q the balance point. Find Z.
  

  b) Balance the meter ruler with its graduated face upwards on a knife
  edge. With the mass M provided at P=10 cm from A as shown,
  

  c) Measure and record distance X and Y.
  

  d) Repeat procedure (b) and (c) for values of P=15, 20, 25, 30 and
  35cm.
  

  e) Tabulate your results including values of (Y-Z) and (X-P).
  

  f) Plot a graph of (Y-Z) against (X-P).
  

  g) Find the slope “S’’ of your graph.
  

  20.5. Archimedes’ principle of the lever and centre of
             gravity of bodies
  

  Activity 20.5
  

  Task 1
  
  

  1. In group, discuss levers using knowledge of O’ level Machines.
  

  2. What is your friend telling you? Is it what you knew before?
  

  Task 2
  

  Given a pencil, a ruler, a notebook or other regular shaped material
  Tray to balance the material using your finger. Is it balanced? What
  causes it to be balanced? How do you call the point of balance? How can
  you locate this point?
  

  20.5.1. Archimedes and the principle of the lever
  Building up from the earliest remaining writings regarding levers date from
  the 3rd century BC and were provided by Archimedes. “Give me a place
  tostand, and I shall move the Earth with it” is a remark of Archimedes who
  formally stated the correct mathematical principle of lever.
  

  Force and levers, law of the lever
  

  A lever is a beam connected to ground by a hinge or pivot called a fulcrum.
  

  In other words we say that the lever is a movable bar that pivots on a fulcrum
  attached to a fixed point. The lever operates by applying forces at different
  distances from the fulcrum, or a pivot.
  

  The ideal lever does not dissipate or store energy, which means there is
  no friction in the hinge or bending in the beam. In this case, the power into
  the lever equals the power out, and the ratio of output to input force is given
  by the ratio of the distances from the fulcrum to the points of application of
  these forces. This is known as the law of the lever.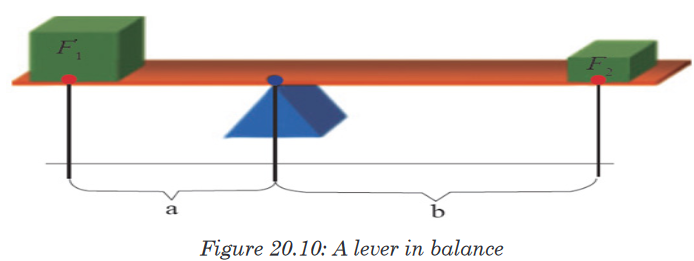
  

  
  

  The mechanical advantage of a lever can be determined by considering the
  balance of moments or torque, τ, about the fulcrum, and we write: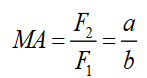
  

  
  

  where F₁ is the input force to the lever and F₂ is the output force. Then
  distances a and b are the perpendicular distances between the forces and
  the fulcrum.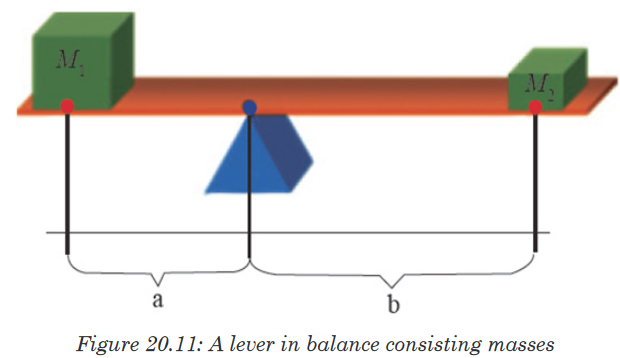
  

  
  

  For the case of the figure 20.11, knowing that the forces considered are
  weights of objects and W = Mg, we can write the mechanical advantage of
  the lever as a ratio,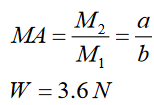

  
  

  20.5.2. Centre of gravity and the total weight centre of gravity of
                  a flat object
  

  In most equilibrium problems, one of the forces acting on the body is the
  weight. We need to be able to calculate the torque of this force. The weight
  doesn’t act at a single point; it is distributed over the entire body. But we can
  always calculate the torque due to the body’s weight by assuming that the
  entire force of gravity (weight) is concentrated at a point called the center
  of gravity (abbreviated “ cg”). The acceleration due to gravity decreases with
  altitude; but if we can ignore this variation over the vertical dimension of
  the body, then the body’s center of gravity is identical to its center of mass
  (abbreviated “cm”), let us prove it.
  

  First let’s review the definition of the center of mass. For a collection of
  particles with masses m₁, m₂,and coordinates (x₁,y₁,z₁ )(x₂,y₂,z₂ ) the
  coordinates and of the center of mass are given by
  

  
  

  Also, x_cm,y_cm and z_cm are components of the position vector of center of mass,
  so this is equivalent to the vector equation
  

  
  

  Now let’s consider gravitational torque on a body of arbitrary shape
  

  We assume that the acceleration due to gravity has the same magnitude and
  direction at every point in the body. Every particle in the body experiences a
  gravitational force, and the total weight of the body is a vector sum of a large
  number of parallel forces. A typical particle has mass and weight . If is the
  position vector of this particle with respect to an arbitrary origin O, then the
  torque vector of the weight with respect to O is,
  

  
  

  
  

  The total gravitational torque is the same as though the total weight were
  acting on the position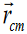 of the center of mass, which we also call the center
  of gravity. If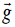 has the same value at all points on a body, its center of gravity
  is identical to its center of mass. Note, however, that the center of mass is
  defined independently of any gravitational effect. While the value of does
  vary somewhat with elevation, the variation is extremely slight. Hence we
  will assume that the center of gravity and the center of mass are identical
  unless explicitly stated otherwise.
  

  20.5.3. Equilibrium of a system of objects
  

  Balancing turning forces

  An object in static equilibrium is one that has no acceleration in any direction.
  While there might be motion, such motion is constant.
  

  Two children on a seesaw: the system is in static equilibrium, showing no
  acceleration in any direction.
  

  When an object is balanced on a pivot the turning effect of the forces
  on one side of the pivot must balance the turning effect of the forces
  on the other side of the pivot - if they didn’t it would not balance.
  In the picture (Figure 20.13(a)) two girls are sitting on a see saw. They have
  moved until it is balanced. They are the same weight and so to balance the
  see saw they must sit the same distance from the pivot.
  

  
  

  In the picture (Figure 20.13(b)) one of the girls gets off and a man sits on
  instead. They move until the see saw is balanced. The girl is much lighter
  than the man and so she has to sit further away from the pivot then he does
  so that she can balance his extra weight.
  

  You should remember that the turning effect of a force is called the moment
  of the force and is found by multiplying the force by its distance from the pivot.
  When the see saw is balanced we say that the anticlockwise moments (those
  trying to turn the object anticlockwise) equal the clockwise moments (those
  trying to turn the object clockwise). In our example the man’s weight tries to
  turn the see saw clockwise and the girl’s weight tries to turn it anticlockwise.
  You can investigate this in the lab by using sets of weights hanging on a
  wooden ruler (Figure 20.14)
  

  
  

  The rule for something to be balanced is called the principle of moments and
  is written as follows: when an object is balanced (in equilibrium) the sum of
  the clockwise moments is equal to the sum of the anticlockwise moments.
  

  Force 1 x perpendicular distance 1 = Force 2 x perpendicular distance 2
  from pivot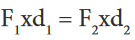
  

  
  

  Example 20.2: Balancing a seesaw.

  A board of mass M = 2.0 kg serves as a seesaw for two children, as shown in
  figure below. Child A has a mass of 30 kg and sits 2.5m from the pivot point,
  P (his center of gravity is 2.5m from the pivot).
  

  At what distance x from the pivot must child B, of mass 25 kg, place herself
  to balance the seesaw? Assume the board is uniform and centered over the
  pivot.
  

  
  

  Approach
  

  We follow the steps of the problem solving box explicitly.
  

  Solution

  1. Free-body diagram. We choose the board as our object, and assume it
  is horizontal. Its free-body diagram is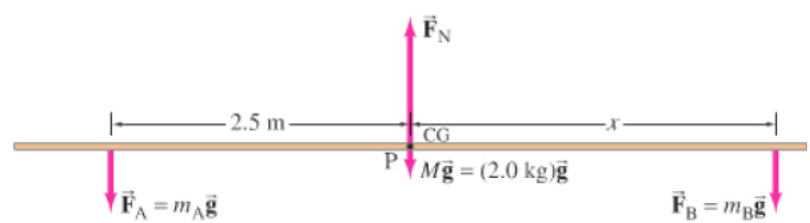
  

  
  

  The forces acting on the board are the forces exerted downward on it
  

  by each child, and  , the upward force exerted by the pivot  and
  the force of gravity on the board (= Mg) which acts at the center of the
  uniform board.
  

  2. Coordinate system. We choose y to be vertical, with positive upward,
  and x horizontal to the right, with origin at the pivot.
  

  3. Force equation. All the forces are in the y (vertical) direction, so
  

  
  

  4. Torque equation. Let us calculate the torque about an axis through the
  board at the pivot point, P. then the lever arm for FN and for weight of
  the board are zero , and they will contribute zero torque (about point P)
  

  in our torque equation. Thus the torque equation will involve only the
  

  forces  and  , which are equal to the weights of children. The torque
  exerted by each child will be mg times the appropriate lever arm, which
  here is the distance of each child from the pivot point. Hence the torque
  equation is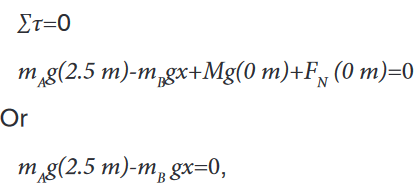
  

  
  

  where two terms were dropped because their lever arms were zero.
  

  5. Solve. We solve the torque equation for x and find

  
  

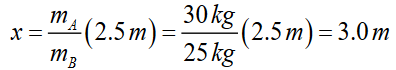
  To balance the seesaw, child B must sit so that her CM is 3.0 m from the
  pivot point. This makes sense: since she is lighter, she must sit farther from
  the pivot than the heavier child.

  Application activity 20.5

  A seesaw consisting of a uniform board of mass M = 10 kg and length l =
  2 m supports a father and a daughter with mass mf and md, 50 kg and 20
  kg respectively as shown in the figure. The support (called the fulcrum) is
  under the centre of gravity of the board. The father is a distance d from
  the center, and the daughter is at distance l/2 from the center.
  

  a) Determine the magnitude of the upward force (reaction) n exerted
  by the support on the board.
  

  b) Determine where the father should sit to balance the system.
  

  
  

  
  

  Skills lab 20
  

  Title: determination of the mass of the meter rule
  Apparatus: 2 meter rules, knife edge, 6 masses of 10 g,
  

  Procedure
  1. Balance the meter rule provided on a knife edge with the graduated
  side facing upwards.
  

  2. Note the balance point P and record its distance from B.
  

  3. Place a mass M of 10 g on the top of mater rule at the 10 cm mark and
  balance the arrangement as shown in figure below.
  

  4. Read and record distance l₁ and l₂
  

  5. Repeat the procedures (3) and (4) from the values of M = 20,30,40,50,
  and 60g.

  6. Record your results in a suitable table including the values of l₂−l₀ and
  

  
  

  7. Plot a graph of M against
  

  8. Find the slope of your graph.

  
  

  End unit assessment 20

  1. ............................ is an example of a scalar quantity
  a) Velocity. b) Force. c) Volume. d) Acceleration.
  

  2. ............................ is an example of a vector quantity
  a) Mass. b) Force. c) Volume. d) Density.
  

  3. A scalar quantity:
  a) Always has mass.
  b) Is a quantity that is completely specified by its magnitude.
  c) Shows direction.
  d) Does not have units.
  

  4. A vector quantity
  a) Can be a dimensionless quantity.
  b) Specifies only magnitude.
  c) Specifies only direction.
  d) Specifies both a magnitude and a direction.
  

  5. A boy pushes against the wall with 50 kilograms of force. The wall
  does not move. The resultant force is:
  a) -50 kilograms.
  b) 100 kilograms.
  c) 0 kilograms.
  d) -75 kilograms.
  

  6. a) State the principle of moment
  b) What are the conditions for equilibrium?
  

  7. Calculate the magnitudes FA and FB of the tensions in the two
  cords that are connected to the vertical cord supporting the 200kg
  chandelier in the following figure.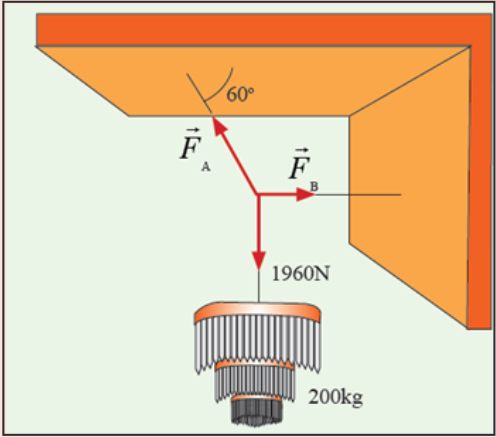
  

  
  

  8. A horizontal rod AB is suspended at its ends by two strings. (See the
  figure below). The rod is 0.6m long and its weight of 3N acts at G
  where AG is 0.4m and BG is 0.2m. Find the tensions X and Y

  
  

  
  

  
  

• UNIT 21: PROJECTILE AND UNIFORM CIRCULAR MOTION

  Key Unit competence: Analyse and solve problems related to
                                                 projectile and circular motion.

  Introductory Activity 21
  1. a) Throw a ball, a stone or any object upwards.
  b) State what happens.
  c) Hold a ball in your hands and release it to fall.
  d) Is the motion of the ball same as in the first case?
  e) Note down your observation.
  f) Relate your observations for bodies moving linearly.

  2. Observe the following image thereafter answer the question below

  

  a) What happen for this bicyclist to turn on level ground easily?

  21.1. Projectile Motion
  
  

  Activity 21.1

  1. a) Kick the football individually.
  b) By observing, the flight of the ball state whether it will cover a
  longer horizontaldistance when it is projected at a large angle or
  a small angle.
  c) Explain your observation and note down any key points in your
  book.

  2. Observe the image below and thereafter answer the next questions:

  

  a) If the rifle is fired directly at the target in a horizontal direction, will
  the bullet hit the center of the target?

  b) Does the bullet fall during its flight?

  Projectile motion is a predictable path traveled by an object that is influenced
  only by the initial launch speed, launch angle, and the acceleration due to
  gravity. You can try it out from where you’re sitting. Pick up an object, and
  gently toss it up and away from you. It will rise as it flies away from you,
  reach a maximum height, and then start falling down to the floor. Toss a few
  more objects while you’re at it. As long as you’re not tossing pieces of paper
  or feathers, the projectile paths should be similar

  Airplanes and birds are not considered projectiles because they are self-
  propelled. Neglecting air resistance, it is relatively easy to calculate the
  height reached, the horizontal distance travelled, and the object’s velocity
  at any point in time, given only the initial velocity and the angle at which the
  projectile was propelled. The path taken is called a trajectory. We have three
  cases: oblique projection, vertical projection and horizontal projection.

  The best angle to kick the football, If I am kicking the ball really slow, a 45°
  would be close to the best angle. At an angle of 45°, you get the best of both
  horizontal velocity and time for the ball to be in the air.

  A projectile, in other words, travels the farthest when it is launched at an
  angle of 45 degrees.

  The greatest distance is achieved using an angle close to 45° if the effects
  of air resistance are negligible.

  Key terms in projectile

  
  • A projectile is any object that is given an initial velocity and then follows
  a path determined entirely by gravitational acceleration. Regardless
  of whether you›re launching a balloon, a baseball, or an arrow, all
  projectiles follow a very predictable path, making them a great tool for
  studying kinematics.

  • Trajectory: The path of aprojectile in motion, a parabola upward and
  across space.

  • Maximum height:The highest vertical position along its trajectory. The
  object is flying upwards before reaching the highest point and it’s falling
  after that point. It means that at the highest point of projectile motion,
  the vertical velocity is equal to 0 (Vy = 0).

  • The horizontal range of a projectile:The distance along the horizontal
  plane it would travel, before reaching the same vertical position as it
  started from.

  • Time of flight: is the amount of time spends in the air. If the ground from
  which the projectile is launched is level, the time of flight only depends
  on the initial velocity V0, the launch angle λ, and the acceleration due
  to gravity.

  • Angle of projection is the angle between the initial velocities of a body
  from a horizontal plane through which the body is thrown.

  Application activity 21.1

  
  1. Make a research on other terms used in projectile motion
  2. Draw an image of an object which can apply different terms used in
      projectile motion thereafter interpret it.

  21.2. Applications of projectile motion
  

  Activity 21.2
  

  Task 1

  1. Analyze the picture below and answer those questions:

  

  a) What is the cause turning back of this kicked ball?

  b) Through your analysis, if the ball is kicked at 450 from horizontal
  for first session and at 60⁰ from horizontal for second session.
  What will happen? Explain your reason.

  Task 2

  
  You may have seen soldiers in the television news firing their rifles into the
  air to celebrate some victory. The bullets travel as high speed projectiles
  and, despite air resistance, return to Earth at high enough speeds to be
  dangerous. Reports indicate that from time to time people are injured by
  the returning bullets.

  a) Explain your reasoning about the above statement

  b) Plot a graph of the motion of rifles they flown

  Task 3

  At the instant horizontally pointed cannon is fired, a cannonball held at
  the cannon’s side is released and drops to the ground. Which cannonball
  strikes the ground first, the one fired from the cannon or the one dropped?

  The first important area which comes to mind is ball games and sports.
  Footballs are heavy enough to follow a nearly parabolic trajectory, without
  spin, with the effect of spin often being spectacular. Footballers have to
  develop a feel for such trajectories.

  A cricket ball is small and dense enough to follow a nearly parabolic path,
  and it is up to the batsman to judge this, in playing his shot. The fielder must
  firstly get himself into the same plane as the flight, and then needs to judge

  where to place himself. The symmetry of the flight means that when it comes
  down to a catchable height, it will be moving at the same speed that it left
  the bat.

  With tennis and table tennis, the constant use of spin, even with lob shots,
  makes parabolic trajectories less important. This is also true in games such
  as golf, where spin predominates, and in rugby, where the shape of the ball
  affects its motion.

  Scoring from distance in basketball is an example of the pure judgement of
  parabolic flight, and can only be mastered by constant practice.

  There are the obvious throwing events, such as javelin, shot put and hammer,
  where there is obviously pure projectile motion, but this is also the case
  in jumping events, where the centre of mass of the body follows a purely
  parabolic trajectory after take off.

  Fundamentally, we can say that whenever anything moves freely, without
  support, we have an example of projectile motion, and there are many that
  are not mentioned, but perhaps we ought to end with satellites and space
  stations. These orbit the earth in circles, but they are still in constant freefall,
  and they are still technically projectiles, and an example of projectile motion.

  21.2.1. Horizontal projection

  
  Along Y-axis the object moves as in a free fall which means that the motion
  is accelerated by g in the opposite direction of the axis. On the X-axis there
  is no acceleration and the object moves as in a URM.

  

  a. General condition
  

  Velocity

  
  

  
  

  
  

  
  

  
  

  
  

  
  

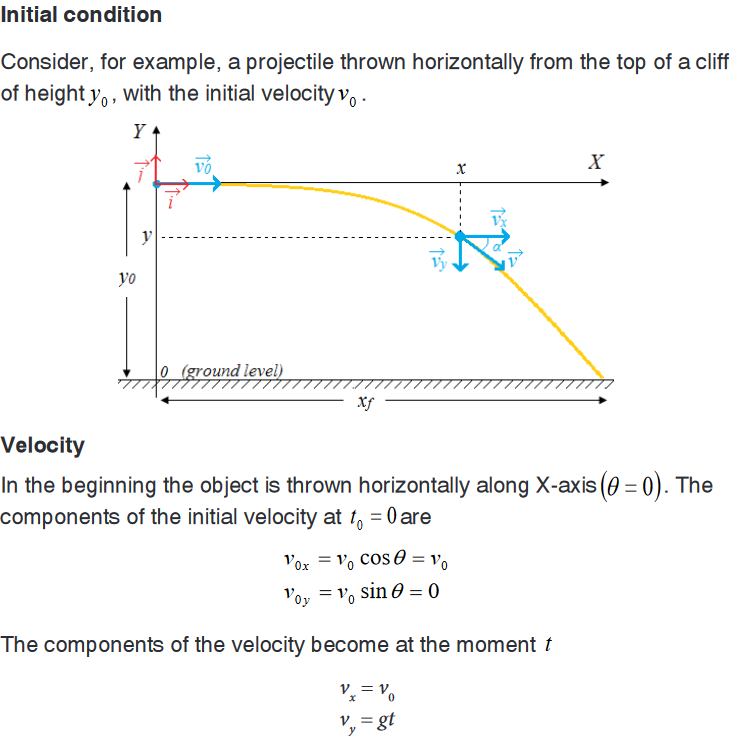
  21.2. Motion of a projectile thrown obliquely
  Now, we are going to examine the more general motion of object moving
  through the air in two dimensions near the Earth’s surface, such as a golf
  ball, athletes doing the long jump or high jump. Specifically, in the absence
  of air resistance, there is no acceleration in the horizontal or x direction and
  the object moves as in the URM. In the y direction, the object moves as in
  

  the UDRM until when the object reaches the maximum height y_m . After, the
  motion proceeds as when the projectile is thrown horizontally.
  

  
  

  Consider now, a projectile fired obliquely with initial velocity  at an angle
  θ above the horizontal axis.
  

  a. General condition
  When an object is fired obliquely, in the upward motion, it goes decelerating.
  After reaching the maximum height, it goes downward accelerating. We
  still can refer to the general conditions of the motion of a projectile thrown
  horizontally
  

  b. Initial condition
     • Position
  The projectile coordinates at the moment t are
  

  
  

  Note that the maximum height for a given initial velocity 0v will be reached
  if the object is launched at  , which the motion of a projectile is thrown
  vertically.

  Motion duration

  The motion of the object from the maximum height is similar to the motion
  of a projectile thrown horizontally from the equivalent height .The time t_g
  it takes the object to reach the ground from the maximum height is also
  deduced similarly.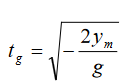
  

  
  

  Then, the total duration of the motion will be the sum of the time to reach
  the maximum height t_m and the time to reach the ground from the maximum
  height t .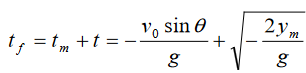
  

  
  

  c. Oblique motion launched from the ground level

  
  

  Motion duration

  If the object is launched from the ground (y₀ =0) , it takes the same time to
  reach the maximum height as to fall back to the ground.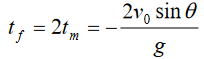
  

  
  

  Range

  We can find how far away the projectile hits the ground as we know that
  

  
  

  
  

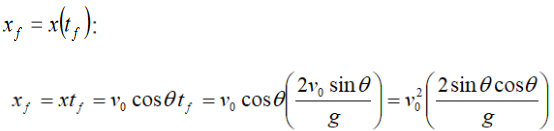
  The maximum range, for a given initial velocity v₀ , is obtained when the sine
  takes on its maximum value of 1, which occurs for  In this case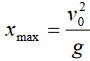
  

  
  

  Notice: The magnitude of g is
  Motion of projectiles thrown obliquely
  

  
  

  The paths of projectiles launched at the same speed but at different
  angles. The paths neglect air resistance. On the figure above the paths of
  several projectiles all having the same initial speed but different projection
  angles. The figure neglects the effects of air resistance, so the paths are all
  parabolas. Notice that these projectiles reach different heights above the
  ground. They also travel different horizontal distances, that is, they have
  different horizontal ranges. The remarkable thing to note form the figure
  above is that the same range is obtained for two different projection angles,
  angles that add up to 90⁰.
  

  For example, an object thrown into the air at an angle of 60⁰ will have the
  same range as if it were thrown at 30⁰ with the same speed. Of course, for
  the smaller angle the object remains in the air for a shorter time.
  

  We have emphasized the special case of projectile motion for negligible air
  resistance.
  

  Example
  A football is kicked at an angle Ɵ₀ = 37.00 with a velocity 20.0 m/s. calculate
      a). The maximum height,
      b). The time of travel before the football hits the ground,
      c). How far away it hits the ground.
      d). The velocity vector at the maximum height,
      e). The acceleration vector at the maximum height. Assume the ball
            leaves the foot at ground level, and ignore air resistance and rotation
            of the ball.

  Solution

  We resolve the initial velocity into its components
  v_x0=v₀ cos37.0⁰ =(20.0 m⁄s)(0.799)=16.0 m⁄s
  v_y0=v₀ sin37.0⁰ =(20.0 m⁄s)(0.602)=12.0 m⁄s
  

  a). We consider a time interval that begins just after the football loses
  contact with the foot until it reaches its maximum height. During this
  time interval, the acceleration is g downward. At the maximum height,
  the velocity is horizontal so, v_y=0 and this occurs at a time given by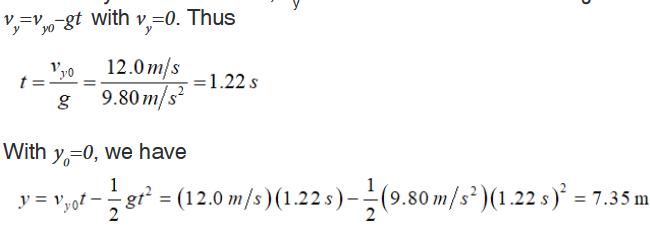
  

  
  

  The maximum height is 7.35 m
  b) To find the time interval it takes for the ball to return to the ground,
  we consider a different time interval, starting at the moment the ball
  leaves the foot (t=0, y₀ = 0) and ending just before the ball touches
  the ground (y = 0).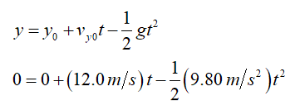
  

  
  

  This equation can be easily factored:
  

  
  

  There are two solutions, t (which corresponds to the initial point, y0),
  and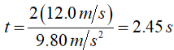
  

  
  

  Which is the total travel time of the football.
  c) The total distance traveled in the x-direction is found by:
  

  
  

  d). At the highest point, there is no vertical component to the velocity. There
  is only the horizontal component (which remains constant through the
  flight), so
  

  
  

  The acceleration vector is the same at the highest point as it is throughout
  the flight, which is 9.80 m⁄s2 downward.
  

  
  

  Application activity 21.2
  
  

  1. There is more than one way to prove that the horizontal and vertical
  components of a projectile’s motion are independent of each other.
  Describe two or three ways that you could use to analyze the motion
  of the two balls.
  

  2. A projectile is launched at an angle into the air. Neglecting
  air resistance, what is its vertical acceleration? Its horizontal
  acceleration? At what point in its path does a projectile have
  minimum speed?
  

  3. A cannon ball is fired with an initial velocity of 100. m/s at an angle
  of 45° above the horizontal. What maximum height will it reach and
  how far will it fly horizontally?
  

  21.3. Circular motion: Meaning and related key terms
  

  Activity 21.3
  
  

  Study carefully the motion of the ball shown below.
  

  1. From your observation of below figure, how can a body move in that
  circular path? Explain your reason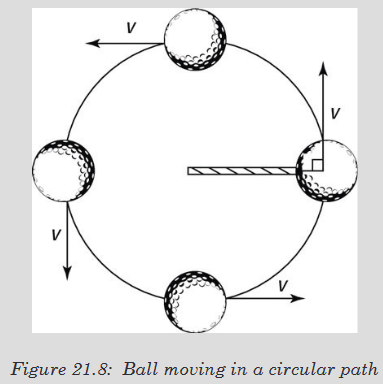
  

  
  

  Circular motion: Movement of an object along the circumference of a circle,
  or rotation along a circular path. It is a motion with constant velocity.
  

  
  

  
  

  
  

  
  

  
  

  To indicate the angular position of a particle, or how far it has rotated we
  specify the angle θ of a line joining the centre of the particle and its position
  with respect to some reference line, such as the x axis. Consider an object
  moving in a circle of radius r with a uniform speed v round a fixed point 0
  as centre.
  

  When an object rotates the angular displacement 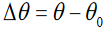, the average
  angular velocity is defined as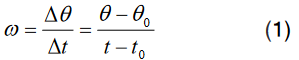
  

  
  

  The linear displacement or the Arc of the object along the circle is
  

  
  

  The linear average velocity

  
  

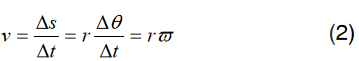
  We define the instantaneous angular velocity as the very small angle θ∆ ,
  through which the object turns in the very short time interval t∆ :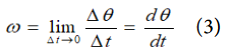
  

  
  

  The instantaneous linear velocity

  
  

  The angular velocity is generally specified in radian per second
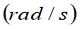
  whereas the instantaneous linear velocity is expressed in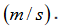
  

  21.4.2. Periodic time and frequency

  The period T is the time needed for the object to make one complete revolution.
  During this time, the object travels a distance equal to the circumference of
  the circle. The frequency f is referred to as the number of revolutions made
  by an object in one second. The unit of frequency is Hertz.
  

  
  

  The object’s angular speed is then represented by

  21.4.3. The average angular acceleration

  The average angular acceleration is defined as the change in angular velocity
  divided by the time required to make this change:
  

  
  

  The average linear acceleration

  
  

  The instantaneous angular acceleration is

  
  

  The instantaneous linear acceleration

  
  

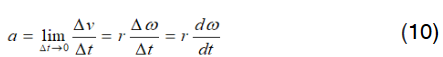
  The angular acceleration is generally specified in radian per second
  whereas the instantaneous linear acceleration is expressed in
  

  
  

  
  

  Application activity 21.4
  1. A ball at the end of a string is revolving uniformly in a horizontal circle
  of radius 2 meters at constant angular speed 10 rad/s. Determine the
  magnitude of the linear velocity of a point located:
  a) 0.5 meters from the center
  b) 1 meter from the center
  c) 2 meters from the center
  

  2. The blades in a blender rotate at a rate of 5000 rpm. Determine the
  magnitude of the linear velocity :
  a) a point located 5 cm from the center
  b) a point located 10 cm from the center
  

  3. A point on the edge of a wheel 30 cm in radius, around a circle at
  constant speed 10 meters/second.
  What is the magnitude of the angular velocity?
  

  4. The angular speed of wheel 20 cm in radian is 120 rpm. What is the
  distance if the car travels in 10 seconds.
  

  21.5. Acceleration in circular motion: Constant and
  tangential acceleration
  

  Activity 21.5
  

  A car executing a turn, after a certain speed limit, a car will start drifting.
  

  Why at that limitation of the speed the car start travelling? Explain your
  reasoning
  

  21.5.1. Tangential and Centripetal acceleration
  

  In the circular motion, the tangential acceleration Ta always points in the
  direction tangent to the circle and changes the rate of velocity in terms of
  magnitude because their vectors are always in the same or opposite direction.
  The tangential acceleration can be considered as the linear acceleration.
  

  The centripetal acceleration (normal acceleration or radial acceleration) Na
  changes the velocity in terms of direction and its vector is perpendicularly
  directed inward the circle.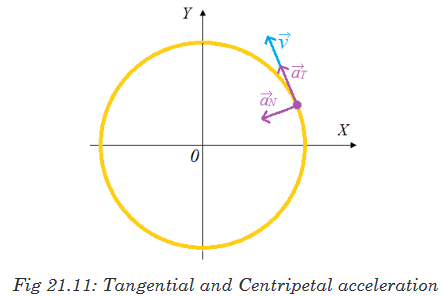
  

  
  

  Since the velocity is constant, the tangential component of acceleration
  doesn’t exist in UCM: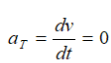

  
  

  Consequently, the tangential component of the acceleration is also zero.
  Only, the normal component of the acceleration exists in UCM. Thus, the
  velocity v changes in direction but not in magnitude. The figure below
  shows the representation of the angular velocityusing a distant reference
  frame
  

  
  

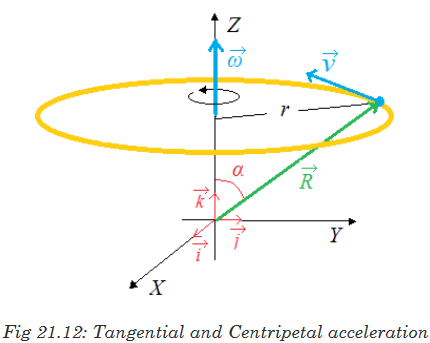
  The centripetal component of the acceleration is directed along the radius.
  From the above figure we can notice that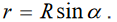
  

  
  

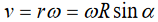
  This relation indicates that the vector can be expressed in the vector form
  by the equation:
  

  
  

  It follows that

  
  

  Introducing the equation (1) into (2)

  
  

  The magnitude of the centripetal acceleration is given by

  
  

  
  

  21.5.2. Acceleration in a non-uniform circular motion

  Circular motion at a constant speed occurs when the acceleration of the object
  is directed toward the centre of the circle (Only the centripetal component is
  available). If the acceleration is not directed toward the centre but is at an
  angle, as shown in figure below, the acceleration has two components; the
  centripetal and the tangential component.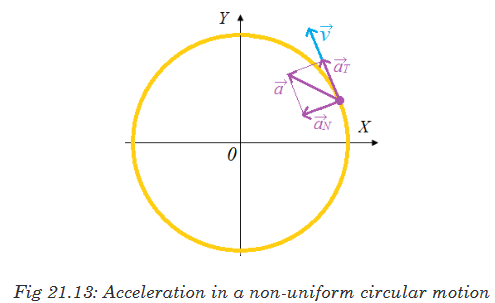
  

  
  

  The tangential component of the acceleration is the rate that changes the
  magnitude of the velocity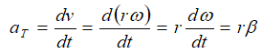

  
  

  The centripetal acceleration arises from the change in direction of the velocity
  and, as we have seen, is given by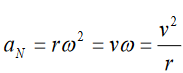

  
  

  If the tangential acceleration is in the direction of motion i.e. parallel to , the
  speed is increasing and if it is antiparallel to  is the speed is decreasing.
  

  In either case,  and 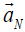are always perpendicular to each other; and their
  directions change continually as the object moves along its circular path.
  The total vector acceleration is the sum of these two: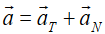
  

  
  

  the magnitude of  at any moment is
  

  
  

  21.5.3. Distance time graph of circular motion

  When an object executes a circular motion of constant radius R, its projec-
  tion on an axis executes a motion of amplitude a that repeats itself back
  and forth, over the same path.
  

  
  

  When M executes a uniform circular motion, its projection on X-axis executes
  a back and forth motion between positions P and P’ about O.

  Considering the displacement and the time, we find the following graph
  

  
  

  Application activity 21.5
  

  1. A ball is attached to a string that is 1.5m long. It is spun so that it
  completes two full rotations every second. What is the centripetal
  acceleration felt by the ball?
  

  2. Imagine a car driving over a hill at a constant speed. Once the
  car has reached the apex of the hill, what is the direction of the
  acceleration?
  

  21.6. Centripetal force
  

  Activity 21.6

  Observe the following figure and answer the question below:
  

  
  

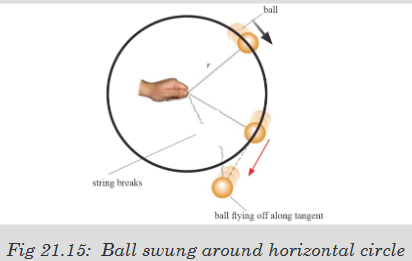
  What would happen when a ball is attached to a string and is swung
  round in horizontal circle? Explain your reasoning.
  

  If you try to move in a circular path, you will finally notice that you keep
  moving in a circle even when you try to stop. There is a force that keeps you
  more in a circular path called centripetal force. Since a body moving in a
  circle (or a circular arc) is accelerating, it follows
  

  from Newton’s first law of motion that there must be force acting on it to
  cause the acceleration.
  

  This force, like the acceleration, will also be directed toward the centre and
  is called the centripetal force. The value F of the centripetal force is given by
  

  Newton’s second law, that is:
  

  Wherem is the mass of the body and v is its speed in circular path of radius

  R. If the angular velocity of the body is ω, we can also say, since V = Rω,

  
  

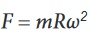
  Application activity 21.6

  1. A 3.0 kg mass is tied to a rope and swung in a horizontal circle. If the
  velocity of the mass is 4.0 m/s and the radius of the circle is 0.75 m,
  what is the centripetal force and centripetal acceleration of the mass?
  

  2. A 200-gram ball, attached to the end of a cord, is revolved in a
  horizontal circle with an angular speed of 5 rad s-1. If cord’s length is
  60 cm, what is the centripetal force?
  

  3. A student of mass 50kg decides to go on the ride. The coefficient of
  static friction between the student and wall is 0.8. If the diameter of
  the ride is 10m, what is the maximum period of the ride’s rotation that
  will keep the student pinned to the wall once the floor drops? g=10m/s2
  

  21.7. Applications of circular motion
  

  Activity 21.7
  

  Task 1
  

  1. What is the difference between horizontal and vertical circular
  motion?
  

  2. Does gravity affect horizontal circular motion? Explain your reason
  

  Task 2

  a) Tie a thread of about 50cm on retort stand.
  b) On a thread, tie a pendulum bob.
  c) Displace the bob through a certain angle. What do you observe?
  d) Release the bob to move through a certain angle so that it moves
  in a horizontal circle.
  e) Try to investigate forces acting in the bob.
  

  Task 3

  Observe the following image and answer the related questions
  

  
  

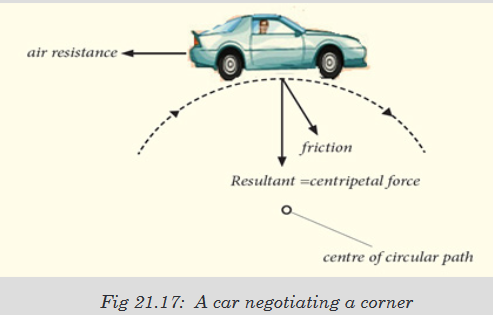
  a) Explain the way the driver will use for not falling down at that
  corner of the above figure
  

  b) Identify different factors needed to travel properly in the corner
  

  21.7.1. Vertical and horizontal circle
  

  1. Vertical circle
  

  Taking the approach that the ball moves in a vertical circle and is not
  undergoing uniform circular motion, the radius is assumed constant, but the
  speed v changes because of gravity. The free-body diagram is shown in the
  figure below for the positions 1 and 2.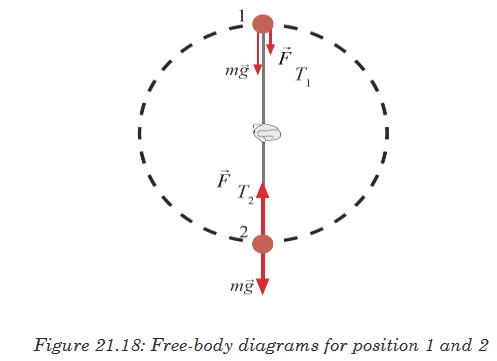
  

  
  

  a) At the top (point 1), two forces act on the ball: the force of gravity and
  the tension force the cord exerts at point 1. Both act downward and their
  vector sum acts to give the ball its centripetal acceleration. We apply
  Newton’s second law, for t a vertical direction, choosing downward as
  positive since the acceleration is downward (toward the centre):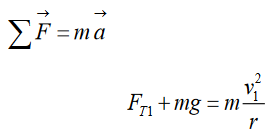
  

  
  

  From this equation, we can see that the tension force F_T1 at point 1 will
  get larger if V₁ (ball’s speed at top of circle) is made larger, as expected.
  But we are asked for the minimum speed to keep the ball moving in a
  circle.

  The cord will remain taut as long as there is tension in it. But the tension
  disappears (because V₁ is too small), the cord can go limp and the ball
  will fall out of its circular path. Thus, the minimum speed will occur if F_T1
  = 0, for which we have (minimum speed at top)
  

  We solve for V₁:
  

  
  

  This is the minimum speed at the top of the circle if the ball is to continue
  moving in a circular path.
  

  b) When the ball is at the bottom of the circle (point 2 in the figure 21.9), the
  cord exerts its tension force upward, whereas the force of gravity, still
  acts downward. So we apply Newton’s second law, this time choosing
  upward as positive since the acceleration is upward (toward the centre):
  

  
  

  We solve for

  
  

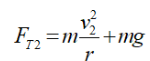
  2. Horizontal circle
  

  The second case is the case of a force on revolving ball (horizontal) which is:
  

  Estimate the force a person must exert on a string attached to a ball to make
  the ball revolve in a horizontal circle of radius r.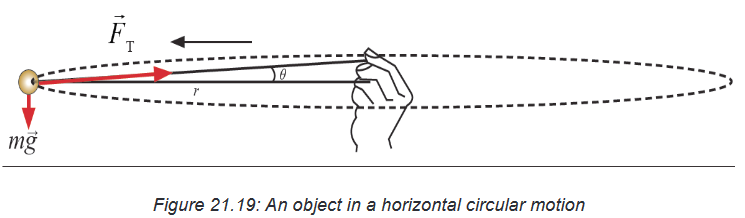
  

  
  

  The forces acting on the ball are the force of gravity, downward, and the
  tension that the string exerts toward the hand at the centre. The free-
  body diagram for the ball is as shown in the figure 21.22. The ball’s weight
  complicates matter and makes it a little difficult to revolve a ball with the cord
  perfectly horizontal.

  We assume the weight is small and put in the figure 21.22. Thus the tension
  will act nearly horizontally and, in any case, provides the force necessary to
  give the ball its centripetal acceleration. We apply Newton’s second law to
  the radial direction ∑F=m_aN where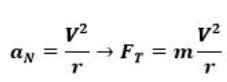
  

  
  

  21.7.2. Conical pendulum
  

  A small object of mass m is suspended from a string of length L. The object
  revolves with constant speed v in a horizontal circle of radius r, as shown
  in Figure 21.9.2. Because the string sweeps out the surface of a cone, the
  system is known as a conical pendulum.
  

  Let us find an expression for v.
  

  
  

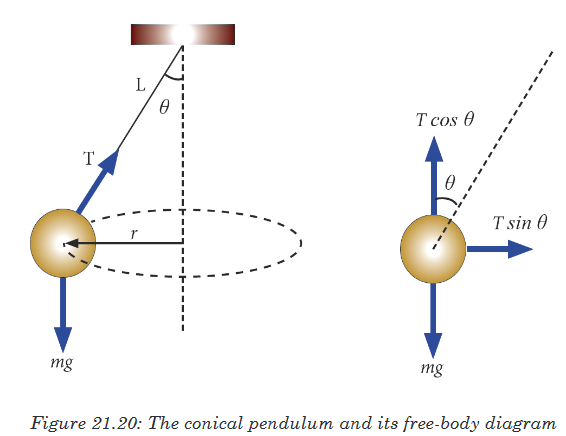
  To analyse the problem, begin by letting θ represent the angle between the
  string and the vertical. In the free-body diagram shown, the force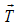 exerted
  by the string is resolved into a vertical component and a horizontal
  component acting toward the centre of revolution. Because the
  object does not accelerate in the vertical direction,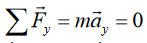 and the
  upward vertical component of must balance the downward gravitational
  force. Therefore;
  

  

  Because the force providing the centripetal acceleration in this example is
  the component , we can use the formula of centripetal acceleration to obtain
  

  
  

  21.7.2. Conical pendulum
  

  
  

  
  

  Where m and v are the mass and the speed respectively of the car and R is
  the radius of the bend.

  Also, the car is assumed to remain in the same horizontal plane and so has
  no vertical acceleration, therefore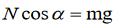

  Hence by division:
  

  
  

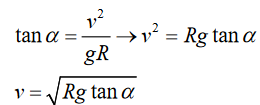
  The equation shows that for a given radius of bend, the angle of banking is
  only correct for one speed.
  

  Example
  A ball on the end of a string is revolved at a uniform rate in a vertical circle
  of radius 72.0 cm, as shown in figure below. If its speed is 4.00 m/s and its
  mass is 0.300 kg; calculate the tension in the string when the ball is
  

  a). At the top of its path,
  b). At the bottom of its path
  

  
  

  Solution
  

  a). Take positive to be downward. Write Newton’s 2nd law in the downward
  direction.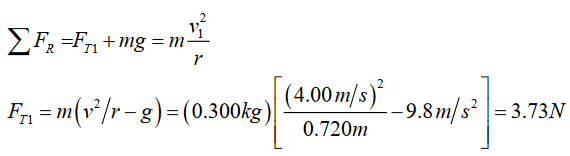
  

  
  

  This a downward force, as expected.

  b). Take positive to be upward. Write Newton’s 2nd law in the upward
  direction.This is an upward force, as expected.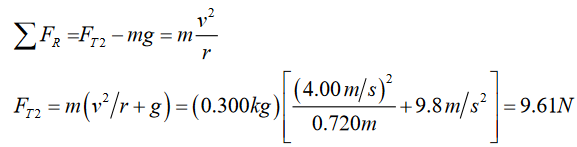
  

  
  

  Application activity 21.7
  1. Why do we give banking to curved roads?
  2. A particle is revolving in a circle increasing its speed uniformly. Which
  of following is constant? why? and why not? Explain the all three of
  option.
  a) Centripetal force b) Tangential acceleration c) Angular
  acceleration
  3. A steel ball of mass 0.5kg is suspended from a light inelastic string of
  length 1m. The ball swings in a horizontal circle of radius 0.5 m. Find
  i. The centripetal force and tension in the string.
  ii. The angular Speed of the ball.
  4. A student twirls a 75 gram weight at the end of a string in a horizontal
  circle of radius 50 cm. If the speed of the weight is 7.0 m/s, what is
  the tension in the string?
  

  Skills lab 21

  Go on youtube.com, watch video about “Trucks fail to Negotiate Dangerous
  Bend in Road ”. It is a social issue which relationship with Circular motion.
  1. What did you see on the video and what happen?
  2. If you are engineer, how you will solve this problem?
  3. Brainstorm with your classmates about the property needed to design a
      safety road by used scientific knowledge in Circular motion.
  

  End unit assessment 21
  1. At the instant a ball is thrown horizontally over a level range, a ball
      held at the side of the first is released and drops to the ground. If air
      resistance is neglected, which ball strikes the ground first?
  

  2. Neglecting air resistance, if you throw a ball straight up with a speed
      of 20m/s, how fast will it be moving when you catch it?
  

  3. A body describes a circumference of radius 2m and the motion is
      uniform. It does 2 rotations in 6s. If π² = 9.86, find the centripetal
      acceleration.
  

  4. A moving body is in uniform circular motion. The radius of the
     circle is 25m. Assuming that the acceleration equals 9m/s², find the
     angular velocity.
  

  5. How many rotations a wheel of 3.20m diameter does in one minute.
      Assuming that the linear speed is equal to 16m/s?

  6. A ball at the end of a string is swinging in a horizontal circle of radius
      1.15m. The ball makes exactly 2.00 revolutions in a second. What is
      its centripetal acceleration?
  

  7. The wheel of an engine of 4m diameter does 90 rotations per minute.
        Calculate:
  h) The linear speed.
  i) The angular speed.
  j) The centripetal acceleration.
  

  8. What is the angular velocity of the earth around its axis? What is the
       linear velocity of a point situated at the equator? The radius of the
       earth is supposed to be 6400km.
  

• UNIT 22: GENERAL STRUCTURE OF SOLAR SYSTEM

  Key Unit competence: To illustrate and describe the general
                                                 structure of the solar system.

  Introductory Activity 22

  Observe the following illustration and answer the questions

  

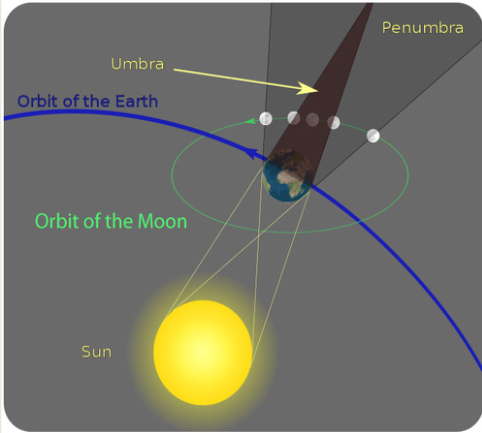
  Questions:
  a) What do you see in the illustration above?
  b) Can you suggest how the bodies identified in the illustration
  above move? Explain to support your decision?
  c) Explain how the earth receives light during the night?
  d) What causes day and night? Explain your answer with possible
  illustrations.
  e) How do Kepler talk about the general structure of the solar
  system? Justify your arguments with possible illustrations.

  22.1. Astronomical scales
  

  Activity 22.1

  1. Student-teachers interpret reality from their perspective of the world
  around them. As a result their everyday thinking about space and time
  is often limited to local conditions; often at most perhaps hundreds of
  kilometre or decades of years. Vast distances and times are central
  ideas in ‘the changing Earth and its place in space’.

  Questions: Read the paragraph above and try to answer the following
  questions;

  a) Explain how these ideas are very difficult for student-teachers to
  grasp.

  b) Explain why it has very important implications for their learning of
  ideas about distances in space or very long spans of time.

  22.1.1. Origin of the solar system

  Our solar system originated from a giant cloud of gas and debris left from
  the explosion of stars five billion years ago. Everything in the universe and
  on Earth is made of this material. Scientific evidence implies that some rock
  near the Earth’s surface is several billion years old.

  The Earth’s surface is shaped by water (including ice) and wind over very
  long times. The change is so slow that it is hard to observe rock erosion and
  soil formation. Biological evolution is also difficult to observe due to the very
  slow changes that occur.

  22.1.2. Astronomical scale

  Astronomy is the study of the universe, and when studying the universe,
  we often deal with unbelievable sizes and unfathomable distances. To help
  us get a better understanding of these sizes and distances, we can put them
  to scale.

  Scale is the ratio between the actual object and a model of that object.
  Some common examples of scaled objects are maps, toy model kits, and
  statues. Maps and toy model kits are usually much smaller than the object it
  represents, whereas statues are normally larger than its analog.

  Our solar system is immense in size. We think of the planets as revolving
  around the sun but rarely consider how far each planet is from the sun or from
  each other. Furthermore, we fail to appreciate the even greater distances to

  the other stars. Astronomers refer to the distance from the sun to the Earth
  as one“astronomical unit” or AU = approximately 150 million kilometres. This
  unit provides an easy way to calculate the distances of the other planets
  from the sun and build a scale model with the correct relative distances.

  Viewed from Earth it is difficult to gauge the scale of the universe but
  astrophysicists have developed techniques to help to do this. Stars and
  galaxies are so far away than a new unit of distance measurement, the
  light-year (ly),is often used. For light travelling at 3 x 108m/s, the distance
  traveled in oneyear is:1 ly = (3 x 108 m/s) x (365 x 24 x 60 x 60 s) = 9.46 x
  1015 m.

  For specifying distances to the Sun and Moon, we usually use metres or
  kilometres, but we could specify them in terms of light. The Earth-Moon
  distance is 384 000 km, which is 1.28 light-seconds. The Earth-Sun distance
  is 1.5 x 1011 m, or 150,000,000 km; this is equal to 8.3 light-minutes. Far out
  in our solar system, the ninth planet, Pluto, is about 6 x 109km from the Sun,
  or 6 x 10-4 ly. The nearest star tous, other than the sun, is Proxima Centauri,
  about 4.3 ly away. (Note that the nearest star is about 10,000 times farther
  from us than the outer reaches of our solar system.)

  The Milky Way or our Galaxy is about 100 000 ly across; our sun is located
  on one

  of the spiral arms of the galaxy at a distance of 28,000 ly from the galactic
  centre.

  Application activity 22.1
  1. Construct a time line to gain perspective of the vastness of time and
       our lifetime in reference to it. Examples of timelines are ‘the origins
       of the solar system’ and ‘life on Earth’. If a helpful scale is used a
       time line representing the age of the Earth can be displayed around
       the walls of their classroom.

  2. Construct a scale model of the solar system with both distances
       and size of planets to scale. If an orange is used to represent the
       size of the sun then the model of the solar system should fit into the
       size of an average school oval.

  22.2. Sun-earth-moon system: eclipses and phases of the
              moon
  

  Activity 22.2

  From our perspective, the three objects that have the greatest impact on
  our lives are the Earth, Sun, and Moon. The Earth, of course, is the planet
  beneath our feet. Without it, well, we wouldn’t have anything at all. The
  Sun warms our planet, and with the Moon, creates the tides. Interpret the
  figure below and try to answer the questions that follow: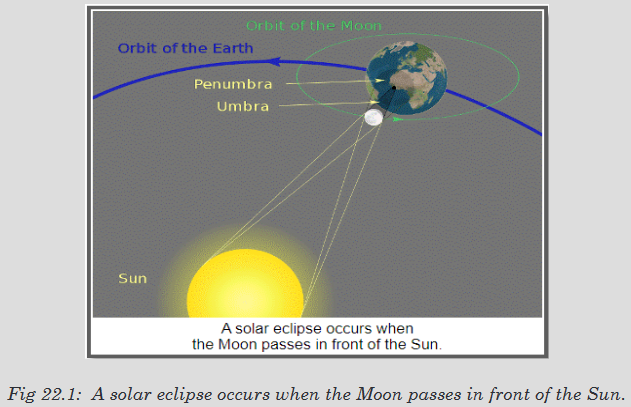

  

  Questions:
  c) Describe how Earth’s movements affect seasons and cause day
       and night.

  d) Explain solar and lunar eclipses.

  e) Describe the phases of the Moon and explain why they occur.

  f) Explain how movements of the Earth and Moon affect Earth’s
      tides

  Eclipse, in astronomy is the obscuring of one celestial body by another,
  particularly that of the sun or a planetary satellite. Two kinds of eclipses
  involve the earth: those of the moon, or lunar eclipses; and those of the sun,
  or solar eclipses. A lunar eclipse occurs when the earth is between the sun
  and the moon and its shadow darkens the moon. A solar eclipse occurs
  when the moon is between the sun and the earth and its shadow moves
  across the face of the earth.

  22.2.1.Lunar Eclipses
  The earth, lit by the sun, casts a long, conical shadow in space. At any point
  within that cone the light of the sun is wholly obscured.

  A total lunar eclipse occurs when the moon passes completely into the
  umbra. If it moves directly through the centre, it is obscured for about 2
  hours. If it does not pass through the centre, the period of totality is less and
  may last for only an instant if the moon travels through the very edge of the
  umbra.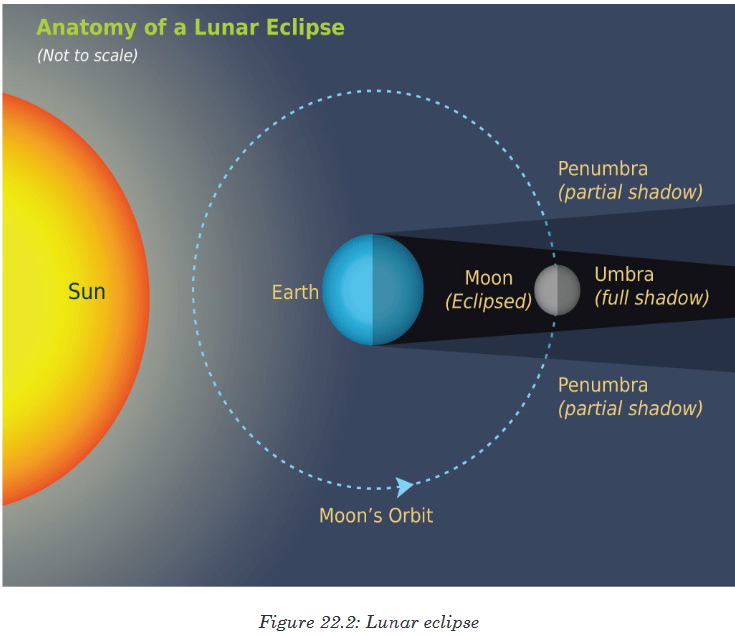

  

  A partial lunar eclipse occurs when only a part of the moon enters the umbra
  and is obscured. The extent of a partial eclipse can range from near totality,
  when most of the moon is obscured, to a slight or minor eclipse, when
  only a small portion of the earth’s shadow is seen on the passing moon.
  Historically,the view of the earth’s circular shadow advancing across the
  face of the moon was the first indication of the shape of the earth.

  
  

  22.2.2.Solar eclipses
  A solar eclipse occurs when the Moon passes in front of the Sun causing a
  shadow to fall on certain portions of the Earth. The eclipse is not seen from
  every place on Earth, but only from the locations where the shadow falls.

  In areas outside the band swept by the moon’s umbra but within the
  penumbra, the sun is only partly obscured, and a partial eclipse occurs.

  Types of Solar Eclipses
  Depending on what part of the shadow you are located in, there are three
  types of eclipses:
  • Total - A total eclipse is where the Sun is covered completely by the
  Moon. The portion of the Earth that is in the umbra experiences a total
  eclipse.
  • Annular - An annular eclipse is when the Moon covers the Sun, but the
  Sun can be seen around the edges of the Moon. An annular eclipse
  occurs when the viewer is within the antumbra.
  • Partial - A partial eclipse is when only a portion of the Sun is blocked
  by the Moon. It occurs when the observer is within the penumbra.
  Caution! Don’t Look at A Solar Eclipse. We should warn you here to never
  look directly at a solar eclipse. Even though it appears darker, the harmful
  rays of the Sun can still damage your eyes.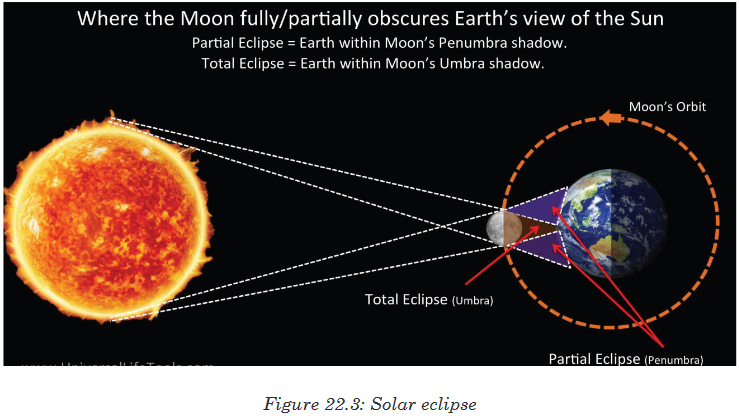

  

  22.2.3. Phases of the moon
  Like everything in the solar system except the Sun, the Moon does not
  produce any light of its own. It only reflects sunlight. As the Moon moves
  around Earth, different portions of the satellite are illuminated. This causes
  the phases of the Moon, so that our view of the Moon goes from fully lit to
  completely dark and back again.

  There are different phases of the Moon that make it appear a little different
  every day, but it looks the same again about every four weeks. The Moon
  can sometimes be seen at night and sometimes during the day.

  Phases of the Moon

  • The Moon is full when Earth is between the Moon and the Sun and the
  Moon’s nearside is entirely lit.

  • The Moon is at first quarter phase about one week later, when the
  Moon appears as a half-circle. Only half of the Moon’s lit surface is
  visible from Earth.

  • The Moon is in a new moon phase when the Moon moves between
  Earth and the Sun and the side of the Moon facing Earth is completely
  dark. Earth observers may be able to just barely see the outline of the
  new moon because some sunlight reflects off the Earth and hits the
  moon.

  • Before and after the quarter-moon phases are the gibbous and crescent
  phases. During the gibbous moon phase, the moon is more than half
  lit but not full. During the crescent moon phase, the moon is less than
  half lit and is seen as only a sliver or crescent shape.

  

  One revolution of the Moon around Earth takes a little over 27 days 7 hours.
  The Moon rotates on its axis in this same period of time, so the same face
  of the Moon is always presented to Earth. Over a period, a little longer than
  29 days 12 hours, the Moon goes through a series of phases, in which the
  amount of the lighted half of the Moon we see from Earth changes. These
  phases are caused by the changing angle of sunlight hitting the Moon. (The
  period of phases is longer than the period of revolution of the Moon, because
  the motion of Earth around the Sun changes the angle at which the Sun’s
  light hits the Moon from night to night).

  Application activity 22.2
  1. What is a solar eclipse?
  a) When the Moon passes in front of the Sun
  b) When the Earth casts a shadow on the Moon
  c) When the Sun is blocked by another planet
  d) All of the above
  e) None of the Above

  2. What do we call the area of a solar eclipse where only a portion of
  the Moon is in front of the Sun?
  a) Umbra b) Antumbra c) Penumbra.

  3) What do we call the area of a solar eclipse where the Moon covers
  the Sun, but the outline of the Sun can still be seen?
  a) Umbra b) Antumbra c) Penumbra

  4) What do we call the area of a solar eclipse where the Moon completely
  covers the Sun?
  a) Umbra b) Antumbra c) Penumbra

  5) What type of solar eclipse occurs when only a portion of the Sun is
  blocked by the Moon?
  a) Total   b) Lunar   c) Special   d) Annular    e) Partial.

  6) What type of solar eclipse occurs when the Sun is completely covered
  by the Moon?
  a) Total    b) Lunar    c) Special    d) Annular    e) Partial.

  7) What is a lunar eclipse?
  a) When the Moon passes in front of the Sun.
  b) When the Earth casts a shadow on the Moon.
  c) When the Sun is blocked by another planet.
  d) All of the above.
  e) None of the Above.

  8) What color will the moon sometimes appear during a lunar eclipse?
  a) Green   b) Blue   c) Yellow    d) Red    e) purple.

  9) Around how long can a solar eclipse last?
  a) 1.5 minutes   b) 7.5 minutes   c) 30minutes    d) 1.5 hours e) 7.5
  hours.

  10) True or False: Looking directly at the Sun during a solar eclipse can
  damage your eyes.

  22.3. Solar system
  

  Activity 22.3
  

  Observe and interpret the image below and try to explain the structure of
  the solar system based on the inner and outer planets.

  

  Solar System is constituted by the Sun and everything that orbits the
  Sun,including the planets and their satellites, the dwarf planets, asteroids,
  and comets, and interplanetary dust and gas...

  22.3.1. Inner planets and outer planets
  In our Solar System, astronomers often divide the planets into two groups:
  the inner planets and the outer planets. The inner planets are closer to
  the Sun and are smaller and rockier. The outer planets are further away,
  larger and made up mostly of gas.

  The inner planets (in order of distance from the sun, closest to furthest)
  are Mercury, Venus, Earth and Mars. After an asteroid belt come the outer
  planets, Jupiter, Saturn, Uranus and Neptune. The interesting thing is, in
  some other planetary systems discovered, the gas giants are actually quite
  close to the sun. This makes predicting how our Solar System formed an
  interesting exercise for astronomers. Conventional wisdom is that the young
  Sun blew the gases into the outer fringes of the Solar System and that is why
  there are such large gas giants there. However, some extra-solar systems
  have “hot Jupiters” that orbit close to their Sun.

  a. The Inner Planets
  The four inner planets are called terrestrial planets because their surfaces
  are solid (and, as the name implies, somewhat similar to Earth — although
  the term can be misleading because each of the four has vastly different
  environments). They’re made up mostly of heavy metals such as iron and
  nickel, and have either no moons or few moons. Below are brief descriptions
  of each of these planets based on this information from National Aeronautic
  and Space Authority of the USA (NASA).

  Mercury
  Mercury is the smallest planet in our Solar System and also the closest. It
  rotates slowly (59 Earth days) relative to the time it takes to rotate around
  the sun (88 days). The planet has no moons, but has a tenuous atmosphere
  (exosphere) containing oxygen, sodium, hydrogen, helium and potassium.
  The NASA MESSENGER (Mercury Surface, Space Environment,
  Geochemistry, and Ranging) spacecraft is currently orbiting the planet.

  

  Venus

  
  Venus was once considered a twin planet to Earth, until astronomers
  discovered its surface is at a lead-melting temperature of 900 degrees
  Fahrenheit (480 degrees Celsius). The planet is also a slow rotator, with
  a 243-day long Venusian day and an orbit around the sun at 225 days. Its
  atmosphere is thick and contains carbon dioxide and nitrogen. The planet
  has no rings or moons and is currently being visited by the European Space
  Agency’s Venus Express spacecraft.

  Earth

  
  Earth is the only planet with life as we know it, but astronomers have found
  some nearly Earth-sized planets outside of our solar system in what could
  be habitable regions of their respective stars. It contains an atmosphere
  of nitrogen and oxygen, and has one moon and no rings. Many spacecraft
  circle our planet to provide telecommunications, weather information and
  other services.

  Mars

  Mars is a planet under intense study because it shows signs of liquid water
  flowing on its surface in the ancient past. Today, however, its atmosphere
  is a wispy mix of carbon dioxide, nitrogen and argon. It has two tiny moons
  (Phobos and Deimos) and no rings. A Mars day is slightly longer than 24
  Earthhours and it takes the planet about 687 Earth days to circle the Sun.
  There’s a small fleet of orbiters and rovers at Mars right now, including the
  large NASA Curiosity rover that landed in 2012.

  b. The Outer Planets
  Sometimes called Jovian planets or gas giants are huge planets swaddled
  in gas. They all have rings and all of plenty of moons each.
  Despite their size, only two of them are visible without telescopes: Jupiter
  and Saturn. Uranus and Neptune were the first planets discovered since
  antiquity, and showed astronomers the solar system was bigger than
  previously thought. Below are brief descriptions of each of these planets
  based on this information from NASA.

  

  Uranus was first discovered by William Herschel in 1781. The planet’s day
  takes about 17 Earth hours and one orbit around the Sun takes 84 Earth
  years.

  Its mass contains water, methane, ammonia, hydrogen and helium
  surrounding a rocky core. It has dozens of moons and a faint ring system.
  There are no spacecraft slated to visit Uranus right now; the last visitor was
  Voyager 2 in 1986.

  Jupiter

  Jupiter is the largest planet in our Solar System and spins very rapidly
  (10 Earth hours) relative to its orbit of the sun (12 Earth years). Its thick
  atmosphere is mostly made up of hydrogen and helium, perhaps surrounding
  a terrestrial core that is about Earth’s size. The planet has dozens of moons,
  some faint rings and a Great Red Spot, a raging storm happening for the
  past 400 years at least (since we were able to view it through telescopes).
  NASA’s Juno spacecraft is en route and will visit there in 2016.

  Saturn
  Saturn is best known for its prominent ring system, seven known rings with
  well-defined divisions and gaps between them.

  How the rings got there is one subject under investigation. It also has dozens
  of moons. Its atmosphere is mostly hydrogen and helium, and it also rotates
  quickly (10.7 Earth hours) relative to its time to circle the Sun (29 Earth
  years). Saturn is currently being visited by the Cassini spacecraft, which will
  fly closer to the planet’s rings in the coming years.

  Uranus

  
  

  Neptune
  Neptune is a distant planet that contains water, ammonia, methane,
  hydrogen and helium and a possible Earth-sized core. It has more than a
  dozen moons and six rings. The only spacecraft to ever visit it was NASA’s
  Voyager 2 in 1989.
  

  Comets
  Comet, small icy body in space that sheds gas and dust. Like rocky asteroids,
  icy comets are ancient objects left over from the formation of the solar system
  about 4.6 billion years ago. Some comets can be seen from Earth with the
  unaided eye.
  

  
  

  Comets typically have highly elliptical (oval-shaped), off-centre orbits that
  swing near the Sun. When a comet is heated by the Sun, some of the ice on
  the comet’s surface turns into gas directly without melting. The gas and dust
  freed from the ice can create a cloud (coma) around the body (nucleus) of
  the comet.
  

  More gas and dust erupt from cracks in the comet’s dark crust. High-energy
  charged particles emitted by the Sun, called the solar wind, can carry the gas
  and dust away from the comet as a long tail that streams into space. Gas in
  the tail becomes ionized and glows as bluish plasma, while dust in the tail is
  lit by sunlight and looks yellowish. This distinctive visible tail is the origin of
  the word comet, which comes from Greek words meaning “long-haired star.”
  

  Humans have observed comets since prehistoric times. Comets were long
  regarded as supernatural warnings of calamity or signs of important events.
  

  Astronomers and planetary scientists now study comets for clues to the
  chemical makeup and early history of the solar system, since comets have
  been in the deep-freeze of outer space for billions of years. Materials in
  comets may have played a major role in the formation of Earth and the origin
  of life. Catastrophic impacts by comets may also have affected the history of
  life on Earth, and they still pose a threat to humans.
  

  
  

  A meteorite is a rock from outer space; it’s a piece of rock that has
  reached Earth from outer space. It can also be defined as a fiery mass of
  rock fromspace, a mass of rock from space that burns up after entering the
  Earth’s atmosphere.
  

  Meteorite, meteor that reaches the surface of Earth or of another planet
  before it is entirely consumed. Meteorites found on Earth are classified into
  types, depending on their composition: irons, those composed chiefly of
  iron, a small percentage of nickel, and traces of other metals such as cobalt;
  stones, stony meteors consisting of silicates; and stony irons, containing
  varying proportions of both iron and stone.
  

  Although most meteorites are now believed to be fragments of asteroids or
  comets, recent geochemical studies have shown that a few Antarctic stones
  came from the Moon and Mars, from which they presumably were ejected
  by the explosive impact of asteroids. Asteroids themselves are fragments of
  planetesimals, formed some 4.6 billion years ago, while Earth was forming.
  Irons are thought to represent the cores of planetesimals, and stones (other
  than the aforementioned Antarctic ones) the crust. Meteorites generally have
  a pitted surface and fused, charred crust. A meteorite that landed in Texas
  in 1998 was found to have water trapped in its rock crystals. The discovery
  helped scientists theorize about whether water exists in other parts of the
  solar system.
  

  The largest known meteorite, estimated to weigh about 60 metric tons, is
  situated at Hoba West near Grootfontein, Namibia. The next largest, weighing
  more than 31 metric tons, is the Ahnighito (the Tent); it was discovered,
  along with two smaller meteorites, in 1894 near Perlernerit (Cape York),
  Greenland, by American explorer Robert Edwin Peary.
  

  Composed chiefly of iron, the three masses had long been used by the Inuit
  as a source of metal for the manufacture of knives and other weapons.
  

  Asteroids
  

  
  

  Asteroid, small rocky or metallic body that orbits the Sun. Hundreds of
  thousands of asteroids exist in the solar system. Asteroids range in size
  from a few metres to over 500km wide. They are generally irregular in shape
  and often have surfaces covered with craters. Like icy comets, asteroids are
  primitive objects left over from the time when the planets formed, making
  them of special interest to astronomers and planetary scientists.
  

  On the figure 12.10, Asteroid Mathilde, left, is the third and the largest
  asteroid ever to be viewed at close range. The Near Earth Asteroid
  Rendezvous(NEAR) spacecraft flew by Mathilde in late June 1997. Asteroids
  Gaspra and Ida, centre and right, photographed by the Galileo orbiter in 1991
  and 1993, respectively, are smaller and more oblong-shaped than Mathilde.
  The three asteroids are partially obscured by shadows.
  

  Most asteroids are found between the orbits of the planets Mars and Jupiter
  in a wide region called the asteroid belt. Scientists think Jupiter’s gravity
  prevented rocky objects in this part of the solar system from forming into
  a large planet. The giant planet Jupiter’s gravity also helped throw objects
  out of the asteroid belt. The hundreds of thousands of asteroids now in the
  asteroid belt represent only a small fraction of the original population.
  

  
  

  Thousands of asteroids have orbits that lie outside the asteroid belt. Some
  of these asteroids have paths that cross the orbit of Earth. Many scientists
  think that an asteroid that hit Earth 65 million years ago caused the extinction
  of the dinosaurs. Because asteroids can pose a danger to people and other
  life on Earth, astronomers track asteroids that come near our planet. Space
  scientists are also studying ways to deflect or destroy an asteroid that might
  strike Earth in the future.
  

  Many scientists believe that a large asteroid or comet struck Earth about
  65 million years ago, changing the Earth’s climate enough to kill off the
  dinosaurs.
  

  
  Application activity 22.3
  1. Which of the following is true about asteroids?
  a) They are made of rock and metal b) The orbit the Sun c) They
  are in outer space d) All of the above e) None of the Above.
  

  2. According to the article, what are most asteroids shaped like?
  a) Ball b) Box c) Potato d) Triangle. e) Orange.
  

  3. What two metals are metallic asteroids mostly made of?
  a) Iron and nickel b) Silver and gold c) Magnesium and copper d)
  Aluminum and zinc e) Lead and iron
  

  4.What is the most common type of asteroid?
  a) Metallic b) Carbon c) Rocky d) Gas e) Round
  

  5. The asteroid belt is located in orbit between what two planets?
  a) Earth and Mars b) Jupiter and Saturn c) Venus and Mercury
  d) Neptune and Saturn e) Mars and Jupiter.
  

  6.What is the largest asteroid in the Solar System?
  a) Vesta b) Ceres c) pallas d) hygiea
  

  7.What is the largest of the carbon asteroids?
  a) Vesta b) Ceres c) pallas d) hygiea
  

  8.What is the brightest asteroid when viewed from Earth?
  a) Vesta b) Ceres c) pallas d) hygiea
  

  9. What asteroid is the largest body in the Solar System that is not
  round?
  b) Vesta b) Ceres c) pallas d) hygiea
  

  10. True or False: Most asteroids that hit the Earth are small enough to
  explode when they hit the Earth's atmosphere.
  

  22.4. Kepler’s Laws
  

  Activity 22.4
  
  

  1. It has been mentioned that planets move not on circle but follow an
  elliptical curve. State laws that govern this type of motion.
  2. How do you relate the period and the mean radius of planet’s orbit?
  

  Johannes Kepler proposed three laws of planetary motion. Kepler was able
  to summarize the carefully collected data of his mentor with three state-
  ments that described the motion of planets in a sun-centered solar system.
  Kepler’s efforts to explain the underlying reasons for such motions are no
  longer accepted; nonetheless, the actual laws themselves are still considered
  an accurate description of the motion of any planet and any satellite.
  Kepler’s three laws of planetary motion can be described as follows:
  

  22.4.1. First Kepler’s law
  

  Statement
  “The path of the planets about the sun is elliptical in shape, with the center
  of the sun being located at one focus.” (The Law of Ellipses)
  

  
  

  Figure 22.10 (a) An ellipse is a curve in which the sum of the distances from
  a point on the curve to two foci (f1 and f2) is a constant. From this definition,
  you can see that an ellipse can be created in the following way. Place a pin
  at each focus, and then place a loop of string around a pencil and the pins.
  Keeping the string taught, move the pencil around in a complete circuit. If
  the two foci occupy the same place, the result is a circle—a special case of
  an ellipse.
  

  Figure 22.10. (b) For an elliptical orbit, if m << M , then m follows an elliptical
  path with M at one focus. More exactly, both m and M move in their own
  ellipse about the common center of mass.
  

  
  22.4.2. Kepler’s Second Law

  Kepler’s second law states that“A line segment joining a planet and the Sun
  sweeps out equal areas during equal intervals of time.”
  

  Therefore, an imaginary line drawn from the center of the sun to the center
  of the planet will sweep out equal areas in equal intervals of time. (The Law
  of Equal Areas).
  

  Consider Figure 22.14 The time it takes a planet to move from position A to
  B, sweeping out area A1, is exactly the time taken to move from position C
  to D, sweeping area A2, and to move from E to F, sweeping out area A3.
  These areas are the same: A1 = A2 = A3.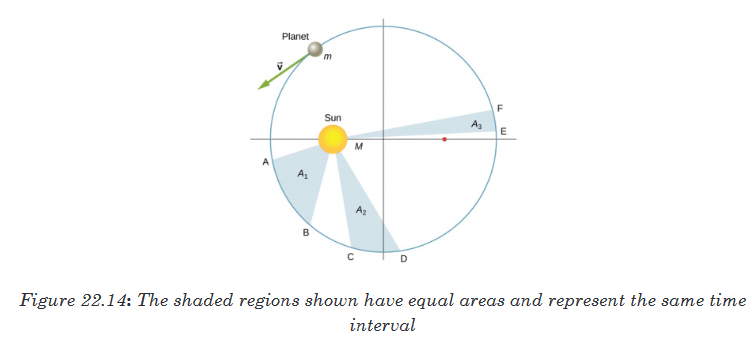
  

  
  

  Comparing the areas in the figure and the distance traveled along the ellipse
  in each case, we can see that in order for the areas to be equal, the planet
  must speed up as it gets closer to the Sun and slow down as it moves away.
  But we will show that Kepler’s second law is actually a consequence of the
  conservation of angular momentum, which holds for any system with only
  radial forces.
  

  22.4.3. Kepler’s Third Law (The Law of Harmonies)
  

  Statement
  

  “The Square of the orbital period of a planet is proportional to the cube of
  the semi-major axis of its orbit”.
  In Satellite Orbits and Energy, we derived Kepler’s third law for the special
  case of a circular orbit.
  

  Application activity 22.4
  1. Write in symbol the law of harmonies
  

  2. Kepler’s second law is the consequence of which physical quantity.
  Write the symbolical definition of that physical quantity.
  

  3. Explain the law of equal area.
  

  22.5. Star Patterns: Constellations
  

  Activity 22.5
  

  1. Research on star patterns and do report about constellations.
  2. Research on uses of constellation.
  

  Constellations
  A constellation is a group of visible stars that form a pattern when viewed
  from Earth. The pattern they form may take the shape of an animal,
  a mythological creature, a man, a woman, or an inanimate object such as a
  microscope, a compass, or a crown.
  

  How many constellations are there? The sky was divided up into 88
  different constellations in 1922. This included 48 ancient constellations
  listed by the Greek astronomer Ptolemy as well as 40 new constellations.
  

  Star Maps
  The 88 different constellations divide up the entire night sky as seen from
  all around the Earth. Star maps are made of the brightest stars and the
  patterns that they make which give rise to the names of the constellations.
  The maps of the stars represent the position of the stars as we see them
  from Earth. The stars in each constellation may not be close to each other
  at all. Some of them are bright because they are close to Earth while
  others are bright because they are very large stars.
  

  Hemispheres and Seasons

  Not all of the constellations are visible from any one point on Earth. The
  star maps are typically divided into maps for the northern hemisphere and
  maps for the southern hemisphere. The season of the year can also affect
  what constellations are visible from where you are located on Earth
  

  Famous constellations
  Here are a few of the more famous constellations:
  

  Orion
  Orion is one of the most visible constellations. Because of its location,
  it can be seen throughout the world. Orion is named after a hunter
  from Greek mythology. Its brightest stars are Betelgeuse and Rigel.
  

  
  

  
  

  Ursa Major
  Ursa Major is visible in the northern hemisphere. It means “Larger Bear”
  in Latin. The Big Dipper is part of the Ursa Major constellation. The Big
  Dipper is often used as a way to find the direction north.
  

  Ursa Minor
  Ursa Minor means “Smaller Bear” in Latin. It is located near Ursa Major and
  also has the pattern of a small ladle called the Little Dipper as part of its
  larger pattern.
  

  
  

  Draco constellation
  The Draco constellation can be viewed in the northern hemisphere. It means
  “dragon” in Latin and was one of the 48 ancient constellations.
  

  Pegasus
  The Pegasus constellation is named after the flying horse by the same name
  from Greek mythology. It can be seen in northern sky.
  

  
  

  
  

  The zodiac
  

  The Zodiac constellations are the constellations that are located within
  a band that is about 200 wide in the sky. This band is considered special
  because it s the band where the sun, the moon and the planets all move.
  There are 13 Zodiac constellations. Twelve of these are also used as signs for
  the zodiac calendar and astrology. These are Capricornus, Aquarius, pisces
  

  Aries, Taurus, Gemini, Cancer, Leo, Virgo, Libra, Scorpius, Sagittarius and
  Ophiuchus.
  

  Uses for Constellations

  Constellations are useful because they can help people to recognize stars in
  the sky. By looking for patterns, the stars and locations can be much easier
  to spot. The constellations had uses in ancient times. They were used to
  help keep track of the calendar. This was very important so that people knew
  when to plant and harvest crops. Another important use for constellations
  was navigation. By finding Ursa Minor it is fairly easy to spot the North
  Star (Polaris). Using the height of the North Star in the sky, navigators
  could figure out their latitude helping ships to travel across the oceans.
  

  Application activity 22.5

  1. What is a constellation?
  a) A group of stars from the same galaxy.
  b) A group of stars that are physically close to each other.
  c) A group of visible stars that make a pattern when viewed from
  Earth.
  d) All of the above.
  e) None of the Above.
  

  2.How many constellations are there?
  a) 12 b) 22 c) 44 d) 88 e) 120
  

  3. What constellation was named after a flying horse?
  a) Orion b) Ursa Minor c) Ursa Major d) Draco e) Pegasus
  

  4. What constellation has the Little Dipper as part of its pattern?
  a) Orion b) Ursa Minor c) Ursa Major d) Draco e) Pegasus
  

  5. What constellation was named after a hunter from Greek mythology?
  a) Orion b) Ursa Minor c) Ursa Major d) Draco e) Pegasus
  

  6. What constellation has the Big Dipper as part of its pattern?
  a) Orion b) Ursa Minor c) Ursa Major d) Draco e) Pegasus
  

  7. True or False: All the constellations are visible from anywhere on
  Earth throughout the year.
  
  

  8. What group of constellations are used in astrology?
  a) Ursa constellations b) Predictive constellations c) Northern
  constellations d) Zodiac constellations e) Ancient constellations.
  

  9. How are constellations useful?
  a) To help locate stars b) To keep track of the calendar c) To
  navigate d) To know when to plant crops. e) All of the above
  

  Skills lab 22
  

  1. With help of internet, visit youtube.com and watch “Seasons- what
  causes seasons”. watch again the video , summarize the causes and
  share the findings with your classmate and schoolmates.
  

  2. Using local materials make a demonstration explaining Moon phases.
  

  
  

  End unit assessment 22
  

  1. Why does the moon seem to change its shape every night? Why
  can I see the moon in the daytime?
  

  2. What are the Moon phases in order?
  

  3. What is an approximation of largest meteorite?
  

  4. What is the role of Constellations?
  

  5. Which physical quantity is conserved in the case of law of areas?
  

  6. With the help of diagrams explain types of eclipses.
  

• Topic 23
• Topic 24
• Topic 25
• Topic 26
• Topic 27
• Topic 28
• Topic 29
• Topic 30
• Topic 31
• Topic 32
• Topic 33
• Topic 34
• Topic 35
• Topic 36
• Topic 37
• Topic 38
• Topic 39
• Topic 40
• Topic 41
• Topic 42