Integrated Science SME

Key Unit competence: Relate Bohr’s model of the atom with
                                              hydrogen spectrum and energy levels, and
                                              interpret graphical information in relation to
                                              ionization energy of elements.

Introductory Activity 16
Observe the images below and answer the questions asked.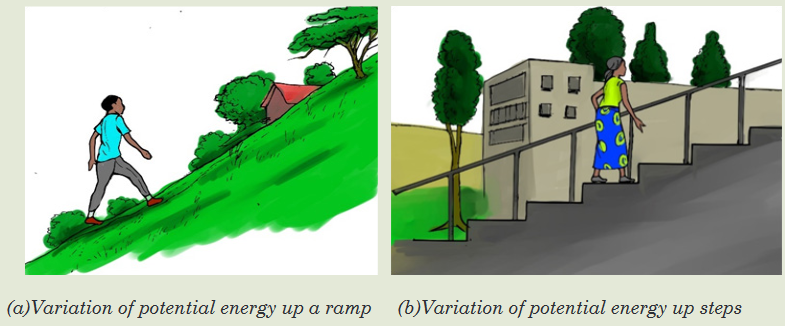

1. What can you see on the image above?
2. What type of motion is performed by the people on the image?
3. How does their potential energy change?

16.1. Bohr’s atomic model: Concept of energy levels and
spectra

Activity 16.1
1. Describe the Rutherford atomic structure?
2. What improvements have been brought by Bohr to the Rutherford
atomic structure
3. Establish a relationship between the Bohr’s atomic model and
the illustration in the introductory activity.

16.1.1 Bohr’s atomic model

From the observations in introductory activity 16, the potential energy of
a person walking up ramp increases in uniform and continuous manner
whereas potential energy of person walking up steps increases in stepwise
and quantized manner. This can be explained by the values of energy
which are continuous for the person walking up ramp while they are discrete
(discontinued) for the person walkingup steps (Figures (a) and b of the
introductory activity).

A model is a simplified representation used to explain the workings of a real
world system or event. A model is useful because it helps you understand
what’s observed in nature. It’s not unusual to have more than one model
represent and help people understand a particular topic.

There are two models of atomic structure in use today: the Bohr model and
the quantum mechanical model. Of these two models, the Bohr model is
simpler and relatively easy to understand.

Have you ever bought colour crystals for your fireplace — to make flames of
different colours? Or have you ever watched fireworks and wondered where
the colours came from?

Colour comes from different elements. If you sprinkle table salt on a fire, you
get a yellow colour. Salts that contain copper give a greenish-blue flame.
And if you look at the flames through a spectroscope, an instrument that
uses a prism to break up light into its various components, you see a number
of lines of various colours. Those distinct lines of colour make up a line
spectrum.

Niels Bohr, a Danish scientist, explained this line spectrum while developing
a model for the atom:

• The Bohr model shows that the electrons in atoms are in orbits of
differing energy around the nucleus (think of planets orbiting around
the sun).

• Bohr used the term energy levels (or shells) to describe these
orbits of differing energy. He said that the energy of an electron
is quantized, meaning electrons can have one energy level or another
but nothing in between.

• The energy level an electron normally occupies is called its ground
state. But it can move to a higher-energy, less-stable level, or shell, by
absorbing energy. This higher-energy, less-stable state is called the
electron’s excited state.

• After it is done being excited, the electron can return to its original
ground state by releasing the energy it has absorbed, as shown in
the diagram below.

• Sometimes the energy released by electrons occupies the portion of
the electromagnetic spectrum (the range of wavelengths of energy)
that humans detect as visible light. Slight variations in the amount of
the energy are seen as light of different colours.

The energy change is accompanied by absorption of radiation energy of
E=E₂ E₁ = h v where, h is a constant called ‘Planck’s constant’ and v is the
frequency of radiation absorbed or emitted.

The value of h is 6.626 x 10^-34 J.s. The absorption and emission of light due
to electron jumps are measured by use of spectrometers.

Bohr found that the closer an electron is to the nucleus, the less energy it
needs, but the farther away it is, the more energy it needs. So Bohr numbered
the electron’s energy levels.

The higher the energy-level number, the farther away the electron is from
the nucleus and the higher the energy.

Bohr also found that the various energy levels can hold differing numbers of
electrons: energy level 1 may hold up to 2 electrons, energy level 2 may hold
up to 8 electrons, and so on.

Weakness of Bohr’s Model
The Bohr model works well for very simple atoms such as hydrogen (which
has 1 electron) but not for more complex atoms. Although the Bohr model
is still used today, especially in elementary textbooks, a more sophisticated
(and complex) model (the quantum mechanical model) is used much more
frequently.

16.2.2. Absorption and emission spectra and energy associated

1. Atomic spectrum

The atomic spectrum is the range of characteristic frequencies or
electromagnetic radiations that are readily absorbed and emitted by an atom.

A spectrum obtained from a glowing source is called an emission spectrum.
When white light is passed through a prism we see a myriad of colours
– specifically what we term to be a rainbow. This dispersion of white light
demonstrates that white light contains all the wavelengths of colour and is
thus considered to be continuous. Each colour blends into the next with
no discontinuity.

When elements are vaporized and then thermally excited, they emit light;
however, this light was not in the form of a continuous spectrum as was
observed with white light. Instead, a discrete line spectrum was seen when
the light was passed through a narrow slit. A series of fine lines of different
colours separated by large black spaces was observed. The wavelengths of
those lines are characteristic of the element producing them – thus, elements
can be identified based on the spectral line data that they produce.

Typically, we can examine the visible line spectra produced by an element
in lab – using electricity, tubes filled with elements in the gaseous state and
a spectroscope or diffraction grating which separates the light emitted by the
gas into its components.

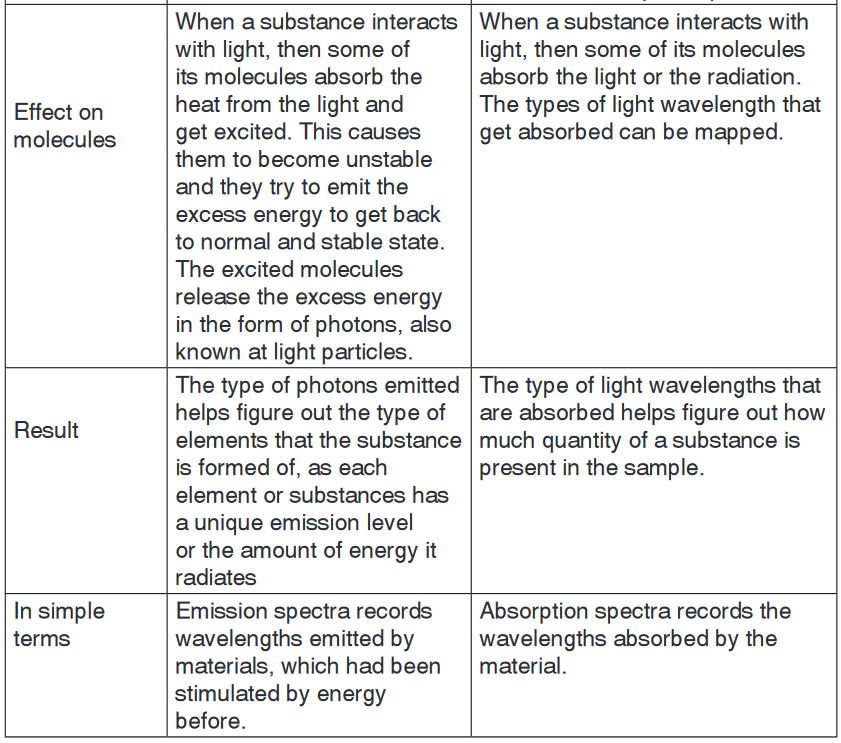
2. Emission and absorption spectra
Emission is the ability of a substance to give off light, when it interacts
with heat. Absorption is the opposite of emission, where energy, light or

radiation is absorbed by the electrons of a particular matter.
Emission and absorption spectra are techniques that are used in chemistry
and physics. Spectroscopy is the interaction of radiation and matter. Using
spectroscopy, a scientist can figure out the composition of a certain matter.
This is really beneficial, of dealing with unknown substances. Emission
spectra and absorption spectra are different from each other but still related.

a. Emission spectrum

Every substances reacts differently when it interacts with light. The material
starts off with being in the ground state, where all molecules are stable and
settled. However when heat, energy or light is applied to a substance, some
of the molecules transition into a higher energy state or an excited state.
During this state the molecules are unstable and try to emit the energy
in order to reach the state of equilibrium. The molecules emit energy
in the form of photons or light. The difference between the substance in
ground state and excited state is then used to determine the emission level
of the substance.

Each element or substances has a unique emission level or the amount
of energy it radiates; this helps the scientists identify elements in unknown
substances. The emission of an element is recorded on an emission
spectrum or atomic spectrum. The emittance of an object measures
how much light is emitted by it. The amount of emission of an object varies
depending on the spectroscopic composition of the object and temperature.
The frequencies on an emission spectrum are recorded in light
frequencies, where the colour of the light determines the frequency.

b. Absorption spectrum
Absorption is the ability of a matter or electron to absorb light or radiation
which makes them transition into a higher energy state. Absorption is
used to determine the absorption level of certain objects and their ability to
retain heat.

Absorption spectrum is the plotting of the energy that is absorbed by
an element or substance. Absorption can be plotted in a wavelength,
frequency or wave number. There are two types of absorption: atomic
absorption spectra and molecular absorption spectra.

Absorption is used to determine the presence of a particular substance
in a sample, or the quantity of the present substance in the sample. They
are also used in molecular and atomic physics, astronomical spectroscopy
and remote sensing. Absorption is primarily determined by the atomic and
molecular composition of the material. They can also depend on temperature,
electromagnetic field, interaction between the molecules of the sample,
crystal structure in solids and temperature.

In order to determine the absorption level of a substance, a beam of
radiation is directed at the sample and the absence of light that is
reflected through the object can be used to calculate the absorption.
The absorption spectrum is usually light coloured, with dark bands that
run through it. These dark bands are used to determine the absorption of
the object.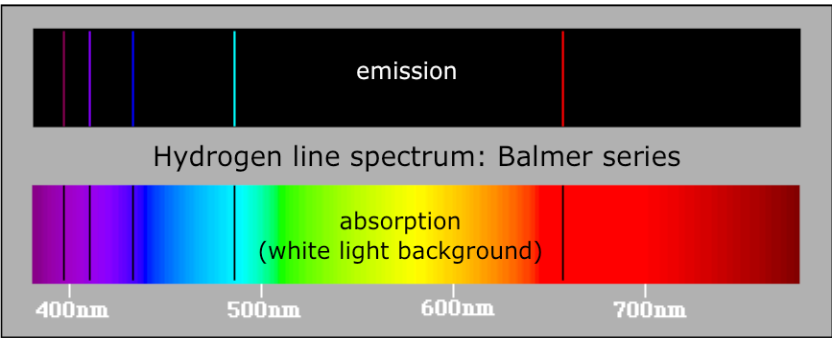

Application activity 16.1
1. Find out two more examples that you can use to illustrate the
concept of quantization.

2. Discuss the main weakness of:
c) Rutherford’s nuclear atom.
d) Bohr’s atomic model.

16.2. Hydrogen spectrum and spectral line series

Activity 16.2

Look at the picture of neon tube light below and do research about how
this neon tube light works to produce light and present your findings.

Bohr’s atomic model allows explaining the emission spectra of atoms. This
happens when excited electrons lose energy in form of electromagnetic ra-
diation and fall to lower energy levels.

The wave-particle nature of the light

Light as a wave

The light is a wave-like phenomenon as shown in Figure 16.1.

It is characterized by its wave length, generally symbolized by the Greek
letter lambda, λ, and its frequency, represented by the Greek letter nu, ν.

As shown in the Figure 16.1 below, the wavelength represents the distance
between two successive summits/peaks (or two successive troughs).

The frequency represents the number of complete wavelengths made by the
light per second, also called cycles per second.

Visible light is composed by different visible lights with different λ and ν.

But all those lights have the same speed, the speed of light, which, in a
vacuum, is equal to: 3.00x10⁸m/s; although different types of light have
different λ and ν, they move at the same speed c. This results in the relation

between the speed of light and its wavelengthand frequency: c = νλ

From this relation, and since c is constant, we can conclude that:

• Light with long wavelength has low frequency, whereas

• Light with short wavelength has high frequency.

Let’s take an example to illustrate: light1 has λ1 equal to 10⁵m whereas light₂
has λ₂ equal to 10^-5m. After 1 second, both would have travelled 3.00x10⁸m,
the speed of light, but their frequencies will be different:

Hence energy in the light is proportional to its frequency; the higher the
frequency of the light, the higher is its energy and vice-versa.

The different colours of the visible light differ by their wavelength as shown
in the Figure 16.2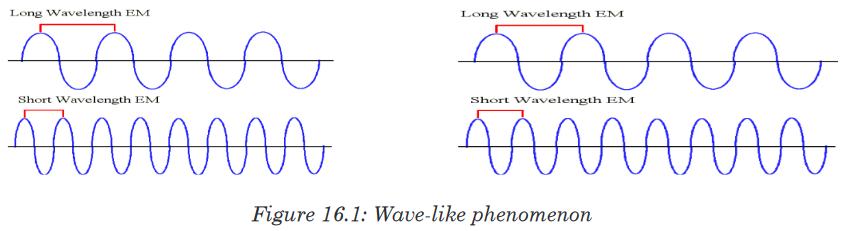

As illustrated in Figure 16.2 below, the right side of the spectrum consists of
high-energy, high-frequency and short wavelength radiations. Conversely,
the left side consists of low-energy,low-frequency and long wavelength
radiations.

When an electron is excited or de-excited, the energy absorbed or emitted
corresponds to the difference of energy, ΔE, between the final energy level
of the electron, E₂, and the starting energy level of the electron,

E₁: E₂ – E₁ =ΔE = hν. ΔE is positive when E₂>E₁, this is the case of absorption
and excitation of electron; on the other hand ΔE may be negative when
E₂<E₁, in case of emission and de-excitation of electron.

Figure 16.3 below shows the different series of emission spectra of hydrogen.
As you can see, the difference between those series is the final energy level
where the electron fall after de-excitation.

The series have been named according to the scientists who discovered
them. Ionization of an atom or loss of an electron corresponds to excitation
of an electron to the level n=∞.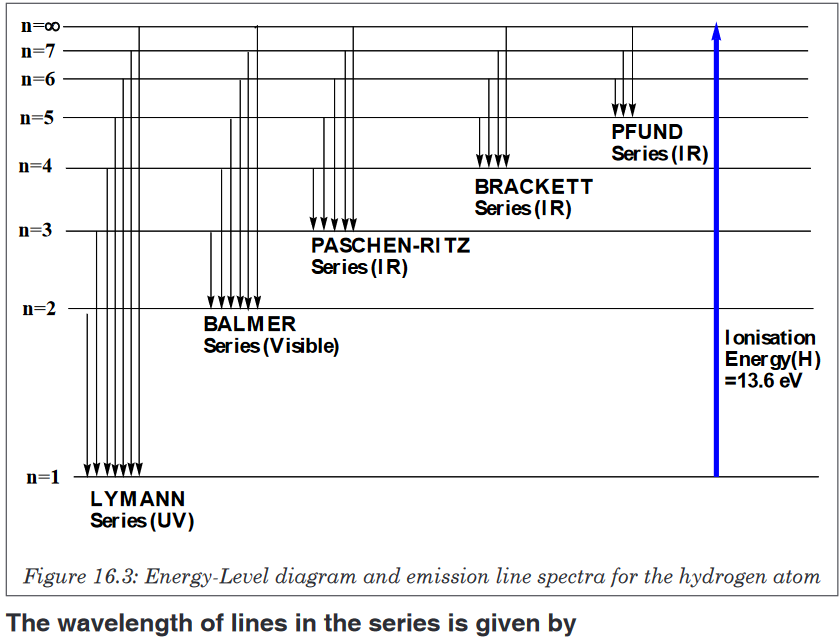

Examples
1. Find the wavelength and frequency in Balmer series associated with a
drop of an electron from the fourth orbit.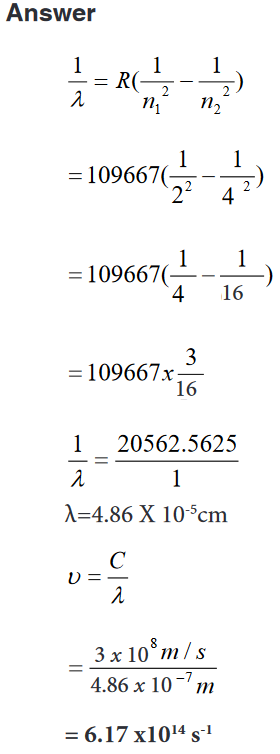

2. Find the wave length, frequency and energy of the third line in the
Lyman series.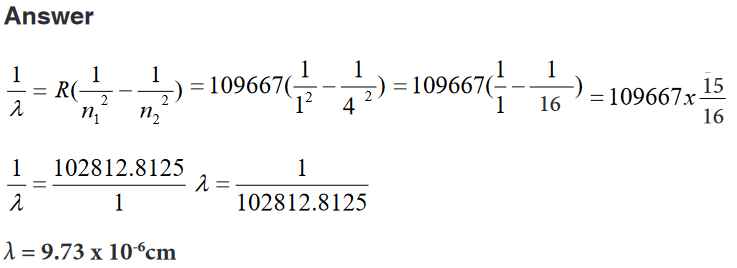

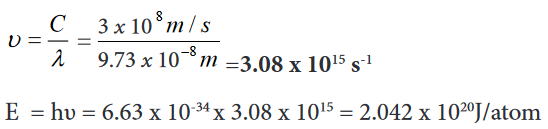
Application activity 16.2
1. What is the meaning of infinity level in the hydrogen spectral lines?

2. Given a transition of an electron from n=5 to n=2. Calculate
c) Energy
d) Frequency
e) Wavelength

3. What is the wavelength (in nanometres) of a photon emitted during
a transition from the ni = 5 state to the nf = 2 state in the hydrogen
atom?

16.3. Quantum theory of the atom
Activity 16.3
1. Recall the Bohr’s model of an atom.

2. What were the limitations of that model?

3. What improvements other scientists have brought to that model?

In 1913, physicist Niels Bohr described as an atom as a small, positively
charged nucleus surrounded by electrons that travel in circular orbits around
the nucleus—similar in structure to the solar system, but with attraction
provided by electrostatic forces rather than gravity. An electron must absorb
or emit specific amounts of energy to transition between these fixed orbits.

1. Despite its success in accounting for spectral lines of the H atom, the
Bohr model failed to predict the spectrum of any other element. The
model worked well for one-electron species, but not for atoms or ions
with more than one electron.

2. According to Bohr, the circular orbits in which electrons revolve are
planar.

3. Bohr’s theory fails to account for Zeeman Effect and Stark Effect.

4. Bohr assumes that the electron revolves around the nucleus in circular
orbits at fixed distance from the nucleus and with a fixed velocity.

In 1926, Erwin Schrödinger used this idea to develop a mathematical
model of the atom how electrons move in wave form, and developed the
Schrodinger equation which describes how the quantum state of a system
changes with time.

This was the beginning of Quantum Mechanics (or Quantum Theory). A
consequence of using waveforms to describe particles is that it is impossible
to obtain precise values for both the position and velocity of a particle at the
same time. This became known as the “uncertainty principle” formulated
by Werner Heisenberg in 1926. This model was able to explain observations
of atomic behaviour that previous models could not. Afterwards the planetary
model of the atom was discarded in favour of one that described atomic
orbital zones around the nucleus where a given electron is most likely to be
observed.

Thus, the quantum mechanical model is based on mathematics. Although it
is more difficult to understand than the Bohr model, it can be used to explain
observations made on complex atoms.

Max Planck proposed that energy emitted is not done so in a continuous
manner but is given off in small packets which he called quanta. He
determined that an atom can emit only certain amounts of energy and
therefore they must contain certain quantities of energy and that those are
fixed. Thus, the energy of an atom is quantized. The change in the atom’s
energy results from the gain or loss of one or more packets of energy. Planck
derived an equation to explain this quantized form of energy (as opposed to
the idea that energy emitted was continuous)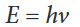

where h = Planck’s constant = 6.626 x 10^-34 J•s and ν = frequency (as above)

According to quantum theory, energy is always emitted in integral multiples
of hν; (hν, 2 hν, 3 hν . . .), but never, for example, 1.67 hν or 4.98 hν. At the
time Planck presented his theory, he could not explain why energies should
be fixed or quantized in this manner.

Therefore, despite the fact that Planck thought that energy was quantized,
physicists continued to think of energy as travelling in waves. Energy as
waves, however, could not explain the photoelectric effect. The quantum
mechanical model is based on quantum theory, which says matter also
has properties associated with waves. According to quantum theory, it is
impossible to know the exact position and momentum of an electron at the
same time. This is known as the Uncertainty Principle.

The quantum mechanical model of the atom uses complex shapes of
orbitals(sometimes called electron clouds), volumes of space in which there
is likely to be an electron. So, this model is based on probability rather than
certainty.

The existence of discrete atomic energy levels is retained from Bohr’s model
in the current atomic model.

The allowed wave-like motion of the electron leads to an atom with certain
fixed energy states much like Bohr assumed. The electron’s exact location
cannot be determined.

Solutions of Schrödinger’s wave equation are functions that describe atomic
orbitals.

Each function describes a fixed-energy state the electron can occupy and
gives the probability of finding it in a given 3-dimensional space.

Applying wave mathematics to the electron wave, Erwin Schrödinger derived
an equation that is the basis for the quantum-mechanical model of hydrogen
atom.

This probability can be shown pictorially by means of an electron probability
density diagram, or simply, an electron density diagram.

Electron probability density in the H atom ground state.

The distinction between atomic orbital and probability of the electron being
at a distance r from the nucleus.

The probability of the electron being far from the nucleus is very small, but
not zero.

The maximum radial probability for the ground-state of H atom appears at
(0.529 Å, or 5.29 x 10 ^–10 m), the same as 1st Bohr orbit.

The electron spends most of its time at the same distance that the Bohr
model predicted it spent all of its time. Each atomic orbital, has a distinctive
radial probability distribution and probability contour diagram.

Four numbers, called quantum numbers, were introduced to describe the
characteristics of electrons and their orbitals:

Principal quantum number: n
Angular momentum quantum number: ℓ
Magnetic quantum number: m_ℓ
Spin quantum number: m_s

Application activity 16.3

Discuss the improvements brought by the quantum theory in the
understanding of the atomic structure

16.3.1. Quantum numbers for energy levels, sub-energy levels
and orbitals

Activity 16.3.1

1. Explain the difference between orbit and orbitals.

2. The energy of both orbit and orbital is determined by a number n
known as principal quantum number. Explain.

3. An electron in an orbital is even described by other quantum numbers.
What are they?

4. Do research to precise the relationship between these quantum
numbers, their role in the description of electrons in orbitals and their
number in each energy level.

We have seen the weakness and critics against the atomic Bohr’s model.
In order to answer the questions not answered by that model, other atomic
models were proposed. One of those models is the Quantum model that
has been developed by the Australian physicist Erwin Schrödinger (1887-
1961). The model is based on a mathematical equation called Schrödinger
equation. This model is based on the following assumptions or hypotheses:

An electron is in continuous movement around the nucleus but cannot be
localized with precision; only the high probability of finding it in a certain
region around the nucleus can be known.

The region where the probability of finding electron is high, at more than
95%, is called “orbital”; in other words, the orbital is the volume or the space
(three-dimensional) around the nucleus where there is a high probability of
finding the electron.

Without going into the mathematical development of the Schrödinger
equation, we can say that the energy of the electron depends on the orbital
where it is located. And an atomic orbital is described by a certain number of
“quantum numbers” according to the solution of Schrodinger equation, i.e. 3
whole numbers:

1. The principal quantum number is a positive integer which varies
from 1 to ∞. The principal quantum number indicates the energy level in
an atom where electrons can be located: the higher the n value, the higher
the energy level. An electron in energy level n=1 has lowest energy in
an atom. The principal quantum number, n, has been traditionally given
names by the letters: K (n=1), L (n=2), M (n=3), N (n=4), O (n=5), P
(n=6).

In the Bohr’s atomic model, K, L, M, … were used to represent different
orbits or shells of electrons. Later on, the term shell sometimes is used to
describe a group of orbitals with the same principal quantum number. The
term subshell describes a group of orbitals with the same principal and
second quantum number. The maximum number of orbitals and electrons
that can be found in an energy level n are n² and 2n², respectively (Table
16.2). The maximum number of sub shells in an energy level n equals n.

In summary:

n = principal quantum number; all orbitals with same n are in the same shell.
l = secondary (azimuthal) quantum number; divides shells into subshells.
ml = magnetic quantum number; divides subshells into individual orbitals.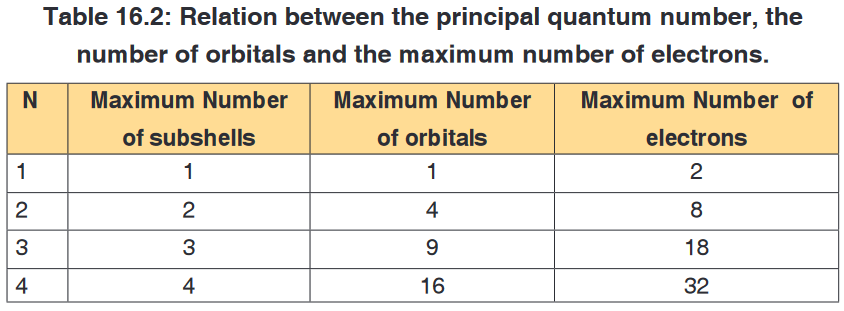

2. The angular momentum quantum number (l)
The second quantum number is the angular quantum number represented
by the letter, l: it is an integer which can take any value from zero or higher
but less than n-1, i.e. equal to: 0, 1, 2, 3,….up to n-1. For example if n= 1, l
is equal to 0, if n = 2, l can be 0, 1.

It is also called secondary or azimuthal quantum number. It indicates the
shape of the orbital and is sometimes called the orbital shape quantum
number. By tradition, those different shapes of orbitals have been given
names or letter symbols: l = 0 = s, l =1 = p, l = 2 = d, l=3 = f

3. Magnetic quantum number (ml)
The magnetic quantum number describes the spatial orientation of the
orbital. It is an integer that varies from -l to +l. For example if: l = 0, ml can
only be 0; if l = 1, ml = -1, 0, +1; if l=2, ml = -2, -1, 0, 1, 2. As you can see
for each value of l there are (2l+ 1) values of ml corresponding to (2l + 1)
orientations under the influence of magnetic field.

It is called the magnetic quantum number because the effect of different
orientations of orbitals was first observed in the presence of a magnetic field.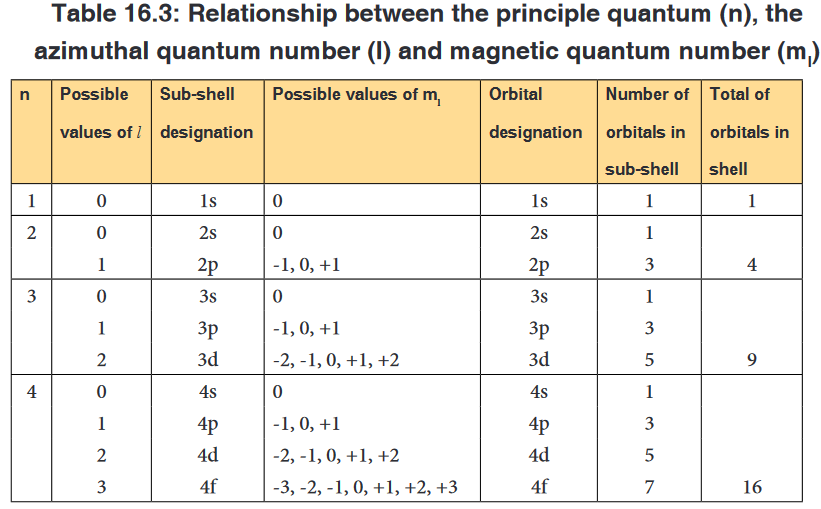

The table 16.3 shows that, apart s sub-level that has only one orbital, other
sub-levels have a certain number of different orbitals; those orbitals have the
same energy but differ in their specific orientations. Example p orbitals are 3
with different orientations: p_xp_yp_z.

4. The spin quantum number (m_s)

The fourth quantum number is the spin quantum number, represented by
the symbol ms. It describes the spin of an electron that occupies a particular
orbital. The electron behaves as a spinning magnet. The spin quantum
number is the property of the electron, not the orbital.

This number describes the spinning direction of the electron in a magnetic
field. The direction could be either clockwise or counter clockwise. The
electron behaves as if it were spinning about its axis, thereby generating a
magnetic field whose direction depends on the direction of the spin. The two
directions for the magnetic field correspond to the two possible values for the
spin quantum number, m_s (S).

Only two values are possible: ms = +1/2 and -1/2 as shown in the Figure 16.4
below.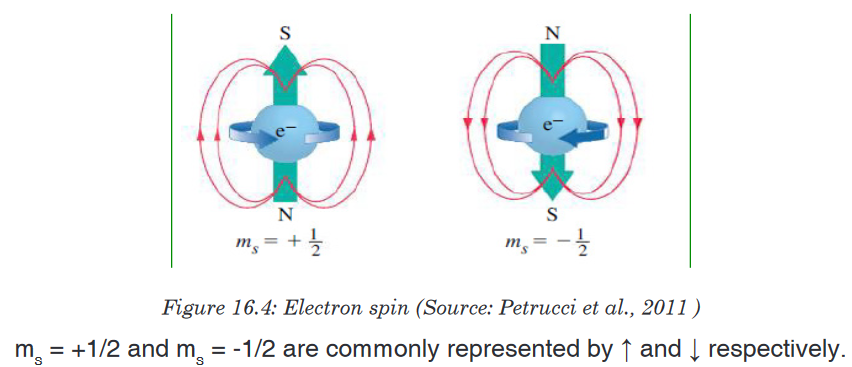

In conclusion an electron in any given atom is described by 4 quantum
numbers: (i) three quantum numbers which describe the orbital where the
electron is located: n, l and ml and (ii) one quantum number describing the
spin of the electron, m_s.

• Electrons will spin opposite each other in the same orbital

16.3.2. Number and shape of “s” and “p” orbitals

Activity 16.3.2

1. Explain the terms orbital and quantum numbers.
2. How the terms explained in 1. above are related?
3. Do research and point out the possible shapes assigned to s and
p orbitals.

An orbital is a region of space around the nucleus in which there is a great
chance (high probability) to find an electron. It is described by three quantum
numbers.

These quantum numbers describe the size, shape, and orientation in space
of the orbitals on an atom.

The principal quantum number (n) describes the size of the orbital.
The angular quantum number (l) describes the shape of the orbital.
The magnetic quantum number (ml), describes the spatial orientation of
a particular orbital.

All electrons that have the same value for n (the principal quantum number)
are in the same shell. Within a shell (same n), all electrons that share the
same value for l( the angular momentum quantum number, or orbital shape)
are in the same subshell. The electrons in subshell have same principal
quantum number, same azimuthal quantum number and differ in magnetic
and spinquantum number. When electrons share the same n, l, and m, they
are said to be in the same orbital. That is, they have the same energy level,
shape, and orientation. The electrons in the same orbital differ only in spin
quantum number.

Chemists describe the shell and subshell in which an orbital belongs with a
two-character code such as 2p or 4f. The first character indicates the shell
(n = 2 or n = 4). The second character identifies the subshell. By convention,
the following lowercase letters are used to indicate different subshells.

The number of subshells in a shell is equal to the principal quantum number
for the shell. For example the n = 3 shell, contains three subshells: the 3s,
3p, and 3d orbitals.

There is only one orbital in the n = 1 shell because there is only one way in
which a sphere can be oriented in space. The only allowed combination of
quantum numbers for which n = 1 is the following.

There is only one orbital in the 2s subshell. But, there are three orbitals in the
2p subshell because there are three directions in which a p orbital can point.
One of these orbitals is oriented along the X axis, another along the Y axis,
and the third along the Z axis of a coordinate system, as shown in the figure
below. These orbitals are therefore known as the 2p_x, 2p_y, and 2p_z orbitals.

The number of orbitals in a shell is the square of the principal quantum
number: 1² = 1, 2² = 4, 3² = 9. There is one orbital in an s subshell (l = 0),
three orbitals in a p subshell (l = 1), and five orbitals in a d subshell (l = 2).
The number of orbitals in a subshell is therefore 2(l) + 1.

Orbitals have shapes that are best described as spherical (l = 0), polar (l =
1), or cloverleaf (l = 2).

Shapes of “s” and “p” orbitals

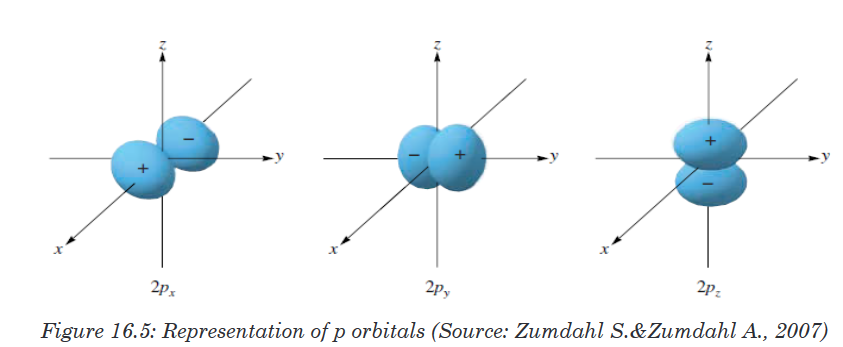
Application activity 16.3.2
1. Determine the number of orbitals that can exist at energy level
corresponding to n=1, 2, 3.
2. Outline diagrams representing the s and p orbitals.

16.4. Electronic configuration of atoms and ions

16.4. 1. Rules governing the electronic configurations

Activity 16.4.1

1. Using your knowledge acquired so far in chemistry, define the term
electron configuration.
2. How this concept can apply to the quantum theory of the atomic
structure?
3. Using available resources, figure out the rules that dictate the
electronic configuration.

The electron configuration is the distribution of electrons of an atom in its
atomic orbitals. The electronic configuration of an atom is governed by three
main rules including Aufbau principle, Pauli Exclusion Principle and Hund’s
rule.

1. Pauli Exclusion Principle

No two electrons in the same atom can have the same set of the four quantum
numbers. If two electrons have the same values of n, l, ml, they must have

different values of ms. Then, since only two values of msare allowed, an
orbital can hold only two electrons, and they must have opposite spins.

2. Hund’s rule
Electrons occupy all the orbitals of a given sublevel singly before pairing
begins.

Spins of electrons in different incomplete orbitals are parallel in the ground
state. The most stable arrangement of electrons in the subshells is the one
with the greatest number of parallel spins.

That is, the most stable arrangement for electrons in orbitals of equal
energy (degenerate) is where the number of electrons with the same spin is
maximized • Example: Carbon - 6 electrons

For example, for an element with atomic number equal to 6, the electronic
configuration is:1s²2s²2p_x¹p_y¹p_z0

When building the electronic configuration of elements, the above principles
are applied. writing the principal quantum number in Arabic number, followed
by the orbitals immediately followed by the number of electrons in the orbital
as superscript.

An atom X: 1s²: has only two electrons in s orbital at the 1^st energy level

An atom Y: 1s²2s²2p³: has electrons in 2 levels of energy: level n=1, and level
n= 2. In level 1, it has 2 electrons in s orbital. In level 2, it has 2 electrons in
s orbital and 3 electrons in p orbitals.

Figure 2.8 is a useful and simple aid for keeping track of the order in which
electrons are first filled for each atomic orbital. The different orbitals are filled
in the order 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f,
6d, 7p.

Notice that as energy levels increase starting from n=3, 4s orbital is filled
before 3d, 5s before 4d, etc… as shown in the diagram below. But when
ionized, 4s electrons are ionized before 3d, and 5s before 4d.

3. Aufbau Principle

The Aufbau principle or build up principle or construction principle state that
“Electrons fill lower energy orbitals (closer to the nucleus) before they fill
higher energy ones”.

Orbitals in atomic ground state electron configuration are filled in order of
increasing n+l. For equal n+l values, the orbital with the lower n is most
often filled first.

Examples:
Using, s, p, d, f notation, write the electronic configuration for elements of
atomic numbers: 16, 23, 37

The s, p, d and f notation uses numbers to designate a principal shell and
the letters to identify a subshell; a superscript number indicates the number
of electrons in a designated subshell

Note that 1s² is read “one s two,” not “one s squared.”

Application activity 16.4.1.a
1. Using the spdf notation, build the electronic configuration of the
following atoms: ₁H, ₃Li, ₅B, ₁₁Na, ₁₈Ar,₁₉K, ₂₁Sc, ₂₄Cr, ₂₆Fe, ₂₉Cu

Expanded notation
Expanded notation is another method of writing the s, p, d and f notation.
The method uses the same concept as s, p, d and f notation except that
each individual orbital of a sub-level having many orbitals is represented
with a subscript letter indicating the orientation of the orbital. This applies for
p, d, and f orbitals.

Considering that p-orbital has three components p_x, p_y, and p_z, the expanded
electronic configuration of some elements is given hereafter.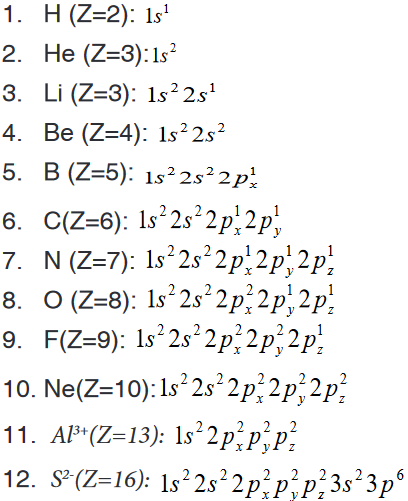

Application activity 16.4.1.b
Write the expanded electronic configuration for each of the following
atom/ions.

S(z=16), P^3-(z=15), Mg²⁺(z=12)

Orbital box representation
An orbital box representation consists of a box for each orbital in a given
energy level, grouped by sublevel, with an arrow indicating an electron and
its spin.

Note that two electrons in the same orbital have necessarily opposite spins
as indicated in the examples below.

The table 16.4 shows the electronic configuration of some elements using
orbital box representation and applying Hund’s rule.
Examples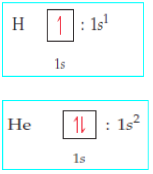

N.B:An orbital box representation doesn’t show the real form of the orbital;
the forms of the different orbitals are shown in Figures 16.4, 16.5 and 16.6
above.

Table 16.4: Electronic configuration using orbital box representation

Application activity 16.4.1.c
Using boxes to represent orbitals, draw the electronic configuration of
N^3- (z=7), Ti⁴⁺(z=22), Mg²⁺(z=12), Ar(z=18)
Identify the isoelectronic species that are present.

Noble Gas Notation or condensed electron configuration

All noble gases have completely filled subshells and can be used as a
shorthand way of writing electron configurations for subsequent atoms.

When using this method, the following steps are respected.
a). Identify the noble gas whose electronic configuration is included in

that of the concerned element.

b). Write the chemical symbol of the identified noble gas within square
brackets. We call this the noble gas core.

c). Add electrons beyond the noble gas core. Note that electrons that
are added to the electronic level of the highest principal quantum
number (the outermost level or valence shell) are called valence
electrons.

Example: Given the electronic configurations of the noble gases Ne and Ar,
one can write the electronic configuration of some elements in
noble gas notation of some elements as:

Application activity 16.4.1.d
Using the noble gas notation, write the electronic configuration of the
following atoms/ions.
a). Ge (Z=32)
b). S (Z=16)
c). Co²⁺ (Z=27)
d). Br- (Z=35)
e). Sr (Z=38)

16.4.2. Electronic configuration and stability

Activity 16.4.2

State the Hund’s rule and explain how the rule is important in the
understanding of the behaviour of an element.

Hund’s rule states that electrons first occupy the similar energy orbitals
that are empty before occupying those which are half-full. This is especially
helpful when determining unpaired electrons. The Aufbau process denotes
the method of “building up” each sub-shell before moving on to the next;

Almost all the elements follow the same trend for writing electronic
configuration.

Sometimes electron configurations of certain elements appear to violate the
rules that govern the electron configuration.

For example, the electron configuration of chromium is [Ar]3d⁵4s¹rather
than the [Ar]3d⁴4s²configuration we might have expected.

Similarly, the configuration of copper is [Ar]3d ¹⁰4s¹instead of [Ar]3d⁹4s².

This anomalous behaviour is largely a consequence of the closeness of the
3d and 4s orbital energies.

The orbitals in which the sub-shell is exactly half-filled or completely filled
are more stable because of the symmetrical distribution of electrons.

Application activity 16.4.2
1. Write the electronic structure of the following chemical species.
K (Z=19), Ne (Z=10), Al³⁺ (Z=13), Cl (Z=17), O^2- (Z=16)

2. a) Write the electronic configuration for each of the following pairs
of ions. State the more stable ion in gaseous state and explain your
choice.

i. Cu+ and Cu²⁺  (ii) Fe²⁺and  Fe³⁺

b) Using information in question (a) specify the species from each pair
has a more stable electronic configuration. Explain.

16.5. Relationship between ionization energy, energy levels
and factors influencing ionization energy

16.5.1. The graphs of ionization energy versus the number of
electrons removed

Activity 16.5.1
1. Write the electronic configuration of the following elements/ions, use
s, p, d, …) Sodium, magnesium, magnesium ion (Mg²⁺), aluminium,
aluminium ion (Al³⁺), oxide ion (O^2-).

2. Identify the common feature of ions in (1) and why do they have such
feature.

3. Suggest what happened to aluminium atom when it changed to
aluminium ion (Al³⁺).

4. Identify the group and the period of aluminium, sodium and oxygen
atom.

Concept of Ionization energy
The ionization energy is a measure of the energy needed for an atom, in
gaseous state, to lose an electron and become positive ion.

The first ionisation energy is the energy required to remove one electron from
an atom in its gaseous state. The example below shows how to represent
the successive ionization energies of an atom M.

First ionisation energy: M(g) →M⁺(g) + e^-

Second ionisation energy and n^th ionisation energy: Two or more
electrons can be removed and we have successive ionization energies.

The ionization energy is usually expressed in kilojoules per mole (kJ.mol-1).
This energy is required to overcome the attractive force between the nucleus
and the electron and then remove the electron. Theoretically there are as
many successive ionisation energies as there are electrons in the original
atom. In figure 2.9, someone can make an interpretation of successive
ionization energies of an atom.

• Successive ionisation energies for an element increase, since the
remaining electrons are pulled closer to the nucleus and are more
tightly held.

• Evidence for the arrangements of electrons in shells of different
energies is provided by values of successive ionisation energies for
elements.

• The figure below shows a graph of the logarithm of the ionisation
energy required for the removal of one electron after another from the
potassium atom.

• A logarithmic scale is used in order to give a condensed graph, since
there is a large range in values of successive ionisation energies.

• The graph that has four parts shows three breaks. These three breaks
are evidence of principal energy level.
• The first break occurs after the first electron has been removed from
the forth energy level (n = 4). The second breaks after the ninth electron
has been removed from the third energy level (n = 3).
• The third break occurs after the 17th electron is removed from a second
energy level.
• The two electrons with the highest ionisation energy are close to the
nucleus and form the n = 1 shell.

Application activity 16.5.1

1. What is meant by the term first ionisation energy?
2. Explain why helium has the highest first ionisation of all the elements.
3. Explain why the first ionisation energy of sodium is less than that of
neon, but the second ionisation energy of sodium is greater than the
second ionisation energy of neon.
4. Sketch a graph to show the successive ionisation energies for
aluminium. What does the shape of your graph tells you about the
electron configuration of aluminium?

16.5.2. Interpretation of a graph of first ionization energy versus
the atomic numbers of elements.

Activity 16.5.2

Using the s, p, d, f notation, predict the electronic configurations of the
first twenty elements.

Use the established electronic configurations to predict the trends in the
first ionisation energy values for the elements above.

Note that the noble gases have high ionization energies, whereas the alkali
metals and alkaline earth metals have low ionization energies.

Note also that, apart from small irregularities, the first ionization energies of
elements in a period increase with increasing atomic number.

Application activity 16.5.2

1. Write an equation to illustrate the process which occurs during the
first ionization of neon.

2. Explain why the value of the first ionization energy of magnesium is
higher than that of sodium.

3. Write an equation to illustrate the process occurring when the second
ionization energy of magnesium is measured.

4. The Ne atom and the Mg²⁺ ion have the same number of electrons.
Give two reasons why the first ionization energy of neon is lower than
the third ionization energy of magnesium.

5. Explain why the first ionization of aluminum is smaller than that of
magnesium greater than the first ionization energy of magnesium.

16.5.3. Factors influencing the magnitude of ionization energy

Activity 16.5.3

1. Why is the first ionisation of neon higher than that of fluorine?

2. Explain why the first ionisation energy of potassium is lower than that
of sodium?

The ionization energy is a physical property of elements that can be influenced
by some factors:

1. Size of atom
The atomic size is the distance between the nucleus and valence shell.
As the number of energy levels (shells) increases, the force of attraction
between nucleus and valence electron decreases. Therefore, the valence
electrons are loosely held to the nucleus and lower energy is required to
remove them, i.e. ionization energy decreases with increase in atomic size
and vice versa. This is what happens when you go down a Group.

2. Nuclear charge
The nuclear charge is the total charge of all the protons in the nucleus. As
the nuclear charge increases, the force of attraction between nucleus and
valence electrons on the same valence energy level increases and hence
makes it difficult to remove an electron from the valence shell. The higher
the nuclear charge, the higher the ionization energy. This is what happens
when you cross a period from left to right.

3. Screening effect or Shielding effect
The Screening effect or Shielding effect is due to the presence of inner
electrons which have a screening or shielding effect against the attraction
of the nucleus towards the outermost electrons. The electrons present in
inner shells between the nucleus and the valence shell reduce the attraction
between nucleus and the outermost electrons. This shielding effect
increases with the increasing number of inner electrons. A strong Shielding
effect makes it easier to remove an external electron and hence lowers the
ionization energy.

4. Electronic Configuration
Electronic configuration plays an important role in determining the value
of ionization energy. Atoms having stable configuration (i.e. fully filled or
half filled) have least tendency to lose electrons and hence have high of
ionization energy values.

Application activity 16.5.3
1. Why is the first ionization energy of krypton lower than the first
ionization energy of argon?

2. Explain why the value of the first ionization energy of sulphur is
lower than that of phosphorus.

3. Explain why the third ionisation energy of magnesium is very
much larger than the second ionisation energy of magnesium.

Skills lab 16
Absorption and emission spectra are like finger prints. Assume that you
have to market some goods using advertising lamps that can emit light with
at least 10 alternating colours. Write paper specifying the chemical elements
that may be involved in the production of these advertising lamps.

End unit assessment 16
1. Which of the following is the correct representation of the ground-
state electron configuration of molybdenum? Explain what is wrong
with each of the others.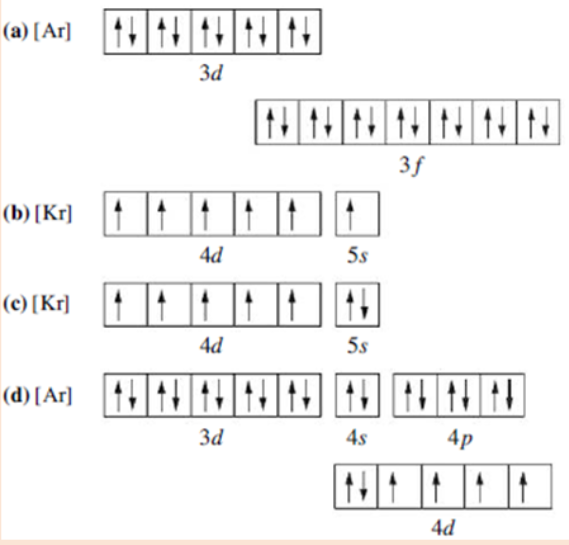

2. Which of the following electron configurations are correct and which
ones are wrong? Explain.

3. Photosynthesis uses 660 nm light to convert CO₂ and H₂O into
glucose and O₂. Calculate the frequency of this light.

4. Which of the following orbital designations are incorrect: 1s, 1p, 7d,
9s, 3f, 4f, 2d?

5. The data encoded on CDs, DVDs, and Blu-ray discs is read by lasers.
What is the wavelength in nanometres and the energy in joules of the
following lasers?
CD laser, v = 3.85 x 10¹⁴ Hz
DVD laser, v = 4.62 x 10¹⁴ Hz
Blu-ray laser, v = 7.41 x 10¹⁴ Hz

6. Concerning the concept of energy levels and orbitals,
a) How many subshells are found in n=3?
b) What are the names of the orbitals in n=3?
c) How many orbitals have the values n=4 and l=3?
d) How many orbitals have the values n=3, l=2 and ml= −2?
e) What is the total number of orbitals in the level n=4?

7. A hypothetical electromagnetic wave is pictured here. What is the
wavelength of this radiation?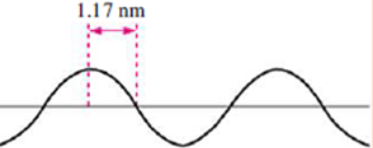

8. Consider the following waves representing electromagnetic radiation:

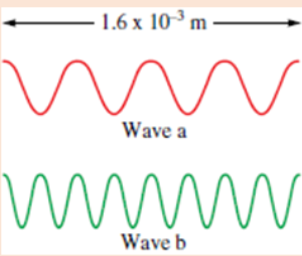
a) Which wave has the longer wavelength?
b) Calculate the wavelengths of the two radiations
c) Which wave has the higher frequency and larger photon energy?

9.Order the orbitals for a multielectron atom in each of the following lists
according to increasing energy:
a). 5p, 5d
b). 4s, 3d
c). 6s, 4d

10. According to the Aufbau principle, which orbital is filled immediately
after each of the following in a multielectron atom?
a) 4s
b) 3d
c) 5f
d) 5p

11. According to the Aufbau principle, which orbital is filled immediately
before each of the following?
a) 3p
b) 4p
c) 4f
d) 5d

12. The ground-state electron configurations listed here are incorrect.
Explain what mistakes have been made in each and write the correct
electron configurations.

13. Four possible electron configurations for a nitrogen atom are shown
below, but only one represents the correct configuration for a
nitrogen atom in its ground state. Which one is the correct electron
configuration? Which configurations violate the Pauli Exclusion
Principle? Which configurations violate Hund’s rule?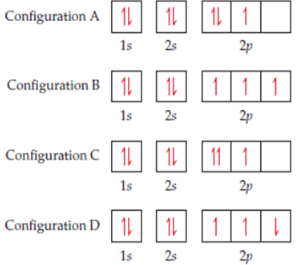

14. Explain the variation in the ionization energies of carbon, as displayed
in this graph.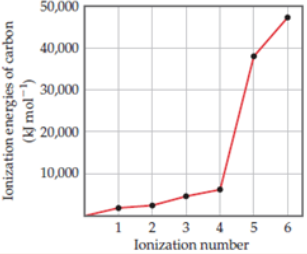

15. The first seven ionization energies of an element W are shown below

What factors determine the magnitude of the first ionization energy

16. The following table shows the ionisation energies ( in kJ mol-1) of the
five elements lettered A, B, C, D and E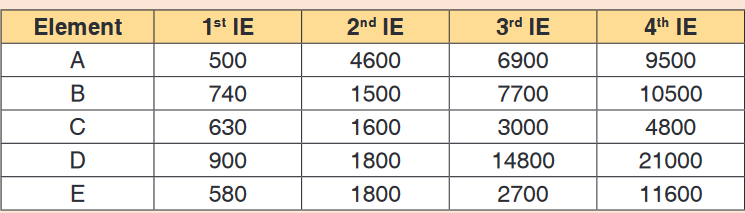

a) Which of these elements is most likely to form an ion with a
charge of 1+? Give reasons for your answer.

b) Which two of the elements are in the same group of the periodic
table? Which group do they belong to?

c) In which group of the periodic table is element E likely to occur?
Give reasons for your answer.

d) Which element would require the least energy to convert one
mole of gaseous atoms into ions carrying two positive charges?