Mathematics SSE

Key Unit competence: Model and solve daily life problems using linear, quadratic equations

or inequalities 

2.0. Introductory Activity

1) By the use of library and computer lab, do the research and explain

the linear equation.

2) If x is the number of pens for a learner, the teacher decides to give

him/her two more pens. What is the number of pens will have a

learner with one pen?

2.1 Linear equations in one unknown and related problems

Activity 2.1

Problems which are expressed in words are known as problems or applied

problems. A word or applied problem involving unknown number or

quantity can be translated into linear equation consisting of one unknown

number or quantity. The equation is formed by using conditions of the

problem. By solving the resulting equation, the unknown quantity can be found.

In solving problem by using linear equation in one unknown the following

steps can be used:

i) Read the statement of the word problems

ii) Represent the unknown quantity by a variable

iii) Use conditions given in the problem to form an equation in the unknown variable

iv) Verify if the value of the unknown variable satisfies the conditions of the problem.

Examples

1) The sum of two numbers is 80. The greater number exceeds the

smaller number by twice the smaller number. Find the numbers.

2.2 Linear inequalities in one unknown and related real life problems

Activity 2.2

CONTENT SUMMARY

2.2.1 Meaning of an inequality

The statement x + = 3 10 is true only when x = 7 . If x is replaced by 5, we

have a statement 5 3 10 + = which is false. To be true we may say that 5 +

3 is less than 10 or in symbol5 3 10 + < . If x is replaced by 8, the statement

8+3=10 is also false. In those two cases we no longer have equality but

inequality.

Suppose that we have the inequality x + <3 10 , in this case we have an

inequality with one unknown. Here the real value of x satisfies this

inequality is not unique. For example 1 is a solution but 3 is also a

solution. In general all real numbers less than 7 are solutions. In this

case we will have many solutions combined in an interval.

Now, the solution set of x + <3 10 is an open interval containing all real

numbers less than 7 whereby 7 is excluded. How?

We solve this inequality as follow

Since any real number times zero is zero and zero is not less or equal to

-1 then the solution set is the empty set. S = ∅

2.2.3 Inequalities products / quotients

Activity 2.2

Explain the method you can use to solve the following inequalities: 

Suppose that we need to solve the inequality of the form(ax b cx d + +< ) 0

For this inequality we need the set of all real numbers that make the

left hand side to be negative. Suppose also that we need to solve the

inequality of the form (ax b cx d + +> ) 0 . For this inequality we need the

set of all real numbers that make the left hand side to be positive.

We follow the following steps:

a) First we solve for (ax b cx d + += ) 0

b) We construct the table called sign table, find the sign of each

factor and then the sign of the product or quotient if we are given

a quotient.

For the quotient the value that makes the denominator to be

zero is always excluded in the solution. For that value we use the

symbol || in the row of quotient sign.

c) Write the interval considering the given inequality sign.

Example

Solve in set of real numbers the following inequalities

Solution

a) (37 20 x x + −< )

2.2.4 Inequalities involving absolute value

Activity 2.2.4

State the set of all real numbers whose number of units from zero, on

a number line, are

1) greater than 4

2) less than 6

2.2.5 Real life problems involving linear inequalities

Activity 2.2.5

Sam and Alex play in the same team at their school. Last Saturday

their team played with another team from other school in the same

district, Alex scored 3 more goals than Sam. But together they scored

less than 9 goals.

What are the possible number of goals Alex scored?

Inequalities can be used to model a number of real life situations. When

converting such word problems into inequalities, begin by identifying

how the quantities are relate to each other, and then pick the inequality

symbol that is appropriate for that situation. When solving these

problems, the solution will be a range of possibilities. Absolute value

inequalities can be used to model situations where margin of error is a

concern.

Examples

1) The width of a rectangle is 20 meters. What must the length be if the

perimeter is at least 180 meters?

The length must be at least 70 meters.

2) John has 1 260 000 Rwandan Francs in an account with his bank.

If he deposits 30 000 Rwanda Francs each week into the account,

how many weeks will he need to have more than 1 820 000 Rwandan

Francs on his account?

Solution:

Let x be the number of weeks

We have total amount of deposits to be made the current balance is

greater to the total amount wanted.

Application activity 2.2

1) Joe enters a race where he has to cycle and run. He cycles a

distance of 25 km, and then runs for 20 km. His average running

speed is half of his average cycling speed. Joe completes the race

in less than 2½ hours, what can we say about his average speeds?

2) Explain your colleague whether or not a solution set for an

inequality can have one element.

2.3 Simultaneous linear equations in two unknowns

(Solving by equating two same variables)

Activity 2.3

In each of the following systems find the value of one variable from one

equation and equalize it with the same value of another variable from

second equation. Calculate the values of those variables

.

CONTENT SUMMARY

To find the value of unknown from simultaneous equation by equating

the same variable in terms of another, we do the following steps:

i) Find out the value of one variable in first equation,

ii) Find out the value of that variable in the second equation,

iii) Equate the same values obtained from the two equations,

iv) Solve the equation obtained to find out the unknown variables.

Example

1) Algebraically, solve the simultaneous linear equation by equating the

same variables.

Activity 2.4

CONTENT SUMMARY

To eliminate one of the variables from either of equations to obtain an 

equation in just one unknown, make one pair of coefficients of the same 

variable in both equations negatives of one another by multiplying both 

sides of an equation by the same number. Upon adding the equations, 

that unknown will be eliminated.

Example

1) Solve the system of equations using elimination method

Application activity 2.4

1) Solve the following system of equation by using elimination 

method.

2.5 Solving graphically simultaneous linear equations 

in two unknowns

Activity 2.5

1) Discuss how you can find the coordinate of the point intercept of 

two lines whose equations are known.

CONTENT SUMMARY

One way to solve a system of linear equations is by graphing. The 

intersection of the graphs represents the point at which the equations 

have the same -value and the same -value. Thus, this ordered pair 

represents the solution common to both equations. This ordered pair is 

called the solution to the system of equations.

The following steps can be applied in solving system of linear equation 

graphically:

1) Find at least two points for each equation.

2) Plot the obtained points in XY plane and join these points to obtain 

the lines. Two points for each equation give one line.

3) The point of intersection for two lines is the solution for the given 

system

Examples

1) Solve the following system by graphical method

The two lines intersect at point(3,1). Therefore the solution set is

S = {(3,1)} .

2) Solve graphically the following system of linear equations

Solve the following equations graphically

Application activity 2.5

1) Solve the graphically the following system of linear equations.

2.6 Solving algebraically and graphically simultaneous 

linear inequalities in two unknowns

Activity 2.6

The following graph illustrates two lines and their equations

CONTENT SUMMARY

A system of inequalities consits of a set of two inequalities with the same 

variables. The inequalities define the conditions that are to be considered 

simultaneously.

Each inequality in the set contains infinetely many ordered pair solutions 

defined by a region in rectangular coordinate plane. When considering 

two of these inequalities together, the intersection of these sets will 

define the set of simultaneous ordered pair solutions

The solution of the system of inequalities is the intersection region of the 

solutions of the three inequalities as it is done in the following figure.

Application activity 2.6

1) Algebraically and graphically, solve the following simultaneous 

inequalities

2.7 Solving quadratic equations by the use of 

factorization and discriminant

Activity 2.7

Smoke jumpers are fire fighters who parachute into areas near forest 

fires. Jumpers are in free fall from the time they jump from a plane 

until they open their parachutes. The function 2 y t =− + 16 1600 gives a 

jumper’s height y in metre after t seconds for a jump from1600m. 

a) How long is free fall if the parachute opens at1000m?

b) Complete a table of values for t = 0, 1, 2, 3, 4, 5 and 6.

CONTENT SUMMARY

Equations which are written in the form of 2 ax bx c a + += ≠ 0 0 are 

called quadratic equations. To find solution of this equation the two main 

ways can be used in solving such equation

a)Use of factorization or finding square roots

Grouping terms or decomposition can be used to factorize the quadratic 

equations; and later help us to find the solution of equation. By having 

the product of and the sum of those two integers which gives , it 

helps you to decompose into a product of factors

Example 

Application activity 2.7

a) Use factorization and discriminant to solve the following equations

2.8 Applications of linear and quadratic equations in 

economics and finance: Problems about supply 

and demand (equilibrium price

Activity 2.8 

Assume that a firm can sell as many units of its product as it can manufacture in a month at 180 Rwandan francs each. It has to pay out 2400 Rwandan francs fixed costs plus a marginal cost of 140 Rwanda francs for each unit produced. How much does it need to produce to break even (where total revenue equals to total cost)?

CONTENT SUMMARY

When only two or single variables and equations are involved, a 

simultaneous equation system can be related to familiar graphical 

solutions, such as supply and demand analysis. 

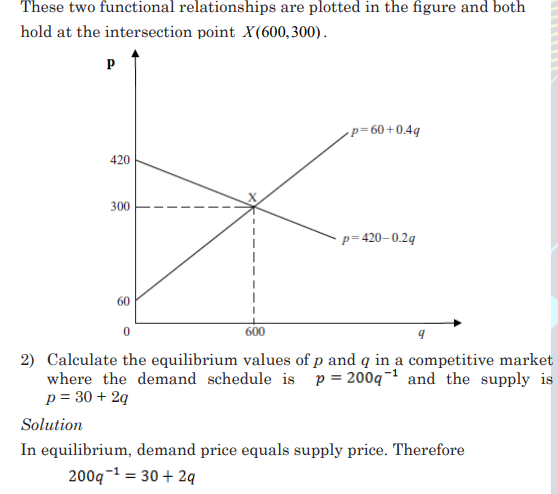
For example, assume that in a competitive market the demand schedule 

is given by 

p = 420 − 0.2q and the supply schedule is given by p = 60 + 0.4q, 

If this market is in equilibrium, the equilibrium price and quantity will 

be where the demand and supply schedules intersect. This requires 

you to solve the system formed by the two simultaneous equations. Its 

solution will correspond to a point which is on both the demand schedule 

and the supply schedule. Therefore, the equilibrium values of p and q 

will be such that both equations (1) and (2) hold.

Example

 1) In a competitive market the demand schedule is given by p = 420 − 0.2q and the supply schedule is given by p = 60 + 0.4q, Solve for p and q the simultaneous equation and determine the point at which the market is in equilibrium.

Solution:

Let us solve the system