UNIT 6:COMPLEX ELECTRICAL CIRCUIT
Key topic competence: By the end of the unit I should be able to
construct and to analyze a complex electrical circuit.
Unit Objectives:
By the end of this unit, I should be able to:
◊ analyse complex electrical circuits well.
◊ use Kirchhoff’s laws in circuit analysis accurately◊ analyse simple potentiometer circuits clearly.
Introductory Activity
Look at the illustration given above.
a. What type of devices available in the illustration above?
b. Can you suggest the names of the available devices in the
illustration above?
c. Is there any complete circuit in the illustration above?
d. What kind of electrical circuits identified in the illustration above?
e. Have you ever used or connected these electrical components
somewhere? If yes, what were the difficulties in handling these
electrical components in circuit construction?
f. What can be considered to select the best electrical device(s) to
be used in electrical circuit construction?
g. What can be put in recognition to minimize risks when
connecting these electrical components in the circuit?
6.0 INTRODUCTION
A complex circuit configuration is one that contains components that are
connected either in parallel or in series with each other. If a circuit can
be reduced to a single resistor, it is a series or parallel circuit. If not, it is
a complex circuit. If the circuit is complex and is mixed with series and
parallel networks of resistors and supplies, we may want to look if it is
feasible to reduce these to a single power supply and a single resistor which
would make them either a series or a parallel simple circuit.
Most electronic devices we use at home have built-in complex circuits to
perform different tasks. Also the concept of this unit is helpful in other
subjects like electrons and conductors (in Chemistry), volume adjustment
circuits in radios.
Opening questions
1. A combination circuit is shown in the diagram of Fig.5.1. Use the
diagram to answer the following questions.
a. The current at location A is _____ (greater than, equal to, less than)
the current at location B.
b. The current at location B is _____ (greater than, equal to, less than)
the current at location E.
c. The current at location G is _____ (greater than, equal to, less than)
the current at location F.
d. The current at location E is _____ (greater than, equal to, less than)
the current at location G.
e. The current at location B is _____ (greater than, equal to, less than)
the current at location F.
f. The current at location A is _____ (greater than, equal to, less than)
the current at location L.
g. The current at location H is _____ (greater than, equal to, less than)
the current at location I.
2. Consider the combination circuit in the diagram of Fig.5.1. Use the
diagram to answer the following questions. (Assume that the voltage
drop in the wires is negligibly small.)
a. The electric potential difference (voltage drop) between points
B and C is _____ (greater than, equal to, less than) the electric
potential difference (voltage drop) between points J and K.
b. The electric potential difference (voltage drop) between points
B and K is _____ (greater than, equal to, less than) the electric
potential difference (voltage drop) between points D and I.
c. The electric potential difference (voltage drop) between points E and
F is _____ (greater than, equal to, less than) the electric potential
difference (voltage drop) between points G and H.
d. The electric potential difference (voltage drop) between points E and
F is _____ (greater than, equal to, less than) the electric potential
difference (voltage drop) between points D and I.
e. The electric potential difference (voltage drop) between points J and
K is _____ (greater than, equal to, less than) the electric potential
difference (voltage drop) between points D and I.
f. The electric potential difference between points L and A is _____
(greater than, equal to, less than) the electric potential difference(voltage drop) between points B and K.
6.1 KIRCHHOFF’S LAWS
Next to Ohm’s Law in the fundamental rules which govern the behaviour
of electric circuits are Kirchhoff’s Circuit Laws. Gustav Kirchhoff in
1845 formulated two circuit laws, one of which essentially establishes
the conservation of charge and the other establishes the conservation ofpotential.
ACTIVITY 6-1
The 16 puzzle pieces associated with this problem represent different
circuit elements. Arrange the circuit pieces to form a four-by-four-piece
square, with the “sun” symbol appearing somewhere within the puzzle.
If all of the puzzle pieces are placed appropriately, the sun will be in aspecific position.
6.1.1 Kirchhoff’s Current Law
Kirchhoff’s first law, known as Kirchhoff’s Current Law (KCL) or Kirchhoff’s
Junction Rule, essentially expresses the conservation of charge, which can
be thought of as the conservation of matter. This implies that charge cannot
appear from anything at any point in a circuit, neither can it disappear into
oblivion at any point.
Kirchhoff’s Current Law states that “the algebraic sum of the currents
flowing at a node or junction in an electric circuit is zero”.
This means that currents are added with respect to their directions. Let usconsider the junction shown on Fig. 6.3 below.

Notes: Any calculated value of current which works out to be negative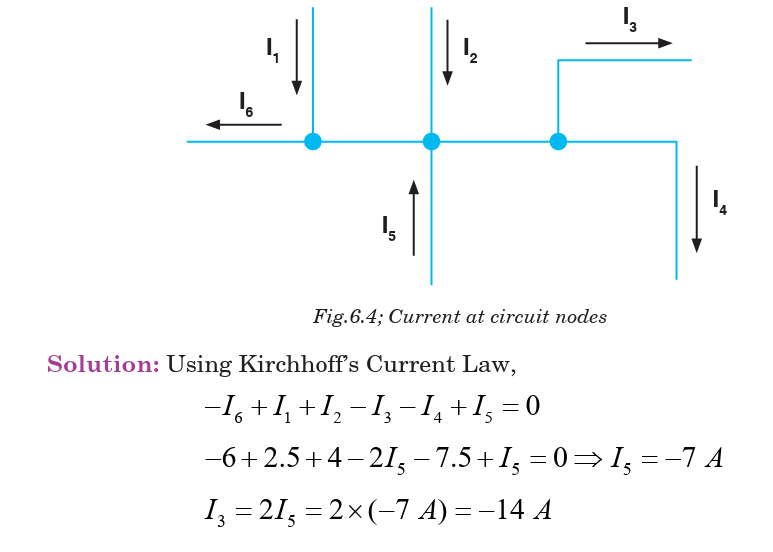
simply indicates that in practice, the current is actually flowing in adirection opposite to that assigned in the schematic diagram of the circuit.
6.1.2 Kirchhoff’s Voltage Law
Kirchhoff’s second circuit law, known as Kirchhoff’s Voltage Law (KVL) or
Kirchhoff’s Loop Rule, essentially formulates the conservation of energy in
the form of electric potential around a circuit in which current is flowing.
This means that no net voltage can be created or destroyed around the loop
of a closed circuit.
Kirchhoff’s Voltage Law states that “the algebraic sum of the potentials
around a closed electric circuit is zero.”Consider an electrical network shown in Fig. 6.5 below.
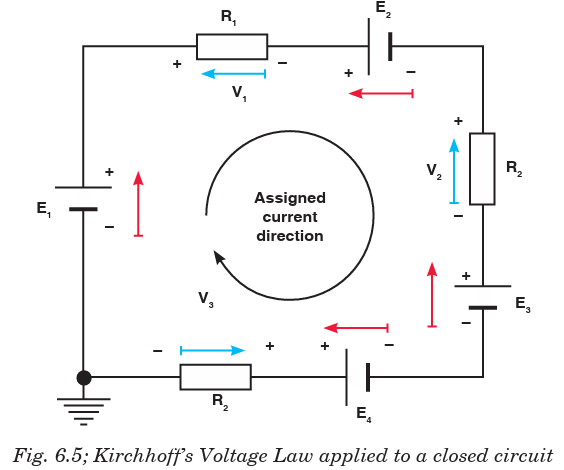
Kirchhoff’s Voltage Law gives:
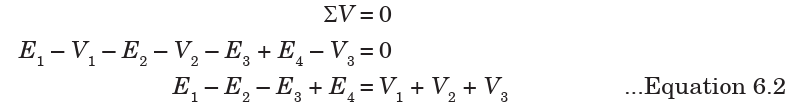
Sign conventions
• The potential change across a resistor is – IR if the loop is traversed
along the chosen direction of current (potential drops across a resistor).
• The potential change across a resistor is + IR if the loop is traversed
opposite the chosen direction of current.
• If an emf source is traversed in the direction of the emf, the change in
potential is positive.
• If an emf source is traversed in the opposite direction of the emf, thechange in potential is negative.
6.2 DESIGN OF COMPLEX AND SIMPLE ELECTRIC CIRCUITS
An electric circuit is a collection of electrical components connected by
conductors. A simple electric circuit consists of a supply with either seriesor parallel network of resistors.
This circuit contains neither simple series nor simple parallel connections.
It contains elements of both. It is complex circuit because the circuit is
a combination of both series and parallel, we cannot apply the rules for
voltage, current and resistance “across the table” to begin its analysis. Thisis shown below;
ACTIVITY 6-2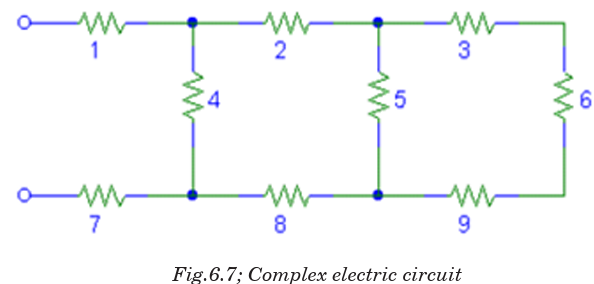
A. A circuit with two or more
braches for the current to flow
B. A material that electrons can
move through
C. Flow of electrons through a
conductor
D. Made up of series and parallel
circuits
E. Device to break a circuit
F. Poor conductor of electricity
G. Unit for measuring rate of
electron flow in a circuit
H. Having too many or too few
electrons
I. A temporary source of electric
current
J. Rate at which a device converts
electrical energy to another form of
energy.
1. Electric charge
2. Insulator
3. Conductor
4. Electroscope
5. Electric current
6. Resistance
7. Battery
8. Circuit
9. Series circuit
10. Parallel circuit
11. Complex circuit
12. Volt
13. Ampere
14. Switch15. Power
K. Path of electric conductors
L. Electric charge built up in one place
M. Device that detects electric charges
N. Opposition to the flow of electricity
O. Electric circuit where current
flows through all parts of the circuitP. Unit to measure electric potential
Aim: to know different components of the circuit and why they are needed
in the circuit.Instructions: match the following terms are used in electric circuits
ACTIVITY 6-3
For each of the following circuits state if it is series, parallel or
complex if any. In each case comment on the current flowing and thebrightness of the bulb.
6.3 RESISTORS AND ELECTROMOTIVE FORCES IN
SERIES AND PARALLEL COMPLEX CIRCUITS
This section examines how Kirchhoff’s voltage and current laws are applied
to the analysis of complex circuits. In the analysis of such series-parallel
circuits, we often simplify the given circuit to enable us to clearly see how
the rules and laws of circuit analysis apply. We might need to redraw
circuits whenever the solution of a problem is not immediately apparent.
Resistors are said to be in series if they are arranged side by side in a
such way that the total potential difference is shared by all resistors and
the current flowing through them is the same. This arrangement is shownbelow:
A parallel circuit is a circuit in which the resistors are arranged with their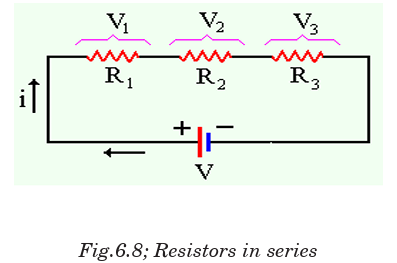
heads connected together, and their tails connected together. The current
in a parallel circuit breaks up, with some flowing along each parallel branch
and re-combining when the branches meet again. The voltage across eachresistor in parallel is the same.
The same idea of series and parallel resistors is applied in series and parallel
cells. For series e.m.fs the total e.m.f is equivalent to the sum of individuale.m.fs with respect to the direction of currents they generate.
When these cells are connected in parallel, the total e.m.f e equivalent to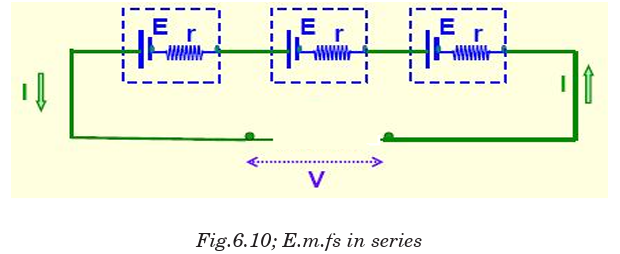
the e.m.f of only one cell.
To solve the resistor circuits using Kirchhoff’s rules,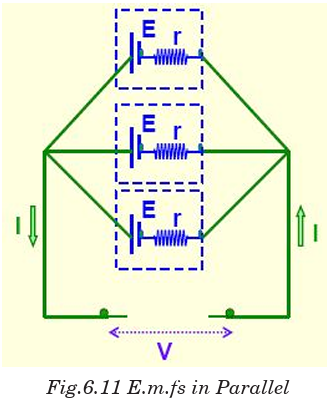
1. Define the various currents
• This can be done by either defining branch (segment) currents for
each element in the circuit, or defining loop currents for each loop in the circuit.
2. If using branch currents, use Kirchhoff’s Junction Rule to look for
interdependent currents. This allows for reducing the number of
variables being solved for.
3. Use Loop Rule to define voltage equations for each loop, using previously
defined currents.4. Solve set of simultaneous equations using algebraic manipulation.
EXAMPLE 6.3
Using Kirchhoff’s rules, calculate the currents I1
, I2 and I3 in the three branches of the circuit in Fig.5.12.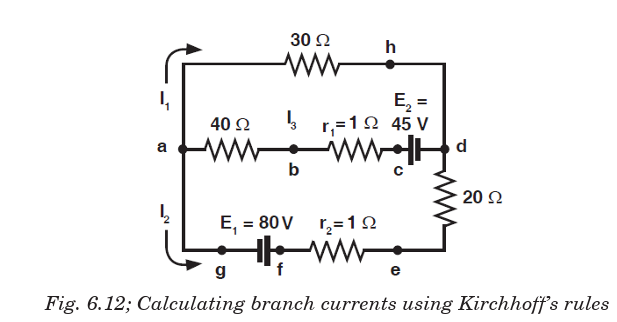

Ammeter
An ammeter is a device which is used to measure electric current flowing
through a branch of a circuit. Electric current is measured in amperes (A).
Smaller currents are measured by milliammeters (mA) and microammeters . Ammeters are of various types–moving coil ammeter, moving magnet
. Ammeters are of various types–moving coil ammeter, moving magnet
ammeter, moving iron ammeter, hot wire ammeter, etc. Nowadays, digital
ammeters are used to measure current accurately which use ADC (analog
to digital converter). An ammeter is connected in series with the circuitthrough which current is flowing.
Voltmeter
A voltmeter is a device which is used to measure electric potential difference
between two points in an electrical circuit. Electric p.d. is measured in
along a calibrated scale in proportion to circuit voltage. Digital voltmeters
are now frequently used to give a display of voltage using ADC. A voltmeter
is always connected in parallel to the component across which p.d. is to bemeasured.

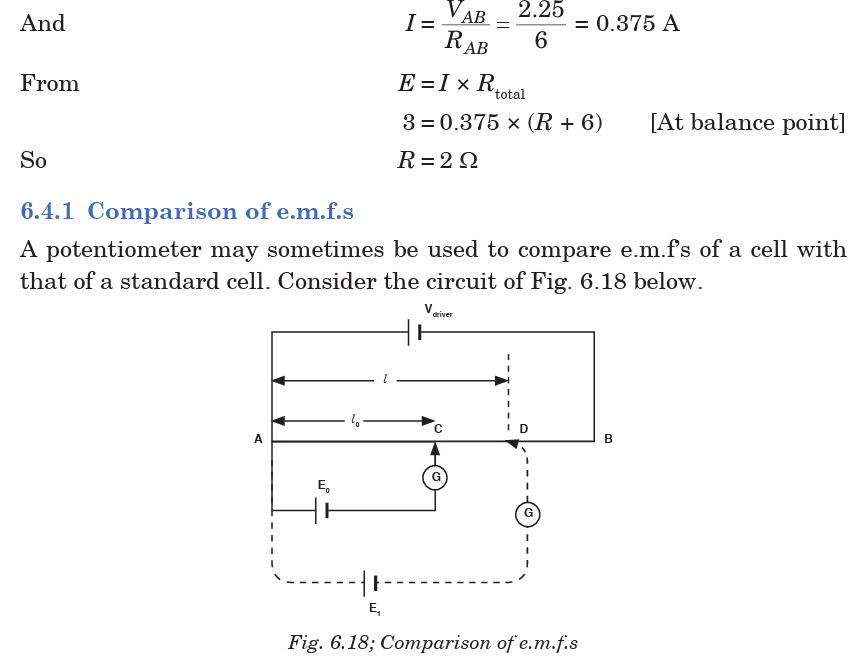
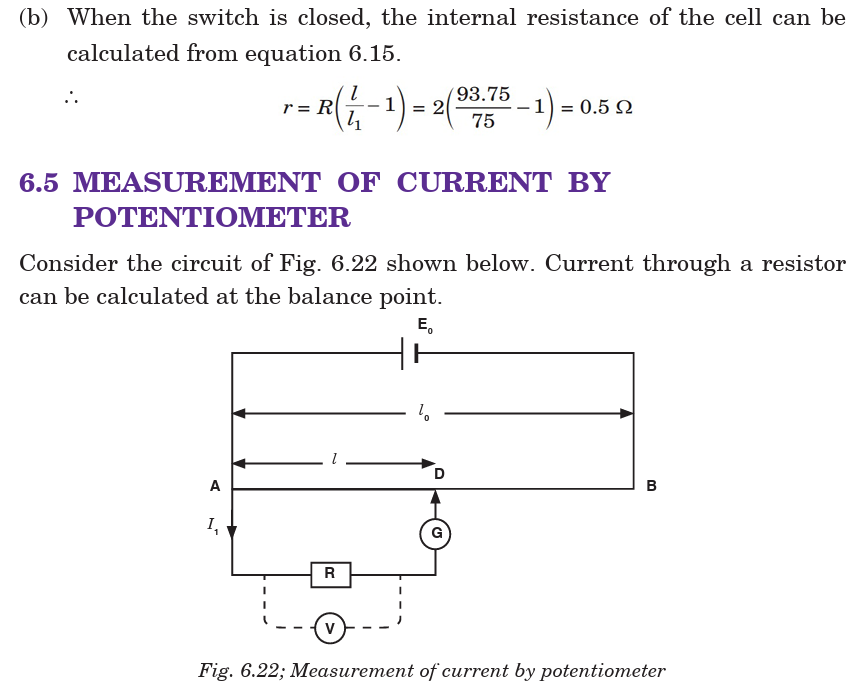
6.4 SIMPLE POTENTIOMETER CIRCUITS
A simple potentiometer is a device used for taking a number of electrical
measurements. It is a piece of resistance wire, usually a metre long, fixed
between two points A and B with a cell of output voltage, V, connected
between the two ends. The potential difference to be measured is put intoa circuit together with an opposing variable p.d. from the voltage divider.
The voltage divider is then adjusted until its p.d., VAC equals the p.d. beingmeasured. Fig. 6.15 illustrates this.
The sliding contact in the above diagram is moved until the galvanometer
indicates zero. This position is referred to as the balance p oint. The current
in the lower part of the circuit is zero because the p.d., VAC equals the p.d.
E provided by the cell under test. The protective resistor serves only to
prevent the galvanometer from the damage.
Electromotive force of the wire is always proportional to the length of thewire. So, the approximate value of E is determined as follows:

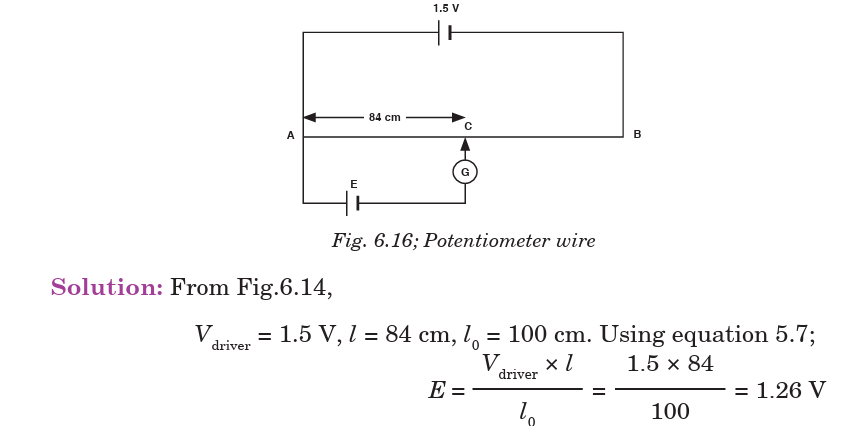
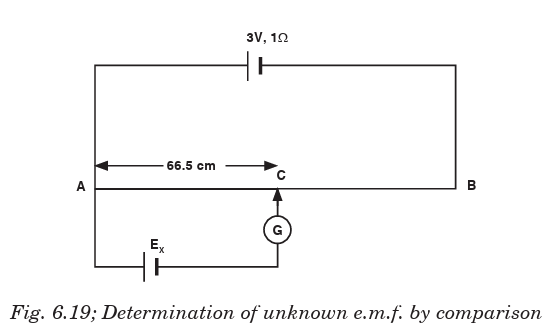
EXAMPLE 6.5
What value of resistance is needed in series with a driver cell of negligible
Solution: At the balance point or null point, no current flows through the
galvanometer, i.e. in the lower loop of the circuit. But in the lower loop ofthe circuit, a current I flows. Since the current in the lower loop is zero.


6.4.2 Measurement of internal resistance of a cell
The circuit is arranged as shown in Fig. 6.20 with the cell, whose internal
resistance r is to be found, is connected in parallel with a resistor with
resistance R and a switch. The driver cell as usual is in the upper loop ofthe circuit.
The balance point l is found with the switch open. Since at balance point, no
current is flowing through G; E is then measured. The switch is then closed
and the new balance point l1 is found. Balance length l1 is proportional tooutput voltage V (across the resistor R); i.e.
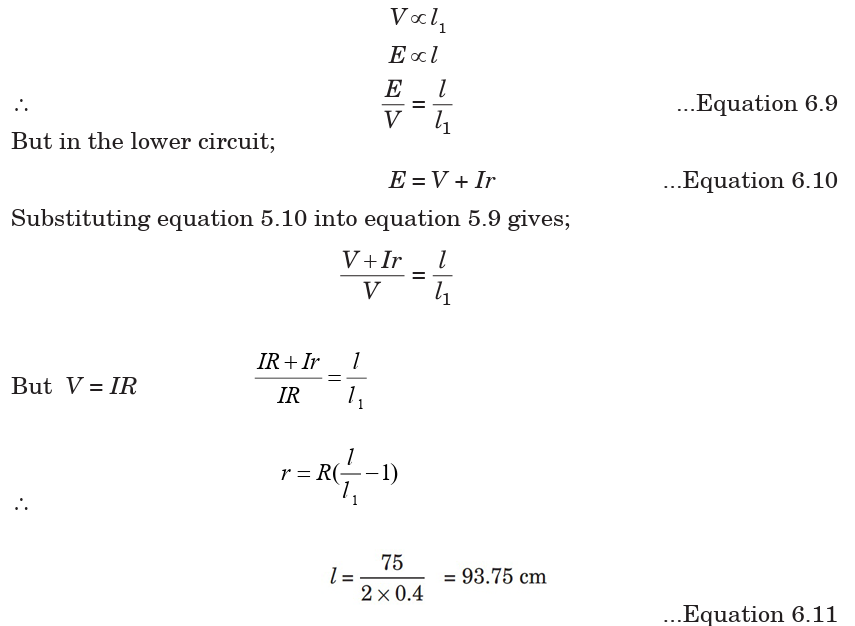
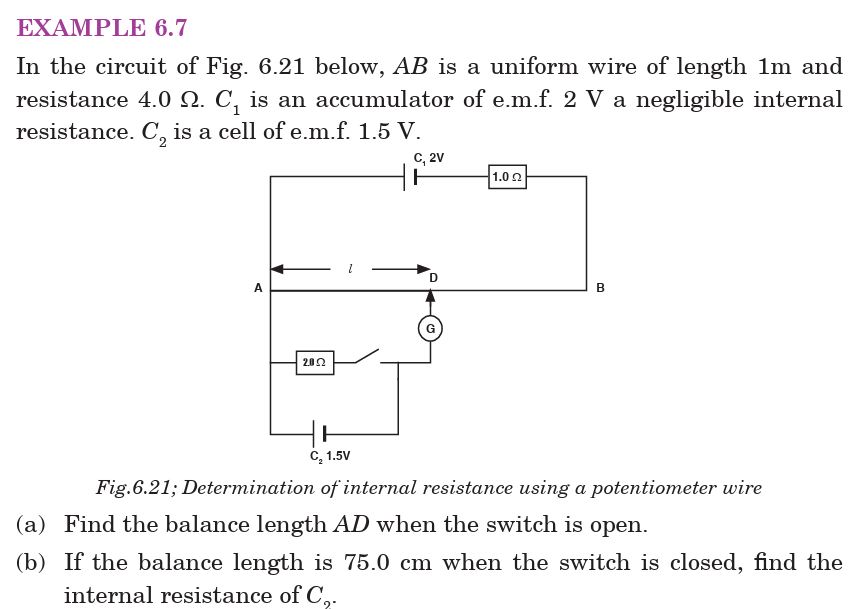

ACTIVITY 6-4
To measure the e.m.f. of an unknown cell using a potentiometer.
Procedure:
(a) Connect the circuit as shown in Fig. 6.23. Voltage supply is set at its
appropriate value, so the current is fairly small. This is to protect
the galvanometer.
(b) Close the DPDT (Double Pole Double Throw) switch to the standard
cell side and calibrate the potentiometer by finding what length of
wire corresponds to the voltage of the standard cell. This is done by
finding the location of the sliding contact where the galvanometer
does not deflect when the key switch is closed.
(c) Calculate the constant, k, using the e.m.f. of the standard cell and
the length, LS
measured to the sliding contact-use equation E = kLs
(d) Throw the DPDT switch to connect the unknown battery in the
circuit and move the sliding contact until the galvanometer indicates
zero current as in Step 2. (Do not adjust Rheostat Rt since this will
change the voltage across the potentiometer wire and upset your
calibration). Read the length Lv
measured on the sliding contact.
(e) Calculate the e.m.f. of the unknown battery by the formula: E = kLv
(f) Now measure the voltage of the unknown battery with the voltmeter.Explain the difference.

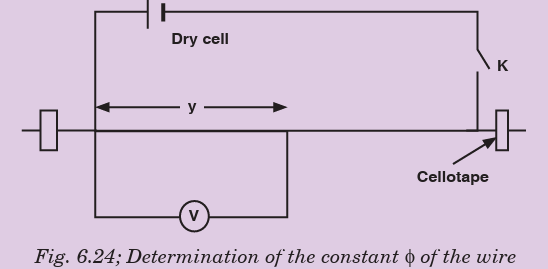
ACTIVITY 6-5
Determination of the constant of the wire.
of the wire.
Procedure:(a) Fix the wire provided firmly on the bench.
Application Activity 6.1
1. A potentiometer is set up as shown in Fig. 6.25. Given that the
balancing point for the unknown e.m.f. E is found to be 74.5 cm
from the left hand end of the meter wire (1 m). If the driver cell has
an e.m.f. of 1.5 V and negligible internal resistance. Find the valueunknown e.m.f.
2. A certain cell is connected to a potentiometer and a balance point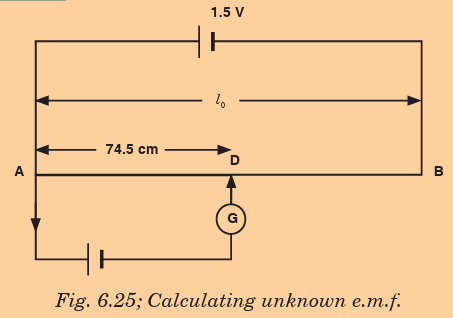
is obtained at 84 cm along the meter wire. When its terminals are
connected to a 5 resistor, the balance point changes to 70 cm.
resistor, the balance point changes to 70 cm.
Calculate the balance when a 5 resistor is now replaced by a 4
resistor is now replaced by a 4 
resistor.
6.6 ADVANTAGES AND DISADVANTAGES OF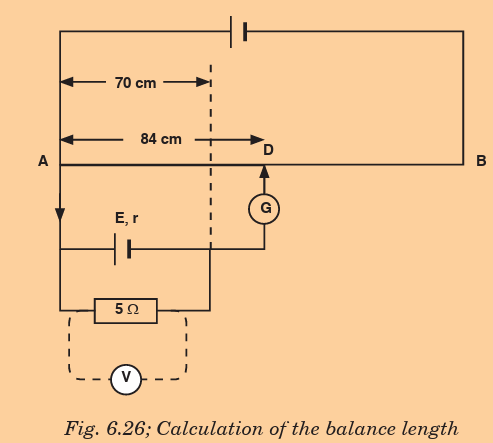
POTENTIOMETER
Wear: Most potentiometers last only a few thousand rotations before the
materials wear out. Although it means years of service in some applications,
it takes special designs to stand up to daily, demanding use. It means they
can’t be used for machine sensing where rapid cycling would wear them out
in a matter of minutes.
Noise: The action of the wiper moving across the element creates a noise
called “fader scratch.” In new pots, this noise is inaudible, but it can get
worse with age. Dust and wear increase the bumpiness of the action and
make the noise noticeable. Small cracks can appear in the element, and
these make noise as the wiper moves over them.
In addition to these mechanically caused noises, carbon elements, in
particular, are prone to producing electrical noise. This noise is heard as a
soft, steady hiss that can degrade sound recordings. The resistive materials
have improved over the years, so newer pots are quieter.
Inertia: The friction between the potentiometer’s wiper and resistive
element creates a drag or inertia that the pot must overcome before it
turns. Although this drag is not large, it prevents the pot from being used
as a rotary sensor in more sensitive applications.
Limited Power: Out of necessity, most potentiometers can dissipate only a
few watts of power. To handle more power, they have to be larger and hence
expensive. Engineers work around this problem by putting the potentiometer
in low-power parts of circuits. They control small currents, which, in turn,control transistors and other components with greater power ratings.
END OF UNIT ASSESSMENT
1. What are Kirchhoff’s rules for understanding a circuit?
2. Explain why Kirchhoff’s junction rule must be true if the Law of
Conservation of Charge (that no charge may be created or destroyed) is true.
3. Explain why Kirchhoff’s loop rule must be true if the Law of Conservation
of Energy is true.4. Find the branch currents of the circuit shown below.


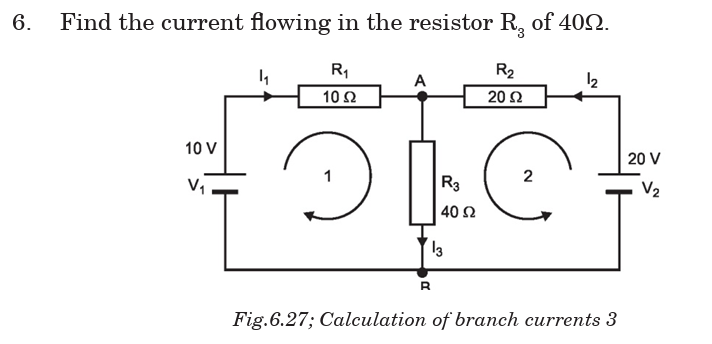


(b) Solve the equations to find the current through each resistor in the circuit.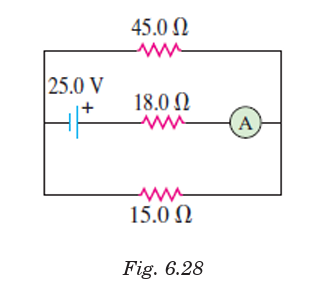
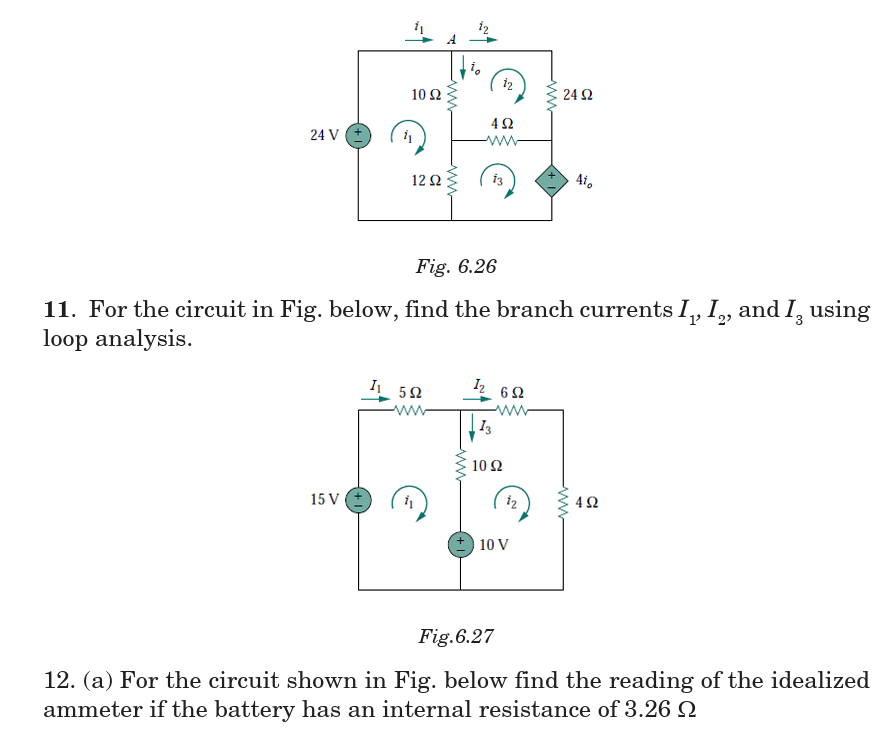
13. (a) Apply Kirchhoff’s rules to the following circuit to find a set ofequations that describe how charges behave inside the circuit
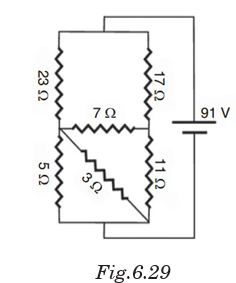
(b) Solve the equations to find the current through each resistor in the circuit.
UNIT SUMMARY
Kirchhoff’s laws
There are two Kirchhoff’s laws: Kirchhoff’s Current Law states that “the
algebraic sum of the currents flowing at a node or junction in an electric
circuit is zero.”
Kirchhoff’s Voltage Law states that “the algebraic sum of the potentials
around a closed electric circuit is zero.”
To solve the resistor circuits using Kirchhoff’s rules
1. Define the various currents
• Can either define branch (segment) currents for each element in the circuit
• Or can define loop currents for each loop in the circuit
2. If using branch currents, use Kirchhoff’s Junction Rule to look for
interdependent currents. This allows for reducing the number of
variables being solved for.
3. Use Loop Rule to define voltage equations for each loop, using previously
defined currents.
4. Solve set of simultaneous equations using algebraic manipulation.
A simple potentiometer is a device used for taking a number of electrical
measurements. It is a piece of resistance wire, usually a metre long,
fixed between two points A and B with a cell of output voltage, V,
connected between the two ends.
Potentiometer can be used to
(i) compare e.m.f.’s of two primary cells.
(ii) measure internal resistance of a cell.
