UNIT 3:FORCED OSCILLATIONS AND RESONANCE OF A SYSTEM
Key unit competence: Analyze the effects of forced oscillations on
systems..
Unit Objectives:
By the end of this unit I will be able to;
◊ Explain the concept of oscillating systems and relate it to the real
life situations.
◊ Solve equations of different types of damped oscillations and derive
the expression for displacement for each.
◊ explain resonance, state its conditions and explain its applicationsin everyday life.
Introductory Activity
Comment on the following situations by giving clear reasons on each;
• A guitar string stops oscillating a few seconds after being
plucked.
• To keep a child moving on a swing, you must keep pushing.
3.0 INTRODUCTION
In the conventional classification of oscillations by their mode of excitation,
oscillations are called forced if an oscillator is subjected to an external
periodic influence whose effect on the system can be expressed by a separate
term, a periodic function of the time, in the differential equation of motion.
We are interested in the response of the system to the periodic external
force. The behaviour of oscillatory systems under periodic external forces is
one of the most important topics in the theory of oscillations. A noteworthy
distinctive characteristic of forced oscillations is the phenomen of resonance,
in which a small periodic disturbing force can produce an extraordinarily
large response in the oscillator. Resonance is found everywhere in physics
and thus, a basic understanding of this fundamental problem is required.
3.1 DAMPED OSCILLATIONS.
Unless maintained by some source of energy, the amplitude of vibration of
any oscillatory motion becomes progressively smaller and the motion is said
to be damped. The majority of the oscillatory systems that we encounter
in everyday life suffer this sort of irreversible energy loss while they are in
motion due to frictional or viscous heat generation generally. We therefore
expect oscillations in such systems to eventually be damped.
Damping is the gradual decrease of amplitude of an oscillating system
due to presence of dissipative forces. As work is being done against
the dissipating force, energy is lost. Since energy is proportional to theamplitude, the amplitude decreases exponentially with time.
ACTIVITY 3-1: Resonance
Clearly observe the figure below and answer the questions thatfollow:
a) How is figure A different from B?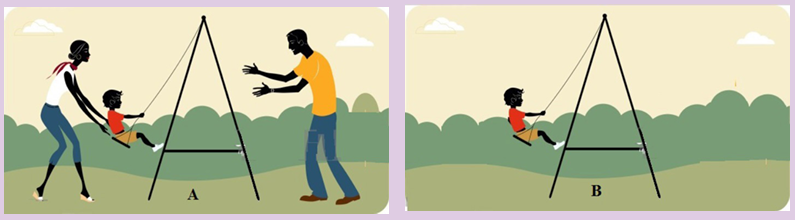
b) What do you think the kid is doing?
c) Assume that the man and woman shown are the kid’s father and
mother. What do you think they are doing?
d) Explain the oscillations in both cases.
e) Compare the two oscillations.
f) Depending on the definition of damping given above, how do you relate
it with the above scenarios?g) Make a clear conclusion.
In everyday life we experience some damped oscillations like:(i) Damping due to the eddy current produced in the copper plate
(ii) Damping due to the viscosity of the liquid
3.2 EQUATION OF DAMPED OSCILLATIONS
Consider a body of mass m attached to one end of a horizontal spring, the
other end of which is attached to a fixed point. The body slides back and
forth along a straight line, which we take as x-axis of a system of Cartesian
coordinates and is subjected to forces all acting in x-direction (they may be
positive or negative). The motion equations for constant mass are based
on Newton’s second law which can be expressed in terms of derivatives. In
all derivations assume that m is the mass of an oscillating object, b is thedamping constant and k is the spring constant.
Where b is the damping constant and the negative sign means that damping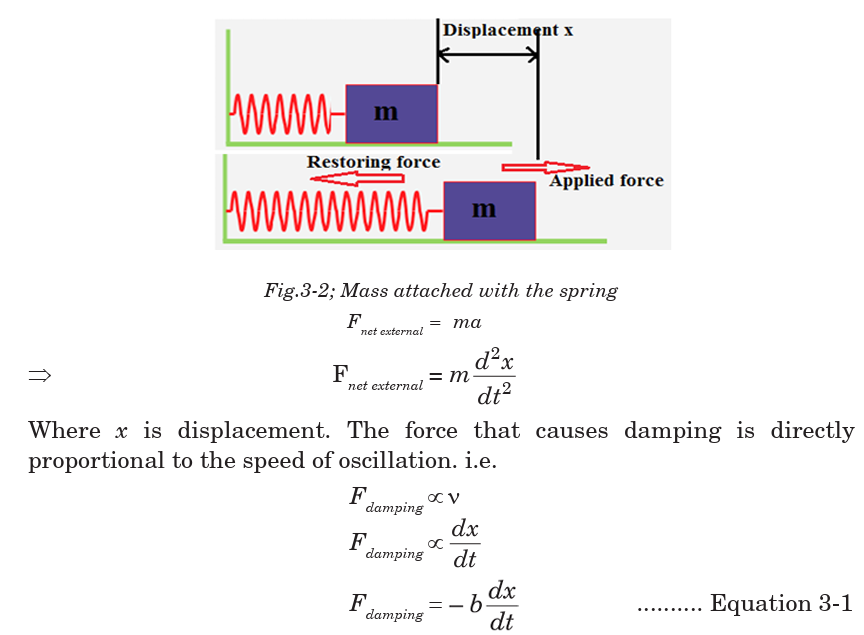
force always opposes the direction of motion of the mass.
The spring itself stores the energy that is used to restore the position of the
mass once released after being slightly displaced. The restoring force of thespring is directly proportional to the displacement.
Where k is the spring constant and the negative sign means that the restoring
force opposes the direction of motion of the mass. With this restoring forceand the resisting force of the spring, the resultant force on the mass is;
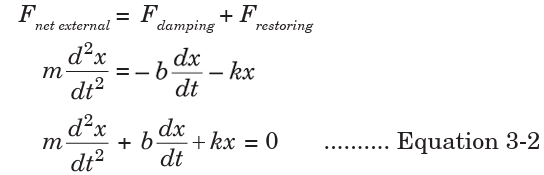
Equation 3.2 is the differential equation of damping.
3.3 THE SOLUTION OF EQUATION OF DAMPINGIn terms of derivatives, the equation of damped oscillation is given by
We see that when the retarding force is small, the oscillatory character of the motion is
preserved but the amplitude decreases in time, with the result that the motion ultimately
ceases. Any system that behaves in this way is known as a damped oscillator.
Figure 3-3 shows the position as a function of time for an object oscillating in thepresence of a retarding force.
The dashed blue lines in Fig.3.3, which define the envelope of the oscillatory curve,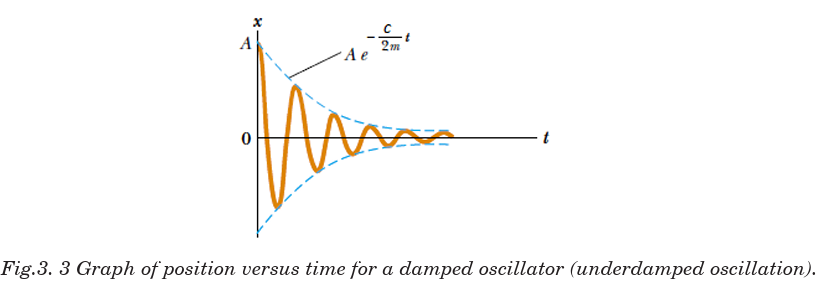
represent the exponential factor in Equation 3-4. This envelope shows that the amplitudedecays exponentially with time.
These cases are respectively classified as overdamped, critically damped, and
oscillatory damped (or, in electrical problems, underdamped) as shown in fig.3.4.
Let us consider these cases separately:
3.4.1 Overdamped or Heavy dampingOverdamped or Heavy damping is also called excessive damped oscillation and occur
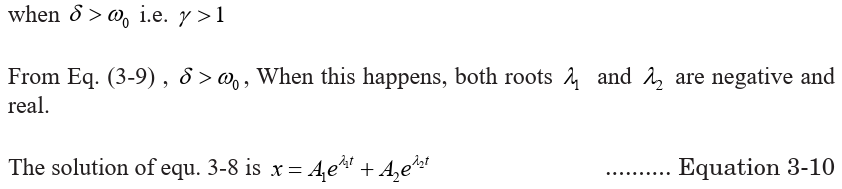
A typical critically damped oscillation is shown in Fig. 3.4). A critically damped system
converges to zero as fast as possible without oscillating.
An example of critical damping is the door closer seen on many hinged doors in pub
lic buildings. An over-damped door-closer will take longer to close than a critically
damped door would.
Examples of Critical damping
(a) Shock Absorber
It critically damps the suspension of the vehicle and so resists the setting up
of vibrations which could make control difficult or cause damage. The viscousforce exerted by the liquid contributes to this resistive force.
(b) Electrical Meters They are critically damped (i.e. dead-beat) oscillators so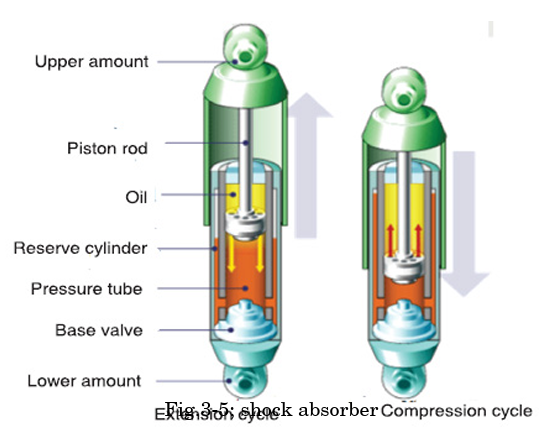
that the pointer moves quickly to the correct position without oscillation.
The system oscillates with the amplitude gradually (slowly) decreasing to zero. In
this situation, the system will oscillate at the natural damped frequency ωd
, which is a
function of the natural frequency and the damping ratio. This system stops after one or
two oscillations.
To continue the analogy, an underdamped door closer would close quickly, but would
hit the door frame with significant velocity, or would oscillate in the case of a swinging
door. Fig.3.4 depicts a typical underdamped response.
Examples of slightly damped oscillations include
Acoustics
(i) A percussion musical instrument (e.g. a drum) gives out a note whose intensity
decreases with time. (slightly damped oscillations due to air resistance)
(ii) The paper cone of a loud speaker vibrates, but is heavily damped so as to lose energy
(sound energy) to the surrounding air.
Plotting equations for damped oscillation on the same amplitude-time axes gives thegeneral curve for damping oscillation as shown on Fig.3-6.
Undamped oscillation (free oscillations): δ= 0
If the oscillating system is isolated (i.e. if no energy is being added to or taken away
from the system) the oscillations are called free oscillations. The system oscillates at
its natural resonant frequency ωo. Free Oscillations can occur whenever a restoring
force capable of transforming potential energy (PE) to kinetic energy (KE) and vice
versa is present. In a free oscillation, since the sum of the PE and KE cannot increase,
the PE must be largest at the extreme points of the oscillation where the KE is zero.
Examples
• Liquid sloshing mode - the restoring forces are due to gravity.
• A vibrating metal plate - elastic restoring forces.
• Stretched string - the restoring force is provided by tension in the string.
In each of these three examples all the oscillating particles together formed astanding wave pattern.
ACTIVITY 3-2 Damping Oscillation
A mass and spring system was set up with three masses of 100g and
radius 2.5 cm. The oscillator (masses) was displaced by 3 cm, released
and the time was measured for the oscillator to come to rest. After this,
pieces of circular cards were inserted between two of the masses and
the experiment was carried out again. Analyse the results obtained astabulated in table 3-1.
Analysis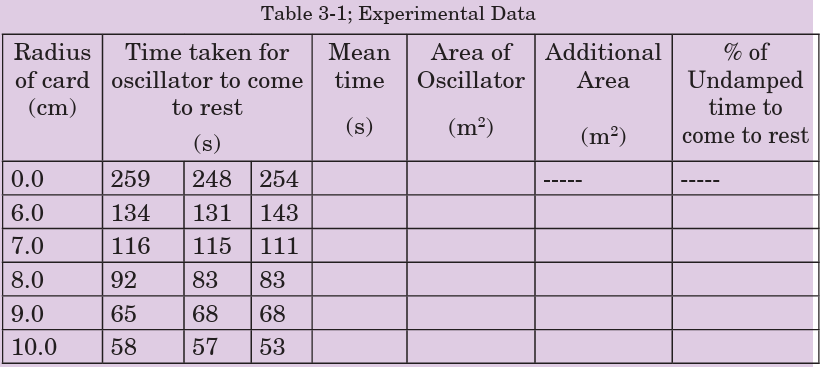
• Calculate mean value for the time taken for the oscillator to come
to rest for each radius of card.
• What is the uncertainty in the time taken to stop when the radius is 6 cm?
• Calculate this as a percentage of the mean value.
• What is the uncertainty in the time taken to stop when the radius is 8 cm?
• Calculate this as a percentage of the shortest time measurement at this radius.
• What is the uncertainty in the time taken to stop when the radius is 10 cm?
• Calculate this as a percentage of the longest time measurement at
this radius.
• What type of error is responsible for the difference in the value of
the time taken to come to rest?
• Calculate the area of the oscillator using A =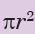
. Write these values
in the column provided.
• What is the precision in the radius of card measurements?
• Calculate the percentage uncertainty in the 7.0 cm measurement.
• What will be the percentage uncertainty in the value of the area?
• Write down the upper and lower limits of the area.
• Plot a graph of radius of Oscillator (on the y axis) against time
taken to come to rest.
• Describe the graph you have plotted.
• What does your graph suggest about the relationship between the
two variables?
• Plot a graph of area of Oscillator (on the y axis) against time taken
to come to rest.
• Describe the graph you have plotted.
• What does your graph suggest about the relationship between
these two variables?
• Complete the final columns of the table by calculating the
additional area each card adds to the oscillator and the time period
as a percentage of the undamped time taken to come to rest.
• Do you notice any patterns or trends?
• Plot a graph of additional area (y axis) against percentage of
undamped time taken to come to rest.
• How are these variables linked?
• Theory states that damping will not affect the time period of the
SHM system. How could you prove this using the experimental setup described above?
3.5 NATURAL FREQUENCY OF A VIBRATION AND
FORCED OSCILLATION.
The natural frequency of an object is the frequency of oscillation when
released. e.g. a pendulum. A forced oscillation is where an object is subjected
to a force that causes it to oscillate at a different frequency than its natural
frequency. e.g. holding the pendulum bob in your hand and moving it along
its path either more slowly or more rapidly than its natural swing. Examples
on forced oscillation include:
A: Barton’s Pendulum
The oscillation of one pendulum by application of external periodic force
causes the other pendulums to oscillate as well due to the transfer of energy
through the suspension string. The pendulum having the same pendulum
length and pendulum bob mass will have the same natural frequency as
the original oscillating pendulum and will oscillate at maximum amplitude
due to being driven to oscillate at its natural frequency causing resonance to occur.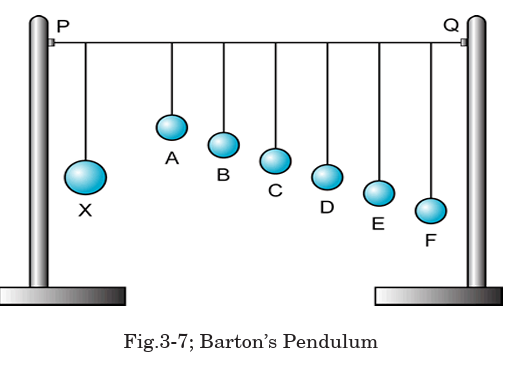
B: Hacksaw blade oscillator
This is another example of resonance in a driven system. If the peiod
of oscillation of the driver is changed by increasing the length of thread
supporting the moving mass, the hacksaw blade will vibrate at a different
rate. if we get the driving frequency right the slave will reach the resonant
frequency and vibrate widely. Moving the masses on the blade will have asimilar effect.
3.6 EQUATION OF FORCED OSCILLATION AND ITS SOLUTION
The mechanical energy of a damped oscillator decreases in time as a result of the resistive
force. It is possible to compensate for this energy decrease by applying an external force
that does positive work on the system. At any instant, energy can be transferred into the
system by an applied force that acts in the direction of motion of the oscillator.
For example, a child on a swing (se Fig.3.5) can be kept in motion by appropriately timed
“pushes.” The amplitude of motion remains constant if the energy input per cycle of
motion exactly equals the decrease in mechanical energy in each cycle that results from
resistive forces.
When a vibrating system is set into motion, it vibrates at its natural frequency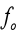
the resistive force decrease the amplitude because there is a loss of energy. To stop the
decrease of amplitude you must give an external energy to the system. The system that
gives energy is called excitatory and one receiving is called resonator. The resonator is
forced to oscillate at the frequency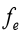
the external force and oscillation is forced.
Symbolically, it is designated by a dashpot, as shown in Fig. below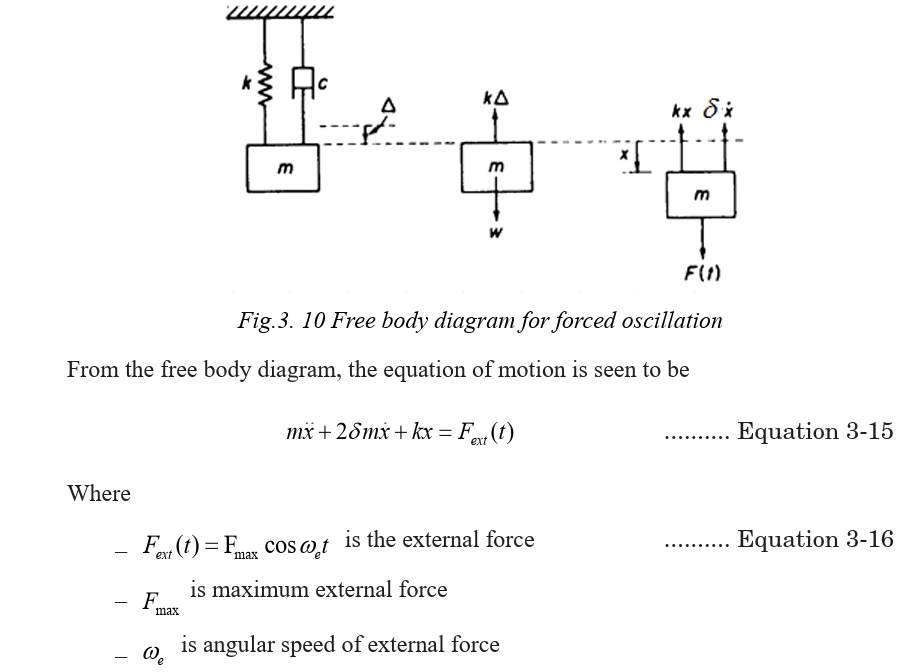
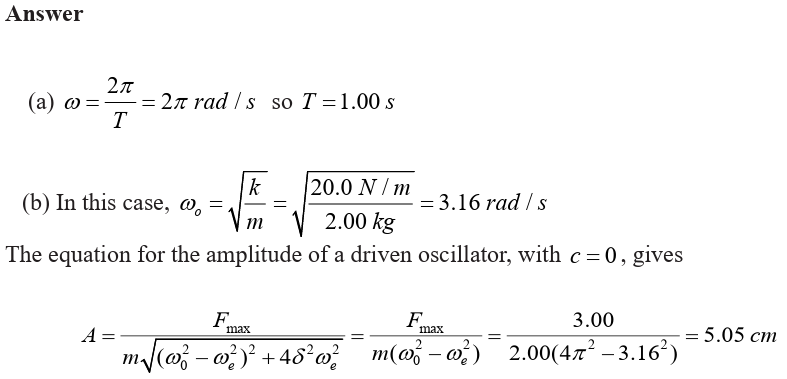
3.7. VARIATION OF FORCED FREQUENCY ON GRAPH AT
AMPLITUDE CLOSE TO NATURAL FREQUENCY OF VIBRATION.
If an oscillating object is made to perform forced oscillations, closer is the
frequency of force applied to the natural frequency, larger is the oscillation.
However the amplitude rises and falls as the object will be assisted to
oscillate for a short time and then the forces will oppose its motion for a short
time. The graph shows the variation of the amplitude of the oscillationswith time.
In figure 3.7, the applied force has a frequency closer to the natural
frequency. The amplitude of the oscillation has increased and there is timewhen the force helps and then hinders the oscillations.
The largest amplitude is produced when the frequency of the applied force
is the same as the natural frequency of the oscillation. When the energy
input from the applied force is equal to the energy loss from the damping,the amplitude stops increasing.
3.8 RESONANCE
When the frequency of excitatory is the same as that of resonator, then
the process is called resonance. The phenomenon of resonance is quicklyincreasing of amplitude when the frequency of exciting force approaches
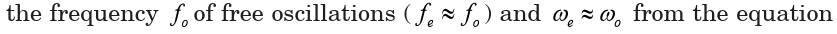
3.9 APPLICATIONS AND EXAMPLES OF RESONANCE
IN EVERYDAY LIFE
The phenomenon of resonance depends upon the whole functional form of
the driving force and occurs over an extended interval of time rather than
at some particular instant. Below are examples of resonance in different
applications;
3.9.1 A washing machine
A washing machine may vibrate quite violently at particular speeds. In
each case, resonance occurs when the frequency of a rotating part (motor,
wheel, drum etc.) is equal to a natural frequency of vibration of the body ofthe machine. Resonance can build up vibrations of large amplitude.
3.9.2 Breaking the glass using voice
Fig.3-14; A washing machine
You must have heard the story of an opera singer who could shatter a glass
by singing a note at its natural frequency. The singer sends out a signal
of varying frequencies and amplitudes that makes the glass vibrate. At
a certain frequency, the amplitude of these vibrations becomes maximum
and the glass fails to support it and breaks it. This scenario is shown onFig.3-10 below.
3.9.3 Breaking the bridge
The wind, blowing in gusts, once caused a suspension bridge to sway with
increasing amplitude until it reached a point where the structure was over
stressed and the bridge collapsed. This is cuased by the oscillations of the
bridge that keep varying depending on the strength of the wind. At a certain
level, the amplitude of oscillation becomes maximum and develops crack onit and suddenly breaks.
3.9.4 Musical instruments
Wind instruments such as flute, clarinet, trumpet etc. depend on the idea
of resonance. Longitudinal pressure waves can be set up in the air inside
the instrument. The column of air has its own natural frequencies at
which it can vibrate. When we blow, we use the mouthpiece to start some
vibrations. Those which happen to match exactly the natural frequencies ofthe instrument are picked out and magnified.
3.9.5 Tuning circuit
The another example of useful resonance is the tuning circuit on a radio
set. Radio waves of all frequencies strike the aerial and only the one which
is required must be picked out. This is done by having a capacitance
inductance combination which resonates to the frequency of the required
wave. The capacitance is variable; by altering its value other frequenciescan be obtained.
3.9.6 Microwave Ovens
Microwave ovens use resonance. The frequency of microwaves almost
equals the natural frequency of vibration of a water molecule. This makes
the water molecules in food to resonate. This means they take in energy
from the microwaves and so they get hotter. This heat conducts and cooks the food.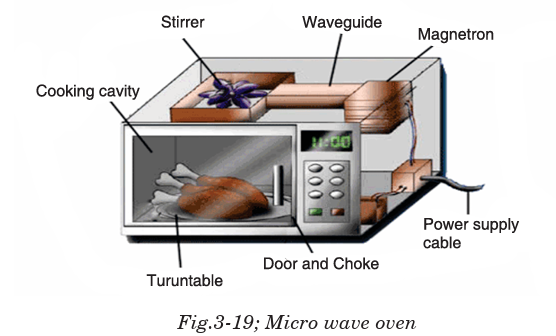
3.9.7 Magnetic Resonance Imaging (MRI)
The picture showing the insides of the body was produced using magnetic
resonance imaging (MRI). Our bodies contain a lot of hydrogen, mostly in
water. The proton in a hydrogen spins. A spinning charged particle has a
magnetic field, so the protons act like small magnets. These are normally
aligned in random directions. Placing a patient in a strong magnetic field
keeps these mini magnets align almost in line. Their field axis just rotateslike a spinning top. This is called processing.
3.10 EFFECT OF RESONANCE ON A SYSTEM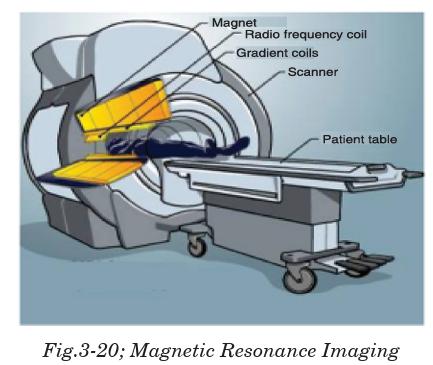
◊ Vibrations at resonance can cause bursting of the blood vessel.
◊ In a car crash a passenger may be injured because their chest is
thrown against the seat belt.
◊ The vibration of kinetic energy from the wave resonates through
the rock face and causes cracks.
◊ It is also used in a guitar and other musical instruments to
give loud notes.
◊ Microphones and diaphragm in the telephone resonate due to radio
waves hitting them.
◊ Hearing occurs when eardrum resonates to sound waves hitting it.
◊ Soldiers do not march in time across bridges to avoid resonance and
large amplitude vibrations. Failure to do so caused the loss of over two
hundred French infantry men in 1850.
◊ If the keys on a piano are pushed down gently enough it is possible to
avoid playing any notes. With the keys held down, if any loud noise
happens in the room (e,g. Somebody shouting), then some of the notes
held down will start to sound.
◊ An opera singer claims to be able to break a wine glass by loudlysinging a note of a particular frequency.
END OF UNIT ASSESSMENT
1. Solve the following initial value problem and determine the naturalfrequency, amplitude and phase angle of each solution.
2. Solve the following initial value problem. For each problem, determine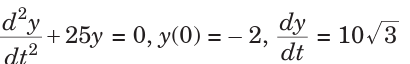
whether the system is under, over, or critically damped.
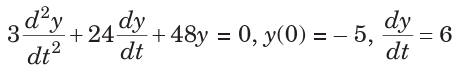
3. Consider a mass-spring system described by the equation
Give the value(s) of k for which the system is under, over, and critically
damped.
4. Damping is negligible for a 0.150 kg object hanging from a light 6.30
N/m spring. A sinusoidal force with an amplitude of 1.70 N drives the
system. At what frequency will the force make the object vibrate with an
amplitude of 0.440 m?
5. A 10.6 kg object oscillates at the end of a vertical spring that has a
spring constant of . The effect of air resistance is represented by the
damping coefficient . Calculate the frequency of the damped oscillation.
6. 1. A body of mass 0.5 kg suspended on a spring constant 50 N/m, describes
the damped oscillation with coefficient of resistance . At the upper end
it is applied the exciting force . Calculate the damping constant and the
amplitude of resonance of this system.
7. A body of mass 0.5 kg suspended on a spring constant 50 N/m, describes
the damped oscillation with coefficient of resistance . At the upper end
it is applied the exciting force . Calculate the damping constant and theamplitude of resonance of this system.
UNIT SUMMARY
Damping is a dissipating force that is always in the opposite direction
to the direction of motion of the oscillating particle and is represented by equation;
The natural frequency of an object is the frequency of oscillation when
released. e.g. a pendulum.
A forced oscillation is where an object is subjected to a force that causes it
to oscillate at a different frequency than natural frequency. It is representedby differential equation;
Resonance occurs when an object capable of oscillating, has a force applied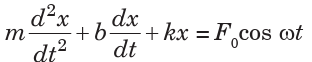
to it with a frequency equal to its natural frequency of oscillation. Resonance
occurs when angular frequency of oscillation is related to natural angularfrequency according to equation;
In real life, resonance is applied in;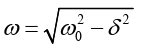
• A washing machine
• Breaking the glass using the voice
• Breaking the bridge
• Musical instruments
• Tuning circuit
• Microwave ovens• Magnetic Resonance Imaging (MRI)