UNIT 2: SIMPLE HARMONIC MOTION
Key unit competence: By the end of the unit I should be able to
analyze energy changes in simple harmonic motion.
Unit Objectives:
By the end of this unit I will be able to;
◊ Determine the periodic time of an oscillating mass by practically
and by calculation accurately.
◊ Derive and apply the equation of simple harmonic motion correctly◊ Determine the periodic time of the simple pendulum correctly.
Introductory Activity
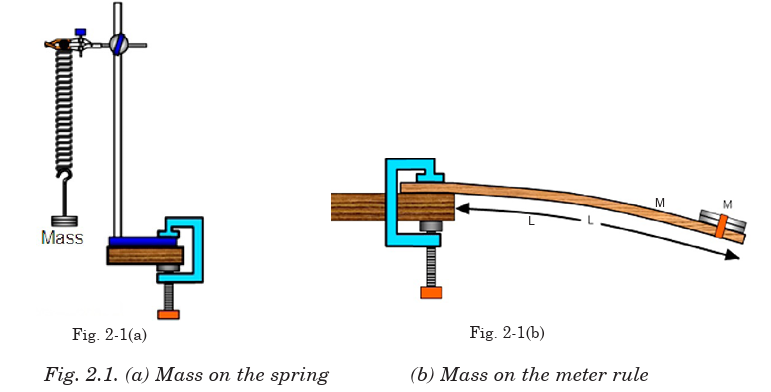
a. Clearly analyze the images of Fig. 2-1 given below and explain
what you think would happen in each case when the mass is displaced.
b. Basing on your daily experiences, what other systems do you
think behave the same way as fig 2.1(shown above) when displaced?
c. Discuss fields where those systems you mentioned in b) aboveare applied.
2.0 INTRODUCTION
You are familiar with many examples of repeated motion in your daily
life. If an object returns to its original position a number of times, we call
its motion repetitive. Typical examples of repetitive motion of the human
body are heartbeat and breathing. Many objects move in a repetitive way,
such as a swing, a rocking chair and a clock pendulum. Probably the first
understanding of repetitive motion grew out of the observations of motion
of the sun and phases of the moon.
Strings undergoing repetitive motion are the physical basis of all string
musical instruments. What are the common properties of these diverse
examples of repetitive motion?
In this unit we will discuss the physical characteristics of repetitive
motion and develop techniques that can be used to analyze this motionquantitatively.
Opening question
Clearly analyze the images of Fig. 2-1 given below and explain what youthink will happen in each case when the mass is displaced.
2.1 KINEMATICS OF SIMPLE HARMONIC MOTION
One common characteristic of the motions of the heartbeat, clock pendulum,
violin string and the rotating phonograph turntable is that each motion has
a well defined time interval for each complete cycle of its motion. Any motion
that repeats itself with equal time intervals is called periodic motion. Its
period is the time required for one cycle of the motion.
In Mechanics we showed that simple harmonic motion occurs when the
force acting on an object or system is directly proportional to its displacement x
from a fixed point and is always directed towards this point:
The negative sign in Eq. 2.01 implies that the force is opposite to the dis
placement.
To stretch the spring a distance x, an (external) force must be exerted onthe free end of the spring with a magnitude at least equal to.
The greater the value of k, the greater the force needed to stretch a spring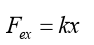
a given distance. That is, the stiffer the spring, the greater the spring constant k.
Consider a physical system that consists of a block of mass m attached to
the end of a spring, with the block free to move on a horizontal, frictionless
surface (Fig. 2.2). When the spring is neither stretched nor compressed, the
block is at the position called the equilibrium position of the system. If disturbed from its equilibrium position such a system oscillates back and forth.
Fig.2. 2 A block attached to a spring moving on a frictionless surface. (a) When the block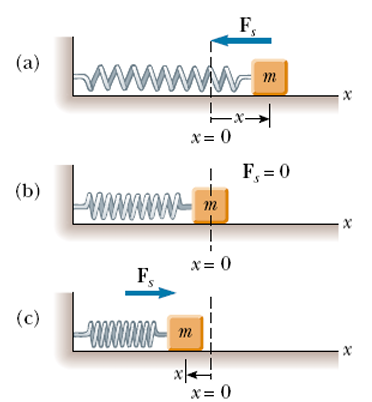
is displaced to the right of equilibrium (x > 0 ), the force exerted by the spring acts to
the left. (b) When the block is at its equilibrium position (x =0 ), the force exerted by the
spring is zero. (c) When the block is displaced to the left of equilibrium (x < 0 ), the forceexerted by the spring acts to the right.
Recall that when the block is displaced a small distance x from equilibrium,
the spring exerts on the block a force that is proportional to the displace
ment and given by Hooke’s law (Eq. 2.01).
We call this a restoring force because it is always directed toward the
equilibrium position and therefore opposite the displacement. That is, when
the block is displaced to the right of in Figure above, then the displacement
is positive and the restoring force is directed to the left. When the block is
displaced to the left of then the displacement is negative and the restoring
force is directed to the right.
Applying Newton’s second law to the motion of the block, together withEquation 2.01, we obtain.
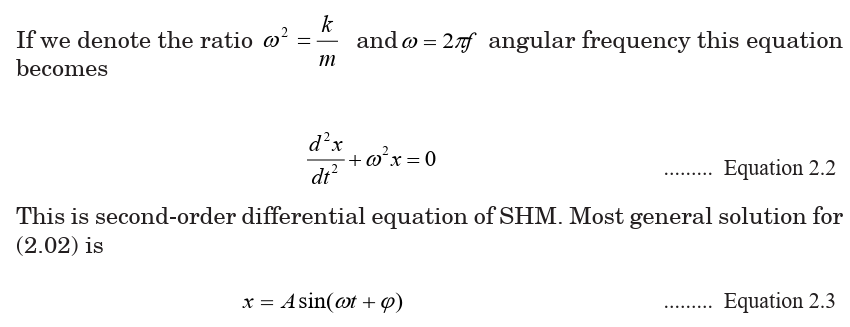
Fig.2. 3 Defining the phase angle for a sinusoidal function that
crosses the horizontal axis with a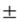
positive slope after 0°
We can obtain the linear velocity of a particle undergoing simple harmonic
motion by differentiating Equation 2.03 with respect to time:
From this equation we see that the acceleration is proportional to the
displacement of the body, and its direction is opposite the direction of the
displacement. Systems that behave in this way are said to exhibit simple
harmonic motion.
The curves in Fig.2.4 show that at the time of zero velocity 2.4a, the acceleration
and the displacement are maximum. At a time of maximum velocityFig.2.4b, the acceleration and the displacement are zero. We say that they
EXAMPLE 2.1
A particle moving with SHM has velocities 4 cm/s and 3 cm/s at distances
3 cm and 4 cm respectively from equilibrium position. Find
(a) the amplitude of oscillation
(b) the period(c) velocity of the particle as it passes through the equilibrium position.
EXAMPLE 2.2
A simple pendulum has a period of 2.0 s and amplitude of swing 5.0 cm.
Calculate the maximum magnitude of
(a) velocity of the bob
(b) acceleration of the bob.
The frequency and period depend only on the mass of the block and on the
force constant of the spring. Furthermore, the angular frequency, the frequency
and period are independent of the amplitude of the motion
EXAMPLE 2.3: PERIOD, FREQUENCY, AND ANGULAR FREQUENCY
1. A car with a mass of 1 300 kg is constructed so that its frame is supported
by four springs. Each spring has a force constant of 20 000 N/m.
(a) If two people riding in the car have a combined mass of 160 kg, find the
frequency of vibration of the car after it is driven over a pothole in the road
and what is the angular frequency.
(b) How long does it take the car to execute two complete vibrations?
Answer
We assume that the mass is evenly distributed. Thus, each spring supports
one fourth of the load. The total mass is 1 460 kg, and therefore each springsupports 365 kg.
ACTIVITY 2-1: Cantilever
Aim of this activity is to determine the periodic time of a cantilever beam.
Required Materials
Metre rule, G-clamp (or a wooden block), stop watch, set of masses(4 × 100 g), Cellotape and pair of scissors (can be shared).
EXAMPLE 2-4The displacement of an object undergoing simple harmonic motion is given
Application Activity 2.1
1. A body of mass 100 g undergoes simple harmonic motion with
amplitude of 20 mm. The maximum force which acts upon it is 0.05
N. Calculate:
(a) its maximum acceleration.
(b) Its period of oscillation.
2. The following graph shows the displacement (x) of a simple harmonic oscillator.
Draw graphs of its velocity, momentum, acceleration and the force acting on it.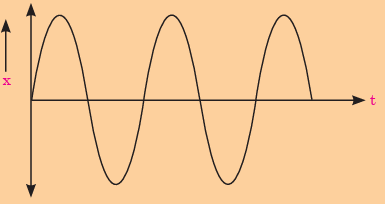
3. A particle undergoes SHM with an amplitude of 8.00 cm and an
angular frequency of 0.250 s-1. At t = 0, the velocity is 1.24 cm/s.
Determine:
(a) The equations for displacement and velocity of the motion.(b) The initial displacement of the particle.
2.2 SIMPLE HARMONIC OSCILLATORS
A simple harmonic oscillator is a physical system in which a particle
oscillates above and below a mean position at one or more characteristic
frequencies. Such systems often arise when a contrary force results from
displacement from a force-neutral position and gets stronger in proportion
to the amount of displacement. Below are some of the physical oscillators;
2.2.1 Simple Pendulum
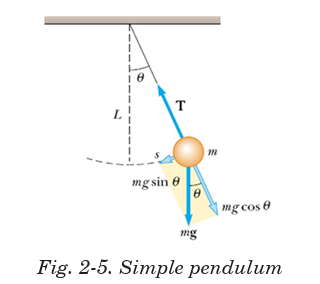
A simple pendulum consists of a small bob of mass m suspended from a
fixed support through a light, inextensible string of length L as shown on
Fig.2-5. This system can stay in equilibrium if the string is vertical. This is
called the mean position or the equilibrium position. If the particle is pulled
aside and released, it oscillates in a circular arc with the center at the pointof suspension ‘O’.
Equation 2-12 shows that acceleration is directly proportional to displace
ment and is opposite to it. So the bob executes S.H.M;Comparing equation 2-7 and equation 2-12 gives
Equation 2-18 represents the periodic time of a simple pendulum. Thus, the
following are the factors affecting the periodic time of the simple pendulum;
• Length of string
• Acceleration due to gravity
EXAMPLE 2.5
A small piece of lead of mass 40 g is attached to the end of a light string of
length 50 cm and it is allowed to hang freely. The lead is displaced to 0.5 cm
above its rest position, and released.
(a) Calculate the period of the resulting motion, assuming it is simple
harmonic.
(b) Calculate the maximum speed of the lead piece. (Take g = 9.81 m.s–2)
Solutions:
(a) To calculate the time periodequation 2-26 can be used
EXAMPLE 2.6
What happens to the period of a simple pendulum if the pendulum’s length
is doubled? What happens to the period if the mass of the suspended bob isdoubled?
ACTIVITY 2-2: Acceleration due to Gravity
The aim of this activity is to determine the acceleration due togravity using oscillation of a simple pendulum Apparatus
2.2.2 Mass suspended from a Coiled Spring
The extension of the spiral spring which obeys Hook’s law is directly
proportional to the extending tension. A mass m is attached to the end of
the spring which exerts a downward tension mg on it and stretches it by eas shown in Fig.2-7 below;
The stretching force is equal to the upward tension and is given by k(x + e)
So, the resultant force acting on the mass downwards is given by;F = Downword force – Upward force .
Form equation 2-17 and 2-18, we conclude that the periodic time of an
oscillation of a mass on a spring will depend on extension and the mass tied on it.
EXAMPLE 2.7
When a family of four with a total mass of
200 kg steps into their 1200 kg car, the car’s
springs get compressed by 3.0 cm.
(a) What is the spring constant of the car’s
springs (Fig.2-9), assuming they act as a
single spring?
(b) How far will the car lower if loaded with300 kg rather than 200 kg?
ACTIVITY 2-3: Acceleration due to Gravity
Aim: The aim of this activity is to determine the acceleration due to
gravity, g, using mass on spring.
Required materials1 retort stand, one spiral
spring, slotted masses (5 × 100g), 1 meter rule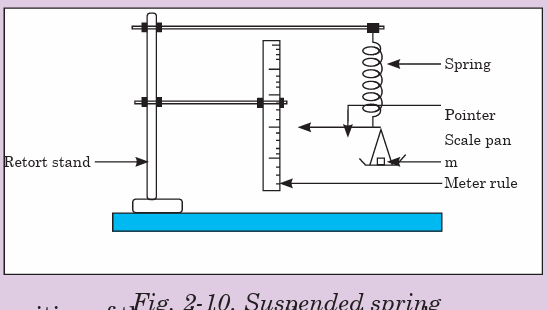
Procedure
(a) Clamp the given spring and a meter rule as shown in the
figure above.
(b) Read and record the position of the pointer on the meter rule.
(c) Place mass m equal to 0.100 kg on the scale pan and record the new
position of the pointer on the meter rule.
(d) Find the extension of the spring x in meters.
(e) Remove the meter rule
(f) Pull the scale pan downwards through a small distance and release it.
(g) Measure and record the time for 20 oscillations. Find the time T for
one oscillation.
Repeat the procedures (f) and (g) for values of m equal to 0.200 kg,
0.300 kg, 0.400 kg and 0.500 kg.
(i) Record your results in a suitable table including values of T2.
(j) Plot a graph of T2 (along the vertical axis) against m (along the horizontal axis).
(k) Find the slope, s, of the graph.
2.2.3 Liquid in a U-tube.
Consider a U-shaped tube filled with a liquid. If the liquid on one side of a
U-tube is depressed by blowing gently down that side, the level of the liquid
will oscillate for a short time about the respective positions O and C beforefinally coming to rest.
Application Activity 2.2
1. A baby in a ‘baby bouncer’ is a real-life example of a mass-on
spring oscillator. The baby sits in a sling suspended from a stout
rubber cord, and can bounce himself up and down if his feet are
just in contact with the ground. Suppose a baby of mass 5.0 kg is
suspended from a cord with spring constant 500 N m–1. Assume g =
10 N kg–1.
(a) Calculate the initial (equilibrium) extension of the cord.
(b) What is the value of angular velocity?
(c) The baby is pulled down a further distance, 0.10 m, and
released. How long after his release does he pass through
equilibrium position?
(d) What is the maximum speed of the baby?
(e) A simple pendulum has a period of 4.2 s. When it is shortened
by 1.0 m the period is only 3.7 s.
(f) Calculate the acceleration due to gravity g suggested by the
data.
2. A pendulum can only be modelled as a simple harmonic oscillator
if the angle over which it oscillates is small. Why is this so?
3. What is the acceleration due to gravity in a region where a simple
pendulum having a length 75.000 cm has a period of 1.7357 s?
State the assumptions made.
4. A geologist uses a simple pendulum that has a length of 37.10 cm
and a frequency of 0.8190 Hz at a particular location on the Earth.What is the acceleration due to gravity at this location?
6. A spring is hanging from a support without any object attached to it
and its length is 500 mm. An object of mass 250 g is attached to the
end of the spring. The length of the spring is now 850 mm.
(a) What is the spring constant?
The spring is pulled down 120 mm and then released from rest.
(b) Describe the motion of the object attached to the end of the spring.(c) What is the displacement amplitude?
2.3 KINETIC AND POTENTIAL ENERGY OF AN
OSCILLATING SYSTEM
Kinetic energy as the energy of a body in motion, change in velocity will also
change it as shown on Fig.2-12. Velocity of an oscillating object at any point
is given by equation:
2.4 ENERGY CHANGES AND ENERGY CONSERVATION
IN AN OSCILLATING SYSTEM
In an oscillation, there is a constant interchange between the kinetic and
potential forms and if the system does no work against resistive force its
total energy is constant. Fig.2-12 illustrates the variation of potential
energy and kinetic energy with displacement x.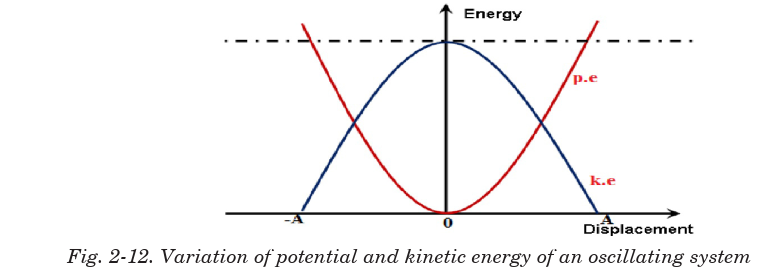
Substituting equation for sinusoidal displacement into equation 2-29 and
equation 2-30 gives;
is independent of displacement x. Since the total energy of an oscillating
particle is constant, it means that potential energy and kinetic energy vary
in such a way that total energy is conserved.
Also substituting equation 2-30 and equation 2-31 into equation 2-32 will
give an expression for the total energy of an oscillating system which isindependent of time taken.
EXAMPLE 2.9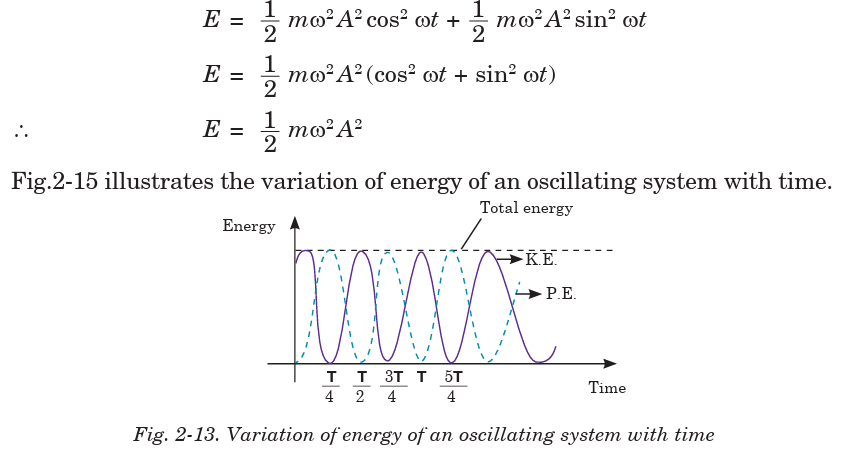
A 0.500 kg cart connected to a light spring for which the force constant is
20.0 N/m oscillates on a horizontal, frictionless air track.
(a) Calculate the total energy of the system and the maximum speed of the
cart if the amplitude of the motion is 3.00 cm.
(b) What is the velocity of the cart when the position is 2.00 cm?
(c) Compute the kinetic and potential energies of the system when the
position is 2.00 cm.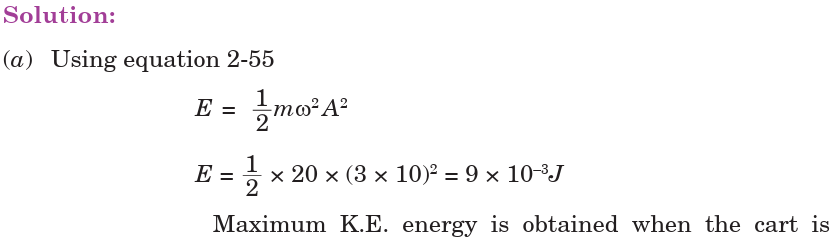
Application Activity 2.3
1.The graph in fig. below shows the variation with displacement of the
kinetic energy with displacement of a particle of mass 0.40 kgperforming SHM.
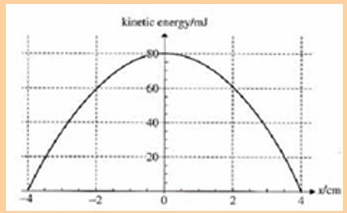
Use the graph to determine:
i. The total energy of the particle.
ii. The maximum speed of the particle.
iii. The amplitude of the motion.
iv. The potential energy when the displacement is 2.0 cm.
v. The period of the motion.
2. A 0.500-kg mass is vibrating in a system in which the restoring
constant is 100 N/m; the amplitude of vibration is 0.200 m.
Find
a. The PE and KE when x = 0.100 m
b. The mechanical energy of the system
c. The maximum velocity
2.5 SUPERPOSITION OF HARMONICS OF SAMEFREQUENCY AND SAME DIRECTION
Consider two simple harmonic oscillations which interfere to produce a
displacement x of the particle along same line. Suppose that both have the
same frequency. The displacement time functions of respective motions are
given by equations 2-39 and 2-40 with A1 and A2 being the amplitude of
individual displacements ( x1and x2) and a1 and a2as their respective
phase angles;
QUESTIONS
1. Give at least 2 examples of the applications of superposition in real life.
2. Derive the expression for the resultant displacement of two oscillations
of the same frequency but acting in opposite directions.
END OF UNIT ASSESSMENT
2. A 200 g block connected to a light spring for which the force constant
is 5.00 N/m is free to oscillate on a horizontal, frictionless surface. The
block is displaced by 5.00 cm from equilibrium and released from rest,as in Fig.2-15.
(a) Find the period of its motion.
(b) Determine the maximum speed of the block.
(c) What is the maximum acceleration of the block?
(d) Express the position, speed, and acceleration as functions of time.
3. (a) A 10 N weight extends a spring by 5 cm. Another 10 N weight is
added, and the spring extends another 5 cm. What is the spring
constant of the spring?
(b) A pendulum oscillates with a frequency of 0.5 Hz. What is the
length of the pendulum?
4. Christian Huygens (1629–1695), the greatest clockmaker in history,
suggested that an international unit of length could be defined as the
length of a simple pendulum having a period of exactly 1 s. How much
shorter would our length unit be had his suggestion been followed?
5. A simple pendulum is suspended from the ceiling of a stationary
elevator, and the period is determined. Describe the changes, if any, in
the period when the elevator
(a) accelerates upward,
(b) accelerates downward, and
(c) moves with constant velocity.
6. Imagine that a pendulum is hanging from the ceiling of a car. As the car
coasts freely down a hill, is the equilibrium position of the pendulum
vertical? Does the period of oscillation differ from that in a stationary car?
7. What is the acceleration due to gravity in a region where a simple
pendulum having a length 75.000 cm has a period of 1.7357 s?
UNIT SUMMARY
Simple Harmonic Motion: Any motion that repeats itself in equal time
intervals is called periodic motion with the force F acting on an object
directly proportional to the displacement x from a fixed point and is always
towards this point.
Periodic Time; is the time taken by the particle to complete one oscillation.
Frequency is defined as number of oscillations occur in one second f = 1/T.
Amplitude is the maximum displacement of the particle from its resting position.
Angular velocity (w): is the rate of change of angular displacement with time.
The extension of the spiral spring (caused by attached mass) which obeys
Hooke’s law is directly proportional to the extending tension. The periodic
time of oscillation caused by releasing the mass is given by;
