Unit 4 Work, Energy and Power
Key Unit Competence
Evaluate the relation between work, energy and power and the resulting
phenomena.
My goals
By the end of this unit, I will be able to:
* define work done, energy and power.
* state the formulae of work, energy and power.
* explain how power depends on energy.
* explain how gravitational potential energy.
* identify the difference between potential energy and kinetic energy
* describe strain and work done in deforming materials
INTRODUCTORY ACTIVITY
Kaliza and Kalisa are classmates in senior four sciences. When Kaliza
mops the class alone; she can do it in only 30 minutes. But when Kalisa
is given the same task of mopping the class, he can do it in 45 minutes.
Questions
1. Discuss the work being done as in the above case study. In your own
words define the term work.
2. Sometimes people do confuse the term work and energy. Are they
different? Are they the same? Explain your choice.
3. Between Kaliza and Kalisa who is more powerful? Why?
4. By research find the meaning of the terms: Work, energy and power
Introduction
In real life, we always use the term work. Which means “task to be
accomplished. But before the task to be done, one must have energy. Then if
a given work is done in a given time, we say that one has power i.e work done
in a given time.
Work
Review of the idea of work
Activity 1
Study and interprete the diagram below
CASE I
Work is done when a force moves its point of application along the
direction of its action.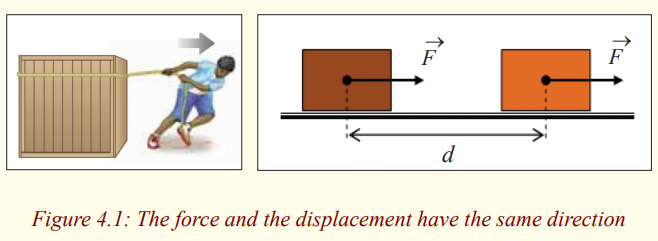
* How is the force applied onto the body?
* Why does it change its position?
* What if the body is 10 times the mass of the boy. Would the body
change its position? Why?
* State the direction of application of force.
From the fig. 4.1 and your deductions, how can you define Work?
CASE II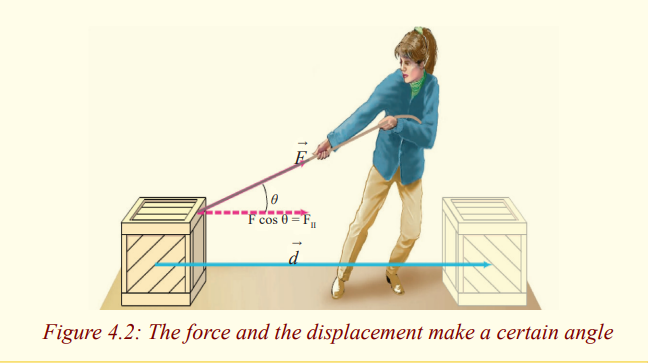
Activity 2
Aim; To relate distance, force and work
Let us as a class visit any where people are constructing a house,a bride,
road.
Ask them why they are paid?
Ask them how they measure what they do.

Expressions of some kinds of work
Work of the gravitational force
Activity 3
a) Hold a book in your hands at a height say h.
b) Leave it to fall vertically onto the ground.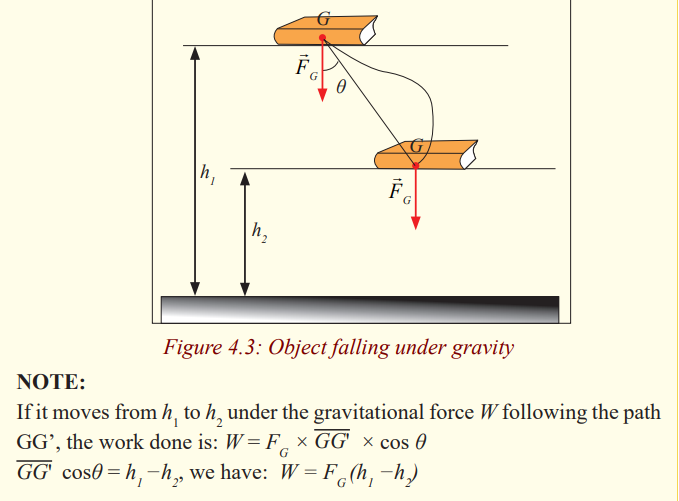
From the deductions, it can be noted that:
The work done by the gravitational force does not depend on the path
followed but on the change of the height.
Work done by the force of pressure
Activity 4
Requirements
* A syringe with a piston.
Aim: To determine work done by a piston.
* Pull the piston through a small distance ∆x as shown in the figure below.
Assuming you applied a force F, What is the work done?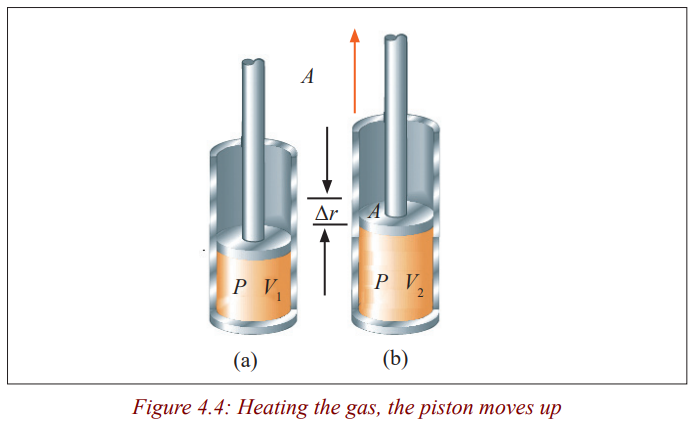

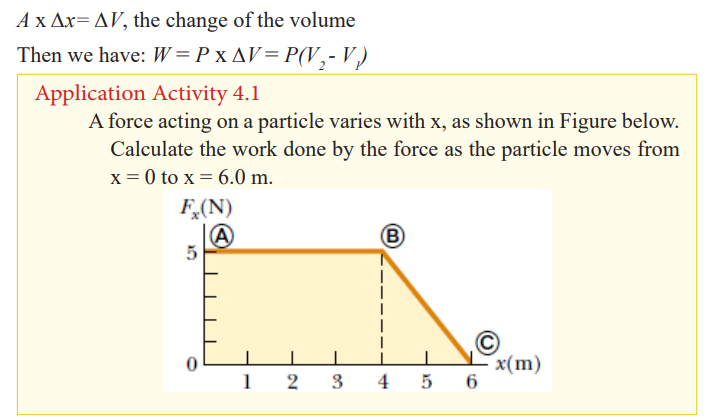
Energy
Activity 5
Ask yourself why some times you feel like not working or bored. What
do you normally say when you are asked why you are not performing any
duty? Use what comes into your mind to define energy.
Normally we say that Energy is ability of a body to do work.
It’s measured in Joules like work. When an interchange of energy occurs
between two bodies, we can consider the work done as a measure of the
quantity of energy transferred between them. It has the same units as work
and heat i.e. Joule.
The displacement is that of the point of application of the force. If the
force is applied to a particle or a non-deformable, non-rotating system, this
displacement is the same as the displacement of the particle or system. For
deformable systems, however, these two displacements are often not the same.
Force is not necessarily the cause of the object’s displacement. For example,
if you lift an object, work is done by the gravitational force, although gravity
is not the cause of the object moving upward! An important consideration
is that work is an energy transfer. If W is the work done on a system and W
is positive, energy is transferred to the system; if W is negative, energy is
transferred from the system. Whenever work is done energy is transferred or
converted from one form to another. Work is performed not only in motion and
displacement (mechanical work); it is done also by fire flame and electricity
in electric lamps.
Example
The gravitational force exerted by the Sun on the Earth holds the Earth in
an orbit around the Sun. Let us assume that the orbit is perfectly circular.
The work done by this gravitational force during a short time interval in
which the Earth moves through a displacement in its orbital path is
(a) zero (b) positive (c) negative (d) impossible to determine.
Solution
(a). The force does no work on the Earth because the force is pointed
toward the center of the circle and is therefore perpendicular to the
direction of the displacement.
Categories of Energy in Our Environment
There are several forms of energy in our environment e.g. mechanical energy,
heat energy, light energy, electromagnetic energy, electric energy, nuclear
energy, sound energy, chemical energy stored in petrol, food and other
materials, moving matter such as water, wind, falling rocks, etc.
Furthermore, one form of energy can be converted to another. For example,
when an electric motor is connected to a battery, the chemical energy in the
battery is converted to electrical energy in the motor, which in turn is converted
to mechanical energy as the motor turns some device.
Scientists classify forms of energy into two major categories: Potential energy
and Kinetic energy.
Potential energy
Activity 6
How do we know that things have energy just because of their height?
Well, let’s think about the following process:
1. You lift a ball off the ground until it is above your head.
2. You drop it.
3. It is moving fast right before it hits the ground.
4. Draw a conclusion.
Potential energy may be defined as the energy possessed by an objects or
bodies due to their position or state of strain or the position of their parts.
Potential energy is energy deriving from position. Potential energy is referred
to as stored energy because it can be looked at as energy which will be used
when time comes for it to be used. Thus a stretched rubber band has elastic
potential energy.
Kinds of potential energy:
a) Chemical potential energy
Activities such as tug of war or riding a bicycle, we use energy provided by
the food we eat. In cars or motorcycles, petrol is used to provide energy. Petrol
contains energy which makes these vehicles move. Food and petrol contain
energy called chemical potential energy. It is called chemical energy because
it is from the chemical bonds found in the food or petrol it is potentially
available for use when it is needed.
b) Elastic potential energy
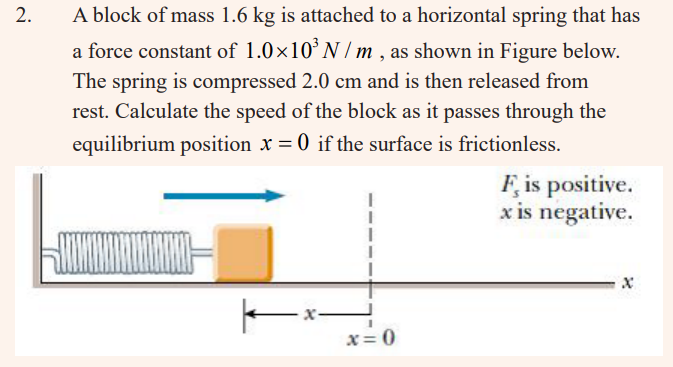
Restoring force
A block on a horizontal, frictionless surface is connected to a spring. If the
spring is either stretched or compressed a small distance from its unstretched
(equilibrium) configuration, it exerts on the block a force that can be expressed
as F = −k x
x is the position of the block relative to its equilibrium (x = 0) position
• k is a positive constant called the force constant or the spring
constant of the spring. The units of k are N/m.
• The negative sign in Equation signifies that the force exerted by
the spring is always directed opposite to the displacement from
equilibrium.
This force law for springs is known as Hooke’s law. Because the spring force
always acts toward the equilibrium position (x = 0), it is sometimes called a
restoring force.

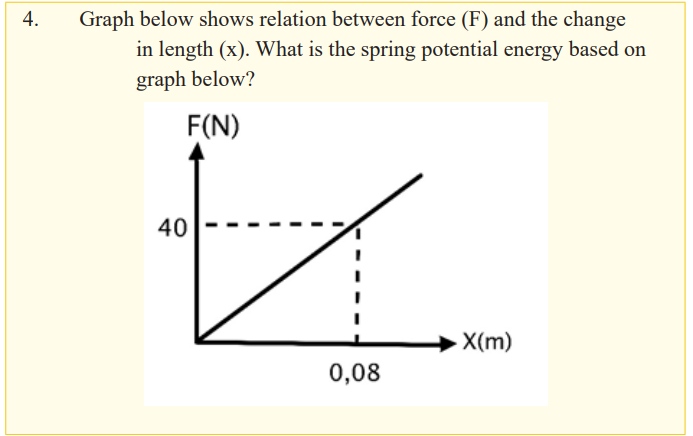
Elastic Potential Energy
Activity 7
Aim; To find out whether there is energy stored in elastic Materials
In laboratory,
* Try to perform experiment arranging your apparatus as shown in the
figure below.
* What do you observe after putting a mass on the spring.
* What would happen if the mass of the body is given a small
displacement downwards?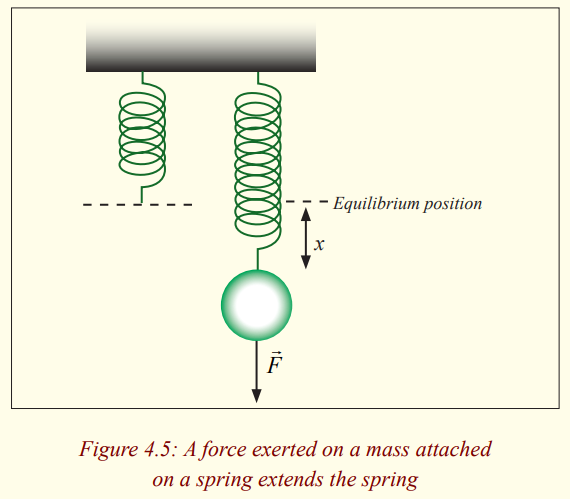
The elastic potential energy of the system can be thought of as the energy
stored in the deformed spring (one that is either compressed or stretched from
its equilibrium position.
Consider Figure below, which shows a spring on a frictionless, horizontal
surface.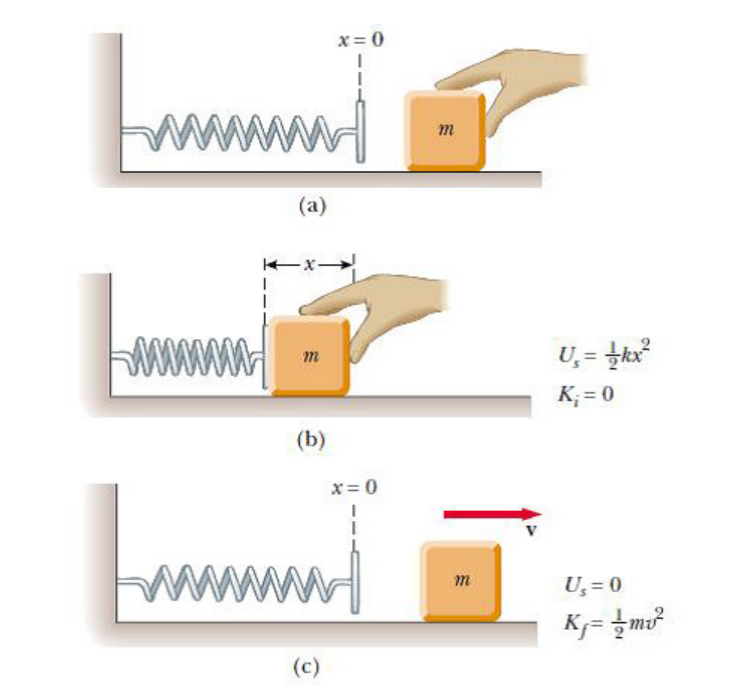



Kinetic energy
Kinetic energy is the form of energy possessed by moving bodies. Such bodies
have the ability to do work e.g. a flying bullet can kill a dangerous wild animal.
Wind (a moving mass of air) flowing streams, falling rocks, heat flowing from
a body at high temperature to one at a lower temperature, electricity (flowing
electrons), moving cars, lorries, busses, etc, all have kinetic energy. Kinetic
energy of a body is dependent upon both the body’s mass and speed.


Total Mechanical energy
Mechanical energy can be either kinetic energy (energy of motion) or potential
energy (stored energy of position). Objects have mechanical energy if they are
in motion and/or if they are at some position relative to a zero potential energy
position (for example, a brick held at a vertical position above the ground or
zero height position).
We call Mechanical energy is the sum of kinetic energy and all forms of potential
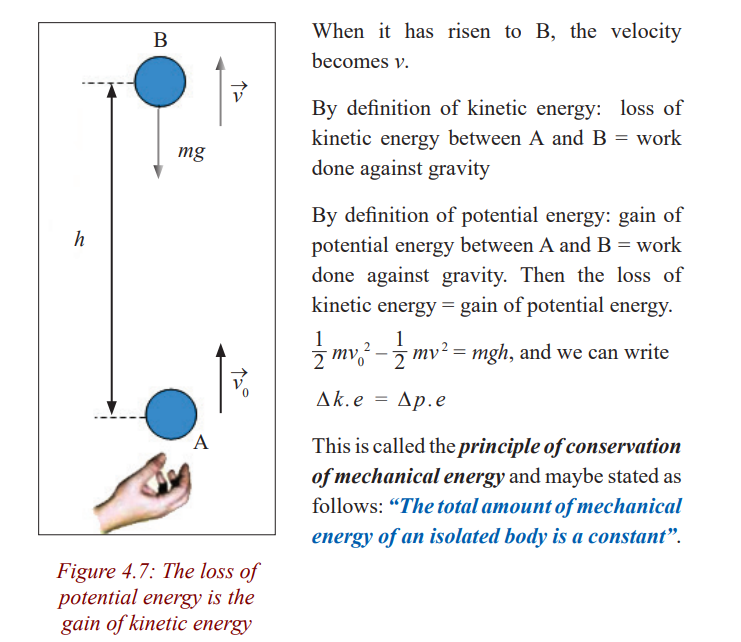
energy associated with an object or group of objects i.e. E PE KE = +Conservation of mechanical energy
If a body of mass m is thrown vertically upwards with an initial velocity v0 atA, it has to do work against the constant force of gravity.
Example
A 6.0 kg block initially at rest is pulled to the right along a horizontal by
a constant horizontal force of 12 N; Find the speed of the block after it
has moved 3.0 m.
a) If the surfaces in contact is frictionless surface.
b) If the surfaces in contact have a coefficient of kinetic friction of
0.15.
c) Suppose the force F is applied at an angle as shown in( Fig.b).
At what angle should the force be applied to achieve the largest
possible speed after the block has moved 3.0 m to the right?
Power
Activity 8
Interpret the diagrams below





Solution
The force is perpendicular to every increment of displacement. Therefore,
p mv =
2. Discuss whether any work is being done by each of the following
agents and, if so, whether the work is positive or negative: (a) a
chicken scratching the ground, (b) a person studying, (c) a crane
lifting a bucket of concrete, (d) the gravitational force on the bucket
in part (c), (e) the leg muscles of a person in the act of sitting down.Solution
(a) Positive work is done by the chicken on the dirt.(b) No work is done,
although it may seem like there is. (c) Positive work is done on the bucket.
(d) Negative work is done on the bucket. (e) Negative work is done on theperson’s torso.
3. When a punter kicks a football, is he doing any work on the ball
while his toe is in contact with it? Is he doing any work on the ball
after it loses contact with his toe? Are any forces doing work on theball while it is in flight?
Solution
Yes. Force times distance over which the toe is in contact with the ball.
No, he is no longer applying a force. Yes, both air friction and gravity dowork.
4. Cite two examples in which a force is exerted on an object withoutdoing any work on the object.
Solution
Force of tension on a ball rotating on the end of a string. Normal forceand gravitational force on an object at rest or moving across a level floor.
5. As a simple pendulum swings back and forth, the forces acting on
the suspended object are the gravitational force, the tension in the
supporting cord, and air resistance. (a) Which of these forces, if
any, does no work on the pendulum? (b) Which of these forces does
negative work at all times during its motion? (c) Describe the workdone by the gravitational force while the pendulum is swinging.
Solution
a) Tension (b) Air resistance (c) Positive in increasing velocity on thedownswing.
Negative in decreasing velocity on the upswing.
Everyday usage of the term momentum is in accord with the definition
above. According to the equation of momentum, a fast-moving car has more
momentum than a slow-moving car of the same mass; a heavy truck has
more momentum than a small car moving with the same speed. The more
momentum an object has, the harder it is to stop it, and the greater effect it will
have if it is brought to rest by striking another object. A football player is more
likely to be stunned if tackled by a heavy opponent running at top speed than
by a lighter or slower-moving tackler. A heavy fast-moving truck can do moredamage than a slow-moving motorcycle.
Momentum (symbol: p) of an object is the product of the mass and velocityof a moving body.
Example
Calculate the linear momentum of the car in the figure below.


Example
A 2250 kg pickup truck has a velocity of 25 m/s to the east. What is themomentum of the truck?
Solution

Conservation of momentum
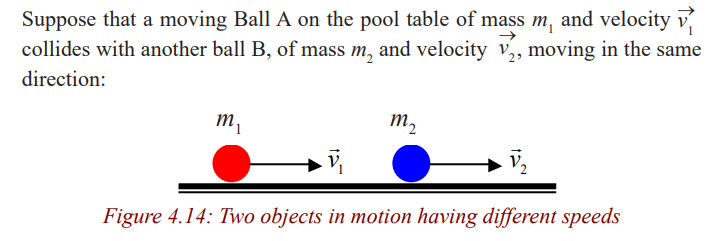
Activity 9: Field work
As a class, visit a place with a pool table.
Let each and every body try to hit the ball using the playing stick.
What happens when one ball hits another?
State and observe what you notice.Draw a conclusion.

Activity 10: Fieldwork
* As a class, visit a place where there is billiard.
* Try to arrange the balls with the help of your teacher or any of the
learners who have ever played it.
* Let one of you hit the white ball to strike/hit the rest.
* State what you observe after the white ball has hit the balls.
* Draw your conclusion from your observations.* Repeat the same procedures using balls in the play grounds.

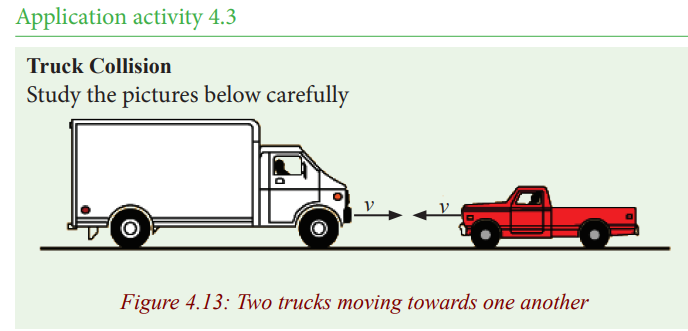
In a head-on collision:
1. Which truck will experience the greatest force?
2. Which truck will experience the greatest change in momentum?
3. Which truck will experience the greatest change in velocity?
4. Which truck will experience the greatest acceleration?5. Which truck would you rather be in during the collision?
Impulse
Activity 11
* Move out the class to the play ground.
* In pairs (one pair at a time), kick a ball so that it is moving with a
low speed. Let your friend stop it. Ask him/her what he/she felt. Let
your friend do the same.
* For the second time, make sure that you kick the ball by applying a
strong force so that it moves faster. Let your friend try to stop it. Ask
him/her what this time he/she has felt?
* Go back in class and summarise what you observed and felt while inthe play ground.






Application activity 4.5
1. Two bodies of mass 3kg and 5kg travelling in opposite directions
on a horizontal surface collide. The velocities of the bodies before
collision are 6m/s and 5m/s respectively. Given that after collision
the two separate and move in the same direction in which the 5kg
body was moving before collision, and the velocity of the 5kg mass
is 1m/s, find the speed of the 3kg body after impact. Find also theloss in the energy.
2. A body of mass 2kg initially moving with a velocity of 1m/s is
acted upon by a horizontal force of 6N for 3seconds. Find
(i) Impulse given to the body(ii) Final speed of the body
Collisions
Activity 12
To know what happens to bodies after impact/colliding.
To know the effect of collision on the velocities and masses of bodies aftercolliding.
Observe the diagram below carefully assuming the black car to have alarger mass than a white one and answer the questions that follow.

Questions about the picture above:
a) Do you think after collision , the two cars continue moving?
Explain why?
b) From what you observed, what is the effect of collision?
c) After separating the cars, do you think the masses of thecars changed? Explain why.
Note: We can define collision as an interaction between bodies in
which the time intervals during which the bodies interactionis small relative to the time for which we can observe them.
In collision the total momentum of colliding objects is always conserved.
Usually, however, their total kinetic energy is not conserved; some of it is
changed to heat or sound energy, which is recoverable. Such collisions aresaid to be inelastic.
For example, when a lump of putty falls to the ground, the total momentum of
putty and earth is conserved, that is, the putty loses momentum and the earth
gains an equal amount of momentum. But all the kinetic energy of putty ischanged to heat and sound on collision.
An Inelastic collision is the collision where the total kinetic energy is not
conserved (total momentum always conserved in any type of collision). If the
total kinetic energy is conserved, the collision is said to be elastic. For example,the collision between two smooth smoker balls is approximately elastic.
Elastic collision
In here, we shall consider objects colliding in a straight line and thereafterthey move with different speeds in the same direction.

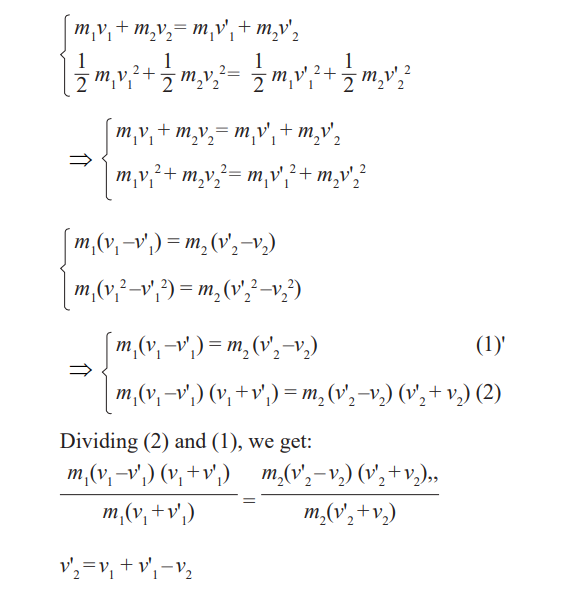

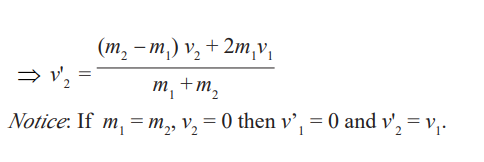
Special cases:
• Consider the case when the mass of one body, is equal to that of the
other. And the particle 2 is initially at rest, when they collide the velocity
of the first become zero and the velocity of the second is equal to thevelocity of the first one before collision.
That is a heavy particle collides with head-on with alight one that is at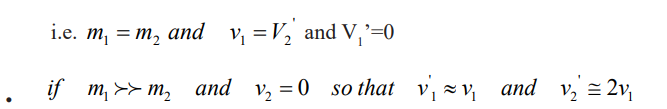
rest , heavy particle continue its motion unaltered after the collision and
the light particle rebounds with a speed equal to about twice the initial
speed of the heavy particle. an example of such collision would be that
of the moving heavy atom such as uranium stricking a light atom such ashydrogen.
That is a light particle collides with head-on with a heavy one that is at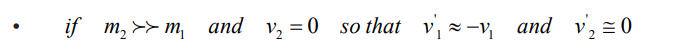
rest, heavy particle remain approximatively at rest , the light particle hasa velocity reversed.
Example is that a golf ball hitting a brick wall. The wall remains at rest,and the ball bounces back with its speed unchanged.
Example
A Ball of 0.1kg makes an elastic head-on collision with a ball of
unknown mass that is initially at rest. If the 0.1 kg ball rebounds at onethird of its original speed. what is the mass of the other ball?
Solution
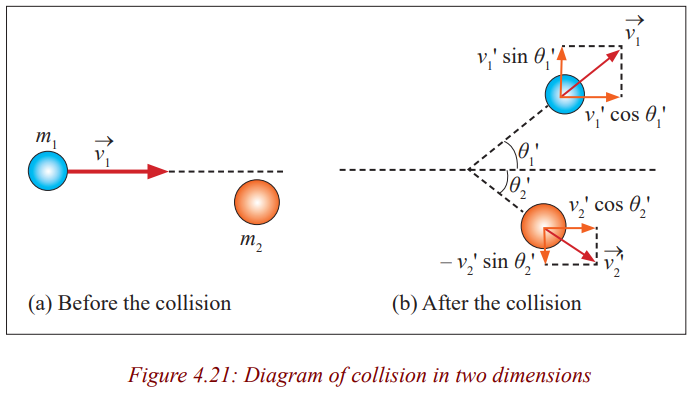
Elastic collision in two or three dimensions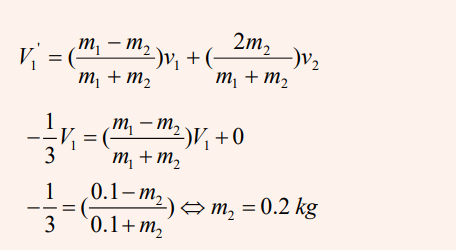
To understand this, use billiards as shown in the previous lesson
Some times after hitting the balls, they do not move in a straight line most
especially (those who know how to play it) when you want to score in the
centre hole. You must make sure that you hit the ball in target so that it movesat a certain angle.
Activity 13
• Try to hit a billiard ball as shown in figure above.
• Observe what happens when one ball hits another.
• Note down your observations.• Present your findings/observation to the whole class.
On Striking the balls ,energy and momentum is conserved.
Conservation of momentum and energy can also be applied to collisions in
two or three dimensions and in this case the vector nature of momentum isimportant.
One common type of non-head-on collision is one for which one particle
(called the “projectile”) strikes a second particle initially at rest (the “tangent”particle). This is the common situation in games such as billiards.




Inelastic collision
Collisions in which kinetic energy is not conserved are called inelastic
collisions. Some of the initial kinetic energy in such collisions is transformedinto other types of energy, such as thermal or potential energy.
A common example of a perfectly inelastic collision is when two objects
collide and then stick together afterwards and move with a common velocityafter colliding.


2. An Object A of mass 2 kg is moving with a velocity of 3 m/s and
collides head on with an object B of mass 1 kg moving in the opposite
direction with a velocity of 4 m/s. After collision both objects sticks,so that they move with a common velocity v. calculate v.
Solution
The phrase “become entangled” tell us that this is a perfectly inelastic
collision.Answer: v=6.67m/s
Other examples of collision
The Ballistic Pendulum
1. The ballistic pendulum (seen figure below) is an apparatus used to
measure the speed of a fast-moving projectile, such as a bullet. A
bullet of mass mB is fired into a large block of wood of mass mw
suspended from some light wires and makes a completely inelastic
collision with it. The bullet embeds in the block, and the entire system
swings through a height h. How can we determine the speed of thebullet from a measurement of h??
Solution
Let configuration (A) be the bullet and block before the collision, and
configuration (B) be the bullet and block immediately after colliding.
The bullet and the block form an isolated system, so we can categorize thecollision between them as a conservation of momentum problem.



An automobile collision
A 1000Kg compact car is travelling North at 15 m/s when it collides with
a 2000 kg truck travelling East at 10m/s. all occupants are wearing seat
belts are there are no injuries, but the two vehicles are thoroughly tangled
and move away from the impact point as one mass. The insurance adjustor
has asked you to find the velocity of the wreckage just after the impact.What do you tell her? The figure below show the situation
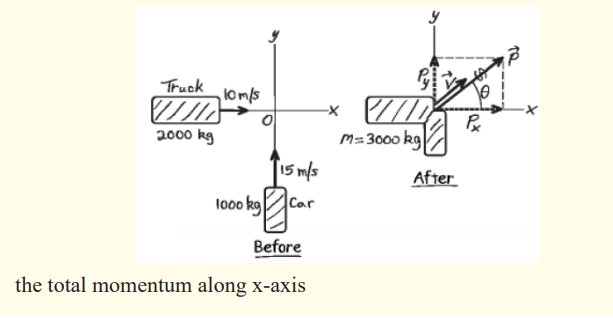
If the velocities of the two objects make a certain angle before collision
and after collision they stick together, analytically we have this situation:


END UNIT ASSESSMENT
“Work, Energy and Power”
1. A worker lifts up a stone of 3.5kg to a height of 1.80m each 30s. Findthe work done in one hour.
2. Calculate the kinetic energy and the velocity required for a 70kg pole
vaulter to pass over a 5.0m high bar. Assume the vaulter’s centre of
mass is initially 0.90m off the ground and reaches its maximum heightat the level of the bar itself.
3. Calculate the power required of a 1400 kg car under the following
circumstances
a) The car climbs a 10° hill at a steady 80km/h and
b) The car accelerates from 90 to 110km/h in 6.0s to pass another
car on a level road. Assume the force of friction on the car is700N in both parts of the problem.
4. A woman of mass 75kg walks up a mountain of height 20m.
a) What is the work done?
b) The walking up being done in 1.5 min, find the power,
c) What time will be taken by this woman to walk up the 20m inorder to develop a power of 73W?






