Unit 3 : Moments and Equilibrium of Bodies
Key Unit Competence
Analyse the principle of moments and equilibrium of bodies. .My goals
By the end of this unit, I should be able to:
* Explain the principle of moments and apply it to equilibrium of a
body.
* Come out with the effects of forces when applied onto a body.* Know the effects of forces.
INTRODUCTORY ACTIVITY
When a patient goes to hospital having a headache and fever, a doctor may
require a blood test for malaria. When a sample of blood is taken, it is not
possible to check whether a patient has malaria or not. But a laboratory
technician may need to test the blood using some instrument and decidewhether the patient has malaria or not.
Questions:
(i) Which instrument do you think may be used to test malaria from
blood sample?
(ii) In summary, discuss how that instrument function.(iii) What other instrument do you think can be used for such purpose?
Introduction
In here, we shall majorly concetrate on the turning effect of force. As you
know, it is very hard to close a door when you apply force near its turning
point. That’s why door handles are always put at the end of the door so that
the distance from the turning point to where force is applied increases. This
increases the turning effect of the force applied. Which is the effect of forceson bodies one of our interest in this unit.
Scalar and vector quantities
Activity 1
Try to stand bricks in a line behind one another. Push one brick.
(i) What happens to other bricks?(ii) What if in the process one brick stops, what would happen?
In daily life, we normally pull the objects from one place to another. When
pulling a goat that is to be tethered, obviously it will take the direction of the
pull. We can call this a force. This is a quantity that changes body’s state ofrest or uniform motion.
You noticed that after pushing your friend he/she changed position and
direction. Hence, a force has both magnitude and direction. This quantity can
be termed as a vector quantity. This is a quantity with both magnitude anddirection.
Activity 2
(i) Using the above example, discuss in groups or as a class other
vector Quantities.
(ii) Analyse the effects of these physical quantities.
(iii) In daily life, how are these quantities utilised?(iv) Ask your friend what time is it?
You will realise that he/she will tell the exact time not even indicating direction.Such a quantity is termed to be a scalar quantity.
A scalar quantity is a physical quantity that is defined by only magnitude(size).
Other examples of scalar quantities are volume, mass, speed, and time
intervals. The rules of ordinary arithmetic are used to manipulate scalarquantities.
Application activity 3.1
Of the following physical quantities, group them in different
sets of scalar and vector quantities: mass, energy, power, weight,
acceleration, velocity, momentum, time, impulse, magnetic flux density,pressure, displacement.
Force as vector
Activity 3
1. As an individual or a group push the desk.
2. What happens to it?
3. What causes the change in position?
a) Let as a class move to:
(i) Football pitch.
(ii)Net ball pitch.
(iii) Basket ball play ground.
Try to kick a ball. What happens to it? What causes it to change its
position?Note what you observe.
Also, as you sit reading this book, you eventually feel tired. This is because ofgravitational force acting on your body and yet you remain stationary.
From the above examples, we can define the “quantity force”. We have to
know the direction and the magnitude. For that matter, we conclude that the
force is vector quantity. We can think of force as that which causes an objectto accelerate.
What happens when several forces act simultaneously on an object? In this case,
the object accelerates only if the net force acting on it is not equal to zero. The
net force acting on an object is defined as the vector sum of all forces acting on
the object. (We sometimes refer to the net force as the total force, the resultantforce, or the unbalanced force.)
Application activity 3.2
1. ............................ is an example of a scalar quantity
a) Velocity.
b) Force.
c) Volume.d) Acceleration.
2. ............................ is an example of a vector quantity
a) Mass.
b) Force.
c) Volume.d) Density.
3. A scalar quantity:
a) always has mass.
b) is a quantity that is completely specified by its magnitude.
c) shows direction.d) does not have units.
4. A vector quantity
a) can be a dimensionless quantity.
b) specifies only magnitude.
c) specifies only direction.d) specifies both a magnitude and a direction.
5. A boy pushes against the wall with 50 kilogrammes of force. The wall
does not move. The resultant force is:
a) -50 kilogrammes.
b) 100 kilogrammes.
c) 0 kilogrammes.d) -75 kilogrammes.
6. A man walks 3 miles north then turns right and walks 4 miles east. The
resultant displacement is:
a) 1 kilometre SW
b) 7 kilometres NE
c) 5 kilometres NEd) 5 kilometres E
7. A plane flying 500km/hr due north has a tail wind of 45 mi/hr the
resultant velocity is:
a) 545 kilometres/hour due south.
b) 455 kilometres/hour north.
c) 545 kilometres/hour due north.d) 455 kilometres/hour due south.
8. The difference between speed and velocity is:
a) Speed has no units.
b) Speed shows only magnitude, while velocity represents both
magnitude (strength) and direction.
c) They use different units to represent their magnitude.d) Velocity has a higher magnitude.
9. The resultant magnitude of two vectors
a) Is always positive.
b) Can never be zero.
c) Can never be negative.d) Is usually zero.
10.Which of the following is not true.
a) Velocity can be negative.
b) Velocity is a vector.
c) Speed is a scalar.d) Speed can be negative.
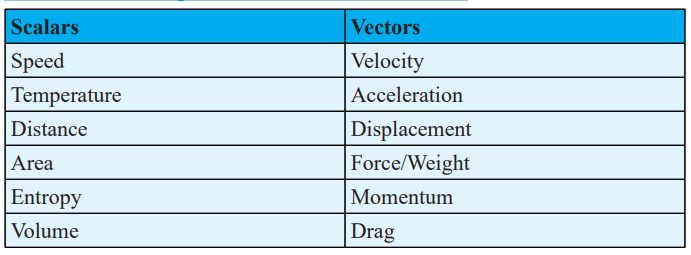
Table summarising Scalar and vector Quantities
Turning effect of force
Moment of a force about a point
Every time we open a door, turn on a tap or tighten up a nut with a spanner,
we exert a turning force. The combined effect of the force and distance which
determines the magnitude of the turning force is called the moment of theforce or torque and is defined as follows:
“The moment (turning effect) of a force about a point is the force multiplied
by the perpendicular distance from the place where the force is applied to thatpoint.” Fig. a
Or Moment is force times lever arm where is the lever arm, and the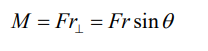
perpendicular symbolreminds us that we must use the distance from the
axis of rotation that is perpendicular to the line of action of the force (Fig.3.1a). The SI unit for moment is N m.
A lever arm or moment arm is the perpendicular distance from the axis ofrotation to a line drawn along the direction of the force.
An equivalent way of determining the torque associated with a force is to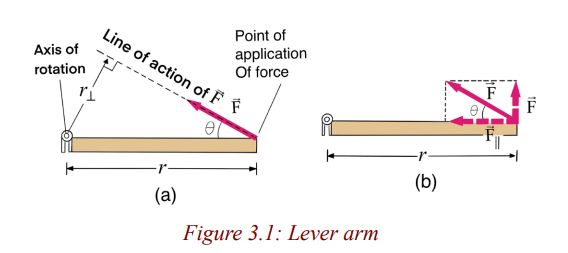
resolve the force into components parallel and perpendicular to the line that
connects the axis to the point of application of the force, as shown in Fig. 3.1b.
The component exerts no torque since it is directed at the rotation axis (its
lever arm is zero). Hence the torque will be equal to times the distance r fromthe axis to the point of application of the force:
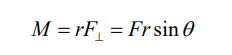
Activity 4
(i) Suspend a meter rule at its middle point, either by passing a string
through a hole or a knife edge. If necessary stick plasticine one one
and to make it balance exactly.
(ii) Tie loops of thread to several
(iii) Hang a 0.5 N weight A (the load) one the left hand side of the ruler
on the 34 cm mark (16 cm ) from the fulcrum)
(iv) Place another weight 0.2 N (the effort) on the other side and moveit until the ruler balances.
(v) Note the distances of the weights from the fulcrum, i.e from the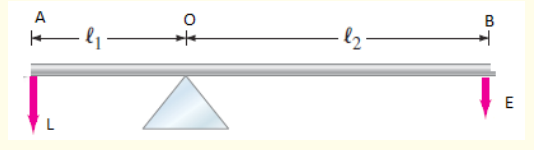
midpoint.(vi) Record the results in a suitable as shown in the table.
(vii) Reapeat several times with (a) the same weights in differentposition, and (b) different weights.
The table suggests that when the turning effects of forces acting
on an object are balanced the sum of clock wise moments is the
same as the sum of anticlockwise moments. This is the principle ofmoment
Principle of moment of force
When a body is in equilibrium (balanced), the sum of the anticlockwise
moments about any point is equal to the sum of the clockwise moments aboutthe same point.
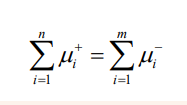
Example
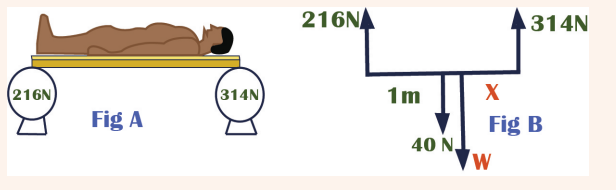
In kinesiology (the study of human motion), it is often useful to know the
location of the center of mass of a person. This can be determined with
the arrangement shown fig A. A plank of weight 40 N is placed on two
scales separated by 2.0 m. A person lies on the plank and the left scale
reads 3214 N and the right scale reads 216 N as shown in fig B. What isthe distance from the left scale to the person’s center of mass?

A torque is a quantity that measures the ability of a force to rotate an
object around some axis. Net torque produces rotation. A torque is positive
or negative; depending on the direction the force tends to rotate an object.Torques that produce counterclockwise rotation are defined to be positive.
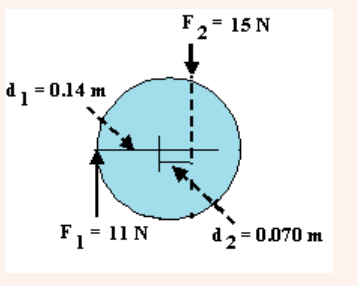
Example
A basketball is being pushed by two basketball players during tip-off.
Assuming each force acts perpendicular to the axis of rotation throughthe centre of ball the ball; find the net torque acting on the ball.
Torque should not be confused with work
Torque (τ = Fd sin θ ) and work (W = Fd cos θ ) can both be expressed in
units of N m, so be careful to distinguish torque and work. The components of
a force that produces work is parallel to a distance (the displacement), while
the component of force that produces torque is perpendicular to a distance (thelever arm).
Torque should not be confused with force. Forces can cause a change in
linear motion, as described by Newton’s second law. Forces can also cause a
change in rotational motion, but the effectiveness of the forces in causing this
change depends on both the forces and the moment arms of the forces, in thecombination that we call torque.
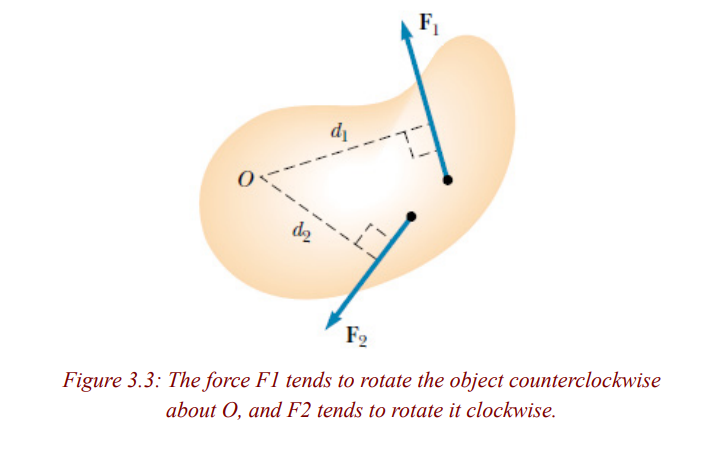
If two or more forces are acting on a rigid object, as shown in Fig.3.3, each
tends to produce rotation about the pivot at O. We use the convention that the
sign of the torque resulting from a force is positive if the turning tendency
of the force is counterclockwise and is negative if the turning tendency isclockwise.
Equilibrium of a body
Conditions for equilibrium
Objects in daily life have at least one force acting on them (gravity). If they are
at rest, then there must be other forces acting on them as well so that the net
force is zero. A book at rest on a table, for example, has two forces acting on
it, the downward force of gravity and the normal force the table exerts upwardon it (Fig. 3.4).
Because the book is at rest, Newton’s second law tells us that the net force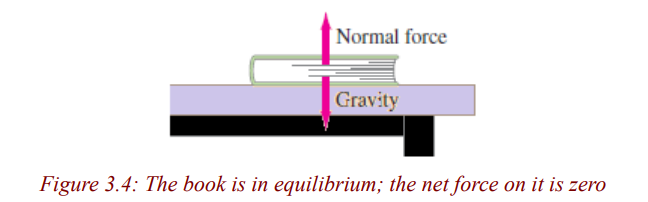
on it is zero. Thus the upward force exerted by the table on the book must be
equal in magnitude to the force of gravity acting downward on the book. Such
an object is said to be in equilibrium (Latin for “equal forces” or “balance”)
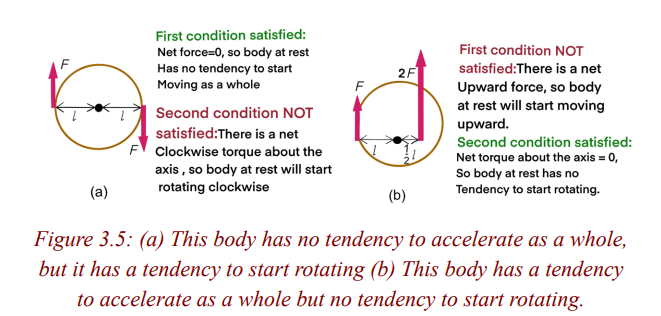
under the action of these two forces. This is often called the first conditionfor equilibrium (Fig.3.5a).
Force not only push or pull but have a turning-effect or moment about an
axis. In cases of equilibrium the moments have also to be considered. If forces
act at different points on an extended body an additional requirement must
be satisfied to ensure that the body has no tendency to rotate: The sum of the
torques about any point must be zero (Fig.3.5.b). This is called the secondcondition for equilibrium.
A rigid body is in mechanical equilibrium when the sum of all forces on all
particles of the system is zero (i.e. when all the particles of the system are
at rest or that its center of mass moves with constant velocity relative to the
observer and the total force on each particle is permanently zero)., and also
the sum of all torques on all particles of the system is zero so that its state of
rotational motion remains constant. The bodies are rigid if they do not deformunder the action of applied forces.
We will apply the first and second conditions for equilibrium to situations
in which a rigid body is at rest (no translation or rotation). Such a body is
said to be in static equilibrium (Fig. 3.6). But the same conditions apply to
a rigid body in uniform translational motion (without rotation), such as an
airplane in flight with constant speed, direction, and altitude. Such a body is inequilibrium but is not static.
The above conditions of equilibrium are also used to determine the resultant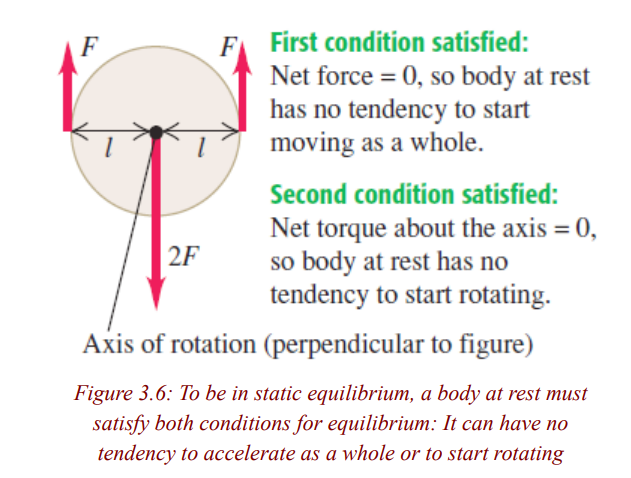
of non-parallel, non-concurrent systems of forces i.e. all of the lines of
action of the forces in this system do not meet at one point. The parallel force
system was a special case of this type. Since all of these forces are not entirely
parallel, the position of the resultant can be established using the graphical oralgebraic methods of resolving co-planar forces
There are a number of ways in which one could resolve the force system that
is shown. One graphical method would be to resolve a pair of forces using the
parallelogram or triangle method into a resultant. The resultant would then be
combined with one of the remaining forces and a new resultant determined,
and so on until all of the forces had been accounted for. This could prove to
be very complex if there are a great number of forces. The algebraic solution
to this system would potentially be simpler if the forces that are applied to thesystem are easy to break into components.
■ Addition of Forces in a Plane (Stevinus law)
If all the forces acting on a body act in a plane, they are called coplanar forces.
If they have a common point of application they are called concurrent forces
Consider a body that is subjected to two forces F1 and F2, whose lines of
action intersect at point A (Fig. 3.7). It is postulated that the two forces can
be replaced by a statically equivalent force R. This postulate is an axiom; it is
known as the parallelogram law of forces. The force R is called the resultant
of F1 and F2 . It is the diagonal of the parallelogram for which F1 and F2 areadjacent sides.
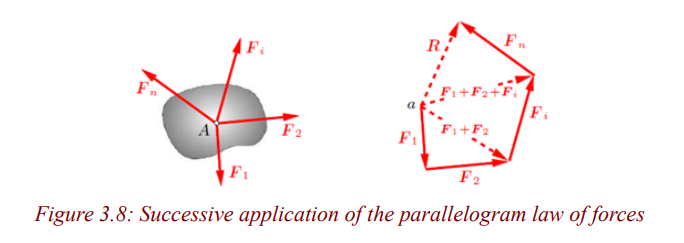
Now consider a system of n forces that all lie in a plane and whose lines of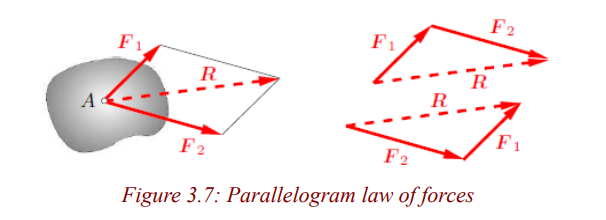
action intersect at point A (Fig. 3.8). Such a system is called a coplanar system
of concurrent forces. The resultant can be obtained through successive
application of the parallelogram law of forces. Mathematically, the summationmay be written in the form of the following vector equation:
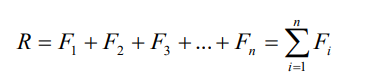
■ Representation in Cartesian Coordinates
It is usually convenient to resolve forces into two components that are
perpendicular to each other. The directions of the components may then be
given by the axes x and y of a Cartesian coordinate system (Fig. 3.8). The
quantities Fx and Fy are called the coordinates of the vector F or componentsof F.
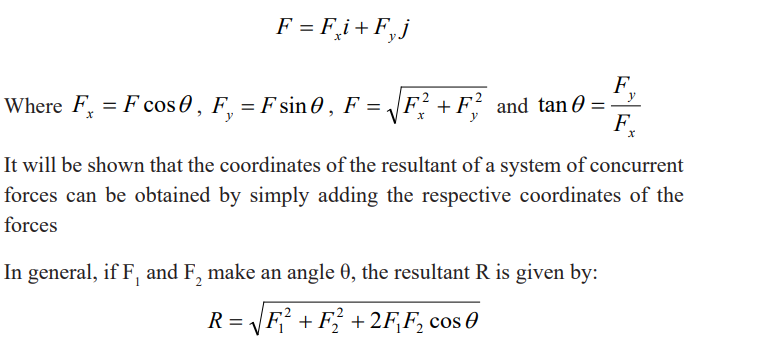
Examples
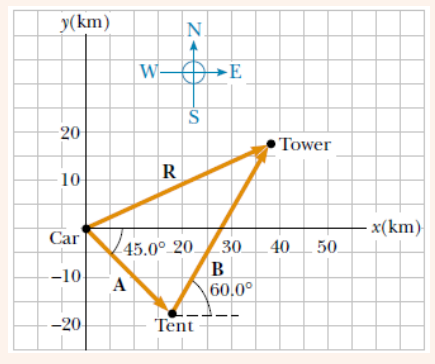
1. A hiker begins a trip by first walking 25.0 km southeast from her car.
She stops and sets up her tent for the night. On the second day, she
walks 40.0 km in a direction 60.0° north of east, at which point she
discovers a forest ranger’s tower.
(a) Determine the components of the hiker’s displacement for each
day.
(b)Determine the components of the hiker’s resultant displacement
R for the trip. Find an expression for R in terms of unit vectors.(c) Determine the magnitude and direction of the total displacement.
Solution
(a) If we denote the displacement vectors on the first and second days by
A and B, respectively, and use the car as the origin of coordinates, weobtain the vectors shown in Figure below.
2. Under what circumstances would a nonzero vector lying in the xy
plane have components that are equal in magnitude?
Solution
Any vector that points along a line at 45° to the x and y axes has componentsequal in magnitude.
3. In what circumstance is the x component of a vector given by themagnitude of the vector times the sine of its direction angle?
Solution
If the direction of a vector is specified by giving the angle of the vector
measured clockwise from the positive y-axis, then the x-component of the
vector is equal to the sine of the angle multiplied by the magnitude of thevector.
4. If A = B, what can you conclude about the components of A and B?
Solution
Any vector that points along a line at 45° to the x and y axes has componentsequal in magnitude.
■ Lami’s theorem
Lami’s theorem gives the conditions of equilibrium for three forces acting at
a point O. Lami’s theorem states that if three forces acting at a point are in
equilibrium, then each of the force is directly proportional to the sine of theangle between the remaining two forces.
Branch of mechanics which deals with state of equilibrium is called statics.
Statics is the branch of mechanics concerned with the analysis of loads
(force, torque/moment) on physical systems in static equilibrium, that is, in
a state where the relative positions of subsystems do not vary over time, or
where components and structures are at a constant velocity. When in static
equilibrium, the system is either at rest, or its center of mass moves at constant
velocity. The study of moving bodies is known as dynamics, and in fact theentire field of statics is a special case of dynamics.
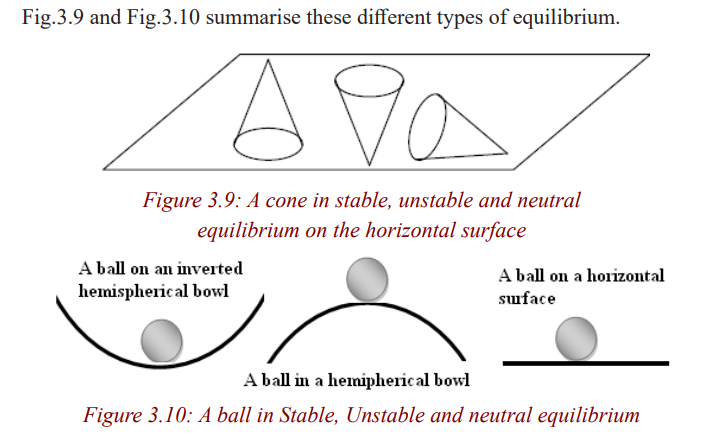
Stability and Balance
An object in static equilibrium, if left undisturbed, will undergo no translational
or rotational acceleration since the sum of all the forces and the sum of all the
torques acting on it are zero. However, if the object is displaced slightly, threeoutcomes are possible:
• Equilibrium is said to be stable if small, externally induced
displacements from that state produce forces that tend to oppose the
displacement and return the body or particle to the equilibrium state.
Examples include a weight suspended by a spring or a brick lying on alevel surface.
• Equilibrium is unstable if the least departure produces forces that tend
to increase the displacement. An example is a ball bearing balanced onthe edge of a razor blade.
• Static Equilibrium (neutral equilibrium) is equilibrium where
all forces are balanced, but it also applies to bodies in uniform or
accelerated motion. For example, a book resting on a table applies a
downward force equal to its weight on the table. According to the third
law, the table applies an equal and opposite force to the book. This
force occurs because the weight of the book causes the table to deformslightly so that it pushes back on the book like a coiled spring.
By summing up
• A system is said to be in stable equilibrium if, when displaced from
equilibrium, it experiences a net force or torque in a direction oppositethe direction of the displacement.
• A system is in unstable equilibrium if, when displaced from equilibrium,
it experiences a net force or torque in the same direction as thedisplacement from equilibrium.
• A system is in neutral equilibrium if its equilibrium is independent ofdisplacements from its original position.
Centre of gravity and center of mass
Concept of centre of gravity and center of mass
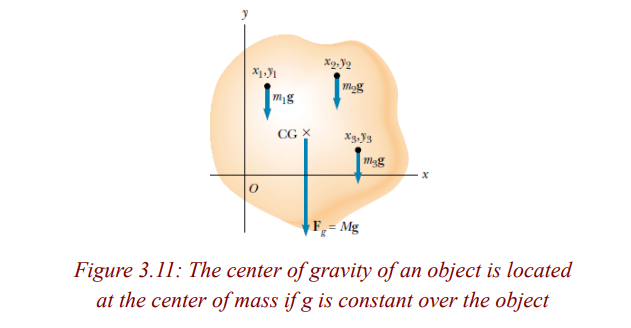
The center of gravity is the average location of the weight of an object. The
centre of gravity is defined as the point of application of the resultant force
due to the earth’s attraction on it. The center of gravity is a geometric propertyof any object.
The centre of gravity of a body also coincides with its centre of mass. The
center of mass of an object may be defined as the point at which an appliedforce produces acceleration but no rotation
Centre of gravity and base of support of a body
1. For balance to exist, the line of gravity must intersect the base of support.
2. If the area of the base of support of an object is increased, this tends to
increase the stability of the object.
3. The lower the center of gravity is above the base of support the more
stable the object tends to be. (This is true even though the size of the
base of support is unchanged.)
4. Objects that are more massive tend to be more stable.
5. For an object, the farther the line of gravity’s intersection is from the
edge of its base of support the more stable the object tends to be in that
direction.Determining the center of gravity
Determining the center of gravity is very important for any flying object. In
general, determining the center of gravity (cg) is a complicated procedure
because the mass (and weight) may not be uniformly distributed throughout the
object. If the mass is uniformly distributed, the problem is greatly simplified.
If the object has a line (or plane) of symmetry, the center of gravity lies on theline of symmetry.
For a solid block of uniform material, the center of gravity is simply at theaverage location of the physical dimensions.
Example
Activity 5
To determine the centre of gravity of different regular shapes
Apparatus* Manila paper, scissors, a pencil and a ruler
Procedure• Make a number of shapes from a manila paper, as below:
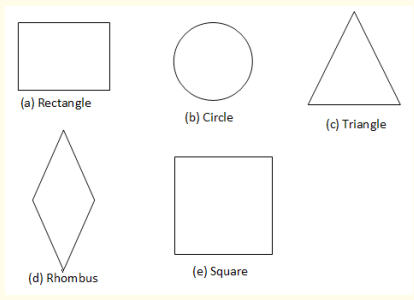
• Find the centre of gravity of those different figures.
Conclusion
The point of intersection of diagonals (a,d and e), bisectors (c) ,diameters(b) is the centre of gravity of those figures
For a general shaped object, there is a simple mechanical way to determinethe center of gravity:
In Step 1, you hang the object from any point and you drop a weighted string(plumb line) from the same point. Draw a line on the object along the string.
For Step 2, repeat the procedure from another point on the object you now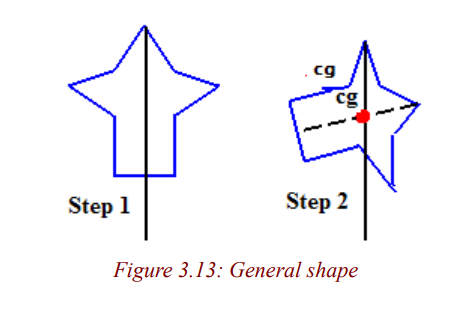
have two lines drawn on the object which intersect. The center of gravity is
the point where the lines intersect. This procedure works well for irregularlyshaped objects that are hard to balance.
Activity 6
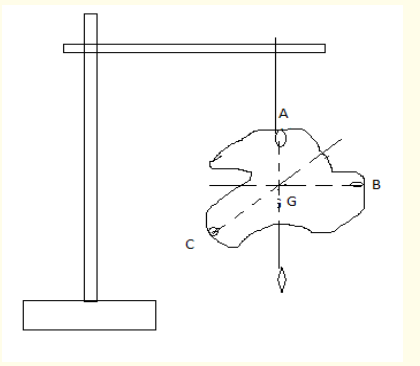
To determine the centre of gravity of an irregularly shaped lamina
Apparatus* A plumb line, a thread, a stand and a cardboard
Procedure
• Make 3 holes, A, B and C on the edges the cardboard.
• Suspend it by a rod through the hole A as shown in Figure2.4
• Tie a plumb line on the rod beside the cardboard.
• After the cardboard and plumb line have stopped swinging, draw
a vertical line on the cardboard as set by plumb line.
• Repeat the experiment using other holes B and C. The lines
intersect at a point noted G
• Balance the cardboard with the tip of a pencil at the point ofintersection of the three lines. What do you observe?
Observation
The suspended object will always rest with its centre of gravity vertically
below the point of support. The object balances on the tip of the pencil ifplaced at its centre of gravit.


Stability and center of gravity
Consider a ball suspended freely from a string is in stable equilibrium, for if it
is displaced to one side, it will return to its original position (Fig. 3.14a) due
to the net force and torque exerted on it. On the other hand, a pencil standing
on its point is in unstable equilibrium. If its center of gravity is directly over
its tip (Fig. 3.14b), the net force and net torque on it will be zero. But if it
is displaced ever so slightly as shown—say, by a slight vibration or tiny air
current—there will be a torque on it, and this torque acts to make the pencil
continue to fall in the direction of the original displacement.
Finally, an example of an object in neutral equilibrium is a sphere resting on a
horizontal tabletop. If it is moved slightly to one side, it will remain in its newposition—no net torque acts on it.
In general, an object whose center of gravity (CG) is below its point of support,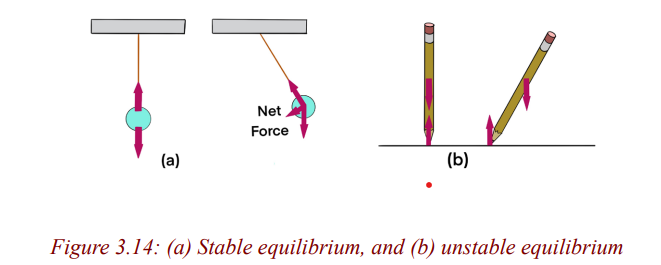
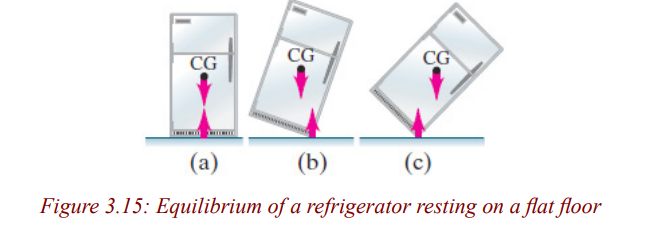
such as a ball on a string, will be in stable equilibrium. Consider a standing
refrigerator (Fig. 3.15a). If it is tipped slightly, it will return to its original
position due to the torque on it as shown in Fig. 3.15b. But if it is tipped too
far, Fig. 3.15c, it will fall over. The critical point is reached when the CG shifts
from one side of the pivot point to the other.When the CG is on one side, the
torque pulls the object back onto its original base of support, Fig. 3.15b. If the
object is tipped further, the CG goes past the pivot point and the torque causesthe object to topple, Fig. 3.15c.
In general,
• an object whose center of gravity is above its base of support will be
stable if a vertical line projected downward from the CG falls within the
base of support. This is because the normal force upward on the object
(which balances out gravity) can be exerted only within the area of
contact, so if the force of gravity acts beyond this area, a net torque will
act to topple the object.
• the larger the base and the lower the CG, the more stable the object.
• an object tends to fall when its center of gravity is away from the basethat supports it.
Applications of equlilibrium
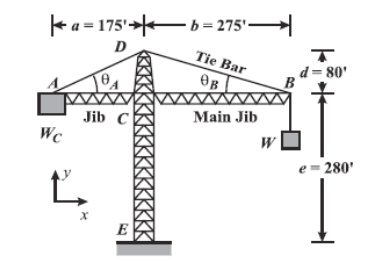
Tower Crane – Method of Joints
The tower crane shown in the figure below consists of tower DCE fixed at the
ground and two jibs AC and CB. The jibs are supported by tie bars AD and
DB, and are assumed to be attached to the tower by pinned connections. Thecounterweight WC weighs and the crane has a lifting capacity of W.
Beam balance
It consist of pivoted horizontal lever of equal length arms called the beam,
with a weighing pan also called scale, scale pan or boson, suspended fromeach arm.
The unknown mass is placed on one pan and standard masses are added on the
other pan until is as close to equilibrium as possible. In precision balances a
slider mass is moved along a graduated scale. The slider position gives a finecollection to the mass value.
Example
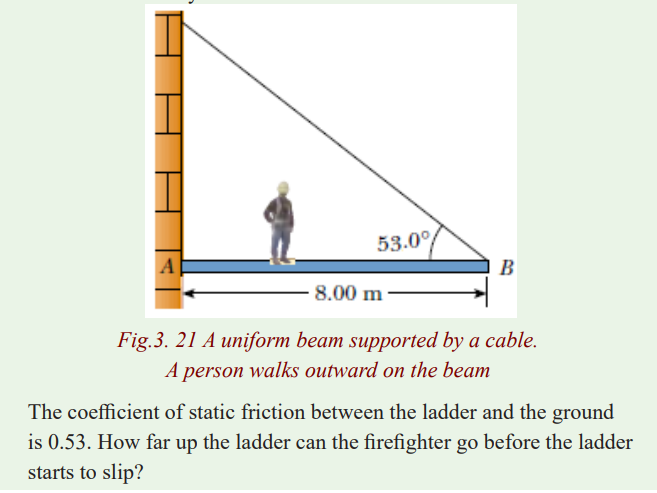
A uniform meter stick supported at the 25 cm mark is in equilibrium
when a 1 kg rock is suspended at the 0 cm end (as shown in Fig.). Is the
mass of the meter stick greater than, equal to, or less than the mass of therock? Explain your reasoning.

Solution

Application Activity 3.3
A friend of yours that has been sick comes from the hospital where he
had gone for medication telling you that he is 62 kg and that is what is
indicated on his medical papers.
Imagine you have the following
* A strong wood bar of a bout 5m (or any length as long as you know
its actual length) and has a mass of 10kg.
* A wood that you can use as a pivot
a)Since you know the exact mass of your friend and that of the
wood. Explain all the procedures you can follow to know your
mass. In your procedures include all the necessary equations and
diagrams you may need to use.
b)Do you think the mass (your mass) you obtained is accurate?
Explain your reasoning.
c)What do you think may be the source of errors in determining
your mass? Or any unknown mass?
d)Basing on your knowledge and understanding you have obtained
from this unit, how can this unit be applied in your career you arepursuing?
END UNIT ASSESSMENT
1. The uniform bar shown below weighs 40 N and is subjected to the
forces shown. Find the magnitude, location, and direction of the forceneeded to keep the bar in equilibrium.
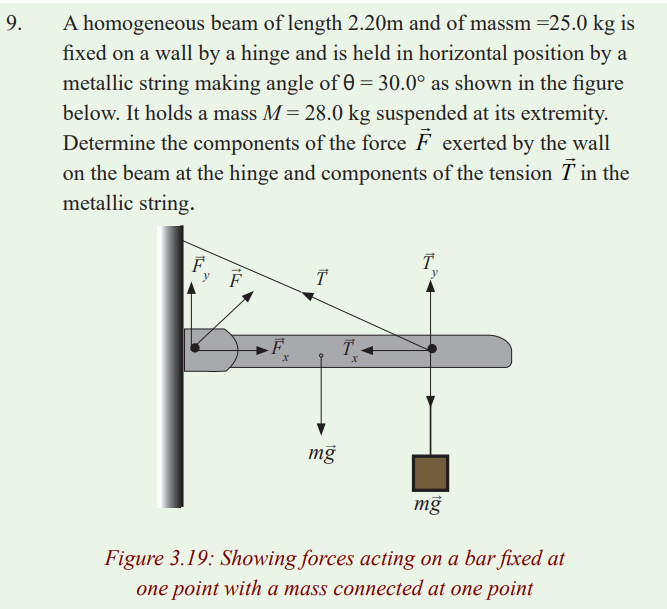
2. System given below is in equilibrium. If the potential energies of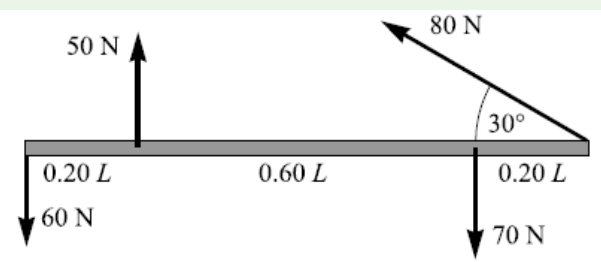
objects A and B are equal, find the mass of object A in terms of G.(Rod is homogeneous and weight of it is G.)
A 172 cm tall person lies on a light (massless) board which is sup-ported by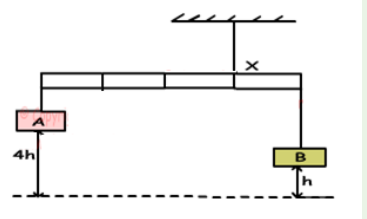
two scales, one under the top of her head and one beneath
the bottom of her feet see Fig. The two scales read respectively 35.1
kg and 31.6 kg. What distance is the center of gravity of this personfrom the bottom of her feet?
3. A) A seesaw consisting of a uniform board of mass M =10kg and
length l=2m supports a father and daughter with masses mf and md, 50and 20kg respectively as shown in the Figure below.
The support (called the fulcrum) is under the center of gravity of the
board, the father is a distance d from the center, and the daughter is adistance l / 2 from the center.
a. Determine the magnitude of the upward force n exerted by thesupport on the board.
b. Determine where the father should sit to balance the system.
B) Three children are trying to balance on a seesaw, which consists of
a fulcrum rock, acting as a pivot at the center, and a very light board3.6 m long (see fig.).
Two playmates are already on either end. Boy A has a mass of 45 kg, and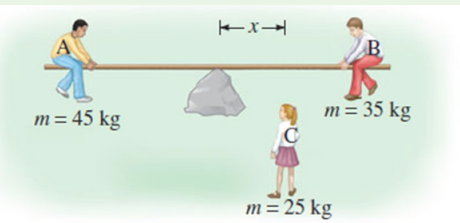
girl B a mass of 35 kg. Where should girl C, whose mass is 25 kg, placeherself so as to balance the seesaw?
4. A uniform 1500kg beam, 20m long, supports a 15,000kg printing press
5 from the right support column, see the figure. Calculate the force oneach of the vertical support columns.
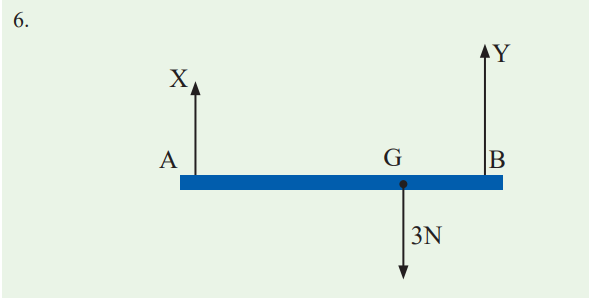
5. A horizontal rod AB is suspended at its ends by two strings. (See the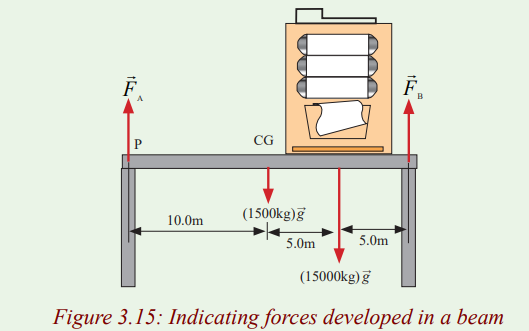
figure below). The rod is 0.6m long and its weight of 3N acts at Gwhere AG is 0.4m and BG is 0.2m. Find the tensions X and Y