◄Unit 6 : Sources of Energy in the WorldUnit 8 :Universal gravitational field and potential►

Unit 7 : Projectile and uniform circular motion

  • Unit 7 : Projectile and uniform circular motion

    Key Unit Competence

    Analyse and solve problems related to projectile and circular motion.

    My goal

    By the end of this unit, I will be able to:

    * define and explain terms used in projectile motion.

    * discuss the different applications of projectile motion.

    * apply concepts of projectile and circular motion in real life.

    * differentiate between projectile motion and circular motion. 

    Introductory activity 

    Take the case of a basketball player shooting the ball into the basket’s net 
    from a given distance at a given angle as shown in the figure below then 

    answer to the following questions.

    C

    1.Discuss on the motion of the ball after being shot
    2.Discuss other situation where one can observe such a king of motion.
    3.Explain how this kind of motion is important in normal life activities.
    4.Contrast between projectile motion and circular motion using typical 

    examples.

    Introduction

    We have different kinds of sports, for examples; football, netball, tennis 
    amongst others. A lot of reasoning is needed while playing football to score 
    one of which is to kick a ball at a certain angle (i.e. to move above the ground). 
    We say that the ball is projected. This also applies to basket ball; the ball to 
    enter the round ring for a score it has to be thrown at a certain angle. Hence, 
    projected. The same principle is used by the military in shooting and launching 

    their missiles.

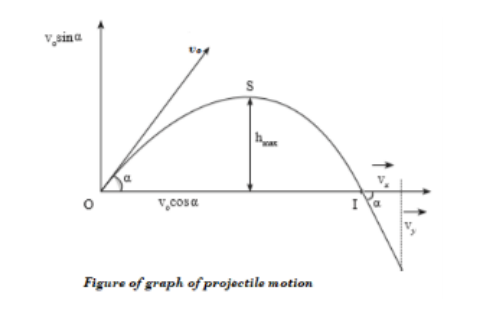
    Projectile Motion

    Activity 1: Field study

    Aim; To study motion of bodies in free space
    a) Out of class, (in pitch,or in school compound), throw a 
    ball,a stone or any body upward.
    b) State what happens.
    c) Hold a ball in your hands and release it to fall.
    d) Is the motion of the ball same as in the first case?
    e) Note down your observation.

    f) Relate your observations for bodies moving linearly. 

    Caution
    While throwing a stone or any body, take care so that it does not harm you.
    We can define a projectile as any body thrown into space/air. The path 
    taken is called a trajectory. The motion of a projectile unless taken otherwise 
    is a free motion under gravity. We assume that air resistance is negligible in 
    this kind of motion. 
    We have three cases: oblique projection, vertical projection and horizontal 

    projection. 

    Projection at an angle above the horizontal
    • Study the picture below carefully.
    • Go outside class and try to kick the ball so that it does not roll on the 
    ground.
    • State when will the ball cover a long horizontal range. (State down 

    the conditions for that to occur).

    C

    From the figure above, if the ball is kicked so that it does not roll on the 

    ground, it will move at certain angle relative to the ground. 

    Activity 2
    a) In the ground, kick the football individually.
    b) By observing, the flight of the ball state whether it will cover a 
    longer horizontal distance when it is projected at a large angle or a 
    small angle.
    c) Explain your observation and note down any key points in your 
    book.
    C
    C

    Upward projection

    From the figure above, a football player can kick the ball and it takes the 

    motion of a projectile.

    C

    C

    C

    C

    C

    C

    C

    C

    C

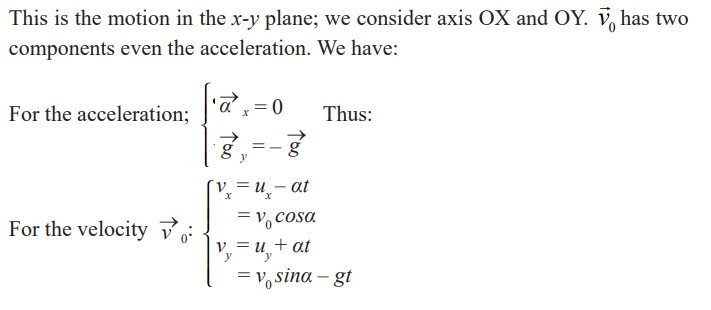
    Horizontal projection

    Activity 3

    Place a stone on top of a table.
    Displace it so that its motion takes the shape below.
    Try to observe the motion carefully.

    Note down what you observe and share it with your class members.

    Take care
    In throwing the stone / displacing it, you should take care so that it does not 

    hit you because it may harm you. 

    C

    C

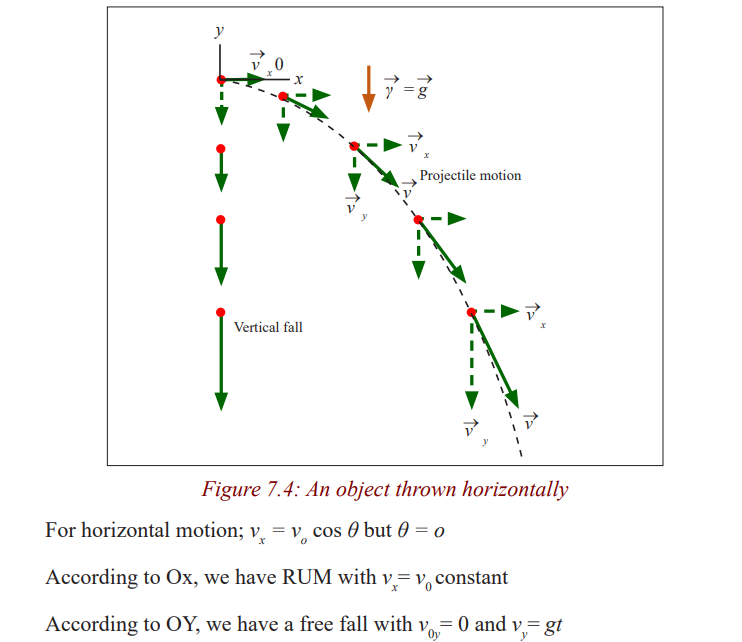
    Activity 4
    Using the information given above;
    a) Derive the equations for the motion.
    b) Study the picture below and do the same.

    c) State the condition when the body attains maximum height.

    C

    Examples of application of projectile motions are as follow:

    • Football kicked in a game

    • A cannonball fired from a cannon.

    • A bullet fired from a gun

    • A disc thrown in the sport of discus throw.

    • The flight of golf ball.

    • A jet of water escaping a hose.

    • Motorcycles and cars jumping in extreme sports

    Application activity 7.1

    1. A gun has a muzzle velocity of (i.e. a shell leaves the gun with 
    an initial speed of ). Find the horizontal range of the gun when 
    the angle of projection is 300. Find also the maximum horizontal 

    range of the gun.

    2. A stone is thrown from the top of a cliff (as shown in figure below) 
    70 m high at an angle of 300 below the horizontal and the sea 20 
    m from the bottom of the cliff. Find the initial speed of the stone 

    and the direction in which it is moving when it hits the sea.

    C

    3. A man fires a rock out of a slingshot directly upward. The rock has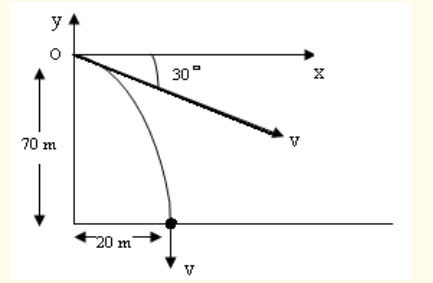 
    an initial velocity of . How long will it take for the rock to return 

    to the level he fired it at?

    Circular motion

    Activity 5

    Study carefully the motion of the ball shown below.
    State what would happen if at any point the thread holding the ball breaks?

    Note and record your observation.

    C

    A motion is said to be circular if the trajectory is a circle of constant 

    radius R.

    The motion is uniform if the body describes in equal angular displacements 
    in equal times.. Even if the motion is uniform, it has an acceleration because 

    the velocity changes after every moment since its direction keeps changing. 

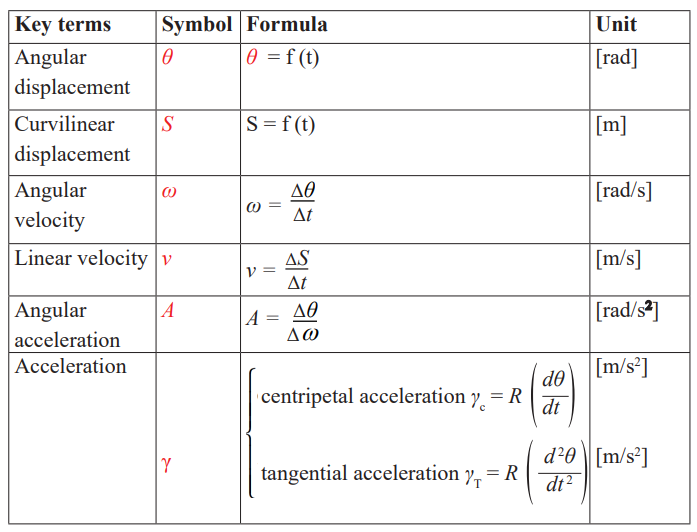
    Angular displacement θ

    Definition of key terms in circular motion

    C

    C

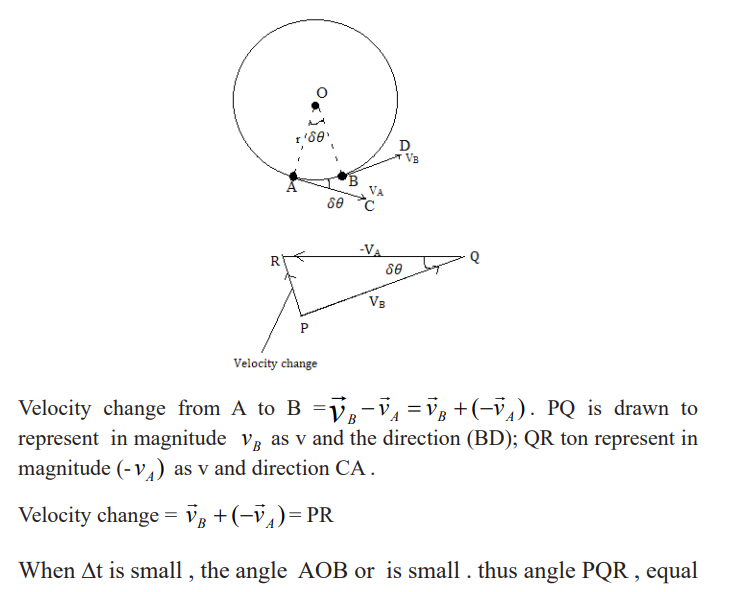
    Centripetal acceleration

    As we said, in a circular uniform motion, there is acceleration. This acceleration 
    is called centripetal acceleration. The easiest way of proofing this formula is 

    as follow: 

    Consider an object moving with a constant speed (a scalar which has no 

    direction) round a circle of radius r.

    C

    C

    Periodic time, frequency

    Activity 6

    * Go to the play ground.

    * Make sure you round the playground two times.

    * Note and observe the time taken to make one complete revolution.

    * What do you call the time taken to move around the play ground.

    C

    From the activity 6, you made two rounds in a given time. The number of 

    rounds made in a Unit time is called frequency

    C

    In summary

    C

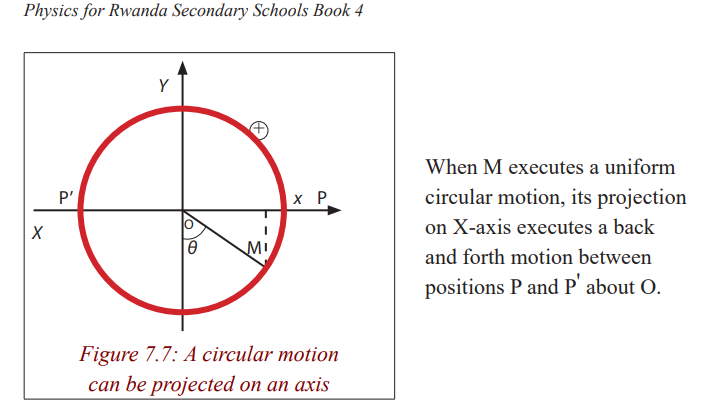
    Distance time-graph of a uniform circular motion

    When an object executes a circular motion of constant radius R, its projection 

    on an axis executes a motion of amplitude a that repeats itself back and forth, 

    over the same path.

    C

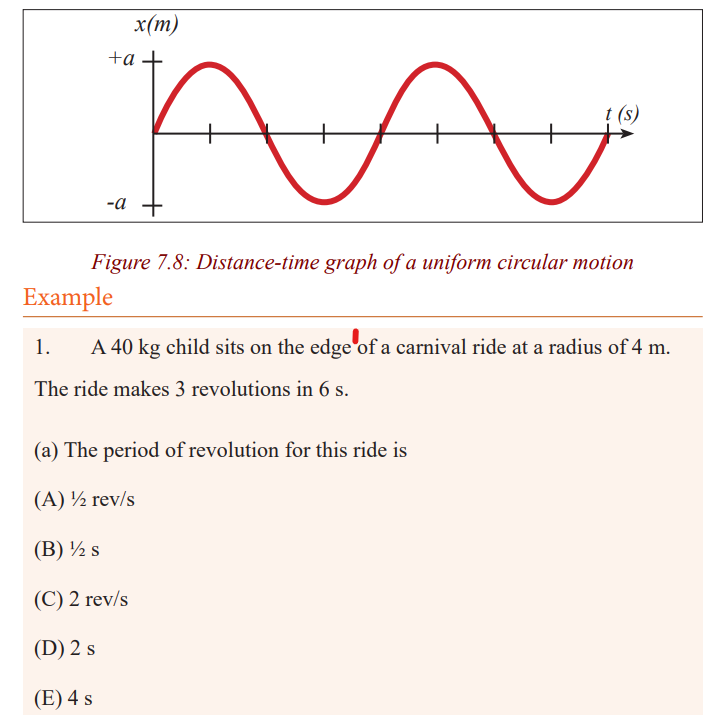
    Considering the displacement and the time, we find the following graph

    C

    (b) The speed of the child is most nearly 

    (A) 4 m/s

    (B) 12 m/s

    (C) 24 m/s

    (D) 120 m/s

    (E) 360 m/s

    Solution

    C

    2.A 150 g ball at the end of a string is revolving uniformly in horizontal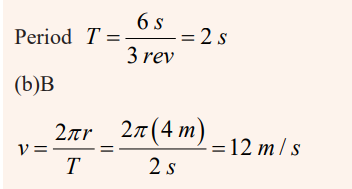 
    circle of radius 0.600 m; the ball makes 2.00 revolutions in a second. What 

    is its centripetal acceleration?

    Solution

    If the ball makes two complete revolutions per second then the Period is 

    C

    Centripetal force
    If you try to move / run in a circular path, you will finally notice that you keep 
    moving in a circle even when you try to stop. There is a force that keeps you 

    more in a circular path called centripetal force.

    Since a body moving in a circle (or a circular arc) is accelerating, it follows 
    from Newton’s first law of motion that there must be force acting on it to cause 

    the acceleration. 

    This force, like the acceleration, will also be directed toward the centre and 
    is called the centripetal force. The value F of the centripetal force is given by 

    Newton’s second law, that is:

    C

    C

    Example
    1. A 40 kg child sits on the edge of a carnival ride at a radius of 4 m. The 
    ride makes 3 revolutions in 6 s. The force which is holding the child on the 

    ride is most nearly

    (A) 30 N
    (B) 160 N
    (C) 320 N
    (D) 1440 N
    (E) 2880 N

    Solution

    C

    Application of circular motion

    Vertical and horizontal circle

    Vertical circle

    Taking the approach that the ball moves in a vertical circle and is not 
    undergoing uniform circular motion, the radius is assumed constant, but the 
    speed v changes because of gravity. Nonetheless, the formula of centripetal 

    acceleration is valid at each point along the circle, and we use it at point 1 and 

    2. The free-body diagram is shown in the figure 8.10 for the positions 1 and 2.

    C

    a) At the top (point 1), two forces act on the ball: the force of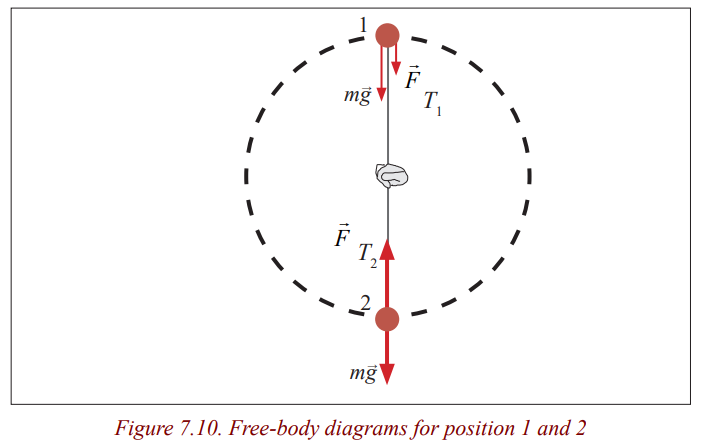 
    gravity and the tension force the cord exerts at point 1. Both 
    act downward and their vector sum acts to give the ball its 
    centripetal acceleration. We apply Newton’s second law, for t 
    a vertical direction, choosing downward as positive since the 

    acceleration is downward (toward the centre):

    C

    C

    C

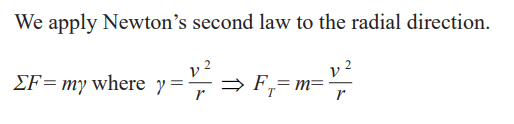
    Example

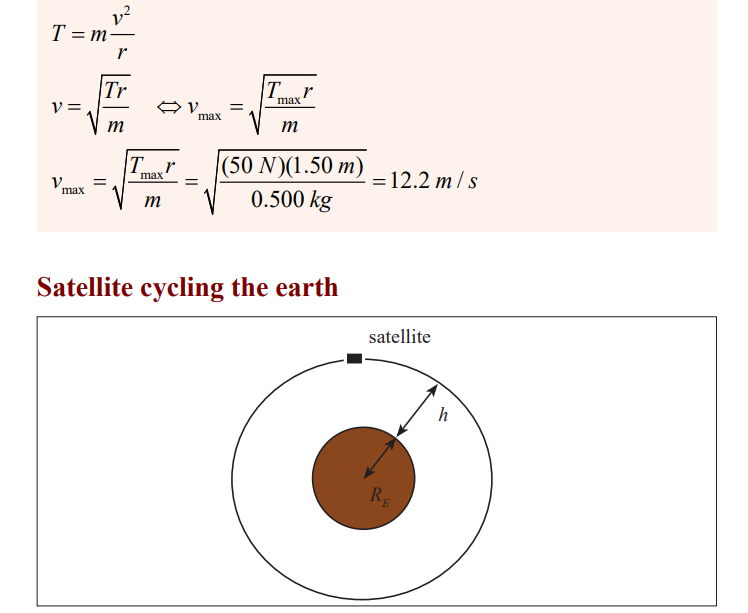
    A puck of mass 0.500 kg is attached to the end of a cord 1.50 m long. The 
    puck moves in a horizontal circle as shown in the figure. If the cord can 
    withstand a maximum tension of 50.0 N, what is the maximum speed at 
    which the puck can

    move before the cord breaks?

    C

    C

    C

    C

    C

    C

    Conical pendulum

    Activity 7

    DO THIS!

    * Tie a thread of about 50cm on retort stand. 

    * On a thread, tie a pendulum bob.

    * Displace the bob through a certain angle. 

    * Displace the bob through a certain angle. What do you observe.

    * Release the bob to move through a certain angle so that it moves in a 

    horizontal circle.

    * Try to investigate forces acting in the bob.

    * Relate your findings to fig. 8.13.

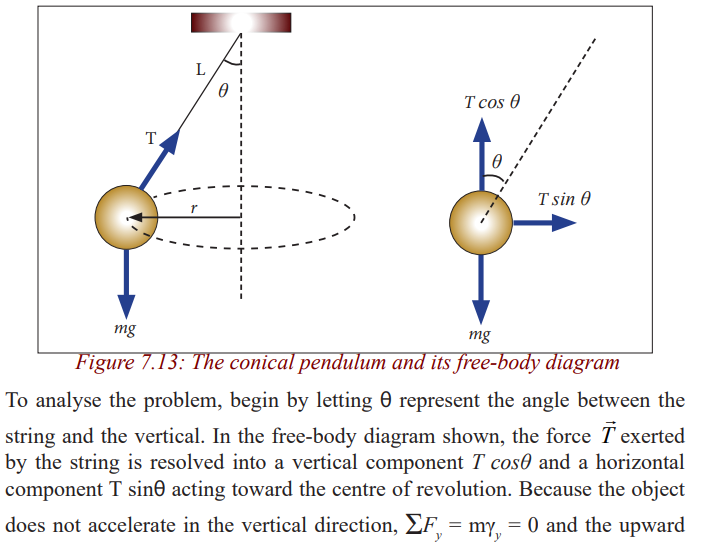
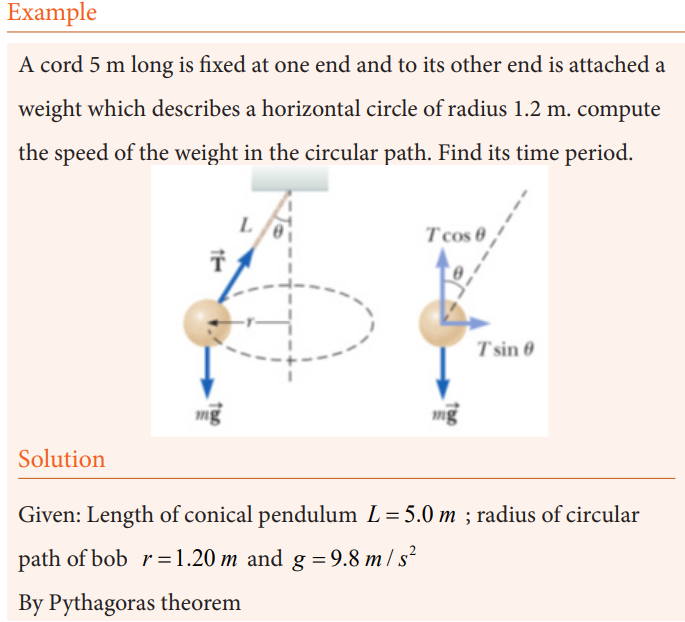
    A small object of massm is suspended from a string of length L. The object 
    revolves with constant speed v in a horizontal circle of radius r, as shown in 
    Figure 8.13. Because the string sweeps out the surface of a cone, the system is 

    known as a conical pendulum. 

    Let us find an expression for v.

    C

    C

    C

    C

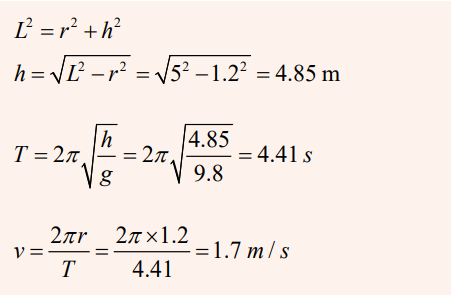
    Road banking 

    Circular motion on JOB

    Activity 8

    A car negotiating a corner

    C

    The successful negotiation of a bend on a flat road therefore depends on the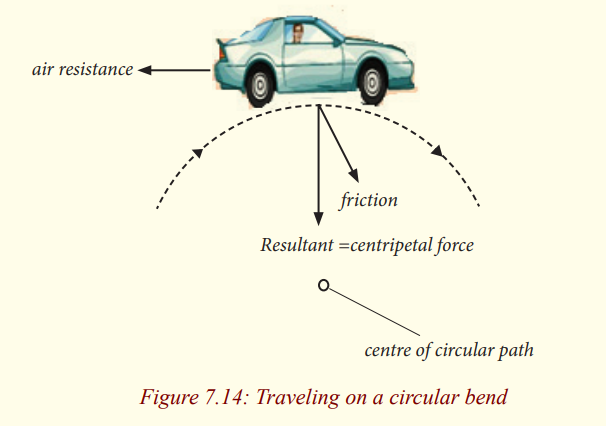 
    tyres and the road surface being in a condition that enables them to provide a 
    sufficiently high frictional force, otherwise skidding occurs. Safe cornering 

    that does not rely on friction is achieved by “banking” the road.

    C

    C

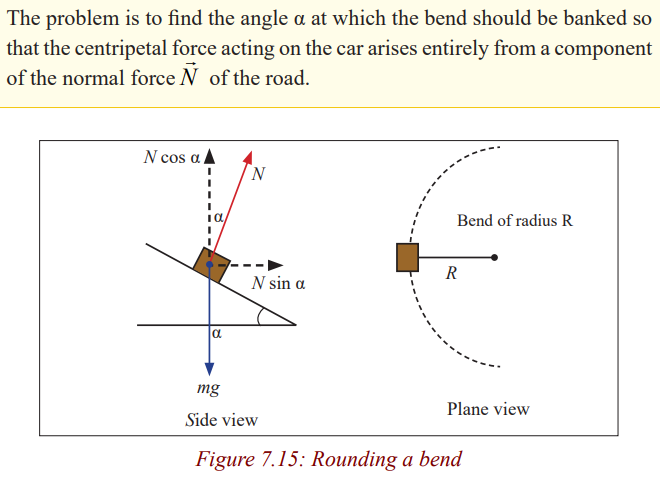
    The equation shows that for a given radius of bend, the angle of banking is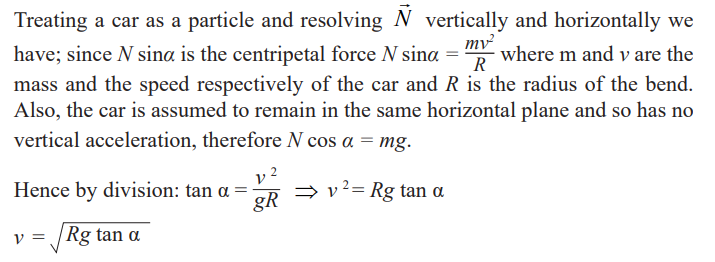 

    only correct for one speed.

    Spinning dryer is also known as tumble dryer is a powered household 
    appliance that is used to remove moisture from a load of clothing, bedding 

    another textures, usually shortly after they are washed in a washing machine.

    Example
    1. The car has a mass m and a speed v as it moves around the track 
    of radius R. Which of the following expressions can be used to find 

    the value of the coefficient of friction between the tires and the road?

    C

    Career centre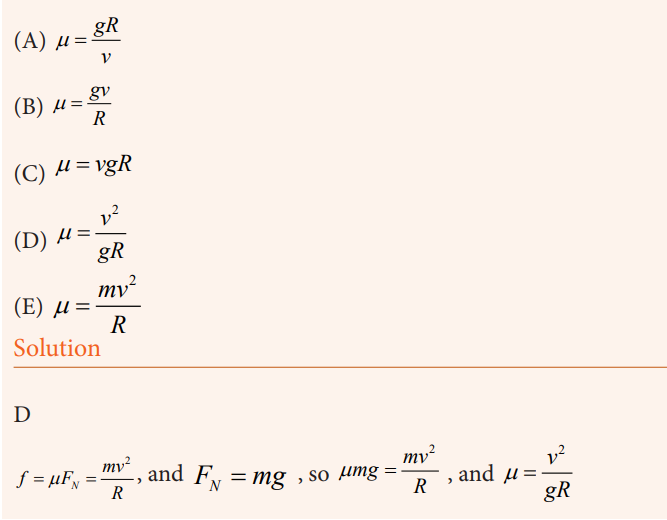 
    Learn more about careers in physics where projectile and circular motion are 

    applied.

    END UNIT ASSESSMENT

    1. A body is projected upwards from the level ground at an angle of 
    500 with the horizontal has an initial speed of 40 m/s. how long will 

    it be before it hits the ground?

    2. A body is projected downwards at an angle of 300 with the 
    horizontal from the top of a building 170m high. Its initial speed is 
    40m/s. 
    a) How long will it take before striking the ground?
    b) Find out how far from the foot of the building the body will 
    strike,

    c) What the angle with the horizontal?

    3. A body is projected from the ground at the angle of 300 with 
    the horizontal at an initial speed of 128m/s, ignoring air friction, 
    determine: 
    a) In how may seconds, it will strike the ground?
    b) How high it will go?

    c) What is its range will be?

    4. A ball is thrown upwards at an angle of 300 to the horizontal and 
    lands on the top edge of a building that is 20m away, the top edge is 

    5m above the throwing point. How fast was the ball thrown?

    5. A projectile is fired with initial velocity v0=95m/s at an angle . 
    After five seconds it strikes the top of hill. What is the elevation of 
    the hill above the point of firing? At what horizontal distance from 

    the gun does the projectile lands?

    6. 6. A ball is thrown from the top of the one building towards a tall 
    building 50m away. The initial velocity of the ball is 20m/s at 400 
    above the horizontal. how far above all below its original level, will 

    the ball strikes the opposite wall?

    7. A projectile is fired with horizontal velocity of 330m/s from the top 
    of a cliff 80m high. 
    a) How long will it take for the projectile to strike the level 
    ground at the base of the cliff?
    b) How far from the foot of the cliff will strike?

    c) With what velocity will it strike?

    8. A 0.3kg mass attached to 1.5m long string is whirled around the 
    horizontal circle at a speed of 6m/s.
    a) What is the centripetal acceleration of the mass?

    b) What is the tension of the string?

    9. (Moderate), a race car, moving at a constant tangential speed 
    of 60m/s, takes one lap around a circular track in 50 seconds. 

    Determine the magnitude of the acceleration of the car.

    10. An object that moves in uniform circular motion has a centripetal 
    acceleration of 13m/s2. If the radius of the motion is 0.02m, what is 

    the frequency of the motion?

    11. Find the centripetal acceleration for a n object on the surface of a 

    planet with the following characteristics: radius and 1day seconds.

    12. An 8.0g cork is swung in a horizontal circle with a radius of 35 cm. 
    it makes 30 revolutions in 12 seconds. What is the tension in the 

    string? (Assume the string in nearly horizontal).

    13. A 15g stopper is swung in a horizontal circle with a radius of 
    0.80meters. The tension in the string is 1.5Newtons. Find the speed 
    of the stopper and determine how long it takes to complete 30 

    revolutions. (assume the string is very nearly horizontally)

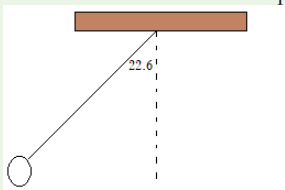
    14. A brass ball with a mass of 120 grams is suspended from that is 
    60.0 cm long. The ball is given a push and it moves in a horizontal 
    circle. The string is not nearly horizontal. It forms an angle of just 
    22.6 degrees from the vertical. (this is sometimes called a conical 
    pendulum because the string sweeps out the surface of a cone.
    a) Draw free body diagram indicating the forces acting on the 
    ball.
    b) What is the y-component of the tension force equal to? how 
    do you know?
    c) Use trigonometry to find the x-component of the tension 
    force.
    d) What is the radius of the ball’s motion?

    e) Use your answer to c and d to find the speed of the ball 

    C

    ◄Unit 6 : Sources of Energy in the WorldUnit 8 :Universal gravitational field and potential►