General
UNIT 9:Area and Land Measurements
Key unit competence
By the end of this unit, a learner should be able to understand area as a two
dimensional (2D) space enclosed by a boundary. The learner should also use
square and land units in solving mathematical problems.
Attitudes and values
Appreciate the need to properly and accurately use different area and land
measurements in daily life situations.9.1 Understanding Area
In the preceding figure, the shaded part (green) is a square of length 1 mm and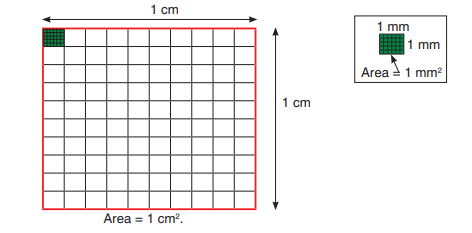
width 1 mm. The area of this part is 1 mm × 1 mm = 1 mm2
.
Now, consider the big square (red). There are 10 small squares along its length
and 10 squares along its width.
So, the area of the big square = 10 mm × 10 mm = 100 mm2.
Important point
If area = 100 mm2, then there are 100 squares each of area 1 mm2.
Activity 9.1
Refer to the area grid shown:
• What is the area of 1 small square?
• What is the area of the big square?
• Count the number of small squares inthe big square.
Exercise 9.1
In the figure below, each small square has both length and width of 1 cm.
(a) What is the area of one small square?
(b) How many small squares are in the figure?(c) What is the area of the whole figure?
9.2 Units of Area
The standard unit of area is the square metre. It is written as m2
. However,
other units for measuring area are km2, hm2, dam2, dm2, cm2 and mm2.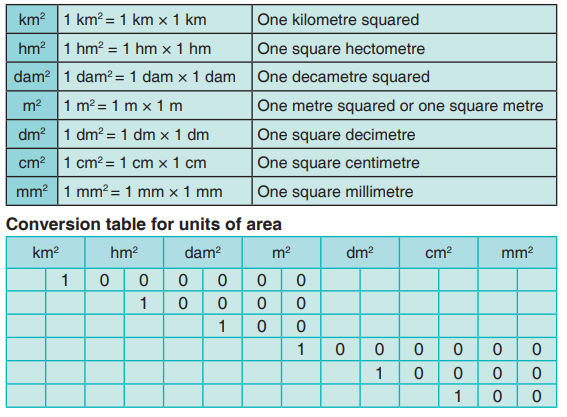
From the conversion table above, we can see that:
1km2 = 1 000 000 m2
1hm2= 10 000 m2
1dam2= 100 m2
1 m2 = 1 000 000 mm2
1dam2= 10 000 dm2
1cm2 = 100 mm2
The meaning of 1 km2
Consider a square plot of land ABCD such that
BC is 1 km long and CD is also 1 km long as
shown.
Area of the plot ABCD = length of side BC x
length of side CD = 1 km x 1 km = 1 km2.
The area of this plot of land is 1 km2, which is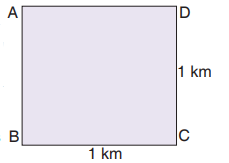
read as “one kilometre squared” or “one square kilometre”.
NOTE:
Since 1 km2 = 1 km x 1 km, then we can easily change 1 km2 in to other units
of area such as m2.
1 km2= 1 km x 1 km = 10 hm x 10 hm = 100 hm2.
Read the following areas aloud:
(a) 50 km2 (b) 600 hectares (c) 40 acres
(d) Our school football field has an area of 7 000 m2
(e) My study table is 320 cm2 (f) The size of my wall photo is 300 mm2.
Exercise 9.2
Change the following units of area as instructed:
(a) 1 km2 = _______ m2
(b) 10 m2 = _______ cm2
(c) 25 dam2 = __________ m2
9.3 Relationship Between Land Measurement and Area
Land area is measured in a larger unit called the hectare. It is written in short as ha.
Other units of area include; are, acre and hectare.
• A plot of land measuring 100 m by 100 m has an area of
1 hectare. So, 1 hectare (1 ha) = 100 m × 100 m = 10 000 m2.
• A plot of land measuring 10 m by 10 m has an area of 1 are.
So, 1 are = 100 m2.
• 1 ca = 1 m2, i.e. 1 centiare = 1 square metre.
• 1 acre = 0.40 hectare and 1 hectare = 2.47 acre.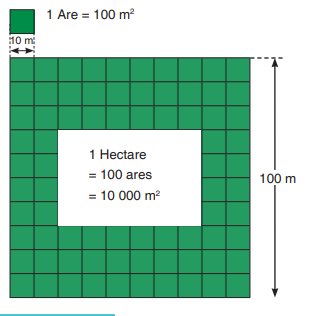
1ha = 100a
1a = 100 ca
1 ha = 10 000ca1ca = 1m2
1 hm2= 1ha, 1dam2= 1a, 1m2= 1ca.
Activity
Study the conversion table above. Discuss with your group members and
answer the following questions:Activity 9.2• 1a = ..........ca• 1dm2= .........ca• 10a = ............ha• 20ca = ............cm2• 5dam2= ............dm2• 25m2= ...............ca• 25ca = ..............a• 5 000 m2 = .......h
In this class activity, you will find the area of a plot of land of length 10 m and
width 5 m by counting the number of square metres in it.
(a) 10 m can not fit into your book, so you will use a scale of 1 cm to represent
1 m. Draw a rectangle of length 10 cm and width 5 cm in your book.
(b) Divide the length into 10 equal parts using vertical lines. Each part
should be equal to 1 cm.
(c) Divide the width into 5 equal parts using horizontal lines as shown in
the diagram below:
(d) Count the number of small squares formed by the lines you have
drawn. You can do this by numbering all the small squares.
(e) Each small square represents an area of 1 m2.(f) Now answer this question: What is the area of the plot of land?
Example 9.1
Convert the following units of area:
(a) 3 m2 to cm2
( b) 5 km2 to dam2
(c) 2.5 hectares to m2
Solution
(a) 3m2 = 30 000cm2
(b) 5km2 = 50 000dam2(c) 2.5 ha = 25 000m2
Exercise 9.3
Convert the following units:
(a) 5 km2 in m2.
(b) 1 hectare in m2.
(c) 10 are in m2. 9.4 Area of Rectangular Piece of Land
9.4 Area of Rectangular Piece of Land
Example 9.2
Find the area of a rectangular piece of land whose length and width are:
(a) 80 m and 20 m. (b) 100 m and 40 m.
Solution
(a) Area = length × width = 80 m × 20 m = 1 600 m2.
(b) Area = 100 m × 40 m = 4 000 m2.
Exercise 9.4
1. The length of a house floor is 10 m and its width is 8 m. What is the
area of the floor?
2. The area of the floor of our classroom is 40 m2. How long is theclassroom if it is 5 m wide?
9.5 Addition and Subtraction of the Area of Land
Activity 9.3
In groups, do the following:
• Measure the length and width of your classroom.
• Also, measure the length and width of another classroom.
• What is the total area? What is the difference between the areas of tworooms? Write the answers in m2.
Activity 9.4
In this class activity, you are going to work in groups and find the area of the
plot of land shown below. Divide the land in two parts. Find the areas of plotseparately. Add the area of the two plots and express in m2.
Assessment Exercise
1. Change the following units of area as instructed.
(a) 2 500 cm2 = ________ m2
(b) 8 000 m2 = ____________ hm2
(c) 6.5 km2 = ____________ dam2
2. A piece of paper has an area of 6 cm2.
If it is 3 cm long, then how wide is the paper?
3. (a) Add 25.32 m2 and 62.28 m2.
(b) Subtract 4.25 ha from 6.75 ha.
4. School A is built on 1 are of land and school B is built on 100 m2 of land.
Which of the two schools has bigger area?
5. On a fruit farm, 1 are of land produces 2 tons of oranges. How many
kilograms of oranges will be produced by 300 m2
of the same farm land?
6. Kenia has a plot of land measuring 100 m by 100 m. Peter’s land has
an area of 3 hectares and Kwame has an area of 200 ares. Who has
the largest land? What is the total Land area in hectares?
7. The total land area of our country Rwanda is 26 338 km2.
Lake Victoria has an area of 69 484 km2.
By how much is Lake Victoria bigger than Rwanda?Internet Resource
Internet Resource http://www.mathplace.com/
