• General

    ◄UNIT 5:Decimal Fractions/NumbersUNIT 7:Capacity Measurements ►

    UNIT 6:Length Measurements

    • UNIT 6:Length Measurements

      Key unit competence
      A learner should be able to know the meaning of length, conversion between 
      units of length and apply them in solving mathematical problems related to 
      daily life situations.

      Attitudes and values
      Learners should appreciate the importance of metric measures in daily life and 
      recognise the importance of using, measuring tools correctly.

      6.1 Meaning of length

      Distance between two points is known as length.

      A

      6.2 Instruments for Measuring Length
      There are many instruments used for measuring length. These types of 
      instruments are used depending on the size of the length to be measured. 
      Some instruments used for measuring length/distances are shown below;
      1. Ruler: It is used to measure short distances like length of a line in a book, 

      length of a table, classroom, height of a door

      W

      2. Tape measure: It is used for measuring longer distances like length of a 

      field, height of a person, length of a cloth, etc.

      3. Yard stick: It is a flat wooden board with markings at regular intervals. It 

      is used for measuring small lengths.

      4. Micrometer screw gauge: It is used for measuring very small distances 
      such as diameter of a pin or the thickness of a paper. A micrometer screw 

      gauge appears like shown below:

      Other instruments used for measuring length are vernier calliper,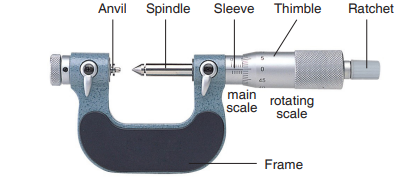 

      Architect’s scale, etc.

      6.3 Units of Length
      6.3.1 Non-standard Units

      2

      We can measure the length using pace, handspan, foot span, cubit, etc. These 
      units vary from persons to persons as they have different pace. This method is 
      used by the same person to measure small distances.
      For example, the length of a table is 6 hand spans, the length of a carpet is 8 

      foot spans.

      E

      Activity 6.1
      • Stand straight up on the floor.
      • Place the metre rule near your foot so that it is 
      parallel to the side of your body.
      • Mark a point on your body where the end of the 
      metre rule touches.
      • Now you have your own metre rule and be sure 
      to tell the length of 1 metre.
      • Cut the stick provided so that its length is 1m.
      • How many times does your foot fit into a metre? 
      • You can now use your foot to measure the length of a classroom.
      S
      Activity 6.2
      • Hold the metre rule as shown in the diagram. 
       The zero mark ofthe metre rule must be 
       at the tip of your finger.
      • Mark a point on your arm/chest where the 
      end of the metre rule touches.
      • This is the length of 1m. Now you have 
      your own metre rule.
      • You can now use it to measure the length 
      of your table.
      • While at home, you can try to measure/estimate the height of a table, your brother, 
      your sister, your parents/guardians, length of your bed.

      Exercise 6.1
      1. Check and write the lengths/heights of the following objects present in your home
      S
      2. Check and write the length/height of the following.


      6.3.2 Standard Units of Measuring Length
      WThe standard unit for measuring 
      length is metre. It is denoted by ‘m’. 
      The other units of length are the kilometre (km), hectometre (hm), decametre 
      (dam), decimetre (dm), centimetre (cm) and millimetre (mm).

      Metric-unit Prefixes      Metric
      prefixes are very useful in converting units of quantities.
      The main metric prefixes dealt with at this level are the kilo, hecto, deca, deci, centi and milli.


      Important mnemonic:
      It is important to remember the order of the above prefixes:
      Kigali Hotel Deserves One Delicious Chocolate Milk, where Kigali kilo, 
      Hotel →hecto, Deserves →deca, One →one (Unit), Delicious→ deci, 
      Chocolate→ centi, and Milk →milli.
      From the above table we can see that;
      • One kilometre = 1 km = 1000 m. 
      • One hectometre = 1 hm = 100 m
      • One decametre = 1 dam = 10 m
      • One decimetre = 1 dm = 0.1 m ( a tenth of a metre)
      • One centimetre = 1 cm = 0.01 m = (hundredth part of a metre)
      • One millimetre = 1 mm = 0.001 m = (a thousandth of a metre)

      Activity 6.3
      M• Place the metre rule on your work table 
      or desk.
      • Identify the 0 cm and the 100 cm marks 
      on the metre rule.
      • Confirm that the metre rule is divided into 
      10 equal parts. How many decimetres 
      make up a metre? {10 dm = 1 m}
      • Look closely at 1 dm.You should be able to see that 1 dm is divided into 
      10 equal parts. Each part is a centimetre (cm). How many cm make up 
      1dm? {10 cm = 1 dm)
      • Look closely at 1 cm. You should be able to see that 1 cm is divided into 
      10 equal parts. Each of these is called a millimetre (mm). How many 
      mm make up a cm? {10 mm = 1 cm}.
      • Now measure the length of your longest finger. Record your answer in 
      dm, cm and mm.

      Exercise 6.2
      Estimate the length of the following in metres.
      (a) length of a car.                                             (b) length of a bus.

      (c) length/height of your handspan.         (d) length of your pace.

      6.4 Estimation of Length
      In this section, we will study to find the length of objects by observing them.
      For example, the length of a notebook is about 12 cm, the length of a pencil is 
      about 5 cm, etc.

      Activity 6.4

      Estimate the length of the following in metres.

      E

      Exercise 6.3
      Since we have practically seen the length of a mm, cm, dm, m, dam, hm and 
      km, it is now time to see how well you can estimate length.
      Estimate the following lengths:
      (a) Length of your foot (in cm).
      (b) Length of your classroom (in m).
      (c) Length of your pencil in mm (or cm).
      (d) Width of your exercise book (in cm).
      (e) Length of your table (in dm).

      (f) Height of your best friend in class (in cm or m).

      6.5 Conversion of Units 
      When converting from one unit of length to another, we can easily use a 
      conversion table.


      Conversion table for length

      2

      From the conversion table, you can see that;
      • 1 km = 10 hm, 1 km = 100 dam, 1 km = 1000 m
      • 1 m = 10 dm, 1 m = 100 cm, 1 m = 1000 mm,
      • 1 hm = 0.1 km, 1 dam = 0.01 km, 1 m = 0.001 km
      • 1 dm = 0.1 m, 1 cm = 0.01 m, 1 mm = 0.001 m.

      Example 6.1
      Convert the following units of length:
      (a) 2 km to m        (b) 2 km to hm        (c) 10 cm to mm

      (d) 3 dam to m     (e) 40 m to mm       (f) 50 dm to cm

      F

      R

      Exercise 6.4
      1. Complete the following:
      (a) 40 km = ............... m                       (b) 350 cm = ............. mm
      (c) 3 hm = .................. m                      (d) 40 cm = .............. dm
      (e) 1 m = ................. mm                      (f) 2 900 mm = ......... cm
      (g) 3 000 000 mm = ............... m        heart 5 000 m = ............. dam

      2. Use the conversion table to convert the following units of length as 
      instructed:
      (a) 2 m = ................ cm                        (b) 3 km = ............... dam
      (c) 2.5 m = ............. cm                        (d) 46 cm = .............. mm
      (e) 2 000 m = ............... km                 (f) 50 mm = ............... cm

      (g) 4500 dm = .............. dam.

      6.6 Addition and Subtraction of Length
      The process of addition or subtraction of length is exactly similar to the addition 
      or subtraction of ordinary numbers.

      Example 6.3
      Add the following:
      (a) 3 km + 200 m = ................... m
      (b) 50 hm + 40 dm = ................... dm
      (c) 16 m + 14 dm = ................... m

      (d) 76 hm + 4 km = ................... m

      Example 6.4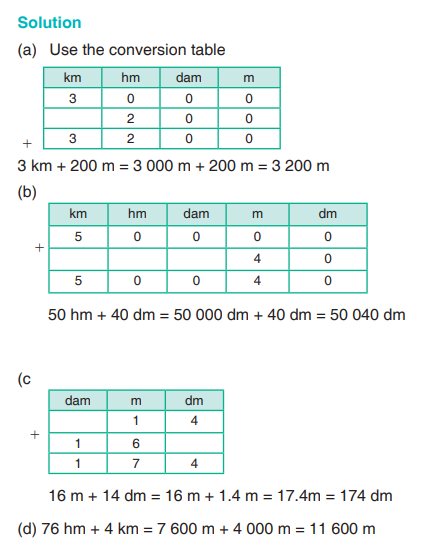
      Subtract: 1) 226 cm – 105 cm
      2) 3 m 15 cm – 1 m 35 cm
       3) 125.2 mm – 87.6 mm
      Solution
      1. 226 cm – 105 cm = 121 cm
      2. 3 m 15 cm = 3 × 100 cm + 15 cm
      = 300 cm + 15 cm
      = 315 cm
      1 m 35 cm = 100 cm + 35 cm
          = 135 cm

      Therefore, 315 cm – 135 cm = 180 cm

      E

      Exercise 6.5
      Workout the following:
      (a) 30 km + 4 000 m = ............... m
      (b) 3 600 m + 44 hm = ............... km
      (c) 65 hm – 25 dam = ............... m
      (d) 30 km – 4 000 m = ............... hm
      (e) 40 hm – 200 dam = ............... dm

      (f) 500 m + 28 000 dm = ............... cm

      6.7 The Perimeter
      The perimeter of a closed figure is the distance around the figure. Since the 
      standard unit of distance or length is the metre (m), then the unit of perimeter 
      is the metre. However, perimeter can also be expressed in km, hm, dam, dm, 
      cm or mm.

      Example 6.5
      The diagram below shows a piece of paper. Length AB = 6 cm, length 
      BC = 2 cm, length CD = 6 cm and length DA = 2 cm. Calculate the distance 

      all round the piece of paper.

      F

      Solution
      Perimeter = length of (AB + BC + CD + DA)
          = 6 cm + 2 cm + 6 cm + 2 cm
          = 16 cm.
      Example 6.6
      The diagram below shows an isosceles piece of cake PQR. The lengths of 
      the sides of the cakes are shown on the diagram. What is the distance all 

      round the figure PQR?

      Solution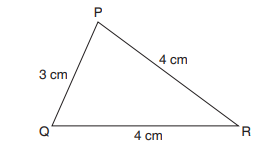
      Perimeter = Distance around PQR = PQ + QR + RP = (3 cm + 4 cm + 4 cm)
      = 11 cm.
      Example 6.7
      The diagram below shows a birthday card for my younger sister Cathy. The 
      length of each side of the card is 5cm. What is the total distance all round 

      the card?

      D

      Solution

      Perimeter = Length of (PQ + QR + PR)
                           = 5 cm + 5 cm + 5 cm
                           = 15 cm

      Example 6.8
      What is the total distance around this plot of land? Express your final answer 

      in metres.

      E

      Solution
      The sides are given in different units. We need to convert all units to metres 

      using the conversion table.

      U

      From the conversion table 
      2 000 mm = 2 m
      20 dam = 200 m
      300 cm = 3 m
      10 dam = 100 m
      20 000 mm = 20 m
      So the required distance = 2 m + 200 m + 3 m + 100 m + 20 m + 90 m = 

      415 m

      4

      6.8 Application of Length
      Sometimes, you find situations where you need to apply length in order to solve 
      them. Study the following examples.

      Example 6.9
      Trees are planted at an intervals of 10 m. If ten trees are planted, find the 

      distance from the first to the last tree.

      M

      First find the number of spaces
       Number of spaces = Total number of trees – one tree = 10 – 1
                                              = 9 spaces
                              1 space = 10 m
                              9 spaces = (10 × 9) m = 90 m
      The distance is 90 metres.

      Example 6.10
      A rectangular garden 50 m by 30 m is to be fenced with poles placed 
      at an interval of 5 m. Find the amount of money required to fence the 

      garden at 3 000 Frw per pole.

      3

      Activity 6.5
      Eleven bundles of wires, each of 125 cm long were needed from Kabuye’s house 

      to the electric pole. How far was Kabuye’s house from the electric pole?

      Assessment Exercise
      1. Estimate the following lengths: 
       (a) Height of your teacher (in m).
      (b) Length of your football field at school (in m).
       (c) Height of the tallest tree at your school (in m).
       (d) Length of your handspan (in cm).
      2. Workout the following:
       (a) 1 100 mm + 1 100 cm = ............... cm
       (b) 800 hm + 5 000 dam = ............... km
       (c) 1 km + 1 hm + 1 dam + 1 m + 1 dm + 1 cm + 1 mm = ................... mm

      3. Find the perimeter of the shape shown in the diagram below:

      z

      4. Electric poles are fixed at intervals of 50 m apart. If 101 poles are 
      fixed, find the distance from the first pole to the last pole.

      5. How many poles are required to make a circular fence of 45 m if the 
      poles are 5 m apart?

      6. Othieno has to fence his rectangular garden of 45 m by 30 m.
       (a) Find the number of poles he will require if the poles are 5 m apart?
       (b) If each pole costs 4 500 Frw, how much does he require to buy the 
      poles?

      7. Find the number of trees required to plant around a circular pond of 

      length 28 m at intervals of 4 m apart.

      8. Luzige’s land is in a shape of trapezium as shown:

      y

      He intends to fence it with poles 5 m apart. How many poles does he 
      require?
      9. Workout:
       (a) 1.25 cm + 7.75 cm

       (b) 9.75 dm + 2.45 dm

      Internet Resource

      For more online support visit www.kidsnumbers.com

      ◄UNIT 5:Decimal Fractions/NumbersUNIT 7:Capacity Measurements ►