General
UNIT 5:Decimal Fractions/Numbers
Key unit competence
A learner should be able to add, subtract and compare decimal numbers using
place values of decimals up to 2 decimal places.
Attitudes and values
Develop personal confidence in the use of decimal numbers and appreciate the
importance of decimal fractions in comparing and sharing.
5.1 The Concept of decimal number
A decimal number is any number which contains a decimal point.
A decimal number is a number which has a decimal part separated from the
integer part using a decimal separator called the decimal point.For example, 28.53 is a decimal number.
Activity 5.1
i. Draw a horizontal line of about 12 cm on your notebook using a ruler
and sharp pencil.
ii. Show the integers –4, –3, –2, –1, 0, +1, +2, +3 and +4 on the number line.
Activity 5.2
In this class activity, you will find some numbers:
(a) Divide the following numbers by 10:- 1400
- 140
- 14
- 1.4
- between 0 and 100?
- between 0 and 10?
- between 0 and 1?
Consider the number line below. The number line shows negative and positivenumbers from –5 to +5.
However, if we zoom into the space between 0 and 1, then we create new
numbers which are not whole. The space between 0 and 1 is divided into 10
equal parts. The decimal numbers 0.1, 0.2, 0.3, 0.4, ...... , 0.9 are produced.Decimals like 0.25 and 0.75 can easily be located as shown below.
By further zooming into the space between 0.1 and 0.2, we can form newdecimal numbers as shown below.
Activity 5.3
In this class activity, you will divide the space between 2.0 and 3.0 into ten
equal parts.
i. Draw a horizontal line of about 10 cm on your notebook using a ruler
and sharp pencil.
ii. Mark the start of the line with the decimal number 2.0.
iii. Mark the end of the line with the decimal number 3.0.
iv. Mark the line drawn into 10 equal parts, each 1 cm long.
v. Show the decimal numbers 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8 and 2.9
on the number line.
Activity 5.4
In this class activity, you will locate the positions of the given decimal
numbers: 8.11, 8.16 and 8.19.
i. Draw a horizontal line in your notebook using a sharp pencil. Length of
the line should be 10 cm.
ii. Mark the line at intervals of 1 cm so that the line has 10 equal parts.
iii. Write the decimal number 8.10 on the first mark and the decimal
number 8.20 on the last mark.
iv. Carefully study the number line you have drawn and write the correct
decimal numbers on the marks drawn.
v. Show the positions of the decimal numbers 8.11, 8.16 and 8.19.
vi. Present your work to the teacher for evaluation.
Exercise 5.1
Show the following on the number line:
(a) 0.6, 0.8, 0.3, 0.1
(b) 0.43, 0.48, 0.25, 0.15
(c) 0.3, 0.1, 0.5, 0.9, 0.2(d) 0.51, 0.50, 0.48, 0.55
5.3 Place Value of decimalsConsider the decimal number 78.46
78.46 is read as “seventy eight point four six”.It is wrong to say “seventy eight point forty six”
We can see that the place value for 7 is ‘tens’, 8 is ‘ones’ or ‘units’, 4 is ‘tenths’,and 6 is ‘hundredths’.
Activity 5.5
i. Let two pupils A and B stand to the right of a tree.
ii. Also, two pupils C and D should stand to the left of the tree.
iii. If we now consider the tree as a decimal point, let each pupil mentionhis/her place.
Example 5.1
Write the places of the underlined digits in the decimal numbers given
below:(a) 0.24 (b) 5.06 (c) 13.56
Solution
(a) Tenths (b) Ones (c) Tens
Exercise 5.2
1. Read the following decimal numbers and write them in words.
(a) 87.09 (b) 12.2 (c) 0.03 (d) 23.56
(e) 19.19 (f) 0.10 (g) 45.45
2. Write the following decimal numbers in figures:
(a) One hundred forty-four point seven.
(b) Twelve point one two.
(c) Seven point seven.
(d) Eighty point seven one.
5.4 Comparing decimals
When comparing decimal numbers, we may use =, < or >.
Example 5.2
Compare the decimal numbers 9.25 and 9.7.
Solution
1. Align the decimal points.
2. Fill in the empty place with zero.3. Compare the digits from left to right until they are different.
Example 5.3
Compare the two numbers: 452.78 and 452.21. Which one is greater?
SolutionArrange the numbers in a table like this:
The first three digits are the same in both decimal numbers. But in the
tenths’ column, 7 is greater than 2. So, 452.78 > 452.21.
Example 5.4
Arrange the following numbers in ascending order:
0.46, 0.64, 0.9, 0.09, 0.57, 0.75
Solution
• All these numbers begin with zero.
• Now we compare the second numbers.
• We can see that the smallest number is 0.09, followed by 0.46......
• 0.57 is smaller than 0.64.
• 0.75 is smaller than 0.9.
Therefore, Ascending order: 0.09, 0.46, 0.57, 0.64, 0.75, 0.9.
This can also be written as 0.09 < 0.46 < 0.57 < 0.64 < 0.75 < 0.9.
Example 5.5
Arrange the following numbers in descending order:
8.6, 7.66, 7.6, 0.76, 0.67, 0.86, 6.08.
Solution
Descending order: 8.6, 7.66, 7.6, 6.08, 0.86, 0.76, 0.67.
Alternatively, 8.6 > 7.66 > 7.6 > 6.08 > 0.86 > 0.76 > 0.67.
Exercise 5.3
1. Arrange the following decimal numbers from the smallest to the largest
(Ascending order)
(a) 3.5, 3.79, 3.42, 3.57, 3.7, 3.62.
(b) 5.7, 5.64, 5.8, 5.4, 5.79, 5.72.
(c) 5.0, 4.7, 4.8, 4.9, 4.3, 4.75
(d) 1.02, 1.7, 1.12, 1.66, 1.71, 1.1
(e) 3.1, 2.5, 2.49, 2.8, 3.48, 2.52
2. Arrange the following decimal numbers from the largest to the smallest
(Descending order).
(a) 8.1, 7.9, 7.92, 8.43, 7.89, 7.97
(b) 6.8, 7.23, 7.32, 6.59, 6.92, 7.02
(c) 2.01, 2.10, 2.63, 2.36, 1.4, 1.7
(d) 3.8, 2.77, 2.75, 3.34, 2.9, 3.(e) 6.4, 7.4, 4.7, 4.6, 4.06, 7.04
5.5 Addition and subtraction of decimal numbers
Adding decimal numbers works exactly the same way as adding whole numbers.
You just line up the decimal points as shown below. For example,
Activity 5.6
In this class activity, you will find any two decimal numbers which add up to
the given whole number:
(a) Find any 3 pairs of decimal numbers which add up to 10.
{e.g. 8.5 + 1.5, 5.5 + 4.5, and 3.55 + 6.45}
(b) Find any 3 pairs of decimal numbers which add up to 1.{e.g. 0.25 + 0.75, 0.8 + 0.2 and 0.77 + 0.23}
Example 5.6
Add 528 + 7.49
Solution
We can write 528 as a decimal number by putting a decimal point after 8and adding zeroes. So, 528 can be written as 528.00
Example 5.7
Add the following decimal numbers:
(a) 206.1 + 223.9 (b) 404.1 + 247.4 (c) 665.2 + 567(d) 435.7 + 65.1 (e) 299.72 + 0.08
Exercise 5.4
Work out the following:(a) 4.7 + 4.7 (b) 2.78 + 3.62 (c) 20.9 + 25.7
(d) 20.23 + 40 (e) 25.26 + 0.72 (f) 400.2 + 400
(g) 18.6 – 8.624.6 – 20.4 (i) 6.25 – 4.25
(j) 80.02 – 0.02 (k) 19.82 – 5.28 (l) 20.82 – 6.27
(m) 20.9 + 25.75.8 + 1.3 (o) 24.7 + 47.2
5.6 Real life problems involving decimals
Example 5.9
Ogolla ate 0.5 of his apple in the morning and 0.2 of it in the afternoon. Howmuch of his apple did he ate altogether?
Example 5.10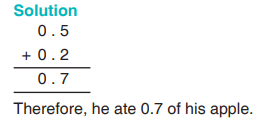
1. Opio bought 4 metres of cloth and used 2.3 metres for making shirts.
Find the length of the remaining cloth.
2. Nankinga weighs 94.2 kg and his brother Hamidu, 87.5 kg.
What is the difference between their weights?
Assessment Exercise
1. Write the following decimal numbers in figures:
(a) Three hundred ninety-nine point nine nine.
(b) One thousand seventy point seven zero.
3. Work out the following:
(a) 84.0 + 79.3 (b) 9.1 – 6.1 (c) 53.3 – 23.2
(d) 92.7 – 20.7 (e) 8.9 – 0.9 (f) 689.6 – 609.8(g) 100.5 – 50.5
4. A boy walks 2.5 km to school and then 1.5 km to his friend’s home.
What is the total distance covered?
5. The masses of four children in our class are 34 kg, 43.4 kg, 36.3 kg
and 38.2 kg. What is their total mass in kg?
6. A lesson starts at 8:30 a.m. and lasts for 50 minutes. At what time does it end?
7. The lengths of four rivers are 2.5 km, 4 km, 10.45 km and 0.95 km
respectively. What is the total length of the four rivers? By how much is
the longest river more than the shortest river?
8. In an athletics school race competition, the time taken to complete
100 m race is given below:
(a) Who won the race? Explain why.
(b) Who came last in the race? Explain why.
(c) For how long did the first competitor wait for the last person tofinish the race?
9. If x = 23.23 and y = 32.32, find the value of:
(a) x + x
(b) x + y
(c) y – x.
10. By how much is 18.5 greater than 14.6?
11. I am 9 years old. My elder sister is 14.5 years old. My mother is 31.5
years older than me.
(a) How old is my mother?
(b) What is the total of all our ages?
12. My wrist watch displays time using figures. The time right now is shownas 8:15 a.m. What time will my watch show after 15 minutes from now?
