General
UNIT 4:Fractions of the Same Denominator
Key Unit Competence
By the end of this unit, a learner should be able to explain the meaning of
fractions, add and subtract same-denominator fractions, multiply and divide
fractions accurately.
Attitude and Values
Appreciate the importance of accuracy in carrying out operations on fractions
and develop the spirit of sharing with others.
4.1 Meaning of fractions
A fraction is a part of a whole number.
A fraction is made up of 2 numbers. The top number is called the numerator
and the bottom number is called the denominator.
How Fractions Arise?
Fractions are obtained when a whole number is divided into two or more thantwo parts. The figures below show an orange divided into 8 equal parts.
Mixed Fractions
Activity 4.1
In this class activity, you will identify the numerator and denominator in thefollowing fractions. You will work in groups of 4.
• This is a clock face with so many numbers, some of which are fractions.
• Write down all the fractions shown on the clock face above.
• For each fraction you have written above, write down the numerator and
denominator.
• Compare your results with other classmates in class.• Present your answers to the teacher for marking.
Activity 4.2
In this class activity, you will write fractions when you are given the numerator
and denominator. You will complete this activity in groups of 4. Complete thetable in your note book, writing down the fraction.
Think!!!
A farmer has a bag of popcorn, a hen and a fox. He wants to cross a river in
a boat. The boat can only take him and only one of the three items he has.
The problem is that the hen can eat popcorn and the fox can eat the hen.How does he cross the river without anything getting eaten up?
Activity 4.3
Look at the following figures. Use coloured pencils or crayons to colour orpaint as instructed below:
4.2 Reading a Fraction
Activity 4.4
(a) In this class activity, you will work in groups of 6 learners.
(b) Three of them will write a half, a fifth and a third on their respectivecards as shown below.
(d) Now, make pairs of similar values of cards.(e) Ask your teacher to check the results.
Activity 4.5
Shade the parts represented by the given fraction.
Exercise 4.1
4.3 Comparing fractions with the same denominator
Activity 4.6
In this class activity, you will work in groups of 5 learners.
(a) Cut the orange given to you into 4 equal parts. Each part shall be
called a slice.
(b) Display the slices on a table and count them to be sure that they are 4.
(c) What fraction represents all the slices you have counted?
(d) Put the slices in 3 groups labelled A, B and C. In A put 1 slice, 2 slices
in B and 1 slice in C.
(e) What fraction represents the number of slices in each group? Answerthis question by completing the table below:



4.4 Addition of Fractions with the Same Denominator
Activity 4.8
(a) Draw a circle of radius 10 cm on a manila paper.
(b) Mark the centre of the circle using letter O.
(c) Draw two lines through the centre of the circle to divide the circle into
four equal parts. Each of these parts is called a sector.
(d) Label the three boxes A, B and C.
(e) Cut out the outline of the circle along the lines drawn.
(f) What fraction does each sector represent? Your answer should be 4/1.
(g) In box A put one sector, put two sectors in B and one sector in C.What fraction is represented by the sectors in boxes A, B and C?
(i) Pick the sectors in box A and box B. Add them together. What total
fraction do you get?(j) Add the sectors in A and C together. What fraction do you get?
Think!!!
Mr. Kamanzi came back home from Kigali with 24 apples. He decided to
share all the apples between his two sons Ted and Ronald. Ted was given
a quarter of a half of the apples and Ronald was given a half of a quarter ofthe apples. Which son got more apples?
Real Life Problems involving Fractions
4.6 Multiplication of Fractions by Whole Numbers
Activity 4.10
Get 8 bottle topsArrange them into four equal groups
What is a quarter of eight bottle tops? Use your arrangement to get the quarter of 8.

4.7 Multiplication of Fractions by Fractions
Solution
Two fractions can be multiplied together using a fraction grid.(a) Draw a rectangle as shown below.
(b) Separate the rectangle into three equal parts using two vertical lines.
(c) Shade two of these parts. The shaded area (blue) represents the
fraction 3/2 .
(d) Now divide the rectangle into four equal parts using three horizontal lines.
(e) Shade three of these parts to represent 4/3 .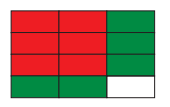
(f) Now count the total number of parts in the rectangle. You will find 12 parts.
(g) Count the number of parts that have been double shaded. There are
6 out of 12 parts which are double shaded. (This is represented by the red parts)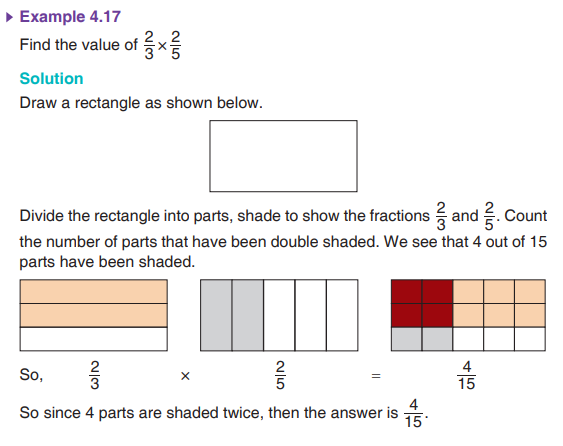
Exercise 4.7Let us multiply the fractions below and reduce them to their simplest form:
4.8 Division of Fractions by Whole Numbers
To divide a fraction by a whole number:
Step 1: Multiply the denominator by the whole number.Step 2: Simplify the fraction where necessary.
Real Life Problems involving Fraction
Example 4.19How many half litre bottles can be filled by a twenty litres jerrycan of water?
Assessment Exercise
1. In the following diagrams, white parts are not shaded. The coloured
parts are shaded. Count the shaded parts carefully and write down thefraction shown by the shaded part (s).
Internet ResourceFor more online support visit www.math-play.com/fractions
