General
UNIT 2:Positive and Negative Integers
Key Unit Competence
A learner should be able to solve problems related to comparing, ordering and
finding distance between negative and positive integers.
Attitudes and values
Appreciate the importance of using positive and negative numbers in practical
contexts.
2.1 Integer
An integer is a number with no fractional part. Integer include all the whole
numbers along with negative numbers.We represent the integers on a number line as follows:
A set of integers includes:
1. All counting numbers (1, 2, 3, 4, 5, 6, 7, ………. 100, ..)
2. Zero {0}
3. And the negatives of all the counting numbers (–1,–2,–3,–4,–5….)
Therefore, the set of integers is (……, –3, –2, –1, 0, +1, +2, +3, …..)
Integers are made up of negative numbers, zero and positive numbers. ‘Zero’is neither positive nor negative.
Activity 2.1
In this class activity, you will discuss positive and negative numbers with your
group members.
You should discuss positive and negative numbers in relation to the following:
(i) Falling into a hole and climbing a tree, what can be the position of zero?
(ii) Profit and loss in business, what is negative and what is positive?
(iii) Sinking into water and rising above earth, what is the position of zero?(iv) Promotion and demotion at work place, what is compared to positive event?
2.2 Explaining Integers
• If I have no money at all, then I can say that I
have ‘0’ money.
• If I have been given some 50 Frw, then I can say
I have some money.
• If I have lost 100, then I can say that I have a
shortage of 100 Frw.
• If a stone is dropped into a pit which is 10 metres
deep, then from the ground level the stone is at
–10 m from the earth surface.Example 2.1• A plane flying above our school at a height of500 m is +500 m above the school.
Study the diagram below and use integers to estimate the position of thefollowing objects from the earth surface.Solution
(a) The position of the plane is +40 m.
(b) The position of the balloon is +35 m.
(c) The position of the ball is +10 m.
(d) The position of the ground is 0 m.
(e) The position of the fish is –5 m.
(f) The position of the stone is –15 m.
Exercise 2.1
Explain and illustrate these expressions using integers:
(a) A pupil got no mark in a Mathematics test _________.
(b) A team scored two points in a game _________ .
(c) A pupil climbed a tree 10 m tall _________ .
(d) My coin fell to the bottom of a swimming pool 2 m deep ______ .
(e) A shopkeeper made a profit of 2 000 Frw _______ .
(f) A shoeseller made a loss of 300 Frw_______ .
2.3 Number Line
A number line is a horizontal line drawn with integers marked along its length.
Positive numbers are marked and written on the right hand side of zero and
negative numbers are marked and written on the left hand side of the zero markas shown below:
• Positive numbers are written with a plus (+) sign in front of them. They may
also be written without any sign in front, e.g. +5 = 5.
• Negative numbers are written with a minus (–) sign in front of them, e.g. –4.
The Temperature ScaleThe temperature is a degree of hotness or coldness of an object.
The temperature of an object is measured using a thermometer.
• The temperature of freezing water is 0°C.
• The temperature of boiling water is 100°C.
• The temperature of a normal person is about 37°C.
The temperature of an object below 0°C is negative. For instance,temperature in the Antarctica can reach as low as –89.2˚C
2.4 The inverse or opposite of an integer
The opposite or inverse of an integer has the same absolute value but with
an opposite sign.
The inverse of +1 is –1. The inverse of +5 is –5.
The inverse of –2 is +2. The inverse of –6 is +6.
The inverse of –3 is +3. The inverse of +7 is –7 and so on.
The inverse property of an integer
The inverse property of integers states that any number added to its inverse
equals to zero. Example: +5 +(-5) = 0
Exercise 2.2
1. Draw a number line. Mark all the integers from –10 to +10.
(a) Which integer is 4 steps to the right of +4?
(b) Which integer is 5 steps to the left of 0?
(c) An integer is 6 steps to the left of 1. What is this integer?
(d) If you are at zero (0) and you move 9 steps in the negative direction,
where will you be on the number line?
(e) An insect moves from -6 to +6. How many steps has it moved?
2. Verify the following:
(a) (+1) + (–1) = 0 (b) (–88) + (+88) = 0
(c) (+100) + (–100) = 0 (d) (+6) + (–6) = 0
3. Name the inverse of each of the following integers:
(a) +12 (b) + 45 (c) –34 (d) –20 (e) –240 (f) –500
2.5 Position of Integers on the Number Line
When locating integers on the number line, we need to take great care of the
direction in which we are moving. We need to establish a system that we will
follow whenever we are locating positions of integers on the number line.
• Our reference point is the zero (0) mark.
• An addition (+) operation means we move towards the right of 0.
• A subtraction (–) operation means we move towards the left of 0.
• We can imagine our face to represent the positive and the back of our
heads to represent the negative.
• For positive integers, we move forwards.
• For negative integers, we move backwards.
Activity 2.2
In this activity, you will need the following materials for your class:
Long string (about 10 m), cotton thread, manila paper of different colours
(red, green and yellow), a pair of scissor, two 6 cm nails, hammer, large
cardboard box and a black marker pen.
(i) Using a hammer, fix two nails into the opposite walls of the classroom.
(ii) Make loops on the string and tie the string on the nails across the
classroom.
(iii) Cut about 10 pieces of red manila papers, 10 pieces of green manila
papers and 1 piece of yellow manila paper (each paper should be
about 15 cm by 15 cm).
(iv) The teacher will guide you to write integers from –10 to +10 on the 21
pieces of manila papers. The red papers should be used for negative
integers, yellow for zero and green for positive integers.
(v) Each pupil picks a cardboard from the box at random, makes a small
hole in the paper and ties it with about 30 cm of cotton thread.
(vi) The pupils will stand in groups according to the colour of papers they
have picked. There is only one pupil with a yellow paper on which 0 is
written.
(vii) The pupil with the yellow paper ties his/her paper to hang exactly in the
middle of the string.
(viii) The other pupils also hang their papers on the correct side of the yellowpaper and at the correct positions.
Activity 2.3
(i) Your teacher will take you to a large play area such as a field.
(ii) Using dry sand, ash or any suitable material, draw a number line on the
ground and mark integers on it so that each pupil has a point to stand on
the number line. The distance between the integers can be about 60 cm.
(iii) Write negative integers on the red papers, 0 on the yellow paper and
positive on the green papers.
(iv) Pick the papers at random and tie a loop on the paper so that you are
able to wear it around your neck.
(v) Move to the position on the number line which has the same number on
your card.
(vi) During this activity, your name is the number that you are wearing on
your neck. Listen carefully as the teacher calls your “name” and follow the
instructions well.
(vii) Everyone should be able to know how far he/she has moved and in whichdirection (positive or negative) he/she has moved.
2.6 Distance between two integers
1. Two integers on the same side of zero:
The magnitude of –3 is 3 and the magnitude of +3 is also 3.Magnitude of a number is the distance from 0 to that number.
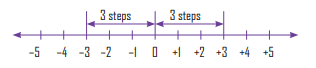
If two numbers are on the same side of zero, the difference between them
is the difference of their magnitudes.
Example 2.2
What is the distance between the following integers on the number line?
(a) + 2 and +10 (b) 0 and +15 (c) –3 and –6 (d) –7 and –2
Solution
(a) Magnitude of +2 = 2 and magnitude of +10 = 10.
so, distance between +2 and +10 = 10 – 2 = 8 steps
(b) In the same way, distance between 0 and +15 = 15 – 0 = 15 steps.
(c) Magnitude of –3 = 3 and magnitude of –6 = 6. So the distance between
–3 and –6 = 6 – 3 = 3 steps.
(d) Distance between –7 and –2 = 7 – 2 = 5 steps.
2. Two integers on opposite sides of 0 on the number line:
If two numbers are on opposite sides of 0 on the number line, the distance
between them is the sum of the magnitudes of the two numbers.
Example 2.3
What is the distance between the following points on the number line?
(a) –5 and +7 (b) –10 and +10
Solution
Distance between – 5 and +7 = 5 steps + 7 steps = 12 steps.
(b) Two numbers on opposite side of zero
magnitude of –10 is 10 and the magnitude of +10 is also 10.
So, the distance between –10 and +10 = 10 + 10 = 20 steps.
Exercise 2.3
Without drawing a number line, state the distance between the following
points on the number line;
(a) 0 and +3 (b) 0 and –3 (c) –2 and +2 (d) –1 and +1
2.7 Comparing integers and Ordering integers
• On a number line integers are always in order from the smallest to the
biggest.
• If you touch two integers at a time, the one to the left is always smaller and
the one to the right is always bigger.
• Any integer is always bigger than the one to its left on the number line.
• Any integer is always smaller than the one to its right on the number line
10 is less than –9 –7 is less than –4 –2 is less than 0
1 is less than 6 +6 is less than +10 0 is greater than –4
+3 is greater than –10 +1 is greater than –1
Example 2.5
Arrange +1, –3, –10, –2, –4, 0, +5 in order starting with the smallest to the
biggest (ascending order)
SolutionWe draw the number line and show the positions of the integers.
Order from the smallest to biggest = –10, –4, –3, –2, 0, +1, +5.
Assessment Exercise
1. Show these expressions using integers:
(a) 3 metres below the ground _________ .
(b) 5 steps forward ________ .
(c) 10 steps backward ________ .
2. Name the inverse of each of the following integers:
(a) –5 890 (b) +100 000 (c) –20 000
3. Without drawing a number line, state the distance between the following
points on the number line;
(a) +3 and –1 (b) –2 and +10 (c) –10 and +10
(d) –10 and –6
4. Arrange these integers from biggest to smallest (descending order)
–3, –7, 0, +4, –13, –31, +13, +31, –301, +310, +301.
5. Arrange these integers from the smallest to biggest (ascending order)
–8, –5, 3, 2, 0, +5, 6, 8, 1Think!!!
A chameleon wants to move from point A to point B, 10 metres apart. It
walks in a very funny way such that within 1 minute, it moves 3 metres
forward followed by 1 metre backward. How long does the chameleon take
to complete its journey to point B?
