• General

    ◄UNIT 15:2D Shapes and their PropertiesUNIT 17:Elementary Statistics►

    UNIT 16:Area and Perimeter of 2D Shapes

    • UNIT 16:Area and Perimeter of 2D Shapes

      Key unit competence
      By the end of this unit, a learner should be able to use area of rectangle to 
      determine the area of a triangle and other shapes.

      Attitudes and values
      Appreciate that the relationship between area and perimeter.

      16.1 Area
      Area is defined as the amount of space inside the boundary of a flat 
      (2-Dimensional) object such as triangle, square, circle etc.

      The area of a closed figure is the measure of the surface enclosed by it.

      16.2 Area of Rectangle
      Activity 16.1
      In this class activity, you will determine the area of a rectangle by counting the 
      number of square grids in the rectangle.
      1. Draw a rectangle of length 6 cm and width 4 cm on a graph paper.
      2. Divide the rectangle into grids by dividing the length into 6 equal parts 
      and width into 4 equal parts.
      3. Count the total number of squares formed in the rectangle, i.e., 24. This 
      is equal to the area of the rectangle.
      4. Now, 6 × 4 = 24 which is equal to the area of rectangle.

      5. Thus, we find the area of rectangle = length × width

      Example 16.1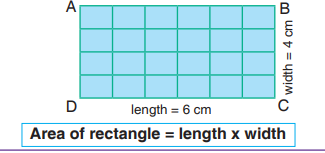
      A rectangular football field measures 100 m by 70 m. What is the area of 
      the field?
      Solution
      Area = length x width = 100 m x 70 m = 7 000 m2.

      16.3 Area of a Square
      As we have seen in above activity that area of rectangle is length × width. Area 
      of square is defined as, the number of square units it takes to completely fill a 

      square. In square all four sides are equal. So, area of square is length × length.

      M

      Example 16.2
      A piece of land is in the form of a square. Its side is 200 m long. What is its 
      area?

      Solution
      Area of square= side x side

      Area of square= 200 m x 200 m= 40 000 m2

      16.4 Area of Triangle

      Activity 16.2

      In this class activity, you are going to find the area of a triangle from a rectangle.
      1. Draw a rectangle of length 8 cm by 4 cm on a graph paper. 
      2. Divide this rectangle into thirty two 1 cm2grids. The area of this rectangle is 32 cm2.
      3. Cut out this rectangle using a pair of scissors along one of its diagonal.
      4. This forms two equal triangles.
      5. What is the area of each triangle?
      6. How does the area of the triangle relate to the area of the rectangle? Now, 

           let’s look at the formula.

      M

      In the figure above, PSRQ is a rectangle with length 8 cm and width 4 cm. SQR 

      is a triangle with base 8 cm and height 4 cm.

      M

      The height of a triangle makes an angle of 90˚ with the base.

      Example 16.3
      A triangle has an area of 100 cm2 and a base of 10 cm. What is the height 
      of the triangle?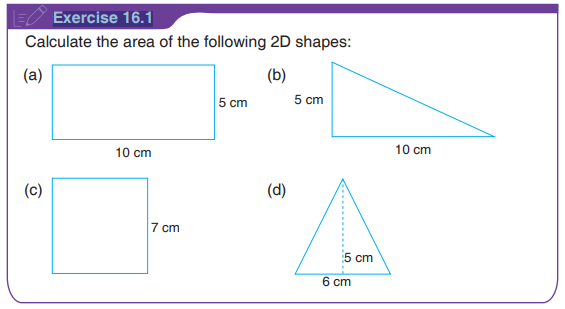

      M

      16.6 Area of Parallelogram

      Activity 16.3
      Consider the parallelogram JHFE of base 8 cm, height 4 cm and width 5 cm as 
      shown in the diagram below:
      D
      If we cut the parallelogram along the height, we get the shaded part EJI. We 
      can paste the shaded part to the right hand side of HF. 
      The new figure formed is EIGF as shown in the figure below:


      The figure EIGF is a rectangle of length 8 cm and width 4 cm.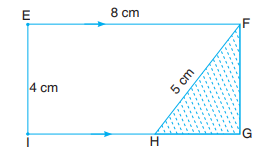

      So, the area of the parallelogram EJHF = area of rectangle EIGF.

      F

      Note: The height of the parallelogram is perpendicular to the base.

      Area of the given parallelogram = 8 cm x 4 cm = 32 cm2

      Example 16.4

      Find the area of the parallelogram given below: 

      Y

      Area of the parallelogram = base × height
      Base of the parallelogram = 20 cm
      Height of the parallelogram = 8 cm
      = 20 × 8 

      = 160 cm2

      Activity 16.4
      In pairs, 
      • Draw a triangle and a rhombus whose perimeter is 36cm.

      • Draw a triangle and a rhombus whose area is 36cm2

      16.7 Area of a Rhombus
      A rhombus is a special type of parallelogram in which all the sides are equal 
      and the diagonals bisect each other at right angle. The area of a rhombus can 

      be given by the formula:

      T

      T

      AC and DB are diagonals. AC = 2b and DB = 2a. The two diagonals divide the 
      rhombus into four equal right angled triangles. Each right angled triangle has a 

      base b and height a.

      Y

      Example 16.5
      A rhombus has diagonals of lengths 20 cm and 32 cm as shown below. 

      Calculate the area of the rhombus.

      T

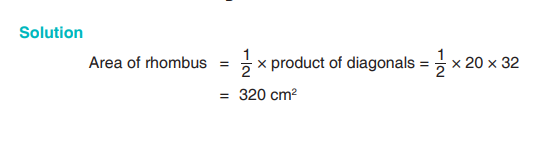
      Activity 16.5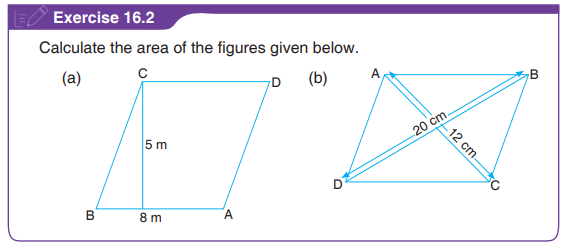
      • Use a squared paper to draw a rectangle of length 6 units and height 4 units. 
      • Use a squared paper to draw a right angled triangle of base 3cm and height 4cm.
      • By counting the number of squares, find the area of the rectangle and the 
      area of the triangle.
      • Join the two shapes together to form one figure. What is the name of this 
      new figure formed?
      • By counting the number of squares, find the area of the new figure formed.
      • What have you learnt from this activity? Discuss your finding with your teacher.

      16.8 Area of a Trapezium
      A trapezium can be divided into two triangles. This makes it easy for the area 

      to be calculated.

      J

      ADCB is a trapezium. Line DB is a diagonal of the trapezium. It divides the 
      trapezium into two triangles namely ADB and DCB.

      Area of trapezium = Area of triangle ADB + Area of triangle DCB

      Example 16.6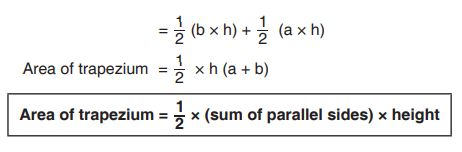

      Find the area of the trapezium given below. 

      Y

      16.9 Perimeter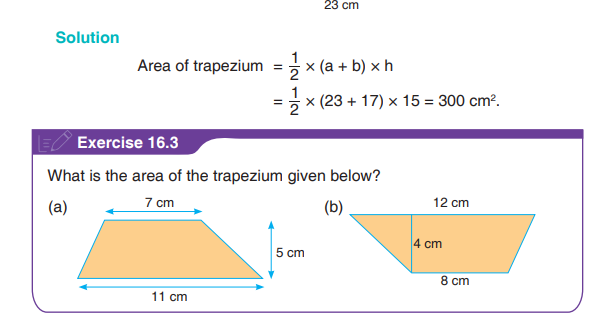

      The perimeter of a closed figure is the total distance around the given figure. 

      Activity 16.6
      In this class activity, you will use straws to draw a triangle and you will find its perimeter.
      E
      (a) You are provided with ordinary drinking straws.
      (b) Cut three straws such that each one has a length of 8 cm.
      (c) Join these straws to form a triangle.

      (d) What is the perimeter of the triangle?

      Activity 16.7
      In this activity, you are going to design a square, rectangle, rhombus, 
      parallelogram and trapezium whose perimeter is 24 cm. You can use straws to 
      design these shapes. 

      To design a rectangle or parallelogram, you need 
      – 2 straws each of 4 cm long and 

      – 2 straws each of 8 cm long

      So, perimeter = 2 × 4 + 2 × 8
       = 2 (4 + 8)
       = 2 × 12
       = 24 cm
      Therefore, Perimeter of rectangle = 2 (length + width)
       Perimeter of parallelogram = 2 (length + width)
      Now, to design a square or rhombus, you need
      – 4 straws each of 6 cm long 

                                   So, Perimeter = 6 + 6 + 6 + 6

                                                                            = 4 × 6 = 24 cm
      Therefore,      Perimeter of square = 4 × side
       Perimeter of rhombus = 4 × side
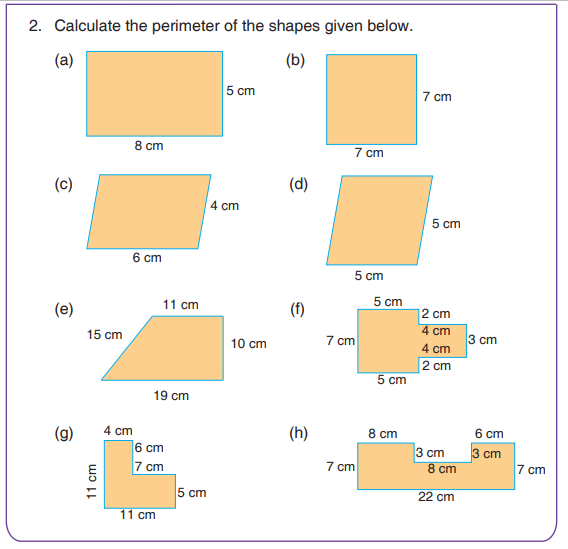
      Since, the sides of a trapezium are different in length.

      Therefore,     Perimeter of trapezium = sum of all the sides.

      Example 16.7

      Find the perimeter of the rectangle and parallelogram given below:

      Solution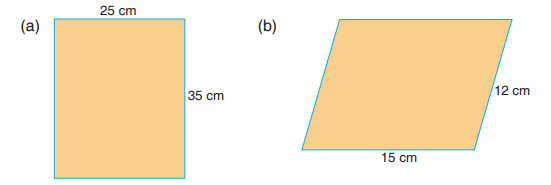
      (a) Perimeter of rectangle = 2(25 + 35) 
                                                            = 120 cm
      (b) Perimeter of parallelogram = 2 (15 + 12) 

                                                                      = 54 cm

      Example 16.8

      Find the perimeter of the square and rhombus given below. 

      M

      Solution
      (a) Perimeter of square = 4 × side = 4 × 8 = 32 cm

      (b) Perimeter of rhombus = 4 × side = 4 × 6 = 24 cm

      Example 16.9

      Find the perimeter of the given trapezium.

      Solution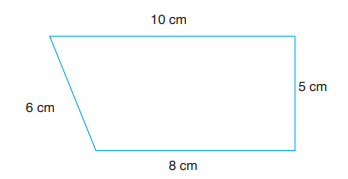

                  Perimeter of trapezium = 10 + 5 + 8 + 6 = 29 cm

      Example 16.10

      Calculate the perimeter of the shape given below.

      M

      Solution
      Perimeter = 30 mm + 9 mm + 6 mm + 7 mm + 5 mm + 8 mm + 15 mm

                                                                                                             + 14 mm = 94 mm

      N

      Internet Resource

      visit:http://www.sheppardsoftware.com/math.htm

      ◄UNIT 15:2D Shapes and their PropertiesUNIT 17:Elementary Statistics►