General
UNIT 14:Types of Lines and Angles
Key unit competence
By the end of this topic, a learner should be able to identify types of lines and
angles and use a protractor to measure angles.
Geometry is a branch of mathematics which deals with the measurement of
shape and size of different figures.
Attitudes and values
Appreciate the importance of lines and angles in daily activities, being confident
and accurate when measuring lines and angles.
14.1 Lines
A line is a long straight mark which joins any two points. It has no end points. Aline has no thickness and extends forever.
• Parallel lines do not meet at all.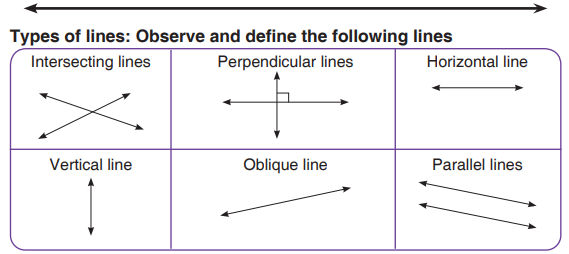
• Intersecting lines are lines which meet at a point.• Perpendicular lines make an angle of 90˚.
Activity 14.1
Using a geometry set, draw the following lines on a manila paper.
• 2 horizontal lines • 2 vertical lines
• 2 intersecting lines • 2 perpendicular lines
• 2 oblique lines not cutting each other • 3 parallel linesLabel the lines according to their names.
14.2 Measuring the length of a line segmentA pair of compass and a ruler can be used to measure the length of line segment.
Activity: Consider the line segment AB shown in the diagram below.
Place one arm of the compass at point A.
Extend the second arm of the compass up to point B.
Transfer the compass on to a ruler as shown below.The length of the line segment can be read from the ruler.
Example 14.1(a) Railway track is an example of parallel lines.
(b) Aluminium wires in electric poles are examples of parallel lines.
14.3 Angles
An angle is the measure of the amount of turn from one direction to another. An
angle is the measure of the space between two intersecting lines. We use an
anticlockwise direction.
The unit for measuring an angle is known as ‘degree’. A degree is written
in short as (°). If you draw a circle and divide the circle into equal parts using
180 diameters, then the amount of turn from one diameter to the other diameteris 1 degree or 1˚.
Activity 14.2
Mark a point ‘X’ at the centre of the line segment AB. Use a protractor to measure
AXB. What will be the size of angle AXB?
14.4. Types of angles
(a) Acute angle: This is an angle which is greater than 0˚ but less than 90˚.Examples of acute angles are 30˚ and 72˚.
(b) Right angle: This is an angle which is formed by intersection of twostraight perpendicular lines. The measure of a right angle is 90˚.
(c) Obtuse angle: This is an angle which is greater than 90˚ but less than180˚. Example of obtuse angle is 135˚.
(d) Straight angle: This is the angle whose value is exactly 180˚. A straight
angle is formed when two straight lines meet end to end and form onestraight line.
(e) Reflex angle: This is an angle whose value is greater than 180˚ but lessthan 360˚. Examples of reflex angles are 339˚ and 285˚.
(f) Complementary angles: These are two angles which add up to 90˚. For
example 27˚ and 63˚ are complementary angles as 27˚ + 63˚ = 90˚. Wecan say, the complement of 27˚ is 63˚ and the complement of 63˚ is 27˚.
(g) Supplementary angles: These are the angles which add up to 180˚. For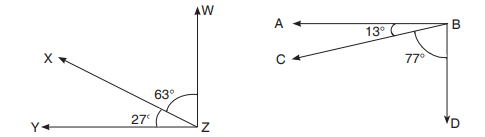
example 90˚ and 90˚ have a sum of 180˚. So, they are supplementary
angles. Other examples of supplementary angles are 121˚ and 59˚, 31˚and 149˚.
Activity 14.3
1. Do you see any objects that form right angles in your classroom? Name them.2. Compare your list with your classmates.
Exercise 14.2
2. Using Set squares and a Ruler, draw perpendicular lines to the givenlines below.
14.5 Measuring Angles
The instrument used for measuring an angle is called a protractor.
The above protractor can be used to measure angles from 0° up to 180°.
Angles can be measured either in a clockwise sense or anti-clockwise sense
depending on where the angle is drawn.
• When measuring the angle between two intersecting lines, we place the
protractor so that its centre is at the point of intersection of the two lines.
• We adjust the protractor so that the horizontal line on it runs along one of
the lines.
• We measure the angle by counting the number of degrees from one line
to the next line.
Measure the following angles with the help of ProtractorExample 14.2
SolutionThe acute angle between the two lines = 63˚.
Example 14.3
Solution
The angle between the two lines is obtuse. We measure it by using theanticlockwise scale of the protractor. The size of this angle is 121˚.
Example 14.4
Solution
The angle between the two lines is measured using the anti-clockwise scaleand its value is 175˚.
Example 14.5
Solution
The angle between the two lines = 130° – 40° = 90°.Alternatively, the angle = 140° – 50° = 90°.
Activity 14.4
In this activity you will make your own protractor.
You will need the following materials:
• Manila paper
• Pencil
• Markers
• Pair of scissors
• Math set
• Paper glue
• Blackboard protractor
1. Place the Manila paper on a large table and spread it flat on the table.
2. Place the blackboard protractor in the middle of the Manila paper.
3. Trace the outline of the protractor on the Manila paper using a pencil.
4. Draw short marks on the manila paper corresponding to the following
angles: 0°, 10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°, 90°, 100°, 110°,
120°, 130°, 140°, 150°, 160°, 170° and 180°.
5. Remove the protractor and mark a point which represents the point
where all lines meet on a protractor.
6. Redraw the lines using a marker.
7. Carefully cut out your Manila protractor using a pair of scissor or
any other useful tool.
8. Cut another piece of Manila paper which is identical to your Manila
protractor. Use paper glue to attach this Manila paper under your
Manila protractor.
You now have a strong Manila protractor.
9. Use your Manila paper to measure different angles in your class
room including the angles at the edges of your table, book etc.Assessment Exercise
3. In the figure below, the protractor is used to measure many angles at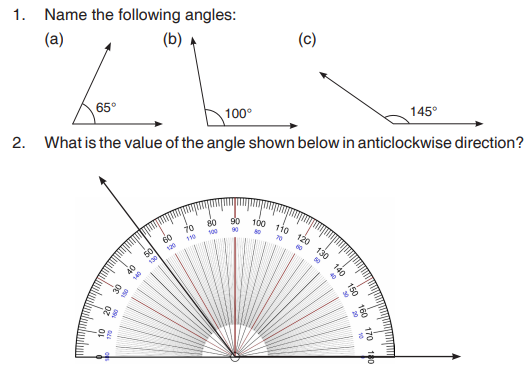
once. Find the angle between;
(a) Line A and line F
(b) Line B and line C
(c) Line D and line A(d) Line B and line E
4. Here are some angles marked using letters a, b, c, d, e and f.Using a protractor, measure and record the angles in degrees.

5. Measure the length of the following line segments by the help of ruler.
