General
UNIT 12:Number Patterns
Key unit competence
A learner should be able to describe and generate number patterns.
Attitudes and values
Appreciate the importance of orderliness in daily life. Learners should be made
to realise the need for orderliness in places such as bus, park, banks, markets,
schools, hospitals and other places in daily life situations.
12.1 What is a Number Pattern?
A list of numbers which form a sequence is called a number pattern.
Ascending order (increasing order)
The term ascending means ‘going up’. While ordering integers in ascending
order, we arrange integers from smallest to the largest.
For example: 1, 3, 6, 8, 9, 23, 56, 400, .....are arranged in ascending order.
Descending order (decreasing order)
The term descending means coming down. While ordering integers in
descending order, we arrange them from largest to smallest.
For example: 45 000, 340, 34, 20, 6, 2, –3, –567, .....,.....,... are arranged in
descending order.
Importance of orderliness in daily life situations
Arranging numbers in order of size helps us to compare numbers easily from agiven set of numbers.
Example 12.1
The list shown below shows the size (area) of some selected countries inthe world. (Source: www.simple.wikipedia.org)
Arrange the land areas of the different countries in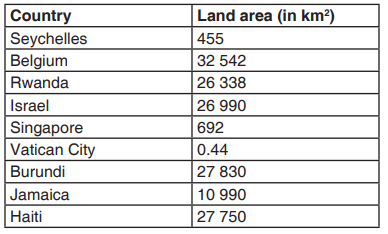
(a) ascending order
(b) descending order
Hence tell the 4th smallest country from this list.
Solution
(a) Ascending order: 0.44, 455, 692, 10 990, 26 338, 26 990, 27 750,
27 830, 32 542.
(b) Descending order: 32 542, 27 830, 27 750, 26 990, 26 338, 10 990, 692,
455, 0.44.
The 4th smallest country has an area of 10 990 km2
. It is the 4th from the left
on the ascending list and it is the 4th from the right on the descending list.
So the answer is Jamaica.
Example 12.2
For example, the figure below shows the number pattern –10, –6, –2, ......,....., .....,
This pattern starts with – 10 and jumps by 4 every time.
Example 12.3Dots like these ones below can also be used to show number patterns.
The number pattern formed is 1, 3, 6, 10, 15,.......This pattern starts with 1 and then you add 2, 3, 4, 5 and so on.
Activity 12.1
Each picture has a number on its face.Can you workout the number patterns and fill the missing numbers?
Compare your answers with the answers of your classmates from the othergroups.
Exercise 12.1
1. Complete the number pattern.
(a) 4, 8, 12, 16, 20, 24, ________
(b) 1, 4, 8, 13, ________
(c) 50, 42, 35, 29, ________
(d) 100, 105, 115, 130, 150, ________
(e) 1, 2, 4, 7, ________, 16
2. The list shown below shows the marks obtained (out of 100) by the
students of class 4 in a maths test:
59, 56, 79, 82, 90, 53, 19, 54, 65, 88, 93, 58, 63, 52, 75.
Arrange the data in the ascending order and find out the third highest mark.12.2 Progression or Series
There are two types of series or progressions namely; Arithmetic series andGeometric series.
12.2.1 Arithmetic Progression
In an arithmetic progression or arithmetic series, the sequence of numbers are
such that the difference between the consecutive terms is constant.
For example: The sequence 3, 5, 7, 9, 11, 13, 15 is an arithmetic progressionwith a common difference of 2.
Activity 12.2
What you need
• 6 empty chalk boxes, labelled A, B, C, D, E and F.
• At least 100 bean seeds.
• Marker pens.
• Manila paper.
What to do
(i) Place one bean seed in box A.
(ii) Record the number of bean seeds in box A on a manila paper.
(iii) Remove the bean seed in box A and transfer it to box B. Add two more
bean seeds in box B.
(iv) Count the number of bean seeds in box B and record the number on the manila paper.
(v) Remove all the bean seeds in box B and place them in box C. Add two more bean seeds in box C.
(vi) Count the number of bean seeds in box C and record the number on a manila paper.
(vii) By adding two bean seeds each time, repeat the procedures for boxes
D, E and F. Record the number of beans in the boxes D, E and F on the manila paper.
The numbers on the manila paper forms an Arithmetic progression with a
first term of 1 and common difference of 2.Use the bean seeds to form other Arithmetic Progressions.
Exercise 12.2
Rewrite the numbers as shown in your exercise book and write down the
next two numbers in the following sequences:
(a) 70, 69, 68, 67, 66, 65, 64, 63,......,......,
(b) 20, 17, 14, 11, 8, 5,......,.......,
(c) 10, 20, 30, 40, 50, 60,.......,.......,(d) 10, 13, 16, 19, 22, 25,......,.......,
12.2.2 Geometric Progression
A geometric progression is a sequence of numbers in which the next number
is obtained by multiplying or dividing the previous number by a fixed number.
Examples of a geometric progression :
40, 20, 10, 5. The first number is 40. The next number of the sequence is got
by dividing by 2 or multiplying by 2/1 .
1, 2, 4, 8, 16, 32, 64, 128,....... The first number is 1 and the next number is gotby multiplying the previous number by 2.
Assessment Exercise
1. Complete the number pattern:
(a) 4, 7, 12, 19, 28, ________ (b) 20, 23, 28, 35, ________
(c) 1, 7, 18, 34, ________
2. Rewrite the numbers as shown in your exercise book and write down
the next two numbers in the following sequences:
(a) +12, +10, +8, +6, +4, ...., ...., (b) 0, 40, 80, 120, 160, ..., ...,
3. On a modern art painting, there are 4 green dots in the first row, 12
green dots in the second row, 36 green dots in the third row, 108 green
dots in the fourth row, and 324 green dots in the fifth row. If this pattern
continues, how many green dots will there be in the sixth row?
4. A restaurant used 2 onions on Friday, 4 onions on Saturday, 6 onions on
Sunday, 8 onions on Monday, and 10 onions on Tuesday. If this sequence
continues, how many onions will the restaurant use on Wednesday?
5. While at work, Mimi is putting papers into folders. She puts 3 papers in
the first folder, 6 papers in the second folder, 9 papers in the third folder,
12 papers in the fourth folder, and 15 papers in the fifth folder. If thissequence continues, how many papers will Mimi put in the sixth folder?
Internet Resource
For more online support visit:http://www.kidsites.com/
