General
UNIT 1:Mathematical Operations on Whole Numbers up to 100,000
Key unit competence
By the end of this unit, a learner should be able to write, compare and calculate
whole numbers up to 100,000.
Attitude and Values
• develop personal confidence in the use of numbers.
• appreciate the importance of addition, subtraction, division and multiplication
of numbers in real life.
• appreciate the need for manipulating numbers.
1.0 Introduction to the Number Systems
A number is a mathematical way of representing how many, how far, how long
or how much a quantity is.
A number (numeral) system or system of numeration is a writing system for
expressing numbers using digits or other symbols in a consistent manner.Three of the most commonly used number systems are:
1. The Hindu-Arabic Numeral System.
2. The Roman Numeral System.
3. The Chinese Numeral System.
We generally use arabic numeral system.
The Hindu-Arabic Numeral System
This numeration system uses ten digits; 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. These
digits can be used to form any number. For example, the digits 3, 9, 7 can be
used to form numbers 397, 379, 973, 937, 793 and 739.
Natural Numbers (Counting Numbers)
When a child is learning to count, he/she says “one, two, three, four... .” Thisset of numbers is called natural numbers or counting numbers
Whole numbersWhole numbers is a set of counting (natural) numbers including zero.
Forming numerals from digits
The digits 0 to 9 are used to form different numbers depending on how you
arrange the digits.
Example 1.1
Write down any 2-digit number formed by the digits 4, 6, 7, 0, 1.
Solution
Pick any two digits given above.
For example
First number = 46
Second number = 67
Other numbers are 40, 10, 70, 71, 76, 61, etc.
Example 1.2
Discuss and give the smallest number or numeral that can be obtained
from the digits 8, 9, 6, 1.
Solution
First, arrange the digits in ascending order (from smallest to biggest).
In ascending order we get 1, 6, 8, 9.
Therefore, the smallest number is 1 689.
Example 1.3Find the biggest number that can be formed from the digits 1, 3, 5, 9, 4?
Solution
Arrange the digits in descending order (from biggest to smallest).
In descending order, we get 9, 5, 4, 3, 1.
Therefore, the biggest number formed is 95 431.
Activity 1.1
In this class activity, you will form numbers from given digits.
(i) Arrange five blank flash cards provided on your table.
(ii) Write the digits 5, 2, 4, 1 and 3 on each flash card.
(iii) Form a 5-digit number starting with 5.
(iv) Form a 5-digit number starting with 2.
(v) Form a 5-digit number starting with 4.
(vi) Form a 5-digit number starting with 1.
(vii) Form a 5-digit number starting with 3.
(viii) Arrange the formed numbers in ascending order.
Exercise 1.1
Given the 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
You can use a digit only once while answering the questions below:
(a) Use the digits above to form all 3-digit numbers beginning with 3 and
ending with 9. {An example is 329}.
(b) What is the largest 2-digit number that can be formed from these
digits?
(c) What is the smallest 2-digit number that can be formed from these
digits?
1.1 Reading and writing numbers in words and in figures
Use one zero ‘0’ to write a ten, two zeroes ‘00’ to write a hundred, three zeroes
‘000’ to write a thousand. For example:
10 = Ten.
30 = Thirty.
100 = One hundred.
370 = Three hundred seventy.
1 000 = One thousand.
8 900 = Eight thousand nine hundred.
50 000 = Fifty thousand.
99 990 = Ninety-nine thousand nine hundred ninety.
100 000 = One hundred thousand.
Activity 1.2
In this class activity, you will play a game of matching numbers.
(i) Divide yourselves into 2 groups: Group A and B.
(ii) Arrange yourselves in a straight line and sit in 2 groups by facing each
other. The pupil seated opposite to you is your opponent.
(iii) Write one large number in words and one large number in figures on
the two manila cards.
(iv) Take turns in playing the game by showing your opponent the numbers
you have written on the cards. He/she should say the number aloud or
write the number on the blackboard. The teacher together with the rest
of the pupils will act as judges.
(v) Correct answer = 3 marks and wrong answer = 0 marks. Add up the
marks for your group and see which group wins.
Example 1.4
Write the following numbers in words:
(a) 97 642
(b) 10 002
(c) 999
(d) 90 001
(e) 1 704
Solution
(a) 97 642 = Ninety-seven thousand six hundred forty-two.
(b) 10 002 = Ten thousand two.
(c) 999 = Nine hundred ninety-nine
(d) 90 001 = Ninety thousand one.(e) 1 704 = One thousand seven hundred four.
Example 1.5
Write the following in figures:
(a) Ninety-nine.
(b) One hundred ninety-nine.
(c) Seven hundred five.
(d) Six hundred fifty.
(e) Twelve thousand five hundred.
(f) Eighty thousand.
(g) Forty thousand one.One hundred thousand.
(i) Nine hundred ninety-seven.
(j) Eleven thousand one hundred eleven.
Solution
Exercise 1.2
1. Read and write the following numbers in words:
(a) 111 (b) 1 011 (c) 54 700
(d) 1 000 (e) 78 999 (f) 15 000
2. Write the following numbers in figures.
(a) Nineteen (b) Ninety (c) Ninety-nine
(d) Nine hundred ninety-nine. (e) Five hundred one.(f) Three thousand one.
1.2. Place Values of Whole Numbers
Place values help us to show the position of a given digit in a number.
Example 1.6Find the value of each digit in 79 846
Example 1.7
Use the table below to work out the value of each digit in the number 43 275.
Solution
Activity 1.3Get an abacus frame
(i) Place 3 beads on the ten thousand’s spike, 4
on the thousand’s spike, 2 on the hundreds
spike, 7 on the ten’s spike and 1 on the ones
spike.(ii) Read the number you have formed.
Exercise 1.3
Write down the place values of the underlined digits in the given numbers:
1. 3 289 3. 87 204 5. 89 434 7. 22 343 9. 29 3212. 94 483 4. 8 724 6. 4 927 8. 88 287
Expanding whole numbers using place values
Example 1.8
Expand the following numbers:
(a) 82 645 (b) 98 067
Solution
(a) 82 645 = 80 000 + 2 000 + 600 + 40 + 5
(b) 98 067 = 90 000 + 8 000 + 60 + 7
Writing expanded numbers in short form
Example 1.9
Write the following expanded numbers in short form:
(a) 10 + 9 (b) 30 000 + 5 000(c) 30 000 + 400 + 40 + 4 (d) 90 000 + 1
Solution
Activity 1.4
Exercise 1.4
1. Write the following numbers in expanded form.
(a) 4 624 (b) 984 (c) 44 484
(d) 93 428 (e) 76 709
2. Write the following in short form.
(a) (7 × 1 000) + (3 × 100) + (8 × 10) + (3 × 1)
(b) (9 × 10 000) + (8 × 1 000) + (3 × 100) + (7 × 10) + (6 × 1)(c) (3 × 10 000) + (9 × 1 000) + (8 × 100) + (6 × 10) + (7 × 1)
1.3 Comparing Numbers
When comparing two numbers, we count the number of digits in each number.- The number with more number of digits is greater than the one with few digits.
- The number with fewer digits is smaller than the other.
- If the two numbers have equal number of digits, then we can consider the value of each digit.
the number which has greater value is greater than
than the other.
The following notations are used while comparing numbers:
< denotes ‘less than’
> denotes ‘greater than’ and
= denotes ‘equal to’.
Activity 1.5
In this class activity, you will write down the biggest number you know.
(i) Form yourselves in groups of 5 learners each.
(ii) Write down the greatest number you know on a flash card.
(iii) Compare the number you have written with the numbers your
classmates have written.
Example 1.10
Use the symbol <, >, or = to compare the following numbers and items:
(a) Four thousand and 4 × 1000 (b) 10 000 and 1 000
(c) 500 Frw and 550 Frw (d) 400 bottles and 400 bottles
Solution
(a) Four thousand is equal to 4 × 1000, because four thousand = 4 × 1000
= 4000.
(b) 10 000 > 1 000 because 10 000 has more digits than 1 000.
(c) 500 and 550 have the same number of digits. The first digit in both
numbers is 5. So, we now compare the next digits which are 0 and 5.
Since 5 > 0, therefore, 500 Frw < 550 Frw.
(d) 400 bottles = 400 bottles. The two numbers are exactly the same sothey are equal.
Think!!!
There is a three-digit number. The second digit is four times as big as the
third digit, while the first digit is three less than the second digit. What is thenumber?
1.4 Operation of numbers
1.4.1 Addition of Whole Numbers
When adding numbers, we arrange the numbers so that the ones are on the
same vertical line, the tens are also on the same vertical line and so on.Addition of Whole Numbers Without Carrying
Example 1.11
1. Evaluate 34 907+54 091
Solution
Add 375 and 8 201.
SolutionNumbers can be easily added by using an addition grid as shown below:
Exercise 1.6
1. Add the following numbers and write your answers in words:
2. Add the following numbers together:
(a) 230 and 230 (b) 21 650 and 32 146
(c) 5 and 21 454 (d) 160 and 610
3. I have three thousand Rwandan Francs and my brother has seven
thousand five hundred Rwandan Francs. How much do I and my
brother have altogether?
4. Town A has 242 cars and Town B has 424 cars. How many cars arethere in the two towns?
Addition with Carrying
When the sum of two or more numbers is more than 9, we carry as we do theaddition as shown in the example given on the next page:
Example 1.12Add 4 999 and 8 294.
Solution
• Add downwards starting from the place of ones on your right.
• A number where the sum above is a two-digit number, write the ones
and carry the tens to the next digit to the left.• So, 4 999 + 8 294 = 13 293.
Exercise 1.7
1. Add the following numbers together:
(a) 53 250 and 32 488 (b) 738 and 262
(c) 1 354 and 9 999 (d) 999 and 111
(e) 999 and 1 110
2. The data below shows the monthly amount of rainfall received by acertain country for a whole year;
(a) How much total rainfall was received between November and
December?
(b) How much rainfall was received in the first three months?
(c) Write down in words, the amount of rainfall received in the
month of May.
(d) Calculate the sum of the least and greatest amount of rainfallduring the year.
Think!!!Using only addition, how do you add eight 8s and get the number 1 000?
1.4.2 Subtraction
Subtraction without Borrowing
Just like we did with addition of numbers, we arrange numbers so that the
Ones, Tens, ... etc. are all aligned.
Example 1.13
Evaluate: 6 989 – 3 453Solution
Subtraction with Borrowing
Example 1.14Evaluate: 2 573 – 1 395
• Arrange the two numbers as we did for addition.
• In ones, 3 – 5 is not possible because 3 is less than 5. We then borrow
1 from the next digit under the tens.
• So, we borrow 1 from 7 tens and remain with 6. The one we have
borrowed becomes 10 and 10 + 3 = 13.
• Now, we subtract 5 from 13 to get 8.
• Now, in tens 6 – 9 is also impossible. So, we borrow 1 from 5 hundreds,
so, 16 – 9 = 7.
• In the hundreds column, we have 4 – 3 = 1 and in the thousands
column, we have 2 – 1 = 1.• So, 2 573 – 1 395 = 1 178.
Example 1.15
a position. We write 94 not 094.
Example 1.16
Eina has 73 567 Frw in her account and Awiza has 89 504 Frw in his
account. What is the difference between the money in Eina’s account andin Awiza’s account.
Solution
Activity 1.6
• Put 256 bean seeds in a tin box.
• Remove 75 bean seeds from the tin box.
• Count the number of seeds which remained in the tin.• How many seeds are left?

Exercise 1.8
1. Evaluate:
(a) 15 789 – 11 000 (b) 86 786 – 63 524
(c) 99 999 – 29 999 (d) 863 – 489
(e) 45 567 – 12 540 (f) 48 487 – 32 450
(g) 32 450 – 16 36054 000 – 543
(i) 65 009 – 222 (j) 90 000 – 1
2. A shirt costs 3 000 Frw and another shirt costs 1999 Frw. What is the
difference in cost of two shirts?
3. I had 304 eggs in a box, out of which 70 got broken. How many eggs
were not broken?
4. One metre of cloth costs 1 250 Frw and another cloth of 1 metre costs
2600 Frw. How much more does the another cloth cost?
5. Kayongo went to the market with 550 Frw and bought mangoes. He
was left with a balance of 120 Frw. How much did he use to buy the
mangoes?
6. By how much is 67 015 more than 67 010?
7. The distance between London City in the U.K and New York City in
USA is 5 546 km. A plane travelling from London to New York has
covered a distance of 4 509 km. What distance has to be covered by
the plane to reach New York?
8. A district had a population of 30 845 in a national census. Of these,
19 678 were females. How many males were in the district?
9. The following people had the given amounts of money on their bankaccounts
(a) What is the difference between the money in Matsiko’s account
and in Lina’s account?
(b) What is the difference of money in Mwiza’s and Peter’s accounts?
10. A town has 98 500 buildings. 70 005 of these buildings are shops. Findthe number of other types of buildings in the town.
1.4.3 Multiplication of Whole NumbersThe Multiplication Table
Example 1.17
Evaluate:
1. 23 × 2 2. 45 × 7
3. 21 × 13 4. 38 × 85
5. 782 × 3 6. 476 × 25
7. 450 × 25 8. 620 × 25Solution
Multiplication of whole numbers by 10, 100, 1 000, 10 000.
When multiplying a whole number by:
• 10, we add a zero (0) at the right hand side of end of the last digit of the
number.
• 100, we add two zeroes at the right hand side of the last digit of the number.
• 1 000, we add three zeroes at the right hand side of the last digit of the
number.
• 10 000, we add four zeroes at the right hand side of the last digit of thenumber.
This is shown in the cases below:
(a) 27 × 10 = 270
(b) 4 × 10 = 40
(c) 2 376 × 10 = 23 760
(d) 24 × 100 = 2 400
(e) 457 × 100 = 45 700
(f) 34 × 1 000 = 34 000
(g) 6 × 10 000 = 60 000
Quick Multiplication by 5:
In order to multiply a whole number by 5, you have to multiply it by 10, then
divide the product by 2.
Therefore, 280 × 5 = (280 × 10) ÷ 2
= 2800 ÷ 2 = 1400
Quick Multiplication by 100 and 1000:
In order to multiply a whole number by 100, we put two zeros on the right hand
side of that number.
Therefore, 82 × 100 = 8200.
In order to multiply a whole number by 1000, we put three zeros on the right
hand side of that number.
Therefore, 46 × 1000 = 46000.
Example 1.18
A square floor of classroom is completely covered with tiles. The length
of square room is covered by 26 tiles. Also number of tiles along its each
boundary is 26. How many tiles are there in the class room.
Solution
Number of tiles along one boundary (length) = 26
Number of tiles along another boundary (width) = 26
Total titles = 26 × 26So,
Exercise 1.9
1. Complete the multiplication table below and learn them by heart.
2. Complete the table below.
3. Work out:
(a) 164 × 6 (b) 40 × 9 9c) 78 × 7 (d) 217 × 5
(e) 450 × 5 (f) 897 × 5 (g) 575 × 3349 × 8
(i) 999 × 9 (j) 35 × 21 (k) 34 × 12 (l) 56 × 23(m) 75 × 25
55 × 60 (o) 39 × 13
Exercise 1.1
1. A rectangular floor is completely covered with tiles. There are 26 tiles
along its length and 15 tiles along its width. How many tiles are there
altogether in the room?
2. There are 10 rows of students at a school assembly. Each row has 28students. How many students are there altogether?
3. Each box contains 500 nails. How many nails are contained in 80 boxes?
4. Kigali Chalk Factory produces 90 cartons of chalk in a day. Each
carton contains 36 boxes of chalk. How many boxes of chalk does the
factory produce per day?
5. The table below shows part of Mr. and Mrs. Bitega’s wedding budget.The cost of the items is in dollars.
Complete the table and find the total cost for the different items.
1.4.4 Division
Division without A Remainder
Example 1.19
Work out the following:
(a) 48 ÷ 2 (b) 245 ÷ 5 (c) 90 ÷ 5(d) 2 170 ÷ 7 (e) 54 000 ÷ 45 (f) 108 ÷ 6
Example 1.20
Divide 5000 pens equally among 5 children.
SolutionDivide 5000 by 5
Exercise 1.11
1. Work out the following:
2. Answer the following questions:
(a) There are 340 bags of cement to be unloaded off from a lorry by
5 men working at the same rate. How many bags will each man unload?
(b) Divide 450 sweets equally among 10 pupils.
(c) The District Agriculture Officer plans to distribute 1 080 Friesian cows
to 10 farmers’ groups. How many cows will each farmers’ group get?
(d) A butcher supplies 10 kg of meat to each school. If he has 1 000 kgof meat, how many schools does he supply?
Division with a Remainder
Example 1.21
Evaluate the following:(a) 25 ÷ 4 (b) 398 ÷ 5 (c) 1 478 ÷ 12
Solution
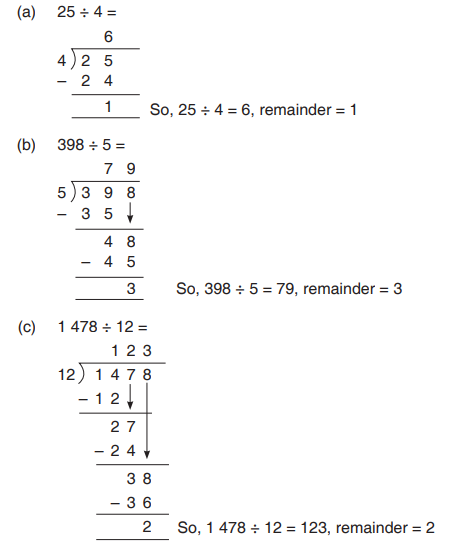
Assessment Exercise
1. What is the largest 5-digit number that can be formed from the digits
0, 3, 2, 4, 1, 5?
2. Write the following numbers in figures:
(a) Twenty-four thousand seven hundred seven.
(b) One hundred twenty-four thousand seven hundred seventy.
(c) Thirty-four thousand seven hundred seventy-seven.
3. Write the following in short form.
(a) (4 × 1 000) + (2 × 100) + (7 × 10) + (3 × 1)
(b) (5 × 10 000) + (5 × 100) + (3 × 10) + (2 × 1)
4. In a school with 888 pupils, three girls were voted for the post of head
girl of the school. The number of votes obtained by each girl is given
below:
Which girl obtained the greatest number of votes?
5. On a certain school trip to Akagera National Game Park, we counted
123 zebras, 10 buffaloes, 21 wild pigs and 14 giraffes.
(a) How many giraffes and zebras did we count?(b) How many wild animals did we count altogether in the park?
6. Fill the missing digits in the addition grids below:
7. A shopkeeper in Kimironko main market in Kigali had the followingdaily records of sales:
(a) What was the value of goods sold on Monday?
(b) What was the value of goods sold on Thursday and Friday?
(c) How much did the shopkeeper get from Monday to Wednesday?
8. A school water tank holds 100 000 litres of water. P5 pupils use 12 500
litres and P6 pupils use 67 500 litres. How much water remains in the
tank?9. By how much is 67 999 greater than 45 908?
10. Work out:
(a) 217 × 11 (b) 234 × 90 (c) 805 × 30 (d) 565 × 20
(e) 680 × 26 (f) 615 × 10 (g) 575 × 33465 × 40
(i) 500 × 100 (j) 895 × 100 (k) 65 × 456
11. Each tray of eggs contain 30 eggs. How many eggs are in 22 trays?
13. A father had 23 sweets and decided to give the sweets to his four
children equally.
(a) How many sweets did each child get?
(b) How many sweets did he remain with?
14. A class has 67 pupils. A teacher wants to form groups of 4 pupils each.
(a) How many groups were formed in the class?(b) How many students remain without a group?
Think!!!
Which 3 numbers have the same answer whether they are added or multipliedtogether?
