Mathematics

Topic outline

• 

  General
• UNIT 1:Mathematical Operations on Whole Numbers up to 100,000

  

  Key unit competence
  By the end of this unit, a learner should be able to write, compare and calculate 
  whole numbers up to 100,000.
  
  Attitude and Values
  • develop personal confidence in the use of numbers.
  • appreciate the importance of addition, subtraction, division and multiplication 
  of numbers in real life.
  • appreciate the need for manipulating numbers.
  
  1.0 Introduction to the Number Systems
  A number is a mathematical way of representing how many, how far, how long 
  or how much a quantity is.
  
  A number (numeral) system or system of numeration is a writing system for 
  expressing numbers using digits or other symbols in a consistent manner.
  

  Three of the most commonly used number systems are:

  1. The Hindu-Arabic Numeral System.
  2. The Roman Numeral System.
  3. The Chinese Numeral System. 
  We generally use arabic numeral system.
  
  The Hindu-Arabic Numeral System
  This numeration system uses ten digits; 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. These 
  digits can be used to form any number. For example, the digits 3, 9, 7 can be 
  used to form numbers 397, 379, 973, 937, 793 and 739.
  
  Natural Numbers (Counting Numbers)
  When a child is learning to count, he/she says “one, two, three, four... .” This 
  

  set of numbers is called natural numbers or counting numbers

  
  

  Whole numbers
  

  Whole numbers is a set of counting (natural) numbers including zero.

  
  

  Forming numerals from digits
  The digits 0 to 9 are used to form different numbers depending on how you 
  arrange the digits.
  
  Example 1.1
  Write down any 2-digit number formed by the digits 4, 6, 7, 0, 1.
  
  Solution
  Pick any two digits given above.
  For example
  First number = 46
  Second number = 67
  Other numbers are 40, 10, 70, 71, 76, 61, etc.
  
  Example 1.2
  Discuss and give the smallest number or numeral that can be obtained 
  from the digits 8, 9, 6, 1.
  
  Solution
  First, arrange the digits in ascending order (from smallest to biggest). 
  In ascending order we get 1, 6, 8, 9.
  Therefore, the smallest number is 1 689.
  
  Example 1.3
  

  Find the biggest number that can be formed from the digits 1, 3, 5, 9, 4?

  Solution
  Arrange the digits in descending order (from biggest to smallest). 
  In descending order, we get 9, 5, 4, 3, 1.
  Therefore, the biggest number formed is 95 431.
  
  Activity 1.1
  In this class activity, you will form numbers from given digits.
  (i) Arrange five blank flash cards provided on your table.
  (ii) Write the digits 5, 2, 4, 1 and 3 on each flash card.
  (iii) Form a 5-digit number starting with 5.
  (iv) Form a 5-digit number starting with 2.
  (v) Form a 5-digit number starting with 4.
  (vi) Form a 5-digit number starting with 1.
  (vii) Form a 5-digit number starting with 3.
  (viii) Arrange the formed numbers in ascending order.
  
  Exercise 1.1
  Given the 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
  You can use a digit only once while answering the questions below:
  (a) Use the digits above to form all 3-digit numbers beginning with 3 and 
  ending with 9. {An example is 329}. 
  (b) What is the largest 2-digit number that can be formed from these 
  digits?
  (c) What is the smallest 2-digit number that can be formed from these 
  digits?
  
  1.1 Reading and writing numbers in words and in figures
  Use one zero ‘0’ to write a ten, two zeroes ‘00’ to write a hundred, three zeroes 
  ‘000’ to write a thousand. For example:
  10 = Ten.
  30 = Thirty.
  100 = One hundred.
  370 = Three hundred seventy.
  1 000 = One thousand.
  8 900 = Eight thousand nine hundred.
  50 000 = Fifty thousand.
  99 990 = Ninety-nine thousand nine hundred ninety.
  100 000 = One hundred thousand.
  
  Activity 1.2
  In this class activity, you will play a game of matching numbers.
  
  (i) Divide yourselves into 2 groups: Group A and B.
  (ii) Arrange yourselves in a straight line and sit in 2 groups by facing each 
  other. The pupil seated opposite to you is your opponent. 
  (iii) Write one large number in words and one large number in figures on 
  the two manila cards.
  (iv) Take turns in playing the game by showing your opponent the numbers 
  you have written on the cards. He/she should say the number aloud or 
  write the number on the blackboard. The teacher together with the rest 
  of the pupils will act as judges. 
  (v) Correct answer = 3 marks and wrong answer = 0 marks. Add up the 
  marks for your group and see which group wins.
  
  Example 1.4
  Write the following numbers in words:
  (a) 97 642 
  (b) 10 002
  (c) 999
  (d) 90 001
  (e) 1 704
  
  Solution 
  (a) 97 642 = Ninety-seven thousand six hundred forty-two.
  (b) 10 002 = Ten thousand two.
  (c) 999 = Nine hundred ninety-nine
  (d) 90 001 = Ninety thousand one.
  

  (e) 1 704 = One thousand seven hundred four.

  Example 1.5
  Write the following in figures:
  (a) Ninety-nine.
  (b) One hundred ninety-nine.
  (c) Seven hundred five.
  (d) Six hundred fifty.
  (e) Twelve thousand five hundred.
  (f) Eighty thousand.
  (g) Forty thousand one.
  One hundred thousand.
  (i) Nine hundred ninety-seven.
  (j) Eleven thousand one hundred eleven.
  
  Solution
  
  
  Exercise 1.2
  1. Read and write the following numbers in words:
   (a) 111              (b) 1 011                    (c) 54 700
   (d) 1 000          (e) 78 999                   (f) 15 000
  2. Write the following numbers in figures.
   (a) Nineteen        (b) Ninety               (c) Ninety-nine
   (d) Nine hundred ninety-nine.        (e) Five hundred one.
  

   (f) Three thousand one.

  1.2. Place Values of Whole Numbers
  Place values help us to show the position of a given digit in a number.
  
  Example 1.6
  

  Find the value of each digit in 79 846

  

  Example 1.7

  Use the table below to work out the value of each digit in the number 43 275.

  Solution

  
  

  Activity 1.3
  Get an abacus frame
  (i) Place 3 beads on the ten thousand’s spike, 4 
  on the thousand’s spike, 2 on the hundreds 
  spike, 7 on the ten’s spike and 1 on the ones 
  spike.
  

  (ii) Read the number you have formed. 

  Exercise 1.3
  Write down the place values of the underlined digits in the given numbers:
  1. 3 289        3. 87 204          5. 89 434       7. 22 343             9. 29 321
  

  2. 94 483     4. 8 724             6. 4 927          8. 88 287

  Expanding whole numbers using place values
  Example 1.8
  Expand the following numbers:
  (a) 82 645              (b) 98 067
  
  Solution
  (a) 82 645 = 80 000 + 2 000 + 600 + 40 + 5
  (b) 98 067 = 90 000 + 8 000 + 60 + 7
  Writing expanded numbers in short form
  
  Example 1.9
  Write the following expanded numbers in short form:
  (a) 10 + 9                                       (b) 30 000 + 5 000 
  

  (c) 30 000 + 400 + 40 + 4         (d) 90 000 + 1

  Solution

  
  

  Activity 1.4
  

  
  

  Exercise 1.4
  1. Write the following numbers in expanded form.
   (a) 4 624          (b) 984               (c) 44 484
   (d) 93 428       (e) 76 709
  2. Write the following in short form.
   (a) (7 × 1 000) + (3 × 100) + (8 × 10) + (3 × 1)
   (b) (9 × 10 000) + (8 × 1 000) + (3 × 100) + (7 × 10) + (6 × 1)
  

   (c) (3 × 10 000) + (9 × 1 000) + (8 × 100) + (6 × 10) + (7 × 1)

  1.3 Comparing Numbers
  When comparing two numbers, we count the number of digits in each number.
  

  • The number with more number of digits is greater than the one with few  digits.
  • The number with fewer digits is smaller than the other.
  • If the two numbers have equal number of digits, then we can consider the value of each digit.
    the number which has greater value is greater than 

  the number which has greater value is greater than the number which has greater value is greater
  than the other.
  

  
  The following notations are used while comparing numbers:
  < denotes ‘less than’ 
  > denotes ‘greater than’ and
  = denotes ‘equal to’. 
  
  Activity 1.5
  In this class activity, you will write down the biggest number you know.
  (i) Form yourselves in groups of 5 learners each.
  (ii) Write down the greatest number you know on a flash card.
  (iii) Compare the number you have written with the numbers your 
  classmates have written.
  
  Example 1.10
  Use the symbol <, >, or = to compare the following numbers and items:
  (a) Four thousand and 4 × 1000                     (b) 10 000 and 1 000
  (c) 500 Frw and 550 Frw                                    (d) 400 bottles and 400 bottles
  
  Solution
  (a) Four thousand is equal to 4 × 1000, because four thousand = 4 × 1000 
  = 4000.
  (b) 10 000 > 1 000 because 10 000 has more digits than 1 000.
  

  (c) 500 and 550 have the same number of digits. The first digit in both 
  

  numbers is 5. So, we now compare the next digits which are 0 and 5. 
  

  Since 5 > 0, therefore, 500 Frw < 550 Frw.
  

  (d) 400 bottles = 400 bottles. The two numbers are exactly the same so 
  

  they are equal.

  Think!!!

  There is a three-digit number. The second digit is four times as big as the 
  third digit, while the first digit is three less than the second digit. What is the 
  

  number?

  

  1.4 Operation of numbers 
  1.4.1 Addition of Whole Numbers
  When adding numbers, we arrange the numbers so that the ones are on the 
  same vertical line, the tens are also on the same vertical line and so on.
  

  Addition of Whole Numbers Without Carrying

  Example 1.11
  1. Evaluate 34 907 
  

                        +54 091

  Solution 
  

  
  

  Add 375 and 8 201.
  

  Solution
  

  Numbers can be easily added by using an addition grid as shown below:

  
  

  Exercise 1.6
  

  1. Add the following numbers and write your answers in words:
  

  
  

  2. Add the following numbers together:
   (a) 230 and 230                                  (b) 21 650 and 32 146
   (c) 5 and 21 454                                  (d) 160 and 610
  
  3. I have three thousand Rwandan Francs and my brother has seven 
  thousand five hundred Rwandan Francs. How much do I and my 
  brother have altogether?
  
  4. Town A has 242 cars and Town B has 424 cars. How many cars are 
  

  there in the two towns?

  Addition with Carrying
  When the sum of two or more numbers is more than 9, we carry as we do the 
  

  addition as shown in the example given on the next page:

  Example 1.12
  

  Add 4 999 and 8 294.

  Solution

  
  

  • Add downwards starting from the place of ones on your right.
  • A number where the sum above is a two-digit number, write the ones 
  and carry the tens to the next digit to the left.
  

  • So, 4 999 + 8 294 = 13 293.

  Exercise 1.7
  1. Add the following numbers together:
   (a) 53 250 and 32 488               (b) 738 and 262
   (c) 1 354 and 9 999                    (d) 999 and 111
   (e) 999 and 1 110
  
  2. The data below shows the monthly amount of rainfall received by a 
  

  certain country for a whole year;

  

  (a) How much total rainfall was received between November and 
         December?
  (b) How much rainfall was received in the first three months?
  (c) Write down in words, the amount of rainfall received in the 
        month of May.
  (d) Calculate the sum of the least and greatest amount of rainfall 
  

        during the year.

  Think!!!
  

  Using only addition, how do you add eight 8s and get the number 1 000?

  1.4.2 Subtraction
  Subtraction without Borrowing
  Just like we did with addition of numbers, we arrange numbers so that the 
  Ones, Tens, ... etc. are all aligned.
  
  Example 1.13
  Evaluate: 6 989 – 3 453
  

  Solution

  
  

  Subtraction with Borrowing

  Example 1.14
  

  Evaluate: 2 573 – 1 395

  
  

  • Arrange the two numbers as we did for addition.
  • In ones, 3 – 5 is not possible because 3 is less than 5. We then borrow 
     1 from the next digit under the tens. 
  • So, we borrow 1 from 7 tens and remain with 6. The one we have 
     borrowed becomes 10 and 10 + 3 = 13.
  • Now, we subtract 5 from 13 to get 8.
  • Now, in tens 6 – 9 is also impossible. So, we borrow 1 from 5 hundreds, 
     so, 16 – 9 = 7.
  • In the hundreds column, we have 4 – 3 = 1 and in the thousands 
     column, we have 2 – 1 = 1.
  

  • So, 2 573 – 1 395 = 1 178.

  Example 1.15

  
  

  a position. We write 94 not 094.
  

  Example 1.16
  Eina has 73 567 Frw in her account and Awiza has 89 504 Frw in his 
  account. What is the difference between the money in Eina’s account and 
  

  in Awiza’s account.

  Solution

  
  

  Activity 1.6
  

  • Put 256 bean seeds in a tin box.
  • Remove 75 bean seeds from the tin box.
  • Count the number of seeds which remained in the tin.
  

  • How many seeds are left?

  
  

  Exercise 1.8

  1. Evaluate:
  (a) 15 789 – 11 000           (b) 86 786 – 63 524
  (c) 99 999 – 29 999           (d) 863 – 489
  (e) 45 567 – 12 540           (f) 48 487 – 32 450
  (g) 32 450 – 16 360            54 000 – 543
  (i) 65 009 – 222                   (j) 90 000 – 1
  
  

  2. A shirt costs 3 000 Frw and another shirt costs 1999 Frw. What is the 
  

  difference in cost of two shirts?
  

  
  3. I had 304 eggs in a box, out of which 70 got broken. How many eggs 
  were not broken?
  
  4. One metre of cloth costs 1 250 Frw and another cloth of 1 metre costs 
  2600 Frw. How much more does the another cloth cost?
  
  5. Kayongo went to the market with 550 Frw and bought mangoes. He 
  was left with a balance of 120 Frw. How much did he use to buy the 
  mangoes?
  
  6. By how much is 67 015 more than 67 010?
  
  7. The distance between London City in the U.K and New York City in 
  USA is 5 546 km. A plane travelling from London to New York has 
  covered a distance of 4 509 km. What distance has to be covered by 
  the plane to reach New York?
  
  8. A district had a population of 30 845 in a national census. Of these, 
  19 678 were females. How many males were in the district?
  
  9. The following people had the given amounts of money on their bank 
  

  accounts

  

  (a) What is the difference between the money in Matsiko’s account 
  and in Lina’s account?
  
  (b) What is the difference of money in Mwiza’s and Peter’s accounts?
  
  10. A town has 98 500 buildings. 70 005 of these buildings are shops. Find 
  

  the number of other types of buildings in the town.

  1.4.3 Multiplication of Whole Numbers
  

  The Multiplication Table

  

  Example 1.17
  Evaluate:
  1. 23 × 2                               2. 45 × 7
  3. 21 × 13                            4. 38 × 85
  5. 782 × 3                            6. 476 × 25
  7. 450 × 25                         8. 620 × 25
  

  Solution

  
  

  
  

  Multiplication of whole numbers by 10, 100, 1 000, 10 000.
  When multiplying a whole number by:
  • 10, we add a zero (0) at the right hand side of end of the last digit of the 
  number.
  • 100, we add two zeroes at the right hand side of the last digit of the number.
  • 1 000, we add three zeroes at the right hand side of the last digit of the 
  number.
  • 10 000, we add four zeroes at the right hand side of the last digit of the 
  

  number.

  This is shown in the cases below:
  (a) 27 × 10 = 270
  (b) 4 × 10 = 40
  (c) 2 376 × 10 = 23 760 
  (d) 24 × 100 = 2 400
  (e) 457 × 100 = 45 700
  (f) 34 × 1 000 = 34 000
  (g) 6 × 10 000 = 60 000
  
  Quick Multiplication by 5:
  In order to multiply a whole number by 5, you have to multiply it by 10, then 
  divide the product by 2. 
  Therefore, 280 × 5 = (280 × 10) ÷ 2
                                      = 2800 ÷ 2 = 1400
  
  Quick Multiplication by 100 and 1000:
  In order to multiply a whole number by 100, we put two zeros on the right hand 
  side of that number. 
  
  Therefore, 82 × 100 = 8200.
  In order to multiply a whole number by 1000, we put three zeros on the right 
  hand side of that number. 
  
  Therefore, 46 × 1000 = 46000.
  
  Example 1.18
  A square floor of classroom is completely covered with tiles. The length 
  of square room is covered by 26 tiles. Also number of tiles along its each 
  boundary is 26. How many tiles are there in the class room.
  
  Solution
  Number of tiles along one boundary (length) = 26
  Number of tiles along another boundary (width) = 26
  Total titles = 26 × 26
  

  So, 

  

  Exercise 1.9

  1. Complete the multiplication table below and learn them by heart.
  

  
  

  2. Complete the table below.
  

  
  

  3. Work out:
   (a) 164 × 6              (b) 40 × 9                  9c) 78 × 7                    (d) 217 × 5
   (e) 450 × 5             (f) 897 × 5                 (g) 575 × 3                    349 × 8
   (i) 999 × 9              (j) 35 × 21                  (k) 34 × 12                   (l) 56 × 23
  

   (m) 75 × 25            55 × 60                  (o) 39 × 13

  Exercise 1.1
  

  1. A rectangular floor is completely covered with tiles. There are 26 tiles 
  along its length and 15 tiles along its width. How many tiles are there 
  altogether in the room?
  2. There are 10 rows of students at a school assembly. Each row has 28 
  

  students. How many students are there altogether?

  

  3. Each box contains 500 nails. How many nails are contained in 80 boxes?
  4. Kigali Chalk Factory produces 90 cartons of chalk in a day. Each 
  carton contains 36 boxes of chalk. How many boxes of chalk does the 
  factory produce per day?
  5. The table below shows part of Mr. and Mrs. Bitega’s wedding budget.
  

   The cost of the items is in dollars.

  

  Complete the table and find the total cost for the different items.

  1.4.4 Division
  Division without A Remainder
  Example 1.19
  Work out the following:
  (a) 48 ÷ 2          (b) 245 ÷ 5                  (c) 90 ÷ 5
  

  (d) 2 170 ÷ 7     (e) 54 000 ÷ 45         (f) 108 ÷ 6

  

  

  

  Example 1.20
  Divide 5000 pens equally among 5 children.
  
  Solution
  

  Divide 5000 by 5

  

  Exercise 1.11

  1. Work out the following:
  

  
  

  2. Answer the following questions:
  (a) There are 340 bags of cement to be unloaded off from a lorry by 
  5 men working at the same rate. How many bags will each man unload?
  (b) Divide 450 sweets equally among 10 pupils.
  

  (c) The District Agriculture Officer plans to distribute 1 080 Friesian cows 
  to 10 farmers’ groups. How many cows will each farmers’ group get?
  (d) A butcher supplies 10 kg of meat to each school. If he has 1 000 kg 
  

  of meat, how many schools does he supply?

  Division with a Remainder

  Example 1.21

  Evaluate the following:
  

  (a) 25 ÷ 4               (b) 398 ÷ 5            (c) 1 478 ÷ 12

  Solution
  

  
  

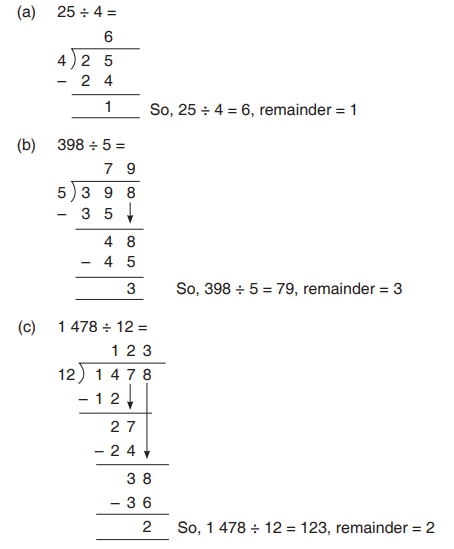
  Assessment Exercise
  

  1. What is the largest 5-digit number that can be formed from the digits 
  0, 3, 2, 4, 1, 5?
  2. Write the following numbers in figures:
   (a) Twenty-four thousand seven hundred seven.
   (b) One hundred twenty-four thousand seven hundred seventy.
   (c) Thirty-four thousand seven hundred seventy-seven.
  3. Write the following in short form.
   (a) (4 × 1 000) + (2 × 100) + (7 × 10) + (3 × 1)
   (b) (5 × 10 000) + (5 × 100) + (3 × 10) + (2 × 1)
  4. In a school with 888 pupils, three girls were voted for the post of head 
  girl of the school. The number of votes obtained by each girl is given 
  below:
  

  

  Which girl obtained the greatest number of votes?
  
  5. On a certain school trip to Akagera National Game Park, we counted 
  123 zebras, 10 buffaloes, 21 wild pigs and 14 giraffes. 
   (a) How many giraffes and zebras did we count?
  

   (b) How many wild animals did we count altogether in the park?

  6. Fill the missing digits in the addition grids below:

  
  

  7. A shopkeeper in Kimironko main market in Kigali had the following 
  

  daily records of sales:

  
  

  (a) What was the value of goods sold on Monday?
   (b) What was the value of goods sold on Thursday and Friday?
   (c) How much did the shopkeeper get from Monday to Wednesday?
  
  8. A school water tank holds 100 000 litres of water. P5 pupils use 12 500 
  litres and P6 pupils use 67 500 litres. How much water remains in the 
  tank?
  

  9. By how much is 67 999 greater than 45 908?

  10. Work out:
   (a) 217 × 11      (b) 234 × 90      (c) 805 × 30       (d) 565 × 20
   (e) 680 × 26     (f) 615 × 10        (g) 575 × 33        465 × 40
  

   (i) 500 × 100     (j) 895 × 100     (k) 65 × 456

  11. Each tray of eggs contain 30 eggs. How many eggs are in 22 trays?

  

  13. A father had 23 sweets and decided to give the sweets to his four 
  children equally. 
   (a) How many sweets did each child get?
   (b) How many sweets did he remain with?
   14. A class has 67 pupils. A teacher wants to form groups of 4 pupils each.
   (a) How many groups were formed in the class?
  

   (b) How many students remain without a group?

  Think!!!

  Which 3 numbers have the same answer whether they are added or multiplied 
  

  together?

• UNIT 2:Positive and Negative Integers

  
  

  Key Unit Competence
  A learner should be able to solve problems related to comparing, ordering and 
  finding distance between negative and positive integers.
  
  Attitudes and values
  Appreciate the importance of using positive and negative numbers in practical 
  contexts.
  
  2.1 Integer
  An integer is a number with no fractional part. Integer include all the whole 
  numbers along with negative numbers.
  

  We represent the integers on a number line as follows:

  
  

  A set of integers includes:
  1. All counting numbers (1, 2, 3, 4, 5, 6, 7, ………. 100, ..)
  2. Zero {0}
  3. And the negatives of all the counting numbers (–1,–2,–3,–4,–5….)
  Therefore, the set of integers is (……, –3, –2, –1, 0, +1, +2, +3, …..)
  Integers are made up of negative numbers, zero and positive numbers. ‘Zero’ 
  

  is neither positive nor negative.

  Activity 2.1
  In this class activity, you will discuss positive and negative numbers with your 
  group members.
  You should discuss positive and negative numbers in relation to the following:
  (i) Falling into a hole and climbing a tree, what can be the position of zero?
  (ii) Profit and loss in business, what is negative and what is positive?
  (iii) Sinking into water and rising above earth, what is the position of zero?
  

  (iv) Promotion and demotion at work place, what is compared to positive event?

  

      2.2 Explaining Integers
   • If I have no money at all, then I can say that I 
  have ‘0’ money.
  • If I have been given some 50 Frw, then I can say 
  I have some money.
  • If I have lost 100, then I can say that I have a 
  shortage of 100 Frw.
  • If a stone is dropped into a pit which is 10 metres 
  deep, then from the ground level the stone is at 
  –10 m from the earth surface.
  

  • A plane flying above our school at a height of 

  500 m is +500 m above the school.

  Example 2.1
  

  Study the diagram below and use integers to estimate the position of the 
  

  following objects from the earth surface.
  
  

  Solution

  (a) The position of the plane is +40 m.

  (b) The position of the balloon is +35 m.

  (c) The position of the ball is +10 m.

  (d) The position of the ground is 0 m.

  (e) The position of the fish is –5 m.

  (f) The position of the stone is –15 m.

  
  

  Exercise 2.1
  Explain and illustrate these expressions using integers:
  (a) A pupil got no mark in a Mathematics test _________. 
  (b) A team scored two points in a game _________ .
  (c) A pupil climbed a tree 10 m tall _________ .
  (d) My coin fell to the bottom of a swimming pool 2 m deep ______ .
  (e) A shopkeeper made a profit of 2 000 Frw _______ .
  (f) A shoeseller made a loss of 300 Frw_______ .
  
  2.3 Number Line
  A number line is a horizontal line drawn with integers marked along its length. 
  Positive numbers are marked and written on the right hand side of zero and 
  negative numbers are marked and written on the left hand side of the zero mark 
  

  as shown below:
  

  
  
  • Positive numbers are written with a plus (+) sign in front of them. They may 
  also be written without any sign in front, e.g. +5 = 5.
  • Negative numbers are written with a minus (–) sign in front of them, e.g. –4. 
  
  The Temperature Scale
  The temperature is a degree of hotness or coldness of an object. 
  The temperature of an object is measured using a thermometer.
  • The temperature of freezing water is 0°C.
  • The temperature of boiling water is 100°C.
  • The temperature of a normal person is about 37°C.
  The temperature of an object below 0°C is negative. For instance, 
  

  temperature in the Antarctica can reach as low as –89.2˚C

  
  

  
  

  2.4 The inverse or opposite of an integer
  The opposite or inverse of an integer has the same absolute value but with 
  an opposite sign.
  
  The inverse of +1 is –1.                                        The inverse of +5 is –5.
  The inverse of –2 is +2.                                         The inverse of –6 is +6.
  The inverse of –3 is +3.                                         The inverse of +7 is –7 and so on.
  
  The inverse property of an integer
  The inverse property of integers states that any number added to its inverse 
  equals to zero. Example: +5 +(-5) = 0
  
  Exercise 2.2
  1. Draw a number line. Mark all the integers from –10 to +10.
  (a) Which integer is 4 steps to the right of +4?
  (b) Which integer is 5 steps to the left of 0?
  (c) An integer is 6 steps to the left of 1. What is this integer?
  (d) If you are at zero (0) and you move 9 steps in the negative direction, 
  where will you be on the number line?
  (e) An insect moves from -6 to +6. How many steps has it moved?
  
  2. Verify the following:
  (a) (+1) + (–1) = 0                   (b) (–88) + (+88) = 0
  (c) (+100) + (–100) = 0          (d) (+6) + (–6) = 0
  3. Name the inverse of each of the following integers:
  (a) +12 (b) + 45        (c) –34         (d) –20       (e) –240      (f) –500
  
  2.5 Position of Integers on the Number Line
  When locating integers on the number line, we need to take great care of the 
  direction in which we are moving. We need to establish a system that we will 
  follow whenever we are locating positions of integers on the number line.
  • Our reference point is the zero (0) mark. 
  • An addition (+) operation means we move towards the right of 0.
  • A subtraction (–) operation means we move towards the left of 0.
  • We can imagine our face to represent the positive and the back of our 
  heads to represent the negative.
  • For positive integers, we move forwards.
  • For negative integers, we move backwards.
  
  Activity 2.2
  In this activity, you will need the following materials for your class:
  Long string (about 10 m), cotton thread, manila paper of different colours 
  (red, green and yellow), a pair of scissor, two 6 cm nails, hammer, large 
  cardboard box and a black marker pen.
  (i) Using a hammer, fix two nails into the opposite walls of the classroom.
  (ii) Make loops on the string and tie the string on the nails across the 
  classroom.
  (iii) Cut about 10 pieces of red manila papers, 10 pieces of green manila 
  papers and 1 piece of yellow manila paper (each paper should be 
  about 15 cm by 15 cm).
  (iv) The teacher will guide you to write integers from –10 to +10 on the 21 
  pieces of manila papers. The red papers should be used for negative 
  integers, yellow for zero and green for positive integers. 
  (v) Each pupil picks a cardboard from the box at random, makes a small 
  hole in the paper and ties it with about 30 cm of cotton thread.
  (vi) The pupils will stand in groups according to the colour of papers they 
  have picked. There is only one pupil with a yellow paper on which 0 is 
  written.
  (vii) The pupil with the yellow paper ties his/her paper to hang exactly in the 
  middle of the string.
  (viii) The other pupils also hang their papers on the correct side of the yellow 
  

  paper and at the correct positions.

  Activity 2.3
  (i) Your teacher will take you to a large play area such as a field. 
  (ii) Using dry sand, ash or any suitable material, draw a number line on the 
  ground and mark integers on it so that each pupil has a point to stand on 
  the number line. The distance between the integers can be about 60 cm. 
  (iii) Write negative integers on the red papers, 0 on the yellow paper and 
  positive on the green papers.
  (iv) Pick the papers at random and tie a loop on the paper so that you are 
  able to wear it around your neck.
  (v) Move to the position on the number line which has the same number on 
  your card.
  (vi) During this activity, your name is the number that you are wearing on 
  your neck. Listen carefully as the teacher calls your “name” and follow the 
  instructions well.
  (vii) Everyone should be able to know how far he/she has moved and in which 
  

  direction (positive or negative) he/she has moved.

  
  2.6 Distance between two integers
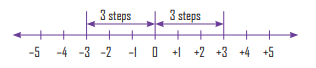
  1. Two integers on the same side of zero:
  The magnitude of –3 is 3 and the magnitude of +3 is also 3. 
  

  Magnitude of a number is the distance from 0 to that number.

  
  If two numbers are on the same side of zero, the difference between them 
  is the difference of their magnitudes.
  
  Example 2.2
  What is the distance between the following integers on the number line?
  (a) + 2 and +10 (b) 0 and +15 (c) –3 and –6 (d) –7 and –2
  
  Solution
  (a) Magnitude of +2 = 2 and magnitude of +10 = 10.
  so, distance between +2 and +10 = 10 – 2 = 8 steps
  (b) In the same way, distance between 0 and +15 = 15 – 0 = 15 steps.
  (c) Magnitude of –3 = 3 and magnitude of –6 = 6. So the distance between 
  –3 and –6 = 6 – 3 = 3 steps.
  (d) Distance between –7 and –2 = 7 – 2 = 5 steps.
  
  2. Two integers on opposite sides of 0 on the number line:
  If two numbers are on opposite sides of 0 on the number line, the distance 
  between them is the sum of the magnitudes of the two numbers.
  
  Example 2.3
  What is the distance between the following points on the number line?
  (a) –5 and +7 (b) –10 and +10
  Solution
  

  

  Distance between – 5 and +7 = 5 steps + 7 steps = 12 steps.
  (b) Two numbers on opposite side of zero
  magnitude of –10 is 10 and the magnitude of +10 is also 10.
  So, the distance between –10 and +10 = 10 + 10 = 20 steps.
  
  Exercise 2.3
  Without drawing a number line, state the distance between the following 
  points on the number line;
  (a) 0 and +3   (b) 0 and –3   (c) –2 and +2   (d) –1 and +1
  
  2.7 Comparing integers and Ordering integers
  • On a number line integers are always in order from the smallest to the 
  biggest. 
  • If you touch two integers at a time, the one to the left is always smaller and 
  the one to the right is always bigger.
  • Any integer is always bigger than the one to its left on the number line.
  • Any integer is always smaller than the one to its right on the number line
  
  10 is less than –9                   –7 is less than –4                    –2 is less than 0
   1 is less than 6                      +6 is less than +10                  0 is greater than –4
  +3 is greater than –10          +1 is greater than –1
  
  Example 2.5
  Arrange +1, –3, –10, –2, –4, 0, +5 in order starting with the smallest to the 
  biggest (ascending order)
  
  Solution
  

  We draw the number line and show the positions of the integers.

  

  Order from the smallest to biggest = –10, –4, –3, –2, 0, +1, +5.
  
  Assessment Exercise
  1. Show these expressions using integers:
  (a) 3 metres below the ground _________ .
  (b) 5 steps forward ________ .
  (c) 10 steps backward ________ .
  
  2. Name the inverse of each of the following integers:
  (a) –5 890    (b) +100 000   (c) –20 000
  
  3. Without drawing a number line, state the distance between the following 
  points on the number line;
  (a) +3 and –1        (b) –2 and +10        (c) –10 and +10
  (d) –10 and –6
  4. Arrange these integers from biggest to smallest (descending order)
  –3, –7, 0, +4, –13, –31, +13, +31, –301, +310, +301.
  5. Arrange these integers from the smallest to biggest (ascending order)
  –8, –5, 3, 2, 0, +5, 6, 8, 1
  

  Think!!!

  
  

  A chameleon wants to move from point A to point B, 10 metres apart. It 
  walks in a very funny way such that within 1 minute, it moves 3 metres 
  forward followed by 1 metre backward. How long does the chameleon take 
  to complete its journey to point B?
  
• UNIT 3:Classifying Numbers by their Properties

  Key Unit Competence
  A learner should be able to classify numbers and appreciate that one number 
  

  may belong to various families of numbers.

  Attitude and Values
  Appreciate the importance of using square roots, being cooperative and 
  

  displaying a teamwork spirit.

  3.1 Natural and whole Numbers 
  The counting numbers starting from 1 are called natural numbers. 
  Natural numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, ...}
  Whole Numbers
  Natural numbers together with 0 are called whole numbers. 
  

  Whole numbers = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...}

  3.2 Odd Numbers

  Odd numbers are natural numbers which are not exactly divisible by 2. When 
  divided by 2 it always has a remainder of 1.
  The following are examples of odd numbers less than 20.
  

  Odd numbers = {1, 3, 5 ,7, 9, 11, 13, 15, 17, 19}

  3.3 Even Numbers

  Even numbers are natural numbers which are exactly divisible by 2. When 
  divided by 2 it leaves no remainder.
  The following are the even numbers found between 0 and 20.
  Even numbers = {2, 4, 6, 8, 10, 12, 14, 16, 18}.
  [Note: 20 is not included in this set of numbers and yet it is an even number. 
  This is because we were asked to list even numbers between 0 and 20 and not 
  

  0 to 20.]Activity 3.1
  In this class activity, you are going to play 
  a game which will help you to learn how 
  to classify numbers as whole, natural, odd 
  and even numbers.
  • The teacher will give you a flashcard 
  with a number written on it.
  • Look at your number carefully and 
  remember it throughout this activity 
  (game). 
  • When the teacher calls out the class to which your number belongs, 
  you will run and stand on the line drawn: Class of odd numbers, even 
  

  numbers, whole numbers and natural numbers.

  Exercise 3.1
  1. List all the odd numbers between 0 and 100. 
  2. List all the even numbers from 0 up to 100.
  
  

  Think!!!
  I am an odd number. Take away one letter and I become even. What number am I?
  
  3.4 Square Numbers
  This is the number obtained when one number is multiplied by itself.
  Study the multiplication table below and use it to identify all the square numbers 
  

  less than 60.

  

  From the table we can see that;
  1 × 1 = 1                               6 × 6 = 36
  2 × 2 = 4                               7 × 7 = 49
  3 × 3 = 9                               8 × 8 = 64
  4 × 4 = 16                            9 × 9 = 81
  

  5 × 5 = 25                           10 × 10 = 100

  So the set of square numbers up to 100 = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}.

  Activity 3.2
  

  Work together in groups and list all the square numbers between 0 and 410.

  3.5 Square root of a number
  Finding the square root of a number is the inverse operation of squaring the 
  number.
  

  

  Exercise 3.2

  
  

  Exercise 3.3
  Complete the multiplication table below and use it to list all the square 
  

  numbers less than 100.

  
  

  3.6 Prime Numbers
  A prime number is any number with only two factors; one factor being 1 and the 
  other one being itself.
  

  Examples of prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, ...

  Activity 3.3
  

  List all the prime numbers between 100 and 150.

  3.7 Composite Numbers
  This is a natural number greater than one which has more than two factors. 
  In fact a composite number is a natural number greater than 1 which is not a 
  prime number.
  The following are examples of composite numbers: 4, 6, 8, 9, 10, 12, 14, 15, 16, ...
  
  Exercise 3.4
  1. What is the smallest prime number?
  2. What is the smallest even number which is a prime number?
  3. What is the smallest odd number which is prime?
  

  4. List the first 10 composite numbers

  Mind Game
  

  I am an even number. I am a counting number and I am a prime number too.
  

  Who am I and what is my square?

  3.8 Multiples of a Number
  The multiples of a whole number are found by taking the product of any counting 
  

  number and that whole number.

  For example:

  

  So, the multiples of 5 are 5, 10,15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, ...

  Exercise 3.5
  List the first 10 multiples of the following numbers: 
  (a) 4              (b) 6             (c) 7           (d) 8                   (e) 9
  (f) 11            (g) 12
  
  3.9 Factors of a Number
  The factors of a number are all those whole numbers that can divide evenly to 
  the number and leave no remainder. 
  The greatest factor of a number is the number itself and the smallest factor of 
  a number is 1.
  
  Activity 3.4
  Work together in groups and list all the numbers between 1 and 30. Which 
  numbers are not multiple of 3?
  
  Example 3.1
  List all the factors of 18.
  
  Solution
  • We already have two factors of 18 namely 1 and 18. 1 is the smallest 
  factor and 18 is the biggest factor. 
  • Try dividing 18 by numbers 2, 3, 4, 5 ...
  • 18 ÷ 2 = 9 and so 2 is the second smallest factor and 9 is the second 
  biggest factor.
  

  • Continue dividing with different numbers until you get all the factors.

  

  • So, the factors of 18 arranged in ascending order are 1, 2, 3, 6, 9, 18.

  Exercise 3.6
  1. List all the factors of the following numbers:
  (a) 8            (b) 12            (c) 24           (d) 36          (e) 48
  (f) 64          (g) 45            23           (i) 96             (j) 100
  2. I think of a number. When I multiply it by itself, the answer is 100. What 
  

  is the number?

  3.10 Lowest Common Multiple (LCM)
  LCM means the Lowest Common Multiple. So, the LCM of two numbers is the 
  smallest multiple which is common to both numbers.
  
  Example 3.2
  Find the LCM of the following numbers:
  (a) 3 and 4                         (b) 5 and 12
  (c) 12 and 15                    (d) 20 and 65
  
  Solution
  Method 1
  (a) LCM of 3 and 4
  Multiples of 3 = {3, 6, 9, 12, 15, 18, 21, 24, 27, ...}
  Multiples of 4 = {4, 8, 12, 16, 20, 24, 28…}
  The common multiples are 12, 24, ........
  

  The smallest common multiple is 12 and so the LCM of 3 and 4 = 12.

  (b) LCM of 5 and 12
  Multiples of 5 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, ...}
  Multiples of 12 = {12, 24, 36, 48, 60, 72, 84, 96, 108, ...}
  The lowest common multiple is 60.
  So, the LCM of 5 and 12 = 60.
  
  (c) LCM of 12 and 15
  Multiples of 12 = {12, 24, 36, 48, 60, 72, 84, 96, 108, ...}
  Multiples of 15 = {15, 30, 45, 60, 75, 90, 105, 120, 135, ...}
  The lowest common multiple is 60.
  So, the LCM of 12 and 15 = 60
  
  (d) LCM of 20 and 65
  Multiples of 20 = {20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 
  240, 260, ...}
  Multiples of 65 = {65, 130, 195, 260, 325, 390, ...}
  The lowest common multiple is 260.
  So, the LCM of 20 and 65 = 260.
  
  Method 2
  Another way of finding the LCM of two or more numbers is to first express 
  them in terms of prime factors. Let’s use this method to find the LCM of 12 
  and 15 and see whether we shall get 60.
  
  Solution
  

  Factorise 12 and 15 in terms of prime factors

  

  The LCM can be got by multiplying all the prime factors of 12 and 15 in the 
  first column on the left.
  

  So, LCM of 12 and 15 = 2 × 2 × 3 × 5 = 60.

  Assessment Exercise

  1. Evaluate the following by finding its square root:
  

  
  

  2. Find the first five multiple of the following numbers: 3, 6, 5, 9, 10
  3. List the first 10 prime numbers.
   (a) Circle all the square numbers.
   (b) Using a pencil, tick all the composite numbers.
  4. Find the highest common factor (HCF) and LCM of the following 
  numbers:
   (a) 2 and 4         (b) 4 and 5      (c) 3 and 6     (d) 4 and 10
  

   (e) 12 and 14     (f) 23 and 46

  Internet Resource
  For more online support visit
  

  https://www.superteacherworksheets.com/least-common-multiple.html

• UNIT 4:Fractions of the Same Denominator

  Key Unit Competence
  By the end of this unit, a learner should be able to explain the meaning of 
  fractions, add and subtract same-denominator fractions, multiply and divide 
  fractions accurately.
  
  Attitude and Values
  Appreciate the importance of accuracy in carrying out operations on fractions 
  and develop the spirit of sharing with others.
  
  4.1 Meaning of fractions
  A fraction is a part of a whole number. 
  A fraction is made up of 2 numbers. The top number is called the numerator 
  and the bottom number is called the denominator. 
  
                                                        
  How Fractions Arise?
  Fractions are obtained when a whole number is divided into two or more than 
  

  two parts. The figures below show an orange divided into 8 equal parts.

  

  

  Mixed Fractions

  
  

  Activity 4.1
  

  In this class activity, you will identify the numerator and denominator in the 
  

  following fractions. You will work in groups of 4.

  
  

  • This is a clock face with so many numbers, some of which are fractions.
  • Write down all the fractions shown on the clock face above.
  • For each fraction you have written above, write down the numerator and 
  denominator.
  • Compare your results with other classmates in class.
  

  • Present your answers to the teacher for marking.

  Activity 4.2

  In this class activity, you will write fractions when you are given the numerator 
  and denominator. You will complete this activity in groups of 4. Complete the 
  

  table in your note book, writing down the fraction.

  
  

  Think!!!

  A farmer has a bag of popcorn, a hen and a fox. He wants to cross a river in 
  a boat. The boat can only take him and only one of the three items he has. 
  The problem is that the hen can eat popcorn and the fox can eat the hen. 
  

  How does he cross the river without anything getting eaten up?

  Activity 4.3
  

  Look at the following figures. Use coloured pencils or crayons to colour or 
  

  paint as instructed below:

  
  

  4.2 Reading a Fraction
  

  
  

  
  

  Activity 4.4
  

  (a) In this class activity, you will work in groups of 6 learners.
  (b) Three of them will write a half, a fifth and a third on their respective 
  

  cards as shown below.

  
  

  (d) Now, make pairs of similar values of cards.
  

  (e) Ask your teacher to check the results.

  Activity 4.5

  Shade the parts represented by the given fraction.
  

  
  

  Exercise 4.1
  

  
  

  4.3 Comparing fractions with the same denominator
  

  Activity 4.6
  

  In this class activity, you will work in groups of 5 learners.
  (a) Cut the orange given to you into 4 equal parts. Each part shall be 
  called a slice.
  (b) Display the slices on a table and count them to be sure that they are 4.
  (c) What fraction represents all the slices you have counted?
  (d) Put the slices in 3 groups labelled A, B and C. In A put 1 slice, 2 slices 
  in B and 1 slice in C.
  (e) What fraction represents the number of slices in each group? Answer 
  

  this question by completing the table below:

  
  

  
  

  
  

  
  

  
  

  
  

  4.4 Addition of Fractions with the Same Denominator
  

  Activity 4.8
  

  
  

  (a) Draw a circle of radius 10 cm on a manila paper.
  (b) Mark the centre of the circle using letter O.
  (c) Draw two lines through the centre of the circle to divide the circle into 
  four equal parts. Each of these parts is called a sector.
  (d) Label the three boxes A, B and C.
  (e) Cut out the outline of the circle along the lines drawn.
  (f) What fraction does each sector represent? Your answer should be 4/1.
  (g) In box A put one sector, put two sectors in B and one sector in C.
  What fraction is represented by the sectors in boxes A, B and C?
  (i) Pick the sectors in box A and box B. Add them together. What total 
  fraction do you get?
  

  (j) Add the sectors in A and C together. What fraction do you get?

  
  

  
  

  Think!!!

  Mr. Kamanzi came back home from Kigali with 24 apples. He decided to 
  share all the apples between his two sons Ted and Ronald. Ted was given 
  a quarter of a half of the apples and Ronald was given a half of a quarter of 
  

  the apples. Which son got more apples?

  
  

  
  

  Real Life Problems involving Fractions
  

  
  

  
  

  4.6 Multiplication of Fractions by Whole Numbers 
  Activity 4.10
  Get 8 bottle tops
  

  Arrange them into four equal groups

  
  

  What is a quarter of eight bottle tops? Use your arrangement to get the quarter of 8.
  

  
  

  
  

  
  

  4.7 Multiplication of Fractions by Fractions
  

  
  

  Solution
  Two fractions can be multiplied together using a fraction grid. 
  

  (a) Draw a rectangle as shown below.

  
  

  (b) Separate the rectangle into three equal parts using two vertical lines. 
  (c) Shade two of these parts. The shaded area (blue) represents the 
  fraction 3/2 .
  
  (d) Now divide the rectangle into four equal parts using three horizontal lines.
  (e) Shade three of these parts to represent 4/3 .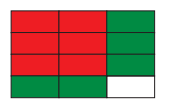
  
  (f) Now count the total number of parts in the rectangle. You will find 12 parts.
  (g) Count the number of parts that have been double shaded. There are 
  6 out of 12 parts which are double shaded. (This is represented by the red parts)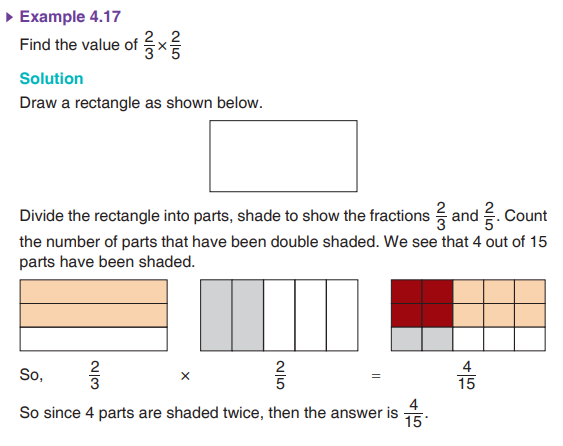
  
  Exercise 4.7
  

  Let us multiply the fractions below and reduce them to their simplest form:

  

  4.8 Division of Fractions by Whole Numbers
  To divide a fraction by a whole number:
  Step 1: Multiply the denominator by the whole number.
  

  Step 2: Simplify the fraction where necessary.

  

  Real Life Problems involving Fraction
  Example 4.19
  

  How many half litre bottles can be filled by a twenty litres jerrycan of water?

  

  Assessment Exercise
  1. In the following diagrams, white parts are not shaded. The coloured 
  parts are shaded. Count the shaded parts carefully and write down the 
  

  fraction shown by the shaded part (s).

  

  

  

  

  

  Internet Resource
  

  For more online support visit www.math-play.com/fractions

• UNIT 5:Decimal Fractions/Numbers

  
  Key unit competence
  A learner should be able to add, subtract and compare decimal numbers using 
  place values of decimals up to 2 decimal places.
  
  Attitudes and values
  Develop personal confidence in the use of decimal numbers and appreciate the 
  importance of decimal fractions in comparing and sharing.
  
  5.1 The Concept of decimal number
  A decimal number is any number which contains a decimal point. 
  A decimal number is a number which has a decimal part separated from the 
  integer part using a decimal separator called the decimal point.
  

  For example, 28.53 is a decimal number.

  

  Activity 5.1

  i. Draw a horizontal line of about 12 cm on your notebook using a ruler 
  and sharp pencil.
  ii. Show the integers –4, –3, –2, –1, 0, +1, +2, +3 and +4 on the number line.
  
  Activity 5.2
  In this class activity, you will find some numbers:
  (a) Divide the following numbers by 10:
  

  •  1400
  •  140
  •  14
  •  1.4

  (b) What number is exactly:
  

  •  between 0 and 100?
  •  between 0 and 10?
  •  between 0 and 1?

  5.2 Decimals on a number line
  Consider the number line below. The number line shows negative and positive 
  

  numbers from –5 to +5.

  

  However, if we zoom into the space between 0 and 1, then we create new 
  numbers which are not whole. The space between 0 and 1 is divided into 10 
  equal parts. The decimal numbers 0.1, 0.2, 0.3, 0.4, ...... , 0.9 are produced. 
  

  Decimals like 0.25 and 0.75 can easily be located as shown below.

  

  By further zooming into the space between 0.1 and 0.2, we can form new 
  

  decimal numbers as shown below. 

  

  Activity 5.3
  In this class activity, you will divide the space between 2.0 and 3.0 into ten 
  equal parts.
  i. Draw a horizontal line of about 10 cm on your notebook using a ruler 
  and sharp pencil.
  ii. Mark the start of the line with the decimal number 2.0.
  iii. Mark the end of the line with the decimal number 3.0.
  iv. Mark the line drawn into 10 equal parts, each 1 cm long.
  v. Show the decimal numbers 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8 and 2.9 
  on the number line.
  
  Activity 5.4
  In this class activity, you will locate the positions of the given decimal 
  numbers: 8.11, 8.16 and 8.19.
  i. Draw a horizontal line in your notebook using a sharp pencil. Length of 
  the line should be 10 cm.
  ii. Mark the line at intervals of 1 cm so that the line has 10 equal parts.
  iii. Write the decimal number 8.10 on the first mark and the decimal 
  number 8.20 on the last mark.
  iv. Carefully study the number line you have drawn and write the correct 
  decimal numbers on the marks drawn.
  v. Show the positions of the decimal numbers 8.11, 8.16 and 8.19.
  vi. Present your work to the teacher for evaluation.
  
  Exercise 5.1
  Show the following on the number line:
  (a) 0.6, 0.8, 0.3, 0.1
  (b) 0.43, 0.48, 0.25, 0.15
  (c) 0.3, 0.1, 0.5, 0.9, 0.2
  

  (d) 0.51, 0.50, 0.48, 0.55

  5.3 Place Value of decimals
  

  Consider the decimal number 78.46

  

  78.46 is read as “seventy eight point four six”. 
  

  It is wrong to say “seventy eight point forty six”

  

  We can see that the place value for 7 is ‘tens’, 8 is ‘ones’ or ‘units’, 4 is ‘tenths’,
  

  and 6 is ‘hundredths’.

  

  Activity 5.5
  i. Let two pupils A and B stand to the right of a tree.
  ii. Also, two pupils C and D should stand to the left of the tree.
  iii. If we now consider the tree as a decimal point, let each pupil mention 
  

  his/her place.

  Example 5.1
  Write the places of the underlined digits in the decimal numbers given 
  below:
  

  (a) 0.24      (b) 5.06       (c) 13.56

  Solution
  (a) Tenths        (b) Ones       (c) Tens
  
  Exercise 5.2
  1. Read the following decimal numbers and write them in words.
   (a) 87.09           (b) 12.2         (c) 0.03          (d) 23.56
   (e) 19.19          (f) 0.10           (g) 45.45
  
  2. Write the following decimal numbers in figures:
   (a) One hundred forty-four point seven.
   (b) Twelve point one two.
   (c) Seven point seven.
   (d) Eighty point seven one. 
  
  5.4 Comparing decimals
  When comparing decimal numbers, we may use =, < or >.
  Example 5.2
  Compare the decimal numbers 9.25 and 9.7.
  
  Solution
  1. Align the decimal points.
  2. Fill in the empty place with zero.
  

  3. Compare the digits from left to right until they are different.

  

  Example 5.3
  Compare the two numbers: 452.78 and 452.21. Which one is greater?
  
  Solution
  

  Arrange the numbers in a table like this:

  

  The first three digits are the same in both decimal numbers. But in the 
  tenths’ column, 7 is greater than 2. So, 452.78 > 452.21.
  
  Example 5.4
  Arrange the following numbers in ascending order:
  0.46, 0.64, 0.9, 0.09, 0.57, 0.75
  
  Solution
  • All these numbers begin with zero.
  • Now we compare the second numbers. 
  • We can see that the smallest number is 0.09, followed by 0.46......
  • 0.57 is smaller than 0.64.
  • 0.75 is smaller than 0.9.
  
  Therefore, Ascending order: 0.09, 0.46, 0.57, 0.64, 0.75, 0.9.
  This can also be written as 0.09 < 0.46 < 0.57 < 0.64 < 0.75 < 0.9.
  
  Example 5.5
  Arrange the following numbers in descending order:
  8.6, 7.66, 7.6, 0.76, 0.67, 0.86, 6.08.
  
  Solution
  Descending order: 8.6, 7.66, 7.6, 6.08, 0.86, 0.76, 0.67.
  Alternatively, 8.6 > 7.66 > 7.6 > 6.08 > 0.86 > 0.76 > 0.67.
  
  Exercise 5.3
  1. Arrange the following decimal numbers from the smallest to the largest 
  (Ascending order)
   (a) 3.5, 3.79, 3.42, 3.57, 3.7, 3.62.
   (b) 5.7, 5.64, 5.8, 5.4, 5.79, 5.72.
   (c) 5.0, 4.7, 4.8, 4.9, 4.3, 4.75
   (d) 1.02, 1.7, 1.12, 1.66, 1.71, 1.1
   (e) 3.1, 2.5, 2.49, 2.8, 3.48, 2.52
  
  2. Arrange the following decimal numbers from the largest to the smallest 
  (Descending order).
   (a) 8.1, 7.9, 7.92, 8.43, 7.89, 7.97
   (b) 6.8, 7.23, 7.32, 6.59, 6.92, 7.02
   (c) 2.01, 2.10, 2.63, 2.36, 1.4, 1.7
   (d) 3.8, 2.77, 2.75, 3.34, 2.9, 3.
  

  (e) 6.4, 7.4, 4.7, 4.6, 4.06, 7.04

  5.5 Addition and subtraction of decimal numbers
  Adding decimal numbers works exactly the same way as adding whole numbers. 
  You just line up the decimal points as shown below. For example,
  
  Activity 5.6
  In this class activity, you will find any two decimal numbers which add up to 
  the given whole number:
  (a) Find any 3 pairs of decimal numbers which add up to 10.
   {e.g. 8.5 + 1.5, 5.5 + 4.5, and 3.55 + 6.45}
  (b) Find any 3 pairs of decimal numbers which add up to 1.
  

   {e.g. 0.25 + 0.75, 0.8 + 0.2 and 0.77 + 0.23}

  Example 5.6
  Add 528 + 7.49
  Solution
  We can write 528 as a decimal number by putting a decimal point after 8 
  

  and adding zeroes. So, 528 can be written as 528.00

  

  Example 5.7
  Add the following decimal numbers:
  (a) 206.1 + 223.9              (b) 404.1 + 247.4                   (c) 665.2 + 567
  

  (d) 435.7 + 65.1                (e) 299.72 + 0.08

  

  Exercise 5.4
  

  Work out the following:
  

  (a) 4.7 + 4.7                (b) 2.78 + 3.62              (c) 20.9 + 25.7
  

  (d) 20.23 + 40            (e) 25.26 + 0.72             (f) 400.2 + 400
  (g) 18.6 – 8.6              24.6 – 20.4                (i) 6.25 – 4.25
  

  (j) 80.02 – 0.02          (k) 19.82 – 5.28             (l) 20.82 – 6.27
  (m) 20.9 + 25.7          5.8 + 1.3                     (o) 24.7 + 47.2
  
  5.6 Real life problems involving decimals
  Example 5.9
  Ogolla ate 0.5 of his apple in the morning and 0.2 of it in the afternoon. How 
  

  much of his apple did he ate altogether?

  

  Example 5.10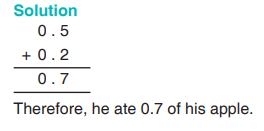
  1. Opio bought 4 metres of cloth and used 2.3 metres for making shirts. 
  Find the length of the remaining cloth.
  2. Nankinga weighs 94.2 kg and his brother Hamidu, 87.5 kg.
   What is the difference between their weights?
  

  
  
  Assessment Exercise
  1. Write the following decimal numbers in figures:
   (a) Three hundred ninety-nine point nine nine.
   (b) One thousand seventy point seven zero.
  
  
  3. Work out the following:
   (a) 84.0 + 79.3            (b) 9.1 – 6.1               (c) 53.3 – 23.2
   (d) 92.7 – 20.7           (e) 8.9 – 0.9                (f) 689.6 – 609.8
  

   (g) 100.5 – 50.5

  4. A boy walks 2.5 km to school and then 1.5 km to his friend’s home. 
  What is the total distance covered?
  5. The masses of four children in our class are 34 kg, 43.4 kg, 36.3 kg 
  and 38.2 kg. What is their total mass in kg?
  6. A lesson starts at 8:30 a.m. and lasts for 50 minutes. At what time does it end?
  7. The lengths of four rivers are 2.5 km, 4 km, 10.45 km and 0.95 km 
  respectively. What is the total length of the four rivers? By how much is 
  the longest river more than the shortest river?
  8. In an athletics school race competition, the time taken to complete 
  100 m race is given below:
  
  
  (a) Who won the race? Explain why.
   (b) Who came last in the race? Explain why.
  (c) For how long did the first competitor wait for the last person to 
  

  finish the race?

  9. If x = 23.23 and y = 32.32, find the value of:
   (a) x + x
   (b) x + y
   (c) y – x.
  10. By how much is 18.5 greater than 14.6?
  11. I am 9 years old. My elder sister is 14.5 years old. My mother is 31.5 
  years older than me.
   (a) How old is my mother?
   (b) What is the total of all our ages?
  12. My wrist watch displays time using figures. The time right now is shown 
  

  as 8:15 a.m. What time will my watch show after 15 minutes from now?

• UNIT 6:Length Measurements

  

  Key unit competence
  A learner should be able to know the meaning of length, conversion between 
  units of length and apply them in solving mathematical problems related to 
  daily life situations.
  
  Attitudes and values
  Learners should appreciate the importance of metric measures in daily life and 
  recognise the importance of using, measuring tools correctly.
  
  6.1 Meaning of length
  

  Distance between two points is known as length.

  

  6.2 Instruments for Measuring Length
  There are many instruments used for measuring length. These types of 
  instruments are used depending on the size of the length to be measured. 
  Some instruments used for measuring length/distances are shown below;
  1. Ruler: It is used to measure short distances like length of a line in a book, 
  

  length of a table, classroom, height of a door

  

  2. Tape measure: It is used for measuring longer distances like length of a 
  

  field, height of a person, length of a cloth, etc.

  

  3. Yard stick: It is a flat wooden board with markings at regular intervals. It 
  

  is used for measuring small lengths.

  

  4. Micrometer screw gauge: It is used for measuring very small distances 
  such as diameter of a pin or the thickness of a paper. A micrometer screw 
  

  gauge appears like shown below:

  

  Other instruments used for measuring length are vernier calliper,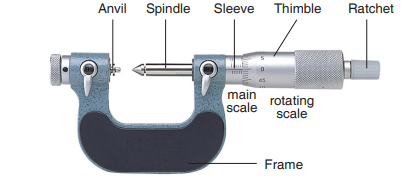 
  

  Architect’s scale, etc.

  6.3 Units of Length
  6.3.1 Non-standard Units

  

  We can measure the length using pace, handspan, foot span, cubit, etc. These 
  units vary from persons to persons as they have different pace. This method is 
  used by the same person to measure small distances.
  For example, the length of a table is 6 hand spans, the length of a carpet is 8 
  

  foot spans.

  

  

  Activity 6.1
  • Stand straight up on the floor.
  • Place the metre rule near your foot so that it is 
  parallel to the side of your body.
  • Mark a point on your body where the end of the 
  metre rule touches.
  • Now you have your own metre rule and be sure 
  to tell the length of 1 metre.
  • Cut the stick provided so that its length is 1m.
  • How many times does your foot fit into a metre? 
  • You can now use your foot to measure the length of a classroom.
  
  Activity 6.2
  • Hold the metre rule as shown in the diagram. 
   The zero mark ofthe metre rule must be 
   at the tip of your finger.
  • Mark a point on your arm/chest where the 
  end of the metre rule touches.
  • This is the length of 1m. Now you have 
  your own metre rule.
  • You can now use it to measure the length 
  of your table.
  • While at home, you can try to measure/estimate the height of a table, your brother, 
  your sister, your parents/guardians, length of your bed.
  

  Exercise 6.1
  1. Check and write the lengths/heights of the following objects present in your home
  
  2. Check and write the length/height of the following.
  
  
  6.3.2 Standard Units of Measuring Length
  The standard unit for measuring 
  length is metre. It is denoted by ‘m’. 
  The other units of length are the kilometre (km), hectometre (hm), decametre 
  (dam), decimetre (dm), centimetre (cm) and millimetre (mm).
  
  Metric-unit PrefixesMetric
  prefixes are very useful in converting units of quantities.
  The main metric prefixes dealt with at this level are the kilo, hecto, deca, deci, centi and milli.
  
  
  Important mnemonic:
  It is important to remember the order of the above prefixes:
  Kigali Hotel Deserves One Delicious Chocolate Milk, where Kigali kilo, 
  Hotel →hecto, Deserves →deca, One →one (Unit), Delicious→ deci, 
  Chocolate→ centi, and Milk →milli.
  From the above table we can see that;
  • One kilometre = 1 km = 1000 m. 
  • One hectometre = 1 hm = 100 m
  • One decametre = 1 dam = 10 m
  • One decimetre = 1 dm = 0.1 m ( a tenth of a metre)
  • One centimetre = 1 cm = 0.01 m = (hundredth part of a metre)
  • One millimetre = 1 mm = 0.001 m = (a thousandth of a metre)
  
  Activity 6.3
  • Place the metre rule on your work table 
  or desk.
  • Identify the 0 cm and the 100 cm marks 
  on the metre rule.
  • Confirm that the metre rule is divided into 
  10 equal parts. How many decimetres 
  make up a metre? {10 dm = 1 m}
  • Look closely at 1 dm.You should be able to see that 1 dm is divided into 
  10 equal parts. Each part is a centimetre (cm). How many cm make up 
  1dm? {10 cm = 1 dm)
  • Look closely at 1 cm. You should be able to see that 1 cm is divided into 
  10 equal parts. Each of these is called a millimetre (mm). How many 
  mm make up a cm? {10 mm = 1 cm}.
  • Now measure the length of your longest finger. Record your answer in 
  dm, cm and mm.
  
  Exercise 6.2
  Estimate the length of the following in metres.
  (a) length of a car.                                             (b) length of a bus.
  

  (c) length/height of your handspan.         (d) length of your pace.

  6.4 Estimation of Length
  In this section, we will study to find the length of objects by observing them.
  For example, the length of a notebook is about 12 cm, the length of a pencil is 
  about 5 cm, etc.
  
  Activity 6.4
  

  Estimate the length of the following in metres.

  

  Exercise 6.3
  Since we have practically seen the length of a mm, cm, dm, m, dam, hm and 
  km, it is now time to see how well you can estimate length.
  Estimate the following lengths:
  (a) Length of your foot (in cm).
  (b) Length of your classroom (in m).
  (c) Length of your pencil in mm (or cm).
  (d) Width of your exercise book (in cm).
  (e) Length of your table (in dm).
  

  (f) Height of your best friend in class (in cm or m).

  6.5 Conversion of Units 
  When converting from one unit of length to another, we can easily use a 
  conversion table.
  

  
  

  Conversion table for length

  
  

  From the conversion table, you can see that;
  • 1 km = 10 hm, 1 km = 100 dam, 1 km = 1000 m
  • 1 m = 10 dm, 1 m = 100 cm, 1 m = 1000 mm,
  • 1 hm = 0.1 km, 1 dam = 0.01 km, 1 m = 0.001 km
  • 1 dm = 0.1 m, 1 cm = 0.01 m, 1 mm = 0.001 m.
  
  Example 6.1
  Convert the following units of length:
  (a) 2 km to m        (b) 2 km to hm        (c) 10 cm to mm
  

  (d) 3 dam to m     (e) 40 m to mm       (f) 50 dm to cm

  
  

  
  

  Exercise 6.4
  1. Complete the following:
  (a) 40 km = ............... m                       (b) 350 cm = ............. mm
  (c) 3 hm = .................. m                      (d) 40 cm = .............. dm
  (e) 1 m = ................. mm                      (f) 2 900 mm = ......... cm
  (g) 3 000 000 mm = ............... m        5 000 m = ............. dam
  
  2. Use the conversion table to convert the following units of length as 
  instructed:
  (a) 2 m = ................ cm                        (b) 3 km = ............... dam
  (c) 2.5 m = ............. cm                        (d) 46 cm = .............. mm
  (e) 2 000 m = ............... km                 (f) 50 mm = ............... cm
  

  (g) 4500 dm = .............. dam.

  6.6 Addition and Subtraction of Length
  The process of addition or subtraction of length is exactly similar to the addition 
  or subtraction of ordinary numbers.
  
  Example 6.3
  Add the following:
  (a) 3 km + 200 m = ................... m
  (b) 50 hm + 40 dm = ................... dm
  (c) 16 m + 14 dm = ................... m
  

  (d) 76 hm + 4 km = ................... m

  

  Example 6.4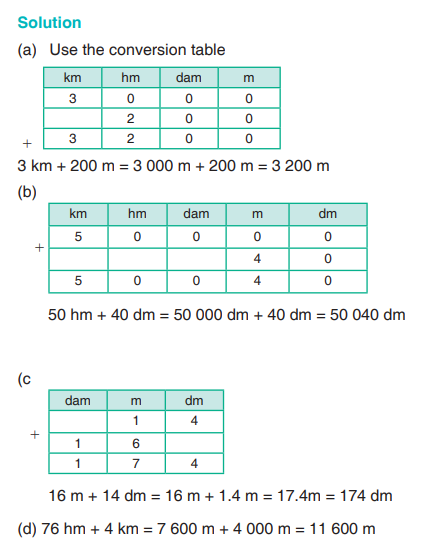
  Subtract: 1) 226 cm – 105 cm
  2) 3 m 15 cm – 1 m 35 cm
   3) 125.2 mm – 87.6 mm
  Solution
  1. 226 cm – 105 cm = 121 cm
  2. 3 m 15 cm = 3 × 100 cm + 15 cm
  

  = 300 cm + 15 cm

  = 315 cm

  1 m 35 cm = 100 cm + 35 cm
  

      = 135 cm

  Therefore, 315 cm – 135 cm = 180 cm

  

  Exercise 6.5
  Workout the following:
  (a) 30 km + 4 000 m = ............... m
  (b) 3 600 m + 44 hm = ............... km
  (c) 65 hm – 25 dam = ............... m
  (d) 30 km – 4 000 m = ............... hm
  (e) 40 hm – 200 dam = ............... dm
  

  (f) 500 m + 28 000 dm = ............... cm

  6.7 The Perimeter
  The perimeter of a closed figure is the distance around the figure. Since the 
  standard unit of distance or length is the metre (m), then the unit of perimeter 
  is the metre. However, perimeter can also be expressed in km, hm, dam, dm, 
  cm or mm.
  
  Example 6.5
  The diagram below shows a piece of paper. Length AB = 6 cm, length 
  BC = 2 cm, length CD = 6 cm and length DA = 2 cm. Calculate the distance 
  

  all round the piece of paper.

  

  Solution
  Perimeter = length of (AB + BC + CD + DA)
  

      = 6 cm + 2 cm + 6 cm + 2 cm

      = 16 cm.

  Example 6.6
  The diagram below shows an isosceles piece of cake PQR. The lengths of 
  the sides of the cakes are shown on the diagram. What is the distance all 
  

  round the figure PQR?

  

  Solution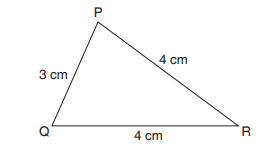
  Perimeter = Distance around PQR = PQ + QR + RP = (3 cm + 4 cm + 4 cm)
  

  = 11 cm.

  Example 6.7
  The diagram below shows a birthday card for my younger sister Cathy. The 
  length of each side of the card is 5cm. What is the total distance all round 
  

  the card?

  

  Solution

  Perimeter = Length of (PQ + QR + PR)
                       = 5 cm + 5 cm + 5 cm
                       = 15 cm
  

  Example 6.8
  What is the total distance around this plot of land? Express your final answer 
  

  in metres.

  

  Solution
  The sides are given in different units. We need to convert all units to metres 
  

  using the conversion table.

  

  From the conversion table 
  2 000 mm = 2 m
  20 dam = 200 m
  300 cm = 3 m
  10 dam = 100 m
  20 000 mm = 20 m
  So the required distance = 2 m + 200 m + 3 m + 100 m + 20 m + 90 m = 
  

  415 m

  

  6.8 Application of Length
  Sometimes, you find situations where you need to apply length in order to solve 
  them. Study the following examples.
  
  Example 6.9
  Trees are planted at an intervals of 10 m. If ten trees are planted, find the 
  

  distance from the first to the last tree.

  

  First find the number of spaces
   Number of spaces = Total number of trees – one tree = 10 – 1
                                          = 9 spaces
                          1 space = 10 m
                          9 spaces = (10 × 9) m = 90 m
  The distance is 90 metres.
  
  Example 6.10
  A rectangular garden 50 m by 30 m is to be fenced with poles placed 
  at an interval of 5 m. Find the amount of money required to fence the 
  

  garden at 3 000 Frw per pole.

  

  Activity 6.5
  Eleven bundles of wires, each of 125 cm long were needed from Kabuye’s house 
  

  to the electric pole. How far was Kabuye’s house from the electric pole?

  Assessment Exercise
  1. Estimate the following lengths: 
   (a) Height of your teacher (in m).
  (b) Length of your football field at school (in m).
   (c) Height of the tallest tree at your school (in m).
   (d) Length of your handspan (in cm).
  2. Workout the following:
   (a) 1 100 mm + 1 100 cm = ............... cm
   (b) 800 hm + 5 000 dam = ............... km
   (c) 1 km + 1 hm + 1 dam + 1 m + 1 dm + 1 cm + 1 mm = ................... mm
  

  3. Find the perimeter of the shape shown in the diagram below:

  

  4. Electric poles are fixed at intervals of 50 m apart. If 101 poles are 
  fixed, find the distance from the first pole to the last pole.
  
  5. How many poles are required to make a circular fence of 45 m if the 
  poles are 5 m apart?
  
  6. Othieno has to fence his rectangular garden of 45 m by 30 m.
   (a) Find the number of poles he will require if the poles are 5 m apart?
   (b) If each pole costs 4 500 Frw, how much does he require to buy the 
  poles?
  
  7. Find the number of trees required to plant around a circular pond of 
  

  length 28 m at intervals of 4 m apart.

  8. Luzige’s land is in a shape of trapezium as shown:

  

  He intends to fence it with poles 5 m apart. How many poles does he 
  require?
  9. Workout:
   (a) 1.25 cm + 7.75 cm
  

   (b) 9.75 dm + 2.45 dm

  Internet Resource
  

  For more online support visit www.kidsnumbers.com

• UNIT 7:Capacity Measurements

  

  Key Unit Competence 
  A learner should be able to understand capacity, convert between units of 
  capacity and apply them in solving mathematical problems related to daily life 
  situations.
  
  Attitudes and values
  • Show an ability to properly use a range of materials to measure different 
  liquids in daily life.
  • Being honest and trustworthy when measuring different capacities.
  • Being able to show respect for one another when working in groups.
  
  7.1 Understanding Capacity
  In our daily conversation, we usually make statements like:
  

  • This is a small plane and that is a big plane.

  

  • My cup is small but Dad’s cup is big.

  

  • An orange is smaller than a pineapple.

  

  • A lion is smaller than an elephant.

  

  All the above statements compares the volume or capacity of one object with 
  another.
  Volume is the space occupied by a given object.
  Capacity, on the other hand, is the amount of liquid or solid an object can hold.
  
  Activity 7.1
  Collect empty containers and compare their capacities by filling water or any 
  

  other liquid.

  

  7.2 Units of volume 
  Consider a container in the form of a cube as shown in the diagram below. 
  Each side of the container is of length 1 cm.
  

  Capacity of the container = length × width × height = 1 cm × 1 cm × 1 cm = 1 cm³.

  

  Activity 7.2
  (a) Measure the length (l), width (w), and height of the matchbox 
  provided. Record your results in millimetres (mm).
  (b) Calculate the volume of one matchbox using the formula; 
                                                              V = l × w × h.
  (c) Pile the matchboxes so as to form a big cuboid of matchboxes.
  (d) What is the volume of the big box you have formed?
  

  (e) Can you design other different big boxes using the same matchboxes?

  Exercise 7.2
  1. The figure below shows several small cubes of different colours joined 
  

  together. Each small cube has a volume of 1 cm³.

  

  (a) How many small cubes are there altogether?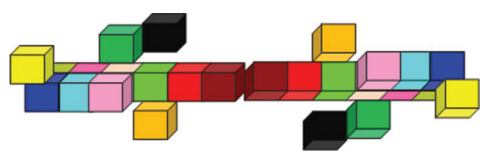
   (b) What is the total volume of all the cubes?
  

  2. Find the volume of the solids if each cube has a volume of 1 m³

  
  

  7.3 Estimating capacities of different containers
  Activity 7.3
  In this class activity, you are going to discuss the statements given with 
  your classmates. State whether you agree or not. You may experiment (if 
  possible) in your classroom.
  (a) The capacity of a tea spoon is about 5 ml or 5 cm³. The capacity of an 
  

  ordinary glass for drinking water is about 300 ml or 300 cm3 or 0.3 litre.

  

  (b) The capacity of a mug is about 0.5 litre. The capacity of a water jug is 
  

  about 2 litres.

  

  (c) The capacity of a small jerrycan is about 5 litres. The capacity of a big 
  

  jerrycan is about 20 litres.

  

  (d) A large water tank has a capacity of about 1 000 litres.

  

  

  Think!!!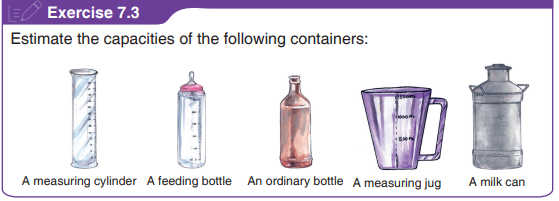
  

  What is full of holes and yet it holds lots of water?

  7.4 Conversion of units for capacity
  

  Conversion table for capacity

  

  We can see that,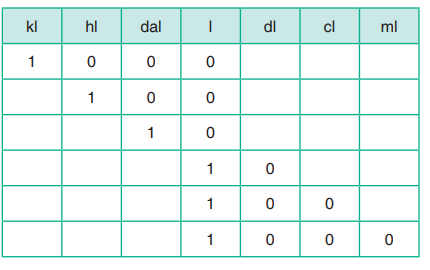
  1kilolitre = 1 kl = 1 000 l
  One hectolitre = 1 hl = 100 l
  One decalitre = 1 dal = 10 l
  One litre = 1 l = 10 dl
  One decilitre = 1 dl = 0.1 l (a tenth of a litre)
  One centilitre = 1 cl = 0.01 l (a hundredth of a litre), e.t.c.
  
  Example 7.1
  Change the following units of capacity as instructed below:
  (a) 20 l to ml          (b) 200 l to hl           (c) 20 kl to l
  (d) 50 kl to dal       (e) 100 dl to ml      (f) 35 hl to dal
  (g) 7 800 cl to l        60 000 ml to l
  
  Solution
  

  We construct a conversion table to enable us convert these units.

  

  (a) 20 l = 20 000 ml         (b) 200 l = 2 hl                         (c) 20 kl = 20 000 l
  (d) 50 kl = 5 000 dal       (e) 100 dl = 10 000 ml            (f) 35 hl = 350 dal
  (g) 7 800 cl = 78 l              60 000 ml = 60 l
  
  Activity 7.4
  A cow produced milk as follows; 
  Monday                  - 2 litres 
  Tuesday                 - 5 litres 
  Wednesday          - 3 litres 
  

  How much milk did it produce in three days? Write answer in ml.

  

  7.5 Addition and Subtraction of Capacity
  Activity 7.5
  In groups, do the following:
  • Measure the capacity of water in a jug.
  • Change this into litres.
  • Now, measure the capacity of a bucket by pouring water using 1 litre 
  bottles.
  • Compare the capacities. Which has more water? Obtain the total volume 
  of water in litre.
  
  Example 7.2
  (a) Add: 900 decalitres + 400 litres
  

  (b) Subtract: 24 litres – 2 400 centilitres

  

                      24 l – 2 400 cl = 2 400 cl – 2 400 cl = 0.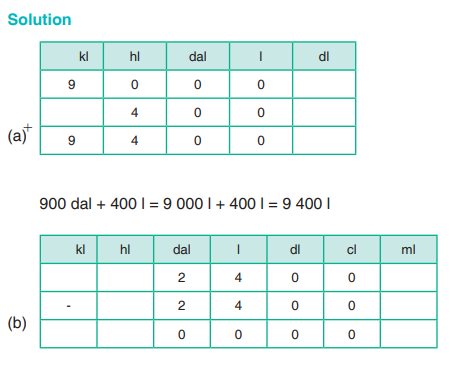
  
  Example 7.3
  (a) 7.50 l + 3.50 l
  

  (b) 6.30 l – 2.30 l

  

  7.6 Application of Capacity
  Example 7.4
  1. A bottle of mineral water has a capacity of 300 ml. How many bottles of 
  mineral water do I need to make 3 litres?
  
  2. Mutoni sells 11 cans of milk to a milk depot every week. If each can 
  of milk has a capacity of 20 litres, how much milk does she sell per 
  month?
  
  Solution
  1. 3 l = 1 000 × 3 = 3 000 ml. Since 3 l = 3 000 ml, therefore, the number 
  of mineral water bottles is given by:
  3000 ml ÷ 300 ml = 10
  
  2. Number of cans sold per week = 11
  Number of cans sold per month = 11 × 4 = 44 cans (1 month = 4 weeks)
  

  Quantity of milk sold in 1 month = 44 × 20 litres = 880 litres.

  Activity 7.6
  

  Study the following figure and answer the given questions:

  

  1. Find how much water should be added so as to fill up the tank fully.
  2. How much water was there earlier in the tank. (Dimensions shown in 
  

  figure are in centimetres)

  Assessment Exercise
  1. Add: (a) 3 l 500 ml + 5 l 700 ml (b) 3.25 l + 6.75 l
  2. Subtract: (a) 5 l 400 ml – 3 l 250 ml (b) 10.5 l – 2.75 l
  3. A restaurant sells 200 l of milk every day. How much milk is sold in
  3 months? (assume 1 month = 30 days).
  4. A school water tank contains 12 000 l of water. Pupils in the school 
  used 40 hectolitres of water. What amount of water is remaining?
  5. The capacity of a milk jug is 750 ml. By how much is this less than a 
  litre?
  6. The cost of milk is 150 Frw per mug (cup). Two such cups make up one 
  litre of milk. How much will a person spend on 4 litres of milk?
  7. On average, each pupil takes 1.5 litres of milk in our school. How much 
  milk is taken by 100 pupils? 
  8. A Friesian cow in a certain farm produces 
  15 litres of milk in the morning and 10 litres 
  of milk in the evening. How much milk does 
  it produce in a week? 
  9. The price of petrol is 900 Frw per litre. A school bus requires 100 litres 
  

  of petrol for a school trip. How much is spent on petrol?

  Internet Resource
  

  For more online support visit www.math-play.com/capacity

• UNIT 8:Mass Measurements

  

  Key unit competence
  By the end of this unit, a learner should be able to convert between units of 
  mass and apply them in solving mathematical problems related to daily life 
  situations.
  
  Attitudes and values
  Appreciate the importance of mass measurement in daily life, show respect 
  for one another, and appreciate difference in opinion while working with other 
  people and show fairness while measuring mass.
  
  8.1 Estimating Mass
  In this section, you will study to estimate the mass of an object by observing it 
  

  only.

  Activity 8.1
  • You will be provided with a stone of 
  mass 500 g (0.5 kg) and another stone 
  of mass 1 kg. Other alternative masses 
  may be provided.
  • Feel the mass of 500 g by holding the 
  stone in your hand.
  • Feel the mass of 1 kg by holding the stone in your hand.
  • You should repeat the experiment a number of times because this will help 
  you estimate masses of different objects.
  • With the help of your teacher, measure the mass of a pen, small stone, a 
  

  small exercise book, your shoes and a bottle top.

  Activity 8.2
  • With the help of your teacher, measure and record your mass in your 
  exercise book.
  • Compare your mass with the masses of your classmates.
  • Record the least and the highest mass in the class.
  • Use your imagination to estimate the mass of the teacher.
  • Ask the teacher to tell the whole class his/her mass after all pupils have 
  given their estimates.
  A butcher at a butchery in Kigali City sells meat. He is 2 m tall, very fat and 
  he puts on the biggest shoe size on market. What does he weigh? 
  
  

  Think!!!

  Exercise 8.1
  Estimate the mass of the following objects:
  (a) mass of a bottle of soda.               (b) mass of a pawpaw fruit.
  (c) mass of a goat.                                   (d) mass of a bull.
  (e) mass of a small car.                          (f) mass of a lorry.
  (g) mass of a knife.                                  mass of a mango leaf.
  (i) mass of a 10 year old pupil.            (j) mass of 10 sheets of paper.
  
  8.2 Measuring of Mass
  Activity 8.3
  Which unit would you use to measure the mass of the following? A kilogram 
  or a gram?
  (a) a tomato         (b) an egg                           (c) a radio
  (d) a baby              (e) an exercise book      (f) a school boy
  

  (g) a chair              an elephant                (i) a mathematical set

  Mass is the quantity of matter contained 
  in a substance. The more the matter, the 
  greater the mass. A house brick and a 
  piece of cotton of the same size have 
  different masses. A house brick has 
  more mass because it has more 
  quantity of matter than the cotton.
  The standard unit for measuring and expressing mass is kilogram. The 
  kilogram is represented by ‘kg’.
  However, mass can also be expressed in ton, denoted by ‘t’ where,
                             1 ton = 1 000 kg.
  
  Instruments for measuring mass
  The following instruments can be used to measure mass:
  

  Top pan balance, beam balance, triple beam balance, electronic balance, etc.

  

  Exercise 8.2
  Which units would you use to measure the following objects:
  (a) mass of a pencil.                          (b) mass of a ball.
  (c) mass of a cycle.                            (d) mass of a TV.
  
  8.3 Conversion between units of Mass
  Metric prefixes are very useful in converting units of quantities. The main metric 
  

  prefixes dealt with at this level are the kilo, hecto, deca, deci, centi and milli.

  

  From the above table we can see that;
  • One kilogram          = 1kg         = 1000g. 
  • One hectogram     = 1hg         = 100g
  • One decagram      = 1 dag       = 10g
  • One decigram       = 1 dg          = 0.1g ( a tenth of a gram)
  • One centigram     = 1cg            = 0.01g        = (hundredth part of a gram)
  • One milligram      = 1mg          = 0.001g       = (a thousandth of a gram)
  
  Note:
  The tonne is equal to one thousand kilograms.
  

  1 tonne (1t) = 1 000kg

  

  1q = 100kg.
  
  Read the following units of mass aloud: 
  (a) 20 t                   (b) 250 kg
  (c) 400 hg             (d) 680 dag
  (e) 500 g                (f) 230 dg
  (g) 100 cg              570 mg
  (i) 45 cg
  
  Example 8.1
  Convert the following units of mass:
  (a) 2 kg to g.                (b) 2 kg to hg.
  (c) 10 kg to g.              (d) 3 dag to g.
  

  (e) 40 g to mg.            (f) 50 dg to cg.

  Solution
  

  Conversion table

  

  (a) 2kg = 2 000g
  (b) 2kg = 20hg
  (c) 10kg = 10 000 000mg
  (d) 3 dag = 30g
  (e) 40g = 40 000mg
  (f) 50dg = 500cg
  
  Example 8.2
  Convert the following units of mass:
  (a) 2 000 g to kg.
  (b) 30 000 g to kg.
  (c) 15 000 cg to g.
  

  (d) 200 dag to hg.

  Solution

  
  

  (a) 2000g = 2kg
  (b) 30 000g = 30kg
  (c) 15 000cg = 150g
  

  (d) 200dag = 20hg

  Exercise 8.3
  1. Convert the following into grams.
   (a) 24 kg         (b) 8 kg           (c) 15 kg            (d) 12 kg          (e) 1.5 kg
   (f) 321 kg       (g) 2.8 kg
  
  2. Express the following in kilograms.
   (a) 15 000 g          (b) 2 400 g      (c) 7 000 g (d) 500 g
   (e) 912 g                 (f) 1 500 g
  
  8.4 Addition and Subtraction of Masses
  Example 8.3
  (a) Add: 4kg + 3hg = ........kg
  (b) Subtract: 29dg – 2.4cg = ........cg
  

  (c) Subtract: 10t – 9 600kg = ........kg

  Solution

  
  

  (a) 4kg + 3hg = 4kg + 0.3kg = 4.3kg
  (b) 29dg – 2.4cg = 290cg – 2.4cg = 287.6cg
  (c) 10t – 9 600kg = 10 000kg – 9 600kg = 400kg
  
  Exercise 8.4
  (a) Add: 3.25 kg and 1.75 kg and express the answer in grams.
  (b) Subtract: 5.25 kg from 25.65 kg and write answer in grams.
  
  8.5 Application of Mass
  In this section, we discuss the problems involving mass in real life situations.
  
  Example 8.4
  A school bought shields and cups for winners and runners-ups. There were 
  2 shields for the overall champions. If the weight of the smaller shield is 
  2 kg 120 g and bigger shield is 2 kg 865 g, then what is the difference in 
  their masses.
  
  Solution
  The weight of the bigger shield = 2 kg 865 g = 2 865 g
  The weight of the smaller shield = 2 kg 120 g = 2 120 g
  \ Difference in weight = 2 865 g – 2 120 g = 745 g
  
  Assessment Exercise
  1. Convert the following into grams.
   (a) 285 kg           (b) 19 kg        (c) 2.5 kg         (d) 196 kg.
  2. Convert the following into kilograms. 
   (a) 2126 g              (b) 9065 g             (c) 850 g
  3. There are 20 tins of biscuits in a shop. Each tin weighs 2 kg 500 g. 
  What is the weight of all the tins in kg?
  4. A car weighs 3 tons. Express this mass in kg
  5. An omnibus (taxi) is licensed to carry passengers with total mass 
  not exceeding 1 140 kg. If 20 people each of mass 60 kg board the 
  omnibus, find whether the omnibus is overloaded.
  6. A truck carries 200 bags of cement. The total weight of all the bags in 
  the truck is 10 tons. What is the mass of only 1 bag of cement?
  7. Each book in a certain bookshop has a mass of 20 dg. How many of 
  these books do I need to have 1 ton of books?
  8. Yesterday, I bought 4 kg of mangoes and ate 2 000 g. How many 
  grams of mangoes are left?
  
  
  9. The mass of 1 chocolate bar is 100 g. What is the mass of 30 chocolate 
  bars in kg?
  10. The mass of 1 toy car is 600 g. What is the total mass of 60 toy cars?
  
  11. Ms Annet packed 24 kg of sugar equally into 8 bags. How many grams 
  of sugar did she pack in each bag?
  12. Peter has a mass of 82 kg. John is 5 kg heavier than Peter. What is the 
  mass of John?
  13. John weighs 80 kg, Peter weighs 70 kg and Eric weighs 90 kg. How 
  

  much do the three people weigh altogether?

  Internet Resource
  

  For more online support visit www.kidsnumbers.com

• UNIT 9:Area and Land Measurements

  

  Key unit competence
  By the end of this unit, a learner should be able to understand area as a two 
  dimensional (2D) space enclosed by a boundary. The learner should also use 
  square and land units in solving mathematical problems.
  
  Attitudes and values
  Appreciate the need to properly and accurately use different area and land 
  measurements in daily life situations.
  

  9.1 Understanding Area

  
  

  In the preceding figure, the shaded part (green) is a square of length 1 mm and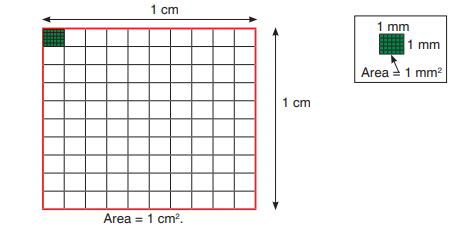 
  width 1 mm. The area of this part is 1 mm × 1 mm = 1 mm²
  .
  Now, consider the big square (red). There are 10 small squares along its length 
  and 10 squares along its width. 
  So, the area of the big square = 10 mm × 10 mm = 100 mm².
  
  Important point
  If area = 100 mm², then there are 100 squares each of area 1 mm².
  

  

  Activity 9.1
  Refer to the area grid shown:
  • What is the area of 1 small square?
  • What is the area of the big square?
  • Count the number of small squares in
  

  the big square.

  Exercise 9.1

  In the figure below, each small square has both length and width of 1 cm.

  

  (a) What is the area of one small square?
  (b) How many small squares are in the figure?
  

  (c) What is the area of the whole figure?

  9.2 Units of Area
  The standard unit of area is the square metre. It is written as m2
  . However, 
  other units for measuring area are km², hm², dam², dm², cm² and mm².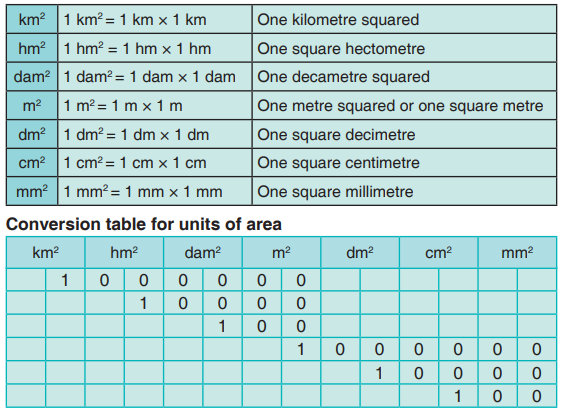
  
  

  From the conversion table above, we can see that:
  1km² = 1 000 000 m²
  1hm²= 10 000 m²
  1dam²= 100 m²
  1 m² = 1 000 000 mm²
  1dam²= 10 000 dm²
  1cm² = 100 mm²
  
  The meaning of 1 km²
  Consider a square plot of land ABCD such that 
  BC is 1 km long and CD is also 1 km long as 
  shown.
  Area of the plot ABCD = length of side BC x 
  length of side CD = 1 km x 1 km = 1 km².
  The area of this plot of land is 1 km², which is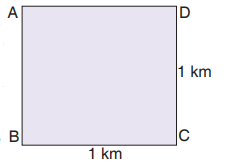
  
  
  read as “one kilometre squared” or “one square kilometre”.
  NOTE:
  Since 1 km² = 1 km x 1 km, then we can easily change 1 km² in to other units 
  of area such as m².
  1 km²= 1 km x 1 km = 10 hm x 10 hm = 100 hm².
  
  Read the following areas aloud:
  (a) 50 km2         (b) 600 hectares         (c) 40 acres
  (d) Our school football field has an area of 7 000 m²
  (e) My study table is 320 cm2 (f) The size of my wall photo is 300 mm².
  
  Exercise 9.2
  Change the following units of area as instructed:
  (a) 1 km²    = _______ m²
  (b) 10 m² = _______ cm²
  (c) 25 dam²  = __________ m²
  

  9.3 Relationship Between Land Measurement and Area
  Land area is measured in a larger unit called the hectare. It is written in short as ha.
  Other units of area include; are, acre and hectare.
  • A plot of land measuring 100 m by 100 m has an area of 
  1 hectare. So, 1 hectare (1 ha) = 100 m × 100 m = 10 000 m².
  • A plot of land measuring 10 m by 10 m has an area of 1 are. 
  So, 1 are = 100 m².
  • 1 ca = 1 m², i.e. 1 centiare = 1 square metre.
  • 1 acre = 0.40 hectare and 1 hectare = 2.47 acre.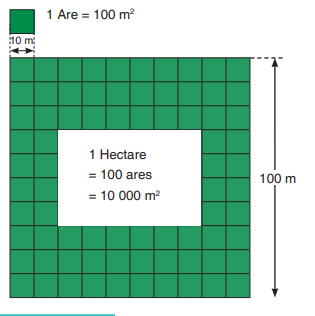
  
  
  
  1ha = 100a
  1a = 100 ca
  1 ha = 10 000ca
  

  1ca = 1m²

  
  

  
  

  1 hm²= 1ha, 1dam²= 1a, 1m²= 1ca.
  
  Activity
  Study the conversion table above. Discuss with your group members and 
  answer the following questions:
  

  • 1a = ..........ca

  • 1dm²= .........ca
  

  • 10a = ............ha

  • 20ca = ............cm²
  

  • 5dam²= ............dm²
  

  • 25m²= ...............ca
  

  • 25ca = ..............a

  • 5 000 m² = ^.......h

  Activity 9.2
  In this class activity, you will find the area of a plot of land of length 10 m and 
  width 5 m by counting the number of square metres in it.
  (a) 10 m can not fit into your book, so you will use a scale of 1 cm to represent 
  1 m. Draw a rectangle of length 10 cm and width 5 cm in your book.
  (b) Divide the length into 10 equal parts using vertical lines. Each part 
  should be equal to 1 cm.
  (c) Divide the width into 5 equal parts using horizontal lines as shown in 
  the diagram below:
  
  (d) Count the number of small squares formed by the lines you have 
  drawn. You can do this by numbering all the small squares.
  (e) Each small square represents an area of 1 m². 
  

  (f) Now answer this question: What is the area of the plot of land?

  Example 9.1
  Convert the following units of area:
  (a) 3 m²  to cm²
  ( b) 5 km² to dam²
  (c) 2.5 hectares to m²
  
  Solution
  
  (a) 3m² = 30 000cm²
  (b) 5km² = 50 000dam²
  

  (c) 2.5 ha = 25 000m²

  Exercise 9.3
  Convert the following units:
  (a) 5 km² in m².
  (b) 1 hectare in m².
  (c) 10 are in m².
  

  9.4 Area of Rectangular Piece of Land
  

  
  Example 9.2
  Find the area of a rectangular piece of land whose length and width are:
  (a) 80 m and 20 m.            (b) 100 m and 40 m.
  
  Solution
  (a) Area = length × width = 80 m × 20 m = 1 600 m².
  (b) Area = 100 m × 40 m = 4 000 m^2.
  
  Exercise 9.4
  1. The length of a house floor is 10 m and its width is 8 m. What is the 
  area of the floor?
  2. The area of the floor of our classroom is 40 m². How long is the 
  

  classroom if it is 5 m wide?

  9.5 Addition and Subtraction of the Area of Land

  Activity 9.3
  

  In groups, do the following:
  • Measure the length and width of your classroom.
  • Also, measure the length and width of another classroom.
  • What is the total area? What is the difference between the areas of two 
  

  rooms? Write the answers in m².

  Activity 9.4

  In this class activity, you are going to work in groups and find the area of the 
  plot of land shown below. Divide the land in two parts. Find the areas of plot 
  

  separately. Add the area of the two plots and express in m².

  

  

  Assessment Exercise
  1. Change the following units of area as instructed.
   (a) 2 500 cm²  = ________ m²
   (b) 8 000 m²  = ____________ hm²
   (c) 6.5 km²   = ____________ dam²
  
  2. A piece of paper has an area of 6 cm².
  If it is 3 cm long, then how wide is the paper?
  
  3. (a) Add 25.32 m² and 62.28 m².
   (b) Subtract 4.25 ha from 6.75 ha.
  
  4. School A is built on 1 are of land and school B is built on 100 m² of land. 
  Which of the two schools has bigger area?
  
  5. On a fruit farm, 1 are of land produces 2 tons of oranges. How many 
  kilograms of oranges will be produced by 300 m²
   of the same farm land?
  
  6. Kenia has a plot of land measuring 100 m by 100 m. Peter’s land has 
  an area of 3 hectares and Kwame has an area of 200 ares. Who has 
  the largest land? What is the total Land area in hectares?
  
  7. The total land area of our country Rwanda is 26 338 km².
  Lake Victoria has an area of 69 484 km².
  By how much is Lake Victoria bigger than Rwanda?
  
  

  Internet Resource

  Internet Resource  http://www.mathplace.com/

  
  

• UNIT 10:Time

  Key unit competence
  The learner should be able to tell, write and convert time appropriately.
  
  Fun Corner
  “Who has two hands but can’t wave?”
  Ans: Eeeehhhh.....ahahaha....Am I not Mr. Clock?
  “You are my friend, I am your friend. You can wait for me but I can never wait 
  for you!” Who am I? 
  Ans: Ahahaha...... I am Mr. Time.
  
  Attitudes and values
  Appreciate the value of time management in daily situations.
  
  9.1 Reading and Telling Time
  

  Time is a measure of durations of events and the intervals between them.

  

  The short hand of the clock is called the hour hand. It measures time in hours. 
  If it rotates once round the clock face, then the time taken is 12 hours.
  The long hand of the clock is the minute hand and it measures time in minutes. 
  One full rotation equals 60 minutes.
  The thinnest hand is the second hand. Of the three, it rotates the fastest. Its 
  

  full rotation equals 60 seconds.

  

  There are two common ways of telling time:
  (i) Say the hour first and then the minutes e.g.
  • 6:25 = It is six twenty-five
  • 8:05 = It is eight O-five (O is said like letter O)
  • 9:11 = It is nine eleven
  • 2:45 = It is two forty-five
  (ii) Say the minutes first and then the hour e.g.
  • 2:16 = It is sixteen past two
  • 11:20 = It is twenty past eleven or it is eleven twenty
  • 8:30 = It is half past thirty or it is eight thirty
  • 8:40 = It is twenty to nine or it is eight forty
  • 11:59 = It is one to twelve or it is eleven fifty-nine
  • 8:51 = It is nine to nine or it is eight fifty-one.
  
  Use of the words ‘past’ and ‘to’
  • If it is 30 minutes or less after the 
  hour, we use the word “past”. For 
  example, if it is 1:16, we can say 
  that the time is sixteen past one. 
  • If it is more than 30 minutes after 
  the hour, we use the word “to”. For 
  example, if the time is 3:55, we see 
  that it is only 5 minutes remaining 
  to reach 4 o’clock. So we can say 
  that the time is 5 to four o’clock.
  
  Quarter past/to and half past
  15 minutes is a quarter of 60 minutes and 30 minutes is half of 60 minutes.
  

  • When it is 15 minutes past the hour we use the words “quarter past” e.g. 
  6:15 = a quarter past six, 9:15 = a quarter past nine etc.
  • When it is 15 minutes to the hour, we use the word “a quarter to”, e.g. 
  10:45 = a quarter to eleven, 4:45 = a quarter to five etc.
  • When it is 30 minutes past the hour, we use the words “half past” not “half 
  to”. e.g. 7:30 = half past seven, 12:30 = it is half past twelve etc.
  
  O’clock
  We use o’clock, when there are no minutes. We use o’clock when the time is 
  exact. For example; 2:00 = two o’clock, 11:00 = eleven o’clock etc.
  
  12:00
  When it is exactly 12:00, we say it is twelve o’clock. There are 2 twelve o’clocks 
  in a day namely:
  • Twelve o’clock midday. This is also referred to as noon.
  

  • Twelve o’clock midnight.

  

  Solution
  (a) The time is 9:40. This may be 9:40 a.m. or 9:40 p.m.
  (b) The time is 5:20. It may be 5:20 a.m. early morning or 5:20 p.m. in the evening.
  (c) It is one o’clock.
  (d) The time is 8:40
  (e) The time is 7:40
  

  (f) The time is 2:20

  Exercise 10.1
  1. Match the digital and analogue clocks which show the same time. You 
  

  may use an arrow.

  

  

  10.2 Writing Time Using a.m. and p.m.
  Time using a.m. is ante meridian, means before midday.
  Time using p.m. is post meridian, means after midday.
  a.m. starts at exactly midnight at a time called 12:00 o’clock up to just before 
  midday (12 noon). p.m. starts at midday at a time called 12 noon and ends just 
  

  before midnight.

  Activity 10.2
  Use a manilla card and plastics to form a model clock as shown below. Your 
  

  teacher will help you. Use it to show the time mentioned below.

  

  Example 10.2
  Express 9 o’clock in the morning using a.m. or p.m.
  
  Solution
  9 o’clock in the morning is 9:00 a.m.
  
  Example 10.3
  What time is a half past 5 o’clock in the evening?
  
  Solution
  A half past 5 o’clock in the evening is 5:30 p.m.
  
  Exercise 10.2
  1. Write the time using ‘a.m.’ or ‘p.m.’: 10 o’clock in the morning?
  2. Express 6 o’clock in the morning as a.m. or p.m.
  3. What time is half past 11 o’clock in the morning?
  4. Express 2 o’clock in the afternoon using a.m. or p.m.
  5. My father left Moroto at a quarter to 7 o’clock in the morning. Write this 
  

  time using a.m. or p.m.

  10.3 Units of Time and Their Conversion
  The standard unit of time is the second. The second is written in short as ‘s’.
  Other units used to express time are minute, hour, day, week, fortnight, month, 
  year, decade, century and millennium, where
  1 minute = 60 second(s).
  1 hour = 60 minutes.
  1 day = 24 hours.
  1 week = 7 days.
  1 fortnight = 2 weeks.
  1 month = 4 weeks.
  1 year = 12 months (365 days).
  1 decade = 10 years.
  1 century = 100 years.
  1 millennium = 1000 years.
  
  • An ordinary (common) year has 365 days and February ends on 28th.
  • A leap year is a year which has 366 days and its February ends on 29th.
  • 2004, 2008, 2012 were leap years and the next leap year is 2016.
  • A full day has both daytime and night time, each of which lasts 12 hours.
  
  Activity 10.3
  In this class activity, you will work in groups and find out the number of
  seconds that are found in:
  (a) 1 minute                           (b) 1 hour                                    (c) 1 day
  (d) 1 week
  
  Example 10.4
  Change 4 hours to minutes.
  
  Solution
  1 hour = 60 minutes
  4 hours = (4 × 60) minutes = 240 minutes.
  
  Example 10.5
  Change 180 minutes to hours.
  
  Solution
  60 minutes = 1 hour
  180 minutes = 180 ÷ 60 = 3 hours
  Therefore, 180 minutes = 3 hours
  

  

  10.4 The Calendar
  A calendar is a chart showing days, weeks and months of a particular year. A 
  calendar helps us to identify days and be informed of special days like Christmas, 
  

  Independence Day, school term opening and closing days, birthdays, etc.

  

  Example 10.6
  Name the days of a week.
  
  Solution
  Days are: Sunday, Monday, Tuesday, Wednesday, Thursday, Friday and Saturday.
  
  Example 10.7
  Name the months of the year.
  
  Solution
  Months are: January, February, March, April, May, June, July, August, 
  September, October, November, December.
  
  Activity 10.4
  In this activity, you will list down all the activities you do in a day right from 
  the time you wake up till you go to sleep.
  
  Activity 10.5
  You will work in small groups with your classmates to finish this activity.
  Carefully follow the teacher’s instructions.
  

  Study the calendar below and answer the following questions:

  

  (a) For which year does the calendar belong?
  (b) For which month of the year is the calendar?
  (c) What does ‘Mo’ stand for in the calendar?
  (d) On what day does the month begin?
  (e) On what day does it end?
  (f) How many week days does the month have?
  (g) Ineza played football for 30 minutes on each weekend days of the 
  month. How many seconds did he spend playing football in the whole month?
  How many days are there in the month?
  (i) On what date is the last Sunday of the month?
   (j) A certain conference started on the first Monday at 9:00 a.m. and
  
  Activity 10.6
  Form yourselves into groups of 4 learners each. Study the calendar and 
  discuss the questions below:
  (a) For which year does this calendar belong?
  (b) How many months are found in a year?
  (c) Which months have 30 days?
  (d) Which months have 31 days?
  (e) What is the last month of the year?
  (f) In which month were you born?
  

  (g) In which month does Rwanda celebrate independence?

  

  Think!!!
  Charles’ mum has three children. The first is called June. The second child
  is called July. What is the name of the third child?
  Exercise 10.4
  Using the given calendar, answer the following:
  1. How many days are there in the months of January, February (not a 
  leap year) and March?
  2. List down all months with 30 days.
  

  3. Write down all months of the year with 31 days.

  10.5 Problems Involving Time
  Example 10.8
  Kato, is a brick layer. He makes 120 bricks every day. How many bricks 
  does he make in the month of January, if he works every day?
  
  Solution
  In one day, he makes 120 bricks. But, January has 31 days.
  Therefore, in 31 days, he makes = 120 × 31 = 3720 bricks
  Therefore, he will make 3 720 bricks.
  
  Example 10.9
  Dorah is a mother of 3 children. She has a job in town and this job enables 
  her to take care of her children. She goes to town everyday except on 
  Sundays. How many times does she go to town in the month of September, 
  if there are 4 Sundays in September?
  
  Solution
  September has 30 days and there are 4 Sundays.
  (30 – 4) days = 26 days
  Therefore, she goes to town 26 times in the month of September.
  
  Example 10.10
  It takes Aminyo 2 hours 30 minutes to travel from Kampala to her village in 
  Luwero. If she walks from Luwero town to her village for 1 hour 10 minutes, 
  

  how much time does she spend moving from Kampala to Luwero town?

  

  Activity 10.7
  1. In groups, study the following class time table and answer the questions 
  

  given below:

  

  (a) How many periods are there before break on Monday?
  (b) On which day is the school’s general assembly held?
  (c) How long is planned for P.E. in the whole week?
  (d) Which subject is given biggest amount of time and how long?
  (e) On Wednesday, the Science teacher came to class at 10:30. He 
  conducted an experiment in our class for 15 minutes. We then used the 
  remaining part of the lesson for doing a test. How long was the test?
  (f) Last Friday, the community service was extended by 55 minutes 
  because of rain. At what time did it end?
  

  Assessment Exercise

  1. Draw the hour and minute hands on the following clock faces to show 
  

  the correct times indicated:

  
  

  2. Our school timekeeper always rings the bell at half past 10 o’clock in the 
  morning. Write this time using a.m. or p.m.
  
  3. A match between Arsenal and Everton started at a quarter past 6 o’clock 
  in the evening on Saturday. Write this time in a.m. or p.m.
  
  4. Express the following as minutes:
   (a) 80 seconds     (d) 150 seconds     (g) 240 seconds    (j) 360 seconds
   (b) 70 seconds    (e) 130 seconds      180 seconds    (k) 720 seconds
   (c) 120 seconds  (f) 480 seconds       (i) 300 seconds      (l) 540 seconds
  
  5. Gloria sold pancakes every day for 2 months as follows:
  September, 200 pancakes every day.
  October, 100 pancakes every day.
   (a) How many pancakes did she sell in September?
   (b) How many pancakes did she sell in October?
   (c) Find the total number of pancakes Gloria sold in the two months.
  
  6. Bwire started washing clothes at 6:30 a.m. and stopped at 7:45 a.m. 
  

  How much time did he take to wash clothes?

  Internet Resource
  

  For more online support visit :http://www.mathplayground.com/

• UNIT 11:Money and Its Financial Applications

  

  Key unit competence
  A learner should be able to understand what money is and know its applications 
  in our daily life.
  
  Attitudes and values
  Appreciate the importance of money in daily life situations and show concern 
  and the need for honesty in spending money.
  
  11.1 What is money?
  Money is a piece of paper or metal which is legally accepted to be used for 
  buying goods and services within a country. 
  A service is something you cannot hold in your hand e.g. education, internet, 
  advice.
  National Bank of Rwanda makes money for use in Rwanda.
  
  Characteristics of money:
  • It cannot be easily damaged.
  • It is very scarce. That means it is hard to get money.
  • It is easy to carry. 
  • It is hard to forge.
  • It should be easily divisible into smaller denominations.
  • It is accepted by everyone.
  
  Uses of money: 
  • It is used for buying goods like books, cars, food, mobile phones.
  • It is used for buying services like education (school fees), medical 
  treatment, airtime, insurance, etc.
  • It is used to keep wealth.
  

  • It is used to pay debts.

  11.2 Rwandan Currency
  The money used in our country (Rwanda) is known as Rwandan francs. It is 
  usually denoted by ‘’. FRW
  

  In Rwanda, we use both notes (paper money) and coins (metallic money).

  Rwandan Currency Coins:

  
  

  Activity 11.1
  In this class activity, you are provided with 6 different Rwandan coins.
  a) Identify the 1, 5, 10, 20, 50 and 100 Frw coins.
  

  b) Discuss with your friends what item can be bought by each coin denomination.

  Rwandan Currency Notes: 

  
  

  Activity 11.2
  In this class activity you are provided with four Rwandan currency notes.
  a) Identify the following notes: 500 Frw, 1 000 Frw, 2 000 Frw and 5 000 Frw.
  b) Discuss with your friends what item each currency note can buy in Rwanda.
  c) Is there any other currency note whose picture is not shown above?
  
  Example 11.1
  My mother gave me money to buy a new school uniform. It was 5 150 Frw 
  in an envelope. In the envelope, there was only one note and two coins. 
  Identify the note and the coins my mother gave me.
  
  Solution 
  Total money = 5 150 Frw. 
  Since there was only one note, it must have been the 5 000 Frw note. There 
  is no coin for 150 Frw, so the two coins are 100 Frw and 50 Frw.
  
  Example 11.2
  Paul bought sweets from a shopkeeper. He paid the shopkeeper 
  550 Frw using only coins of 50 Frw each. How many coins did he gave to 
  

  the shopkeeper?

  

  Exercise 11.1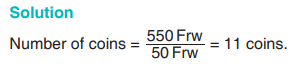
  1. What do we call the national currency used in Rwanda?
  2. Which Rwanda note has the highest value? 
  3. A mother gave three notes of 1 000 Frw and five coins of 50 Frw to her
  son to buy school uniform. What was the total amount of money given 
  by the mother?
  4. Three men shared 15 000 Frw equally. How much money did each 
  

  man get?

  Sample Currency Notes from Other Countries

  

  11.3 Planning According to Needs and Wants
  A need is something you cannot live without. A need is something you must 
  have for you to survive. Examples of needs are food, shelter, clothing and 
  medical care.
  
  A want is something you would like to have but you can live without it. It is not 
  absolutely necessary but it would be a good thing to have. Examples of wants 
  are music, TV, computer, car, toys, mobile phone, radio, electricity.
  
  Scarcity and Budgeting
  Those in towns and cities buy most of their needs and wants including food, 
  clothes, etc. Those in villages may get food from their gardens and also live in 
  their own houses for free. However, everyone needs money to buy salt, sugar, 
  medicine, airtime, soda, bicycle, clothes etc. One of the biggest problems that 
  we all have is scarcity of money. We don’t always have money for everything 
  that we need or want.
  
  Therefore, every time we have money, we need to plan carefully for the money 
  

  so that we buy only the most important things. This planning is called budgeting.

  Activity 11.3
  

  a) Identify the basic needs from the below list

  

  b) Plan your budget according to your priorities. How will you spend 5 000 Frw?

  11.4 Buying and Selling

  
  

  A person who buys goods or services and sells to others is called a trader or 
  businessman or businesswoman. 
  Selling is the act of giving out goods to someone in order to get money.
  Buying is the act of giving money to someone in order to get goods that you 
  

  need.

  Cost Price and Selling Price
  A shop keeper goes to a factory and buys 1 crate of soda at 4 500 Frw. If he 
  sells the crate to a customer at 6 500 Frw, then the cost price is 4 500 Frw
  and the selling price is 6 500 Frw.
  
  11.5 Profit and Loss
  • If the selling price is more than the cost price, then the shopkeeper makes 
  a profit. This means he gets extra money and he becomes richer.
  • If the selling price is less than the cost price, then the shopkeeper suffers 
  a loss. This means he loses some money and he becomes poorer.
  
  Example 11.3
  Manzi was given 3 000 Frw by his father as pocket money for school 
  use. He bought a pen at 200 Frw, a book at 500 and geometry set at 
  900 Frw. How much money is left with him? 
  
  Solution
  

  Cost of a pen = 200 Frw
  

  Cost of a book = 500 Frw
  Cost of a geometry set = 900 Frw
  Total amount of money spent by Manzi = (200 + 500 + 900) Frw
  = 1 600 Frw
  Pocket money given to Manzi by his father = 3 000 Frw
  Money left with Manzi = (3 000 – 1 600) Frw
  

  = 1 400 Frw

  Example 11.4
  A trader went to the market and bought a goat at 20 000 Frw, a sheep at 
  15 500 Frw and a cock at 5 000 Frw. How much money did he spend in the 
  market?
  
  Solution
  Price of a goat = 20 000 Frw
  Price of a sheep = 15 500 Frw
  Price of a cock = 5 000 Frw
  Total amount of money spent by the trader = (20 000 + 15 500 + 5 000) Frw
  

  = 40 500 Frw

  Example 11.5

  Christa bought a tray of eggs at 2 000 Frw and sold it to Sandra at 
  2 200c Frw. Sandra sold it to James at 3 000 Frw and James also sold it to 
  Alex at 2 500 Frw.
  a) What profit did Sandra get?
  

          b) What loss did James bear?

  Solution

  a) Sandra: Cost price = 2 200 Frw
   Selling price = 3 000 Frw
  Sandra’s profit = Selling price – Cost price
                                                          = (3 000 – 2 200) Frw
                                                          = 800 Frw
  
  b) James: Cost price = 3 000 Frw
                     Selling price = 2 500 Frw
   James’ loss = Cost price – Selling price
                           = (3 000 – 2 500) Frw
                          = 500 Frw
  Activity 11.4
  (a) You will do this activity in pairs, suppose a shopkeeper purchases goods 
  at 2 500 Frw and sells the goods at 3 000 Frw. What extra money does 
  the shopkeeper get? Discuss with your teacher. 
  (b) Shina went to the market and bought a dress at 5 000 Frw. The dress 
  was too big and so she decided to sell it at 6 000 Frw. Did she gain from 
  

  the sale of her dress? Discuss with your friend.

  Assessment Exercise

  1. If the cost of one pen is 500 Frw, then what will be the cost of 4 pens?
  
  2. Keza has 450 Frw. She buys an eraser at 250 Frw and a sweet at 
  125 Frw. How much does she remain with?
  
  3. One metre of cloth costs 2 600 Frw. Maria went with one 5 000 Frw 
  and one 2 000 Frw note. She bought two metres of cloth. How much 
  balance was she given?
  
  4. A plot of land was sold at 30 000 Kenyan shillings. This resulted in a 
  profit of 4 500 Kenyan shillings. What was the cost price of the land?
  
  5. The bus fare from Kigali to Kampala is 12 000 Frw. How much does 
  one spend from Kigali to Kampala and back to Kigali?
  
  6. The price of a litre of petrol is 1 200 Frw. A car fuel tank has a storage 
  capacity of 100 litres. How much does it cost to fill up the tank?
  
  7. MTN charges 60 Frw per minute on calls to Kenya. How long do I 
  speak to a friend in Kenya if I have 1 200 Frw airtime in my phone?
  
  8. A Samsung TV costs $ 340. How much will be charged for 2 similar 
  TV sets?
  
  9. The price of a mobile phone is marked as 79 500 Frw. The trader sells 
  it to me and makes a loss of 3 500 Frw. How much do I pay for the 
  phone?
  
  10. A refrigerator costs 80 500 Frw. Kamanda wants to buy the refrigerator 
  and he has 76 900 Frw. How much more money does he need to buy 
  the refrigerator?
  
  11. A group of students are on a school trip to Gisenyi to tour the Methane 
  Gas Plant on Lake Kivu. The fare for each student is 6 250 Frw. There 
  are 40 students in the bus. How much does the conductor of the bus 
  

  collect from the students?

  Internet Resource

  For more online support visit :http://www.math-play.com/fractions

• UNIT 12:Number Patterns

  

  Key unit competence 
   A learner should be able to describe and generate number patterns.
  
  Attitudes and values
  Appreciate the importance of orderliness in daily life. Learners should be made 
  to realise the need for orderliness in places such as bus, park, banks, markets, 
  schools, hospitals and other places in daily life situations.
  
  12.1 What is a Number Pattern?
  A list of numbers which form a sequence is called a number pattern.
  
  Ascending order (increasing order)
  The term ascending means ‘going up’. While ordering integers in ascending 
  order, we arrange integers from smallest to the largest.
  For example: 1, 3, 6, 8, 9, 23, 56, 400, .....are arranged in ascending order.
  
  Descending order (decreasing order)
  The term descending means coming down. While ordering integers in 
  descending order, we arrange them from largest to smallest.
  For example: 45 000, 340, 34, 20, 6, 2, –3, –567, .....,.....,... are arranged in 
  descending order.
  
  Importance of orderliness in daily life situations
  Arranging numbers in order of size helps us to compare numbers easily from a 
  

  given set of numbers.

  Example 12.1

  The list shown below shows the size (area) of some selected countries in 
  

  the world. (Source: www.simple.wikipedia.org)

  
  

  Arrange the land areas of the different countries in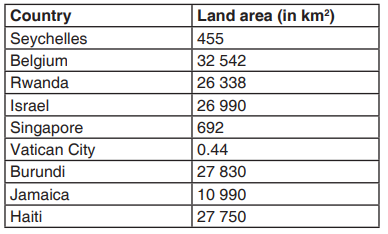
  (a) ascending order
  (b) descending order
  Hence tell the 4th smallest country from this list.
  
  Solution
  (a) Ascending order: 0.44, 455, 692, 10 990, 26 338, 26 990, 27 750, 
  27 830, 32 542. 
  (b) Descending order: 32 542, 27 830, 27 750, 26 990, 26 338, 10 990, 692, 
  455, 0.44.
  The 4th smallest country has an area of 10 990 km2
  . It is the 4th from the left 
  on the ascending list and it is the 4th from the right on the descending list.
  So the answer is Jamaica.
  
  Example 12.2
  For example, the figure below shows the number pattern –10, –6, –2, ......, 
  

  ....., .....,

  

  This pattern starts with – 10 and jumps by 4 every time.

  Example 12.3
  

  Dots like these ones below can also be used to show number patterns.

  

  The number pattern formed is 1, 3, 6, 10, 15,.......
  

  This pattern starts with 1 and then you add 2, 3, 4, 5 and so on.

  Activity 12.1

  Each picture has a number on its face.
  

  Can you workout the number patterns and fill the missing numbers?

  
  

  Compare your answers with the answers of your classmates from the other 
  

  groups.

  Exercise 12.1
  1. Complete the number pattern.
   (a) 4, 8, 12, 16, 20, 24, ________
   (b) 1, 4, 8, 13, ________
   (c) 50, 42, 35, 29, ________
   (d) 100, 105, 115, 130, 150, ________
   (e) 1, 2, 4, 7, ________, 16
  2. The list shown below shows the marks obtained (out of 100) by the 
  students of class 4 in a maths test: 
   59, 56, 79, 82, 90, 53, 19, 54, 65, 88, 93, 58, 63, 52, 75. 
  Arrange the data in the ascending order and find out the third highest mark.
  
  

  12.2 Progression or Series

  There are two types of series or progressions namely; Arithmetic series and 
  

  Geometric series.

  12.2.1 Arithmetic Progression

  In an arithmetic progression or arithmetic series, the sequence of numbers are 
  such that the difference between the consecutive terms is constant.
  For example: The sequence 3, 5, 7, 9, 11, 13, 15 is an arithmetic progression 
  

  with a common difference of 2. 

  Activity 12.2
  

  
  

  What you need
  • 6 empty chalk boxes, labelled A, B, C, D, E and F.
  • At least 100 bean seeds.
  • Marker pens.
  • Manila paper.
  
  What to do
  (i) Place one bean seed in box A.
  (ii) Record the number of bean seeds in box A on a manila paper.
  (iii) Remove the bean seed in box A and transfer it to box B. Add two more 
  bean seeds in box B.
  (iv) Count the number of bean seeds in box B and record the number on the manila paper.
  (v) Remove all the bean seeds in box B and place them in box C. Add two more bean seeds in box C.
  (vi) Count the number of bean seeds in box C and record the number on a manila paper.
  (vii) By adding two bean seeds each time, repeat the procedures for boxes 
  D, E and F. Record the number of beans in the boxes D, E and F on the manila paper.
  
  The numbers on the manila paper forms an Arithmetic progression with a 
  first term of 1 and common difference of 2.
  

  Use the bean seeds to form other Arithmetic Progressions.

  Exercise 12.2
  Rewrite the numbers as shown in your exercise book and write down the 
  next two numbers in the following sequences:
  (a) 70, 69, 68, 67, 66, 65, 64, 63,......,......,
  (b) 20, 17, 14, 11, 8, 5,......,.......,
  (c) 10, 20, 30, 40, 50, 60,.......,.......,
  

  (d) 10, 13, 16, 19, 22, 25,......,.......,

  12.2.2 Geometric Progression
  A geometric progression is a sequence of numbers in which the next number 
  is obtained by multiplying or dividing the previous number by a fixed number.
  Examples of a geometric progression :
  40, 20, 10, 5. The first number is 40. The next number of the sequence is got 
  by dividing by 2 or multiplying by 2/1 .
  1, 2, 4, 8, 16, 32, 64, 128,....... The first number is 1 and the next number is got 
  

  by multiplying the previous number by 2.

  Assessment Exercise
  1. Complete the number pattern:
   (a) 4, 7, 12, 19, 28, ________               (b) 20, 23, 28, 35, ________
   (c) 1, 7, 18, 34, ________
  
  2. Rewrite the numbers as shown in your exercise book and write down 
  the next two numbers in the following sequences:
   (a) +12, +10, +8, +6, +4, ...., ...., (b) 0, 40, 80, 120, 160, ..., ...,
  
  3. On a modern art painting, there are 4 green dots in the first row, 12 
  green dots in the second row, 36 green dots in the third row, 108 green 
  dots in the fourth row, and 324 green dots in the fifth row. If this pattern 
  continues, how many green dots will there be in the sixth row?
  
  4. A restaurant used 2 onions on Friday, 4 onions on Saturday, 6 onions on 
  Sunday, 8 onions on Monday, and 10 onions on Tuesday. If this sequence 
  continues, how many onions will the restaurant use on Wednesday?
  
  5. While at work, Mimi is putting papers into folders. She puts 3 papers in 
  the first folder, 6 papers in the second folder, 9 papers in the third folder, 
  12 papers in the fourth folder, and 15 papers in the fifth folder. If this 
  

  sequence continues, how many papers will Mimi put in the sixth folder?

  Internet Resource

  For more online support visit:http://www.kidsites.com/

• UNIT 13:Filling in the Missing Numbers

  Key unit competence
  By the end of this unit, a learner should be able to solve missing number 
  problems involving addition and subtraction.
  
  Attitudes and values
  Appreciate the importance of inverse operations when solving missing number 
  problems and checking answers.
  
  Arithmagon
  An arithmagon is a polygon with numbers at its vertices and sum of these 
  numbers determine the numbers written on its edges. 
  

  Example:

  Here, the numbers 7, 9 and 12 are at the vertices of the Arithmagon and the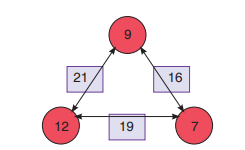 
  numbers 16, 21 and 19 are at the edges.
  You can see that 12 + 9 = 21, 12 + 7 = 19 and 9 + 7 = 16.
  So, add the numbers at the vertex to get the number on the edge. This rule 
  applies to this arithmagon only. Other arithmagons have different rules. You 
  

  can study them carefully and discover the rules by yourself.

  
  

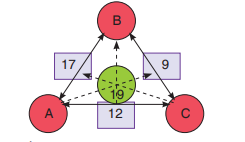
  In the arithmagon shown above 
  

  A = 19 – 9 = 10

  B = 19 – 12 = 7

  C = 19 – 17 = 2

  Activity 13.1
  You will complete this task in groups of 5
  learners.
  (a) Find the value of b
  

  (b) Find the value of c

   Example 13.1
  

  Fill in the missing number.

  

  Solution
  In the arithmagon above, there are 4 numbers at the vertices namely 2, 7, 3 
  

  and 12. You can see that 2 + 7 = 9, 7 + 3 = 10, 3 + 12 = 15 and 12 + 2 = 14.

  

  

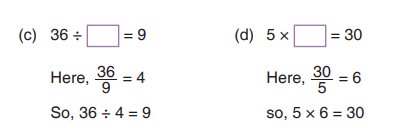
  Assessment Exercise

  1. Study the arithmagons below and complete them by inserting appropriate 
  

  numbers:

  
  

  2. Complete the Arithmagon below by inserting correct numbers
  

  
  

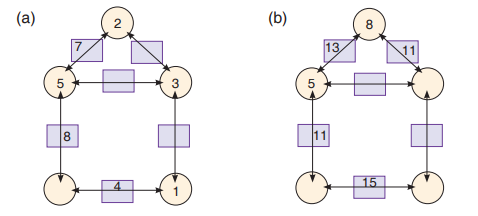
  3. Fill in the missing numbers to make the arithmagon correct.
  

  
  

   4. Complete the arithmagons below by filling in the right numbers in the
  

  circles

  
  

  5. If a number is multiplied by 6, the answer will be 24. What will be the 
  value of the number.
  

  6. If ‘X’ is added to 6. The number obtained is 19. What is the value of ‘X’.

  Think!!!

  If you were running a race and you run past the one in second position, what 
  

  position would you be in now?

  Internet Resource

  For more online support visit:http://www.sheppardsoftware.com/math.htm
  

• UNIT 14:Types of Lines and Angles

  

  Key unit competence
  By the end of this topic, a learner should be able to identify types of lines and 
  angles and use a protractor to measure angles.
  Geometry is a branch of mathematics which deals with the measurement of 
  shape and size of different figures.
  
  Attitudes and values
  Appreciate the importance of lines and angles in daily activities, being confident 
  and accurate when measuring lines and angles.
  
  14.1 Lines
  A line is a long straight mark which joins any two points. It has no end points. A 
  

  line has no thickness and extends forever.

  

  • Parallel lines do not meet at all.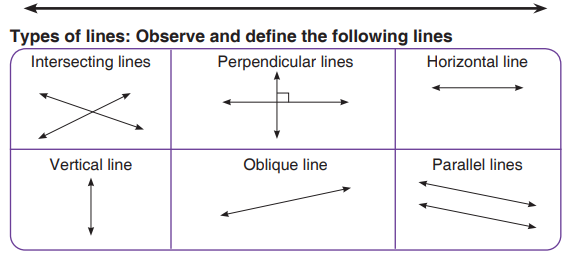
  • Intersecting lines are lines which meet at a point.
  

  • Perpendicular lines make an angle of 90˚.

  Activity 14.1
  Using a geometry set, draw the following lines on a manila paper. 
  • 2 horizontal lines                                                              • 2 vertical lines
  • 2 intersecting lines                                                          • 2 perpendicular lines
  • 2 oblique lines not cutting each other                    • 3 parallel lines
  

  Label the lines according to their names.

  14.2 Measuring the length of a line segment
  

  A pair of compass and a ruler can be used to measure the length of line segment.

  

  Activity: Consider the line segment AB shown in the diagram below.

  

  Place one arm of the compass at point A.
  Extend the second arm of the compass up to point B.
  Transfer the compass on to a ruler as shown below.
  

  The length of the line segment can be read from the ruler.

  

  Example 14.1
  

  (a) Railway track is an example of parallel lines.

  

  (b) Aluminium wires in electric poles are examples of parallel lines.

  

  

  14.3 Angles
  An angle is the measure of the amount of turn from one direction to another. An 
  angle is the measure of the space between two intersecting lines. We use an 
  anticlockwise direction.
  
  The unit for measuring an angle is known as ‘degree’. A degree is written 
  in short as (°). If you draw a circle and divide the circle into equal parts using 
  180 diameters, then the amount of turn from one diameter to the other diameter 
  

  is 1 degree or 1˚.

  

  Activity 14.2

  
  

  Mark a point ‘X’ at the centre of the line segment AB. Use a protractor to measure 
  AXB. What will be the size of angle AXB?
  14.4. Types of angles
  (a) Acute angle: This is an angle which is greater than 0˚ but less than 90˚. 
  

  Examples of acute angles are 30˚ and 72˚. 

  

  (b) Right angle: This is an angle which is formed by intersection of two 
  

  straight perpendicular lines. The measure of a right angle is 90˚.

  

  (c) Obtuse angle: This is an angle which is greater than 90˚ but less than 
  

  180˚. Example of obtuse angle is 135˚.

  

  (d) Straight angle: This is the angle whose value is exactly 180˚. A straight 
  angle is formed when two straight lines meet end to end and form one 
  

  straight line.

  

  (e) Reflex angle: This is an angle whose value is greater than 180˚ but less 
  

  than 360˚. Examples of reflex angles are 339˚ and 285˚.

  

  (f) Complementary angles: These are two angles which add up to 90˚. For 
  example 27˚ and 63˚ are complementary angles as 27˚ + 63˚ = 90˚. We 
  

  can say, the complement of 27˚ is 63˚ and the complement of 63˚ is 27˚.

  

  (g) Supplementary angles: These are the angles which add up to 180˚. For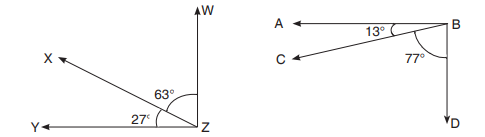 
  example 90˚ and 90˚ have a sum of 180˚. So, they are supplementary 
  angles. Other examples of supplementary angles are 121˚ and 59˚, 31˚ 
  

  and 149˚.

  

  Activity 14.3

  1. Do you see any objects that form right angles in your classroom? Name them.
  

  2. Compare your list with your classmates.

  Exercise 14.2
  

  
  

  2. Using Set squares and a Ruler, draw perpendicular lines to the given 
  

  lines below.

  
  

  14.5 Measuring Angles

  The instrument used for measuring an angle is called a protractor.

  

  The above protractor can be used to measure angles from 0° up to 180°. 
  Angles can be measured either in a clockwise sense or anti-clockwise sense 
  depending on where the angle is drawn.
  • When measuring the angle between two intersecting lines, we place the 
  protractor so that its centre is at the point of intersection of the two lines.
  • We adjust the protractor so that the horizontal line on it runs along one of 
  the lines.
  • We measure the angle by counting the number of degrees from one line 
  to the next line.
  
  Measure the following angles with the help of Protractor
  

  Example 14.2

  
  

  Solution
  

  The acute angle between the two lines = 63˚.

  Example 14.3
  

  
  

  Solution
  The angle between the two lines is obtuse. We measure it by using the 
  

  anticlockwise scale of the protractor. The size of this angle is 121˚.

  Example 14.4

  
  

  Solution
  The angle between the two lines is measured using the anti-clockwise scale 
  

  and its value is 175˚.

  Example 14.5
  

  
  

  Solution
  The angle between the two lines = 130° – 40° = 90°.
  

  Alternatively, the angle = 140° – 50° = 90°.

  Activity 14.4
  

  In this activity you will make your own protractor.
  You will need the following materials:
  • Manila paper
  • Pencil
  • Markers
  • Pair of scissors
  • Math set
  • Paper glue
  • Blackboard protractor
  1. Place the Manila paper on a large table and spread it flat on the table.
  
  2. Place the blackboard protractor in the middle of the Manila paper.
  
  3. Trace the outline of the protractor on the Manila paper using a pencil.
  
  4. Draw short marks on the manila paper corresponding to the following 
  angles: 0°, 10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°, 90°, 100°, 110°, 
  120°, 130°, 140°, 150°, 160°, 170° and 180°.
  
  5. Remove the protractor and mark a point which represents the point 
  where all lines meet on a protractor.
  
  6. Redraw the lines using a marker.
  
  7. Carefully cut out your Manila protractor using a pair of scissor or 
  any other useful tool.
  
  8. Cut another piece of Manila paper which is identical to your Manila 
  protractor. Use paper glue to attach this Manila paper under your 
  Manila protractor. 
   You now have a strong Manila protractor.
  
  9. Use your Manila paper to measure different angles in your class 
  room including the angles at the edges of your table, book etc.
  

  Assessment Exercise

  
  

  
  

  3. In the figure below, the protractor is used to measure many angles at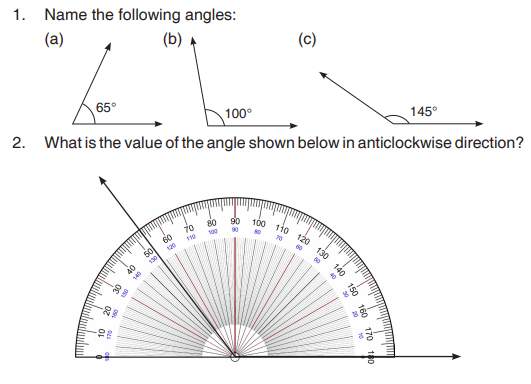 
  

  once. Find the angle between;

  

  (a) Line A and line F
  (b) Line B and line C
  (c) Line D and line A
  

  (d) Line B and line E

  4. Here are some angles marked using letters a, b, c, d, e and f. 
  

  Using a protractor, measure and record the angles in degrees.

  

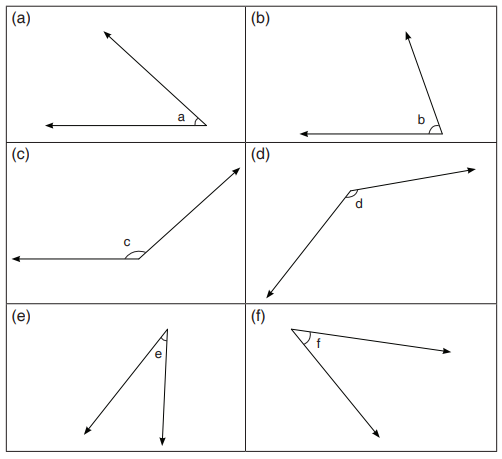
  5. Measure the length of the following line segments by the help of ruler.

  

• UNIT 15:2D Shapes and their Properties

  

  Key Unit Competency
  A learner should be able to use geometric properties to classify shapes.
  
  Attitudes and values
  Appreciate the use of properties to distinguish shapes and recognise that 
  special quadrilaterals are a subset of all quadrilaterals.
  
  15.1 2D Shapes
  2D shapes/figures are two dimensional shapes or figures. These shapes 
  have only two dimensions, i.e., length and width. They do not have thickness. 
  Examples of 2D shapes are triangle, square, rectangle, rhombus, parallelogram, 
  

  kite, trapezium, pentagon, etc.

  15.2 Triangle 
  A triangle is a closed three sided figure. It has three angles and three sides.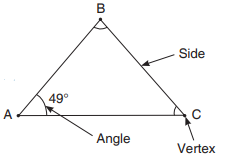
  
  Vertex
  A vertex is a point where any two sides meet. The plural of vertex is vertices. 
  

  So, a triangle has 3 sides, 3 vertices and 3 angles.

  Types of triangles
  Triangles can be classified according to their sides or angles.
  

  Triangles in terms of sides

  

  • A scalene triangle is a triangle in which all sides are unequal.
  • An isosceles triangle is a triangle in which two sides are equal.
  

  • An equilateral triangle is a triangle in which all sides are equal.

  Activity 15.1

  Complete this activity in groups of 5 learners 
  

  • You are provided with the following paper/card objects:

  
  

  • Identify the triangles by putting them separately from the other paper 
  objects.
  • How many sides does a triangle have?
  • How many angles does a triangle have?
  

  • How many vertices does a triangle have?

  

  • Obtuse angled triangle is a triangle in which one angle is obtuse, i.e., more 
  than 90°.
  • Acute angled triangle is a triangle in which all the angles are acute, i.e., 
  less than 90˚.
  

  • Right angled triangle is a triangle in which one angle is a right angle (90°).

  Example 15.2
  

  Write the names of the triangles in terms of their angles.

  

  Solution
  (a) Right angled triangle                      (b) Obtuse angled triangle
  

  (c) Acute angled triangle

  

  15.3 Quadrilaterals 
  A closed plane figure bounded by line-segment is called a polygon. The line 
  segments are called its sides and the points of intersection of consecutive sides 
  are called vertices. Line segments joining non-consecutive vertices are called 
  

  diagonals.

  Activity 15.2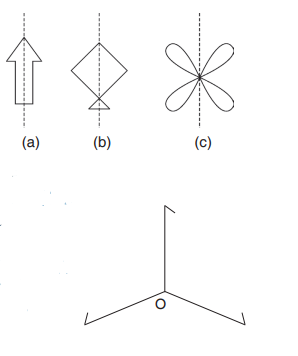
  (a) Look at the following plane figures:
  From the above figures we observe 
  that if these figures are folded along 
  a specific line (dotted line). Each 
  figure on the left hand of the dotted 
  line fits exactly on the figure on the 
  right hand side of dotted line.
  Therefore, if a figure is divided into 
  two coincident parts (mirror images) by a line, then 
  the figure is called symmetrical about that line and 
  the line is called the line of symmetry.
  (b) Look at the following figure:
  The figure shown above does not have any lines 
  of symmetry or point of symmetry. Yet it 
  

  seems balanced and has regularity of shape.

  Let this figure be rotated through one complete turn (clockwise or anticlockwise) 
  about a point O. These are three occasions when it looks the same as it did 
  in its starting positions these are when it has been rotated through 120°, 
  240° and 360°. We say that this figure has a rotational symmetry of order 3.
  

  Definition: A quadrilateral is a 4 sided, closed and 2 dimensional figure.

  
  
  

  

  Activity 15.3

  Identify the 2D shapes given below by writing their names on each shape:
  

  
  

  Activity 15.4
  (a) Move around your classroom, library and the whole school compound. 
  Identify atleast 10 objects which have two dimensional (2D) shapes. 
  (b) With reasons, explain to your classmates whether the object is a 
  

  square, rectangle, rhombus, trapezium, triangle, etc.

  

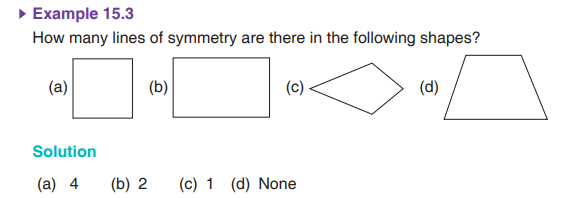
  Assessment Exercise

  
  

  
  

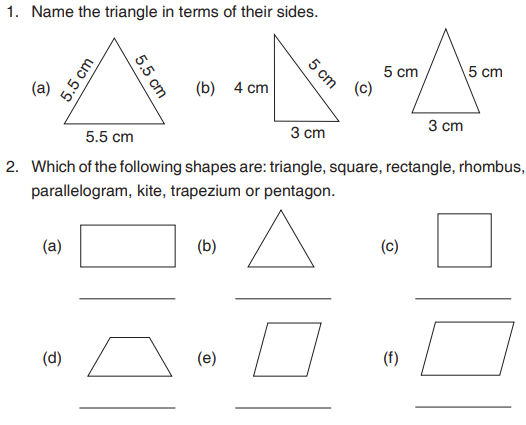
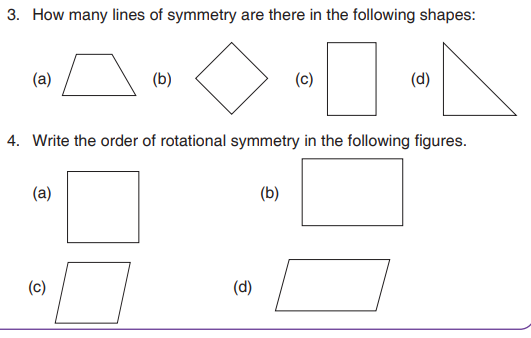
• UNIT 16:Area and Perimeter of 2D Shapes

  Key unit competence
  By the end of this unit, a learner should be able to use area of rectangle to 
  determine the area of a triangle and other shapes.
  
  Attitudes and values
  Appreciate that the relationship between area and perimeter.
  
  16.1 Area
  Area is defined as the amount of space inside the boundary of a flat 
  (2-Dimensional) object such as triangle, square, circle etc.
  

  The area of a closed figure is the measure of the surface enclosed by it.

  16.2 Area of Rectangle
  Activity 16.1
  In this class activity, you will determine the area of a rectangle by counting the 
  number of square grids in the rectangle.
  1. Draw a rectangle of length 6 cm and width 4 cm on a graph paper.
  2. Divide the rectangle into grids by dividing the length into 6 equal parts 
  and width into 4 equal parts.
  3. Count the total number of squares formed in the rectangle, i.e., 24. This 
  is equal to the area of the rectangle.
  4. Now, 6 × 4 = 24 which is equal to the area of rectangle.
  

  5. Thus, we find the area of rectangle = length × width

  

  Example 16.1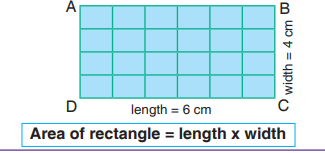
  A rectangular football field measures 100 m by 70 m. What is the area of 
  the field?
  Solution
  Area = length x width = 100 m x 70 m = 7 000 m².
  
  16.3 Area of a Square
  As we have seen in above activity that area of rectangle is length × width. Area 
  of square is defined as, the number of square units it takes to completely fill a 
  

  square. In square all four sides are equal. So, area of square is length × length.

  

  Example 16.2
  A piece of land is in the form of a square. Its side is 200 m long. What is its 
  area?
  
  Solution
  Area of square= side x side
  

  Area of square= 200 m x 200 m= 40 000 m²

  16.4 Area of Triangle
  

  Activity 16.2

  In this class activity, you are going to find the area of a triangle from a rectangle.
  1. Draw a rectangle of length 8 cm by 4 cm on a graph paper. 
  2. Divide this rectangle into thirty two 1 cm²grids. The area of this rectangle is 32 cm².
  3. Cut out this rectangle using a pair of scissors along one of its diagonal.
  4. This forms two equal triangles.
  5. What is the area of each triangle?
  6. How does the area of the triangle relate to the area of the rectangle? Now, 
  

       let’s look at the formula.

  
  

  In the figure above, PSRQ is a rectangle with length 8 cm and width 4 cm. SQR 
  

  is a triangle with base 8 cm and height 4 cm.

  

  The height of a triangle makes an angle of 90˚ with the base.

  Example 16.3
  A triangle has an area of 100 cm² and a base of 10 cm. What is the height 
  of the triangle?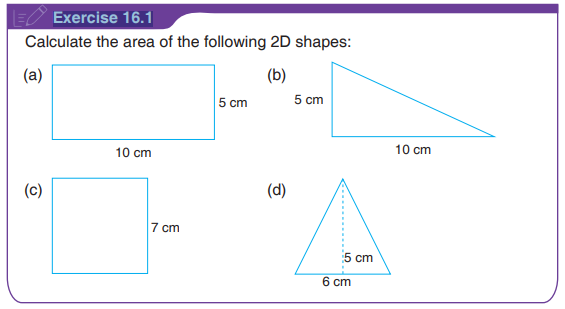
  

  

  

  16.6 Area of Parallelogram

  Activity 16.3
  Consider the parallelogram JHFE of base 8 cm, height 4 cm and width 5 cm as 
  shown in the diagram below:
  
  If we cut the parallelogram along the height, we get the shaded part EJI. We 
  can paste the shaded part to the right hand side of HF. 
  The new figure formed is EIGF as shown in the figure below:
  

  
  

  The figure EIGF is a rectangle of length 8 cm and width 4 cm.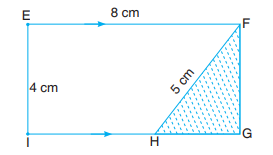
  

  So, the area of the parallelogram EJHF = area of rectangle EIGF.

  
  

  Note: The height of the parallelogram is perpendicular to the base.
  

  Area of the given parallelogram = 8 cm x 4 cm = 32 cm²

  Example 16.4
  

  Find the area of the parallelogram given below: 

  

  Area of the parallelogram = base × height
  Base of the parallelogram = 20 cm
  Height of the parallelogram = 8 cm
  = 20 × 8 
  

  = 160 cm²

  Activity 16.4
  In pairs, 
  • Draw a triangle and a rhombus whose perimeter is 36cm.
  

  • Draw a triangle and a rhombus whose area is 36cm²

  16.7 Area of a Rhombus
  A rhombus is a special type of parallelogram in which all the sides are equal 
  and the diagonals bisect each other at right angle. The area of a rhombus can 
  

  be given by the formula:

  

  

  AC and DB are diagonals. AC = 2b and DB = 2a. The two diagonals divide the 
  rhombus into four equal right angled triangles. Each right angled triangle has a 
  

  base b and height a.

  

  Example 16.5
  A rhombus has diagonals of lengths 20 cm and 32 cm as shown below. 
  

  Calculate the area of the rhombus.

  

  

  

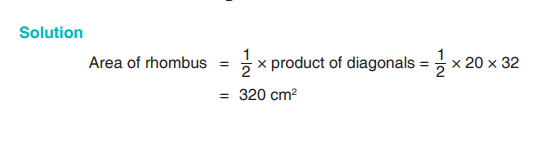
  Activity 16.5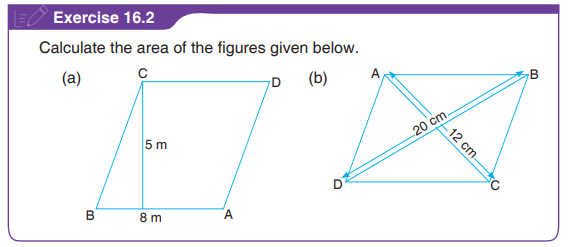
  • Use a squared paper to draw a rectangle of length 6 units and height 4 units. 
  • Use a squared paper to draw a right angled triangle of base 3cm and height 4cm.
  • By counting the number of squares, find the area of the rectangle and the 
  area of the triangle.
  • Join the two shapes together to form one figure. What is the name of this 
  new figure formed?
  • By counting the number of squares, find the area of the new figure formed.
  • What have you learnt from this activity? Discuss your finding with your teacher.
  
  16.8 Area of a Trapezium
  A trapezium can be divided into two triangles. This makes it easy for the area 
  

  to be calculated.

  

  ADCB is a trapezium. Line DB is a diagonal of the trapezium. It divides the 
  trapezium into two triangles namely ADB and DCB.
  

  Area of trapezium = Area of triangle ADB + Area of triangle DCB

  

  Example 16.6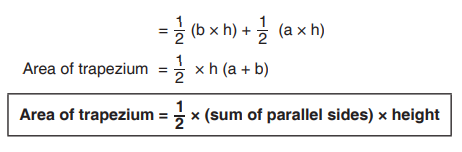
  

  Find the area of the trapezium given below. 

  

  

  16.9 Perimeter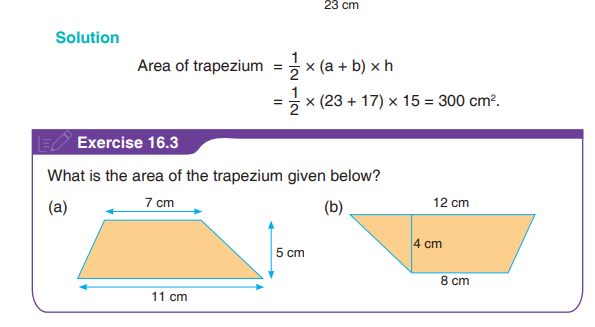
  

  The perimeter of a closed figure is the total distance around the given figure. 

  Activity 16.6
  In this class activity, you will use straws to draw a triangle and you will find its perimeter.
  
  (a) You are provided with ordinary drinking straws.
  (b) Cut three straws such that each one has a length of 8 cm.
  (c) Join these straws to form a triangle.
  

  (d) What is the perimeter of the triangle?

  Activity 16.7
  In this activity, you are going to design a square, rectangle, rhombus, 
  parallelogram and trapezium whose perimeter is 24 cm. You can use straws to 
  design these shapes. 
  
  To design a rectangle or parallelogram, you need 
  – 2 straws each of 4 cm long and 
  

  – 2 straws each of 8 cm long

  So, perimeter = 2 × 4 + 2 × 8

   = 2 (4 + 8)

   = 2 × 12

   = 24 cm

  Therefore, Perimeter of rectangle = 2 (length + width)
   Perimeter of parallelogram = 2 (length + width)
  Now, to design a square or rhombus, you need
  – 4 straws each of 6 cm long 
  

                               So, Perimeter = 6 + 6 + 6 + 6

                                                                        = 4 × 6 = 24 cm
  Therefore,      Perimeter of square = 4 × side
   Perimeter of rhombus = 4 × side
  Since, the sides of a trapezium are different in length.
  

  Therefore,     Perimeter of trapezium = sum of all the sides.

  Example 16.7
  

  Find the perimeter of the rectangle and parallelogram given below:

  

  Solution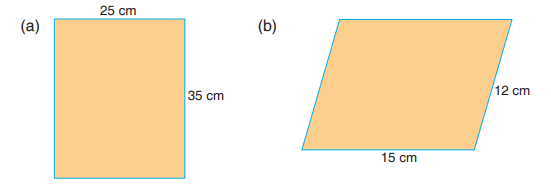
  (a) Perimeter of rectangle = 2(25 + 35) 
                                                        = 120 cm
  (b) Perimeter of parallelogram = 2 (15 + 12) 
  

                                                                  = 54 cm

  Example 16.8
  

  Find the perimeter of the square and rhombus given below. 

  

  Solution
  (a) Perimeter of square = 4 × side = 4 × 8 = 32 cm
  

  (b) Perimeter of rhombus = 4 × side = 4 × 6 = 24 cm

  Example 16.9
  

  Find the perimeter of the given trapezium.

  

  Solution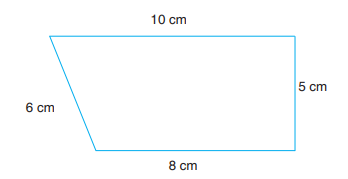
  

              Perimeter of trapezium = 10 + 5 + 8 + 6 = 29 cm

  Example 16.10
  

  Calculate the perimeter of the shape given below.

  

  Solution
  Perimeter = 30 mm + 9 mm + 6 mm + 7 mm + 5 mm + 8 mm + 15 mm
  

                                                                                                         + 14 mm = 94 mm

  

  

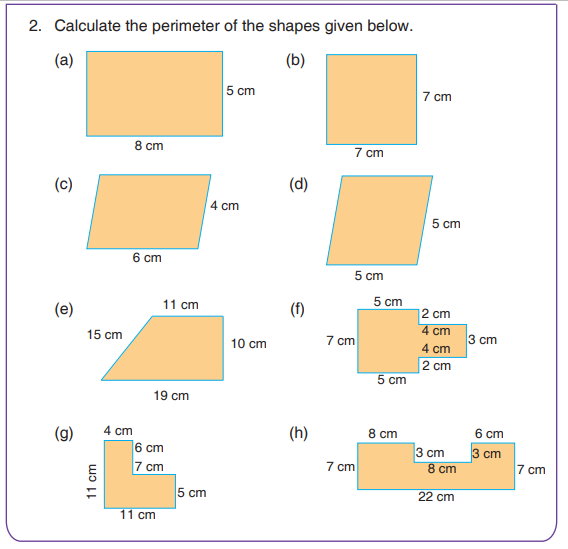
  Internet Resource

  visit:http://www.sheppardsoftware.com/math.htm
  

• UNIT 17:Elementary Statistics

  

  Key unit competence
  By the end of this unit, you should be able to collect, represent and interpret 
  data.
  Attitudes and values
  • Appreciate the importance of data collection in daily life situations.
  • Appreciate the importance of interpreting and extracting information from 
  tables.
  • Appreciate the importance of statistics tables and graphs in daily life 
  situations
  
  17.1 Statistics and data
  It is the branch of mathematics which deals with collection, representation, 
  interpretation and retrieval of data.
  
  Meaning of data
  A collection of information in the form of numerical figures is called data. 
  Examples of data are:
  • Ages of pupils in P4 in our class.
  • Heights of all pupils in our school.
  • Masses of goats in a market.
  • Prices of milk in different markets.
  

  • Number of children born in Rwanda per day.

  17.2 Qualitative and Quantitative data
  Quantitative data is the type of data which can be expressed in terms of 
  numbers. For example: 
  • Number of cars that pass through a certain town per day.
  • Number of pregnant cows in a kraal.
  • Marks obtained by pupils in a Math test.
  • Ages of people in a market
  
  Qualitative data is a type of data which cannot be expressed in terms of 
  numbers. In other words, it cannot be quantified. We use other attributes other 
  than numbers to describe qualitative data.
  
  Examples of qualitative data
  • A person’s skin colour; I am black, brown or white.
  • A person’s sex; I am either a male or female.
  • Someone’s nationality; I am a Rwandan, my friend is a Ugandan and our 
  neighbour is Congolese.
  • My favourite soda; the answer can be coca cola, fanta orange or pepsi.
  
  17.3 Ways of collecting data
  There are many ways of collecting data which may include the following:
  1. Questionnaire
  A questionnaire is a written set of questions that are given to people in order to 
  collect facts or opinions (data) about something.
  
  2. Census
  A census is a study that obtains data from every member of a population. A 
  census is very expensive because it is very hard to reach everybody. A national 
  population is carried out to determine the number of people in a country. 
  In Rwanda, the last Housing and Population census was carried out in August 2012.
  
  3. Sample survey 
  A sample survey is a study that obtains data from a very small group of a 
  population. The result of the sample survey is used to make conclusion for the 
  whole population.
  
  4. Observation
  This is where the person collecting the data makes observations and compiles 
  his/her data accordingly. For instance, a person can simply observe and count 
  

  the number of girls in a class without necessarily talking to anyone.

  5. Interview
  

  In this method of collecting data, people are asked some questions directly.

  17.4 Presentation of Data
  Presentation of data is a method of displaying data in a very simple way so that 
  the data collected can be easily understood. Data can be displayed in many 
  

  forms namely: 

  • Table
  • Bar graph
  • Pie chart
  • Line graph
  

  • Pictograph

  However, at this level, we shall look at table and bar graph only.

  17.4.1 Table
  This is a very simple way of presenting data. The data is presented in columns 
  

  and rows.

  Example 17.1
  The data below shows the results of football matches by three teams in a 
  football league:
  Kanombe United:   Win = 6,   Draw = 3,    Loss = 1
  Kigali Stars: Win =    6, Draw = 0,                 Loss = 4
  Gisenyi Boys: Win = 4, Draw = 2,                  Loss = 4
  

  (a) Present the information on a table.
  

  (b) If a win is worth 3 points, a draw 1 point and a loss is worth 0 point, 
  

  which team has got the highest points?

  Solution

  (a) Let us arrange our data in a table like the one below:
  

  
  

  (b) Total points:

  Kanombe United = (6 × 3) + (3 × 1) + (1 × 0) = 18 + 3 + 0 = 21 points.
  Kigali Stars = (6 × 3) + (0 × 1) + (4 × 0) = 18 + 0 + 0 = 18 points.
  Gisenyi Boys = (4 × 3) + (2 × 1) + (4 × 0) = 12 + 2 + 0 = 14 points.
  

  Kanombe United has the highest points = 21 points.

  Activity 17.1
  In this class activity, each pupil will ask the age of all the pupils of the class 
  

  and represent this data in a table.

  Example 17.2
  The data below shows the marks obtained (out of 100) by some pupils in a 
  

  Maths test:

  56 56 76 23 09 89 90 43 23 12 64 88
  43 54 76 23 22 43 12 54 29 66 74 50
  (a) Represent this data in a table.
  (b) How many pupils did appear for the test?
  (c) How many pupils scored 76% marks?
  (d) How many pupils got less than 50% marks?
  

  (e) What was the highest marks scored?

  Solution

  
  

  (b) Total number of pupils who appeared for the test = 24 pupils.
  (c) 2 pupils scored 76% marks.
  (d) Number of students who got less than 50% 
                           = 1 + 2 + 1 + 3 + 1 + 3 = 11 pupils.
  

  (e) The highest mark scored was 90%.

  Exercise 17.1
  20 pupils are asked for their favourite colour. The answers are as follows:
  Red, Red, Blue, Black, Yellow, Green, Green, Black, Pink, Pink, Pink, Blue, 
  Blue, Yellow, Green, Red, Black, Red, Red, Pink
  

  (a) Represent this data in a table.
  (b) Which colour is liked by the most number of pupils?

  (c) Which colour is liked by the least number of pupils?

  17.4.2 Bar graph
  A bar graph is drawn by representing the data on two perpendicular axis. The 
  

  vertical axis is called the y-axis and the horizontal axis is called the x-axis.

  Example 17.3
  

  The data below shows the number of boys from P1 to P5 in GS Gisozi.
  

  
  

  The vertical axis shows the number of boys and the horizontal axis represents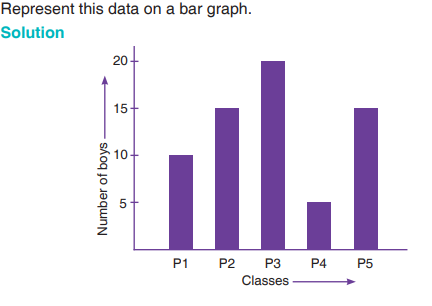 
  the classes. The height of a bar correspond to the number of boys on the 
  Y- axis. 
  From the graph we can see that;
  • P1 has 10 boys, P2 has 15 boys, P3 has 20 boys, P4 has 5 boys and P5 
  has 15 boys.
  • P3 has the most number of boys and P4 has the least number of boys.
  

  • Total number of boys from P1 to P5 = 10 +15 + 20 + 5 + 15 = 65 boys.

  Activity 17.2
  Ask each pupil about their favourite fruit. Write the number of pupils of each 
  

  fruit, and collect the data in a table. Represent this data by a bar graph.

  Example 17.4
  A survey was carried out in a certain school to find out the means of transport 
  used by pupils to go to school. It was found out that each pupil go to school by 
  

  bus, on foot or by bicycle. The data is shown in the bar graph below: 

  

  (a) What quantity is represented on the vertical axis?
  (b) What quantity is represented on the horizontal axis?
  (c) How many pupils go to school by bus in P4?
  (d) How many pupils go to school by bus in P3?
  (e) How many pupils go to school by bicycle in the whole school?
  (f) Which class has the largest number of pupils?
  
  Solution
  (a) “Number of pupils” is represented on the vertical axis.
  (b) “Classes” is represented on the horizontal axis.
  (c) 4 pupils go to school by bus in P4.
  (d) There is no bar for the bus in P3. This means no pupil in P3 goes to 
  school by bus.
  (e) Total number of pupils who go to school by bicycle = 2 + 4 + 7 + 5 + 3 
  + 4 = 25 pupils.
  (f) There are 16 pupils in P4. So P4 has the largest number of pupils in 
  

  the school.

  Assessment Exercise
  1. The birth rate per thousand of five countries over a period of time is 
  

  shown below:

  

  Represent above data in a bar graph.
  2. The table given below shows the monthly expenditure (in percentage) on 
  

  various items, in a family.

  

  Represent the above data in a bar graph.
  3. The graph below shows the salary of five ladies who work in a certain 
  

  factory. Use it to answer the questions that follow.

  

  (a) How much money does each lady get?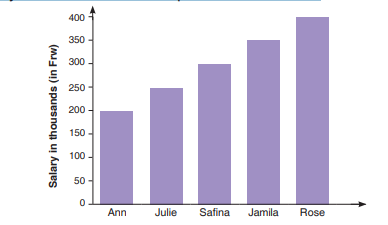
  (b) Find the sum of Safina’s and Ann’s salary.
  

  (c) Find the average of Julie’s, Safina’s and Rose’s salary.

• UNIT 18:Introduction to Probability

  

  Key unit competence
  By the end of this unit, a learner should be able to play games based on the 
  probability.
  
  Attitudes and values
  Appreciate the importance of following rules and taking turns when playing 
  games of cards and coins, throwing dice, snakes and ladders and bingo with 
  probability.
  
  Meaning of Probability
  Probability is a branch of Mathematics which deals with the possibility of 
  something happening. The possibility of something happening is also called 
  the chance or likelihood of something happening.
  Games such as tossing a coin, cards, throwing dice, snakes and ladders and 
  

  bingo etc. are played based on probability.

  Activity 18.1
  Tossing a coin 
  • Pair up with one of your classmates.
  • Together with your friend, you will decide which side of 
  the coin is the head and which one is the tail. Confirm 
  

  with the teacher which side is the head (H) or tail (T).

  • Each one of you will draw a table like the one shown below in your book.

  

  • You will toss the coin, allow it to fall on the floor and note the side facing 
  up. If the head is facing up in the 1st toss, then write H in the table. 
  Otherwise, write T for a tail facing up.
  • Repeat the experiment 9 more times and record your results as honestly 
  as possible in the table.
  • Let your friend also repeat what you have done and help him/her record 
  his/her results in a table.
  

  • Compare your results and see who has more heads than the other.

  Activity 18.2
  Tossing 3 coins at once
  • In this activity, you will pair up with a 
  classmate.
  • Carefully observe the coin faces and 
  decide which the heads are.
  • You will be required to toss all the three coins at the same time and 
  note the sides of the coin facing up. It is good to decide on a winning 
  combination before starting the game. For instance, the winning 
  combination may be getting 2 heads and 1 tail (HHT). If you get anything 
  else, then you have lost.
  • Toss the three coins at once and note the sides facing up. Record your 
  result as a win or a loss. 
  • Give the three coins to your friend and let him/her toss. 
  

  • Repeat the experiment several times and see who gets 10 wins first.

  Activity 18.3

  
  

  In this class activity, you will play a game of cards and discover how lucky you 
  are!!!!
  (a) Open the pack of playing cards. Count the total number of cards and 
  record your answer.
  (b) Group the cards of the same type together. You should have 5 groups of 
  cards namely; hearts, spades, clubs, diamonds and jokers.
  (c) Count and record the number of each suit of cards.
  (d) How many picture cards are there altogether?
  (e) Shuffle the pack of playing cards very well. Deal 5 cards to your neighbour. 
  (f) Open the cards so that everybody can see. Count the number of aces he/
  she has got and record the number down.
  (g) Repeat the shuffling and dealing for everybody in the group. 
  Play the game for a number of times, each time recording the number of 
  aces each pupil has got.
  (i) The pupil who gets 10 aces first is the winner of this game.
  (j) Is the game fair? If you think it is unfair, discuss how you could make it 
  

  fair for everyone.

  Assessment Exercise
  1. Discuss the following questions: (Refer Activity 18.1)
   (a) Was the game fair?
   (b) Are there some winning strategies for getting a head up?
   (c) Some people believe that girls will get more “heads” up than 
  “tails”. Do you agree?
  (d) Some people think that tossing the coin first makes you get “tails” 
  only. Is this true?
  2. Discuss the following questions: (Refer Activity 18.2)
   (a) Were we very sincere while doing the experiment?
   (b) Is it possible to get 2 heads and a tail?
   (c) Some people believe that small coins show heads only and big 
  

  coins show tails only. Do you agree with this?

  Internet Resource

  For more online support visit:http://www.sheppardsoftware.com/

  GLOSSARY

  Abacus: a table or frame used 
  for performing arithmetical calculations.
  Acre: a unit of land measure equivalent to 4046 square metres.
  Addends: the numbers being added together.
  Angle: circular measure of the space between two intersecting lines.
  Acute angle: Angle less than 90˚.
  A.M. : Ante Meridian, time before midday.
  Architect: Stet person who designs and constructs buildings.
  Area: measure of the 2D space surrounded by lines.
  Arithmagon: a polygon with numbers at its vertices which determine 
  the numbers written on its edges.
  Arithmetic: branch of mathematics that deals with calculations.
  Calculator: instrument used to help adding, subtracting, multiplying and
  dividing numbers.
  Calendar: an arrangement of dates, days and months of the year.
  Capacity: the amount of liquid a given container can carry.
  Circle: closed figure with all points at equal distance from the centre.
  Circumference: distance around a circle.
  Cube: closed figure with six equal faces.
  Coin: metallic money in the form of a small disc.
  Compass: device for telling the direction.
  Data: any information collected for statistics.
  Denominator: the lower number in a fraction.
  Diagonal: a line (which is not a side) 
  joining any two vertices of a polygon.
  Diameter: distance from one point on a circumference to the other 
  through the centre. It is twice the radius of a circle.
  Digit: a numeral or number.
  Edge: the boundary line of a surface.
  Even number: a number which is divisible by 2.
  Equivalent fractions: two fractions 
  which have the same numerical value.
  Estimate: to approximate something.
  Face: any of the flat surface of a solid figure.
  Factors: any two numbers multiplied together to form another number.
  Fraction: ratio of two numbers; the numerator and the denominator.
  Gram: a unit of mass equivalent to 0.001 kg.
  Graph: a diagram displaying data showing the relation between two 
  quantities.
  G.C.F. : Greatest Common Factor.
  H.C.F. : Highest Common Factor.
  Intersect: for lines, to meet at a point.
  L.C.M.: Lowest Common Multiple.
  Line: a straight path through two or 
  more points.
  Litre: the unit of capacity equivalent to 1000 cm³.
  Multiple: a number that may be divided by another number with 
  no remainder.
  Numerator: the lower number of a fraction.
  Oblique line: a line which is neither horizontal nor vertical. It is a 
  sloping/slanting line.
  Pair of compasses: a tool consisting of two arms used to draw circles.
  Parallel lines: these are lines which do not meet at all.
  Pentagon: a 5-sided closed figure.
  Perimeter: the distance around a given figure
  Perpendicular lines: two or more lines which intersect at an angle 
  of 90°.
  Plane: a flat surface.
  Point: a small dot used to represent the location of something.
  Polygon: a closed figure bounded by straight or curved edges.
  Prime number: a number with only two factors. One factor being 1 
  and the other one is itself.
  Probability: this is the chance or likelihood of something happening.
  Protractor: This is a geometrical instrument used for measuring angles.
  Quadrilateral: This is any 4-sided closed figure.
  Radius: this is the distance from the centre of a circle to any point on 
  the circumference of the circle. It is half the diameter.
  Range: this is the difference between the largest and smallest numbers 
  in a data.
  Ratio: it refers to the division of two numbers.
  Remainder: a number which is left when two numbers are divided.
  Right angle: an angle which is equal to 90°.
  Square: a closed 4-sided figure with all sides equal.
  Symmetrical shape: a shape that can be separated into two exactly 
  equal parts which can overlap.
  Tossing a coin: throwing a coin in air so that it falls with one side facing upwards.
  Triangle: a closed figure with three sides, three angles and three vertices.
  Vertex: a point on a polygon where two lines meet.
  Volume: the space occupied by an object.
  X-axis: the horizontal line on the Cartesian plane.
  Y-axis: the vertical line on the Cartesian plane
  

• Topic 19