General
- Y1: Integrated Science ECLPE SB File Uploaded 17/08/22, 09:41
- Y1: Integrated Science ECLPE TG File Uploaded 17/08/22, 09:44
UNIT 4: UNIFORM CIRCULAR MOTION
Key unit competence
Analyse and solve problems related to circular motion.
Introductory Activity 4
Read the following statement and analyse them how it happens thereafter
answer the next questions
a) The rotation of the blades on the ceiling fan.
b) A ball rolling on a floor in a constant velocity.
c) An artificial satellite orbiting the Earth at a constant height.
d) A stone which is tied to a rope and is being swung in circles.
e) A car turning through a curve in a race track.”
1. Refer to the above examples, elaborate other examples on where
circular motion can be applied in real life situation
2. From what you elaborate what are the factors that help the body
to be in circular motion?
3. Observe the following image thereafter answer the question below
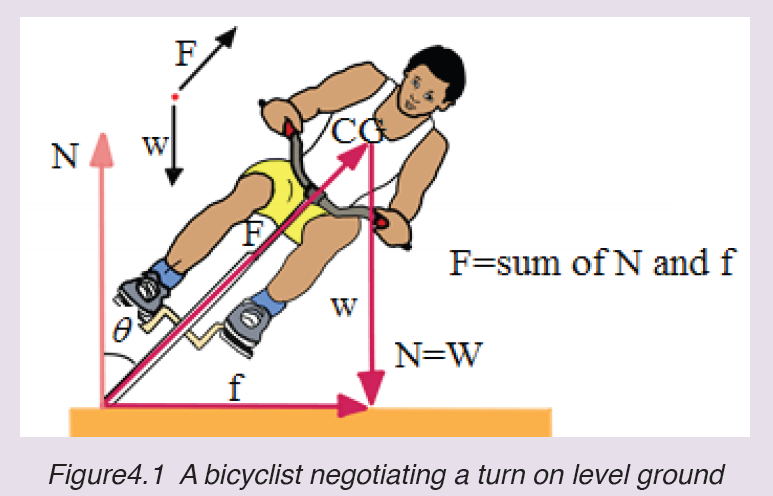
What happen for this bicyclist to turn on level ground easily? T
4.1. Definition of key terms in circular motion
Activity 4.1
Study carefully the motion of the ball shown below.
From your observation of below figure, how can a body move in that circular
path? Explain your reason
Circular motion: is movement of an object along the circumference of a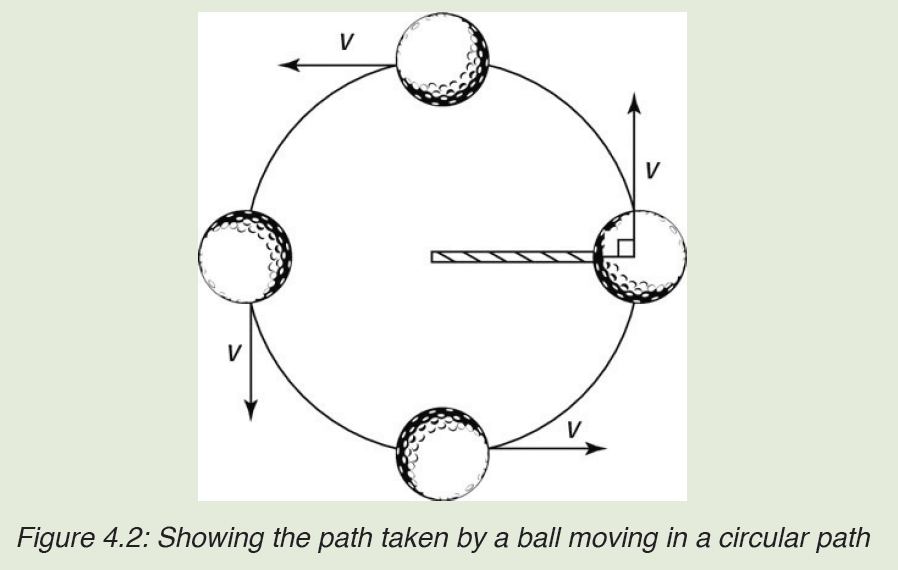
circle, or rotation along a circular path. It is a motion with constant.
Angular displacement: is the angle in radians (degrees, revolutions)
through which a point revolves around a centre or line has been rotated in a
specified sense about a specified axis.
Linear velocity: is themeasure of how fast the dot is moving along the
circumference of the circle
Angular velocity: is the rate at which the central angle swept out by
the object changes as the object moves around the circle, and it is thus
measured in radians per unit time.
Period: The period is the time taken for a full revolution of the motion.
Frequency: is the number of rotation per unit time.
Angular acceleration: also called rotational acceleration, is a quantitative
expression of the change in angular velocity that a spinning object undergoes
per unit time. It is a vector quantity, consisting of a magnitude component
and either of two defined directions or senses.Linear acceleration: is the rate of change of linear velocity
Application activity 4.1
After observing the above pictures, what A, B, C and D represent in circular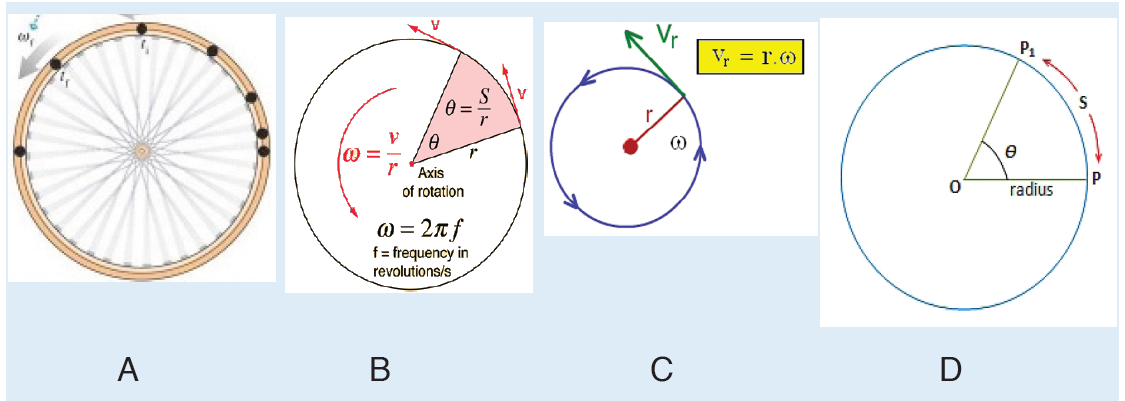
motion?
4.2 Relationship between angular and linear parameters
Activity 4.2
Write your observation on the image below
1. What do variables v, ω and r mean in the expression illustrated on the figure 4.3
2. What does ω show in the movement of the wheel in the illustration above.
4.2.1 Angular Velocity
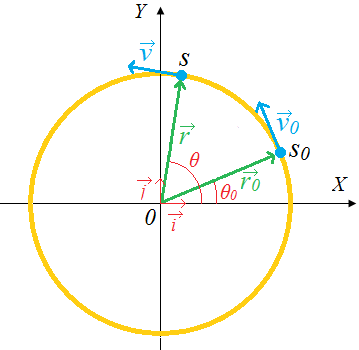
Figure 4.4. Uniform circular motion
To indicate the angular position of a particle, or how far it has rotated we
specify the angle θ of a line joining the centre of the particle and its position
with respect to some reference line, such as the x axis. Consider an object
moving in a circle of radius r with a uniform speed v round a fixed point 0
as centre.
When an object rotates the angular displacement 0 Δθ =θ −θ , the average
angular velocity is defined as
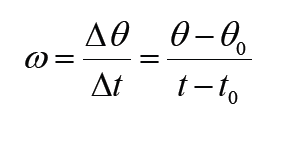
The linear displacement or the Arc of the object along the circle is
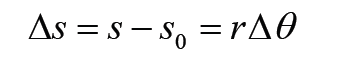
The linear average velocity
We define the instantaneous angular velocity as the very small angle Δθ ,
through which the object turns in the very short time intervalΔt :
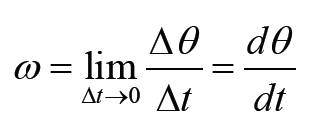
The instantaneous linear velocity
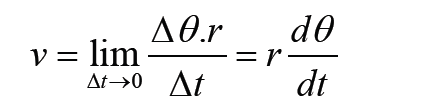
The angular velocity is generally specified in radians per second (rad / s)
whereas the instantaneous linear velocity is expressed in (m / s).
4.2.2 Periodic time and frequency
The period T is the time needed for the object to make one complete revolution.
During this time, the object travels a distance equal to the circumference of
the circle. The frequency f is referred to as the number of revolutions made
by an object in one second. The unit of frequency is Hertz.
The object’s angular speed is then represented by
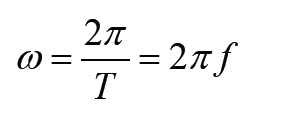
4.2.3 The average angular acceleration
The average angular acceleration is defined as the change in angular velocity
divided by the time required to make this change:
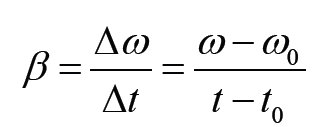
The average linear acceleration
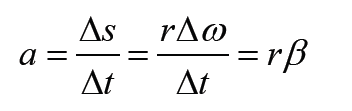
The instantaneous angular acceleration is
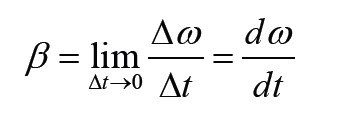
The instantaneous linear acceleration
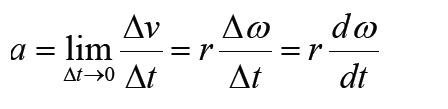
The angular acceleration is generally specified in radians per second (rad / s2)
whereas the instantaneous linear acceleration is expressed in (m / s2).
Application activity 4.2
1. A ball at the end of a string is revolving uniformly in a horizontal
circle of radius 2 meters at constant angular speed 10 rad/s.
Determine the magnitude of the linear velocity of a point located :
a) 0.5 meters from the center
b) 1 meter from the center
c) 2 meters from the center
2. The blades in a blender rotate at a rate of 5000 revolution per minute. Determine the magnitude of the linear velocity :
a) a point located 5 cm from the center
b) a point located 10 cm from the center
3. A point on the edge of a wheel 30 cm in radius, around a circle at constant speed 10 meters/second.
What is the magnitude of the angular velocity?
4. The angular speed of wheel 20 cm in radians is 120 revolutions per minute. What is the distance if the car travels in 10 seconds.
4.3 Acceleration in circular motion
Activity 4.4
A car executing a turn, after a certain speed limit, a car will start drifting.
a) Why at that limitation of the speed the car start travelling? Explain your reasoning
4.3.1. Tangential and Centripetal acceleration
In the circular motion, the tangential acceleration aT always points in the
direction tangent to the circle and changes the rate of velocity in terms of
magnitude because their vectors are always in the same or opposite direction.
The tangential acceleration can be considered as the linear acceleration.
The centripetal acceleration (normal acceleration or radial acceleration)
aN changes the velocity in terms of direction and its vector is perpendicularly
directed inward the circle.
Since the velocity is constant, the tangential component of acceleration doesn’t exist in UCM:
Consequently, the tangential component of the acceleration is also zero. Only, the normal component of the acceleration exists in UCM. Thus, the velocity
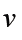changes in direction but not in magnitude. The figure below shows the representation of the angular velocity
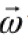using a distant reference frame
The centripetal component of the acceleration is directed along the radius.
From the above figure we can notice that
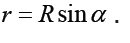
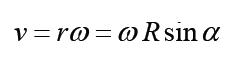
This relation indicates that the vector v can be expressed in the vector form by the equation:
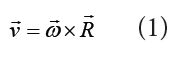
It follows that
Introducing the equation (1) into (2)
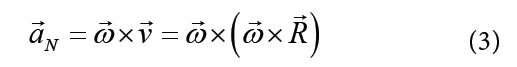
The magnitude of the centripetal acceleration is given by
4.3.2. Acceleration in a non-uniform circular motion
Circular motion at a constant speed occurs when the acceleration of the object
is directed toward the centre of the circle (Only the centripetal component is
available). If the acceleration is not directed toward the centre but is at an
angle, as shown in figure below, the acceleration has two components; thecentripetal and the tangential component.
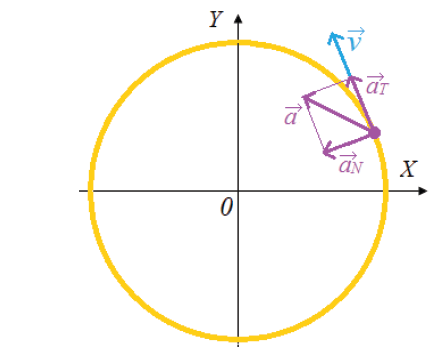
The tangential component of the acceleration is the rate that changes the magnitude of the velocity
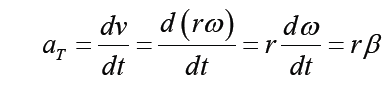
The centripetal acceleration arises from the change in direction of the velocity and, as we have seen, is given by
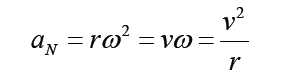
4.3.3. Distance time graph of circular motion
When an object executes a circular motion of constant radius R, its projection on an axis executes a motion of amplitude a that repeats itself back and forth, over the same path.
When M executes a uniform circular motion, its projection on X-axis executes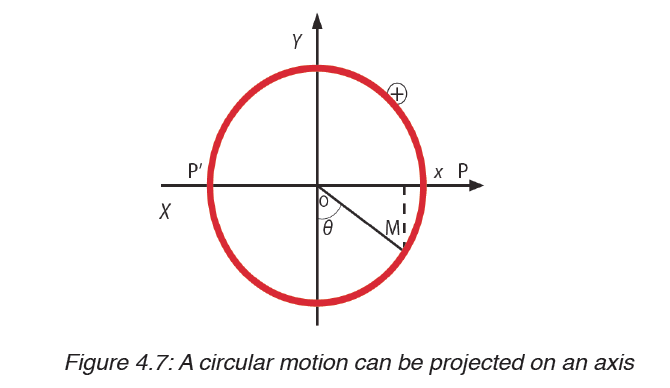
a back and forth motion between positions P and P’ about O.
Considering the displacement and the time, we find the following graph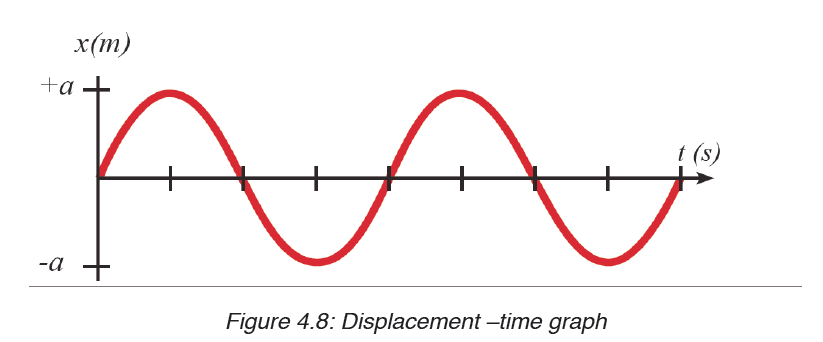
Application activity 4.3
1. A ball is attached to a string that is 1.5m long. It is spun so that it
completes two full rotations every second. What is the centripetalacceleration felt by the ball?
2. Imagine a car driving over a hill at a constant speed. Once the
car has reached the apex of the hill, what is the direction of theacceleration?
4.4 Centripetal force
Activity 4.4
Observe the following figure and answer the question below:
What would happen when a ball is attached to a string and is swung round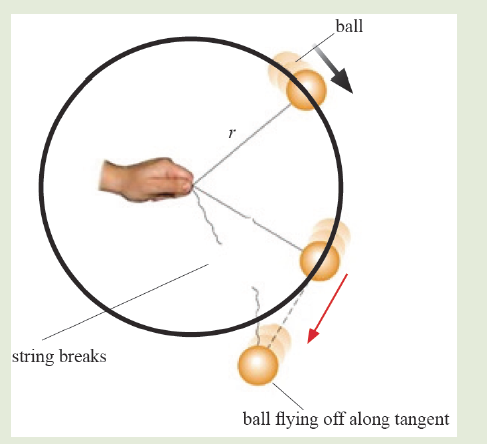
in horizontal circle? Explain your reasoning
If you try to move / run in a circular path, you will finally notice that you keep
moving in a circle even when you try to stop. There is a force that keeps you
more in a circular path called centripetal force. Since a body moving in a
circle (or a circular arc) is accelerating, it follows from Newton’s first law of
motion that there must be force acting on it to cause the acceleration.
This force, like the acceleration, will also be directed toward the centre and
is called the centripetal force. The value F of the centripetal force is given byNewton’s second law, that is:
Application activity 4.4
1. A 3.0 kg mass is tied to a rope and swung in a horizontal circle. If
the velocity of the mass is 4.0 m/s and the radius of the circle is
0.75 m, what is the centripetal force and centripetal acceleration
of the mass?
2. A 200-gram ball, attached to the end of a cord, is revolved in a
horizontal circle with an angular speed of 5 rad s-1. If cord’s length
is 60 cm, what is the centripetal force?
3. A student of mass 50kg decides to go on the ride. The coefficient
of static friction between the student and wall is 0.8. If the diameter
of the ride is 10m, what is the maximum period of the ride’s rotation
that will keep the student pinned to the wall once the floor drops?
g =10m/s2
SKILLS LAB
Go on YouTube, watch video about “Trucks fail to Negotiate Dangerous
Bend in Road”. It is a social issue which relationship with Circular motion.
1. What did you see on the video and what happen?
2. If you are engineer, how you will solve this problem?
3. Brainstorm with your classmates about the property needed to Design asafety road by used scientific knowledge in Circular motion.
End unit assessment 4
1. Why do we need a force to keep a body moving uniformly along a circular path?
2. When an object moves in a circular path the net force is called?
Explain your answer
3. When a particle moves in a circle with constant speed its
acceleration is? Explain your reason
4. Is acceleration constant in circular motion? Defend your reasoning
5. A hot wheels track has a vertical loop with a radius of 20 cm.
a) What is the minimum speed the car can have at the highest point
without falling off of the track?
b) If the actual speed is 1.8 m/s, what is the normal force? (use m=20
grams)
6. A 1200 kg car drives at a constant speed of 14 m/s around a
circular track (r=80.0 m).
a) What is the size of the net force acting on the car?
b) What is the physical agent providing that force?
c) What is the maximum frictional force that can act on the tires if the
static coefficient
of friction is 0.30? Will the car’s tires start slide? If not, how fast can
the car move before it does start sliding?
7. A0.45kg ball, attached to the end of a horizontal cord, is rotated in
a circle of radius 1.3m on a friction less horizontal surface. If the
cord will break when the tension in it exceeds 75N, what is the
maximum speed the ball can have?