Mathematics ECLPE

Key Unit competence: Use Mathematical logic as a tool of reasoning and argumentation in daily situation

4.1 Definition

4.1.1 Simple statement and compound statements

true or false, but never both, and to always have the same truth value. The two truth values of proposition are true and false and are denoted by the symbols T and F respectively. Occasionally they are also denoted by the symbols 1 and 0 respectively.

Application activity 4.1.1

1. Find out which of the following sentences are statements and which are not. Justify your answer.

a) Uganda is a member of East African Community.

b) The sun is shining.

c) Come to class!

d) The sum of two prime numbers is even.

e) It is not true that China is in Europe.

f) May God bless you!

2. Write down the truth value (T or F) of the following statements

a) Paris is in Italy.

b) 13 is a prime number.

c) Kigeri IV Rwabugiri was the king of the Kingdom of Rwanda 

d) Lesotho is a state of South Africa.

e) Tanzania is in east of Rwanda and is in SADC (Southern African Development Community)

4.1.2 Truth tables

Activity 4.1.2

Suppose we are given two simple statements, named p and q to get a compound statement C pq ( , ).

a) What are the possibilities for the truth-values of p and of q? 

b) Using a table, 

i) How many possibilities are there, for their pairs of truth-values? 

ii) How many possibilities are there, for the triples of truth-values of three statements p, q and r?

The way we will define compound statements is to list all the possible combinations of the truth-values (abbreviated T and F) of the simple statements (that are being combined into a compound statement) in a table, called a truth table. The name of each statement is at the top of a column of the table. The truth values used to define the truth-value of the compound statement appear in the last column.

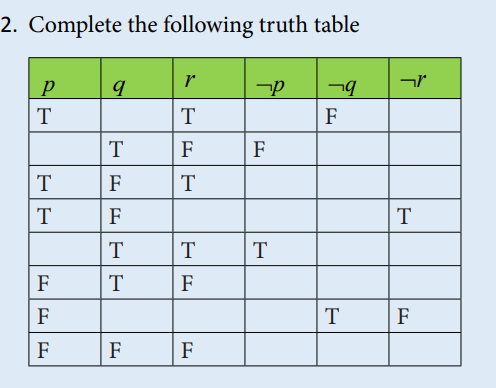
Application activity 4.1.2

 Write down the truth table for three propositions p, q and r

4.2 Logical connectives

4.2.1 Negation

Activity 4.2.1

Let p, q, r, s be the propositions 

1. It is raining

2. Uganda is African country

3. London is in France

4. Kagabo reads Newsweek

Give a verbal sentence which describes the opposite proposition

Application activity 4.2.1

1. Write the negation of each of the following statements.

a) Today is raining.

b) Sky is blue

c) My native country is Rwanda.

d) Benimana is smart and healthy.

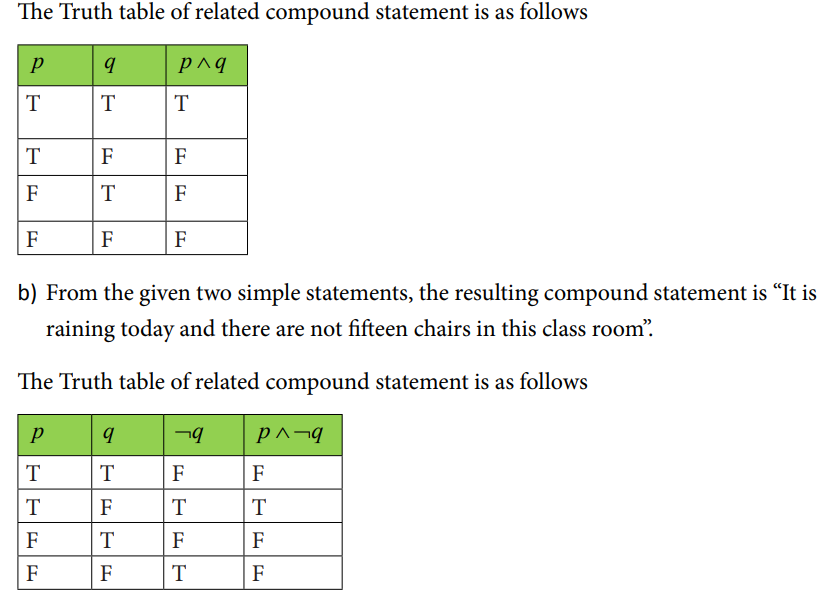
4.2.2 Conjunction

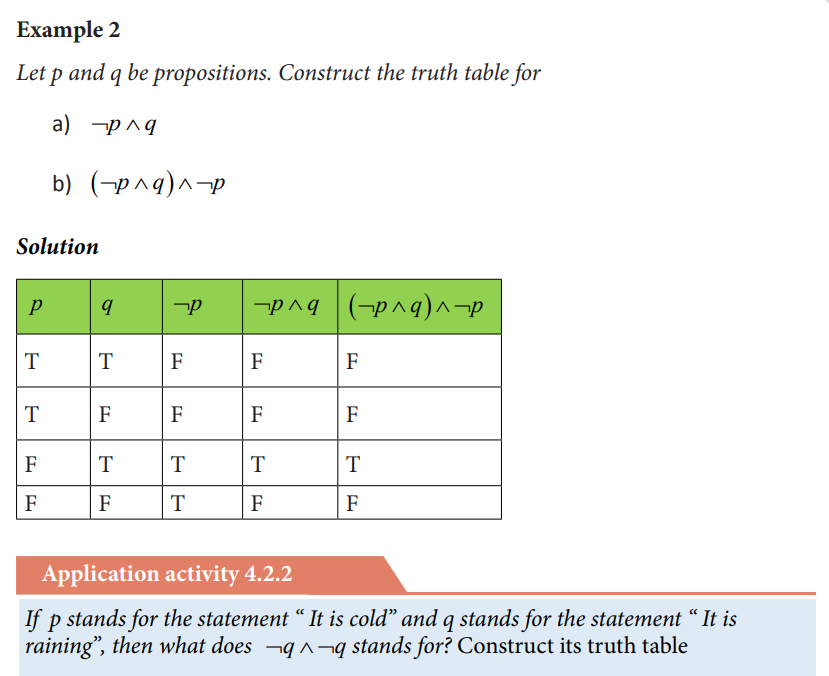
4.2.3 Disjunction

Determine the truth value of each of the following statements

1. Paris is in France or 4 + 4= 8

2. The sun is a planet or the Jupiter is a star.

3. Paris is in Japan or 3 +4 =7

4. The first president of United States of America is George Washington or was inaugurated in 1879.

5. Nairobi is the capital of Tanzania or1+1 =2

6. The French revolution started in 1789 or ended in 1799

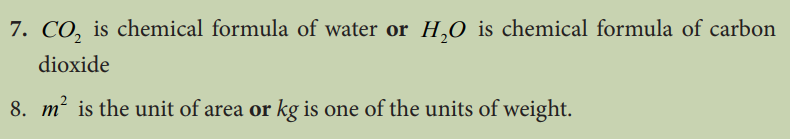
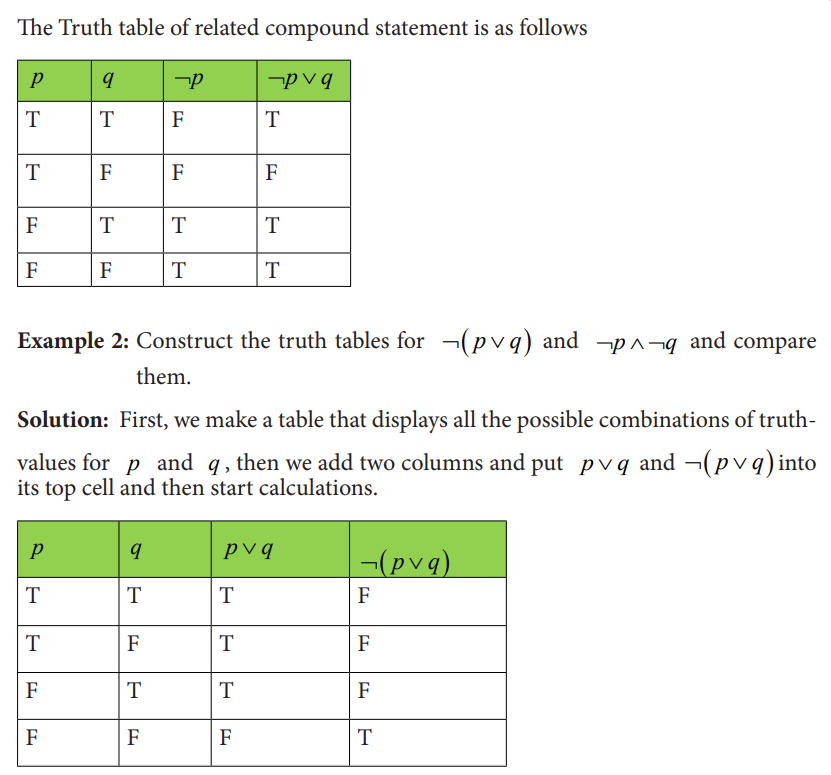
4.2.4 Conditional statement 

Activity 4.2.4

Rephrase the following statements without changing the meaning

1. If you buy me a pen, I will go to school

2. If the earth is flat, then mars is flat

3. If you are tall, then you will be a member of our volleyball team

4. If you do not buy these shoes, then I will not go with you

5. If you do not pay school fees, then you will not get you school report

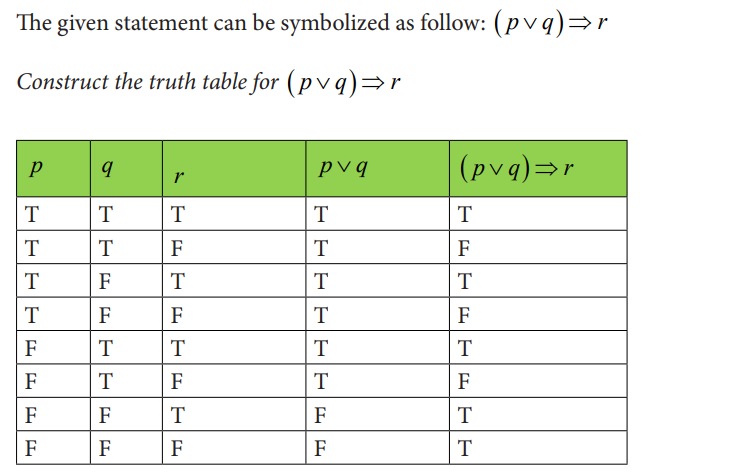
Application activity 4.2.4

1. Using the statements p :Mico is fat and p :Mico is happy

 Assuming that “not fat” is thin, write the following statements in symbolic form

a) If Mico is fat then she is happy

b) Mico is unhappy implies that Mico is thin

2. Write the following statements in symbolic form and their truth table

a) If n is prime, then n is odd or n is 2.

b) If x is nonnegative, then x is positive or x is 0.

c) If Tom is Ann’s father, then Jim is her uncle and Sue is her aunt.

4.2.5 Bi-conditional statements

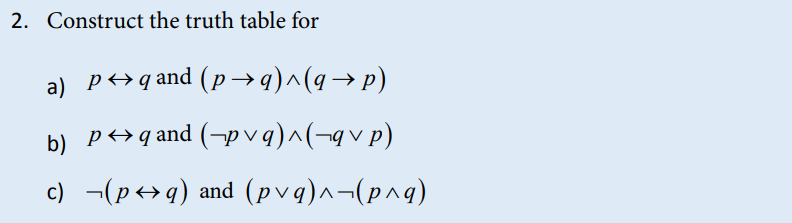
4.2.6 Tautologies and Contradictions

CONTENT SUMMARY

A tautology is a compound statement that is always true regardless of the truth values of the individual statements substituted for its statement variables. 

Example 

• The statement “The main idea behind data compression is to compress data” is a tautology since it is always true.

• The statement “I will either get paid or not get paid” is a tautology since it is always true 

If you are given a statement and want to determine if it is a tautology, then all you need to do is construct a truth table for the statement and look at the truth values in the final column. If all of the values are T (for true), then the statement is a tautology.

The statement “I will either get paid or not get paid” is a tautology since it is always true. We can use p to represent the statement “I will get paid” and not p (written ¬p) to represent “I will not get paid.”

4.3 Quantifiers and their negations: Existential and Universal quantifiers 

4.3.1 Predicates

4.3.2 Quantifiers

4.3.3 Negation of quantifiers 

Activity 4.3.3

Negate the following statements

1. All grapefruit are pink.

2. Some celebrities are modest.

3. No one weighs more than two thousand pounds.

4. Some people are more than ten feet tall.

5. All snakes are poisonous.

6. Some whales can stay under water for two days without surfacing for air.

7. All birds can fly

Application activity 4.3.3

Negate each of the following statements and write the answer in symbolic form

1. Some students are math majors

2. Every real number is positive, negative or zero

3. Every good boy does fine

4. There is a broken desk in our classroom

5. Lockers must be turned in by the last day of class

6. Haste makes waste

4.4 END UNIT ASSESSMENT 4