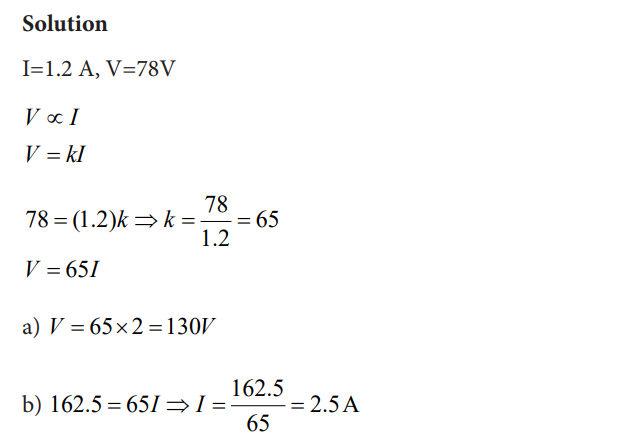Mathematics ECLPE

Key Unit competence: Apply ratios, proportions and multiplier proportion change to solve real life related problems

3.0. Introductory Activity 3

In daily life people compare quantities, share proportionally things or objects for different reasons. Do you ever wonder why ratio and proportion are necessary in daily life situations?

For example, look at your classmates:

a. Find out the number of boys, then the number of girls. Can you express the number of boys or girls in terms of fraction or ratio?

b. Can you equally share a certain number of Mathematics textbooks to different groups in your classroom and then figure out the ratio of Mathematics textbooks per learner?

c. Give examples where the concept of ratio and proportion are used in daily life situations 

3.1 Equal and unequal share, Ratio, Direct and indirect proportions.

3.1.1 Equal and unequal share, Ratio and proportion

Activity 3.1.1

1. Suppose that two brothers from your village received 7 000 Frw from their child who lives in the city. The condition to share this amount of money is that for every 2 Frw that the young brother gets, the other one gets 3 Frw. The two brothers have come to you for help after they disagreed on how to share such money.

(i) In what ratio would you share the money between them? 

(ii) Tell your partner how you would share the money and how much each would get.

2. Read carefully the following word problem and express the given data into fraction or ratio. 

a. John and Lucy partnered to save money for x time and later buy a taxi. For every 800 Frw that John saved, Lucy saved 120 Frw. In what fraction or ratio were their contributions? What other simplest fraction or ratio is same as this?

b. Jane and David sold milk to a vendor in the morning. Jane sold 4 500 ml while David sold 7.5 litres. In what fraction or ratio are their milk sales?

CONTENT SUMMARY

• Equal and unequal share

There are many cases in real life where people or organizations need to share items or resources equally or unequally. For example, a father may want to share 24 acre of land among his two sons. One of them who is disabled gets double of what the other son gets. In such case, the land is unequally shared. 

Ratios:

The mathematical term ‘ratio’ defines the relationship between two numbers of the same kind. The relationship between these numbers is expressed in the form “a to b” or more commonly in the form a b

A ratio is used to represent how much of one object or value there is in relation to another object or value. 

Example: If there are 10 apples and 5 oranges in a bowl, then the ratio of apples to oranges would be 10 to 5 or 10: 5. This is equivalent to 2:1. In contrast, the ratio of oranges to apples would be 1:2.

Ratios occur in many situations such as in business where people compare profit to loss, in sports where compare wins to losses etc.

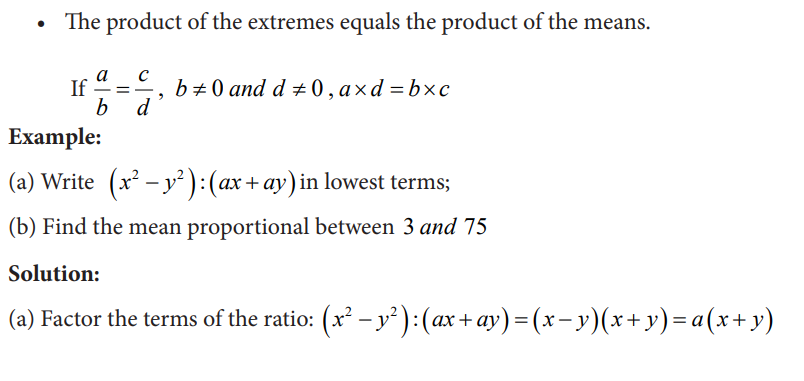
Application activity 3.1.1

Ingabire, Mugenzi and Gahima have jointly invested in buying and selling of shares in the Rwanda stock exchange market. In one sale as they invested different amount of money, they realised a gain of 1 080 000 Frw and intend to uniquely share it in the ratio 2:3:4 respectively. How much did Mugenzi get?

3.1.2 Direct and indirect proportions

CONTENT SUMMARY

• Direct proportion

The mathematical term ‘proportional’ describes two quantities which always have the same relative size or ‘ratio’. 

Example: An object weighs 2kg on the 1st day. If weight is proportional to age, then the object will weigh 4kg on the 2nd day, 6kg on the 3rd day, 8kg on the 4th day, 10kg on the 5th day and so on.

There are many phenomena in real life that involve a squared relationship. 

For example: • The area (A) of a circle varies directly with the square of the radius r

• The value (V) of a diamond varies directly with the square of its mass (M) make the following comparison:

3.2 Calculation of proportional and compound proportional change 

Activity 3.2

1. Discuss with your classmate what you understand by the word multiplier. 

• Consider a shirt that is sold at a 20% discount. 

• What is the percentage of the selling price? 

• Convert this percentage you have gotten into fraction. What do you notice? 

2. Consider a shirt with a marked price of 500 Frw. After negotiating with the customer, the shirt is sold at a 10% lower. Discuss with your classmate the change in price and the new price (selling price) of the shirt in Frw.

3. Consider that 3 people working at the same rate can cultivate 2 acres of land in 3 days. What do you think will happen if the working days are increased to five and people are still working at the same rate? Discuss.

2. A farmer gets 80 litres of milk from his cow. The amount of milk from the cow reduced by 5% after illness. What is the new amount of milk produced by the cow? 

Repeated proportional change is an extremely useful mathematical process because it can be used to calculate real world financial problems such as compound interest.

‘Compound interest’ refers to the interest added to a deposit or loan. The added interest will also earn interest as time passes. To calculate the compound interest of a loan, we may use repeated proportional change.

Example

(a) £500 is borrowed for 6 years at 5 % compound interest. Calculate the amount of compound interest which will be paid

Solution

(a) From the question, we know that 5% compound interest is added each year. This means that there will be 105% of the original amount borrowed at the end of the first year or 1.05.

With 1.05 as your multiplier, you can calculate the total amount of money borrowed after 6 years. The money was borrowed for 6 years, so you must raise 1.05 to the power of 6. Therefore:

Total amount of money borrowed is 500 x (1.05) 6 = 670.047= £670

The question has asked you to calculate the amount of compound interest. To do so, you must subtract the original amount borrowed (£500) from the value you have just generated:

670 - 500 = 170. As a result, the amount of compound interest which will be paid is £170

To calculate compound proportionality problems, one can use the unitary method or compound rule of three

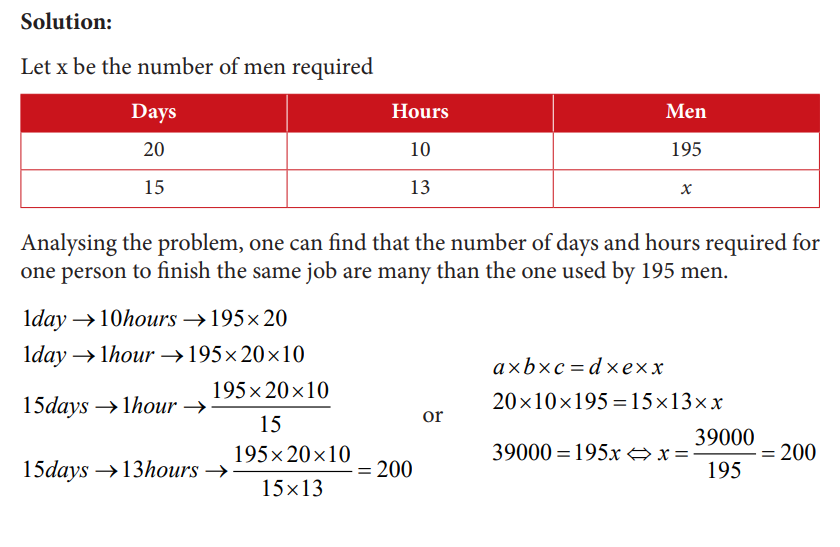
Example: 9 men working in a factory produce a certain number of pans in 6 working days. How long will it take 12 men to produce the same number of pans if they work at the same rate?

Application activity 3.2

1. What is the multiplier of 45% decrease?

2. Deborah’s salary last year was 15 000 Frw. This year it was increased by 20%. What is her salary this year?

3. In 2004 a company processed 800 tonnes of maize. In 2005, the company decreased production by 30 %. How many tonnes did the company process in 2005?

4. Four men working at the same rate can dig a piece of land in ten days. How long would it take five men to do the same job?

3.3 Problems involving direct and indirect proportions

Activity 3.3

Read carefully the given problems and discuss how can you solve problems involving direct and indirect proportions.

1. F is directly proportional to x. When F is 6, x is 4. Find the value of F when x is 5.

2. A is directly proportional to the square of B. When A is 10, B is 2. Find the value of A when B is 3.

3. A is inversely proportional to B. When A is 10, B is 2. Find the value of A when B is 8

4. F is inversely proportional to the square of x. When F is 20, X is 3. Find the value of F when x is 5.

CONTENT SUMMARY

Two values x and y are directly proportional to each other when the ratio x : y or x y ∝  is a constant (i.e. always remains the same). This would mean that x and y will either increase together or decrease together by an amount that would not change the ratio.

Knowing that the ratio does not change allows you to form an equation to find the value of an unknown variable.

Example:

If two pencils cost $1.50, how many pencils can you buy with $9.00?

Problem solving plan 

1. Understand the problem: Think what information is given and what information is required

2. Decide on a strategy: List the strategies with which you think the solution can be found

3. Apply the strategy: Find the solution using the strategy you have chosen

4. Look back:

• Have you verified your solution?

• Are there other solutions?

• Can you solve a simpler problem?

• Have you answered the question as it was initially stated?

Example

1. The voltage V(volts) across an electrical circuit is directly proportional to the current I (Amperes) flowing through the circuit. When I=1.2 A, V=78V

a) Express V in terms of I

b) Find V when I=2A

c) Find I when V=162.5V