Mathematics ECLPE

Key Unit competence: Classify numbers into naturals, integers, rational and irrationals.

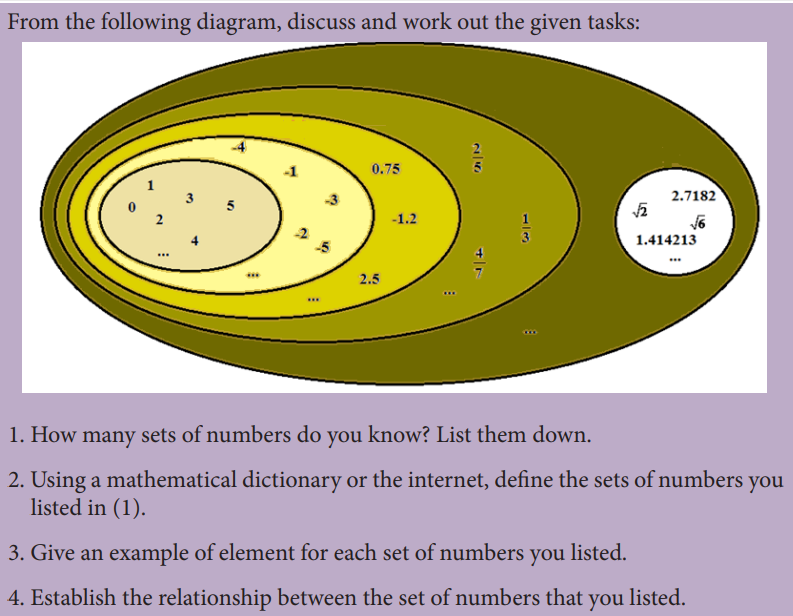
1.0. Introductory Activity 1

1.1. Natural numbers 

1.0.1. Definition

Activity 1.1.1

For any school or organization, they register their different assert for good 

management.

For example 

1. The number of desks may be 152

2. The number of Mathematics textbooks may be 2000. 

3. The number of classrooms is 15

4. The number of kitchen may be 1

5. The number of car may be 0

6. And so on

All of these numbers are elements of a set. Which set do you think, they can 

belong to?

Can you give other example of elements of that set?

CONTENT SUMMARY

Usually, when counting, people begin by one, followed by two, then three and so 

on. The numbers we use in counting including zero, are called Natural numbers. 

The set of natural numbers is denoted by  = … 0, 1, 2, 3, 4, . { }

On a number line, natural numbers are represented as follows:

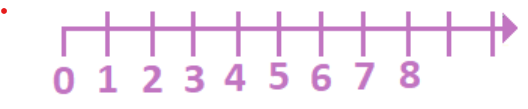
Application activity 1.1.1

1. Write down, first ten elements of natural numbers starting from zero.

2. Apart from recording assets, give two examples of where natural 

numbers can be used in daily life

2 Mathematics ECLPE | TTC Year 1

1.1.2. Sub sets of natural numbers

Activity 1.1.2

Carry out the following tasks. 

(a) Use a dictionary or internet to define the terms: even, odd and prime numbers.

(b) You are given the set of natural numbers between 0 and 20, 

(i) make a set of odd numbers. 

(ii) make a set of even numbers. 

(iii) make a set of prime numbers. 

(iv) identify even numbers which are prime numbers? 

(v) How many odd numbers are prime numbers? 

(c) Represent the information from (b) in a Venn diagram.

CONTENT SUMMARY

There are several subsets of natural numbers:

(a)Even numbers

Even numbers are numbers which are divisible by 2 or numbers which are multiples of 2. 

Even numbers from 0 to 20 are 0, 2, 4, 6, 8, 10,12, 14, 16, 18 and 20. 

The set of even numbers is E = {2,4,6,8,} and it is a subset of natural numbers.

(b) Odd numbers 

Odd numbers are numbers which leave a remainder of 1 when divided by 2. Odd 

numbers between 0 and 20 are 1,3,5,7,9,11,13,15,17 and 19. The set of odd numbers 

is O = {1,3,5,7,} and it is a subset of natural numbers.

(c) Prime numbers 

Prime number is a number that has only two divisors 1 and itself. Prime numbers 

between 0 and 20 are 2, 3, 5, 7, 11, 13, 17 and 19. The set of prime numbers is 

P = {2,3,5,7,11,13,19,} and it is a subset of natural numbers.

Application activity 1.1.2

Given E = {1, 4, 8, 11, 16, 25, 49, 53, 75}, list the elements of the following subsets 

(a) Even numbers 

(b) Odd numbers 

(c) Prime numbers 

Represent the above information on a Venn diagram.

1.1.3 Operations and properties on natural numbers

Activity 1.1.3

1. From the given any three natural numbers a ,b and c , investigate the following operations

a) is a b + always a natural number? Use example to justify your answer.

b) is a b + and b a + always giving the same answer? Use example to justify your 

answer.

c) is a bc + + and (ab c + +) always giving the same answer? Use example to 

justify your answer.

2. Given any three natural numbers a ,b and c , investigate the following operations: 

a b − and b a − , a bc − − and ab c − −

What do you notice? Is always the answer an element of natural numbers? 

Justify your answer.

3. Given any three natural numbers a ,b and c , investigate the following 

operations : a b × , a b × and b a × , a bc × × and ab c × × , a bc × + and 

ab ac + , a bc × − and ab ac −

4. Given any two natural numbers a ,b different from zero, investigate the 

following operations a b ÷ , a b ÷ and b a ÷ ,

CONTENT SUMMARY

Addition 

(i) Closure property:  The sum of any two natural numbers is always a natural 

number. This is called ‘Closure property of addition’ of natural numbers. Thus,  is 

closed under addition. If a and b are any two natural numbers, then (a + b) is also a 

natural number.

Example: 2 + 4 = 6 is a natural number.

(ii) Commutative property:  If a and b are any two natural numbers, then, a+b=b+a. 

Addition of two natural numbers is commutative.

Example: 2+ 4 = 6 and 4 + 2 = 6. Hence, 2 + 4 = 4 + 2

(iii) Associative property:

If a, b and c are any three natural numbers, then a + (b + c) = (a + b) + c. Addition 

of natural numbers is associative.

Example: 2 + (4 + 1) = 2 + (5) = 7 and (2 + 4) + 1 = (6) + 1 = 7. Hence, 2+(4+1)=(2+4)+1

Subtraction

(i) Closure property: The difference between any two natural numbers need not be 

a natural number. Hence  is not closed under subtraction.

Example:  2 - 5 = -3 is a not natural number. 

(ii) Commutative property:  If a and b are any two natural numbers, then 

(a-b) ≠ (b-a). Subtraction of two natural numbers is not commutative.

Example:  5 - 2 = 3 and 2 - 5 = -3. Hence, 5 - 2 ≠ 2 – 5. Therefore, Commutative 

property is not true for subtraction.

(iii) Associative property: If a, b, c and d are any three natural numbers, then 

a - (b - d) ≠ (a - b) – d. Subtraction of natural numbers is not associative.

Example: 2 - (4 - 1) = 2 - 3 = -1 and (2 - 4) - 1 = -2 - 1 = -3 

Hence, 2 - (4 - 1)   ≠  (2 - 4) – 1. Therefore, Associative property is not true for 

subtraction.

Multiplication

(i) Closure property: If a and b are any two natural numbers, then a x b = ab is also 

a natural number. The product of two natural numbers is always a natural number. 

Hence  is closed under multiplication.

Example: 5 x 2 = 10 is a natural number. 

(ii) Commutative property: If a and b are any two natural numbers, then 

a x b = b x a. Multiplication of natural numbers is commutative.

Example:  5 x 9  =  45 and 9 x 5  =  45. Hence, 5 x 9  =  9 x 5. Therefore, Commutative 

property is true for multiplication.

(iii) Associative property: If a, b and c  are any three natural numbers, 

then a x (b x c)  =  (a x b) x c. Multiplication of natural numbers is associative.

Example: 2 x (4 x 5)  =  2 x 20  =  40 and (2 x 4) x 5  =  8 x 5  =  40 , Hence, 

2 x (4 x 5)  =  (2 x 4) x 5. Therefore, Associative property is true for multiplication.

(iv) Multiplicative identity: a is any natural number, then a x 1 = 1 x a  =  a. The 

product of any natural number and 1 is the whole number itself. ‘One’ is the 

multiplicative identity for natural numbers.

Example: 5 x 1 = 1 x 5 = 5

Division

(i) Closure property: When we divide of a natural number by another natural number, 

the result does not need to be a natural number.  Hence,  is not closed under 

multiplication. 

Example: When we divide the natural number 3 by another natural number 2, we 

get 1.5 which is not a natural number. 

(ii) Commutative property: If a and b are two natural then a ÷ b   ≠  b ÷ a. Division 

of natural numbers is not commutative.

Example: 2 ÷ 1  =  2 and 1 ÷ 2  =  1.5. Hence, 2 ÷ 1  ≠  1 ÷ 2

Therefore, Commutative property is not true for division.

(iii) Associative property: If a, b and c  are any three natural numbers, 

then a ÷ (b ÷ c)  ≠  (a ÷ b) ÷ c. Division of natural numbers is not associative.

Example : 3 ÷ (4 ÷ 2)  =  3 ÷ 2  =  1.5 and (3 ÷ 4) ÷ 2  =  0.75 ÷ 2  =  0.375 

Hence, 3 ÷ (4 ÷ 2)  ≠  (3 ÷ 4) ÷ 2. Therefore, Associative property is not true for 

division.

Distributive Property

(i) Distributive property of multiplication over addition :

If a, b and c  are any three natural numbers, then a x (b + c)  =  ab + ac. Multiplication 

of natural numbers is distributive over addition.

Example : 2 x (3 + 4)  =  2 x 3 + 2 x 4  =  6 + 8  =  14

2 x (3 + 4)  =  2 x (7)  =  14. Hence, 2 x (3 + 4)  =  2 x3 + 2 x 4

Therefore, Multiplication is distributive over addition.

(ii) Distributive property of multiplication over subtraction:

If a, b and c  are any three natural numbers, then a x (b - c)  =  ab – ac. Multiplication 

of natural numbers is distributive over subtraction.

Example: 2 x (4 - 1)  =  (2x4) - (2x1)  =  8 - 2  =  6

2 x (4 - 1)  =  2 x (3)  =  6. Hence, 2 x (4 - 1)  =  (2x4) - (2x1)

Therefore, multiplication is distributive over subtraction.

Application activity 1.1.3

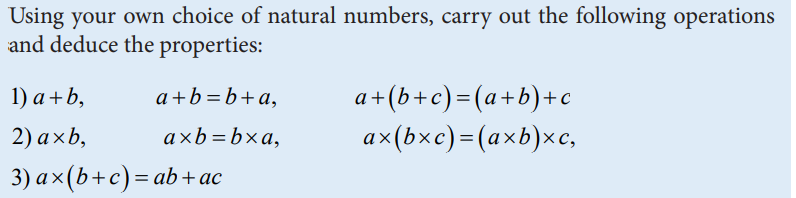
1.2 Integers

1.2.1 Definition

Activity 1.2.1

Carry out the following activities 

1. Using a Maths dictionary, define what an integer is. 

2. What integer would you give to each of the following situation?

(a) A fish which is 50 m below the water level. 

(b) Temperature of the room which is 42ºC. 

(c) A boy who is 2 m below the ground level in a hole. 

(d) A bird which is 3 m high on a tree

CONTENT SUMMARY

Integers are whole numbers which have either negative or positive sign and include 

zero. The set of integers is represented by  . Iintegers can be negative {-1,-2,-3,-4,-5,... }, 

positive {1, 2, 3, 4, 5, ... }, or zero {0}

The set of integers is represented using Carly brackets as follow : 

{ ..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ... }

Example 1:

Taking 4 steps forward can be considered as +4 (positive 4). This means it is 4 steps 

ahead of the starting point.

Taking 4 steps backward is considered as -4 (negative 4). This means it is 4 steps 

behind the starting point.

Example 2:

Application activity 1.2.1

 John borrowed $3 to pay for his lunch. 

 Alex borrowed $5 to pay for her lunch. 

 Virginia had enough money for lunch and has $3 left over.

Place these people on the number line to find who is poorest and who is richest 

given that they will pay the same amount.

1.2.2 Sub sets of integers

Activity 1.2.2

Discuss the following: 

From integers between 12 and +20, form small sets which contain; 

a) odd numbers

b) even numbers

c) factors of 6 

d) multiples of 3. 

CONTENT SUMMARY

Integers have several subsets such as set of natural numbers, set of even numbers, 

set of odd numbers, set of prime numbers, set of negative numbers and so on. 

Some of special subset of integers are the following:

Application activity 1.2.2

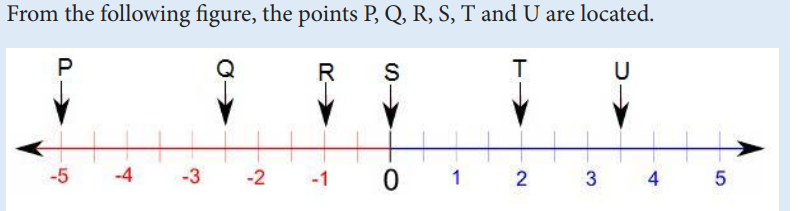
Among them, 

• which are negative integers?

• Which are positive integers?

• Which are neither positive nor negative integers?

• Which are not integers?

1.2.3 Operations and properties on integers

Activity 1.2.3

1. Work out the following on a number line: 

(a) (+3) + (+2) (b) –(5) + - (3) (c) (+4) + (-3) 

(d) Which side of the number line did you move when adding a negative 

number to a positive number? 

(e) Which side of the number line did you move when adding the given 

numbers which are all negative?

2. Work out the following and show your solutions on a number line. 

(a) (-4)-(+3) (b) (+5) – (+3) (c) (–6) – (-6) 

(d) On your number line, which direction do you move when subtracting two 

negative numbers? 

(e) In case you have two positive numbers that you are finding the difference, 

which side of the number line would you move?

3. Work out the following:

(a) (+5) × (-6) (b) (+5) × (+6) (c) (-5) × (+6) (d) (-5) × (-6) 

(e) Did you obtain the same results in all the four tasks?

4. Work out the following and show your solutions on a number line. 

(a) (-4) ÷(+4) (b) (+4) ÷ (+4) (c) (–4) ÷ (-4) (d) (+4) ÷ (-4) 

(e) Did you obtain the same results in all the four questions above?

CONTENT SUMMARY

The table below shows how addition, subtraction, multiplication and division of 

integers are performed.

Application activity 1.2.3

A common example of negative integer usage is the thermometer.  

Thermometers are similar to number lines, but vertical. They have positive 

integers above zero and negative integers below zero. Commonly, people recognize a temperature of -25°C as cold.  People use this number system to measure and represent the temperature of the air. Also, if it is -23°C outside, and 

the temperature drops 3 degrees, what is temperature now? If we picture the thermometer, we know that as the temperature drops, we look downwards on the thermometer

1.3 Rational and irrational numbers

1.3.1 Definition of rational numbers 

Activity 1.3.1

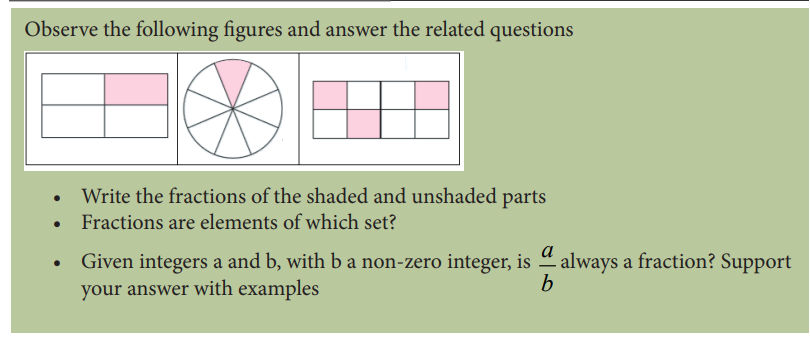
CONTENT SUMMARY

From any two integers a and b , we deduce fractions expressed in the form a/b , where b is a non-zero integer. A rational number is a number that can be expressed as a fraction where both the numerator and the denominator in the fraction are integers; the denominator in a rational number cannot be zero. As fractions are rational numbers, thus set of fractions is known as a set of rational numbers.

Application activity 1.3.1

From research on internet or using reference books, identify different type of fractions and give example for each type.

1.3.2 Sub sets of rational numbers

Activity 1.3.2

Knowing that a rational number is a number that can be in the form of  p q, where p and q are integers and q is not zero. Tell whether the given statements are true or false. Explain your choice.

1. All integers are rational numbers.

2. No rational numbers are whole numbers.

3. All rational numbers are integers.

4. All whole numbers are rational numbers

CONTENT SUMMARY

From the concept of subset and definition of a set of rational numbers we can establish some subsets of rational numbers; among them we have:

• Integers and its subsets: 0 , , , ,... +−+ Z Z;Z Z..........

• Natural numbers and its subsets: , , + N N prime numbers, odd numbers, even numbers,…

• Counting numbers and its subsets: ,+ N square numbers, prime numbers, odd numbers, even numbers …

Application activity 1.3.2

Using Venn diagram, establish the relationship between the following sets: 

Natural numbers; Integers and rational numbers.

1.3.3 Operations and properties on rational numbers

Activity 1.3.3

CONTENT SUMMARY

The following table shows how addition, subtraction, multiplication and division of rational numbers are performed 

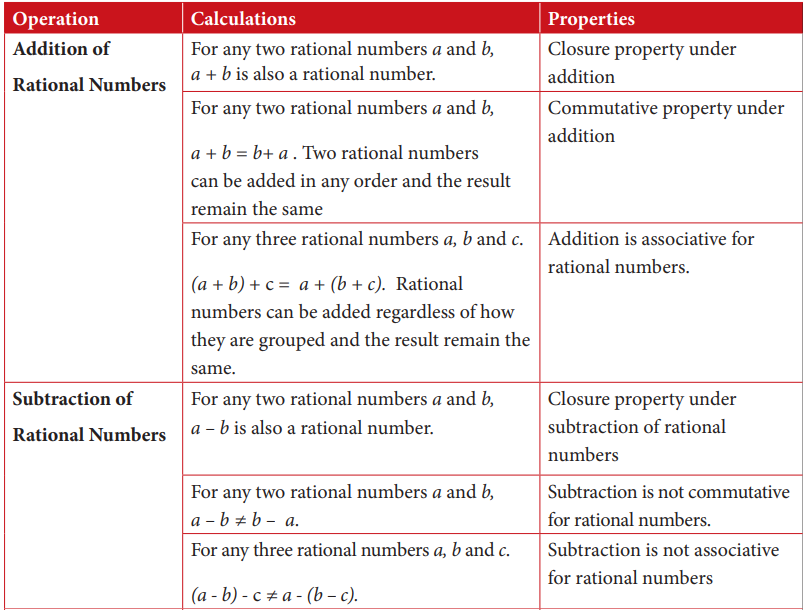
Application activity 1.3.3

Read carefully the following text and make a research to find out two more examples where fractions or rational numbers are used in real life and then present your findings in written and oral forms.“Imagine you are shopping with your $100 in birthday money. You really want a few items you have had your eye on for a while, but they are all very expensive. You are waiting for the items to go on sale, and when they do, you rush down to the store. Instead of being marked with a new price, though, the store has a large sign that reads: All items are currently 75% off. This sounds like great news, but without doing some Math, there is no way to know if you have enough money. Knowing that 75% is ¾ off the cost of each item is the best way to get started”. 

1.3.4 Definition of irrational numbers

Activity 1.3.4

CONTENT SUMMARY

Application activity 1.3.4

Using internet or reference books, from your own choice of appropriate numbers, verify and discuss if the given statement is always true, sometimes true or never true.

1. The sum of rational number and irrational number is irrational.

2. The product of rational number and irrational number is irrational.

3. The sum of two irrational numbers is irrational.

4. The product of two irrational numbers is irrational.

5. Between two rational numbers, there is an irrational number.

6. If you divide an irrational number by another, the result is always an irrational number

1.4 Real numbers

1.4.1 Definition

Activity 1.4.1

From the following Venn diagram, representing the set of counting numbers, natural numbers, integers, decimals, rational numbers and irrational numbers, verify and discuss if the given statement is whether true or false.

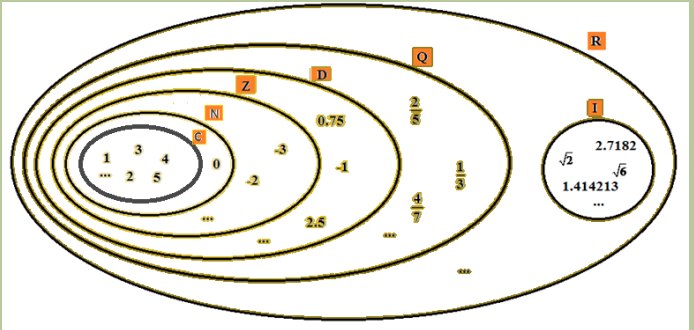
1. The set of counting numbers is a subset of natural numbers.

2. The intersection of set of integers and counting numbers is the set of natural numbers.

3. The intersection of set of integers and natural numbers is the set of counting numbers.

4. The union of set of natural numbers and counting numbers is the set of natural numbers.

5. The intersection of set of rational numbers and irrational numbers is the set of irrational numbers.

6. The union of set of rational numbers and irrational numbers is a set of irrational numbers.

CONTENT SUMMARY

The set of rational numbers and the set of irrational numbers combined together, form the set of real numbers. The set of real numbers is denoted by R . Real numbers are represented on a number line as infinite points or they are set of decimal numbers found on a number line. This is illustrated on the number line below

Application activity 1.4.1

Some examples of applications of real numbers in our daily life are identified below. From research activity; find out at least 3 examples of other applications of real numbers in our daily life.

Real numbers help us to count and to measure out quantities of different items. For instance, in catering you may have to ask the client how many sandwiches they need for the event. Certainly, those working in accounts and other financial related jobs may use real numbers mostly. Even when relaxing at the end of the day in front of the television flicking from one channel to the next you are using real numbers.

1.4.2 Subsets of real numbers and intervals

Activity 1.4.2

Carry out research on sets of real numbers to determine its subsets and present your finds using a number line.

Application activity 1.4.2

Note that, in writing intervals, it is also possible to include only one endpoint in an interval. Included point is geometrically represented by the solid dot. From this notice, complete the following table.

1.4.3 Operations and properties on real numbers

CONTENT SUMMARY

The following table shows how addition, subtraction, multiplication and division of real numbers are performed 

Application activity 1.4.3

1. Discuss whether Closure property under division for real numbers is satisfied.

2. Ngoma District wants to sell two fields on the same price. One has width of 60m out 160m of length. Another one has the width of 100m as it is its length. Among these fields, what is biggest? Interpret your result.

1.4. END UNIT ASSESSMENT 1

1. List three rational numbers between 0 and 1 

2. Identify the sets to which each of the following numbers belong by ticking (˅) in the appropriate boxes (cells).