UNIT 4: INDEX NUMBERS AND APPLICATIONS
Key unit Competence: Apply index numbers in solving financial related
problems, interpreting a value index, and drawingappropriate decisions.
Introductory activity
An industrial worker was earning a salary of 100,000Frw in the year 2000.Today, he earns 1,200,000Frw.
i. Can his standard of living be said to have risen 12 times during thisperiod?
ii. Which statistical measure used to detect changes in a variable (risingor decreasing)
iii. By how much should his salary be raised so that he is as well off asbefore?
iv. Describe the methods can be used detect the rise of the price
4.1. Introduction to index numbers
4.1.1 Meaning, types and characteristics of index number
Learning activity 4.1.1
If a businessman wants to measure changes in the price level for a specific
group of consumers in his region of business.
a) Which statistical measure he can use to detect changes in a variable
or group of variables in his business
b) Help him how he can calculate consumer price index for industrial
workers, city workers and agricultural workers.1. Meaning of index number
An index number is a statistical measure used to detect changes in a variable
or group of variables. In addition, a single ratio (or percentage) that measures
the combined change of several variables between two different times, places,
or situations is referred to as an index number. Index numbers are expressedas percentages.
The relative change in price, quantity, or value in comparison to a base period.
An index number is used to track changes in raw material prices, employee andcustomer numbers, annual income and profits.
A simple index is one that is used to measure the relative change in only
one variable, such as wages per hour in manufacturing. A composite index
is a number that can be used to measure changes in the value of a group of
variables such as commodity prices, volume of production in different sectorsof an industry, production of various agricultural crops and cost of living.
The index number measures the average change in a group of related variables
over two different situations, such as commodity prices, volume of production
in various sectors of an industry, production of various agricultural crops, and
cost of living. Index numbers measure the changing value of a variable over
time in relation to its value at some fixed point in time, the base period, when itis given the value of 100
2. Characteristics of index numbers
Index numbers have the following important characteristics:
– Index numbers are of the type of average that measures the relative
changes in the level of a particular phenomenon over time. It is a special
type of average that can be used to compare two or more series made up ofdifferent types of items or expressed in different units.
– Index numbers are expressed as percentages to show the level of relativechange.
– Index numbers are used to calculate relative changes. They assess the
relative change in the value of a variable or a group of related variablesover time or between locations.
– Index numbers can also be used to quantify changes that are not directly
measurable. For example, the cost of living, price level, or business activity
in a country are not directly measurable, but relative changes in these
activities can be studied by measuring changes in the values of variables/factors that affect these activities.
3. Types of index numbers
a) Consumer price index
A consumer price index (CPI) tracks price changes in a basket of consumer
goods and services purchased by households. CPI measures changes in the price
level for a specific group of consumers in a given region. CPI can be calculated
for industrial workers, city workers and agricultural workers. Consumer priceindex is given by:

e) Uses of index numbers
The price indices such as CPI and PPI used to:
• Measure the cost of living;
• Measure of inflationary and deflationary tendencies in the economy,
• Means of adjusting income payments: nominal interest rates, wage
determination, taxes and other allowancesThe quantity/production Indices used to
• Used in national accounts to assess the performance of the economy
• Good indicator of the economic progress taking place in differentsectors, regions and countries to facilitate comparisons
Application activity 4.1.1
1. Discuss why index numbers are called as economic barometer2. Explain the characteristics of index number.
4.1.2. Construction of indices
Learning activity 4.1.2
For the given data of prices in certain country, answer the questions thatfollows:
a) How do you describe these prices over the given years?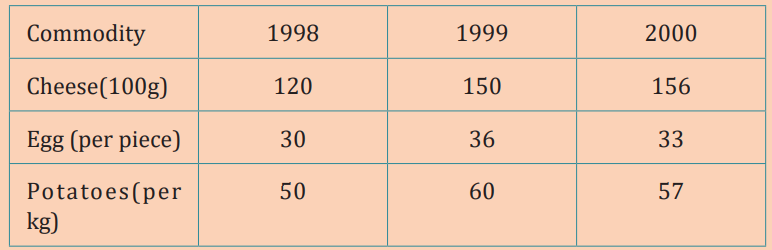
b) Describe the methods can be used to detect changes in these variable?
c) Find simple aggregative index for the year 1999 over the year 1998
d) Find the simple aggregative index for the year 2000 over the year1998
The construction of index numbers considers the definition of the purpose of
the index, selection of the base period, selection of commodities, obtaining price
quotations, choice of an average, selection of weights and then selection of a
suitable formula. Price index numbers are used to explain the various methods
of index number construction. Price index number construction methods canbe divided into three broad categories, as shown below:
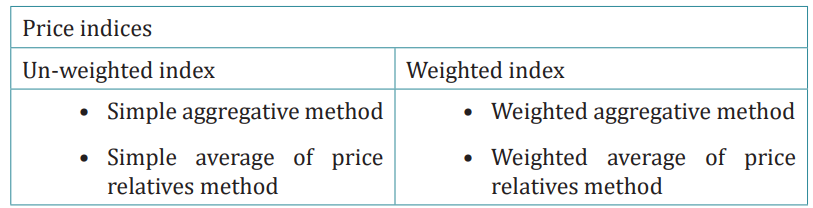
Un-weighted index
Weights are not assigned to the various items used in the calculation of the
un-weighted index number. The following are two un-weighted price indexnumbers:
i. Simple Aggregate Method
This method assumes that different items and their prices are quoted in the
same units. All of the items are given equal weight. The following is the formulafor a simple aggregative price index:
From the following data compute price index number for the year 2014 taking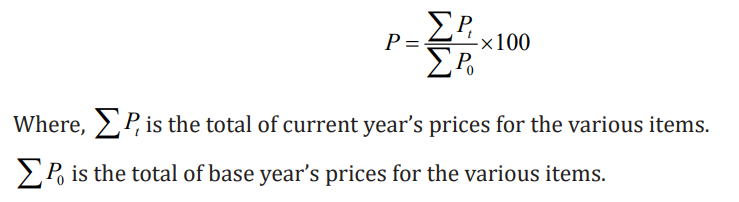
2013 as the base year using simple aggregative method:
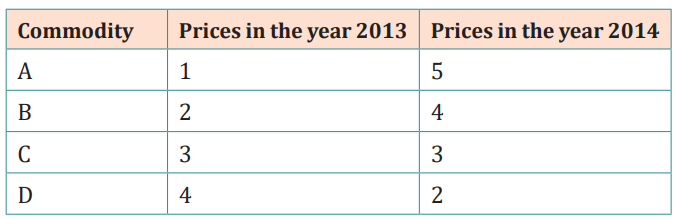
This price index of 140 indicates that the aggregate of the prices of the given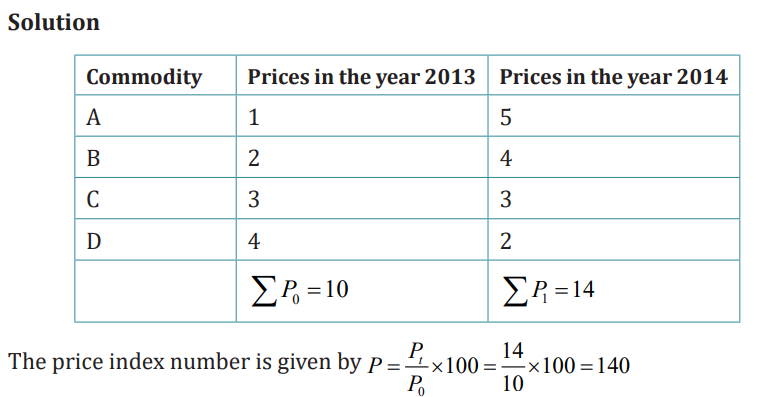
group of commodities increased by 40% between 2013 and 2014. This price
index number, calculated using a simple aggregative method, is only of limitedutility. The following are the reasons:
a) This method disregards the relative importance of the variouscommodities used in the calculation.
b) The various items must be expressed in the same unit. In practice, thevarious items may be expressed in different units.
c) The index number obtained by this method is untrustworthy because it
is influenced by the unit in which the prices of various commodities arequoted.
ii. Simple Average of Price Relatives Method
This method is superior to the previous one because it is unaffected by the
unit in which the prices of various commodities are quoted. Because the price
relatives are pure numbers, they are independent of the original units in which
they are quoted. The price index number is defined using price relatives asfollows:
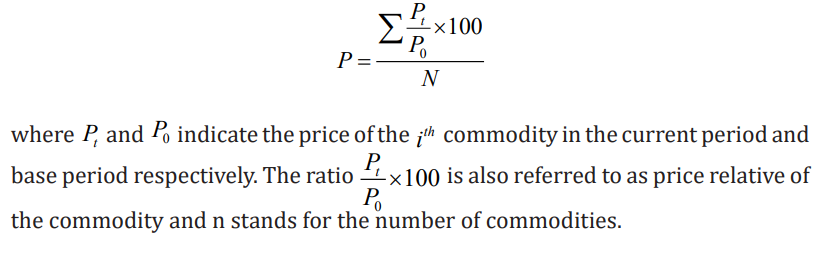
Example1:
Using the data of example 1 the index number using price relative method canbe calculated as follows:
As a result, the price in 2014 is 112.5% higher than in 2013. The index number,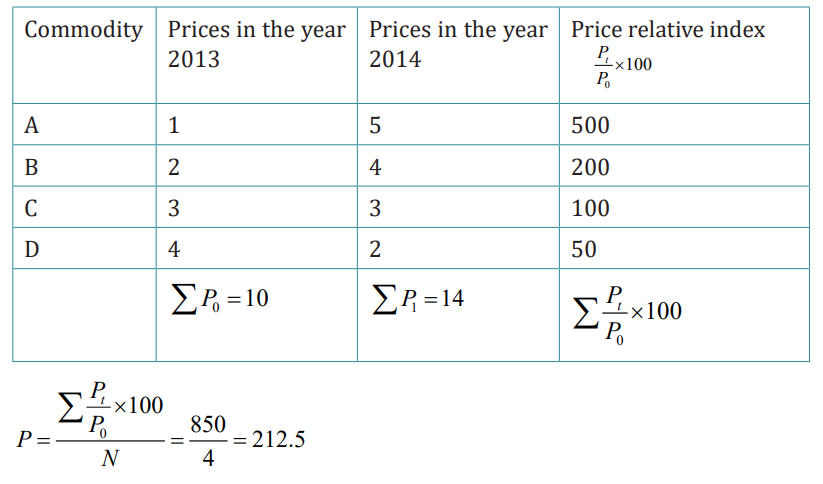
which is based on a simple average of price relatives, is unaffected by the units
in which the commodities’ prices are quoted. However, this method, like the
simple aggregative method, gives equal weight to all items, ignoring theirrelative importance in the group.
Weighted Index Number
All items or commodities are given rational weights in a weighted index number.
These weights indicate the relative importance of the items used in the index
calculation. In most cases, the quantity of usage is the most accurate indicatorof importance.
i. Weighted Aggregative Price Indices
Weights are assigned to each item in the basket in various ways in weighted
aggregative price indices, and the weighted aggregates are also used in various
ways to calculate an index. In most cases, the price index number is calculated
using the quantity of usage. The two most important methods for calculating
weighted price indices are Laspeyre’s price index and Paasche’s price index.
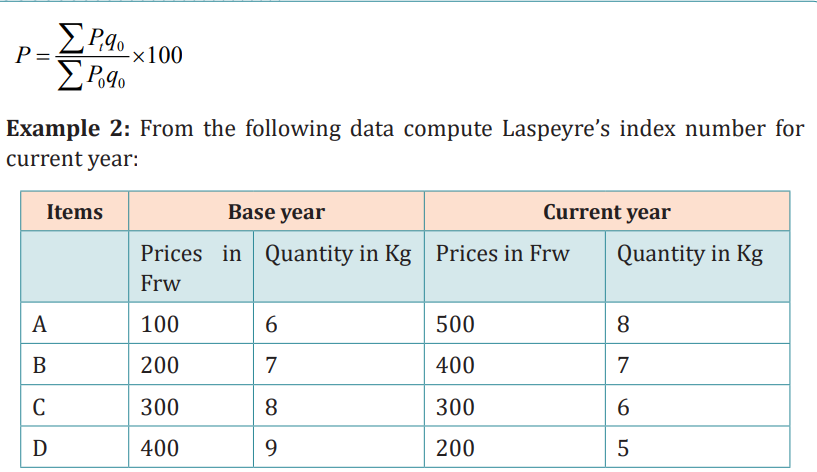
Laspeyre’s price index number is a weighted aggregative price index numberthat uses the quantity from the base year as the weights. It is provided by:
In the given example 2 (above), Paasche’s price index number can be calculated
as follows:
Weights in a weighted price relative index can be determined by the proportion
or percentage of total expenditure on them during the base or current period.
The base period weight is generally preferred over the current period weight.It is due to the inconvenience of calculating the weight every year.
Example 3: From the following data compute an index number by usingweighted average of price relative method:

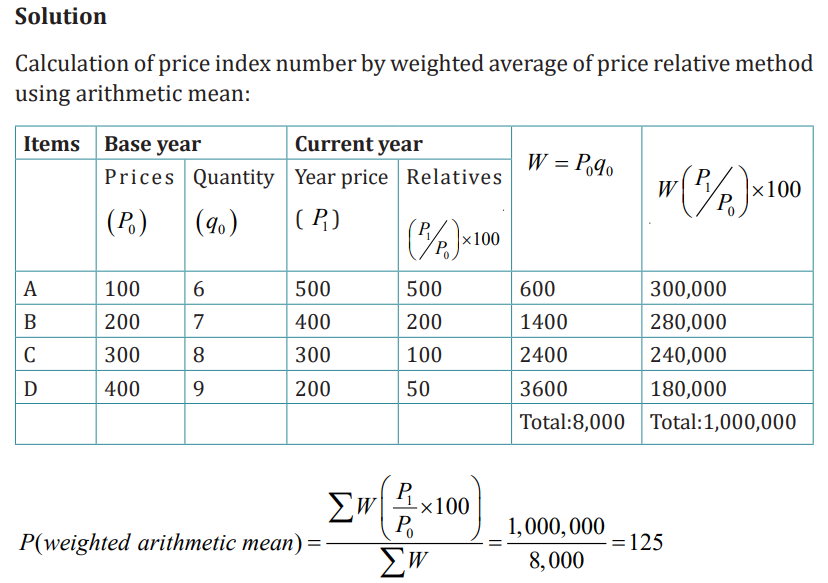
Application activity 4.1.2
Compute Laspeyre’s and Paasche’s index numbers for 2000 from the followingdata

4.2 End unit assessment
1. Calculate cost of living index number using Family Budget method fromthe following data (Price in dollars).
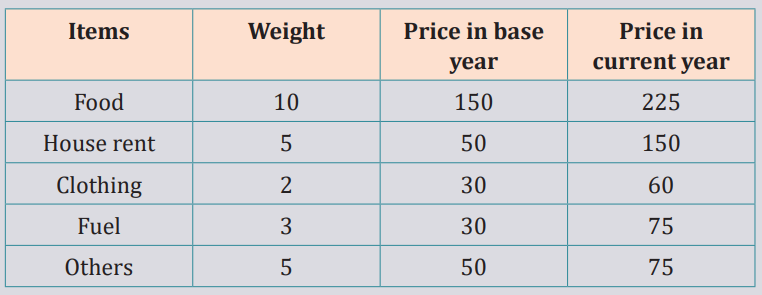

i. Calculate the Laspeyre’s index
ii. Paasche’s index
3. Collect data from the local vegetable market over a week for, at
least 10 items. Try to construct the daily price index for the week.
What problems do you encounter in applying both methods for theconstruction of a price index?
