UNIT 3: INTEGRALS
Key unit Competence: Use integration to solve mathematical and financial
related problems involving marginal cost, revenuesand profits, elasticity of demand, and supply
Introductory activity

3.1 Indefinite integral
3.1.1 Definition and properties
Learning activity 3.1.1



Application activity 3.1.1
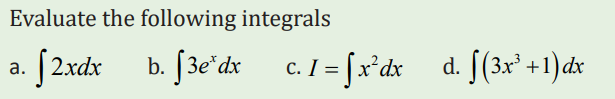
3.1.2 Properties of indefinite integral
Learning activity 3.1.2
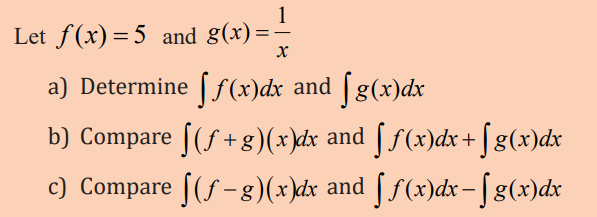

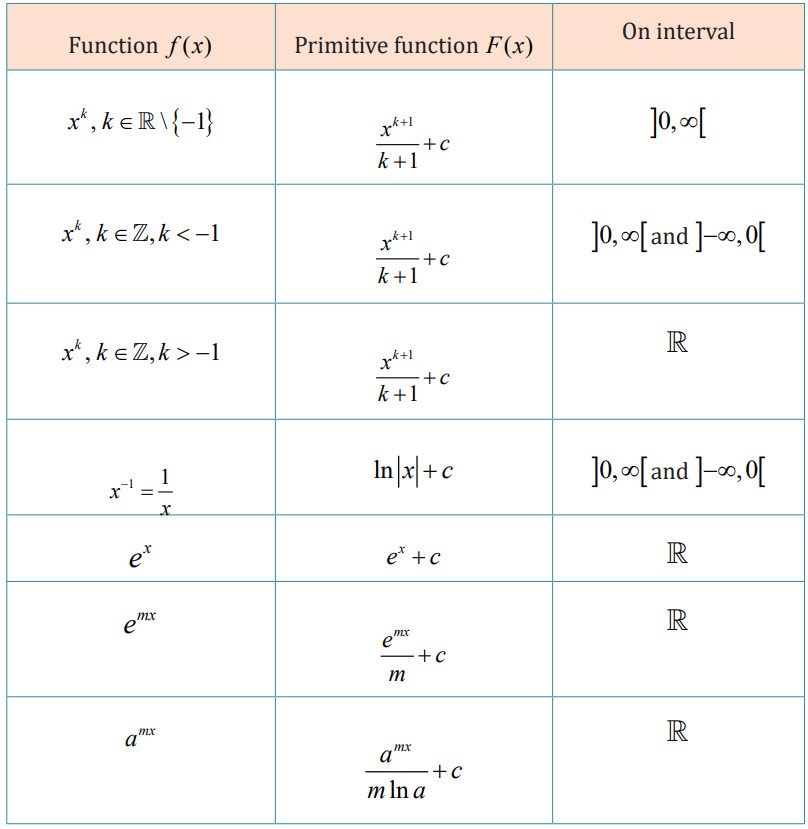
Note: Integration is a process which is the inverse of differentiation. In
differentiation, we are given a function and we are required to find its derivative
or differential coeffient. In integration, we find a function whose differential
coeffient is given. The process of finding a function is called integration and itreverses the operation of differentiation.
Application activity 3.1.2

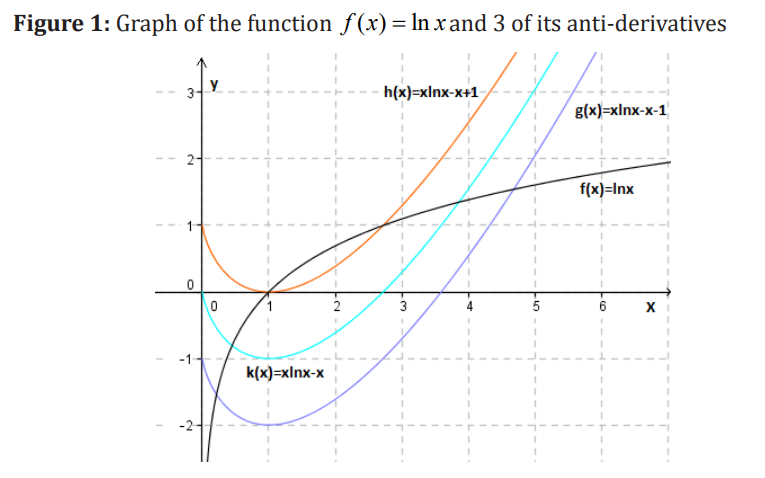
3.1.3 Primitive functions
Learning activity 3.1.3



Application activity 3.1.3
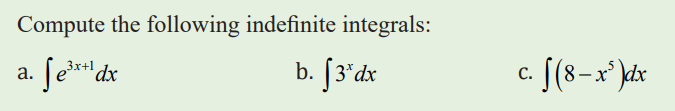
3.2 Techniques of integration
3.2.1 Integration by substitution or change of variable
Learning activity 3.2.1
Integration by substitution is based on rule of differentiating composite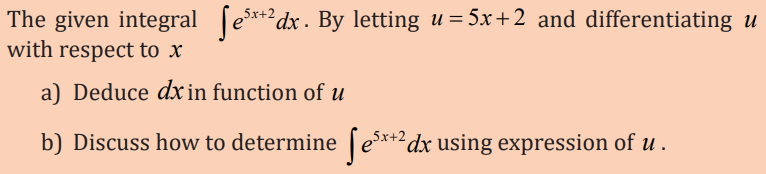
functions. As well as, any given integral is transformed into a simple form
of integral using this method of integration by substitution by substituting
other variables for the independent variable. When we make a substitution
for a function whose derivative is also present in the integrand, the method
of integration by substitution is extremely useful. As a result, the function
becomes simpler, and the basic integration formulas can be used to integratethe function.

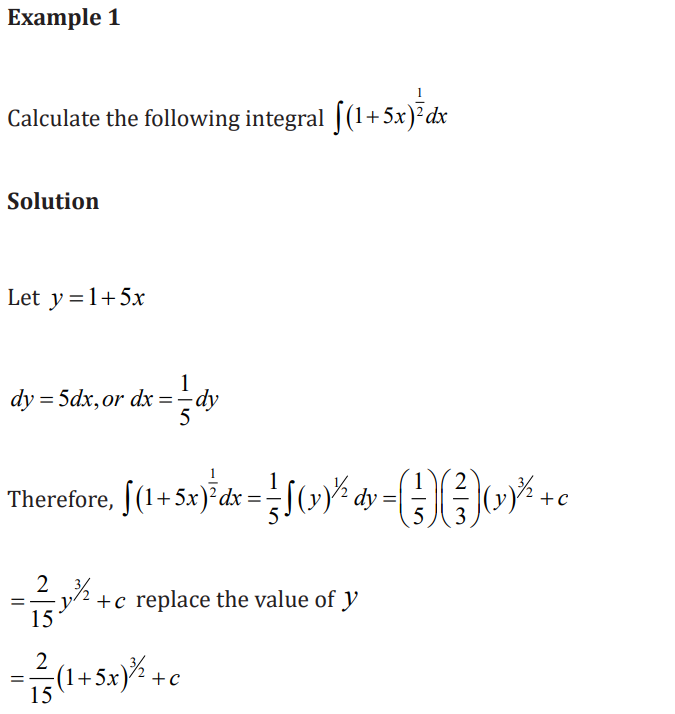

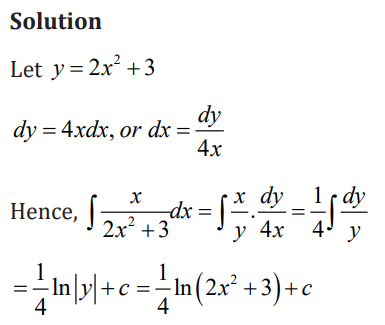
Application activity 3.2.1
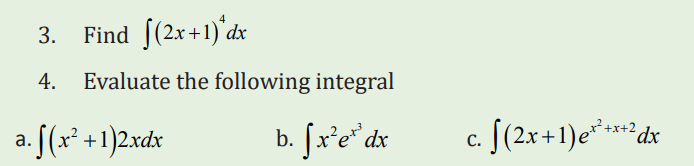
3.2.2 Integration by Parts
Learning activity 3.2.2
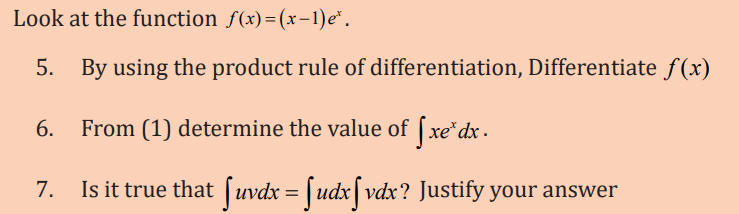





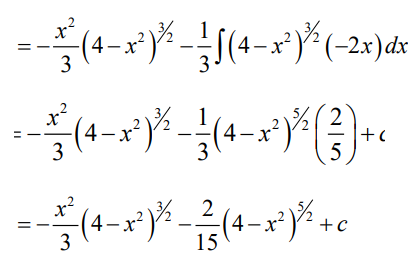
Application activity 3.2.2
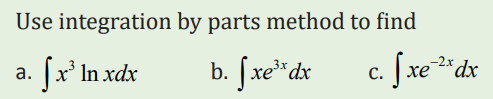
3.2.3 Integration by Decomposition/ Simple fraction
Learning activity 3.2.3
A rational expression is formed when a polynomial is divided by another
polynomial. In a proper rational expression, the degree of the numerator is
less than the degree of the denominator. In an improper rational expression,
the degree of the numerator is greater than or equal to the degree of the
denominator. The integration by decomposition known as integration of partial
fractions found by firstly decompose a proper fraction into a sum of simplerfractions.
Partial fractions decomposition
CASE 1: The denominator is a product of distinct linear factors.
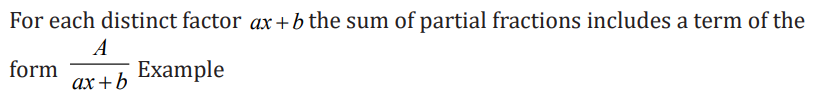





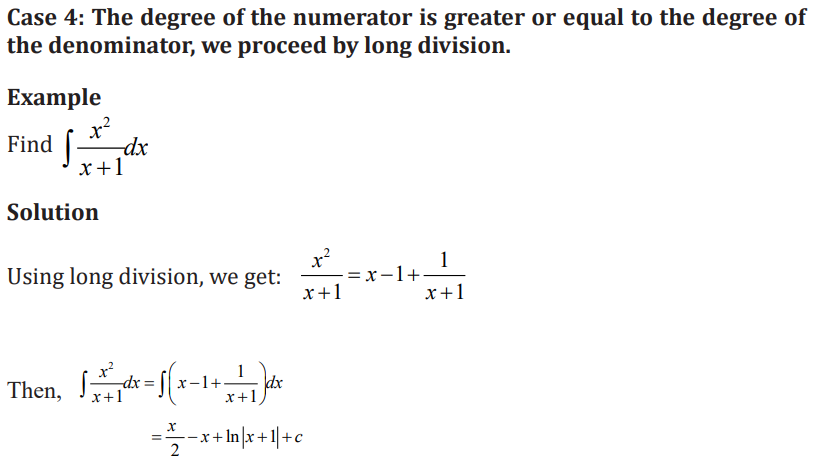
Application activity 3.2.3
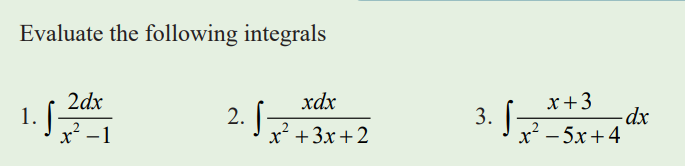
3.3. Definite integral
3.3.1 Definition and properties of definite integrals
Learning activity 3.3.1
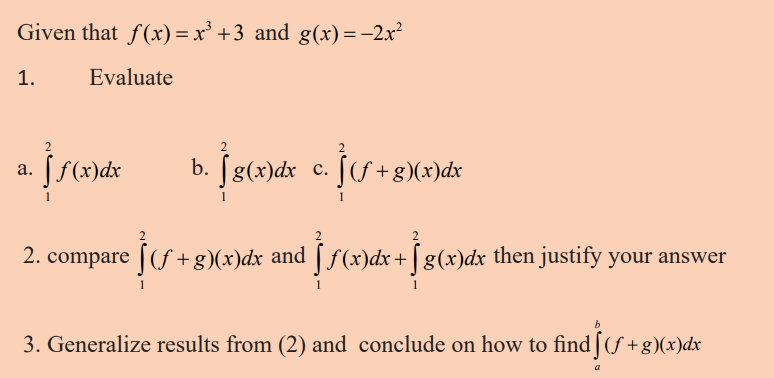




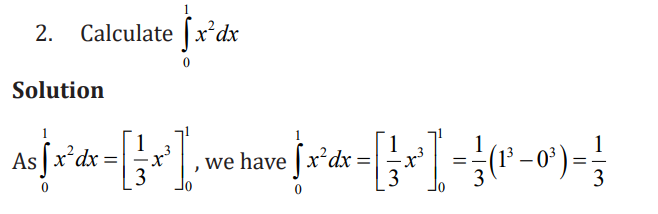
Application activity 3.3.1
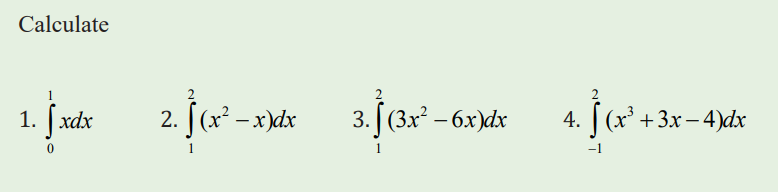
3.3.2 Techniques of integration of definite integral
Learning activity 3.3.2
There is time that some functions cannot be integrated directly. In that case
we have to adopt other techniques in finding the integrals. The fundamental
theorem in calculus tells us that computing definite integral of f xrequires
determining its anti-derivative, therefore the techniques used in determiningindefinite integrals are also used in computing definite integrals.
a) Integration by substitution
The method in which we change the variable to some other variable is called“Integration by substitution”.




c) Decomposition or simple fractions
The partial fraction decomposition method is useful for integrating proper
rational functions. Divide our more complex rational fraction into smaller,
and more easily integrated rational functions. When splitting up the rational
function, the rules to follow are the same as from the indefinite integral. Here arethe steps for evaluating definite integrals using the method of partial fractions :
step 1: Factor the denominator of the integrand
step2: Split the rational function into a sum of partial fractions
step3: Set partial fractions decomposition equal to the original function
step 4: solve for numerators of each of the partial fractions
step 5: Take the definite integral of each of the partial fractions, and sumtogether

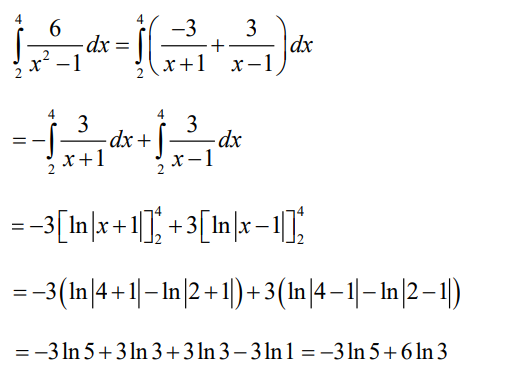
Application activity 3.3.2

3.4 Application of integration
3.4.1 Calculation of marginal cost, revenues and profits
Learning activity 3.4.1

a) Cost function and profit function
If the variable under consideration varies continuously, integration allows us to
recover the total function from the marginal function. As a result, total functionssuch as cost, revenue, production, and saving can be derived from them.
The marginal function is obtained by differentiating the total function. Now,
when marginal function is given and initial values are given, the total functioncan be obtained using integration.





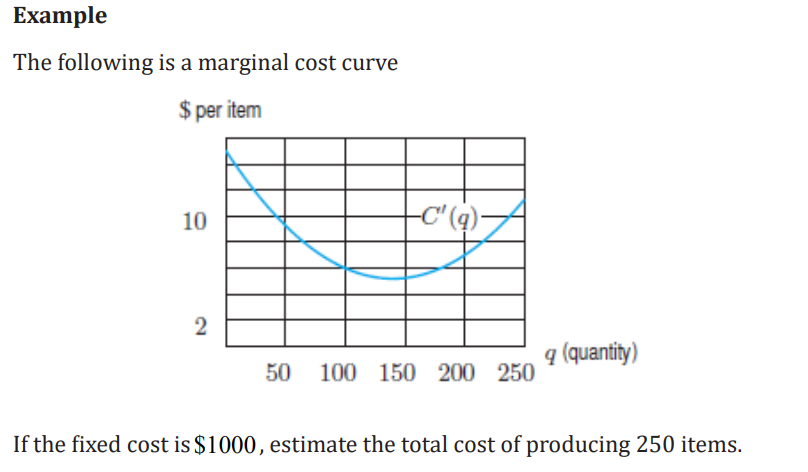
Solution
The total cost of production is fixed cost + Variable cost. The variable cost ofproducing 250 items is represented by the area under the marginal cost curve.



Application activity 3.4.1

3.4.2 Elasticity of demand and supply
Learning activity 3.4.2
The table below shows information about the demand and supply
functions for a product. For both functions, q is the quantity and p is theprice, in dollars
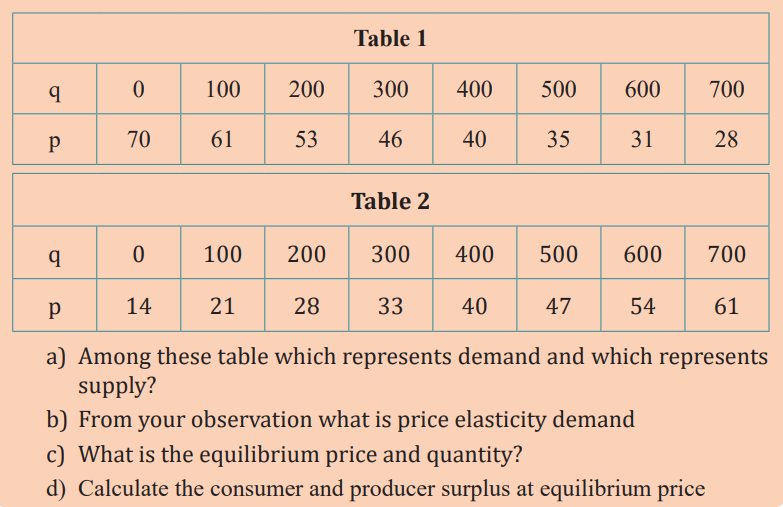

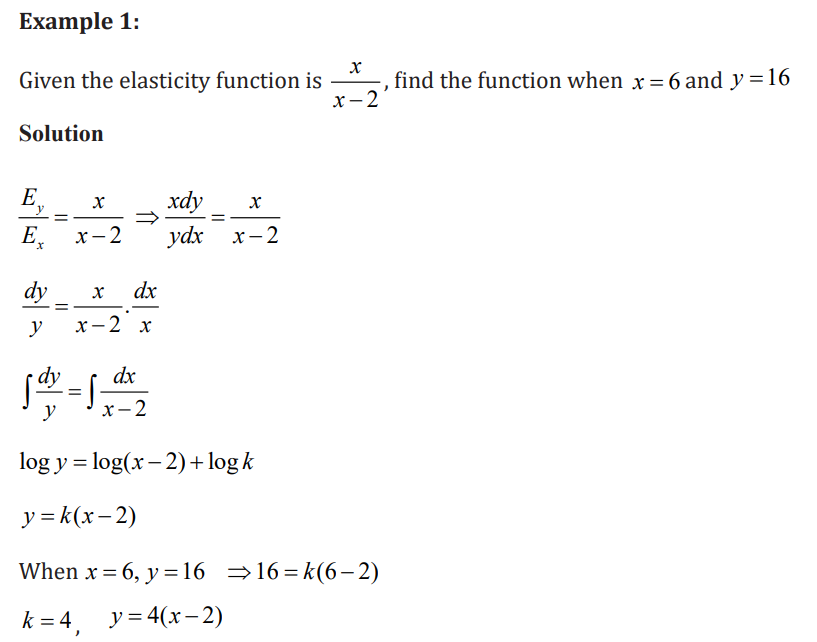


Application activity 3.4.2

3.4.3 Present, Future Values of an Income Stream and Growth Rates
Learning activity 3.4.3
A company is considering purchasing a new machine for its production
floor. The machine costs $65,000. The company estimates that the
additional income from the machine will be a constant $7000 for the first
year, then will increase by $800 each year after that. In order to buy the
machine, the company needs to be convinced that it will pay for itself by
the end of 8 years with this additional income. Money can earn 1.7% peryear, compounded continuously. Should the company buy the machine?
to calculate the present and future value of a continuous income stream as
long as we can model the flow of income with a function. The idea here is that
each little bit of income in the future needs to be multiplied by the exponentialfunction to bring it back to the present, and then we’ll add them all up.

Example 2
Find the present and future values of a constant income stream of $1000 per
year over a period of 20 years, assuming an interest rate of 6% compoundedcontinuously


Further applications in production and consumption
The supply function or supply curve shows the quantity of a product or service
that producers will supply over a period of time at any given price. Both theseprice-quantity relationships are usually considered as functions of quantity Q
Generally, the demand function P = D( Q) is decreasing, because consumers are
likely to buy more of a product at lower prices. Unlike the law of demand, the
supply function P = S(Q ) increasing, because producers are willing to deliver agreater quantity of a product at higher prices.

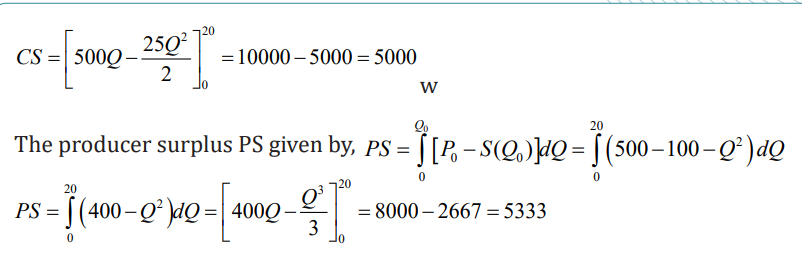
Application activity 3.4.3
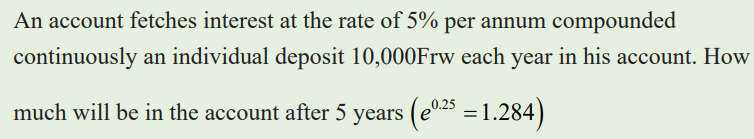
3.5 End unit assessment


