UNIT8:Conditional Probability and Bayes Theorem
Introductory activity
A box contains 3 red pens and 4 blue pens. One pen is taken
from the box and is not replaced. Another pen is taken from the
box. Let A be the event “the first pen is red” and B be the event
“the second pen is blue.”
Is the occurrence of event B affected by the occurrence of event
A? Explain.
Give more other examples of real life problems involving
probability.
Some academic fields based on the probability theory are statistics,
communication theory, computer performance evaluation, signal
and image processing, game theory...
In medical decision-making, clinical estimate of probability
strongly affects the physician’s belief as to whether or not a patient
has a disease, and this belief, in turn, determines actions: to rule
out, to treat, or to do more tests, doctors may use conditional
probability to calculate the probability that a particular patient
has a disease, given the presence of a particular set of symptoms....
Some applications of the probability theory are character
recognition, speech recognition, opinion survey, missile control
and seismic analysis, etc.
In addition, the game of chance formed the foundations ofprobability theory
Objectives
By the end of this unit, a student will be able to:
ᇢ use tree diagram to find probability of events.
ᇢ find probability of independent events.
ᇢ find probability of one event given that the other
event has occurred.ᇢ use and apply Bayes theorem.
8.1. Independent events
Activity 8.1
A bag contains books of two different subjects. One book is
selected from the bag and is replaced. A book is also selected
in the bag. Is the occurrence of the event for the secondselection affected by the event for the first selection? Explain

Example 8.2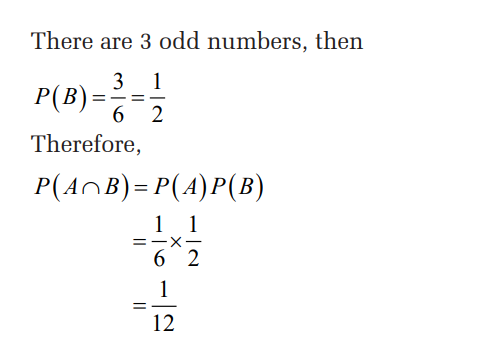
A factory runs two machines. The first machine operates for 80%
of the time while the second machine operates for 60% of the time
and at least one machine operates for 92% of the time. Do thesetwo machines operate independently?

Application activity 8.1
1. A dresser drawer contains one pair of socks with each of
the following colors: blue, brown, red, white and black.
Each pair is folded together in a matching set.
You reach into the sock drawer and choose a pair of socks
without looking. You replace this pair and then choose
another pair of socks. What is the probability that you
will choose the red pair of socks both times?
2. A coin is tossed and a single 6-sided die is rolled. Find
the probability of landing on the head side of the coin androlling a 3 on the die.
8.2. Conditional probability
Activity 8.2
A bag contains books of two different subjects. One book is
selected from the bag and is not replaced. Another book is
selected in the bag. Is the occurrence of the event for the second
selection affected by the event for the first selection? Explain.
When the outcome or occurrence of the first event affects the
outcome or occurrence of the second event in such a way that
the probability sample space is changed, the events are said to be
dependent.
The probability of an event B given that event A has occurredis called the conditional probability of B given A and is written


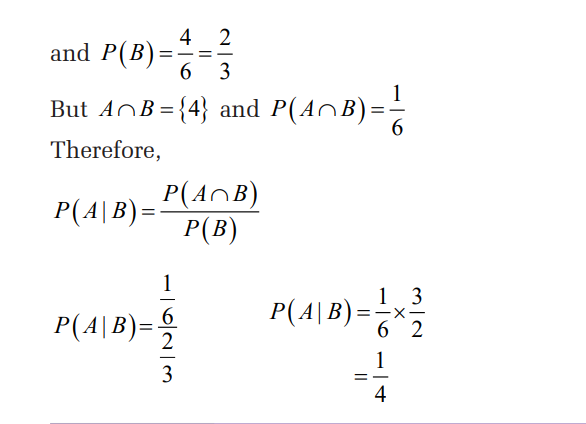
Notice: contingency table
Contingency table (or Two-Way table) provides a different way
of calculating probabilities. The table helps in determining
conditional probabilities quite easily. The table displays
sample values in relation to two different variables that may be
dependent or contingent on one another.
Below, the contingency table shows the favorite leisure activities
for 50 adults, 20 men and 30 women. Because entries in thetable are frequency counts, the table is a frequency table.
Entries in the total row and total column are called marginal
frequencies or the marginal distribution. Entries in the body of
the table are called joint frequencies.
Example 8.6
Suppose a study of speeding violations and drivers who use carphones produced the following fictional data:
d) P(person is a car phone user OR person had no violation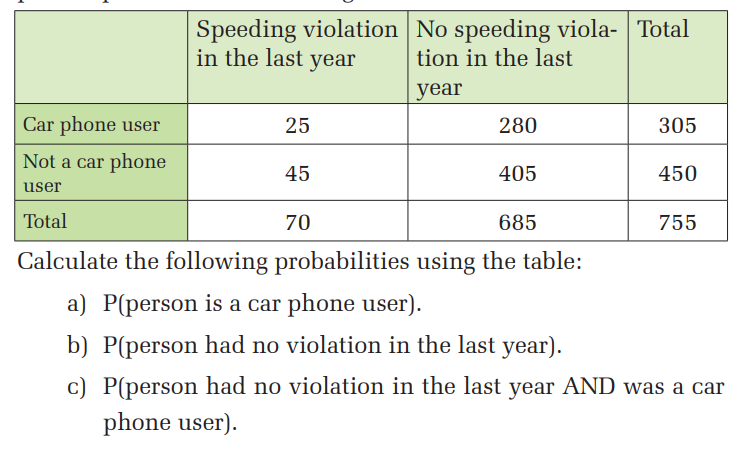
in the last year).
e) P(person is a car phone user GIVEN person had a violation
in the last year).
f) P(person had no violation last year GIVEN person was nota car phone user).

Application activity 8.2
1. A coin is tossed twice in succession. Let A be the event
that the first toss is heads and let B be the event that the
second toss is heads. Find P(B\A)
2. Calculate the probability of a 6 being rolled by a die if it is
already known that the result is even.
3. A jar contains black and white marbles. Two marbles are
chosen without replacement. The probability of selecting
a black marble and then a white marble is 0.34, and the
probability of selecting a black marble on the first draw is
0.47. What is the probability of selecting a white marble
on the second draw, given that the first marble drawn wasblack?
8.3. Bayes theorem and its applications



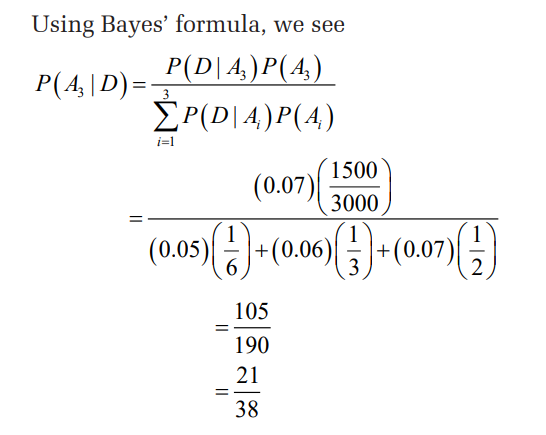



Thus, the most likely diagnosis in the presence of rebound
tenderness/ painfulness is acute appendicitis. Since surgery
is generally not required for either pancreatitis or NSAP, but is
indicated for appendicitis, it is very useful to know the probability
that the patient showing rebound tenderness has appendicitis as
compared to the probability that s/he has one of the other twoconditions.
3. The probability of having an accident in a factory that
triggers an alarm is 0.1. The probability of it sounding
after the event of an incident is 0.97 and the probability
of it sounding after no incident has occurred is 0.02. In
an event where the alarm has been triggered, what is the
probability that there has been no accident?
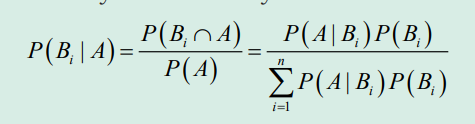
End of Unit Assessment
1. The probability that it is Friday and that a student is
absent is 0.03. Since there are 5 school days in a week, the
probability that it is Friday is 0.2. What is the probability
that a student is absent given that today is Friday?
2. At Kennedy Middle School, the probability that a student
takes Technology and Spanish is 0.087. The probability that
a student takes Technology is 0.68. What is the probability
that a student takes Spanish given that the student is taking
Technology?
3. A car dealership is giving away a trip to Rome to one of
their 120 best customers. In this group, 65 are women,
80 are married and 45 married women. If the winner is
married, what is the probability that it is a woman?
4. A card is chosen at random from a deck of 52 cards. It is
then replaced and a second card is chosen. What is the
probability of choosing a jack and then an eight?
5. A jar contains 3 red, 5 green, 2 blue and 6 yellow marbles.
A marble is chosen at random from the jar. After replacing
it, a second marble is chosen. What is the probability of
choosing a green and then a yellow marble?
6. A school survey found that 9 out of 10 students like pizza.
If three students are chosen at random with replacement,
what is the probability that all three students like pizza?
7. A nationwide survey found that 72% of people in the
United States like pizza. If 3 people are selected at random,
what is the probability that all three like pizza?
8. A bag contains 2 red, 3 green and 2 blue balls. Two balls
are drawn at random. What is the probability that none of
the balls drawn is blue?
9. For married couples living in a certain suburb, the probability
that the husband will vote on a bond referendum is 0.21,
the probability that his wife will vote in the referendum is
0.28, and the probability that both the husband and wife
will vote is 0.15. What is the probability that:
a) at least one member of a married couple will vote?
b) a wife will vote, given that her husband will vote?
c) a husband will vote, given that his wife does not
vote?
10.In 1970, 11% of Americans completed four years of college,
43% of them were women. In 1990, 22% of Americans
completed four years of college; 53% of them were women.
(Time, Jan.19, 1996).
a) Given that a person completed four years of college
in 1970, what is the probability that the person was
a woman?
b) What is the probability that a woman would finish
four years of college in 1990?
c) What is the probability that in 1990 a man would
not finish college?
11.If the probability is 0.1 that a person will make a mistake
on his or her state income tax return, find the probability
that:
a) four totally unrelated persons each make a mistake
b) Mr. Jones and Ms. Clark both make a mistake andMr. Roberts and Ms. Williams do not make a mistake.
12.The probability that a patient recovers from a delicate
heart operation is 0.8. What is the probability that:
a) exactly 2 of the next 3 patients who have this
operation will survive?
b) all of the next 3 patients who have this operation
survive?
13.In a certain federal prison, it is known that 2/3 of the
inmates are under 25 years of age. It is also known that
3/5 of the inmates are male and that 5/8 of the inmates are
female or 25 years of age or older. What is the probability
that a prisoner selected at random from this prison is
female and at least 25 years old?
14.A certain federal agency employs three consulting firms
(A, B and C) with probabilities 0.4, 0.35, 0.25, respectively.
From past experience it is known that the probabilities
of cost overrun for the firms are 0.05, 0.03, and 0.15
respectively. Suppose a cost overrun is experienced by the
agency.
a) What is the probability that the consulting firm
involved is company C?
b) What is the probability that it is company A?
15.In a certain college, 5% of the men and 1% of the women
are taller than 180 cm. Also, 60% of the students are
women. If a student is selected at random and found to be
taller than 180 cm, what is the probability that this student
is a woman?
References
[1] A. J. Sadler, D. W. S. Thorning: Understanding Pure
Mathematics, Oxford University Press 1987.
[2] Arthur Adam Freddy Goossens: Francis Lousberg.
Mathématisons 65. DeBoeck,3e edition 1991.
[3] David Rayner, Higher GCSE Mathematics, Oxford
University Press 2000
[4] Direction des Progammes de l’Enseignement Secondaire.
Géometrie de l’Espace 1er Fascule. Kigali, October 1988
[5] Direction des Progammes de l’Enseignement Secondaire.
Géometrie de l’Espace 2ème Fascule. Kigali, October 1988
[6] Frank Ebos, Dennis Hamaguchi, Barbana Morrison & John
Klassen, Mathematics Principles & Process, Nelson Canada
A Division of International Thomson Limited 1990
[7] George B. Thomas, Maurice D. Weir & Joel R. Hass,
Thomas’ Calculus Twelfth Edition, Pearson Education, Inc.
2010
[8] Geoff Mannall & Michael Kenwood, Pure Mathematics 2,
Heinemann Educational Publishers 1995
[9] H.K. DASS... Engineering Mathematics. New Delhi, S.
CHAND&COMPANY LTD, thirteenth revised edition 2007.
[10] Hubert Carnec, Genevieve Haye, Monique Nouet,
ReneSeroux, Jacqueline Venard. Mathématiques TS
Enseignement obligatoire. Bordas Paris 1994.
[11] James T. McClave, P.George Benson. Statistics for Business
and Economics. USA, Dellen Publishing Company, a
division of Macmillan, Inc 1988.
[12] J CRAWSHAW, J CHAMBERS: A concise course in
A-Level statistics with worked examples, Stanley Thornes
(Publishers) LTD, 1984.
[13] Jean Paul Beltramonde, VincentBrun, ClaudeFelloneau,
LydiaMisset, Claude Talamoni. Declic 1re S Mathématiques.
Hachette-education, Paris 2005.
[14] JF Talber & HH Heing, Additional Mathematics 6th Edition
Pure & Applied, Pearson Education South Asia Pte Ltd 1995
[15] J.K. Backhouse, SPTHouldsworth B.E.D. Copper and P.J.F.
Horril. Pure Mathematics 2. Longman, third edition 1985,
fifteenth impression 1998.
[16] M.Nelkon, P. Parker. Advanced Level Pysics, Seventh
Edition. Heinemann 1995
[17] Mukasonga Solange. Mathématiques 12, Analyse
Numérique. KIE, Kigali2006.
[18] N. PISKOUNOV, Calcul Différential et Integral tom II 9ème
édition. Editions MIR. Moscou, 1980.
[19] Paule Faure- Benjamin Bouchon, Mathématiques
Terminales F. Editions Nathan, Paris 1992.
[20] Peter Smythe: Mathematics HL & SL with HL options,
Revised Edition, Mathematics Publishing Pty. Limited,
2005.
[21] Rwanda Education Board (2015), Subsidiary Mathematics
Syllabus S4-S6, Ministry of Education: Rwanda.
[22] Robert A. Adms & Christopher Essex, Calculus A complete
course Seventh Edition, Pearson Canada Inc., Toronto,
Ontario 2010
[23] Seymour Lipschutz. Schaum’s outline of Theory and
Problems of linear algebra. McGraw-Hill 1968.
[24] Shampiyona Aimable : Mathématiques 6. Kigali, Juin 2005.
[25] Tom Duncan, Advanced Physics, Fourth edition. John
Murray (Publishers) Ltd, London 1998
[26] Yves Noirot, Jean–Paul Parisot, Nathalie Brouillet. Cours de
Physique Mathématiques pour la Physique. Paris, DUNOD,
1997.
[27] http://www.tiem.utk.edu/~gross/bioed/webmodules/
lungcapacity.html
[28] https://prezi.com/kdrzbkm8yuye/trigonometry-and-medicin
e/?frame=b5001c61a02311bb8f2927d84e8643b207d0c72c
[29] file:///C:/Users/IT%20ZONE/Desktop/Reference%20books/Good%20Applied%20calculus.pd
