UNIT4:Trigonometric Functions and their Inverses

Objectives:
By the end of this unit, a student will be able to:
ᇢ find the domain and range of trigonometric
functions and their inverses.
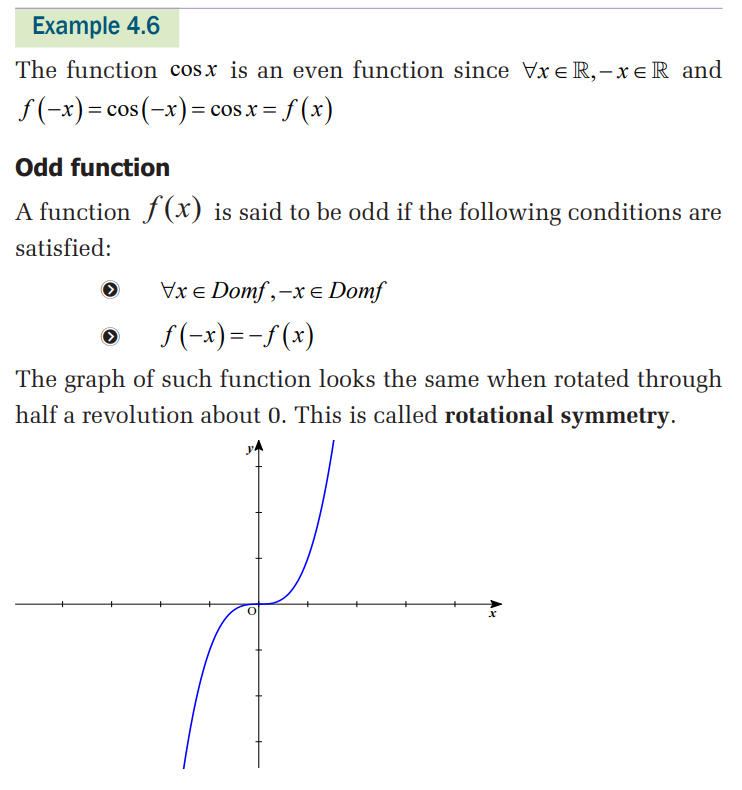
ᇢ study the parity of trigonometric functions.
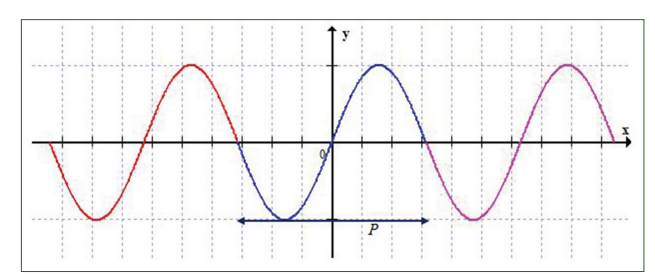
ᇢ study the periodicity of trigonometric functions.
ᇢ evaluate limits of trigonometric functions.
ᇢ differentiate trigonometric functions and theirinverses.
4.1. Generalities on trigonometric functions and
their inverses
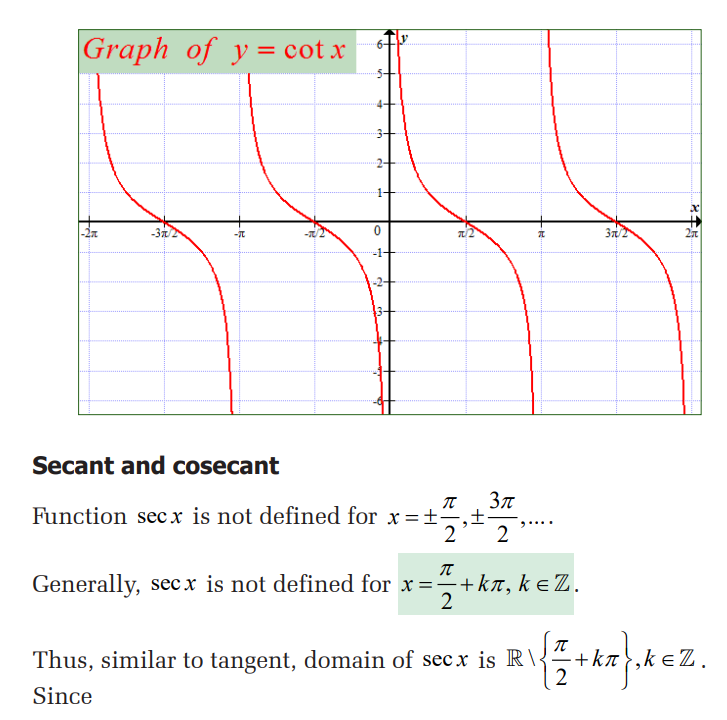
4.1.1. Domain and range of six trigonometric
functions
Activity 4.1
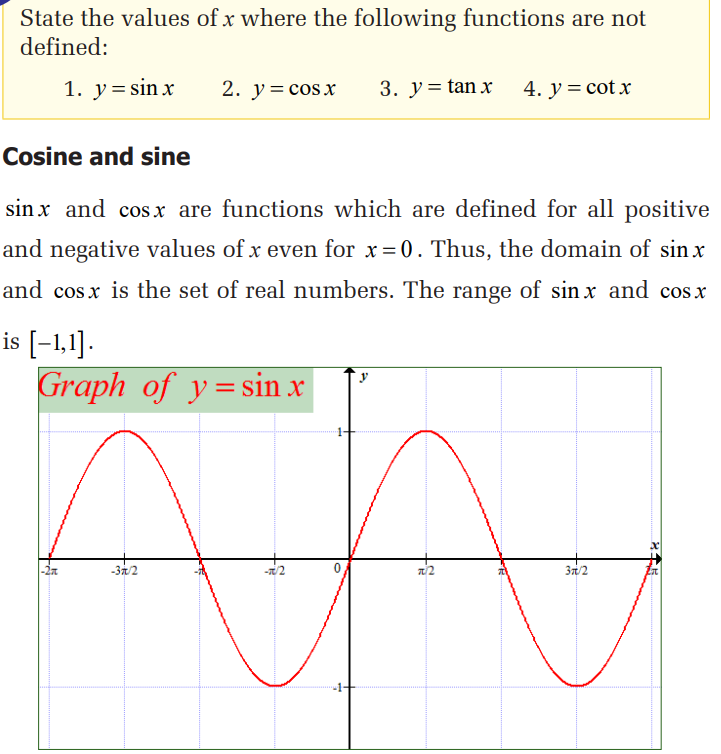
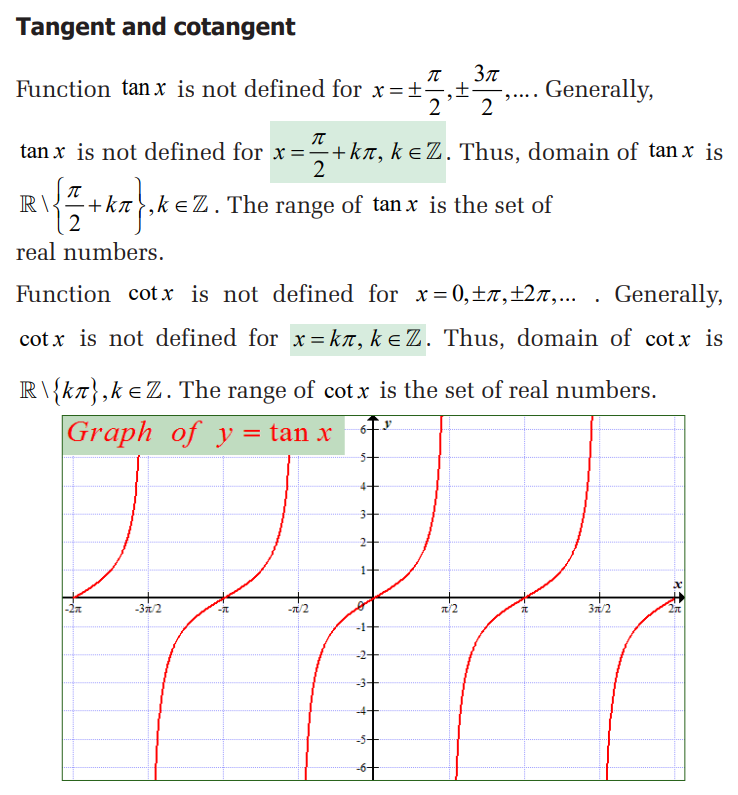
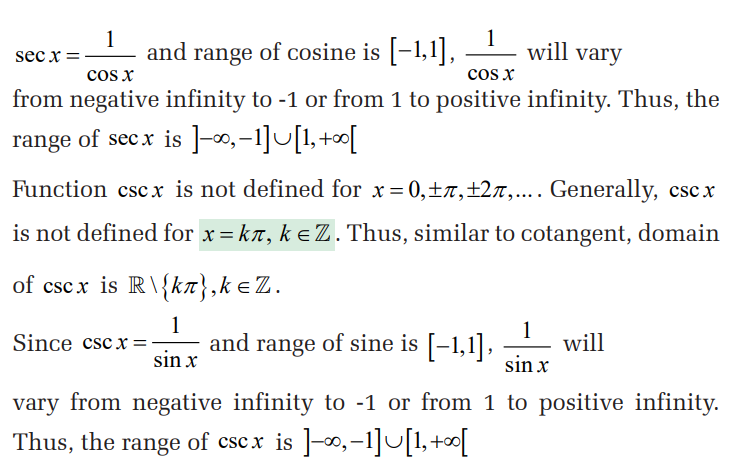


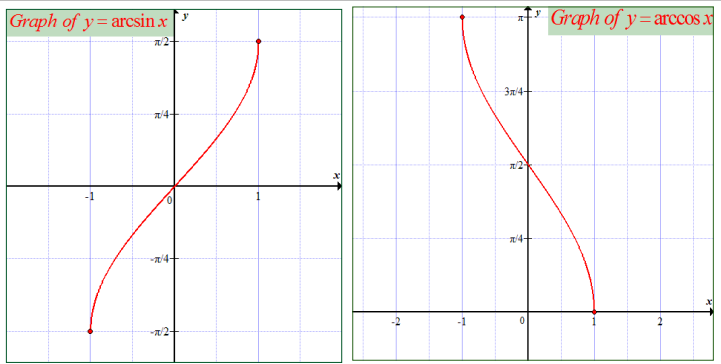
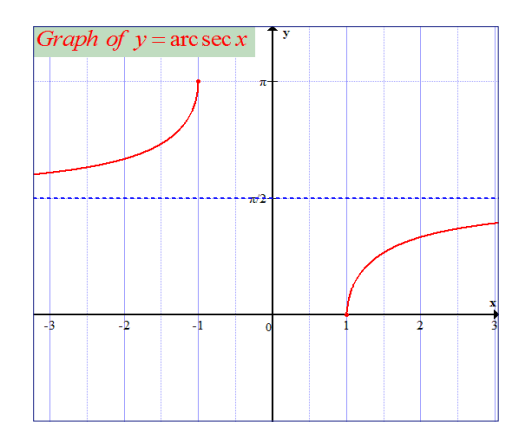
4.1.2. Domain and range of inverses of
trigonometric functions
Activity 4.2

Remark
The inverses of the trigonometric functions are not functions,
they are relations. The reason they are not functions is that for a
given value of x , there is an infinite number of angles at which the
trigonometric functions take on the value of x . Thus, the range of
the inverses of the trigonometric functions must be restricted to
make them functions. Without these restricted ranges, they areknown as the inverse trigonometric relations.



Example 4.2



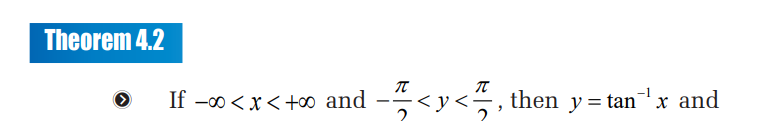
tan y x = are equivalent









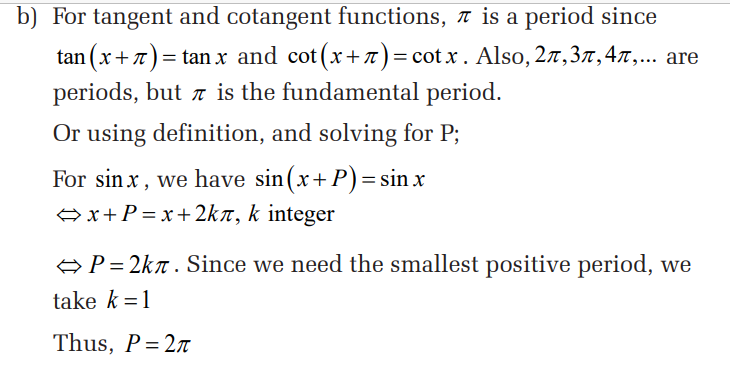





Consider the following case:
If a function repeats every 2 units, then it will also repeat every
6 units. So if we have one function with fundamental period 2,
and another function with fundamental period 8, we have got no
problem because 8 is a multiple of 2, and both functions will cycle
every 8 units.
So, if we can patch up the periods to be the same,we know that
if we combine them, we will get a function with the patched up
period.
What we have to do is to find the Lowest Common Multiple (LCM)
of two periods.
What about if one function has period 4 and another has period 5?
We can see that in 20 units, both will cycle, so they are fine.




4.2. Limits of trigonometric functions and their
inverses
4.2.1. Limits of trigonometric functions
Activity 4.6
We do this until the indeterminate case is removed. Other methods
used to remove indeterminate cases are also applied.


4.3. Differentiation of trigonometric functions
and their inverses
4.3.1. Derivative of sine and cosine
Activity 4.8














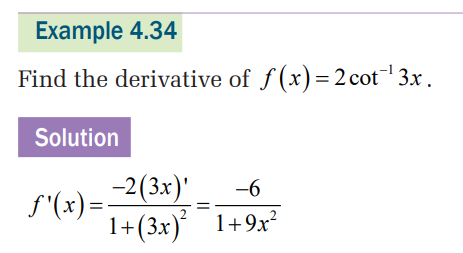

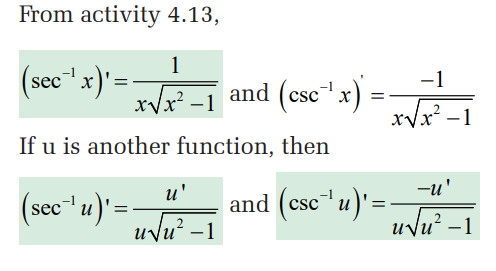






4.4. Applications
Simple harmonic motion
Activity 4.15


Solution