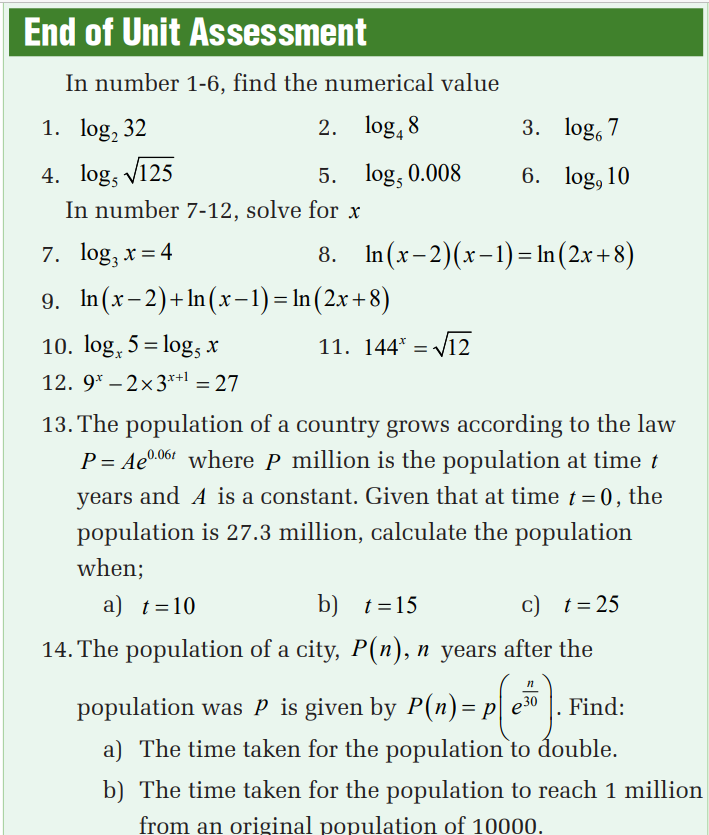UNIT 1:Logarithmic and Exponential Equations
Objectives
By the end of this unit, a student will be able to:
ᇢ solve exponential equations.
ᇢ solve logarithmic equations.
ᇢ apply exponential and logarithmic equations inreal life problems.
3.1. Introduction to Exponential and logarithmic functions
Activity 3.1



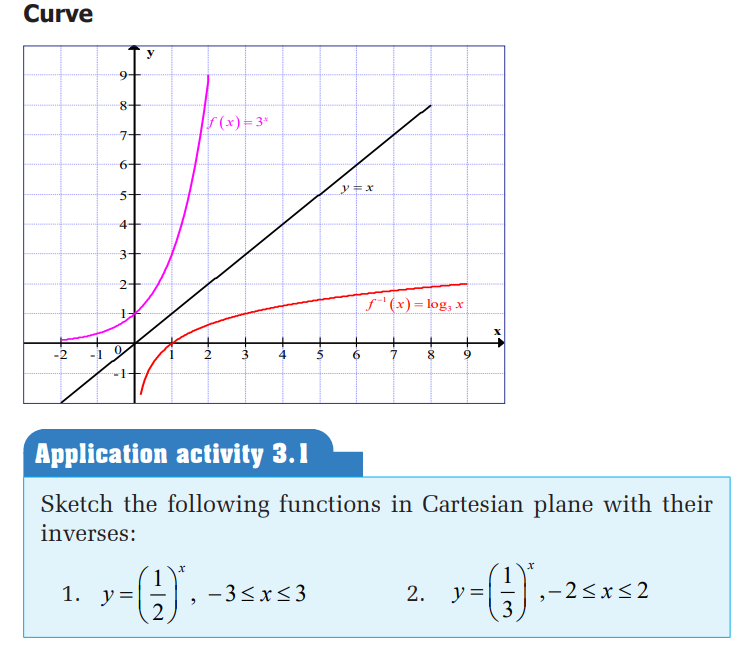

Activity 3.2


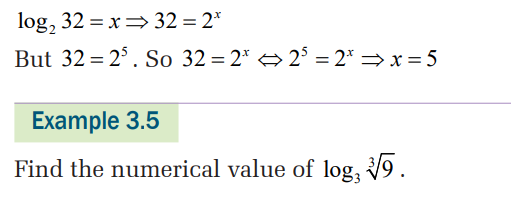
Solution
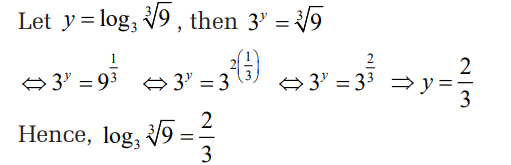

Activity 3.3
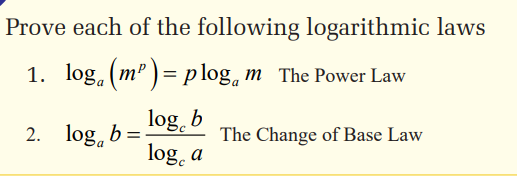






3.3. Applications
Exponential growth
Activity 3.4









Example 3.15
Jack operates an account with a certain bank which pays a
compound interest rate of 13.5% per annum. He opened the account
at the beginning of the year with 500,000 Frw and deposits the
same amount of money at the beginning of every year. Calculate
how much he will receive at the end of 9 years. After how longwill the money have accumulated to Frw 3.32 million?







Application activity 3.4
1. A certain cell culture grows at a rate proportional to the
number of cells present. If the culture contains 500 cells
initially 800 after 24h , how many cells will be there after
a further 12h ?
2. A radioactive substance decays at a rate proportional to
the amount present. If 30% of such a substance decays in
15 years, what is the half-life of the substance?
3. A colony of bacteria is grown under ideal conditions in
laboratory so that the population increases exponentially
with time. At the end of three hours there are 10,000
bacteria. At the end of 5 hours there are 40,000. How many
bacteria were present initially?
4. A radioactive material has a half-life of 1,200 years.
a) What percentage of the original radioactivity of a
sample is left 10 years?
b) How many years are required to reduce the
radioactivity by 10%?
5. Scientists who do carbon-14 dating use a figure of 5700
years for its half-life. Find the age of a sample in which
10% of the radioactive nuclei originally present have
decayed.
6. How much money needs to be invested today at a nominal
rate of 4% compounded continuously, in order that it
should grow to Frw 10,000 in 7 days?
7. The number of people cured is proportional to the number
y that is infected with the disease.
a) Suppose that in the course of any given year the
number of cases of disease is reduced by 20 %. If
there are 10,000 cases today, how many years will it
take to reduce the number to 1000?
b) Suppose that in any given year the number of cases
can be reduced by 25% instead of 20% .
(i) How long will it take to reduce the number of
cases to 1000?
(ii) How long will it take to eradicate the disease,
that is, to reduce the number of cases to lessthan 1?
Unit Summary