UNIT 2:Sequences
Introductory activity
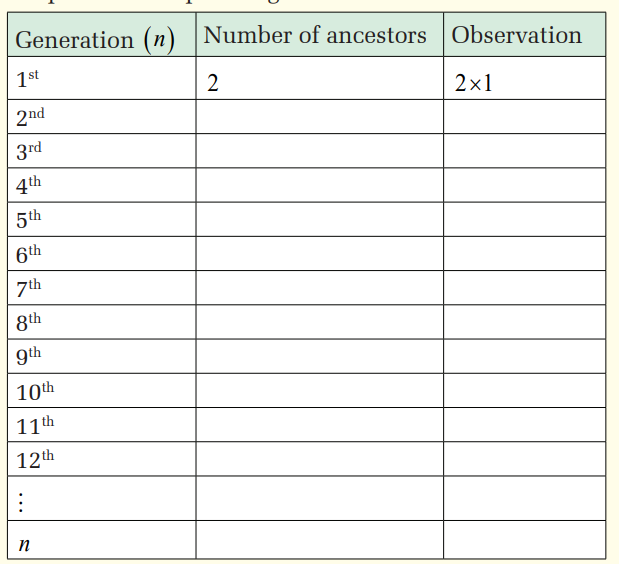
Suppose that an insect population is growing in such a way
that each new generation is 2 times as large as the previous
generation. If there are 126 insects in the first generation, on a
piece of paper, write down the number of insects that will bethere in second, third, fourth,…nth generation.


2.1. Arithmetic and harmonic sequences
2.1.1. Definition
Activity 2.1





Solution











2.1.4. Sum of arithmetic sequence
Activity 2.4


2.1.5. Harmonic sequences
Activity 2.5


Remark
To find the term of harmonic sequence, convert the sequence
into arithmetic sequence then do the calculations using the
arithmetic formulae. Then take the reciprocal of the answer
in arithmetic sequence to get the correct term in harmonicsequence.




2.2. Geometric sequences
2.2.1. Definition
Activity 2.6
Take a piece of paper which is in a square shape.
1. Cut it into two equal parts.
2. Write down a fraction corresponding to one part
according to the original piece of paper.
3. Take one part obtained in step (2) and cut, repeat step (1)
and then step 2).
4. Continue until you remain with a small piece of paper
that you are not able to cut it into two equal parts.
5. Observe the sequence of numbers you obtained and give
the relationship between any two consecutive numbers.


2.2.2. General term of a geometric sequence
Activity 2.7







Example 2.28

2.2.4. The sum of n terms of a geometric sequenceActivity 2.9









2.3. Convergent or divergent sequences
Activity 2.11



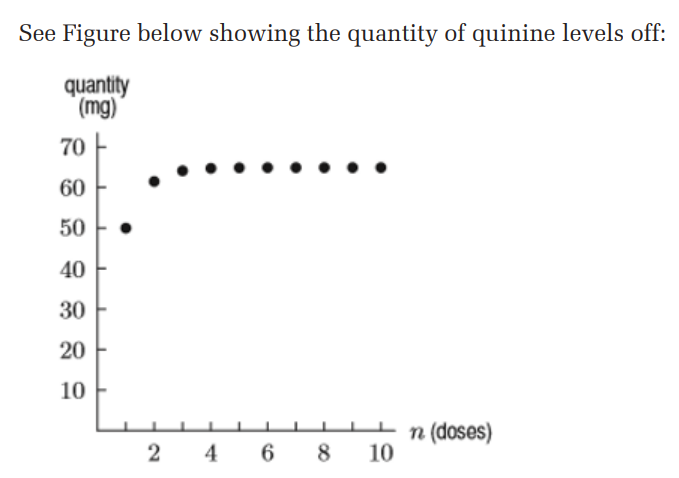
2.4. Applications of sequences in real life
Activity 2.12
















20. The third, fifth and seventeenth terms of an arithmetic
progression are in geometric progression. Find the common
ratio of the geometric progression.
21. A mathematical child negotiates a new pocket money deal
with her unsuspecting father in which he/she receives
1 pound on the first day of the month, 2 pounds on the
second day, 4 pounds on the third day, 8 pounds on the
fourth day, 16 pounds on the fifth day, … until the end of
the month. How much would the child receive during the
course of a month of 30 days? (Give your answer to the
nearest million pounds.)
22. Find the common ratio of a geometric progression that has
a first term of 5 and sum to infinity of 15.
23. The sum of the first two terms of a geometric progression
is 9 and the sum to infinity is 25. If the common ratio is
positive, find the common ratio and the first term.
24. A culture of bacteria doubles every 2 hours. If there are
500 bacteria at the beginning, how many bacteria will
there be after 24 hours?
25. You complain that the hot tub in your hotel suite is not
hot enough. The hotel tells you that they will increase the
temperature by 10% each hour. If the current temperature
of the hot tub is 75º F, what will be the temperature of the
hot tub after 3 hours, to the nearest tenth of a degree?
26. The sum of the interior angles of a triangle is 180º, of a
quadrilateral is 360º and of a pentagon is 540º. Assuming
this pattern continues, find the sum of the interior angles
of a dodecagon (12 sides).
