Course: S5: Mathematics

Topic outline

General
Unit 1 Matrices and determinants
Key Unit competence: Use matrices and determinants notations and properties to solve simple production, financial, economical, and mathematical related problems.
Introductory activity
The table below shows the revenue and expenses (in Rwandan francs) of a family over three consecutive months:

a) What was the family’s revenue in October?
b) By how much money did the family’s revenue increase from October to November?
1.1 Generalities on matrices
1.1.1. Definitions and notations
Learning Activity 1.1.1
A shop selling shirts records the number of each type of shirts it sells over a period of two weeks. In the first week, it sells 12 small size shirts, 8 medium shirts and 5 large shirts.
In the second week, it sells only 9 small size shirts and 3 medium size shirts.
a) What are the two criteria the shopkeeper will use to record these data?
b) Record this information in a rectangular array consisting of double entries.
c) Such a table is called a “matrix”. Describe the components of a matrix.

CONTENT SUMMARY
– A matrix is a rectangular arrangement of numbers, in rows and columns,
within brackets or [ ]. A matrix is denoted by a capital letter: A, B, C, ….
Rows are counted from the top of the matrix to the bottom of the matrix;
columns are counted from the leftmost side of the matrix to the rightmost side
of the matrix.
– The numbers in the matrix are called entries or elements.
The position of an entry in the matrix is shown by lower subscripts, such as ^aj :the entry on the i^th row and j^th column.
– If matrix A has n rows and p columns, then we say that the matrix A is of order n × p , read n by p, where the product n × p is the number of entries in the matrix.
Note: In finding the order of a matrix, we do not perform the multiplication n × p , we just write n × p , but for finding the number of entries of a matrix given by its order n × p ,we calculate the product n × p .
If A is a matrix of order n× p , then A can generally be written as A = (a_ij) ,where
i and j are positive integers, and; 1≤ i ≤ n ;1≤ j ≤ p .
– A matrix with only one row is said to be a row matrix; that is a matrix of order1× p .
Thus, (2 4 7) is a row matrix.
A matrix with only one column is said to be a column matrix; that is a matrix
of order n×1.
– A square matrix is a matrix in which the number of rows is equal to the number of columns; that is, matrix A of order n× p is a square matrix if and only if n = p ;
In this case, instead of saying a matrix of order n× n , we, sometimes, simply say a matrix of order n .
Application activity 1.1.1
1. Write down the order of each of the following matrices:

2. A shoe shop sells shoes for men and ladies. The first week, it sold 7
pairs of men’s shoes and 15 pairs of ladies’ shoes. The second week, it sold 9 pairs of ladies ‘shoes and 4 pairs of men’s shoes. Record this information as a 2× 2 matrix, stating what the rows stand for, and what the columns stand for
1.1.2. Equality of matrices
Learning Activity 1.1.2

Consider the following situations:
Situation1:
A class consists of boys and girls who are boarders or day scholars. The class teacher records the data by the matrix

and the rows represent the numbers of boarders and day scholars.
Situation2:
Two brothers sell shirts and shoes, in two different shop I and II, for two consecutive weeks. The Elder brother records his data by the matrix

shoes, and the rows represent the numbers of items sold in week1, and in
week2.
where the columns represent the numbers of shirts and shoes, and the rows
represent the numbers of items sold in week1, and in week2. Comment on the following, for matrices A, B and C:

a) Number of rows and columns
b) Corresponding entries (that is entries occupying the same
positions)
c) Nature of the elements.
d) Predict which two of the matrices above (A, B and C) are equal.
e) What are the conditions for two matrices to be equal?
CONTENT SUMMARY
Two matrices A = (a_ij)and B = (b_ij) are equal if and only if:
i) they have the same order;
ii) the corresponding entries (that is the entries occupying the same position,
in terms of rows and columns) are equal.
iii) The nature of the entries in the two matrices is the same.
Note: When discussing the equality of matrices, we assume the nature of the
entries in the two matrices to be the same.
A matrix, in which all the entries are zeros is said to be the null matrix or the
zero matrix.
For matrices, the equality A.B = 0 does not imply A = 0 or B = 0 , that is , the
product of two matrices can be the null matrix, yet none of the factors is a null
matrix.
1. 1. Determine whether the following matrices A and B are equal or not:

find the values of x, y, z and t .
1.2. Operations on matrices
1.2.1. Addition and subtraction of matrices
Learning Activity 1.2.1
A retailer sells two products, P and Q, in two shops, S and T.
She recorded the numbers of items sold for the last three weeks in each
shop by the following matrices:

a) Write down the order of each of the two matrices S and T. How are
these two orders?

b) Determine a single matrix for the total sales for this retailer for
the last three weeks in the two shops.

c) Predict the conditions for two matrices to be added and how to
obtain the sum of two matrices.

CONTENT SUMMARY
Matrices that have the same order can be added together, or subtracted. The
addition, or subtraction, is performed on each of the corresponding elements.

Application activity 1.2.1
1. Say, with reason, whether matrices A and B can be added or not. In
case they can be added, find their sum and the difference A− B
2. In a sector of a district, there are three secondary schools, A, B and C
having both boarding and day sections for both boys and girls. The
distribution of the students in the three schools are given, respectivel

where the first rows indicate the number of girls, the second rows
the number of boys, the first columns the number of boarders and
the second columns the number of day scholars in the three schools.

The Sector Education Officer (S.E.O) would like to record these data as a
single matrix S.
a) Which operation should he/she perform on the three matrices to
obtain matrix S?
b) Write down matrix S.
c) Use matrix S to answer the following questions:
i) How many day scholars are there from these three schools?
ii) How many girls are boarders from these three schools?
1.2.2. Scalar multiplication
Learning Activity 1.2.2
The monthly rental prices (in thousand Rwandan Francs) of three apartments without VAT (Value Added Tax)
are recorded by the matrix below:

M = (150 120 300) .
a) How do you calculate the VAT on an item?
b) What is the single operation to use in order to obtain the matrix M’
representing the monthly rental prices of the three apartments,
including 18% of VAT?
c) How do you obtain matrix M’?
d) Write down matrix M’

CONTENT SUMMARY
A matrix can be multiplied by a specific number; in this case, each entry of the matrix is multiplied by the given
number. This type of multiplication is called
scalar multiplication, since the matrix is multiplied by a single real number, and real numbers are also called scalars.

Example 1.2.2.

Solution:

Application activity 1.2.2

columns, and the numbers of shoes and clothes are in rows.
Since the festive period of Christmas is approaching, the shop
expects to double the number of each item to sell. Express the
resulting matrix D.
1.2.3. Multiplication of matrices
Learning Activity 1.2.3
Two friends Agnes(A) and Betty(B) can buy sugar, rice and beans at one

a) Compare the number of columns of M to the number of rows of P .
b) Calculate the shopping bill of each of the two friends at each of the
two supermarkets. Express the answer as matrix C .
c) How many rows and how many columns does C have?
d) Use matrix M and P to explain how each entry of C is obtained.

CONTENT SUMMARY
Let A and B be matrices of order n× p , and m× r , respectively. Matrices A and
B can be multiplied, in this order, if and only if p = m, that is, the number of
columns of the first matrix is equal to the number of rows of the second matrix.
In this case, we say that matrices A and B, in this order, are conformable for
multiplication. The product A× B is of order n× r , that is the product A× B
has the same number of rows as matrix A , and the same number of columns
as matrix B.
Practically, we proceed as follows:
1. Determine the order of the product:

Determine whether A and B , in any order, are conformable for
multiplication or not.
b) In case, they are conformable for multiplication, find the order of the
products A.B and B.A.What do you conclude about the multiplication
of matrices?
c) Find the matrix A.B
Solution:
a)
A : 2× 3
B : 3× 2
A.B : 2 × 2
A and B are conformable for multiplication, since the number of columns of A
is equal to the number of rows of B
In the same way,

B: 3× 2
A : 2× 3
B.A : 3 × 3
B and A are conformable for multiplication, since the number of columns of B
is equal to the number of rows of A.
b) The order of the product A.B is 2× 2 , and the order of the product
B.Ais 3×3 .
Multiplication of matrices is not commutative. In general, for matrices A and
B, A.B ≠ B.A

We can predict that multiplication of matrices is associative, that is, for all
matrices A, B and C , conformable for multiplication, (A.B).C = A.(B.C)

A matrix, in which all the entries are zeros is said to be the null matrix or the
zero matrix.
For matrices, the equality A.B = 0 does not imply A = 0 or B = 0 , that is , the
product of two matrices can be the null matrix, yet none of the factors is a null
matrix.
Application activity 1.2.3
1. Determine whether matrices A and B, in this order, are conformable
for multiplication or not. In case, they are conformable, find the
product:

represent the suppliers and the columns represent the prices.
Obtain the matrix for the total input bill for the next two months for both
suppliers.
1.2.4. Inversion of matrices
Learning Activity 1.2.4

CONTENT SUMMARY
– A square matrix with each element along the main diagonal (from
the top left to the bottom right) being equal to 1 and with all other
elements being 0 is said to be the identity matrix, it is denoted by I;
For any square matrix A of order n× n , and the identity matrix I of order n× n, we have:

A.I = A and I.A = A, that is, I is the identity element for multiplication of
matrices.
In particular,

– If for a square matrix A of order n × n , there exists a square matrix B of
order n × n , such that A.B = I and B.A = I , where I is the identity matrix of
order n× n , then B is said to be the inverse of matrix A , and written B = A⁻¹
– To find the inverse of a square matrix A ,of order n× n , by Gaussian method,
we, practically, proceed as follows:
Write ( A / I ) , a matrix of order n×(2n) , since the number of columns doubled,
but the number of rows is unchanged. Matrix ( A / I ) is an augmented matrix;
Transform the matrix ( A / I ) , using elementary row operations, to (I / B) .
Then B = A⁻¹ .
– The following are the elementary row operations:
1. Interchanging two rows. For example, if row 1 and row 2 are interchanged,
then the entries of row 1 become the respective entries of row2, and vice
versa; we write R₁ ↔ R₂
2. Multiplying each entry of a non-zero real number k .For example, if the
entries of row3 are multiplied by, say 2, we write R₃ → 2R₃
3. Adding to each entry of a row any multiple from any other row, for
example, R₁→ R₁ + kR₂
If matrices B exists, then we say that A is invertible or regular;
If B does not exist, then we say that A is a singular matrix.
Example 1.2.4.

Application activity 1.2.4

1.3. Determinants of square matrices
1.3.1.Definition and calculation of determinants of matrices of orders 2× 2 and 3×3

Learning Activity 1.3.1

CONTENT SUMMARY

Therefore, the determinant of a square matrix equals the sum of the products of
the entries on a row (or column) by their corresponding cofactors.
If the determinant of a square matrix is zero, then the matrix is singular; it has
no inverse.
If the determinant of a square matrix is not zero, then the matrix is invertible
or regular.
Example 1.3.1.

Solution:
The expansion along the second row will make the calculation of the
determinant easier.

Application activity 1.3.1

1.3.2. Properties of determinants
Learning Activity 1.3.2
1. Without calculation, predict the value of the determinant of each of
the following matrices:

CONTENT SUMMARY
A square matrix can be changed into simpler form
before calculating its determinant through properties including the following:
1. If all the entries of a row or column of a square matrix are zeros, then the
determinant of the matrix is zero.
2. If all the entries of a row (or column) of a square matrix are multiplied
by a real number k , then the determinant of the matrix is multiplied by

3. If two rows or columns of a square matrix are identical or proportional,
then the determinant of the matrix is zero.
4. If square matrix B is obtained by interchanging two rows or two columns
of square matrix A , then the determinant of B is the opposite of the
determinant of A .
5. 5)If a row or column of a square matrix B is obtained by adding or
subtracting any nonzero multiple of another row or column of matrix
A , the other rows or columns of B being the same as those of A ,then
the determinant of matrices A and B remains unchanged. Thus,

a) Column 2 and column 3 of matrix A are interchanged (C₂ ↔C₃ )

Application activity 1.3.2

1.4. Finding the inverse and solving simultaneous linear equations
1.4.1. Inverse of a matrix
Learning Activity 1.4.1

c) Perform the following:
i) Find det A
ii) Obtain matrix C ,where each entry of A is replaced by its cofactor
iii) Obtain matrix (denote it Adj(A) ) by writing the entries of the
first row of C as respective entries of the first column of Adj(A) ,
the entries on the second row of C as the respective entries of the
second column of Adj(A) , and the entries on the third row of C as
the respective entries of the third column of Adj(A)

CONTENT SUMMARY
Let A be a square matrix of order 2× 2 or 3×3 .Then the inverse of A . Can also
be calculated through the following four steps:
1. Find the determinant of A , that is det A;
2. Find the matrix C of cofactors of A : each entry of A is replaced by its cofactor.
3. Find the adjoint of matrix A , denoted, Adj(A) : the transpose of the matrix of cofactors;

Application activity 1.4.1

1.4.2. Solving simultaneous linear equations using inverse of a matrix
Learning Activity 1.4.2
A business makes floor tiles and wall tiles.
The table below shows the number of tiles of each type and the labor (in
hours) for making the tiles:

Given that the total cost for floor tiles is 53 (thousand) FRW and the total cost
for wall tiles is 37(thousand) FRW, find the material cost and the labor cost
by answering the following questions:
a) Label x the material cost and y the labor cost, and then model the
problem by simultaneous linear equations in x and y
b) Express the information in the table above as a matrix A of order
2× 2 , the total floor tile cost and the total wall tile cost as a matrix B
of order 2×1, and the material cost and the labor cost as a matrix X
of order 2×1
c) Perform the operation A.X = B and compare it to the simultaneous
equations obtained in part a)
d) Find the inverse matrix A⁻¹ and the product A⁻¹.B
e) Using X = A⁻¹.B ,find the values of x and y .
CONTENT SUMMARY
The two simultaneous linear equations in two unknowns, x and y ,

Therefore, the solution set of the simultaneous equations is S = {(2,3,−2)}
Application activity 1.4.2
Use matrices to solve the following simultaneous equations:

1.4.3. Solving simultaneous linear equations using Cramer’s rule
Learning Activity 1.4.3

1. a) Multiply both sides of equation(1) by b' to get equation(3), and
multiply both sides of equation (2) by −bto get equation(4)

b) Perform the addition (3) + (4) to obtain equation (5)
c) Make x the subject of formula in equation (5) , precising the
condition for this operation to be valid(possible).Label (6) this
equation.
d) Express the numerator and the denominator of (6) as determinants
of matrices of order 2× 2
2. a) Multiply both sides of equation(1) by −a ' to get equation (3') and
multiply both sides of equation (2) by a to get equation (4')
b) Perform the addition (3') + (4') to obtain equation (5')
c) Make x the subject of formula in equation (5') , precising the
condition for this operation to be valid(possible).Label (6') this
equation.
d) Express the numerator and the denominator of (6') as
determinants of matrices of order 2× 2
3. Use the formulas you have obtained above to solve the simultaneous
equations:

CONTENT SUMMARY
To solve the two simultaneous linear equation_s in t_wo unknowns ^x and ^y,
Cramer’s rule requires to go through the following steps:
In the same way, for the three simultaneous linear equations in three
Application activity 1.4.3
Use Cramer’s rule to solve the following simultaneous equations:

End of unit assessment 1
1. Write down the order of each of the following matrices:

2. Given that matrices A and B are equal, find the values of the letters:

3. Perform each of the following operations:

4. Invertible 2× 2matrices A, B and X are such that 4A− 5BX = B
a) Make X the subject of the formula
b) Find X if A = 2B
Unit 2 Differentiation/Derivatives
Key Unit competence: Solve Economical, Production, and Financial related
problems using derivatives.
Introductory activity
Consider functions y = 3x − 2 (1), and y = x² +1 (2)
a) complete the following table for each of the two functions:

2.1 Differentiation from first principles
2.1.1. Average rate of change of a function
Learning Activity 2.1.1
Suppose that the profit by selling x units of an item is modeled by the
equation, P(x) = 4x² − 5x + 3, and x assumes values 2 and 5 ,respectively.
Find:
a) The change in x
b) The values of P for x = 2 and x = 5, respectively. Hence, find the
change in P
c) Find the ratio of the change in P to the change in x
d) Give a word with the same meaning as ratio
CONTENT SUMMARY
The average rate of change of function , y = f (x) as the independent variable
Application activity 2.1.1

2.1.2. Instantaneous rate of change of a function

Learning Activity 2.1.2
Consider function y = f (x) = x² +1, and the changes in x from x₀ = 2 to
x₁ , where x₁ assumes consecutively values x₁ = 2.1; x₁ = 2.01; x₁= 2.001;...
a) Complete the following table:

CONTENT SUMMARY

Application activity 2.1.2

2.2. Rules for differentiation
2.2.1. Differentiation of polynomial functions
Learning Activity 2.2.1

CONTENT SUMMARY

Application activity 2.2.1

2.2.2. Differentiation of product functions
Learning Activity 2.2.2

CONTENT SUMMARY
Application activity 2.2.2

2.2.3. Differentiation of power functions
Learning Activity 2.2.3

CONTENT SUMMARY

Application activity 2.2.3

2.2.4. Differentiation of the composite function (The chain rule)
Learning Activity 2.2.4

CONTENT SUMMARY

Application activity 2.2.4
Use the chain rule to find the derivative of:
a) y = (7x + 8)²
b) y = (4x − 5)³
2.2.5. Differentiation of quotient functions
Learning Activity 2.2.5

CONTENT SUMMARY

Application activity 2.2.4

2.2.6. Differentiation of logarithmic functions
Learning Activity 2.2.6
CONTENT SUMMARY

Application activity 2.2.6

2.2.7. Differentiation of exponential functions
Learning Activity 2.2.7

CONTENT SUMMARY

2.3. Some applications of derivatives in Mathematics
2.3.1. Equation of the tangent to the graph of a function at a point.
Learning Activity 2.3.1

CONTENT SUMMARY

Application activity 2.3.1

2.3.2. Hospital’s rule.
Learning Activity 2.3.2

CONTENT SUMMARY

Application activity 2.3.2
Evaluate the following limits:

End of unit assessment 2
Unit 3 Applications of derivatives in Finance and in Economics
Key Unit competence: Apply differentiation in solving Mathematical problems
that involve financial context such as marginal cost,
revenues and profits, elasticity of demand and supply

Introductory activity
A can company produces open cans, in cylindrical shape, each with
constant volume of 300 cm³. The base of the can is made from a
material that costs 50 FRW per cm² , and the remaining part is made of
material that costs 20 FRW per cm² .
a) Express the height of one can as function of the base radius x of the can.

b) Express the total cost of the material to make a can, as function
of the base radius x of the can.

c) Find the dimensions of the can that will minimize the total cost
of the material to make a can.
3.1. Marginal quantities
3.1.1. Marginal cost
Learning Activity 3.1.1
A company found that the total cost y of producing x items is given by
y = 3x²+ 7x +12 .
a) Find the instantaneous rate of change in the total cost, when x = 3
b) How is the instantaneous rate of change in the total cost called?
CONTENT SUMMARY

The marginal cost is the instantaneous rate of change of the cost.
It represents the change in the total cost for each additional unit of production.
Suppose a manufacturer produces and sells a product. Denote C(q) to be the
total cost for producing and marketing q units of the product. Thus, C is a
function of q and it is called the (total) cost function. The rate of change of C
with respect to q is called the marginal cost, that is,

Application activity3.1.1

3.1.2. Marginal revenue
Learning Activity 3.1.2
A firm has the following demand function: P =100 −Q .
Find: a) in terms of Q, the total revenue function
b) The instantaneous rate of change of the total revenue when Q =11.
CONTENT SUMMARY

Application activity 3.1.2

3.2. Minimization and maximization of functions
3.2.1. Minimization of the total cost function
Learning Activity 3.2.1
Consider the following problem: A can company produces open cans, in
cylindrical shape, each with constant volume of 300 cm³ . The base of the
can is made from a material that costs 50 FRW per cm² , and the remaining
part is made of material that costs 20 FRW per cm² . Assume you are the
manager of the company, and you have to buy the material for constructing
the can. Which question do you ask yourself regarding the dimensions of
the can and the money to use for buying the material?
CONTENT SUMMARY

Application activity 3.2.1
Find the value of Q for which the total cost is minimum, and find the
minimum total cost in each of the following cases:

3.2.2. Maximization of the total revenue function
Learning Activity 3.2.1
Consider the following problem: A company has to buy a plot for the building
of its factory. The plot must have a rectangular shape with a constant
perimeter of 400 meters, and the cost of the plot is constant. Assume you
are the manager of the company, and you have to choose the dimensions of
the rectangular plot located in a flat uniform area. Which question do you
ask yourself regarding the dimensions of the plot and the area of the plot?
CONTENT SUMMARY

Application activity 3.2.2
Given the demand function, P = 24 − 3Q, find the value of Q at which the
total revenue is maximum, and find the maximum revenue.
3.3. Price elasticity
3.3.1. Elasticity of demand
Learning Activity 3.3.1

CONTENT SUMMARY

Application activity 3.3.1
Find the price elasticity of the demand if the quantity demanded d Q and
the price P are related by:

3.3.2. Elasticity of supply
Learning Activity 3.3.2

CONTENT SUMMARY

Application activity 3.3.1
Find the price elasticity of the supply if the quantity supplied s Q and the
price P are related by:

End of unit assessment 3
Unit 4 Univariate Statistics and Applications
Key Unit competence: Apply univariate statistical concepts to collect, organise,
analyse, interpret data, and draw appropriate decisions
Introductory activity
1. (a) How do you think collecting and keeping data is important
daily?
b) In your field of study, which kind of data can a person collect?
And give an example of each kind of data.
c) Is collecting, organizing, and interpreting data helpful in making
a family budget? What do you think about a national budget?
2. Suppose you have a shop selling food, and you want to know the
type of food most people prefer to buy:
i) Which statistical information will you need to collect?
ii) How will you collect such information?
iii) Which statistical measure will help you know the most
preferred food?
3. During an accounting exam, out of 10, ten students scored the
following marks: 3, 5, 6, 3, 8, 7, 8, 4, 8, 6.
a) Determine the mean mark of the class.
b) What is the mark that many students obtained?
c) Compare and discuss the mean mark of the class and the mark
for every student. What advice could you give to an accounting
teacher?
4.1 Basic concepts in univariate statistics
4.1.1. Statistical concepts
Learning Activity 4.1.1
1. Using the internet or any other resources, do research.
i) What do you understand by the term statistics?
ii) What are the different branches of statistics?
iii) What are the key terms used in statistics?
2. Suppose your company is given a market for supplying milk and
fruits to all primary school students in Rwanda. If the student must
choose between milk and fruits, what should a company do to ensure
that it will supply what students want?
CONTENT SUMMARY
Statistics is the branch of mathematics that deals with data collection,
data organization, summarization, analysis, interpretation, and drawing of
conclusions from numerical facts or data.
Statistics plays a vital role in nearly all businesses and forms the backbone for
all future development strategies. Every business plan starts with extensive
research, which is all compiled into statistics that can influence a final decision.
Statistics helps the businessman to plan production according to the taste of
customers.
Branches of statistics
There are two branches of statistics, namely descriptive, and inferential
statistics.
a. Descriptive statistics
Descriptive statistics deals with describing the population under study. It
consists of the collection, organization, summarization, and presentation of
data in a convenient and usable form.
Examples of descriptive statistics
• The average score of accounting students on the mathematics test.
• The average monthly salary of the employees in a company.
• The average age of the people who voted for the winning candidate in the
last election.
b. Inferential statistics
Inferential statistics consists of generalizing from samples to populations,
performing estimations and hypothesis tests, determining relationships among
variables, and making predictions.
The results of the analysis of the sample can be deduced to the larger population
from which the sample is taken. It consists of a body of methods for drawing
conclusions or inferences about characteristics of a population based on
information contained in a sample taken from the population. This is because
populations are almost very large; investigating each member of the population
would be impractical and expensive.
Examples of inferential statistics
• Collecting the monthly savings data of every family that constitutes your
population may be challenging if you are interested in the savings pattern
of an entire country. In this case, you will take a small sample of families
from across the country to represent the larger population of Rwanda. You
will use this sample data to calculate its mean and standard deviation.
• Suppose you want to know the percentage of people who love shopping
at SIMBA supermarket. We take the sample of the population and find
the proportion of individuals who love the SIMBA supermarket. With the
assistance of probability, this sample proportion allows us to make a few
assumptions about the population proportion.
In statistics, we generally want to study a population. Because it takes a lot
of time and money to examine an entire population, we select a sample to
represent the whole population.
The population is a collection of persons, things, or objects under the study.
The population is also defined as the universe, or the entire category under
consideration.
A sample is the portion of the population that is available, or to be made
available, for analysis. A sample is also defined as a subset of the population
studied. From the sample data, we can calculate a statistic.
A statistic is a number that represents a property of the sample. For example, if
we consider one district in Rwanda to be a sample of the population of districts,
then the average (mean) income generated by that one district at the end of
the financial year is an example of a statistic. The statistic is an estimate of a
population parameter, in this case the mean.
A parameter is a numerical characteristic of the whole population that can be
estimated by a statistic. Since we considered all districts to be the population,
then, the average (mean) income generated by district over the entire district
is an example of a parameter.
Application activity 4.1.1
1. Using an example, differentiate descriptive statistics from inferential
statistics.
2. We want to know the average (mean) amount of money senior five
students spend at Kiziguro secondary school on school supplies
that do not include books. We randomly surveyed 100 first-year
students at the school. Three of those students spent 1500Frw,
2000Frw, and 2500Frw, respectively. In this example, what could
be the population, sample, statistic and parameter?
4.1.2 Variables and types of variables
Learning Activity 4.1.1
Gisubizo conducted research on clients’ satisfaction with bank services.
She wanted to understand the relationship between clients’ satisfaction
and the amount of money they saved in that bank.
a) What could be the variables to consider in her research?
b) Will those variables give qualitative or quantitative information?
CONTENT SUMMARY
A variable is a characteristic of interest for each person or object in a population.
A variable is a characteristic under study that takes different values for different
elements. A variable, or random variable, is a characteristic or measurement
that can be determined for each member of a population. For example, if we
want to know the average (mean) amount of money senior five students spend
at Kiziguro secondary school on school supplies that do not include books.
We randomly surveyed 100 first year students at the school. Three of those
students spent 1500Frw, 2000Frw, and 2500Frw, respectively. In this example,
the variable could be the amount of money spent (excluding books) by one
senior five student. Le_t X = the amount of money spent (excluding books) by
one senior five student attending Kiziguro secondary school. Another example,
if we collect information about income of households, then income is a variable.
These households are expected to have different incomes; also, some of them
may have the same income.
Note that a variable is often denoted by a capital letter like X , Y, Z,.... and
their values denoted by small letters for example x, y, z,....The value of a
variable for an element is called an observation or measurement.

In statistics, we can collect data on a single variable or many variables. For
example, if we are interested in knowing how well the company is paying its
employees, we shall only collect data on the salaries of the workers in the
company. In this case, we will categorize these statistics as univariate statistics.
This unit only discusses univariate statistics and its application. When one
variable causes change in another, we call the first variable the independent
variable or explanatory variable. The affected variable is called the dependent
variable or response variable. There are mainly two types of variables:
qualitative variables and quantitative variables.
• Qualitative variables
Qualitative variables are variables that cannot be expressed using a number.
They express a qualitative attribute, such as hair color, religion, race, gender,
social status, method of payment, and so on. The values of a qualitative variable
do not imply a meaningful numerical ordering.
Qualitative variables are sometimes referred to as categorical variables.
For example, the variable sex has two distinct categories: ‘male’ and ‘female.’
Since the values of this variable are expressed in categories, we refer to this as
a categorical variable. Similarly, the place of residence may be categorized as
urban and rural and thus is a categorical variable. Categorical variables may
again be described as nominal and ordinal. Ordinal variables can be logically
ordered or ranked higher or lower than another but do not necessarily establish
a numeric difference between each category, such as examination grades (A+, A,
B+, etc., and clothing size (Extra large, large, medium, small). Nominal variables
are those that can neither be ranked nor logically ordered, such as religion, sex,
etc.
• Quantitative variables
Quantitative variables also called numeric variables, are those variables that
are expressed in numerical terms, counted or compared on a scale. A simple
example of a quantitative variable is a person’s age. Age can take on different
values because a person can be 20 years old, 35 years old, and so on. Likewise,
family size is a quantitative variable because a family might be comprised of one,
two, or three members, and so on. Each of these properties or characteristics
referred to above varies or differs from one individual to another. Note that
these variables are expressed in numbers, for which we call quantitative or
sometimes numeric variables. A quantitative variable is one for which the
resulting observations are numeric and thus possess a natural ordering or
ranking.
Quantitative variables are again of two types: discrete, and continuous. Variables
such as some children in a household or the number of defective items in a box
are discrete variables since the possible scores are discrete on the scale. For
example, a household could have three or five children, but not 4.52 children.
Other variables, such as ‘time required to complete a test’ and ‘waiting time in a
queue in front of a bank counter,’ are continuous variables. The time required
in the above examples is a continuous variable, which could be, for example,
1.65 minutes or 1.6584795214 minutes.
Application activity 4.1.2
Suppose you have a company that sells electronic devices.
i) If you are interested in understanding how your clients are satisfied
with your products. Which variable (s) will you consider in collecting
the data? Is this a univariate statistics? Why?
ii) If you are interested in understanding the relationship between
clients’ satisfaction and educational levels. Which variable (s) will
you consider in collecting the data? Is this a univariate statistics?
Why?
4.1.3 Data and types of data
Learning Activity 4.1.3
Using the internet or any other resources, do research. What do you
understand by the term data? Give an example.
CONTENT SUMMARY
Data are individual items of information that come from a population or sample.
Data is also defined as a set of observations. Data are the values (measurements
or observations) that the variables can assume. They may be numbers, or they
may be words. Datum is a single value. Data may come from a population or
from a sample. Lower case letters like x or y generally are used to represent
data values.
The observations or values that differ significantly from others are called
outliers. Outliers are at the extreme ends of a dataset. Dataset is a collection
of data of any particular study without any manipulation. Information are
facts about something or someone. Most data can be put into the following
categories: qualitative, and quantitative.
Qualitative data are the result of categorizing or describing attributes of a
population. Qualitative data are also often called categorical data. Clients’
satisfaction, quality of goods, color of the car a person bought are some
examples of qualitative (categorical) data. Qualitative (categorical) data are
generally described by words or letters.
Quantitative data are the result of counting or measuring attributes of a
population. Quantitative data are always numbers. Amount of money, number
of items bought in a supermarket, and numbers of employees of the company
are some examples of quantitative data. Quantitative data may be either
discrete or continuous. Data is discrete if it is the result of counting (such
as the number of students of a given gender in a class or the number of books
on a shelf). Data is continuous if it is the result of measuring (such as distance
traveled or weight of luggage). All data that are the result of counting are called
quantitative discrete data.
These data take on only certain numerical values. If you count the number of
phone calls you receive for each day of the week, you might get values such as
zero, one, two, or three. Data that are not only made up of counting numbers,
but that may include fractions, decimals, or irrational numbers, are called
quantitative continuous data.
Example
You go to the supermarket and purchase three soft drinks (500ml soda, 1ml
milk and 300ml juice) at 5000frw, four different kinds of fruits (apple, mango,
banana and avocado) at 800frw, two different kinds of vegetables (broccoli and
carrots) at 500frw, and two desserts (ice cream and biscuits) at 1000frw.

In this example,
• Number of soft drinks, different kinds of fruits, different kinds of vegetables,
and desserts purchased are quantitative discrete data because you count
them.
• The prices (5000frw, 800frw, 500frw, and 1000frw) are quantitative
continuous data.
• Types of soft drinks, vegetable, fruits, and desserts are qualitative or
categorical data.
A collection of information which is managed such that it can be updated
and easily accessed is called a database. A software package which can be
used to manipulate, validate and retrieve this database is called a Database
Management System. For example, Airlines use this software package to book
tickets and confirm reservations which are then managed to keep a track of the
schedule.
Application activity 4.2.1
Describe the data and types of data used in the following study. We want
to know the average amount of money spent on school uniforms annually
by families with children at G.S Kayonza. We randomly survey ten families
with children in the school. Ten families spent 65000Frw, 45000Frw,
65000Frw, 15000Frw, 55000Frw, 35000Frw, 25000Frw, 45000Frw,
85000Frw and 95000Frw, respectively.
4.1.4. Levels of measurement scale
Learning Activity 4.1.4
A researcher surveyed 100 people and asked them what type of place
they visited (rural or urban) and how satisfied (very satisfied, satisfied,
somehow satisfied, not satisfied) they were with their most recent visit to
that place. Those people were also asked to provide their ages. What are
the variables involved in this research?
Classify those variables according to how their data values could be
categorized or measured. Is it possible to rank data values obtained from
those variables?
If yes, rank them. Is it possible to find the difference between the data
values of each variable?
CONTENT SUMMARY
Variables classified according to how they are categorized or measured. For
example, the data could be organized into specific categories, such as major
field (accounting, finance, etc.), nationality or gender. On the other hand, can the
data values could be ranked, such as grade (A, B, C, D, F) or rating scale (poor,
good, excellent), or they can be classified according to the values obtained from
measurement, such as temperature, heights, or weights.
Therefore, we need to distinguish between them through the measurement
scale used. A scale is a device or an object used to measure or quantifies any
event or another object. In statistics, the variables are defined and categorized
using different levels of measurements. Level of measurement or scale of
measure is a classification that describes the nature of data within the values
assigned to variables (Kirch, 2008).
There are four levels or scales of the measurement: Nominal, Ordinal, Interval,
and Ratio.
Nominal scale
A nominal scale is used to name the categories within the variables by providing
no ranking or ordering of values; it simply provides a name for each category
within a variable so that you can track them among your data (Crossman, 2020).
The nominal level of measurement is also known as a categorical measure and
is considered qualitative in nature.
Examples
• Nominal tracking of gender (male or female)
• Nominal tracking of travel class (first class, business class and economy
class).
When the classification takes ranks into consideration, the ordinal level of
measurement is preferred to be used.
Ordinal scale
The ordinal level of measurement classifies data into categories that can be
ordered, however precise differences between the ranks do not exist. Ordinal
scales are used when people want to measure something that is not easily
quantified, like feelings or opinions. Within such a scale the different values
for a variable are progressively ordered, which is what makes the scale useful
and informative. However, it is important to note that the precise differences
between the variable categories are unknowable. Ordinal scales are commonly
used to measure people’s views and opinions on social issues, like quality of the
products, services, or how people are satisfied with something.

Examples
• if you have a business and you wish to know how people are happy with
your products or services, you could ask them a question like “How happy
are you with our products or services?” and provide the following response
options: “Very happy,” “Somehow happy,” and “Not happy.”
• To test the quality of the canned product, people can use the rating scale
either excellent or good or bad.

Interval scale
Unlike nominal and ordinal scales, an interval scale is a numeric one that allows
for ordering of variables and provides a precise, quantifiable understanding of
the differences between them.
Example
It is common to measure people’s income as a range like 0Frw-100,000Frw;
100,001Frw-200,000Frw; 200,001Frw-300,000Frw, and so on. These ranges
can be turned into intervals that reflect the increasing level of income, by using
1 to signal the lowest category, 2 the next, then 3, etc.
Ratio scale
The ratio scale is the interval level with additional property that there is also
a natural zero starting point. In this type of scale zero means nothingness.
Another difference lies in that we can attribute some of the quantities to others.
Example
The value of salary for someone is a measurement of type ratio level, where
we can attribute values of wages to each other, as if to say that the person X
receives a salary twice the salary of the person Y. And zero here means that the
person did not receive a salary.
Application activity 4.2.1
Classify each according to the level of measurement with the interpretation
of the meaning of zero if it exists.
i) Ages of the company workers (in years).
ii) Color of clothes in a shop.
iii) Temperatures inside the room (in Celsius).
iv) Nationalities of the company workers.
v) Salaries of the company employees.
vi) Weights of boxes of fruits
4.1.5. Sampling and Sampling methods
Learning Activity 4.1.5
Suppose that a certain Secondary School has 10,000 boarding students
(the population).
We are interested in the average amount of money a boarding student
spends on meals and accommodation in the year. Asking all 10,000 students
is almost an impossible task. What would you advise that school to do so
that it gets the needed information to know the average amount of money
students are spending?
How will it be done so that the information the school gets represents the
population?
CONTENT SUMMARY
Collecting data on entire population is costly or sometimes impossible.
Therefore, a subset or subgroup of the population can be selected to represent
the entire population. The process of selecting a sample from an entire
population is called sampling. Since the sample selected is representing the
whole population under study, the samplemust have the same characteristics as
the population. There are several ways of selecting sample from the population.
Some of the methods used in selecting samples are simple random sampling,
stratified sampling, cluster sampling, and systematic sampling.
In stratified sampling, the population is divided into groups called strata
and then takes a proportionate number from each stratum. For example, you
can stratify (group) taxpayers by their Ubudehe categories then choose a
proportionate simple random sample from each stratum (Ubudehe category)
to get a stratified random sample. To choose a simple random sample from each
category, number each member of the first category, number each member
of the second category, and do the same for the remaining categories. Then
use simple random sampling to choose proportionate numbers from the first
category and do the same for each of the remaining categories. Those numbers
picked from the first category, picked from the second category, and so on
represent the members who make up the stratified sample.
In cluster sampling, the population is divided the population into clusters
(groups) and then randomly select some of the clusters. All the members from
these clusters are in the cluster sample.
For example, if you randomly sample your costumers by gender (males,

females, those who prefer not to say), the three groups make up the cluster
sample. Number each group, and then choose four different numbers using
simple random sampling. All members of the three groups with those numbers
are the cluster sample.
In systematic sampling, we randomly select a starting point and take
every nth piece of data from a listing of the population.
For example, suppose you have to do a phone survey. Your phone book contains
20,000 customers listings. You must choose 400 names for the sample. Number
the population 1–20,000 and then use a simple random sample to pick a
number that represents the first name in the sample. Then choose every fiftieth
name thereafter until you have a total of 400 names (you might have to go back
to the beginning of your phone list). Systematic sampling is frequently chosen
because it is a simple method. All the above-mentioned sampling methods are
random.
A type of sampling that is non-random is convenience sampling. Convenience
sampling involves using results that are readily available.
For example, a computer software store conducts a marketing study by
interviewing potential customers who happen to be in the store browsing
through the available software. The results of convenience sampling may be
very good in some cases and highly biased (favor certain outcomes) in others.
Application activity 4.1.5
A school account conducted a study to determine the average school fees
parents pay yearly. Each parent in the following samples is asked how
much fee he or she paid for each term. What is the type of sampling in each
case?
a) A random number generator is used to select a parent from the
alphabetical listing of all parents. Starting with that student,
every 50th parent is chosen until 75 parents are included in the
sample.
b) A completely random method is used to select 75 parents. Each
parent has the same probability of being chosen at any stage of
the sampling process.
c) The parents who have students in nursery, primary, and
secondary are numbered one, two, and three, respectively. A
random number generator is used to pick two of those years. All
students in those two years are in the sample.
d) A sample of 100 parents having students at a school is taken
by organizing the parents’ names by classification as a nursery
(parents whose kids are in the nursery), junior (parents whose
kids are in primary), or senior (parents whose kids are in
secondary), and then selecting 25 parents from each.
e) An accountant is requested to ask the first ten parents he
encounters outside the school what they paid for tuition fees.
Those ten parents are the sample.
4.2 Organizing and graphing data
4.2.1. Frequency table
Learning Activity 4.2.1
The weekly revenues paid (in Frw) by 20 businesspeople are below. 27000,
31000, 24000, 31000, 26000, 36000, 21000, 22000, 34000, 29000, 25000,
29000, 27000, 39000, 27000, 23000, 28000, 29000, 24000, 27000. Which
revenue has been paid by many people? Represent this data in a tabular
form (revenue and the number of people who paid each revenue).
CONTENT SUMMARY
Frequency tables are a great starting place for summarizing and organizing
your data. Once you have a set of data, you may first want to organize it to see
the frequency, or how often each value occurs in the set. Frequency tables can
be used to show either quantitative or categorical data.
Example
Assume that a sample of 50 taxpayers in a district was selected to understand
how taxpayers are satisfied with the taxes they are paying. The responses of
those taxpayers are recorded below where (v) means very high satisfied, (s)
means somewhat satisfied and means not satisfied. v, n, v, n, v, s, n, n, n, n, s,
s, v, n, n, n, s, n, n, s, n, n, n, s, s, s, v, v, s, v, s, v, n, n, n, n, s, v, v, v, v, v, v, v, s, v, v, v, v, v
From the recorded data above, we note that:
• Eleven of them were not satisfied with the taxes they were paying.
• Five of them were somewhat satisfied with the taxes were paying.
• Four of them were very high satisfied with the taxes were paying.
This information can be presented in a tabular form which lists the type of
satisfaction (very high satisfied, somewhat satisfied, and not satisfied) and the
number of students corresponding to each category. Clearly the variable is the
type of satisfaction, which is qualitative variable.
Note that, each of the students belongs to one and only one of the categories.
The number of students who belong to a certain category is called the frequency
of that category. A frequency table shows how the frequencies are distributed
over various categories.
Table 4.1: Frequency table

Application activity 42.1
Consider the data on the marital status of 50 people who were interviewed.

4.2.2. Bar graph
Learning Activity 4.2.1
August 27, 1991, Wall Street Journal (WSJ) article reported that the
industry’s biggest companies are absorbing increasing numbers of small
software firms. According to WSJ, the result of this dominance by a few
giants is that the industry has become tougher for software entrepreneurs to
break into. The newspaper printed the chart in the accompanying figure to
depict software companies’ market share breakdown. From entrepreneurs
to corporate giants: market share among the top 100 software companies,
based on total 1990 revenue of $5.7 billion. Refer to this chart to answer
the following questions:
a) List the companies in descending order of market share.
b) What is the combined market share for Lotus Development and
WordPerfect?
c) What is the combined market share for Micro soft, Lotus
Development, and Novell?

CONTENT SUMMARY
A bar chart or bar graph is a chart or graph that presents numerical data with
rectangular bars with heights or lengths proportional to the values that they
represent. The bars can be plotted vertically or horizontally. A vertical bar chart
is sometimes called a line graph.
To construct a bar graph, we use the following steps:
• Represent the categories on the horizontal axis (remember to represent all
categories with equal intervals).
• Mark the frequencies (or percentages) on the vertical axis.
• Draw one bar for each category that corresponds to its frequency (or
percentage) on the vertical axis.
Example 1
The table below shows number of learners per class in a certain school in
Rwanda.
a) Represent the data in a bar chart
b) How many learners are in the whole school?
b) The number of learners that are in the whole school
= 45 + 40 + 50 + 60 + 55 + 45 = 295
The school has 295 learners.
Exampe2
An insurance company determines vehicle insurance premiums based on
known risk factors. If a person is considered a higher risk, their premiums will
be higher. One potential factor is the color of your car. The insurance company
believes that people with some color cars are more likely to get in accidents. To
research this, they examine police reports for recent total loss collisions. The
data is summarized in the frequency table below:
a) From the frequency table above, identify the highest frequency and
the lowest frequency.
b) Present the car data on bar chart indicating frequency against vehicle
color involved in total loss collision.
Solution
a) From the bar chart, the highest frequency is 52 and the lowest
frequency is 23
b) The bar chart indicating frequency against vehicle color involved in
total loss collision
Application activity 42.2
1. Iyamuremye is approaching retirement with a portfolio consisting
of cash and money market fund investments worth 1,350,000,
bonds worth 1,650,000, stocks worth 1,850,000, and real estate
worth 12,000,000. Present these data in a bar chart.
2. By the end of 2022, MTN Rwanda had over 5 million users. The table
below shows three age groups, the number of users in each age
group, and the proportion (%) of users in each age group. Construct
a bar graph of this data.
4.2.3 Histogram and polygon
Learning Activity 4.2.3
The graph below indicates the number of hours people work during a week.
The vertical axis represents the number of people, while the horizontal axis
represents the number of hours people spend at work.
a) How many people spend more hours at work? How many hours
do those people spend?
b) In total, how many people participated in this study?
c) What is the name of this graph?
CONTENT SUMMARY
After you have organized the data into a frequency distribution, you can
present them in graphical form. The purpose of graphs in statistics is to
convey the data to the viewers in pictorial form. It is easier for most people to
comprehend the meaning of data presented graphically than data presented
numerically in tables or frequency distributions.
The three most commonly used graphs in research are
a) The histogram.
b) The frequency polygon.
c) The cumulative frequency graph or ogive (pronounced o-jive).
a. The Histogram
The histogram is a graph that displays the data by using contiguous vertical
bars (unless the frequency of a class is 0) of various heights to represent the
frequencies of the classes.
Example1: suppose the age distribution of personnel at a small business is:
25, 24, 29, 20, 32, 39, 36, 30, 30, 39, 40, 42, 45, 47, 48, 43, 49, 50, 54, 58, 50,
65, 79.
Form classes by grouping ages of these personnel in categories as follows: 20-
29, 30-35, 39, 40-49, 50-59, 60-69, 70-79.
For each group, write the number of times numbers in that group are
occurring. To construct a histogram, we need to enter a scale on the horizontal
axis. Because the data are discrete, there is a gap between the class intervals,
say between 20 and 29 and 30–39.
In such a case, we will use the midpoint between the end of one class and the
beginning of the next as our dividing point. Between the 20–29 interval and
respectively. We find the dividing point between the remaining classes
similarly.
Example2: Construct a histogram to represent the data shown for the record
high temperatures for each of the 50 states.
Step 1: Draw and label the x and y axes. The x axis is always the horizontal axis,
and the y axis is always the vertical axis.
Step 2: Represent the frequency on the y axis and the class boundaries on the
x axis.
Step 3: Using the frequencies as the heights, draw vertical bars for each class.
See Figure below
b. The Frequency Polygon
The frequency polygon is a graph that displays the data by using lines that
connect points plotted for the frequencies at the midpoints of the classes. The
frequencies are represented by the heights of the points.
Example:
Using the frequency distribution given in Example 2, construct a frequency
polygon
Step 1: Find the midpoints of each class. Recall that midpoints are found by
adding the upper and lower boundaries and dividing by 2:
Step 2: Draw the x and y axes. Label the x axis with the midpoint of each class,
and then use a suitable scale on the y axis for the frequencies.
Step 3: Using the midpoints for the x values and the frequencies as the y values,
plot the points.
Step 4: Connect adjacent points with line segments. Draw a line back to the
x axis at the beginning and end of the graph, at the same distance that the
previous and next midpoints would be located, as shown in figure.
The frequency polygon and the histogram are two different ways to represent
the same data set. The choice of which one to use is left to the discretion of the
researcher.
c. The cumulative frequency graph or Ogive.
The ogive is a graph that represents the cumulative frequencies for the classes
in a frequency distribution.
Step 1: Find the cumulative frequency for each class.
Step 2: Draw the x and y axes. Label the x axis with the class boundaries. Use
an appropriate scale for the y axis to represent the cumulative frequencies.
(Depending on the numbers in the cumulative frequency columns, scales such
as 0, 1, 2, 3, . . . , or 5, 10, 15, 20, . . . , or 1000, 2000, 3000, . . . can be used.
Do not label the y axis with the numbers in the cumulative frequency column.)
In this example, a scale of 0, 5, 10, 15, . . . will be used.
Step 3: Plot the cumulative frequency at each upper class boundary, as shown
in Figure below. Upper boundaries are used since the cumulative frequencies
represent the number of data values accumulated up to the upper boundary of
each class.
Step 4: Starting with the first upper class boundary, 104.5, connect adjacent
points with line segments, as shown in the figure. Then extend the graph to the
first lower class boundary, 99.5, on the x axis.
Cumulative frequency graphs are used to visually represent how many values
are below a certain upper class boundary. For example, to find out how many
record high temperatures are less than 114.5 0F, locate 114.5 0F on the x axis,
draw a vertical line up until it intersects the graph, and then draw a horizontal
line at that point to the y axis. The y axis value is 28, as shown in the figure.
Application activity 42.3
Consider the following data:
45,50,55,60,65,70,75,47,51,56,61,66,71,76,48,52,57,62,67,72,77,49,53,5
8,63,68,73,78,49,54,59,64,68,74,49,51,55,61,68,71,51,56,61,69,71,52,56,
62,66,72,53,57,62,67,72,54,58, 63,67,74,58,63,68,58,64,68,59,64,69,55,6
4,69,56,64,68,61, 61,62,62,63.
Then:
a) Make this data in a frequency distribution table with Class
boundaries width equal to 5 and containing Class boundaries,
Midpoints, Frequencies, Relative frequencies, Percentages, and
Cumulative frequencies.
b) Draw the histogram for the frequencies, relative frequencies,
percentages, and percentage frequencies in the distribution
table.
4.2.4 Time series graph
Learning Activity 4.2.4
The graph below shows the number of buyers per quarter (per three
months) who have visited a supermarket.
From the graph,
a) In which quarter did few people visit the supermarket?
b) How many people did buy at the supermarket in the second
quarter of 2005?
c) In total, how many buyers did visit the supermarket from 2005
to 2007?
CONTENT SUMMARY
In most graphs and charts, the independent variable is plotted on the horizontal
axis (the X − axis ) and the dependent variable on the vertical axis (the Y − axis ).
A time series is defined as having the independent variable of time and the
dependent variable as the value of the variable being studied.
A time series graph is a line graph that shows data such as measurements,
sales or frequencies over a given time.
Frequently, “time” is plotted along the x-axis. Such a graph is known as a timeseries
graph because on it, changes in a dependent variable (such as GDP: Gross
Domestic Production, inflation rate, or stock prices) can be traced over time.
They can be used to show a pattern or trend in the data and are useful for
making predictions about the future such as weather forecasting or financial
growth.
To create the time series graph,
• Start off by labeling the time-axis in chronological order.
• Label the vertical axis and horizontal axis. The horizontal axis always
shows the time, and the vertical axis represents the variable being
recorded against time.
• After labelling, plot the points given in the data set.
• Finish the graph by connecting the dots with straight lines.
Example
In a week, a certain company is making a profit of 10000 FRW on the first
day, 15000FRW on the second day, 12000FRW on the third day, 13000FRW
on the fourth day, 9000FRW on the fifth day, 10000FRW on the sixth day, and
9000FRW on the seventh day. In a tabular form, this can be presented as

The time series graph is

Application activity 4.2.4
The following data shows the Annual Consumer Price Index each month
for ten years. Construct a time series graph for the Annual Consumer Price
Index data only.

4.2.5 Pie chart
Learning Activity 4.2.5
The chart below presents data on why teenagers drink. Use the information
shown in the chart to answer the following questions:
a) For what reason do the highest numbers of teenagers drink?
b) What percentage of teenagers drink because they are bored or
upset?
CONTENT SUMMARY
A pie chart, sometimes called a circle chart, is a way of summarizing a set of
data in circular graph. This type of chart is a circle that is divided into sections
or wedges according to the percentage of frequencies in each category of the
distribution. Each part is represented in degrees.
To present data using pie chart, the following steps are respected:
Step 1: Write all the data into a table and add up all the values to get a total.
Step 2: To find the values in the form of a percentage divide each value by
the total and multiply by 100. That means that each frequency must also be
converted to a percentage by using the formula

Step 3: To find how many degrees for each pie sector we need, we take a full
circle of 360° and use the formula:

Since there are 360⁰ in a circle, the frequency for each class must be converted
into a proportional part of the circle. This conversion is done by using the
formula:
Step 4: Once all the degrees for creating a pie chart are calculated, draw a circle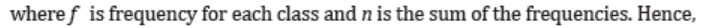
(pie chart) using the calculated measurements with the help of a protractor,
and label each section with the name and percentages or degrees.
Example.
1. In the summer, a survey was conducted among 400 people about their
favourite beverages: 2% like cold-drinks, 6% like Iced-tea, 12% like
Cold-coffee, 24% like Coffee and 56% like Tea.
a) How many people like tea?
b) How many more people like coffee than cold coffee?
c) What is the total central angle for iced tea and cold-drinks?
d) Draw a pie chart to represent the provided information.
Example 2:
A person spends his time on different activities daily (in hours):
a) Find the central angle and percentage for each activity.
b) Draw a pie chart for this information
c) Use the pie chart to comment on these findings.
b) Using a protractor, graph each section and write its name and
corresponding percentage, as shown in the Figure below
Application activity 4.2.5
After selling fruits in a market, Aisha had a total of 144 fruits remaining.
The pie chart below shows each type of fruit that remained.

a) Find the total cost of mangoes and pawpaws if a mango sells at
30 FRW and pawpaw at 160 FRW each.
b) Which types of fruit remained the most?
c) Draw a frequency table to display the information on the pie
chart.
4.2.6 Graph interpretation
Learning Activity 4.2.4
The graph below shows the sizes of sweaters worn by 30 year 1 students
in a certain school. Observe it and interpret it by answering the questions
below:
a) How many students are with small size?
b) How many students with medium size, large size and extra large
size are there?
CONTENT SUMMARY
Once data has been collected, they may be presented or displayed in various
ways including graphs. Such displays make it easier to interpret and compare
the data.
Examples
1. The bar graph shows the number of athletes who represented five
African countries in an international championship.
a) What was the total number of athletes representing the five countries?
b) What was the smallest number of athletes representing one country?
c) What was the most number of athletes representing a country?
d) Represent the information on the graph on a frequency table.
Solution:
We read the data on the graph:
a) Total number of athletes are: 18 + 10 + 22 + 6 + 16 = 72 athletes
b) 6 athletes
c) 22 athletes
d) Representation of the given information on the graph on a frequency
table.
2. Use a scale vertical scale 2cm: 10 students and Horizontal scale 2cm: 10
represented on histogram below to answers the questions that follows
a) estimate the mode
b) Calculate the range
Solution:
a) To estimate the mode graphically, we identify the bar that represents
the highest frequency. The mass with the highest frequency is 60 kg.
It represents the mode.
b) The highest mass = 67 kg and the lowest mass = 57 kg
Then, The range=highest mass-lowest mass=67kg − 57kg =10kg
Application activity 4.2.5
The line graph below shows bags of cement produced by CIMERWA
industry cement factory in a minute.

a) Find how many bags of cement will be produced in: 8 minutes, 3
minutes12 seconds, 5 minutes and 7 minutes.
b) Calculate how long it will take to produce: 78 bags of cement.
c) Draw a frequency table to show the number of bags produced
and the time taken.
4.3 Numerical descriptive measures
4.3.1 Describing data using mean, median, and mode
Learning Activity 4.3.1
Consider a portfolio that has achieved the following returns: Q₁=+10%,
Q₂=-3%, Q₃=+8%, Q₄=+12%, Q₅=-7%, Q₆=+12% and Q₇=+3% over seven
quarters.
a) What is the average return on investment?
b) Which return of the portfolio is in the middle?
c) Which return of the portfolio that has been achieved frequently?
CONTENT SUMMARY
A measure of central tendency is very important tool that refer to the centre
of a histogram or a frequency distribution curve. There are three measures of
central tendency:
• Mean
• Median
• Mode
Difference between the mean, median and mode
• Mean is the average of a data set.
• The median is the middle value in a set of ranked observations. It is also
defined as the middle value in a list of values arranged in either ascending
or descending orders.
• Mode is the most frequently occurring value in a set of values.
How to find mean
The most used measure of central tendency is called mean (or the average).
Here the main of interest is to learn how to calculate the mean when the data
set is raw data.
The following steps are used to calculate the mean:
Step 1: Add the numbers
Step 2: Count how many numbers there are in the data set
Step 3: Find the mean by dividing the sum of the data values by the number of
data values
Mathematically, mean is calculated as follows:
Here, the mean can also be calculated by multiplying each distinct value by its
frequency and then dividing the sum by the total number of data values.
How to find median
• Rank the given data sets (in increasing or decreasing order)
• Find the middle term for the ranked data set that obtained in step 1.
• The value of this term represents the median.
In general form, calculating the median depends on the number of
observations (even or odd) in the data set, therefore applying the above steps
requires a general formula.
Consider the ranked data x_1, x_2, x_3,..., x_n the formula for calculating the median
for the two cases (even and odd) is given by:
Example 1
To understand the three statistical concepts, consider the following example:
A Supermarket recently launched a new mint chocolate chip ice cream flavour.
They want to compare customer traffic numbers to their store in the past seven
days since the launch to understand whether their new offering intrigued
customers. Here is the customer data from last week: Monday =92 customers,
Tuesday =92 customers, Wednesday =121 customers, Thursday =120
customers, Friday = 132 customers, Saturday = 118 customers, and Sunday
=128 customers. To make sense of this data, we can calculate the average:
• Find the sum by adding the customer data together, 92 + 92 + 118 + 120 +
121 + 128 + 132 = 803
• Number of days is equal to 7.
The mode is 92 customers because on Monday and Tuesday, 92 customers
were received. To find the median, we need to arrange data as follows: 92, 92,
118, 120, 121, 128, 132. Then, the middle value is 120. Therefore, the median
is 120.
The value at the fourth position in the ranked data above is 120. Hence,
median is 120.
Example 2
Calculate the mean of the pocket money of some 5 students who get
2500 FRW, 4000 FRW, 5500 FRW, 7500 FRW and 3000 FRW.
Sum all the pocket money of five students
= (2500 + 4000 + 5500 + 7500 + 3000) FRW = 22500FRW.
Divide the sum by the number of students = 22500 / 5 = 4500FRW .
The mean of the pocket money of 5 students is 4500FRW .
Application activity 4.3.1
Find the average and median monthly salary (FRW) of all six secretaries
each month earn (in thousands) 104, 340, 140, 185, 270, and 258 each,
respectively.
4.3.2 Summarizing data using variance, standard deviation,
and coefficient of variation
Learning Activity 4.3.2
You and your friends have just measured the heights of your dogs (in
millimeters):

The heights (at the shoulders) are 600mm, 470mm, 170mm, 430mm, and
300mm.
a) Work out the mean height of your dogs.
b) For each height subtract the mean height and square the difference
obtained (the squared difference).
c) Work out the average of those squared differences. What do you
notice about the average?
Variance
Variance measures how far a s t of numbers is spread out. A variance of zero
indicates that all the values are identical. Variance is always non-negative: a
small variance indicates that the data points tend to be very close to the mean
and hence to each other, while a high variance indicates that the data points are
very spread out around the mean and from each other.
• For the population, the variance is denoted and defined by:
How to find variance
To calculate the variance follow these steps:
• Work out the mean (the simple average of the numbers)
• Then for each number: subtract the Mean and square the result (the squared
difference).
• Then work out the average of those squared differences.
Example1:
The heights (in meters) of six children are 1.42, 1.35, 1.37, 1.50, 1.38 and 1.30.
Calculate the mean height and the variance of the heights.
Example2:
The number of customers served lunch in a restaurant over a period of 60 days
is as follows:
Find the mean and variance of the number of customers served lunch using this
grouped data.
Solution
To find the mean from grouped data, first we determine the mid-interval values
for all intervals;
Standard deviation
A most used measure of variation is called standard deviation denoted by ( σ
for the population and S for the sample). The numerical value of this measure
helps us how the values of the dataset corresponding to such measure are
relatively closely around the mean.
Lower value of the standard deviation for a data set, means that the values
are spread over a relatively smaller range around the mean. Larger value of
the standard deviation for a data set means that the values are spread over a
relatively smaller range around the mean.
How to find standard deviation
Take a square root of the variance. The population standard deviation is defined
as: square root of the average of the squared differences from the population
mean.
Example:
The six runners in a 200 meter race clocked times (in seconds) of 24.2, 23.7,
25.0, 23.7, 24.0, 24.6.
Find the mean and standard deviation of these times.
Range
The range for a data set is depends on two values (the smallest and the largest
values) among all values in such data set. The range is defined as the difference
between the largest value and the lowest value.
Mean deviation
Another measure of variation is called mean deviation; it is the mean of the
distances between each value and the mean.
Coefficient of variation
A coefficient of variation (CV) is one of well-known measures that used to
compare the variability of two different data sets that have different units of
measurement.
Moreover, one disadvantage of the standard deviation that its being a measure
of absolute variability and not of relative variability.
The coefficient of variation, denoted by (CV), expresses standard deviation as a
percentage of the mean and is computed as follows:
Using coefficient of variation, find in which plant, C or D there is greater
variability in individual wages.
In which plant would you prefer to invest in?
Solution
To find which plant has greater variability, we need to find the coefficient of variation.
The plant that has a higher coefficient of variation will have greater variability.
Coefficient of variation for plant C:
Using coefficient of variation formula,
Plant C has CV = 0.36 and plant D has CV = 0.4
Hence plant D has greater variability in individual wages.
I would prefer to invest in plant C as it has lower coefficient (of variation)
because it provides the most optimal risk-to-reward ratio with low volatility
but high returns.
Application activity 4.3.2
A music school has budgeted to purchase three musical instruments. They
plan to purchase a piano costing $3,000, a guitar costing $550, and a drum
set costing $600. The mean cost for a piano is $4,000 with a standard
deviation of $2,500. The mean cost for a guitar is $500 with a standard
deviation of $200. The mean cost for drums is $700 with a standard
deviation of $100. Which cost is the lowest, when compared to other
instruments of the same type? Which cost is the highest when compared
to other instruments of the same type. Justify your answer.
4.3.3 Determining the position of data value using quartiles
Learning Activity 4.3.3
Consider the prices of 11 items arranged in order of rank in the table below.

i) Identify the median price.
ii) How many items were bought at a price below the median price?
iii) How many items were bought at a price above the median price?
iv) Find the middle price of the lower half of the set of prices.
v) Find the middle price of the upper half of the set of prices.
vi) Together with the median price, what do the middle prices in (iv) and
(v) do to the given data? Discuss.
CONTENT SUMMARY
Any data set can be divided into four equal parts by using a summary measure
called quartiles.
There are three quartiles that used to divide the data set which is denoted by Q_i
for ⁱ=1,2,3 . The following definition is illustrated the meaning of the quartiles.
Quartiles are three summary measures that divide a ranked data set into four
equal parts. The following are three quartiles:
• First quartile (Q₁ ) is the middle term among the observations that are less
than the median.
• Second quartile ( Q₂) is the same as the median.
• Third quartile (Q₃) is the value of the middle term among the observations
that are greater than the median.
How to find quartiles

Application activity 4.3.3
The heights in cm of 13 boys are: 163, 162, 170, 161, 165, 163, 162, 163,
164, 160, 158, 153, 165. Determine the three quartiles.
4.5 Measure of symmetry
4.5.1 Skewness
Learning Activity 4.3.4
Consider the two data sets that were recorded for the temperature:
Dataset1: 78, 78, 79,77,76,72,74,75,74,75,76,77, 76; Dataset2: 66, 65, 58,
59, 61, 59, 61, 58, 60, 64, 59, 64, 60, 59, 58, 59, 61, 58, 60, 61, 58, 60, 63, 58,
60, 63, 58, 60, 63, 59.
a) Represent the two datasets using bar graphs.
b) Find the mean, median, and mode of each dataset.
c) Compare the mean, median, and mode of each dataset. Do all
measures of a central tendency (mean, median, and mode) lie in
the middle?
CONTENT SUMMARY
Sometimes data are distributed equally on the right and left of the mean value.
Such data are said to be normally distributed or bell curved. They are also called
symmetric. This means that the right and the left of the distribution are perfect
mirror images of one another.
Not all data is symmetrically distributed. Sets of data that are not symmetric are
said to be asymmetric. The measure of how data are asymmetric or symmetric
can be is called skewness. The mean, median and mode are all measures of the
center of a set of data. The skewness of the data can be determined by how
these quantities are related to one another. There are three types of skewness:
• Right skewness
• Zero skewness
• Left skewness.

Data skewed to the right (Positive skewness).
Data that are skewed to the right have a long tail that extends to the right. An
alternate way of talking about a data set skewed to the right is to say that it is
positively skewed. Generally, most of the time for data skewed to the right, the
mean will be greater than the median and both are greater than the mode.

In summary, for a data set skewed to the right: Mode > Median >Mode.

Data skewed to the left (Negative skewness).
Data that are skewed to the left have a long tail that extends to the left. An
alternate way of talking about a data set skewed to the left is to say that it is
negatively skewed. Generally, most of the time for data skewed to the left, the
mean will be less than the median and both less than the mode.
In summary, for a data set skewed to the left: Mode > Median >Mode.
Zero skewness
The symmetrical data has zero skewness as all measures of a central tendency
lies in the middle.
In summary, for a data set skewed to the left: Mode = Median = Mean .
Measure of skewness
It’s one thing to look at two sets of data and determine that one is symmetric
while the other is asymmetric. It’s another to look at two sets of asymmetric
data and say that one is more skewed than the other. It can be very subjective
to determine which is more skewed by simply looking at the graph of the
distribution. This is why there are ways to numerically calculate the measure
of skewness.
One measure of skewness, called Pearson’s first coefficient of skewness, is
to subtract the mean from the mode, and then divide this difference by the
standard deviation of the data.

The reason for dividing the difference is so that we have a dimensionless
quantity. This explains why data skewed to the right has positive skewness.
If the data set is skewed to the right, the mean is greater than the mode, and
so subtracting the mode from the mean gives a positive number. A similar
argument explains why data skewed to the left has negative skewness.
Pearson’s second coefficient of skewness is also used to measure the asymmetry
of a data set. For this quantity, we subtract the mode from the median, multiply
this number by three and then divide by the standard deviation.
Examples in real life
Incomes are skewed to the right because even just a few individuals who
earn millions of dollars can greatly affect the mean, and there are no negative
incomes.
Data involving the lifetime of a product, such as a brand of light bulb, are skewed
to the right. Here the smallest that a lifetime can be is zero, and long lasting
light bulbs will impart a positive skewness to the data.
Application activity 4.3.3
Discuss the skewness of the data represented in the histograms below.

4.5.2 Chebyshev’s theorem and Empirical rule
Learning Activity 4.5.2

a) Find the mean price and the standard deviation.
b) How many items with prices falling within one standard deviation
from the mean?
c) How many items with prices falling within two standard deviations
from the mean?
d) How many items with prices falling within three standard
deviations from the mean?
CONTENT SUMMARY
There are two ways in which we can use the standard deviation to make a
statement regarding the proportion of measurements that fall within various
intervals of values centered at the mean value. The information depends on the
shape of histogram.
• If the histogram is bell shaped (symmetric data), the Empirical Rule is used.
• Other
wise (If data are asymmetric), Chebyshev’s theorem is used.
The Empirical Rule
The Empirical Rule makes more precise statements, but it can be applied
only to symmetric data (normally distributed data). For such a sample of
measurements, the Empirical Rule states that:

Application activity 4.5.2
Sweets are packed into bags with a normal mass of 75g. Ten bags are
picked at random from the production line and weighed.
Their masses in grams are 76, 74.2, 75.1, 73.7, 72, 74.3, 75.4, 74, 73.1, and
72.8.
a) Find the mean mass and the standard deviation. It was later
discovered that the scale was reading 3.2g below the correct
weight.
b) What was the correct mean mass of the ten bags and the correct
standard deviation?
c) Compare your answer in a) and b) and comment.
4.6 Examples of applications of univariate statistics
in mathematical problems that involve finance,
accounting, and economics.
Learning Activity 4.6
Referring to the concepts you have learnt in this unit, list down concepts
and give examples of how those concepts are applied in solving problems
related to finance, accounting, and economics.
CONTENT SUMMARY
With the use of descriptive statistics, we can summarize data related to revenue,
expenses, and profit for companies. For example, a financial analyst who works
for a retail company may calculate the following descriptive statistics during
one business quarter:
• Mean and median number of daily sales
• Standard deviation of daily sales
• Total revenue and total expenses
• Percentage change in new customers
• Percentage of products returned by customers.
• The mean household income.
• The standard deviation of household incomes.
• The sum of gross domestic product.
• The percentage change in total new jobs.
Using these metrics, the analyst can gain a strong understanding of the current
financial state of the company and also compare these metrics to previous
quarters to understand how the metrics are trending over time. Analyst can
then use these metrics to inform the organization on areas that could use
improvement to help the company increases revenue or reduce expenses.
Application activity 4.6
1. As the controller of the XXX Corporation, you are directed by the
board’s chairman to investigate the problem of overspending
by employees with expense accounts. You ask the accounting
department to provide records of the number of FRW spent by each
of 25 top employees during the past month. The following record
is provided: 292000, 494000, 600000, 807000, 535000, 435000,
870000, 725000, 299000, 602000, 322000, 397000, 390000,
420000, 469000, 712000, 520000, 575000, 670000, 723000,
560000, 298000, 472000, 905000, 305000. The questions the
board of directors wanted to be answered are:
a) How many of our 25 top executives spent more than 600000FRW
last month?
b) On average, how much do employees spend?
2. Consider the data on household size, annual income (in thousands
(FRW)), and the number of cows for each household.
End of unit assessment 4
1. You are assigned by your general manager to examine each of last
month’s sales transactions. Find their average, find the difference
between the highest and lowest sates figures, and construct a
chart showing the differences between charge account and cash
customers. Is this a problem in descriptive or inferential statistics?
2. When a cosmetic manufacturer tests the market to determine
how many women will buy eyeliner that has been tested for safety
without subjecting animals to injury, is it involved in a descriptive
statistics problem or an inferential statistics problem? Explain your
answer.
3. Suppose a real estate broker, is interested in the average price of a
home in a development comprising 100 homes.
a) If she uses 12 homes to predict the average price of all 100 homes,
is she using inferential or descriptive statistics?
b) If she uses all 100 homes, is she using inferential or descriptive
statistics?
4. The number of sales a salesman had in the previous 7 days are: 5, 1,
2, 1, 6, 5, and 1. Calculate the variance and standard deviation.
5. Five people waiting in line at a bank were randomly chosen and
asked how much cash they had in their pocket. The amounts in
dollars are: 16, 17, 18, 19, and 15. Find the variance and standard
deviation.
6. Refer to the table below, in which annual macroeconomic data
including GDP, CPI, prime rate, private consumption, private
investment, net exports, and government expenditures from 1995
to 2000 are given. Answer the following questions.
a) How many observations are in the data set?
b) How many variables are in the data set?
c) Which of the variables are qualitative and which are quantitative
variables?
Unit 5 Bivariate statistics and Applications
Key unit competence: Apply bivariate statistical concepts to collect, organise,
analyse, present, and interpret data to draw appropriate
decisions.
Introductory activity
In Kabeza village, after her 9 observations about farming, UMULISA saw
that in every house observed, where there is a cow (X) if there is also
domestic duck (Y), then she got the following results:
(1,4) , (2,8) , (3,4) , (4,12) , (5,10)
(6,14) , (7,16) , (8,6) , (9,18)
a) Represent this information graphically in (x, y) − coordinates .
b) Find the equation of line joining any two point of the graph and
guess the name of this line.
c) According to your observation from (a), explain in your own
words if there is any relationship between Cows (X) and
domestic duck (Y).
5.1 Introduction to bivariate statistics.
5.1.1. Key concepts of bivariate statistics
Learning Activity 5.1.1

If a businessman wants to make future investments based on how ice cream
sales relate to the temperature,
i) Which statistical measure and variables will he use?
ii) Which variable depends on the other?
iii) In statistics, how do we call a variable which depends on the other?
iv) Plot the corresponding points (x, y) on a Cartesian plane and describe
the resulting graph. Can you draw a line roughly representing the
points in your graph?
v) Can you obtain a rule relating x and y ? Explain your answer.
CONTENT SUMMARY
Bivariate data is data that has been collected in two variables, and each data
point in one variable has a corresponding data point in the other value. Bivariate
data is observation on two variables, whilst univariate data is an observation on
only one variable. We normally collect bivariate data to try and investigate the
relationship between the two variable sand then use this relationship to inform
future decisions.
Bivariate statistics deals with the collection, organization, analysis,
interpretation, and drawing of conclusions from bivariate data. Data sets that
contain two variables, such as wage and gender, and consumer price index and
inflation rate data are said to be bivariate. In the case of bivariate or multivariate
data sets we are often interested in whether elements that have high values of
one of the variables also have high values of other variables.
In bivariate statistics, we have independent variable and dependent variable.
Dependent variable refers to variable that depends on the other variable (s).
Independent variable refers to variable that affects the other variable (s).
Scatter diagram is the graph that represents the bivariate data in x and y
cartesian plane. The points do not lie on a line or a curve, hence the name. A
scatter graph of bivariate data is a two-dimensional graph with one variable on
one axis, and the other variable on the other axis. We then plot the corresponding
points on the graph. We can then draw a regression line (also known as a line of
best fit), and look at the correlation of the data (which direction the data goes,
and how close to the line of best fit the data points are).For example, the scatter
diagram showing the relationship between secondary school graduate rate and
the % of residents who live below the poverty line.

Examples of bivariate statistics
• Collecting the monthly savings and number of family members’ data
of every family that constitutes your population if you are interested in
finding the relationship between savings and number of family members.
In this case, you will take a small sample of families from across the country
to represent the larger population of Rwanda. You will use this sample to
collect data on family monthly savings and number of family members.
• We can collect data of outside temperature versus ice cream sales, these
would both be examples of bivariate data. If there is a relationship showing
an increase of outside temperature increased ice cream sales, then shops
could use this information to buy more ice cream for hotter spells during
the summer.
Application activity 5.1.1
1. Using an example, differentiate univariate statistics from bivariate
statistics.
2. Using an example, differentiate dependent variable from
independent variable.
5.2 Measures of linear relationship between two variables:
covariance, Correlation, regression line and analysis,
and spearman’s coefficient of correlation.
5.2.1 Covariance and correlation.
Learning Activity 5.2.1
As students of economics, you might be interested in whether people with
more years of schooling earn higher incomes. Suppose you obtain the data
from one district for the population of all that district households. The data
contain two variables, household income (measured in FRW) and a number
of years of education of the head of each household.
i) Which statistical measure will you use to know whether people with
more years of schooling earn higher incomes.
ii) If you want to know how household income and year of schooling
covariate, which statistical measure will you consider?
CONTENT SUMMARY
Covariance is a statistical measure that describes the relationship between a
pair of random variables where change in one variable causes change in another
variable. It takes any value between -infinity to + infinity, where the negative
value represents the negative relationship whereas a positive value represents
the positive relationship. It is used for the linear relationship between variables.
It gives the direction of relationship between variables.
The covariance of annual household income and schooling years from the
learning activity 5.2.1 is given by
The covariance of variables x and y is a measure of how these two variables
change together. If the greater values of one variable mainly correspond with the
greater values of the other variable, and the same holds for the smaller values,
i.e., the variables tend to show similar behavior, the covariance is positive. In
the opposite case, when the greater values of one variable mainly correspond
to the smaller values of the other, i.e., the variables tend to show opposite
behavior, the covariance is negative. If covariance is zero, the variables are said
to be uncorrelated, meaning that there is no linear relationship between them.
Correlation
The Pearson’s coefficient of correlation (or product moment coefficient of
correlation or simply coefficient of correlation), denoted by r , is a measure
of the strength of linear relationship between two variables. The coefficient
There are three types of correlation:
• Negative correlation
• Zero correlation
• Positive correlation
If the linear coefficient of correlation takes values closer to -1, the correlation is
strong and negative, and will become stronger the closer r approaches -1.
If the linear coefficient of correlation takes values close to 1, the correlation is
strong and positive, and will become stronger the closer r approaches 1. If the
linear coefficient of correlation takes values close to 0, the correlation is weak.
If r = 1 or r=-1, there is perfect correlation and the line on the scatter plot is
increasing or decreasing respectively. If r = 0, there is no linear correlation.

Application activity 5.1.1
The production manager had ten newly recruited workers under him. For
one week, he kept a record of the number of times that each employee
needed help with a task and make a scatter diagram for the data. What
type of correlation is there?
5.2.2 Regression line and analysis
Learning Activity 5.2.2
In a village, Emmanuella visited nine families and their farming
activities. For each visited family there were x number of cows,
and y goats. Emmanuella recorded her observations as follows:
(1, 4),(2,8),(3, 4),(4,12),(5,10),(6,14),(7,16),(8,6),(9,18) .
a) Represent Emmanuella’s recorded observations graphically in
cartesian plane.
b) Connect any two points on the graph drawn above to form a
straight line and find equation of that line. How are the positions
of the non-connected points vis-à-vis that line?
c) According to your observation from a., is there any relationship
between the variation of the number of cows and the number of
goats? Explain.
CONTENT SUMMARY
Bivariate statistics can help in prediction of a value for one variable if we know
the value of the other. We use the regression line to predict a value of y for any
given value of x and vice versa. The “best” line would make the best predictions:
the observed y-values should stray as little as possible from the line. This straight
line is the regression line from which we can adjust its algebraic expressions
and it is written as y = ax + b .
Deriving regression line equation
The regression line y on x has the form y = ax + b . We need the distance from
this line to each point of the given data to be small, so that the sum of the square
of such distances be very small.
1. Differentiate relation (1) with respect to b . In this case, x, y and a will
be considered as constants.
2. Equate relation obtained in 1 to zero, divide each side by n and give the
value of b .
• Take the value of b obtained in 2 and put it in relation obtained in 1.
Differentiate the obtained relation with respect to Variance for variable x
Application activity 5.1.1
Consider the following data:

Find the regression line of y on x and deduce the approximated value of y
when x=64.
5.2.3 Spearman’s coefficient of correlation
Learning Activity 5.2.2
The death rate data from 1995 to 2000 for developed and underdeveloped
countries are displayed in the table below.

i) Write the death rate for developed countries and the death rate for
underdeveloped countries in ascending order.
ii) Rank the death rate for developed countries and the death rate for
underdeveloped countries such that the lowest death rate is ranked 1
and the highest death rate is ranked 6.
iii) Complete the table below using the information above.
Application activity 5.2.3
Calculate Spearman’s coefficient of rank correlation for the series.

5.2.4 Application of bivariate statistics
Learning Activity 5.2.4
Referring to what you have learnt in this unit, discuss how bivariate
statistics is used in our daily life.
CONTENT SUMMARY
Bivariate statistics can help in prediction of the value for one variable if we know
the value of the other. Bivariate data occur all the time in real-world situations
and we typically use the following methods to analyze the bivariate data:
• Scatter plots
• Correlation Coefficients
• Simple Linear Regression
The following examples show different scenarios where bivariate data appears
in real life.
Businesses often collect bivariate data about total money spent on advertising
and total revenue. For example, a business may collect the following data for 12
consecutive sales quarters:
This is an example of bivariate data because it contains information on exactly
two variables: advertising spend and total revenue. The business may decide to
fit a simple linear regression model to this dataset and find the following fitted
model:
Total Revenue = 14,942.75 + 2.70*(Advertising Spend). This tells the business
that for each additional dollar spent on advertising, total revenue increases by
an average of $2.70.
• Economists often collect bivariate data to understand the relationship
between two socioeconomic variables. For example, an economist may
collect data on the total years of schooling and total annual income among
individuals in a certain city:
He may then decide to fit the following simple linear regression model:
Annual Income = -45,353 + 7,120*(Years of Schooling). This tells the economist
that for each additional year of schooling, annual income increases by $7,120
on average.
• Biologists often collect bivariate data to understand how two variables are
related among plants or animals. For example, a biologist may collect data
on total rainfall and total number of plants in different regions:
The biologist may then decide to calculate the correlation between the two
variables and find it to be 0.926. This indicates that there is a strong positive
correlation between the two variables. That is, higher rainfall is closely
associated with an increased number of plants in a region.
• Researchers often collect bivariate data to understand what variables
affect the performance of students. For example, a researcher may collect
data on the number of hours studied per week and the corresponding GPA
for students in a certain class:
She may then create a simple scatter plot to visualize the relationship between
these two variables:
Clearly there is a positive association between the two variables: As the
number of hours studied per week increases, the GPA of the student tends to
increase as well.
With the use of bivariate data we can quantify the relationship between
variables related to promotions, advertising, sales, and other variables.
Time series forecasting allows financial analysts to predict future revenue,
expenses, new customers, sales, etc. for a variety of companies.
Application activity 5.2.3
A company is to replace its fleet of cars. Eight possible models are
considered and the transport manager is asked to rank them, from 1 to 8,
in order of preference. A saleswoman is asked to use each type of car for
a week and grade them according to their suitability for the job (A-very
suitable to E-unsuitable). The price is also recorded:

a) Calculate the Spearman’s coefficient of rank correlation between:
i) Price and transport manager’s rankings,
ii) Price and saleswoman’s grades.
b) Based on the result of a, state, giving a reason, whether it would
be necessary to use all the three different methods of assessing
the cars.
c) A new employee is asked to collect further data and to do some
calculations. He produces the following results: The coefficient of
correlation between
i) Price and boot capacity is 1.2,
ii) Maximum speed and fuel consumption in miles per gallons is -0.7,
iii) Price and engine capacity is -0.9. For each of his results, say giving
a reason, whether you think it is reasonable.
d) Suggest two sets of circumstances where Spearman’s coefficient
of rank correlation would be preferred to the Pearson’s coefficient
of correlation as a measure of association.
End of unit assessment 5
1. Table below shows the marks awarded to six students in accounting
competition:
Calculate a coefficient of rank correlation.
2. At the end of a season, a league of eight hockey clubs produced the
following table showing the position of each club in the league and
the average attendance (in hundreds) at home matches.

Calculate Spearman’s coefficient of rank correlation between the position
in the league and average attendance. Comment on your results.
3. The following results were obtained from lineups in Accounting
and Finance examinations:
Find both equations of regression lines. Also estimate the value of y for
x=30.
4. The following results were obtained from records of age (x) and
systolic blood pressure of a group of 10 men:
Find both equations of the regression lines. Also estimate the blood
pressure of a man whose age is 45.
REFERENCES
1. Arem, C. (2006). Systems and Matrices. In C. A. DeMeulemeester, Systems
and Matrices (pp. 567-630). Demana: Brooks/Cole Publishing 1993 &
Addison-Wesley1994.
2. Kirch, W. (Ed.). (2008). Level of MeasurementLevel of measurement BT
- Encyclopedia of Public Health (pp. 851–852). Springer Netherlands.
https://doi.org/10.1007/978-1-4020-5614-7_1971
3. Crossman, Ashley. (2020). Understanding Levels and Scales of
Measurement in Sociology. Retrieved from https://www.thoughtco.
com/levels-of-measurement-3026703
4. Markov. ( 2006). Matrix Algebra and Applications. In Matrix Algebra and
Applications (pp. p173-208.).
5. REB, R.E (2020). Mathematics for TTCs Year 2 Social Studies Education.
Student’s book.
6. REB, R.E (2020). Mathematics for TTCs Year 3 Social Studies Education.
Student’s book
7. REB, R.E (2020). Mathematics for TTCs Year 1 Science Mathematics
Education. Students’ book
8. REB, R.E (2020). Mathematics for TTCs Year 1 Social Studies Education.
Student’s book
9. Rossar, M. (1993, 2003). Basic Mathematics For Economists. London and
New York: Taylor & Francis Group.
Topic 6
Topic 7
Topic 8
Topic 9

Topic outline

Table of contents